Analysis of Kink Behaviour of KdV-mKdV Equation under Caputo Fractional Operator with Non-Singular Kernel
Abstract
:1. Introduction
2. Preliminaries
3. Analysis of Fractional KdV-mKdV Equation
Existence Theory
4. Solution of the Equation
5. Convergence and Stability Analysis
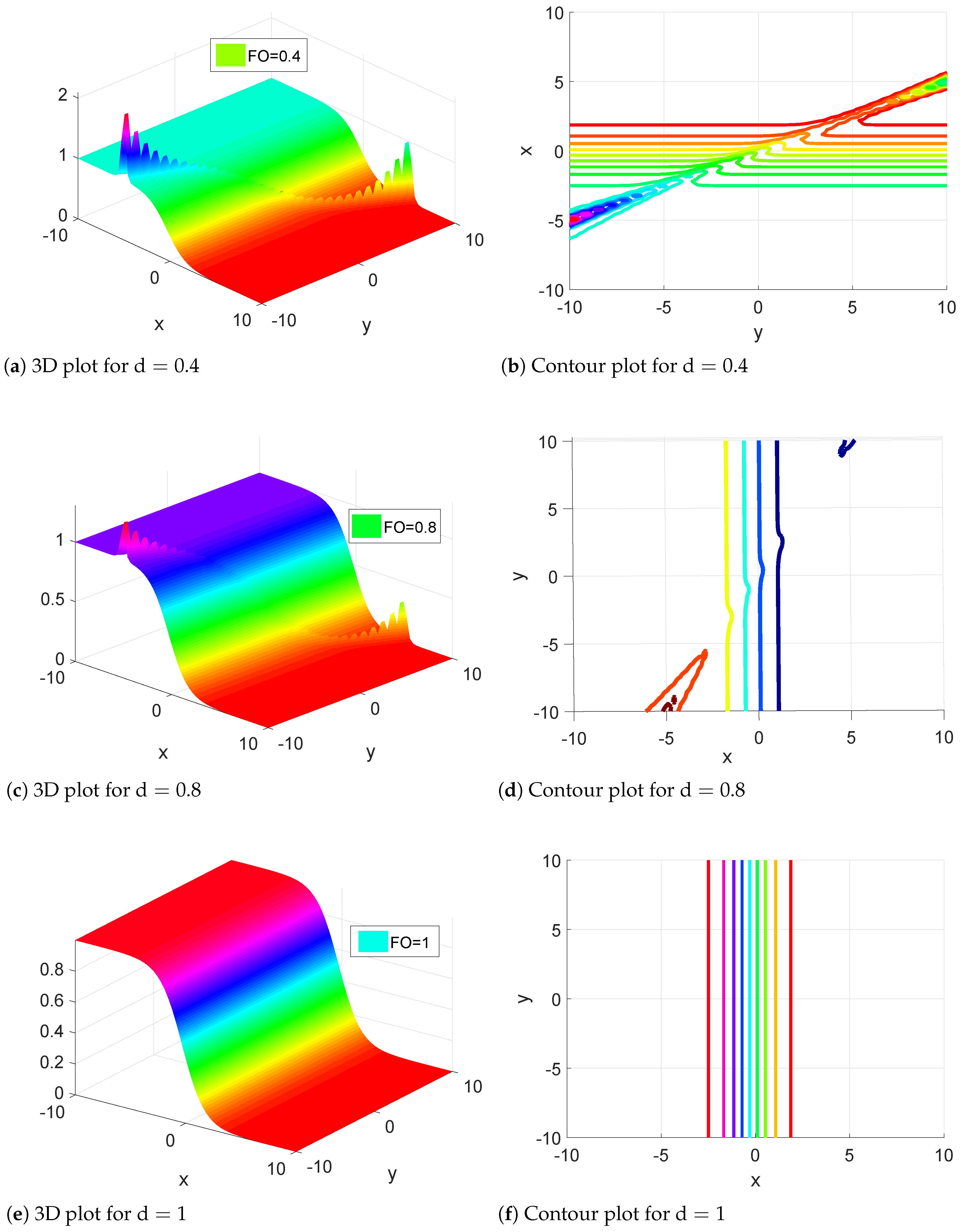
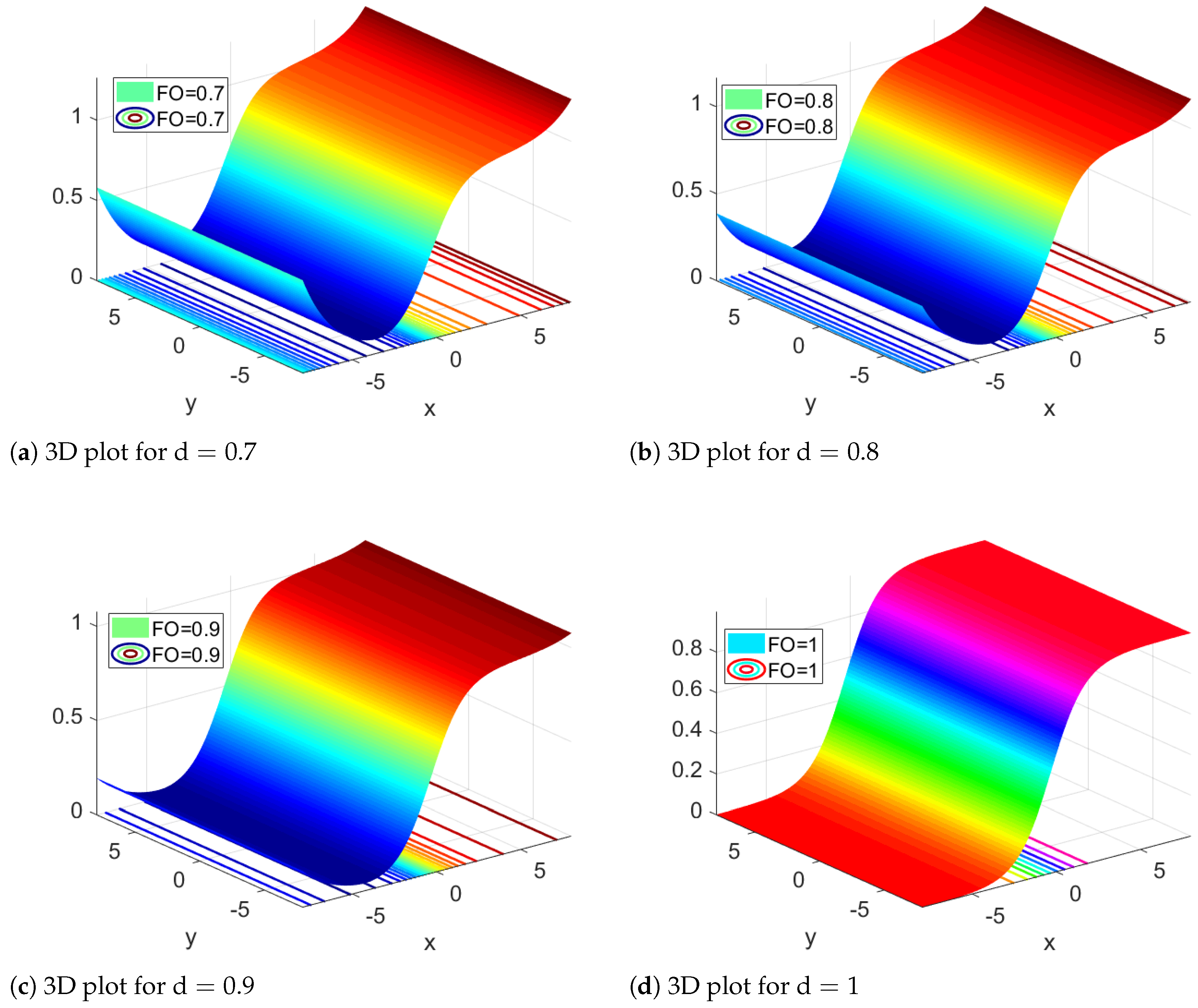
6. Simulations and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wazwaz, A.M. Partial Differential Equations and Solitary Waves Theory; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Salas, A.; Kumar, S.; Yildirim, A.; Biswas, A. Cnoidal waves, solitary waves and painlevé analysis of the 5th order KdV equation with dual-power law nonlinearity. Proc. Rom. Acad. A 2013, 14, 28–34. [Google Scholar]
- Ji, J.L.; Zhu, Z.N. On a nonlocal modified Korteweg-de Vries equation: Integrability, Darboux transformation and soliton solutions. Commun. Nonlinear Sci. Numer. Simul. 2017, 42, 699–708. [Google Scholar] [CrossRef]
- Gurses, M.; Pekcan, A. Nonlocal modified KdV equations and their soliton solutions by Hirota method. Commun. Nonlinear Sci. Numer. Simul. 2019, 67, 427–448. [Google Scholar] [CrossRef]
- Alquran, M. Optical bidirectional wave-solutions to new two-mode extension of the coupled KdV–Schrodinger equations. Opt. Quantum Electron. 2021, 53, 588. [Google Scholar] [CrossRef]
- Malik, S.; Kumar, S.; Das, A. A (2+1)-dimensional combined KdV–mKdV equation: Integrability, stability analysis and soliton solutions. Nonlinear Dyn. 2022, 107, 2689–2701. [Google Scholar] [CrossRef]
- Alqahtani, R.T.; Ahmad, S.; Akgül, A. Dynamical analysis of bio-ethanol production model under generalized nonlocal operator in Caputo sense. Mathematics 2021, 9, 2370. [Google Scholar] [CrossRef]
- Khan, Z.A.; Khan, J.; Saifullah, S.; Ali, A. Dynamics of hidden attractors in four-dimensional dynamical systems with power law. J. Funct. Spaces 2022, 2022, 3675076. [Google Scholar] [CrossRef]
- Saifullah, S.; Ali, A.; Irfan, M.; Shah, K. Time-fractional Klein–Gordon equation with solitary/shock waves solutions. Math. Probl. Eng. 2021, 2021, 6858592. [Google Scholar] [CrossRef]
- Baleanu, D.; Jajarmi, A.; Mohammadi, H.; Rezapour, S. A new study on the mathematical modelling of human liver with Caputo–Fabrizio fractional derivative. Chaos Solitons Fractals 2020, 134, 109705. [Google Scholar] [CrossRef]
- Baleanu, D.; Jajarmi, A.; Hajipour, M. A new formulation of the fractional optimal control problems involving Mittag–Leffler nonsingular kernel. J. Optim. Theory Appl. 2017, 175, 718–737. [Google Scholar] [CrossRef]
- Gulalai; Rihan, F.A.; Ahmad, S.; Ullah, A.; Al-Mdallal, Q.M.; Akgül, A. Nonlinear analysis of a nonlinear modified KdV equation under Atangana Baleanu Caputo derivative. AIMS Math. 2022, 7, 7847–7865. [Google Scholar] [CrossRef]
- Liua, X.; Arfan, M.; ur Rahman, M.; Fatima, B. Analysis of SIQR type mathematical model under Atangana-Baleanu fractional differential operator. Comput. Methods Biomech. Biomed. Eng. 2022, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Sadiq, G.; Ali, A.; Ahmad, S.; Nonlaopon, K.; Akgül, A. Bright Soliton Behaviours of Fractal Fractional Nonlinear Good Boussinesq Equation with Nonsingular Kernels. Symmetry 2022, 14, 2113. [Google Scholar] [CrossRef]
- Shah, N.A.; Alyousef, H.A.; El-Tantawy, S.A.; Shah, R.; Chung, J.D. Analytical Investigation of Fractional-Order Korteweg–De-Vries-Type Equations under Atangana–Baleanu–Caputo Operator: Modeling Nonlinear Waves in a Plasma and Fluid. Symmetry 2022, 14, 739. [Google Scholar] [CrossRef]
- Ahmad, H.; Tariq, M.; Sahoo, S.K.; Askar, S.; Abouelregal, A.E.; Khedher, K.M. Refinements of Ostrowski Type Integral Inequalities Involving Atangana–Baleanu Fractional Integral Operator. Symmetry 2021, 13, 2059. [Google Scholar] [CrossRef]
- Cao, Q.H.; Dai, C.Q. Symmetric and Anti-Symmetric Solitons of the Fractional Second- and Third-Order Nonlinear Schrödinger Equation. Chin. Phys. Lett. 2021, 38, 090501. [Google Scholar] [CrossRef]
- Li, P.; Li, R.; Dai, C. Existence, symmetry breaking bifurcation and stability of two-dimensional optical solitons supported by fractional diffraction. Opt. Express 2021, 29, 3193–3210. [Google Scholar] [CrossRef]
- Mou, D.S.; Dai, C.Q. Vector solutions of the coupled discrete conformable fractional nonlinear Schrödinger equations. Optik 2022, 258, 168859. [Google Scholar] [CrossRef]
- Chen, Y.X. Combined optical soliton solutions of a (1+1)-dimensional time fractional resonant cubic-quintic nonlinear Schrödinger equation in weakly nonlocal nonlinear media. Optik 2020, 203, 163898. [Google Scholar] [CrossRef]
- Fang, J.J.; Mou, D.S.; Zhang, H.C.; Wang, Y.Y. Discrete fractional soliton dynamics of the fractional Ablowitz-Ladik model. Optik 2021, 228, 166186. [Google Scholar] [CrossRef]
- Bo, W.B.; Liu, W.; Wang, Y.Y. Symmetric and antisymmetric solitons in the fractional nonlinear schrödinger equation with saturable nonlinearity and PT-symmetric potential: Stability and dynamics. Optik 2022, 255, 168697. [Google Scholar] [CrossRef]
- Ullah, I.; Ali, A.; Saifullah, S. Analysis of time-fractional non-linear Kawahara Equations with power law kernel, Chaos, Solitons. Fractals X 2022, 9, 100084. [Google Scholar]
- Saifullah, S.; Ali, A.; Khan, Z.A. Analysis of nonlinear time-fractional Klein-Gordon equation with power law kernel. AIMS Math. 2021, 7, 5275–5290. [Google Scholar] [CrossRef]
- Khan, A.; Akram, T.; Khan, A.; Ahmad, S.; Nonlaopon, K. Investigation of time fractional nonlinear KdV-Burgers equation under fractional operators with nonsingular kernels. AIMS Math. 2023, 8, 1251–1268. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef] [Green Version]
- Cresson, J.; Szafrańska, A. Comments on various extensions of the Riemann–Liouville fractional derivatives: About the Leibniz and chain rule properties. Commun. Nonlinear Sci. Numer. Simul. 2020, 82, 104903. [Google Scholar] [CrossRef]
- Tarasov, V.E. No violation of the Leibniz rule. Fract. Deriv. 2013, 18, 2945–2948. [Google Scholar]
- Ortigueiram, M.D. Comments on “Modeling fractional stochastic systems as non-random fractional dynamics driven Brownian motions”. Appl. Math. Model. 2009, 33, 2534–2537. [Google Scholar]
| (x, y, t) | Exact | Approximate | ∣Exact-Approximate∣ |
|---|---|---|---|
| (−10, −10, 0.05) | −1.0000 + 0.0000i | −0.9999 + 0.0000i | 0.0001 |
| (−8, −8, 0.05) | −1.0000 + 0.0000i | −0.9996 + 0.0001i | 0.0005 |
| (−6, −6, 0.05) | −1.0000 + 0.0000i | −0.9967 + 0.0009i | 0.0034 |
| (−4, −4, 0.05) | −1.0000 + 0.0000i | −0.9760 + 0.0062i | 0.0247 |
| (−2, −2, 0.05) | −0.9967 + 0.0009i | −0.8454 + 0.0343i | 0.1550 |
| (0, 0, 0.05) | −0.5182 + 0.0648i | −0.4458 + 0.0657i | 0.0724 |
| (2, 2, 0.05) | −0.0038 + 0.0010i | −0.0870 + 0.0208i | 0.0855 |
| (4, 4, 0.05) | −0.0000 + 0.0000i | −0.0126 + 0.0033i | 0.0130 |
| (6, 6, 0.05) | −0.0000 + 0.0000i | −0.0017 + 0.0005i | 0.0018 |
| (8, 8, 0.05) | −0.0000 + 0.0000i | −0.0002 + 0.0001i | 0.0002 |
| (10, 10, 0.05) | −0.0000 + 0.0000i | −0.0000 + 0.0000i | 0.0000 |
| (x, y, t) | Exact | Approximate | ∣Exact-Approximate∣ |
|---|---|---|---|
| (−10, −10, 0.05) | −0.0004 − 0.0001i | −0.0101 + 0.0167i | 0.0194 |
| (−8, −8, 0.05) | −0.0033 − 0.0009i | −0.0070 + 0.0053i | 0.0072 |
| (−6, −6, 0.05) | −0.0240 − 0.0062i | −0.0256 − 0.0039i | 0.0028 |
| (−4, −4, 0.05) | −0.1548 − 0.0342i | −0.1561 − 0.0335i | 0.0015 |
| (−2, −2, 0.05) | −0.5820 − 0.0632i | −0.5835 − 0.0629i | 0.0016 |
| (0, 0, 0.05) | −0.9132 − 0.0208i | −0.9144 − 0.0203i | 0.0013 |
| (2, 2, 0.05) | −0.9874 − 0.0033i | −0.9887 − 0.0018i | 0.0020 |
| (4, 4, 0.05) | −0.9983 − 0.0005i | −1.0011 + 0.0037i | 0.0050 |
| (6, 6, 0.05) | −0.9998 − 0.0001i | −1.0070 + 0.0114i | 0.0135 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, S.; Ullah, A.; Ahmad, S.; Nonlaopon, K.; Akgül, A. Analysis of Kink Behaviour of KdV-mKdV Equation under Caputo Fractional Operator with Non-Singular Kernel. Symmetry 2022, 14, 2316. https://doi.org/10.3390/sym14112316
Ali S, Ullah A, Ahmad S, Nonlaopon K, Akgül A. Analysis of Kink Behaviour of KdV-mKdV Equation under Caputo Fractional Operator with Non-Singular Kernel. Symmetry. 2022; 14(11):2316. https://doi.org/10.3390/sym14112316
Chicago/Turabian StyleAli, Sajjad, Aman Ullah, Shabir Ahmad, Kamsing Nonlaopon, and Ali Akgül. 2022. "Analysis of Kink Behaviour of KdV-mKdV Equation under Caputo Fractional Operator with Non-Singular Kernel" Symmetry 14, no. 11: 2316. https://doi.org/10.3390/sym14112316







