Rogue Waves Generator and Chaotic and Fractal Behavior of the Maccari System with a Resonant Parametric Forcing
Abstract
:1. Introduction
2. The Approximate Solution
3. The Model System
4. Solving the Model System
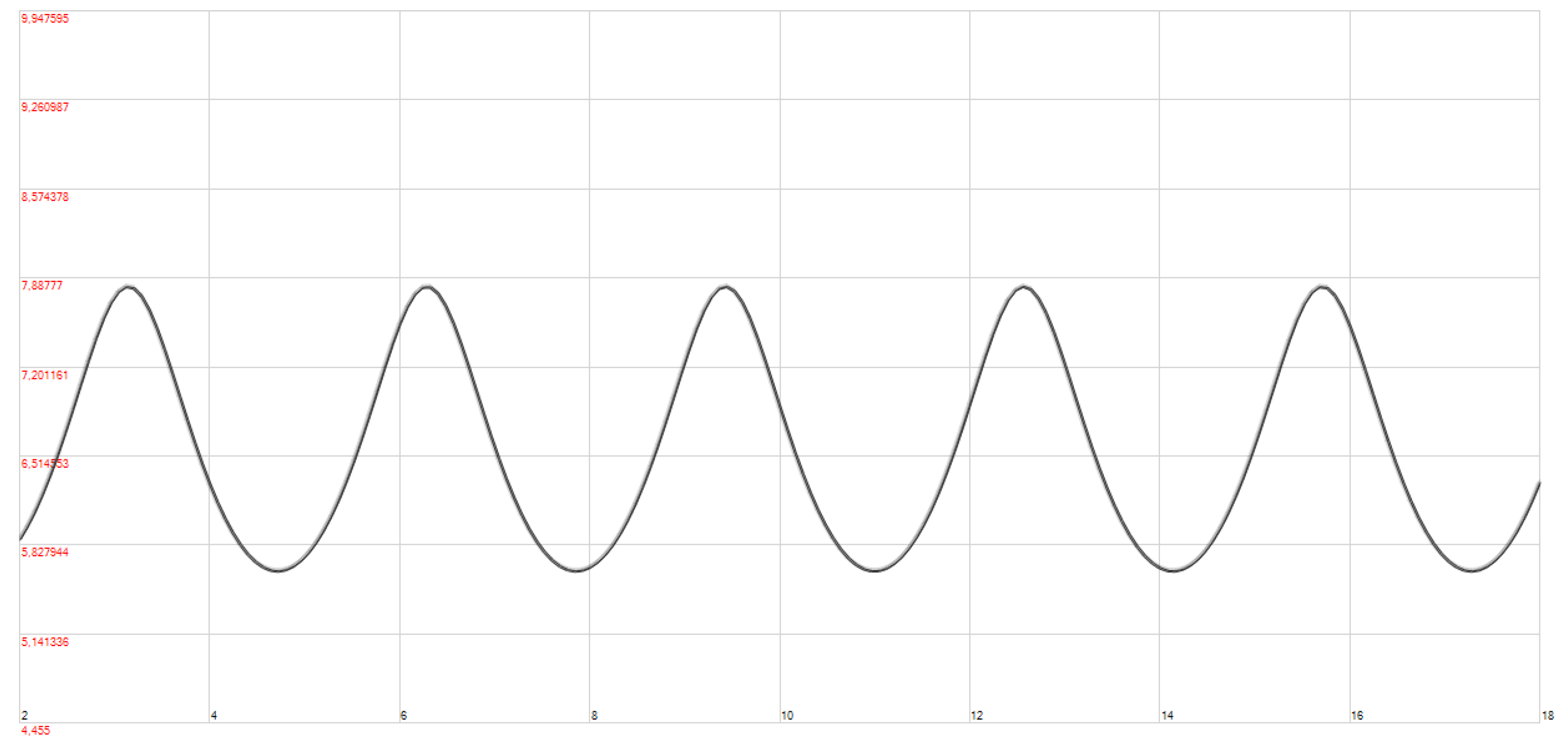
5. Chaotic and Fractal Solutions
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ablowitz, M.J.; Clarkson, P.A. Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Wazwaz, A.M. Partial Differential Equations and Solitary Waves Theory; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Chen, S.H.; Baronio, F.; Soto-Crespo, J.M.; Grelu, P.; Mihalache, D. Versatile rogue waves in scalar, vector, and multidimensional nonlinear systems. J. Phys. A Math. Theor. 2017, 50, 463001. [Google Scholar] [CrossRef] [Green Version]
- Ling, L.M.; Zhao, L.C.; Yang, Z.Y.; Guo, B.L. Generation mechanisms of fundamental rogue wave spatial-temporal structure. Phys. Rev. E 2017, 96, 022211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peregrine, D.H. Water Waves, Nonlinear Schrödinger Equations and Their Solutions. J. Aust. Math. Soc. B 1983, 25, 16–43. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Jin, X.X.C. Phase portraits and optical soliton solutions of coupled nonlinear Maccari systems describing the motion of solitary waves in fluid flow. Results Phys. 2022, 41, 105932. [Google Scholar] [CrossRef]
- Jiang, Y.; Rao, J.G.; Mihalache, D.; He, J.S.; Cheng, Y. Rogue breathers and rogue lumps on a background of dark line solitons for the Maccari system. Commun. Nonlinear Sci. 2021, 102, 105943. [Google Scholar] [CrossRef]
- Liu, L.; Yuan, Y.Q.; Sun, Y. Bright and dark N-soliton solutions for the (2+1)-dimensional Maccari system. Eur. Phys. J. Plus 2018, 133, 72. [Google Scholar] [CrossRef]
- Akbar, Y.; Afsar, H.; Abbas, S.; Javed, W.M.; Ullah, N. Dromions for the coupled Maccari’s system in fluid mechanics. Chaos Solitons Fractals 2021, 150, 111114. [Google Scholar] [CrossRef]
- Cheemaa, N.; Chen, S.; Seadawy, A.R. Propagation of isolated waves of coupled nonlinear (2+1)-dimensional Maccari system in plasma physics. Results Phys. 2020, 17, 102987. [Google Scholar] [CrossRef]
- Chen, Z.X.; Manafian, J.; Raheel, M.; Zafar, A.; Alsaikhan, F.; Abotaleb, M. Extracting the exact solitons fo time-fractional three coupled nonlinear Maccari’s system with complex form via four different methods. Results Phys. 2022, 36, 105400. [Google Scholar] [CrossRef]
- Jiang, Y.; Xian, D.Q.; Kang, X.R. Homoclinic breather and rogue wave solutions to Maccari equation. Comput. Math. Appl. 2020, 79, 1890–1894. [Google Scholar] [CrossRef]
- Thilakavathy, J.; Amrutha, R.; Subramanian, K.; Mani Rajan, M.S. Different wave patterns for (2+1) dimensional Maccari’s equation. Nonlinear Dyn. 2022, 108, 445–456. [Google Scholar] [CrossRef]
- Cheemaa, N.; Younla, M. New and more exact traveling wave solutions to integrable (2+1)-dimensional Maccari systems. Nonlinear Dyn. 2016, 83, 1395–1401. [Google Scholar] [CrossRef]
- Neirameh, A. New analytical solutions for the coupled nonlinear Maccari’s system. Alex. Eng. J. 2016, 55, 2839–2847. [Google Scholar] [CrossRef] [Green Version]
- Baskonus, H.M.; Sulaiman, T.A.; Bulut, H. On the novel wave behaviors to the coupled nonlinear Maccari’s systems with complex structure. Optik 2017, 131, 1036–1043. [Google Scholar] [CrossRef]
- Alkhidhr, H.A.; Abdelrahman, M.A.E. Wave structures to the three coupled nonlinear Maccari’s systems in plasma physics. Results Phys. 2022, 33, 105092. [Google Scholar] [CrossRef]
- Islam, T.; Akbar, A.; Rezazadeh, H.; Bekir, A. New-fashioned solitons of coupled nonlinear Maccari systems describing the motion of solitary waves in fluid flow. J. Ocean Eng. Sci. 2022, in press. [CrossRef]
- Bilal, M.; Ahmad, J. Investigation of diverse exact soliton solutions to the nonlinear dynamical model via three mathematical methods. J. Ocean Eng. Sci. 2022, in press. [CrossRef]
- Ciancio, A.; Baskonus, H.M.; Sulaiman, A.; Bulut, M. New structural dynamics of isolated vaves via the coupled nonlinear Maccari’s system with complex structure. Indian J. Phys. 2022, 92, 1281–1290. [Google Scholar] [CrossRef]
- Xia, P.; Zhang, Y.; Zhang, H.; Zhuang, Y. Some novel dynamical behavior of localized solitary waves for the Maccari system. Nonlinear Dyn. 2022, 108, 533–541. [Google Scholar] [CrossRef]
- Asli, P. Local and nonlocal (2+1)-dimensional Marccari systems and their soliton solutions. Phys. Scr. 2021, 96, 035217. [Google Scholar]
- Maccari, A. The Maccari system as model system for rogue waves. Phys. Lett. A 2020, 384, 126740. [Google Scholar] [CrossRef]
- Maccari, A. A Parametric Resonance for the Hirota-Maccari Equation. Symmetry 2022, 14, 1444. [Google Scholar] [CrossRef]
- Maccari, A. Chaotic and fractal patterns for interacting nonlinear waves. Chaos Solitons Fractals 2010, 43, 86–95. [Google Scholar] [CrossRef]
- Tang, X.Y.; Lou, S.-Y.; Zhang, Y. Localized excitations in (2+1)-dimensional systems. Phys. Rev. E 2022, 66 Pt 2, 046601. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maccari, A. Rogue Waves Generator and Chaotic and Fractal Behavior of the Maccari System with a Resonant Parametric Forcing. Symmetry 2022, 14, 2321. https://doi.org/10.3390/sym14112321
Maccari A. Rogue Waves Generator and Chaotic and Fractal Behavior of the Maccari System with a Resonant Parametric Forcing. Symmetry. 2022; 14(11):2321. https://doi.org/10.3390/sym14112321
Chicago/Turabian StyleMaccari, Attilio. 2022. "Rogue Waves Generator and Chaotic and Fractal Behavior of the Maccari System with a Resonant Parametric Forcing" Symmetry 14, no. 11: 2321. https://doi.org/10.3390/sym14112321





