A Moment Inequality for the NBRULC Class: Statistical Properties with Applications to Model Asymmetric Data

Abstract

In this paper, the moment inequalities for some aging distributions are derived based on a mathematical class entitled “a new better than renewal used in Laplace transform order in increasing convex order class (NBRULC)”. The introduced inequalities can be utilized as a new mathematical test for the exponentiality property versus NBRULC. If the mean life is finitely based on these inequalities, then all higher-order moments exist. Pitman’s asymptotic efficiency of the new mathematical test is derived and studied in detail for some asymmetric probability models. The new mathematical test’s power is estimated in reliability studies for a few well-known alternative asymmetric models. The problem in the case of right-censored data is also handled. After that, applying the suggested test to practical issues is demonstrated using asymmetric, real datasets.

1. Introduction

For more than three decades, aging theories have been the focus of research and have been crucial to reliability theory. Age-related improvements or declines in a population of units or systems are described by concepts of aging. We look at some statistical characteristics and probability distributions before looking at various classes of aging-related life distributions. Gaining greater efficiency is the major goal of creating new tests. Many authors used moment inequalities to compare certain classes of life distributions; Ahmad [1] studied the tests of exponentiality against increasing failure rate (IFR), new better than used (NBU), and new better than used in expectation (NBUE). Ahmad and Mugdadi [2] developed the tests of new better than used convex ordering (NBUC), increasing failure rate average (IFRA), and decreasing mean residual life (DMRL), while Mahmoud et al. [3,4] studied the tests of new better than renewal used in Laplace transform order (NBRUL) and new renewal better than used in Laplace transform order (NRBUL). El-Arishy et al. [5] created a test statistic to compare the exponentiality to the class renewal new better than used in moment generating function (RNBU${}_{mgf}$) using the moment inequalities of this class. Further, the new better than renewal used in moment generating function order (NBRU${}_{mgf}$), used better than aged in convex ordering (UBAC), and overall decreasing life (ODL) classes have been studied by Hassan and Said [6], Abu-Youssef [7], and Diab and El-Atfy [8].

The main classes of life distributions that have been introduced in the literature are based on NBU, NBUC, new better than used convex ordering moment generation function (NBUC${}_{{}_{mgf}}$), new better than used in increasing convex in Laplace transform order (NBUCL), exponential better than equilibrium life in convex (EBELC), new better than used in the increasing convex average order (NBUCA), new better than renewal used (NBRU), and new better than renewal used in Laplace transform order at age t${}_{\circ }$ (NBRUL-t${}_{\circ }$). Numerous academics have advocated comparing some kinds of classes of life distributions with testing the exponentiality from various angles. For more details, one can refer to Kumazawa [9], Cao and Wang [10], Abu-Youssef et al. [11], Mahmoud et al. [12], Mahmoud et al. [13], Al-Gashgari et al. [14], Abouammoh et al. [15], EL-Sagheer et al. [16], Bryson and Siddiqui [17], and Barlow and Proschan [18].

The paper is set up as follows: We provide some definitions for NBRU, NBRUL, and NBRULC classes of life distributions in the remainder of this section. In Section 2, the moment inequalities for the NRBULC class are obtained. In Section 3, testing the exponentiality versus NRBULC is investigated. In Section 4, we obtained the Pitman asymptotic for some asymmetric distributions. Section 5 simulates the critical values and power estimates for Monte Carlo null distributions. Section 6 dealt with right-censored data and critical values. Finally, the use of the proposed test on some real asymmetric data is discussed in Section 7.

Definition 1.

Assume that X and Y are random variables with the cumulative distribution functions $F\left(x\right)$ and $G\left(y\right)$, respectively, and the survival functions $\overline{F}\left(x\right)$ and $\overline{G}\left(y\right)$. It is stated that X is smaller than Y in the following cases:

(i)

Usual stochastic order (${\le }_{st}$), symbolized by $X{\le }_{st}Y$ if

$$\overline{F}\left(x\right)\le \overline{G}\left(y\right),\forall x,y.$$

(ii)

Increasing convex order (${\le }_{icx}$), symbolized by $X{\le }_{icx}Y$ if

$${\int }_x^{\infty }\overline{F}\left(u\right)du\le {\int }_y^{\infty }\overline{G}\left(u\right)du.$$

Definition 2.

A random variable X is said to be

(i)

New better than renewal used ($NBRU$), symbolized by $X\in NBRU$, if

$${\overline{W}}_F\left(x+t\right)\le \overline{F}\left(x\right){\overline{W}}_F\left(t\right),x,t\ge 0.$$

(ii)

New better than renewal used in Laplace transform order ($NBRUL$), symbolized by $X\in NBRUL$, if

$${\int }_0^{\infty }{e}^{-sx}{\overline{W}}_F\left(x+t\right)dx\le {\overline{W}}_F\left(t\right){\int }_0^{\infty }{e}^{-sx}\overline{F}\left(x\right)dx,x,t,s\ge 0,$$

or

$${\int }_0^{\infty }{\int }_{x+t}^{\infty }{e}^{-sx}\overline{F}\left(u\right)dudx\le {\int }_0^{\infty }{\int }_t^{\infty }{e}^{-sx}\overline{F}\left(x\right)\overline{F}\left(u\right)dudx,$$

where ${\overline{W}}_F\left(x+t\right)=\frac{1}{\mu }{\int }_{x+t}^{\infty }\overline{F}\left(u\right)du$ and μ is the expected value of $x.$ Now, depending on definitions (1) and (2), Etman et al. [19] introduced a new class named $NBRULC$ as follows

Definition 3.

The random variable X is said to be $NBRULC$, if

$${\int }_0^{\infty }{e}^{-sx}\mathsf{\Gamma }(x+t)dx\le {\int }_0^{\infty }{e}^{-sx}\overline{F}\left(x\right)\mathsf{\Gamma }\left(t\right)dx,x,t,s\ge 0,$$

where $\mathsf{\Gamma }(x+t)={\int }_{x+t}^{\infty }{\overline{W}}_F\left(t\right)du.$ It is obvious that $NBRU\subset NBRUL\subset NBRULC.$

2. Moment’s Inequalities

Theorem 1.

Suppose F is an NBRULC life distribution with finite moments and all moments existing, then for integers $r,s\ge 0$, we get

$$\begin{array}{ccc}\hfill \frac{{\mu }_{(r+3)}.[1-\varphi \left(s\right)]}{s(r+1)(r+2)(r+3)}& \ge \hfill & \frac{-{(-1)}^{r}r!}{s^{r+2}}[\frac{{\mu }_{\left(2\right)}}{2}-\frac{\mu }{s}+\frac{1}{s^2}(1-\varphi \left(s\right))]+\hfill \\ \hfill & \hfill & \frac{r!}{s^{r+1}}\sum _{i=0}^r\frac{{(-1)}^i{s}^{r-i}}{(r-i+3)!}.{\mu }_{(r-i+3)},\hfill \end{array}$$

(1)

where

$${\mu }_{\left(r\right)}=E\left(X^r\right)={\int }_0^{\infty }{x}^{r}dF\left(x\right)=r{\int }_0^{\infty }{x}^{r-1}\overline{F}\left(x\right)dx\mathrm{and}\varphi \left(s\right)=E\left(e^{-sX}\right)=\underset{0}{\overset{\infty }{\int }}{e}^{-sx}dF\left(x\right).$$

Proof. 

Since $F\left(x\right)$ is NBRULC, then

$${\int }_0^{\infty }{e}^{-sx}\mathsf{\Gamma }(x+t)dx\le {\int }_0^{\infty }{e}^{-sx}\overline{F}\left(x\right)\mathsf{\Gamma }\left(t\right)dx,x,t\ge 0.$$

(2)

Making use of Equation (2), yields

$${\int }_0^{\infty }{t}^r{\int }_0^{\infty }{e}^{-sx}\mathsf{\Gamma }(x+t)dxdt\le {\int }_0^{\infty }{t}^r\mathsf{\Gamma }\left(t\right){\int }_0^{\infty }{e}^{-sx}\overline{F}\left(x\right)dxdt.$$

(3)

Now, we can formulate the expression for the right-hand side of Equation (3) as follows

$${\int }_0^{\infty }{t}^r\mathsf{\Gamma }\left(t\right){\int }_0^{\infty }{e}^{-sx}\overline{F}\left(x\right)dxdt=E{\int }_0^{\infty }{t}^r\mathsf{\Gamma }\left(t\right){\int }_0^{\infty }{e}^{-sx}I(X>x)dxdt,$$

observe that

$$E{\int }_0^{\infty }{e}^{-sx}I(X>x)dx=\frac{1}{s}(1-\varphi \left(s\right)),$$

and

$$\begin{array}{ccc}\hfill {\int }_0^{\infty }{t}^r\mathsf{\Gamma }\left(t\right)dt& =& {\int }_0^{\infty }{t}^r{\int }_t^{\infty }{\overline{W}}_F\left(u\right)dudt={\int }_0^{\infty }{\overline{W}}_F\left(t\right){\int }_0^t{u}^{r}dudt\hfill \\ & =& \frac{1}{r+1}{\int }_0^{\infty }{t}^{r+1}{\overline{W}}_F\left(t\right)dt=\frac{{\mu }_F^{-1}}{r+1}E{\int }_0^{\infty }{t}^{r+1}(X-t)I(X>t)dt\hfill \\ & =& \frac{{\mu }_F^{-1}}{r+1}E{\int }_0^X(X-t)t^{r+1}dt=\frac{{\mu }_F^{-1}}{r+1}E[X{\int }_0^X{t}^{r+1}dt-{\int }_0^X{t}^{r+2}dt]\hfill \\ & =& \frac{{\mu }_F^{-1}}{r+1}E[\frac{1}{r+2}{X}^{r+3}-\frac{1}{r+3}{X}^{r+3}]\hfill \\ & =& {\mu }_F^{-1}[\frac{{\mu }_{(r+3)}}{(r+1)(r+2)}-\frac{{\mu }_{(r+3)}}{(r+1)(r+3)}]=\frac{{\mu }_F^{-1}{\mu }_{(r+3)}}{(r+1)(r+2)(r+3)}.\hfill \end{array}$$

Thus,

$${\int }_0^{\infty }{t}^r\mathsf{\Gamma }\left(t\right){\int }_0^{\infty }{e}^{-sx}\overline{F}\left(x\right)dxdt=\frac{{\mu }_F^{-1}{\mu }_{(r+3)}}{s(r+1)(r+2)(r+3)}(1-\varphi \left(s\right)).$$

(4)

The left side of Equation (3) can be formulated as

$${\int }_0^{\infty }{t}^r{\int }_0^{\infty }{e}^{-sx}\mathsf{\Gamma }(x+t)dxdt={\int }_0^{\infty }{e}^{-sv}\mathsf{\Gamma }\left(v\right){\int }_0^v{u}^r{e}^{su}dudv,$$

(5)

where

$$I={\int }_0^{\infty }{t}^r{\int }_0^{\infty }{e}^{-sx}\mathsf{\Gamma }(x+t)dxdt,$$

$$u=x+t,v=t⟹\mid J\mid =1\mathrm{and}0<x<\infty ⟹v<u<\infty ,$$

then

$$\begin{array}{ccc}\hfill I& =& {\int }_0^{\infty }{\int }_v^{\infty }{v}^r{e}^{-s(u-v)}\mathsf{\Gamma }\left(u\right)dudv={\int }_0^{\infty }{\int }_0^v{u}^r{e}^{-s(v-u)}\mathsf{\Gamma }\left(v\right)dudv\hfill \\ & =& {\int }_0^{\infty }{e}^{-sv}\mathsf{\Gamma }\left(v\right){\int }_0^v{u}^r{e}^{su}dudv,\hfill \end{array}$$

such as

$${\int }_0^v{u}^r{e}^{su}du=\frac{r!}{s^{r+1}}[-{(-1)}^r+\sum _{i=0}^r{(-1)}^i\frac{{\left(vs\right)}^{(r-i)}}{(r-i)!}{e}^{sv}].$$

Moreover, by making some mathematical simplifications, Equation (5) can be formulated as

$$\begin{array}{ccc}\hfill {\int }_0^{\infty }{t}^r{\int }_0^{\infty }{e}^{-sx}\mathsf{\Gamma }(x+t)dxdt& =\hfill & \frac{r!}{s^{r+1}}\sum _{i=0}^r{(-1)}^i\frac{s^{r-i}}{(r-i+3)!}.{\mu }_{(r-i+3)}\hfill \\ \hfill & \hfill & -\frac{{(-1)}^{r}r!}{s^{r+2}}{\mu }_F^{-1}[\frac{{\mu }_{\left(2\right)}}{2}-\frac{\mu }{s}+\frac{1}{s^2}(1-\varphi \left(s\right))].\hfill \end{array}$$

(6)

From Equations (4) and (6), the theorem is proven. □

Remark 1.

When $r=1$, Theorem 1 reduces to

$$\frac{{\mu }_{\left(4\right)}}{24s}[1-\varphi \left(s\right)]\ge \frac{1}{s^3}[\frac{{\mu }_{\left(2\right)}}{2}-\frac{\mu }{s}+\frac{1}{s^2}(1-\varphi \left(s\right))]+\frac{1}{s^2}[\frac{s}{24}{\mu }_{\left(4\right)}-\frac{1}{6}{\mu }_{\left(3\right)}],$$

(7)

where ${\mu }_{\left(r\right)}={\int }_0^{\infty }{x}^{r}dF\left(x\right)$.

3. Testing Exponentiality vs. NBRULC Class

We may test that the null hypothesis $H_{\circ }:F\left(x\right)$ is exponential versus $H_1:F\left(x\right)$ is NBRULC and not exponential by using the inequality in Equation (7), where $\delta \left(s\right)$ has been used as the following

$$\delta \left(s\right)=\frac{{\mu }_{\left(3\right)}}{6s^2}-\frac{{\mu }_{\left(4\right)}\varphi \left(s\right)}{24s}-\frac{{\mu }_{\left(2\right)}}{2s^3}+\frac{\varphi \left(s\right)}{s^5}+\frac{\mu }{s^4}-\frac{1}{s^5}.$$

(8)

Under $H_{\circ }$m the value of $\delta \left(s\right)=0,$ whereas based on $H_1,$ the value of $\delta \left(s\right)>0$. Let $X_1,X_2,X_3,...,X_n$ be a random sample from a distribution $F\left(x\right)$. The empirical estimate ${\delta }_n\left(s\right)$ of $\delta \left(s\right)$ can be obtained as

$${\delta }_n\left(s\right)=\frac{1}{n^2}\sum _{i=1}^n\sum _{j=1}^n[\frac{1}{6s^2}{X}_i^3-\frac{1}{24s}{X}_i^4{e}^{-s{X}_j}-\frac{1}{2s^3}{X}_i^2+\frac{1}{s^5}{e}^{-s{X}_i}+\frac{1}{s^4}{X}_i-\frac{1}{s^5}].$$

To make the test invariant, let ${\Delta }_n\left(s\right)=\frac{{\delta }_n\left(s\right)}{{\overline{X}}^5},$ where $\overline{X}={\sum }_{i=1}^n\frac{X_i}{n}$ is the sample mean. Then,

$${\Delta }_n\left(s\right)=\frac{1}{n^2{\overline{X}}^5}\sum _{i=1}^n\sum _{j=1}^n[\frac{1}{6s^2}{X}_i^3-\frac{1}{24s}{X}_i^4{e}^{-s{X}_j}-\frac{1}{2s^3}{X}_i^2+\frac{1}{s^5}{e}^{-s{X}_i}+\frac{1}{s^4}{X}_i-\frac{1}{s^5}].$$

(9)

It is simple to demonstrate $E\left({\Delta }_n\left(s\right)\right)=\delta \left(s\right).$ Now, set

$${\varphi }_s(X_i,X_j)=\frac{1}{6s^2}{X}_i^3-\frac{1}{24s}{X}_i^4{e}^{-s{X}_j}-\frac{1}{2s^3}{X}_i^2+\frac{1}{s^5}{e}^{-s{X}_i}+\frac{1}{s^4}{X}_i-\frac{1}{s^5},$$

(10)

and define the symmetric kernel

$${\psi }_s(X_i,X_j)=\frac{1}{2!}\sum _R{\varphi }_s(X_i,X_j),$$

where the summation is over all arrangements of $X_i$ and $X_j$. Then, ${\Delta }_n\left(s\right)$ in Equation (9) is equivalent to the $U_n$-statistic given by

$$U_n=\frac{1}{\left({}_2^n\right)}\sum _{i<j}{\psi }_s(X_i,X_j).$$

(11)

The following theorem encapsulates the asymptotic normality of ${\Delta }_n\left(s\right)$.

Theorem 2.

(i) As $n\to \infty ,\sqrt{n}({\Delta }_n\left(s\right)-\delta \left(s\right))$ is asymptotically normal with a mean of 0 and a variance of ${\sigma }^2\left(s\right),$ where

$$\begin{array}{ccc}\hfill {\sigma }^2\left(s\right)& =\hfill & Var\{\frac{X^3}{6s^2}-\frac{X^4}{24s}\varphi \left(s\right)-\frac{X^2}{2s^3}+\frac{e^{-sx}}{s^5}+\frac{X}{s^4}+\frac{1}{6s^2}{\mu }_{\left(3\right)}\hfill \\ \hfill & \hfill & -\frac{e^{-sx}}{24s}{\mu }_{\left(4\right)}-\frac{1}{2s^3}{\mu }_{\left(2\right)}+\frac{1}{s^5}\varphi \left(s\right)+\frac{1}{s^4}\mu -\frac{2}{s^5}\}.\hfill \end{array}$$

(12)

(ii) Under $H_{\circ },$ the variance ${\sigma }_{\circ }^2\left(s\right)$ is

$${\sigma }_{\circ }^2\left(s\right)=\frac{s^3+43s^2+103s+69}{{(1+s)}^5(1+2s)}.$$

(13)

Proof. 

As in Lee [20], based on the U-statistic theory,

$${\sigma }^2\left(s\right)=V\{E[{\varphi }_s(X_1,X_2)\mid X_1]+E[{\varphi }_s(X_1,X_2)\mid X_2]\}.$$

Looking at Equation (10), it follows that it is easy to formulate the following expression

$$E({\varphi }_s(X_1,X_2)\mid X_1)=\frac{X^3}{6s^2}-\frac{X^4}{24s}{\int }_0^{\infty }{e}^{-sx}dF\left(x\right)-\frac{X^2}{2s^3}+\frac{e^{-sx}}{s^5}+\frac{X}{s^4}-\frac{1}{s^5},$$

and

$$\begin{array}{ccc}\hfill E({\varphi }_s(X_1,X_2)& \mid & X_2)=\frac{1}{6s^2}{\int }_0^{\infty }{x}^{3}dF\left(x\right)-\frac{e^{-sx}}{24s}{\int }_0^{\infty }{x}^{4}dF\left(x\right)-\frac{1}{2s^3}{\int }_0^{\infty }{x}^{2}dF\left(x\right)\hfill \\ & & +\frac{1}{s^5}{\int }_0^{\infty }{e}^{-sx}dF\left(x\right)+\frac{1}{s^4}{\int }_0^{\infty }xdF\left(x\right)-\frac{1}{s^5}.\hfill \end{array}$$

Therefore,

$$\begin{array}{ccc}\hfill {\sigma }^2\left(s\right)& =& Var\{\frac{X^3}{6s^2}-\frac{X^4}{24s}{\int }_0^{\infty }{e}^{-sx}dF\left(x\right)-\frac{X^2}{2s^3}+\frac{e^{-sx}}{s^5}+\frac{X}{s^4}\hfill \\ & & \frac{1}{6s^2}{\int }_0^{\infty }{x}^{3}dF\left(x\right)-\frac{e^{-sx}}{24s}{\int }_0^{\infty }{x}^{4}dF\left(x\right)-\frac{1}{2s^3}{\int }_0^{\infty }{x}^{2}dF\left(x\right)\hfill \\ & & +\frac{1}{s^5}{\int }_0^{\infty }{e}^{-sx}dF\left(x\right)+\frac{1}{s^4}{\int }_0^{\infty }xdF\left(x\right)-\frac{2}{s^5}\}.\hfill \end{array}$$

Under $H_{\circ }$

$${\sigma }_{\circ }^2\left(s\right)=\frac{s^3+43s^2+103s+69}{{(1+s)}^5(1+2s)}.$$

 □

4. Pitman Asymptotic Efficiency (PAE)

The PAEs are calculated and compared with various other tests for the following other option distributions to assess the effectiveness of this technique.

(i)

The WD,

$${\overline{F}}_1\left(u\right)=e^{-u^{\theta }},u,\theta >0.$$

(ii)

The LFRD,

$${\overline{F}}_2\left(u\right)=e^{-u-\frac{\theta }{2}{u}^2},u,\theta >0.$$

(iii)

The MD,

$${\overline{F}}_3\left(u\right)=e^{-u-\theta \left(u+e^{-u}-1\right)},u,\theta >0.$$

The PAE is defined by

$$PAE\left({\Delta }_n\left(s\right)\right)=\frac{1}{{\sigma }_{\circ }\left(s\right)}{\left|\frac{d}{d\theta }\delta \left(s\right)\right|}_{{}_{\theta \to {\theta }_{\circ }}}.$$

(14)

$${\delta }_{\theta }\left(s\right)=\frac{{\mu }_{3\theta }}{6s^2}-\frac{{\mu }_{4\theta }{\varphi }_{\theta }\left(s\right)}{24s}-\frac{{\mu }_{2\theta }}{2s^3}+\frac{{\varphi }_{\theta }\left(s\right)}{s^5}+\frac{{\mu }_{\theta }}{s^4}-\frac{1}{s^5},$$

where

$$\begin{array}{ccc}\hfill {\mu }_{\theta }& =& {\int }_0^{\infty }{\overline{F}}_{\theta }\left(u\right)du,{\mu }_{2\theta }=2{\int }_0^{\infty }u{\overline{F}}_{\theta }\left(u\right)du,{\mu }_{3\theta }=3{\int }_0^{\infty }{u}^2{\overline{F}}_{\theta }\left(u\right)du\hfill \\ \hfill {\mu }_{4\theta }& =& 4{\int }_0^{\infty }{u}^3{\overline{F}}_{\theta }\left(u\right)du,\mathrm{and}{\varphi }_{\theta }\left(s\right)={\int }_0^{\infty }{e}^{-su}d{F}_{\theta }\left(u\right).\hfill \end{array}$$

Hence,

$$\frac{d}{d\theta }{\delta }_{\theta }\left(s\right)=\frac{{\mu }_{3\theta }^{‵}}{6s^2}-\frac{1}{24s}({\mu }_{4\theta }{\varphi }_{\theta }^{‵}\left(s\right)+{\mu }_{4\theta }^{‵}{\varphi }_{\theta }\left(s\right))-\frac{{\mu }_{2\theta }^{‵}}{2s^3}+\frac{{\varphi }_{\theta }^{‵}\left(s\right)}{s^5}+\frac{{\mu }_{\theta }^{‵}}{s^4},$$

where

$$\begin{array}{ccc}\hfill {\mu }_{\theta }^{‵}& =& {\int }_0^{\infty }{\overline{F}}_{\theta }^{‵}\left(u\right)du,{\mu }_{2\theta }^{‵}=2{\int }_0^{\infty }u{\overline{F}}_{\theta }^{‵}\left(u\right)du,{\mu }_{3\theta }^{‵}=3{\int }_0^{\infty }{u}^2{\overline{F}}_{\theta }^{‵}\left(u\right)du,\hfill \\ \hfill {\mu }_{4\theta }^{‵}& =& 4{\int }_0^{\infty }{u}^3{\overline{F}}_{\theta }^{‵}\left(u\right)du,\mathrm{and}{\varphi }_{\theta }^{‵}\left(s\right)=-{\int }_0^{\infty }{e}^{-su}d{\overline{F}}_{\theta }^{‵}\left(u\right).\hfill \end{array}$$

Based on PAE expression in Equation (14), we get

$$PAE\left(\delta \left(s\right)\right)=\frac{1}{{\sigma }_{\circ }\left(s\right)}\mid \frac{{\mu }_{3{\theta }_{\circ }}^{‵}}{6s^2}-\frac{1}{24s}({\mu }_{4{\theta }_{\circ }}{\varphi }_{{\theta }_{\circ }}^{‵}\left(s\right)+{\mu }_{4{\theta }_{\circ }}^{‵}{\varphi }_{{\theta }_{\circ }}\left(s\right))-\frac{{\mu }_{2{\theta }_{\circ }}^{‵}}{2s^3}+\frac{{\varphi }_{{\theta }_{\circ }}^{‵}\left(s\right)}{s^5}+\frac{{\mu }_{{\theta }_{\circ }}^{‵}}{s^4}\mid .$$

At $s=5$, this leads to

$$PAE[{\Delta }_n\left(5\right),WD]=0.707,PAE[{\Delta }_n\left(5\right),LFR]=0.769,$$

and

$$PAE[{\Delta }_n\left(5\right),MD]=0.155,\mathrm{where}{\sigma }_{\circ }\left(5\right)=0.14442.$$

Table 1. The results of comparing the proposed test with previous tests based on PAE.

Test	WD	LFRD	MD
Kango [21]	0.13215	0.43325	0.14434
Mugdadi and Ahmad [22]	0.17034	0.40812	0.03903
Mahmoud and Abdul Alim [23]	0.05026	0.21743	0.14415
Our test ${\Delta }_n\left(5\right)$	0.70727	0.76918	0.15526

lists some computations for PAE ${\Delta }_n\left(5\right)$ that outperforms the other tests based on the PAEs.

5. Critical Points

In this section, the upper percentile of ${\Delta }_n\left(5\right)$ for $90\%,95\%,$ and $99\%$ are computed using Mathematica v.12 based on a generated sample size of $10,000$. The empirical results are listed in

Table 2. The upper percentile of ${\Delta }_n\left(5\right)$ with 10,000 iterations.

n	90%	95%	99%
10	0.0175447	0.0215082	0.0307057
15	0.0146700	0.0178336	0.0235737
20	0.0133767	0.0158393	0.0208921
25	0.0124196	0.0143009	0.0190445
30	0.0118450	0.0135788	0.0172333
35	0.0112132	0.0128815	0.0164041
39	0.0108867	0.0123794	0.0155672
40	0.0107201	0.0122105	0.0152138
43	0.0105867	0.0118786	0.0147576
45	0.0103980	0.0117976	0.0146368
50	0.0101641	0.0114157	0.0142009

and Figure 1. From Table 2 and Figure 1, we note that the critical values are increasing as the confidence level increases. Further, the critical values decrease as the sample size n increases. In addition, when the significance level decreases, the critical value increases, which indicates the strength of the proposed test.

The Power Estimates of Test ${\Delta }_n\left(5\right)$

For some famous models, such as LFRD, WD, and GaD, based on 10,000 samples listed in

Table 3. Power estimates of ${\Delta }_n\left(5\right)$.

n	$\mathit{\theta }$	LFRD	WD	GaD
10	2 3 4	0.399942 0.564153 0.678434	1.000000 1.000000 1.000000	0.997213 0.999836 0.998924
20	2 3 4	0.793316 0.922933 0.970625	1.000000 1.000000 1.000000	0.995113 0.999812 1.000000
30	2 3 4	0.955823 0.993732 0.999421	1.000000 1.000000 1.000000	0.994913 0.999842 1.000000

, the power of ${\Delta }_n\left(5\right)$ will be calculated at the $(1-\alpha )\%$ confidence level, where $\alpha =0.05$ with adequate parameter values of $n=10,$ 20, and 30. As we can see, ${\mathsf{\Lambda }}_n\left(5\right)$ has good power for all other choices.

6. Testing for Randomly Right-Censored Data

A test statistic is suggested to compare $H_{\circ }$ to $H_1$ with randomly right-censored data (RRCD). Such censored data are typically the only ones accessible in a life-testing model or clinical trial where patients may be lost before the study is finished. The following formal model applies to this experimental situation. Assume n items are tested, with $X_1,X_2,\dots ,X_n$ designating each object’s actual lifetime. Let $X_1,X_2,\dots ,X_n$ be a continuous, independent and identically distributed life distribution $F\left(x\right)$. Let $Y_1,Y_2,\dots ,Y_n$ be by a continuous, independent and identically distributed life distribution $G\left(y\right)$. In addition, we presume X’s and Y’s are independent. In the RRCD, we notice the pairs $(Z_j,{\delta }_j),$$j=1,\dots ,n$, where $Z_j$$=min(Xj$,$Y_j)$ and

$${\delta }_j=\left\{\begin{array}{ccc}1,\hfill & \mathrm{if}\hfill & Z_j=X_j\hfill \\ 0,\hfill & \mathrm{if}\hfill & Z_j=Y_j\hfill \end{array}\right..$$

Let $Z_{\left(0\right)}=0<Z_{\left(1\right)}<Z_{\left(2\right)}<....<Z_{\left(n\right)}$ denote the ordered Z’s and ${\delta }_{\left(j\right)}$ is ${\delta }_j$ corresponding to $Z_{\left(j\right)}.$ Using the censored data ($Z_j$, ${\delta }_j$),$j=1,\dots \dots ,n$, Kaplan and Meier [24] proposed the product limit estimator,

$${\overline{F}}_n\left(X\right)=\prod _{[j:Z(j)\le X]}{\{(n-j)/(n-j+1)\}}^{{\delta }_{\left(j\right)}},X\in [0,Z_{\left(n\right)}].$$

Now, for testing $H_{\circ }:{\Delta }_c\left(s\right)=0$ versus $H_1:{\Delta }_c\left(s\right)>0,$ we suggest the following test statistic based on RRCD

$${\Delta }_c\left(s\right)=\frac{{\mu }_{\left(3\right)}}{6s^2}-\frac{{\mu }_{\left(4\right)}\varphi \left(s\right)}{24s}-\frac{{\mu }_{\left(2\right)}}{2s^3}+\frac{\varphi \left(s\right)}{s^5}+\frac{\mu }{s^4}-\frac{1}{s^5},$$

where $\varphi \left(s\right)=\underset{0}{\overset{\infty }{\int }}{e}^{-sx}d{F}_n\left(x\right)$. To simplify the computation, ${\widehat{\Delta }}_c\left(s\right)$ may be rewritten as

$${\Delta }_c\left(s\right)=\frac{1}{6s^2}\mathsf{\Phi }-\frac{1}{24s}\mathsf{\Psi }\eta -\frac{1}{2s^3}\tau +\frac{1}{s^5}\eta +\frac{1}{s^4}\mathsf{\Omega }-\frac{1}{s^5},$$

such that

$$\begin{array}{ccc}\hfill \mathsf{\Omega }& =& \sum _{s=1}^n[\prod _{m=1}^{s-1}{C}_m^{\delta \left(m\right)}\left(Z_{\left(s\right)}-Z_{(s-1)}\right)],\hfill \\ \hfill \eta & =& \sum _{j=1}^n{e}^{-k{Z}_{\left(j\right)}}[\prod _{p=1}^{j-2}{C}_p^{\delta \left(p\right)}-\prod _{p=1}^{j-1}{C}_p^{\delta \left(p\right)}],\hfill \\ \hfill \tau & =& 2\sum _{i=1}^n[\prod _{v=1}^{i-1}{Z}_{\left(i\right)}{C}_v^{\delta \left(v\right)}\left(Z_{\left(i\right)}-Z_{(i-1)}\right)],\hfill \\ \hfill \mathsf{\Phi }& =& 3\sum _{i=1}^n[\prod _{v=1}^{i-1}{Z}_{\left(i\right)}^2{C}_v^{\delta \left(v\right)}\left(Z_{\left(i\right)}-Z_{(i-1)}\right)],\hfill \\ \hfill \mathsf{\Psi }& =& 4\sum _{i=1}^n[\prod _{v=1}^{i-1}{Z}_{\left(i\right)}^3{C}_v^{\delta \left(v\right)}\left(Z_{\left(i\right)}-Z_{(i-1)}\right)],\hfill \end{array}$$

and

$$d{F}_n\left(Z_j\right)={\overline{F}}_n\left(Z_{j-1}\right)-{\overline{F}}_n\left(Z_j\right),c_s=\left[n-s\right]{\left[n-s+1\right]}^{-1}.$$

In order to install the test, let

$${\widehat{\Delta }}_c=\frac{{\Delta }_c}{{\overline{Z}}^5},\overline{Z}=\sum _{i=1}^n\frac{Z_{\left(i\right)}}{n}.$$

Table 4. The upper percentile of ${\widehat{\Delta }}_c$ at $s=5$.

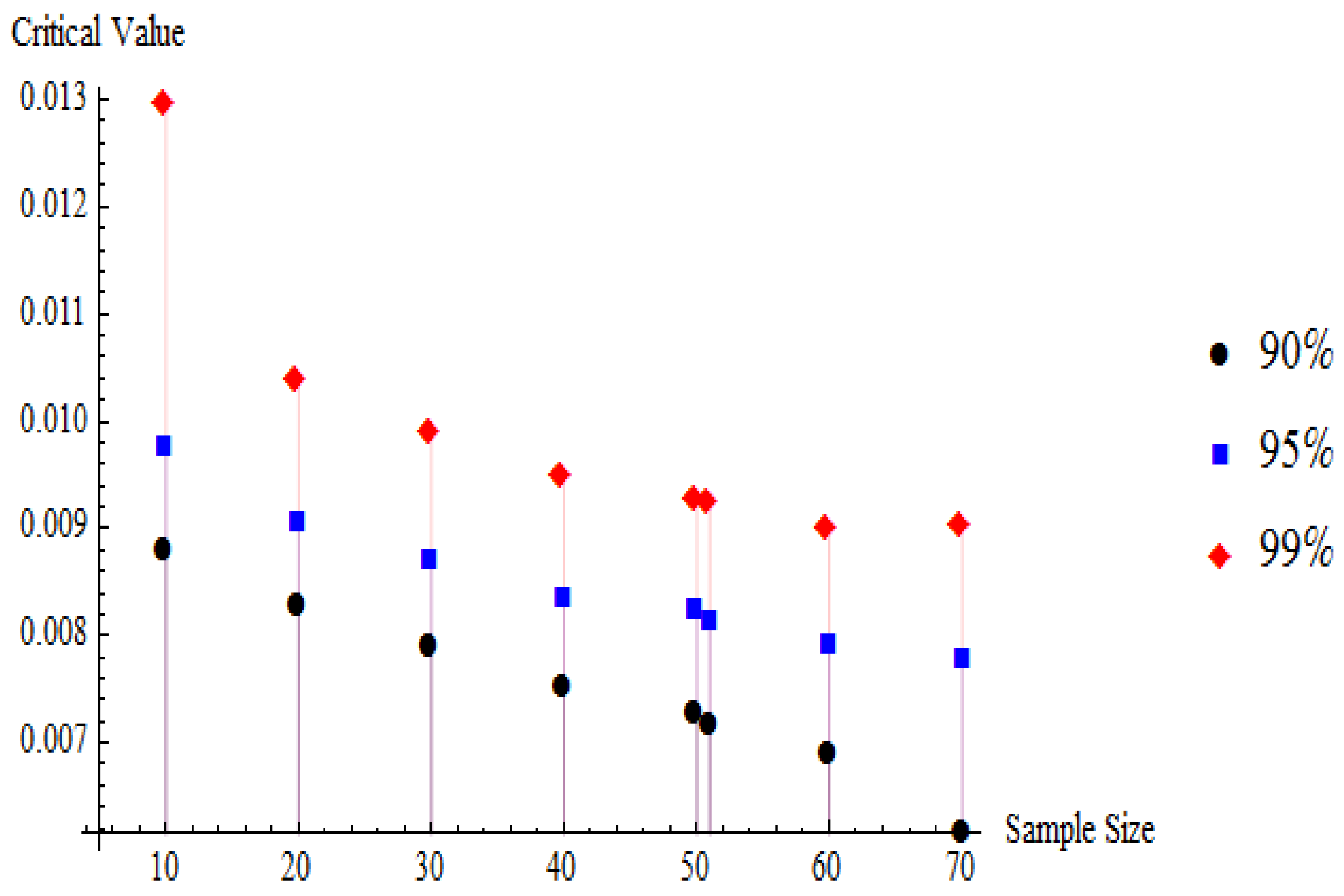
n			90%			95%			99%
10			0.0087888			0.0097737			0.0129660
20			0.0082862			0.0090777			0.0103938
30			0.0078870			0.0087021			0.0098945
40			0.0075253			0.0083648			0.0095017
50			0.0072847			0.0082420			0.0092806
51			0.0071650			0.0081415			0.0092612
60			0.0068861			0.0079237			0.0089990
70			0.0061488			0.0078003			0.0090270

shows the critical values’ percentiles for the ${\widehat{\Delta }}_c$ test.

Using Mathematica v. 12, the critical values of the Monte Carlo null distribution at $s=5$ and 10,000 replications from ED are shown. The empirical results can be sketched in Figure 2. Table 4 and Figure 2 show that the critical values increase as the confidence level increases and decrease as the sample sizes increase.

The Power Estimates of the Test ${\widehat{\Delta }}_c\left(s\right)$

With occasion parameter values of $n=10,20$, and 30, our test’s power is evaluated at the significance level $\alpha =0.05$ concerning three choices. The findings demonstrate that the power estimates of our test ${\widehat{\Delta }}_c\left(5\right)$ are good powers for all other options using Weibull, LFR, and gamma distributions based on 10,000 samples (see

Table 5. Power estimates of ${\widehat{\Delta }}_c\left(5\right)$.

n	$\mathit{\theta }$	WD	LFRD	GaD
10	2 3 4	0.923136 0.993822 1.000000	0.980764 0.994943 0.998454	1.000000 1.000000 1.000000
20	2 3 4	0.835751 0.981332 0.998114	0.963156 0.989671 0.996762	1.000000 1.000000 0.999999
30	2 3 4	0.802954 0.975626 0.998434	0.965674 0.933957 0.879062	1.000000 1.000000 0.999998

).

7. Real-Life Data Analysis

Here, we apply our test to a few real datasets with a $95\%$ confidence level for both censored and uncensored data.

7.1. Uncensored Data

Example 1.

Take a look at the data in Abouammoh et al. [15]. The data are an assortment of 43 patients with blood cancer (leukemia) from a ministry of health hospital in Saudi Arabia, the order values in years are:

0.315	0.496	0.699	1.145	1.208	1.263	1.414	2.025	2.036	2.162
2.211	2.370	2.532	2.693	2.805	2.910	2.912	3.192	3.263	3.348
3.348	3.427	3.499	3.534	3.718	3.751	3.858	3.986	4.049	4.244
4.323	4.323	4.381	4.392	4.397	4.647	4.753	4.929	4.973	5.074
5.203	5.274	5.384

$\widehat{\Delta }\left(5\right)=0.000774434$ is achieved, which is less than the similar critical value in Table 2. It is evident at the significance level $\alpha =0.05$. This indicates that the type of data does not match the NBRULC property.

Example 2.

Consider the Kotz and Johnson [25] dataset, which shows the survival periods (in years) following diagnosis for 43 patients with a specific kind of leukemia.

0.019	0.129	0.159	0.203	0.485	0.636	0.748	0.781	0.869	1.175
1.206	1.219	1.219	1.282	1.356	1.362	1.458	1.564	1.586	1.592
1.781	1.923	1.959	2.134	2.413	2.466	2.548	2.652	2.951	3.038
3.6	3.655	3.754	4.203	4.690	4.888	5.143	5.167	5.603	5.633
6.192	6.655	6.874

We get $\widehat{\Delta }\left(5\right)=0.00157194$, which is less than the critical value in Table 2. Then, the null hypotheses are accepted, which shows that the dataset has exponential properties.

Example 3.

Consider the data in Mahmoud et al. [26]. This data represents 39 patients with liver cancer from the Elminia Cancer Center, according to the Ministry of Health in Egypt, who entered in (1999). The ordered lifetimes (in days) are

10	14	14	14	14	14	15	17	18	20
20	20	20	20	23	23	24	26	30	30
31	40	49	51	52	60	61	67	71	74
75	87	96	105	107	107	107	116	150

In this case, $\widehat{\Delta }\left(5\right)=8.7902\times {10}^{-6}$, which is less than the similar critical value in Table 2. It is evident at the significance level $\alpha =0.05$. This indicates that the type of data does not match the NBRULC property.

7.2. Censored Data

Example 4.

Consider the data in Susarla and Vanryzin [26]. These data represent the survival times of 82 patients with melanoma. Forty-six represent whole lifetimes (non-censored data), and the observed values are

13	14	19	19	20	21	23	23	25	26	26	27
27	31	32	34	34	37	38	38	40	46	50	53
54	57	58	59	60	65	65	66	70	85	90	98
102	103	110	118	124	130	136	138	141	234

The ordered censored observations are

16	21	44	50	55	67	73	76	80	81	86	93
100	108	114	120	124	125	129	130	132	134	140	147
148	151	152	152	158	181	190	193	194	213	215

Taking into account the whole set of survival data (both censored and uncensored), we get ${\widehat{\Delta }}_c\left(5\right)=-2.57685\times {10}^{127}$, which is less than the critical value from Table 4. Then, it is evident to reject $H_1$ at $\alpha =0.05,$ which states that the set of data has an NBRULC property.

Example 5.

Consider the data in Mahmoud et al. [27]. This data represents 51 patients with liver cancer from the Elminia Cancer Center, according to the Ministry of Health in Egypt, who entered in (1999). Out of these, 39 represent non-censored data, and the others represent censored data. The ordered lifetimes (in days) are

Non-censored data

10	14	14	14	14	14	15	17	18	20
20	20	20	20	23	23	24	26	30	30
31	40	49	51	52	60	61	67	71	74
75	87	96	105	107	107	107	116	150

Censored data

30

30

30

30

30

60

150

150

150

150

150

185

Considering the whole set of survival data (both censored and uncensored), it was found that ${\widehat{\Delta }}_c\left(5\right)=-457.328$, which is less than the critical value in Table 4. It is evident at the significance level $\alpha =0.05$. This indicates that the type of data does not match the NBRULC property.

8. Concluding Remarks

In this article, a new mathematical test for the exponentiality property has been established. Quality criteria of the new test have been discussed using Pitman asymptotic efficiency in the case of censored and non-censored data to show the test’s usefulness. It was found that the proposed test is more flexible compared to the other mathematical tools here. We have noticed that Pitman’s efficiency of our test is higher compared to the other tests, and this is illustrated by the comparison made in Table 1. In general, we can conclude that the introduced inequalities can be utilized as a new mathematical test for the exponentiality property versus NBRULC. These inequalities demonstrate that if the mean life is finite, then all higher-order moments exist.