Dynamics Analysis of a Class of Stochastic SEIR Models with Saturation Incidence Rate
Abstract
:1. Introduction
2. The Gradual Progression of the Solution near Disease-Free Equilibrium State of the Deterministic System
3. The Final Behavior of the Infectious Disease
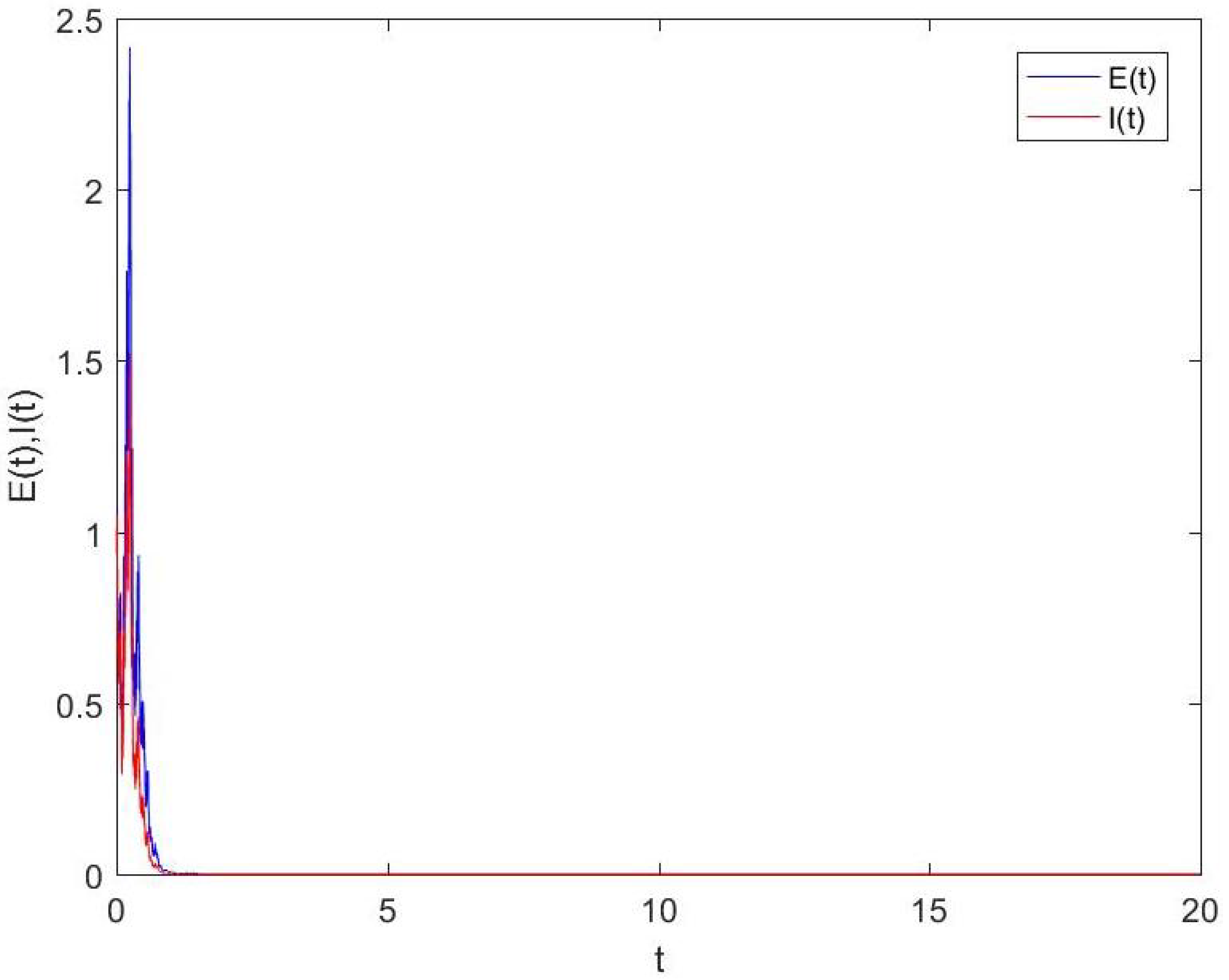
3.1. The Infected Person Persists
3.2. Extermination of Infectious Diseases
3.3. Numerical Simulation
4. Stationary Distribution
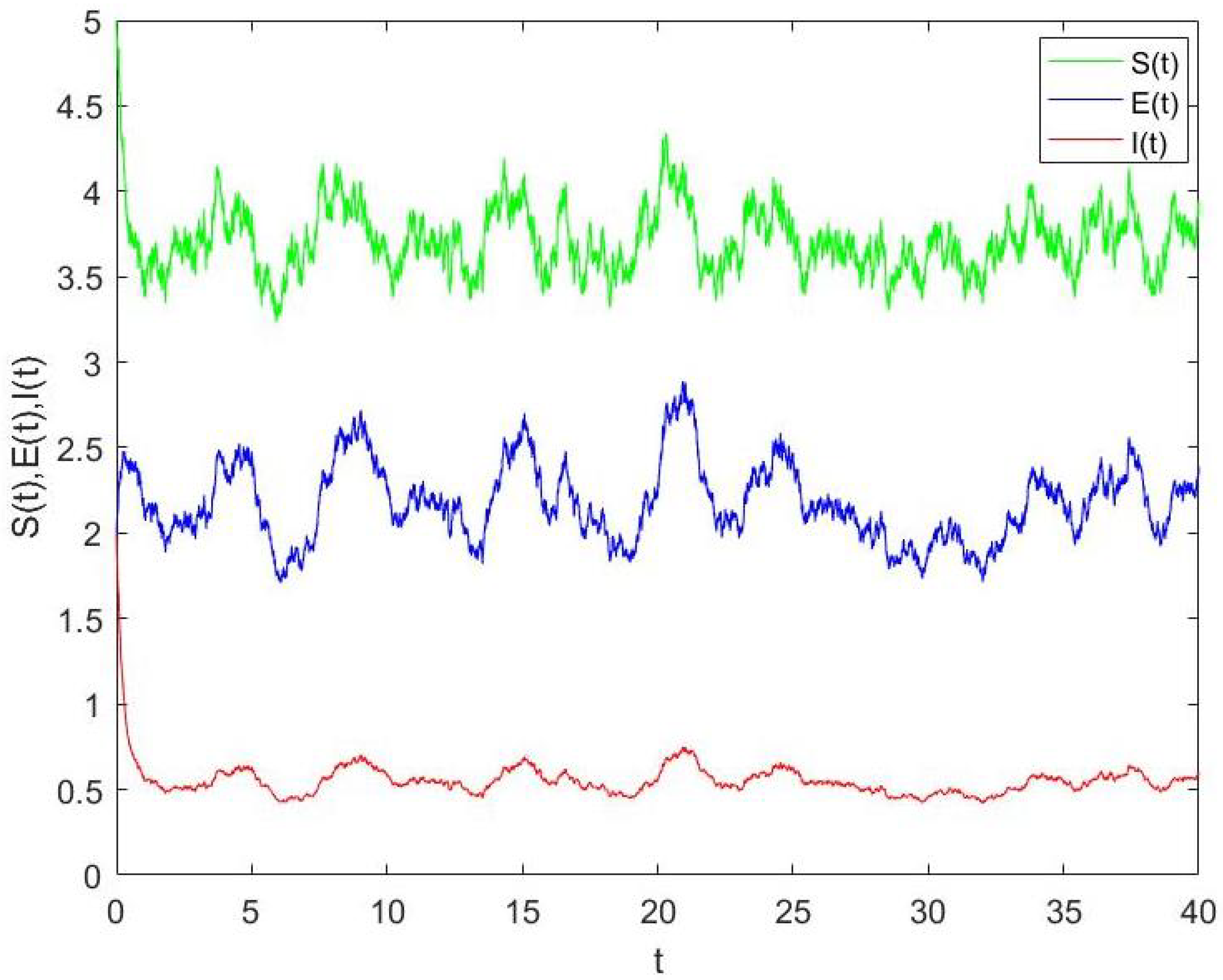
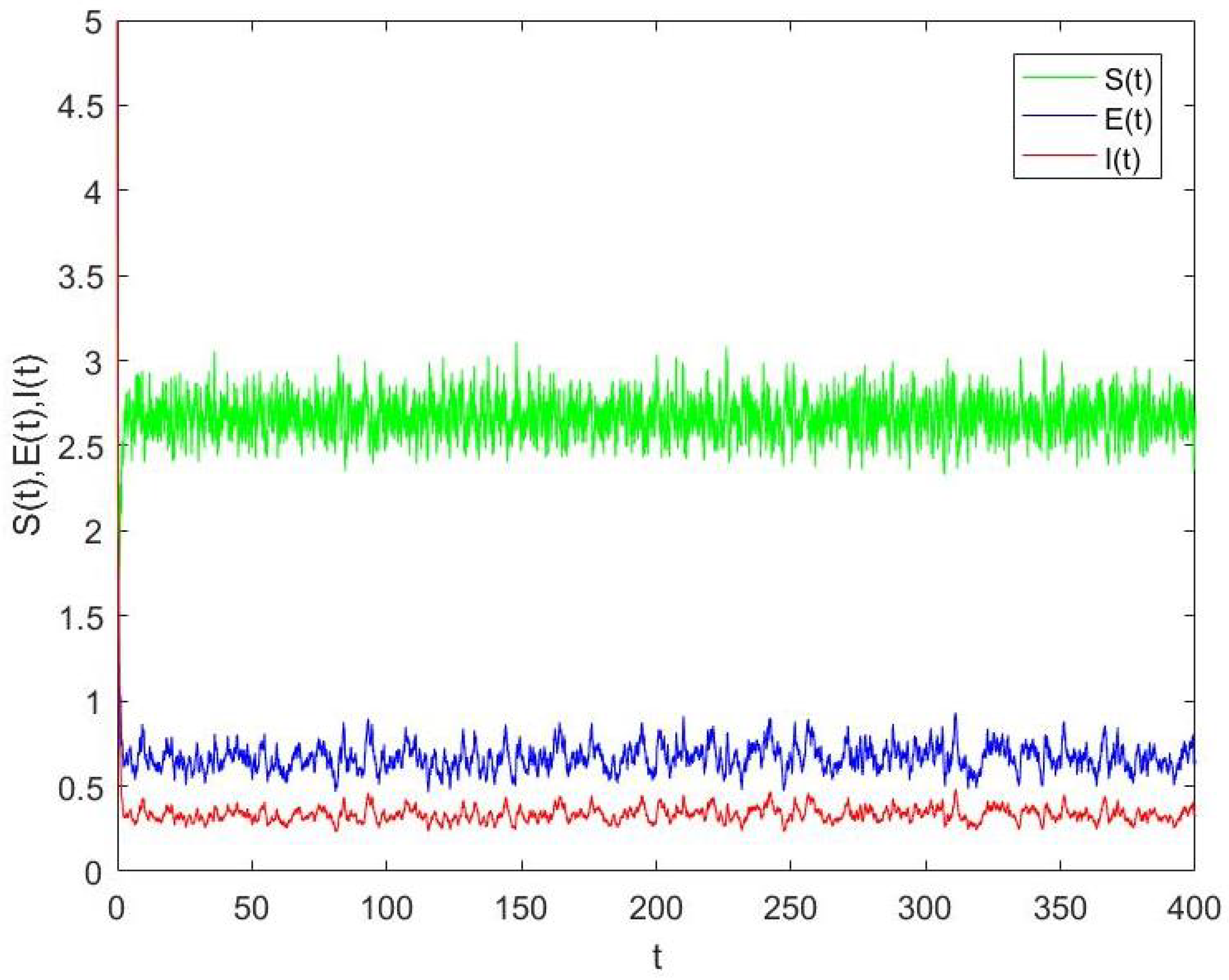
4.1. The Stationary Distribution and Its Ergodicity
4.2. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Ezekiel, D.; Iyase, S.A.; Anake, T.A. Stability Analysis of an SIR Infectious Disease Model. In Proceedings of the 2nd International Conference on Recent Trends in Applied Research (ICoRTAR 2021), Virtual, 8–9 October 2021. [Google Scholar]
- Abdelaziz, M.A.M.; Ismail, A.I.; Abdullah, F.A.; Mohd, M.H. Discrete-Time Fractional Order SIR Epidemic Model with Saturated Treatment Function. Int. J. Nonlinear Sci. Numer. Simul. 2020, 21, 397–424. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, R. Global Stability of an SIS Epidemic Model with Age of Vaccination. Differ. Equ. Dyn. Syst. 2022, 30, 1–22. [Google Scholar] [CrossRef]
- Kaddar, A. Stability analysis in a delayed SIR epidemic model with a saturated incidence rate. Nonlinear Anal. Model. Control. 2010, 3, 299–306. [Google Scholar] [CrossRef]
- Xu, C.; Yu, Y.; Ren, G. Dynamic analysis of a stochastic predator–prey model with Crowley–Martin functional response, disease in predator, and saturation incidence. J. Comput. Nonlinear Dyn. 2020, 15, 071004. [Google Scholar] [CrossRef]
- Shatanawi, W.; Arif, M.S.; Raza, A.; Rafiq, M.; Bibi, M.; Abbasi, J.N. Structure-Preserving Dynamics of Stochastic Epidemic Model with the Saturated Incidence Rate. Comput. Mater. Contin. 2020, 64, 797–811. [Google Scholar] [CrossRef]
- Liu, C.; Cui, R. Qualitative analysis on an SIRS reaction–diffusion epidemic model with saturation infection mechanism. Nonlinear Anal. Real World Appl. 2021, 62, 103364. [Google Scholar] [CrossRef]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. A COVID-19 epidemic model with latency period. Infect. Dis. Model. 2020, 5, 323–337. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Z.C.; Zhao, X.Q. Threshold dynamics of a time periodic reaction–diffusion epidemic model with latent period. J. Differ. Equ. 2015, 258, 3011–3036. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Zhao, X.Q. Dynamics of a climate-based periodic Chikungunya model with incubation period. Appl. Math. Model. 2020, 80, 151–168. [Google Scholar] [CrossRef]
- Dietz, K. The estimation of the basic reproduction number for infectious diseases. Stat. Methods Med. Res. 1993, 2, 23–41. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, D.; Hayat, T.; Alsaedi, A. Stationary distribution of an HIV model with general nonlinear incidence rate and stochastic perturbations. J. Frankl. Inst. 2019, 356, 6610–6637. [Google Scholar] [CrossRef]
- Liu, Q.; Kan, B.; Wang, Q.; Fang, Y. Cluster synchronization of Markovian switching complex networks with hybrid couplings and stochastic perturbations. Phys. Stat. Mech. Its Appl. 2019, 526, 120937. [Google Scholar] [CrossRef]
- Zeb, A.; Kumar, S.; Tesfay, A.; Kumar, A. A stability analysis on a smoking model with stochastic perturbation. Int. J. Numer. Methods Heat Fluid Flow 2021, 32, 915–930. [Google Scholar] [CrossRef]
- Allen, J.C.; Hobbs, S.L. Spectral estimation of non-stationary white noise. J. Frankl. Inst. 1997, 334, 99–116. [Google Scholar] [CrossRef]
- Allen, E.J.; Novosel, S.J.; Zhang, Z. Finite element and difference approximation of some linear stochastic partial differential equations. Stoch. Int. J. Probab. Stoch. Process. 1998, 64, 117–142. [Google Scholar] [CrossRef]
- Funaki, T.; Gao, Y.; Hilhorst, D. Existence and uniqueness of the entropy solution of a stochastic conservation law with a Q-Brownian motion. Math. Methods Appl. Sci. 2020, 43, 5860–5886. [Google Scholar] [CrossRef]
- Prakasa Rao, B.L.S. Parametric inference for stochastic differential equations driven by a mixed fractional Brownian motion with random effects based on discrete observations. Stoch. Anal. Appl. 2022, 40, 236–245. [Google Scholar] [CrossRef]
- Zhang, N.; Jia, G. W-symmetries of backward stochastic differential equations, preservation of simple symmetries and Kozlov’s theory. Commun. Nonlinear Sci. Numer. Simul. 2021, 93, 105527. [Google Scholar] [CrossRef]
- Raza, A.; Rafiq, M.; Baleanu, D.; Shoaib Arif, M.; Naveed, M.; Ashraf, K. Competitive numerical analysis for stochastic HIV/AIDS epidemic model in a two-sex population. IET Syst. Biol. 2019, 13, 305–315. [Google Scholar] [CrossRef]
- Raza, A.; Arif, M.S.; Rafiq, M.; Bibi, M.; Naveed, M.; Iqbal, M.U.; Butt, Z.; Naseem, H.A.; Abbasi, J.N. Numerical treatment for stochastic computer virus model. Comput. Model. Eng. Sci. 2019, 120, 445–465. [Google Scholar] [CrossRef]
- Briat, C.; Khammash, M. Robust and structural ergodicity analysis of stochastic biomolecular networks involving synthetic antithetic integral controllers. IFAC-PapersOnLine 2017, 50, 10918–10923. [Google Scholar] [CrossRef]
- Bachar, M.; Batzel, J.; Ditlevsen, S. Stochastic Biomathematical Models; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Kazeroonian, A.; Theis, F.J.; Hasenauer, J. Modeling of stochastic biological processes with non-polynomial propensities using non-central conditional moment equation. IFAC Proc. Vol. 2014, 47, 1729–1735. [Google Scholar] [CrossRef] [Green Version]
- Jorge, J. On the average dynamical behaviour of stochastic population models. IFAC Proc. Vol. 2014, 47, 5270–5275. [Google Scholar]
- Hening, A.; Tran, K.Q. Harvesting and seeding of stochastic populations: Analysis and numerical approximation. J. Math. Biol. 2020, 81, 65–112. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Li, W.; Liu, M.; Wang, K. Dynamics of a stochastic Holling II one-predator two-prey system with jumps. Phys. Stat. Mech. Its Appl. 2015, 421, 571–582. [Google Scholar] [CrossRef]
- Catuogno, P.; Olivera, C. Time-dependent tempered generalized functions and Itô’s formula. Appl. Anal. 2014, 93, 539–550. [Google Scholar] [CrossRef] [Green Version]
- Li, J. Orbital Stability of Peakons for the Modified Camassa—Holm Equation. Acta Math. Sin. Engl. Ser. 2022, 38, 148–160. [Google Scholar] [CrossRef]
- Fu, T.; Wang, Y. Orbital stability around the primary of a binary asteroid system. J. Guid. Control Dyn. 2021, 44, 1607–1620. [Google Scholar] [CrossRef]
- Zhang, T.; Teng, Z. Pulse vaccination delayed SEIRS epidemic model with saturation incidence. Appl. Math. Model. 2008, 32, 1403–1416. [Google Scholar] [CrossRef]
- Rajasekar, S.P.; Pitchaimani, M.; Zhu, Q. Dynamic threshold probe of stochastic SIR model with saturated incidence rate and saturated treatment function. Phys. Stat. Mech. Its Appl. 2019, 535, 122300. [Google Scholar] [CrossRef]
- Faranda, D.; Alberti, T. Modeling the second wave of COVID-19 infections in France and Italy via a stochastic SEIR model. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 111101. [Google Scholar] [CrossRef] [PubMed]
- Han, B.; Jiang, D.; Hayat, T.; Alsaedi, A.; Ahmad, B. Stationary distribution and extinction of a stochastic staged progression AIDS model with staged treatment and second-order perturbation. Chaos Solitons Fractals 2020, 140, 110238. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Liu, Y.J.; Chen, A.; Tong, S.; Chen, C.L. Integral barrier Lyapunov function-based adaptive control for switched nonlinear systems. Sci. China Inf. Sci. 2020, 63, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Cao, W.; Zhu, Q. Razumikhin-type theorem for pth exponential stability of impulsive stochastic functional differential equations based on vector Lyapunov function. Nonlinear Anal. Hybrid Syst. 2021, 39, 100983. [Google Scholar] [CrossRef]
- Wang, R.; Zong, G.; Shen, H.; Shi, K. A new-gain analysis framework for discrete-time switched systems based on predictive Lyapunov function. Int. J. Robust Nonlinear Control. 2022, 32, 101–125. [Google Scholar] [CrossRef]
- Lahrouz, A.; Omari, L. Extinction and stationary distribution of a stochastic SIRS epidemic model with non-linear incidence. Stat. Probab. Lett. 2013, 83, 960–968. [Google Scholar] [CrossRef]
- Hendricks, W.J. The stationary distribution of an interesting Markov chain. J. Appl. Probab. 1972, 9, 231–233. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, X.; Din, A. Stationary distribution and extinction of a stochastic SEIQ epidemic model with a general incidence function and temporary immunity. AIMS Math. 2021, 6, 12359–12378. [Google Scholar] [CrossRef]
- Chen, Z.; Gan, S. Convergence and stability of the backward Euler method for jump–diffusion SDEs with super-linearly growing diffusion and jump coefficients. J. Comput. Appl. Math. 2020, 363, 350–369. [Google Scholar] [CrossRef]
- Bayram, M.; Partal, T.; Buyukoz, G.O. Numerical methods for simulation of stochastic differential equations. Adv. Differ. Equ. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Yousef, A. A New Approach to Compare the Strong Convergence of the Milstein Scheme with the Approximate Coupling Method. Fractal Fract. 2022, 6, 339. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Tan, X. Dynamics Analysis of a Class of Stochastic SEIR Models with Saturation Incidence Rate. Symmetry 2022, 14, 2414. https://doi.org/10.3390/sym14112414
Liu P, Tan X. Dynamics Analysis of a Class of Stochastic SEIR Models with Saturation Incidence Rate. Symmetry. 2022; 14(11):2414. https://doi.org/10.3390/sym14112414
Chicago/Turabian StyleLiu, Pengpeng, and Xuewen Tan. 2022. "Dynamics Analysis of a Class of Stochastic SEIR Models with Saturation Incidence Rate" Symmetry 14, no. 11: 2414. https://doi.org/10.3390/sym14112414



