MHD and Thermal Slip Effects on Viscous Fluid over Symmetrically Vertical Heated Plate in Porous Medium: Keller Box Analysis
Abstract
:1. Introduction and Literature Review
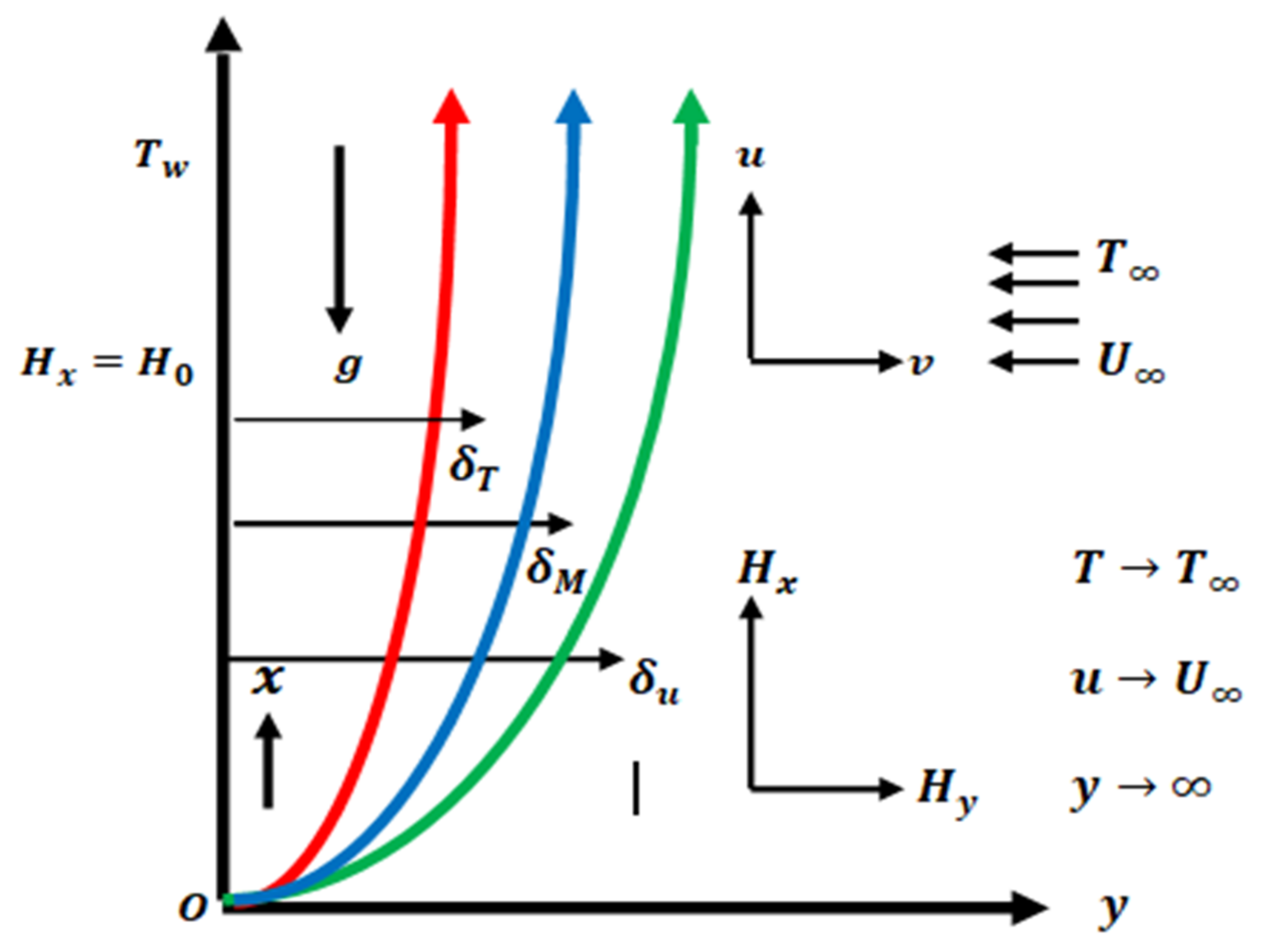
2. Flow Problem and Mathematical Description
3. The Similarity Transformation and Stream Function Formulation
4. The Solution and Computing Techniques
5. The Arrangement of Difference Equations in Vector Notation/Matrix
6. Analysis and Discussion of Results
7. Conclusions
- It is obtained that the velocity profile increased at = but decreased at = with a prominent variation. Due to slip flow, the frictional resistance between the viscous fluid and the surface is eliminated, and the fluid velocity booststhe heat transfer and skin friction along the surface;
- The prominent variations are obtained in the magnetic profile for each value of R, and the prominent thermalslip response is observed in temperatures with a strong magnetic field. As the magnetic Prandtl number increases, the viscosity of fluid increases, and fluid becomes thicker, and consequently, the boundary layer thickness decreases;
- It is concluded that the skin friction is increased at = but the smaller quantity of skin friction is obtained at = withbuoyancy and magnetic force. With the increase in value of , the magnetic field becomes stronger along the surface, which is a clear indication that the Lorentz force is more effective in this case;
- It is presumed that skin friction is maximum at smaller = but minimum at higher = in the presence of temperature slip. Increasing means the medium is more porous, and the fluid permeability in the porous layer is increased and thus yields resistance in the fluid flow;
- Due to the strong buoyancy number which acts like a pressure gradient and dominatesover the resistance, skin friction is increased, and slight changes in heatand magnetic intensityare noted.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| , | Velocity along and normal to surface (m s−1) | Ambienttemperature (K) | |
| , | Magnetic coordinates of velocities in direction (Tesla) | Renolds number | |
| Dynamic viscosity (kg m−1 s−1) | Grashof number | ||
| Constant applied magnetic field | Nusselt number | ||
| Wall temperature (K) | Skin friction | ||
| Radiative heat flux | Magnetic intensity | ||
| Thermal slip factor | Local Darcy number | ||
| Kinematicalviscosity (m2 s−1) | |||
| Greek symbols | |||
| Fluid density (kg m−3) | Thermal conductivity parameter | ||
| Gravity acceleration (m s−2) | Magnetic force parameter | ||
| Coefficient of thermalexpansion (K−1) | Mixedconvective number | ||
| Magnetic diffusivity (H m−1) | Dimensionless temperature | ||
| Thermaldiffusivity (m2 s−1) | MagneticPrandtl parameter | ||
| T | Fluid temperature (K) | Pr | Prandtl parameter |
| Specific heat (J kg−1 K−1) | Magnetic permeability | ||
| Characteristic length | Similarity variable | ||
| Free stream velocity (m s−1) | Thermal conductivity parameter | ||
| Electrical conductivity (s m−1) | permeability of porous medium | ||
| Porous medium parameter | Thermal slip parameter | ||
| Constant temperature | Radiation parameter | ||
Appendix A
References
- Mukhopadhyay, S. Effect of thermal radiation on unsteady mixed convection flow and heat transfer over a porous stretching surface in porous medium. Int. J. Heat Mass Transf. 2009, 52, 3261–3265. [Google Scholar] [CrossRef]
- Sarada, K.; Gowda, R.J.P.; Sarris, I.E.; Kumar, R.N.; Prasannakumara, B.C. Effect of magnetohydrodynamics on heat transfer behaviour of a non-Newtonian fluid flow over a stretching sheet under local thermal non-equilibrium condition. Fluids 2021, 6, 264. [Google Scholar] [CrossRef]
- Abbas, A.; Shafqat, R.; Jeelani, M.B.; Alharthi, N.H. Significance of Chemical Reaction and Lorentz Force on Third-Grade Fluid Flow and Heat Transfer with Darcy–Forchheimer Law over an Inclined Exponentially Stretching Sheet Embedded in a Porous Medium. Symmetry 2022, 14, 779. [Google Scholar] [CrossRef]
- Kumar, A. Numerical study of effect of induced magnetic field on transient natural convection over a vertical cone. Alex. Eng. J. 2016, 55, 1211–1223. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharyya, K.; Mukhopadhyay, S.; Layek, G.C. Similarity solution of mixed convective boundary layer slip flow over a vertical plate. Ain Shams Eng. J. 2013, 4, 299–305. [Google Scholar] [CrossRef] [Green Version]
- Muhammad, A.; Chamkha, A.J.; Iqbal, S.; Ahmad, M. Effects of temperature-dependent viscosity and thermal conductivity on mixed convection flow along a magnetized vertical surface. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 1580–1592. [Google Scholar] [CrossRef] [Green Version]
- Chawla, S.S. Magnetohydrodynamic oscillatory flow past a semi-infinite flat plate. Int. J. Non-Linear Mech. 1971, 6, 117–134. [Google Scholar] [CrossRef]
- Cheng, W.; Liu, Y.L.; Yang, F. A Modified Regularization Method for a Spherically Symmetric Inverse Heat Conduction Problem. Symmetry 2022, 14, 2102. [Google Scholar] [CrossRef]
- Chen, J.; Du, W.; Kong, B.; Wang, Z.; Cao, J.; Wang, W.; Yan, Z. Numerical Investigation on the Symmetric Breakup of Bubble within a Heated Microfluidic Y-Junction. Symmetry 2022, 14, 1661. [Google Scholar] [CrossRef]
- Garia, R.; Rawat, S.K.; Kumar, M.; Yaseen, M. Hybrid nanofluid flow over two different geometries with Cattaneo–Christov heat flux model and heat generation: A model with correlation coefficient and probable error. Chin. J. Phys. 2021, 74, 421–439. [Google Scholar] [CrossRef]
- Yaseen, M.; Rawat, S.K.; Kumar, M. Cattaneo–Christov heat flux model in Darcy–Forchheimer radiative flow of MoS2–SiO2/kerosene oil between two parallel rotating disks. J. Therm. Anal. Calorim. 2022, 147, 10865–10887. [Google Scholar] [CrossRef]
- Yaseen, M.; Rawat, S.K.; Shafiq, A.; Kumar, M.; Nonlaopon, K. Analysis of Heat Transfer of Mono and Hybrid Nanofluid Flow between Two Parallel Plates in a Darcy Porous Medium with Thermal Radiation and Heat Generation/Absorption. Symmetry 2022, 14, 1943. [Google Scholar] [CrossRef]
- Yaseen, M.; Rawat, S.K.; Kumar, M. Falkner–Skan Problem for a Stretching or Shrinking Wedge with Nanoparticle Aggregation. J. Heat Transf. 2022, 144, 102501. [Google Scholar] [CrossRef]
- Agrwal, A.; Kasana, V. [Fesipmim] Cl as highly efficient and reusable catalyst for solventless synthesis of dihydropyridine derivatives through Hantzsch reaction. J. Chem. Sci. 2020, 132, 67. [Google Scholar] [CrossRef]
- Agrwal, A.; Kumar, V.; Kasana, V. Preparation and application of highly efficient and reusable TBAPIL@ Si (CH2)3@nano-silica-based nano-catalyst for preparation of benzoxanthene derivatives. J. Iran. Chem. Soc. 2021, 18, 2583–2595. [Google Scholar] [CrossRef]
- Chaudhary, P.; Agrwal, A.; Sharma, D.K.; Kumar, V. Synthesis and screen-printing of sol-gel developed pure and Yb-doped ZnO films towards optoelectronic analysis. J. Sol-Gel Sci. Technol. 2022, 104, 425–433. [Google Scholar] [CrossRef]
- Chamkha, A.J. On laminar hydromagnetic mixed convection flow in a vertical channel with symmetric and asymmetric wall heating conditions. Int. J. Heat Mass Transf. 2002, 45, 2509–2525. [Google Scholar] [CrossRef]
- Valentino, M.; Tran, L.; Ricklick, M.; Kapat, J. Comparison of heat transfer and friction augmentation for symmetric and non-symmetric wedge turbulators on two opposite walls. In Proceedings of the 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, San Diego, CA, USA, 31 July–3 August 2011; p. 6021. [Google Scholar]
- Sinanoglu, A.; Karaca, I.Y.; Tokmak, F.; Senlik, T. Existence of three symmetric positive solutions for a second-order multi-point boundary value problem on time scales. Adv. Differ. Equ. 2014, 2014, 81. [Google Scholar] [CrossRef] [Green Version]
- Mahmood, M.; Asghar, S.; Hossain, M.A. Hydromagnetic flow of viscous incompressible fluid past a wedge with permeable surface. ZAMM-J. Appl. Math. Mech. Z. Für Angew. Math. Mech. Appl. Math. Mech. 2009, 89, 174–188. [Google Scholar] [CrossRef]
- Ilyas, A.; Ashraf, M.; Rashad, A.M. Periodical analysis of convective heat transfer along electrical conducting cone embedded in porous medium. Arab. J. Sci. Eng. 2021, 47, 8177–8188. [Google Scholar] [CrossRef]
- Al-Mdallal, Q.; Prasad, V.R.; Basha, H.T.; Sarris, I.; Akkurt, N. Keller box simulation of magnetic pseudoplastic nano-polymer coating flow over a circular cylinder with entropy optimisation. Comput. Math. Appl. 2022, 118, 132–158. [Google Scholar] [CrossRef]
- Islam, M.T. Heat Transfer through Parallel Plate Microchannels at Symmetric and Asymmetric Constant Wall Temperature. Acad. J. Appl. Math. Sci. 2018, 4, 22–33. [Google Scholar]
- Wang, C.Y. Boundary layers on rotating cones, discs and axisymmetric surfaces with a concentrated heat source. Acta Mech. 1990, 81, 245–251. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Mondal, I.C.; Chamkha, A.J. Casson fluid flow and heat transfer past a symmetric wedge. Heat Transf. Asian Res. 2013, 42, 665–675. [Google Scholar] [CrossRef]
- Ullah, Z.; Ashraf, M.; Sarris, I.E.; Karakasidis, T.E. The Impact of Reduced Gravity on Oscillatory Mixed Convective Heat Transfer around a Non-Conducting Heated Circular Cylinder. Appl. Sci. 2022, 12, 5081. [Google Scholar] [CrossRef]
- Murdock, J.W. The solution of sharp-cone boundary-layer equations in the plane of symmetry. J. Fluid Mech. 1972, 54, 665–678. [Google Scholar] [CrossRef]
- Charvátová, H.; Janáčová, D.; Kolomazník, K. Study of non-stationary Heat conduction in a Plane Plate for Symmetric and Asymmetric Problem. WSEAS Trans. Heat Mass Transf. 2011, 6, 11–20. [Google Scholar]
- Aldoss, T.; Al-Nimr, M.; Jarrah, M.; Al-Sha, B. Magnetohydrodynamic mixed convection from a vertical plate embedded in a porous medium. Numer. Heat Transf. Part A Appl. 1995, 28, 635–645. [Google Scholar] [CrossRef]
- Ullah, Z.; Yasmin, S.; Younis, J.; Abdullah, A.; Abbas, S.; Shah, A. Dynamics of Unsteady Flow of Chemically Reactive Upper-Convected Maxwell Fluid with Temperature-Dependent Viscosity: Keller Box Analysis. Math. Probl. Eng. 2022, 2022, 5344759. [Google Scholar] [CrossRef]
- Rees, D.A.S.; University of Bath, Bath, UK. The numerical solution of ordinary and partial differential equations using the Keller-box method. Private communication, 1998. [Google Scholar]
- Hirschhorn, J.; Madsen, M.; Mastroberardino, A.; Siddique, J.I. Magnetohydrodynamic boundary layer slip flow and heat transfer of power law fluid over a flat plate. J. Appl. Fluid Mech. 2015, 9, 11–17. [Google Scholar] [CrossRef]
- Sarada, K.; Gamaoun, F.; Abdulrahman, A.; Paramesh, S.O.; Kumar, R.; Prasanna, G.D.; Gowda, R.P. Impact of exponential form of internal heat generation on water-based ternary hybrid nanofluid flow by capitalizing non-Fourier heat flux model. Case Stud. Therm. Eng. 2022, 38, 102332. [Google Scholar]
- Kumar, R.N.; Gamaoun, F.; Abdulrahman, A.; Chohan, J.S.; Gowda, R.P. Heat transfer analysis in three-dimensional unsteady magnetic fluid flow of water-based ternary hybrid nanofluid conveying three various shaped nanoparticles: A comparative study. Int. J. Mod. Phys. B 2022, 36, 2250170. [Google Scholar] [CrossRef]
- Sunitha, M.; Gamaoun, F.; Abdulrahman, A.; Malagi, N.S.; Singh, S.; Gowda, R.J.; Gowda, R.P. An efficient analytical approach with novel integral transform to study the two-dimensional solute transport problem. Ain Shams Eng. J. 2022, 101878. [Google Scholar] [CrossRef]
- Asogwa, K.K.; Alsulami, M.D.; Prasannakumara, B.C.; Muhammad, T. Double diffusive convection and cross diffusion effects on Casson fluid over a Lorentz force driven Riga plate in a porous medium with heat sink: An analytical approach. Int. Commun. Heat Mass Transf. 2022, 131, 105761. [Google Scholar] [CrossRef]
- Punith Gowda, R.J.; Sarris, I.E.; Naveen Kumar, R.; Kumar, R.; Prasannakumara, B.C. A Three-Dimensional Non-Newtonian Magnetic Fluid Flow Induced due to Stretching of the Flat Surface with Chemical Reaction. J. Heat Transf. 2022, 144, 113602. [Google Scholar] [CrossRef]
- Punith Gowda, R.J.; Naveen Kumar, R.; Jyothi, A.M.; Prasannakumara, B.C.; Sarris, I.E. Impact of binary chemical reaction and activation energy on heat and mass transfer of marangoni driven boundary layer flow of a non-Newtonian nanofluid. Processes 2021, 9, 702. [Google Scholar] [CrossRef]








| Mehmood et al. [20] | Ilyas et al. [21] | Present Analysis | |
|---|---|---|---|
| 0.1 | 7.948792987522230 | 0.469004024822659 | 0.872763001306980 |
| 1.0 | 5.444255951510843 | 0.411585485704276 | 0.459271245066785 |
| 3.0 | 3.650283616517952 | 0.363853736639147 | 0.230932235434102 |
| 6.0 | 2.679220347371918 | 0.333775556097965 | 0.134087127559919 |
| 0.1 | 1.570888903060684 | 0.250664877643679 | 0.287615619132488 |
| 0.4 | 1.020219932907417 | 0.221789130911155 | 0.257375444745247 |
| 0.7 | 0.693273907560712 | 0.198738070735411 | 0.231620888575782 |
| 1.0 | 0.504794793668375 | 0.181464431569163 | 0.211274951578891 |
| 0.1 | 1.383648476977060 | 0.376890740587770 | 0.133671961466489 |
| 1.0 | 1.694272623828378 | 0.412795831386895 | 0.124460477822591 |
| 3.0 | 2.091203704461853 | 0.454926644631236 | 0.113299983497299 |
| 5.0 | 2.335649688218721 | 0.478692890887229 | 0.106502575270043 |
| Hirschhorn et al. [32] | Present Analysis | |
|---|---|---|
| 0.0 | 0.34768 | 0.34174 |
| 0.3 | 0.31484 | 0.32909 |
| 0.6 | 0.28767 | 0.31976 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, Z.; Bilal, M.; Sarris, I.E.; Hussanan, A. MHD and Thermal Slip Effects on Viscous Fluid over Symmetrically Vertical Heated Plate in Porous Medium: Keller Box Analysis. Symmetry 2022, 14, 2421. https://doi.org/10.3390/sym14112421
Ullah Z, Bilal M, Sarris IE, Hussanan A. MHD and Thermal Slip Effects on Viscous Fluid over Symmetrically Vertical Heated Plate in Porous Medium: Keller Box Analysis. Symmetry. 2022; 14(11):2421. https://doi.org/10.3390/sym14112421
Chicago/Turabian StyleUllah, Zia, Muhammad Bilal, Ioannis E. Sarris, and Abid Hussanan. 2022. "MHD and Thermal Slip Effects on Viscous Fluid over Symmetrically Vertical Heated Plate in Porous Medium: Keller Box Analysis" Symmetry 14, no. 11: 2421. https://doi.org/10.3390/sym14112421
APA StyleUllah, Z., Bilal, M., Sarris, I. E., & Hussanan, A. (2022). MHD and Thermal Slip Effects on Viscous Fluid over Symmetrically Vertical Heated Plate in Porous Medium: Keller Box Analysis. Symmetry, 14(11), 2421. https://doi.org/10.3390/sym14112421








