A Reliable Way to Deal with the Coupled Fractional Korteweg-De Vries Equations within the Caputo Operator
Abstract
1. Introduction
2. Preliminaries
- 1.
- 2.
- 3.
3. Idea of LRPS
- and for each
- .
4. Numerical Problem
4.1. Problem
4.2. Problem
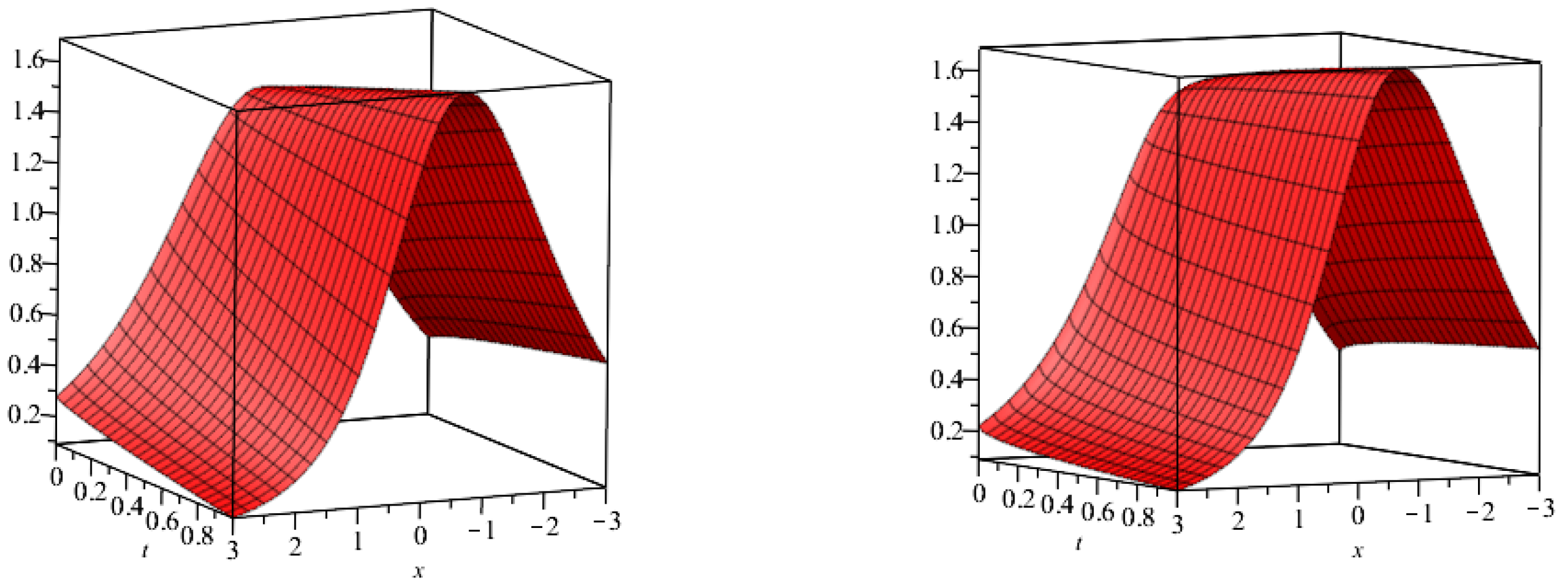
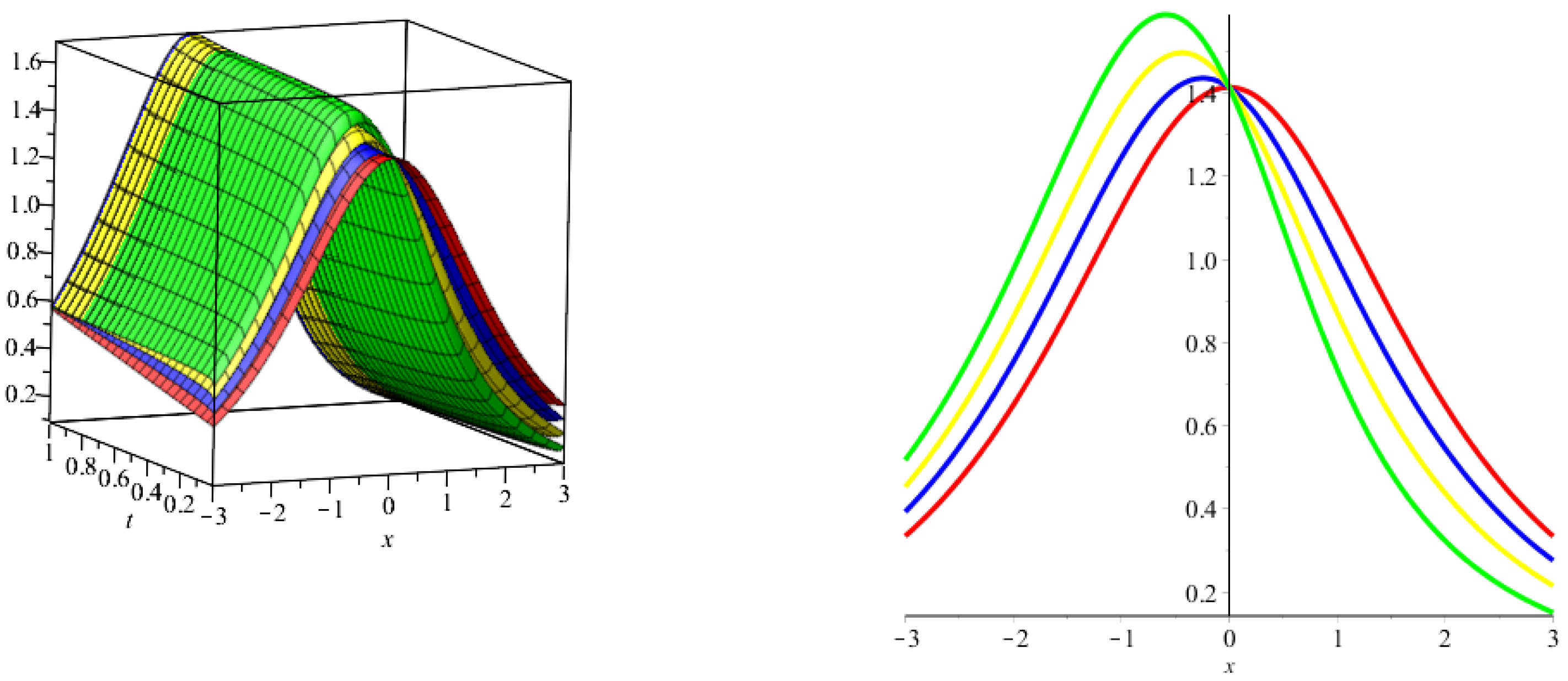
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Odibat, Z.M.; Momani, S. Application of Variational Iteration Method to Nonlinear Differential Equations of Fractional Order. Int. J. Nonlinear Sci. Numer. Simul. 2006, 7, 27–34. [Google Scholar] [CrossRef]
- Razminia, K.; Razminia, A.; Machado, J.A.T. Analytical Solution of Fractional Order Diffusivity Equation With Wellbore Storage and Skin Effects. J. Comput. Nonlinear Dyn. 2016, 11, 011006. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N. Analysis of Fractional Differential Equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef]
- Diethelm, K. An algorithm for the numerical solution of differential equations of fractional order. Electron. Trans. Numer. Anal. 1997, 5, 1–6. [Google Scholar]
- Luchko, Y.; Srivastava, H. The exact solution of certain differential equations of fractional order by using operational calculus. Comput. Math. Appl. 1995, 29, 73–85. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Kumar, S.; Singh, B.P. Numerical computation of nonlinear shock wave equation of fractional order. Ain Shams Eng. J. 2015, 6, 605–611. [Google Scholar] [CrossRef]
- Bulut, H.; Belgacem, F.B.M.; Baskonus, H.M. Some new analytical solutions for the nonlinear time-fractional KdV-Burgers-Kuramoto equation. Adv. Math. Stat. Sci. 2015, 2015, 118–129. [Google Scholar]
- Kumar, D.; Singh, J.; Baleanu, D. Numerical Computation of a Fractional Model of Differential-Difference Equation. J. Comput. Nonlinear Dyn. 2016, 11, 061004. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Nieto, J.J. A Reliable Algorithm for a Local Fractional Tricomi Equation Arising in Fractal Transonic Flow. Entropy 2016, 18, 206. [Google Scholar] [CrossRef]
- Choudhary, A.; Kumar, D.; Singh, J. Numerical simulation of a fractional model of temperature distribution and heat flux in the semi infinite solid. Alex. Eng. J. 2016, 55, 87–91. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Morales-Delgado, V.F.; Taneco-Hernández, M.A.; Baleanu, D.; Escobar-Jiménez, R.F.; Al Qurashi, M.M. Analytical solutions of the electrical RLC circuit via Liouville-Caputo operators with local and non-local kernels. Entrop 2016, 18, 402. [Google Scholar] [CrossRef]
- Coronel-Escamilla, A.; Gómez-Aguilar, J.F.; Baleanu, D.; Escobar-Jiménez, R.F.; Olivares-Peregrino, V.H.; Abúndez-Pliego, A. Formulation of Euler-Lagrange and Hamilton equations involving fractional operators with regular kernel. Adv. Differ. Equat. 2016, 2016, 283. [Google Scholar] [CrossRef]
- Dai, B.; Zhang, B.; Niu, Z.; Feng, Y.; Liu, Y.; Fan, Y. A Novel Ultrawideband Branch Waveguide Coupler With Low Amplitude Imbalance. IEEE Trans. Microw. Theory Tech. 2022, 70, 3838–3846. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, B.; Liu, Y.; Niu, Z.; Fan, Y.; Chen, X. A D-Band Manifold Triplexer With High Isolation Utilizing Novel Waveguide Dual-Mode Filters. IEEE Trans. Terahertz Sci. Technol. 2022, 12, 678–681. [Google Scholar] [CrossRef]
- Kovalnogov, V.N.; Kornilova, M.I.; Khakhalev, Y.A.; Generalov, D.A.; Simos, T.; Tsitouras, C. New family for Runge-Kutta-Nyström pairs of orders 6(4) with coefficients trained to address oscillatory problems. Math. Methods Appl. Sci. 2022, 45, 7715–7727. [Google Scholar] [CrossRef]
- Hao, R.-B.; Lu, Z.-Q.; Ding, H.; Chen, L.-Q. A nonlinear vibration isolator supported on a flexible plate: Analysis and experiment. Nonlinear Dyn. 2022, 108, 941–958. [Google Scholar] [CrossRef]
- Luo, G.; Yuan, Q.; Li, J.; Wang, S.; Yang, F. Artificial Intelligence Powered Mobile Networks: From Cognition to Decision. IEEE Netw. 2022, 36, 136–144. [Google Scholar] [CrossRef]
- Wang, J.; Tian, J.; Zhang, X.; Yang, B.; Liu, S.; Yin, L.; Zheng, W. Control of Time Delay Force Feedback Teleoperation System with Finite Time Convergence. Front. Neurorobot. 2022, 16, 877069. [Google Scholar] [CrossRef]
- Lu, S.; Ban, Y.; Zhang, X.; Yang, B.; Liu, S.; Yin, L.; Zheng, W. Adaptive control of time delay teleoperation system with uncertain dynamics. Front. Neurorobot. 2022, 16, 928863. [Google Scholar] [CrossRef]
- Abdilraze, A. Adomian Decomposition Method: Convergence Analysis and Numerical Approximations. Master’s Dissertation, McMaster University Hamilton, Hamilton, ON, Canada, 2008. [Google Scholar]
- Khan, A.; Khan, T.S.; Syam, M.I.; Khan, H. Analytical solutions of time-fractional wave equation by double Laplace transform method. Eur. Phys. J. Plus 2019, 134, 163. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, S.; Yan, S.-P. Residual Power Series Method for Fractional Diffusion Equations. Fundam. Informaticae 2017, 151, 213–230. [Google Scholar]
- Baleanu, D.; Ghanbari, B.; Asad, J.H.; Jajarmi, A.; Pirouz, H.M. Planar System-Masses in an Equilateral Triangle: Numerical Study within Fractional Calculus. Comput. Model. Eng. Sci. 2020, 124, 953–968. [Google Scholar] [CrossRef]
- Zhang, Y.-Z.; Yang, A.-M.; Long, Y. Initial boundary value problem for fractal heat equation in the semi-infinite region by Yang-Laplace transform. Therm. Sci. 2014, 18, 677–681. [Google Scholar] [CrossRef]
- Spiga, G.; Spiga, M. Two-Dimensional Transient Solutions for Crossflow Heat Exchangers With Neither Gas Mixed. J. Heat Transf. 1987, 109, 281–286. [Google Scholar] [CrossRef]
- Hassan, H.E.; Kilicman, A. A note on solutions of wave, Laplace’s and heat equations with convolution terms by using a double Laplace transform. Appl. Math. Lett. 2008, 21, 1324–1329. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel: Theory and application to heat transfer model. Therm Sci. 2016, 20, 763–785. [Google Scholar] [CrossRef]
- Alshehry, A.S.; Imran, M.; Khan, A.; Shah, R.; Weera, W. Fractional View Analysis of Kuramoto–Sivashinsky Equations with Non-Singular Kernel Operators. Symmetry 2022, 14, 1463. [Google Scholar] [CrossRef]
- Botmart, T.; Agarwal, R.P.; Naeem, M.; Khan, A.; Shah, R. On the solution of fractional modified Boussinesq and approximate long wave equations with non-singular kernel operators. AIMS Math. 2022, 7, 12483–12513. [Google Scholar] [CrossRef]
- Alaoui, M.K.; Nonlaopon, K.; Zidan, A.M.; Khan, A.; Shah, R. Analytical Investigation of Fractional-Order Cahn–Hilliard and Gardner Equations Using Two Novel Techniques. Mathematics 2022, 10, 1643. [Google Scholar] [CrossRef]
- Shah, N.A.; Hamed, Y.S.; Abualnaja, K.M.; Chung, J.-D.; Shah, R.; Khan, A. A Comparative Analysis of Fractional-Order Kaup–Kupershmidt Equation within Different Operators. Symmetry 2022, 14, 986. [Google Scholar] [CrossRef]
- Shah, N.A.; El-Zahar, E.R.; Akgül, A.; Khan, A.; Kafle, J. Analysis of Fractional-Order Regularized Long-Wave Models via a Novel Transform. J. Funct. Spaces 2022, 2022, 2754507. [Google Scholar] [CrossRef]
- Alharthi, M.R.; Alharbey, R.A.; El-Tantawy, S.A. Novel analytical approximations to the nonplanar Kawahara equation and its plasma applications. Eur. Phys. J. Plus 2022, 137, 1172. [Google Scholar] [CrossRef]
- Alyousef, H.A.; Salas, A.H.; Matoog, R.T.; El-Tantawy, S.A. On the analytical and numerical approximations to the forced damped Gardner Kawahara equation and modeling the nonlinear structures in a collisional plasma. Phys. Fluids 2022, 34, 103105. [Google Scholar] [CrossRef]
- Alyousef, H.A.; Salas, A.H.; Alharthi, M.R.; El-Tantawy, S.A. New Periodic and Localized Traveling Wave Solutions to a Kawahara-Type Equation: Applications to Plasma Physics. Complexity 2022, 2022, 9942267. [Google Scholar] [CrossRef]
- Naeem, M.; Zidan, A.; Nonlaopon, K.; Syam, M.; Al-Zhour, Z.; Shah, R. A New Analysis of Fractional-Order Equal-Width Equations via Novel Techniques. Symmetry 2021, 13, 886. [Google Scholar] [CrossRef]
- Iqbal, N.; Akgül, A.; Shah, R.; Bariq, A.; Al-Sawalha, M.M.; Ali, A. On Solutions of Fractional-Order Gas Dynamics Equation by Effective Techniques. J. Funct. Spaces 2022, 2022, 3341754. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Zidan, A.M.; Yao, S.-W.; Shah, R.; Inc, M. The comparative study for solving fractional-order Fornberg-Whitham equation via ρ-Laplace transform. Symmetry 2021, 13, 784. [Google Scholar] [CrossRef]
- Qasim, A.F.; Al-Amr, M.O. Approximate solution of the Kersten-Krasil’shchik coupled Kdv-mKdV system via reduced differential transform method. Eurasian J. Sci. Eng. 2018, 4, 1–9. [Google Scholar]
- Kalkanli, A.K.; Sakovich, S.Y.; Yurdusen, I. Integrability of Kersten-Krasil’shchik coupled KdV-mKdV equations: Singularity analysis and Lax pair. J. Math. Phys. 2003, 44, 1703–1708. [Google Scholar] [CrossRef]
- Hon, Y.C.; Fan, E.G. Solitary wave and doubly periodic wave solutions for the Kersten-Krasil’shchik coupled KdV-mKdV system. Chaos Solitons Fract. 2004, 19, 1141–1146. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Khan, A.; Ababneh, O.Y.; Botmart, T. Fractional view analysis of Kersten-Krasil’shchik coupled KdV-mKdV systems with non-singular kernel derivatives. AIMS Math. 2022, 7, 18334–18359. [Google Scholar] [CrossRef]
- Hietarinta, J. Introduction to the Hirota bilinear method. In Integrability of Nonlinear Systems; Springer: Berlin/Heidelberg, Germany, 1997; pp. 95–103. [Google Scholar]
- Shah, N.A.; Agarwal, P.; Chung, J.D.; El-Zahar, E.R.; Hamed, Y.S. Analysis of optical solitons for nonlinear Schrödinger equation with detuning term by iterative transform method. Symmetry 2020, 12, 1850. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Alyousef, H.A.; El-Tantawy, S.A.; Khan, A.; Wyal, N. Solving Fractional-Order Diffusion Equations in a Plasma and Fluids via a Novel Transform. J. Funct. Spaces 2022, 2022, 1899130. [Google Scholar] [CrossRef]
- Alaroud, M.; Al-Smadi, M.; Ahmad, R.R.; Din, U.K.S. Computational Optimization of Residual Power Series Algorithm for Certain Classes of Fuzzy Fractional Differential Equations. Int. J. Differ. Equations 2018, 2018, 8686502. [Google Scholar] [CrossRef]
- Prakasha, D.G.; Veeresha, P.; Baskonus, H.M. Residual Power Series Method for Fractional Swift–Hohenberg Equation. Fractal Fract. 2019, 3, 9. [Google Scholar] [CrossRef]
- Bataineh, M.; Alaroud, M.; Al-Omari, S.; Agarwal, P. Series Representations for Uncertain Fractional IVPs in the Fuzzy Conformable Fractional Sense. Entropy 2021, 23, 1646. [Google Scholar] [CrossRef]
- Alaroud, M. Application of Laplace residual power series method for approximate solutions of fractional IVP’s. Alex. Eng. J. 2022, 61, 1585–1595. [Google Scholar] [CrossRef]
- Burqan, A.; El-Ajou, A.; Saadeh, R.; Al-Smadi, M. A new efficient technique using Laplace transforms and smooth expansions to construct a series solution to the time-fractional Navier-Stokes equations. Alex. Eng. J. 2022, 61, 1069–1077. [Google Scholar] [CrossRef]
- Alquran, M.; Ali, M.; Alsukhour, M.; Jaradat, I. Promoted residual power series technique with Laplace transform to solve some time-fractional problems arising in physics. Results Phys. 2020, 19, 103667. [Google Scholar] [CrossRef]
- Alderremy, A.A.; Aly, S.; Fayyaz, R.; Khan, A.; Shah, R.; Wyal, N. The Analysis of Fractional-Order Nonlinear Systems of Third Order KdV and Burgers Equations via a Novel Transform. Complexity 2022, 2022, 4935809. [Google Scholar] [CrossRef]
- Zidan, A.M.; Khan, A.; Shah, R.; Alaoui, M.K.; Weera, W. Evaluation of time-fractional Fishe’s equations with the help of analytical methods. AIMS Math. 2022, 7, 18746–18766. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Ababneh, O.Y.; Shah, R.; Khan, A.; Nonlaopon, K. Numerical analysis of fractional-order Whitham-Broer-Kaup equations with non-singular kernel operators. AIMS Math. 2023, 8, 2308–2336. [Google Scholar] [CrossRef]
- Areshi, M.; Khan, A.; Shah, R.; Nonlaopon, K. Analytical investigation of fractional-order Newell-Whitehead-Segel equations via a novel transform. AIMS Math. 2022, 7, 6936–6958. [Google Scholar] [CrossRef]
- Abu Arqub, O.; El-Ajou, A.; Momani, S. Constructing and predicting solitary pattern solutions for nonlinear time-fractional dispersive partial differential equations. J. Comput. Phys. 2015, 293, 385–399. [Google Scholar] [CrossRef]
- Alshehry, A.S.; Shah, R.; Shah, N.A.; Dassios, I. A Reliable Technique for Solving Fractional Partial Differential Equation. Axioms 2022, 11, 574. [Google Scholar] [CrossRef]
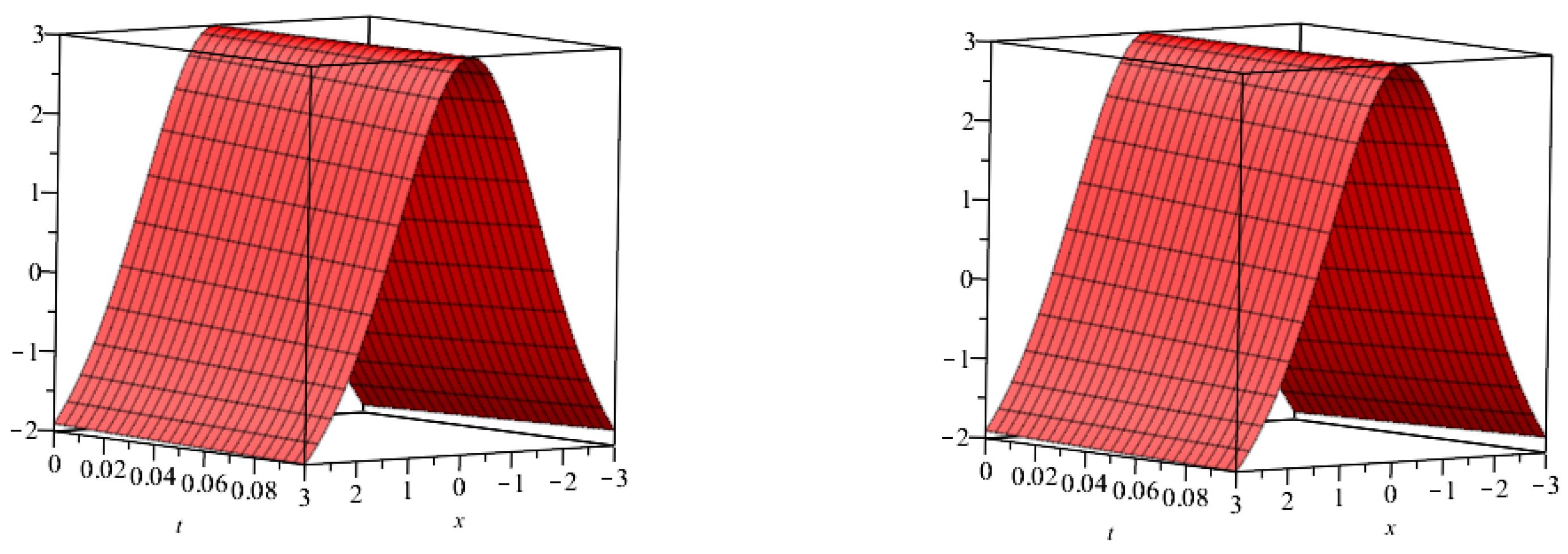
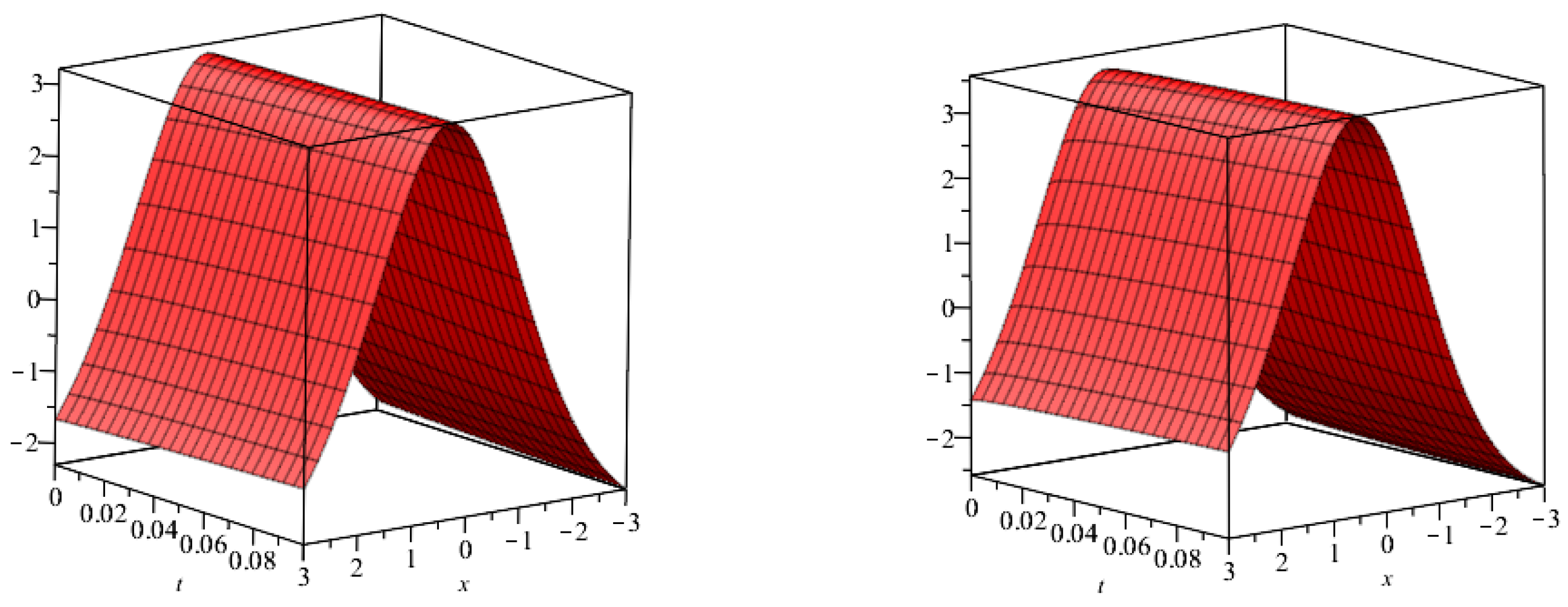

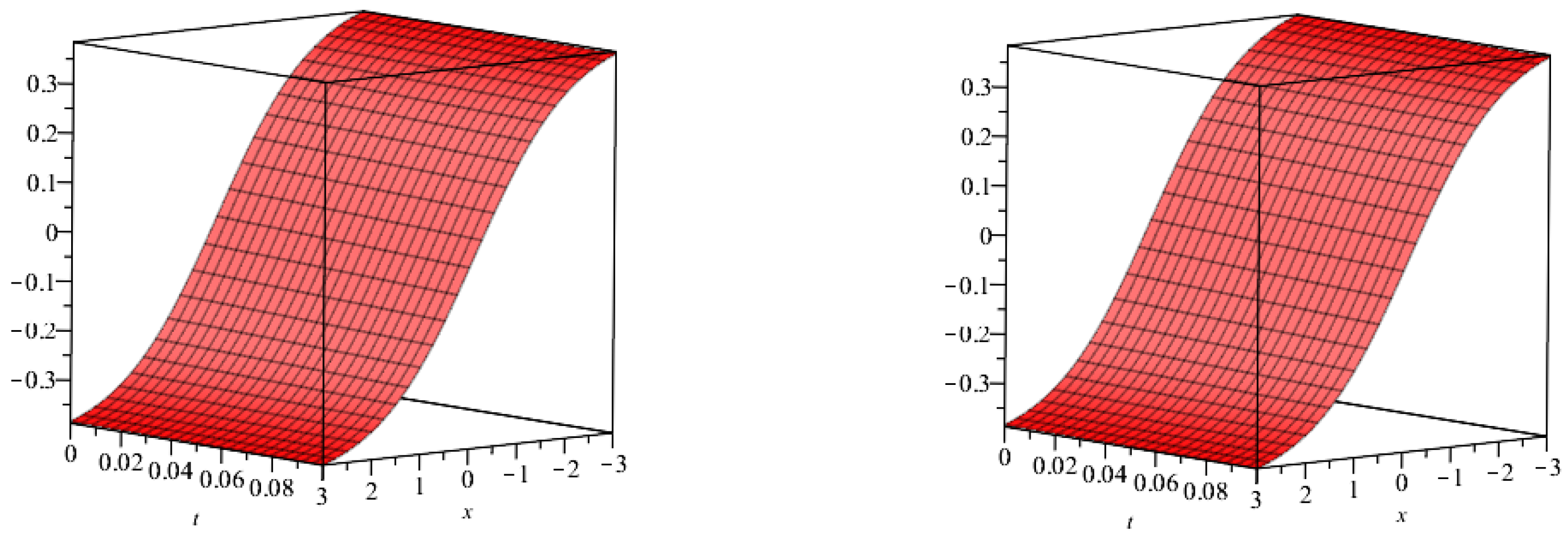


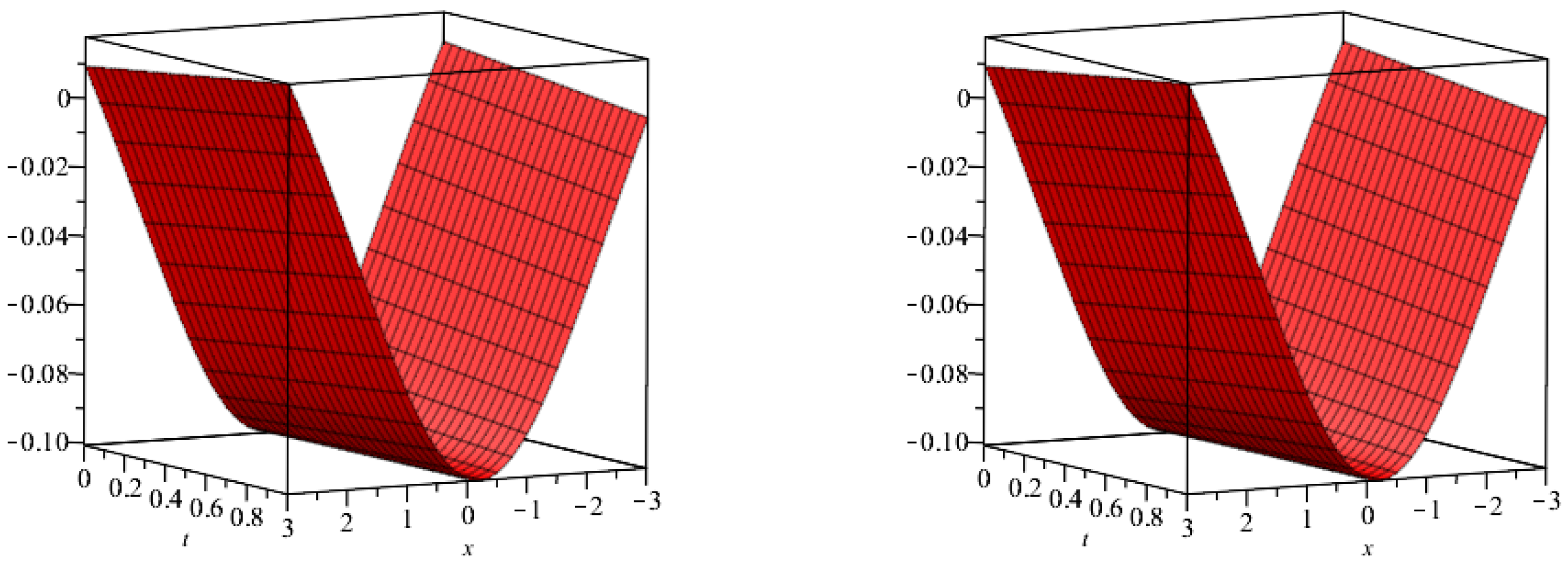



| at 0.5 | at 0.75 | at 1 | Exact Result | |
|---|---|---|---|---|
| (0.2, 0.01) | 2.9522951 | 2.9463031 | 2.9403977 | 2.9403977 |
| (0.4, 0.01) | 2.7892015 | 2.7772263 | 2.7662578 | 2.7662578 |
| (0.6, 0.01) | 2.5227923 | 2.5068021 | 2.4908217 | 2.4908217 |
| (0.2, 0.02) | 2.9523242 | 2.9463522 | 2.9403977 | 2.9403977 |
| (0.4, 0.02) | 2.7892041 | 2.7762190 | 2.7662578 | 2.7662578 |
| (0.6, 0.02) | 2.5227863 | 2.5068015 | 2.4908217 | 2.4908217 |
| (0.2, 0.03) | 2.9523245 | 2.9463621 | 2.9403977 | 2.9403977 |
| (0.4, 0.03) | 2.7891987 | 2.7762124 | 2.7662578 | 2.7662578 |
| (0.6, 0.03) | 2.5227921 | 2.5068105 | 2.4908217 | 2.4908217 |
| (0.2, 0.04) | 2.9523183 | 2.9463561 | 2.9403977 | 2.9403977 |
| (0.4, 0.04) | 2.7892124 | 2.7762321 | 2.7662578 | 2.7662578 |
| (0.6, 0.04) | 2.5227833 | 2.5068103 | 2.4908217 | 2.4908217 |
| (0.2, 0.05) | 2.9523133 | 2.9463562 | 2.9403977 | 2.9403977 |
| (0.4, 0.05) | 2.7892189 | 2.7762488 | 2.7662578 | 2.7662578 |
| (0.6, 0.05) | 2.5228021 | 2.5068111 | 2.4908216 | 2.4908216 |
| at 0.5 | at 0.75 | at 1 | Exact Result | |
|---|---|---|---|---|
| (0.2, 0.01) | −0.0004074 | −0.0004127 | −0.0004228 | −0.0004228 |
| (0.4, 0.01) | −0.0008051 | −0.0008202 | −0.0008373 | −0.0008373 |
| (0.6, 0.01) | −0.0011923 | −0.0012126 | −0.0012359 | −0.0012359 |
| (0.2, 0.02) | −0.0004024 | −0.0004087 | −0.0004228 | −0.0004228 |
| (0.4, 0.02) | −0.0008051 | −0.0008212 | −0.0008373 | −0.0008373 |
| (0.6, 0.02) | −0.0012003 | −0.0012217 | −0.0012359 | −0.0012359 |
| (0.2, 0.03) | −0.0004034 | −0.0004126 | −0.0004228 | −0.0004228 |
| (0.4, 0.03) | −0.0008111 | −0.0008202 | −0.0008373 | −0.0008373 |
| (0.6, 0.03) | −0.0012004 | −0.0012127 | −0.0012359 | −0.0012359 |
| (0.2, 0.04) | −0.0004024 | −0.0004106 | −0.0004228 | −0.0004228 |
| (0.4, 0.04) | −0.0008061 | −0.0008203 | −0.0008374 | −0.0008374 |
| (0.6, 0.04) | −0.0012005 | −0.0012127 | −0.0012359 | −0.0012359 |
| (0.2, 0.05) | −0.0004033 | −0.0004126 | −0.0004228 | −0.0004228 |
| (0.4, 0.05) | −0.0008072 | −0.0008213 | −0.0008374 | −0.0008374 |
| (0.6, 0.05) | −0.0012016 | −0.0012137 | −0.0012359 | −0.0012359 |
| at 0.5 | at 0.75 | at 1 | Exact Result | |
|---|---|---|---|---|
| (0.2, 0.01) | −0.0991522 | −0.0991843 | −0.0992005 | −0.0992005 |
| (0.4, 0.02) | −0.0967362 | −0.0967994 | −0.0968306 | −0.0968306 |
| (0.6, 0.03) | −0.0928263 | −0.0929185 | −0.0929647 | −0.0929647 |
| (0.2, 0.01) | −0.0991503 | −0.0991826 | −0.0991989 | −0.0991989 |
| (0.4, 0.02) | −0.0967322 | −0.0967953 | −0.0968275 | −0.0968275 |
| (0.6, 0.03) | −0.0928212 | −0.0929134 | −0.0929601 | −0.0929601 |
| (0.2, 0.01) | −0.0991480 | −0.0991812 | −0.0991973 | −0.0991973 |
| (0.4, 0.02) | −0.0967281 | −0.0967922 | −0.0968244 | −0.0968244 |
| (0.6, 0.03) | −0.0928152 | −0.0929094 | −0.0929556 | −0.0929556 |
| (0.2, 0.01) | −0.0991473 | −0.0991795 | −0.0991957 | −0.0991957 |
| (0.4, 0.02) | −0.0967250 | −0.0967891 | −0.0968212 | −0.0968212 |
| (0.6, 0.03) | −0.0928102 | −0.0929044 | −0.0929510 | −0.0929510 |
| (0.2, 0.01) | −0.0991454 | −0.0991776 | −0.0991941 | −0.0991941 |
| (0.4, 0.02) | −0.0967214 | −0.0967866 | −0.0968181 | −0.0968181 |
| (0.6, 0.03) | −0.0928051 | −0.0928992 | −0.0929464 | −0.0929464 |
| at 0.5 | at 0.75 | at 1 | Exact Result | |
|---|---|---|---|---|
| (0.2, 0.01) | 0.6311140 | 0.6311641 | 0.6311902 | 0.6311902 |
| (0.4, 0.02) | 0.6272731 | 0.6273743 | 0.6274244 | 0.6274244 |
| (0.6, 0.03) | 0.6210090 | 0.6211581 | 0.6212322 | 0.6212322 |
| (0.2, 0.01) | 0.6311112 | 0.6311624 | 0.6311876 | 0.6311876 |
| (0.4, 0.02) | 0.6272672 | 0.6273683 | 0.6274194 | 0.6274194 |
| (0.6, 0.03) | 0.6210013 | 0.6211506 | 0.6212248 | 0.6212248 |
| (0.2, 0.01) | 0.6311083 | 0.6311596 | 0.6311851 | 0.6311851 |
| (0.4, 0.02) | 0.6272620 | 0.6273632 | 0.6274144 | 0.6274144 |
| (0.6, 0.03) | 0.6209921 | 0.6211423 | 0.6212175 | 0.6212175 |
| (0.2, 0.01) | 0.6311052 | 0.6311564 | 0.6311826 | 0.6311826 |
| (0.4, 0.02) | 0.6272561 | 0.6273583 | 0.6274094 | 0.6274094 |
| (0.6, 0.03) | 0.6209844 | 0.6211358 | 0.6212101 | 0.6212101 |
| (0.2, 0.01) | 0.6311023 | 0.6311457 | 0.6311800 | 0.6311800 |
| (0.4, 0.02) | 0.6272500 | 0.6273532 | 0.6274044 | 0.6274044 |
| (0.6, 0.03) | 0.6209764 | 0.6211275 | 0.6212027 | 0.6212027 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Botmart, T.; Alotaibi, B.M.; Shah, R.; El-Sherif, L.S.; El-Tantawy, S.A. A Reliable Way to Deal with the Coupled Fractional Korteweg-De Vries Equations within the Caputo Operator. Symmetry 2022, 14, 2452. https://doi.org/10.3390/sym14112452
Botmart T, Alotaibi BM, Shah R, El-Sherif LS, El-Tantawy SA. A Reliable Way to Deal with the Coupled Fractional Korteweg-De Vries Equations within the Caputo Operator. Symmetry. 2022; 14(11):2452. https://doi.org/10.3390/sym14112452
Chicago/Turabian StyleBotmart, Thongchai, Badriah M. Alotaibi, Rasool Shah, Lamiaa S. El-Sherif, and Samir A. El-Tantawy. 2022. "A Reliable Way to Deal with the Coupled Fractional Korteweg-De Vries Equations within the Caputo Operator" Symmetry 14, no. 11: 2452. https://doi.org/10.3390/sym14112452
APA StyleBotmart, T., Alotaibi, B. M., Shah, R., El-Sherif, L. S., & El-Tantawy, S. A. (2022). A Reliable Way to Deal with the Coupled Fractional Korteweg-De Vries Equations within the Caputo Operator. Symmetry, 14(11), 2452. https://doi.org/10.3390/sym14112452







