Strain Monitoring-Based Fatigue Assessment and Remaining Life Prediction of Stiff Hangers in Highway Arch Bridge
Abstract
:1. Introduction
2. Strain Monitoring-Based Fatigue Assessment Method
3. Field Measurement on Tian Yuan Bridge
3.1. Introduction of Tian Yuan Bridge
3.2. Vehicle–Bridge Interaction (VBI) Model
3.3. Strain Measurement
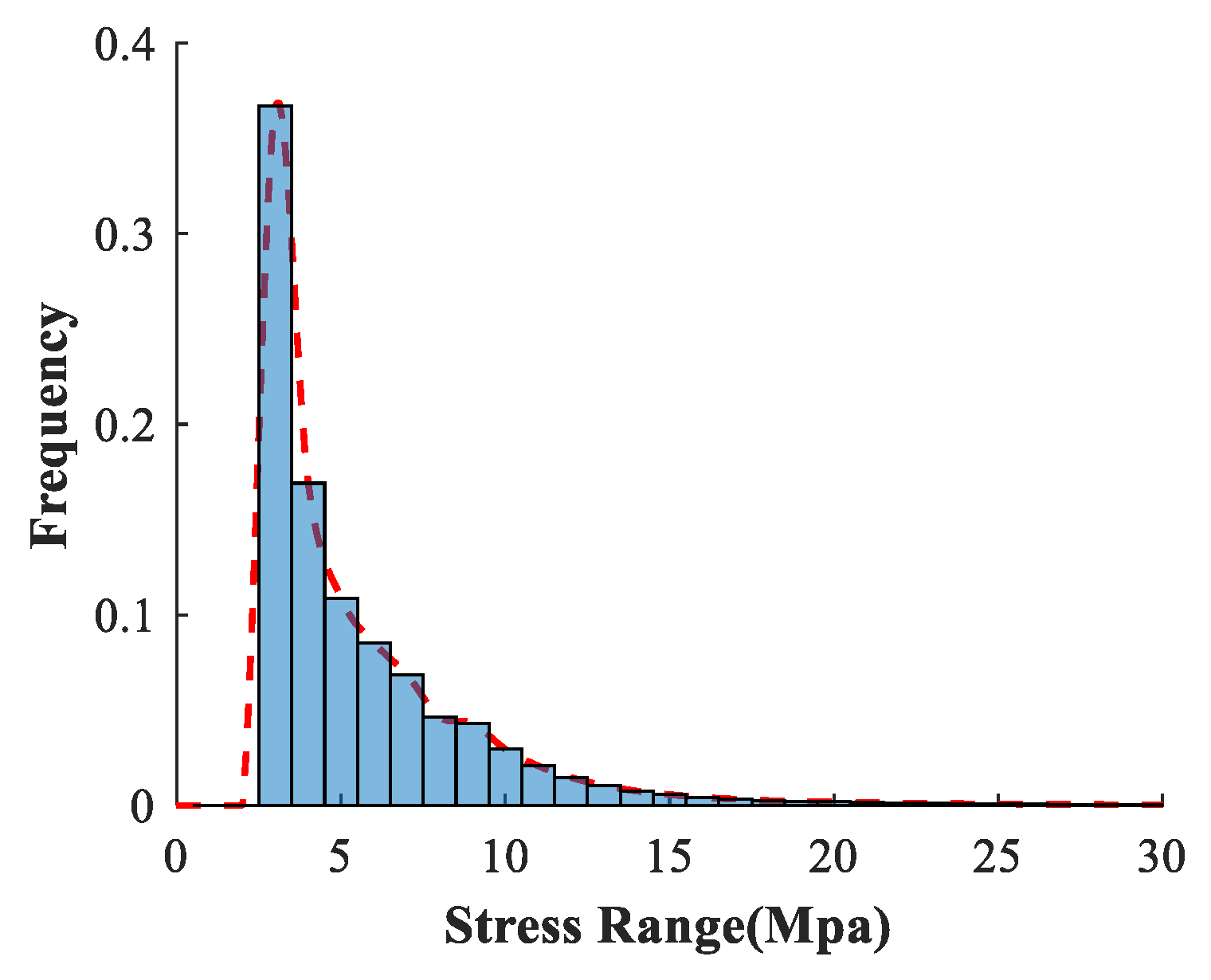
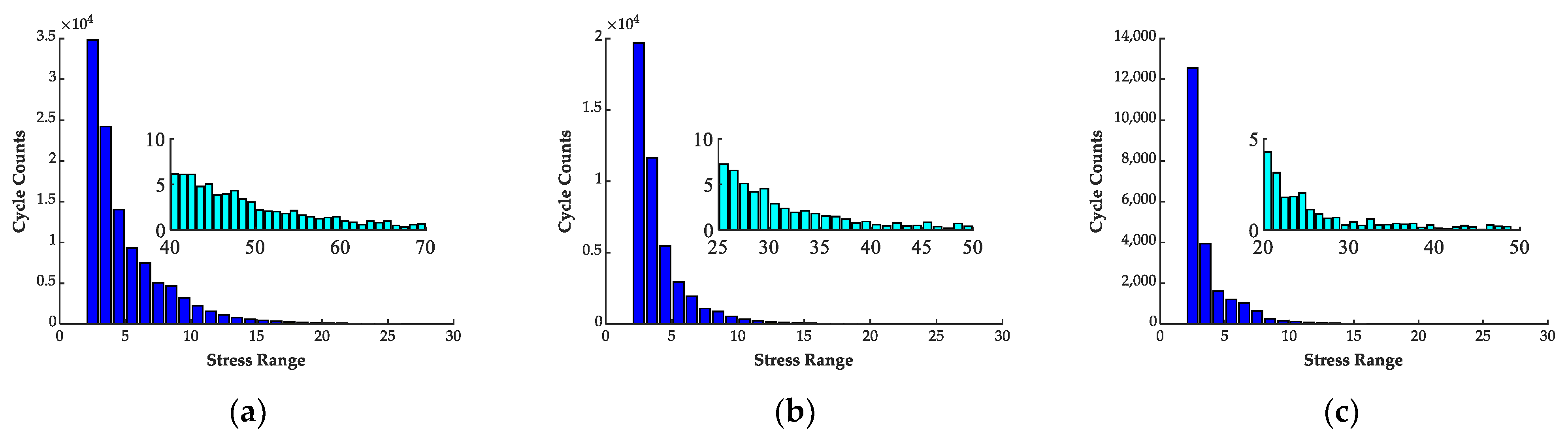
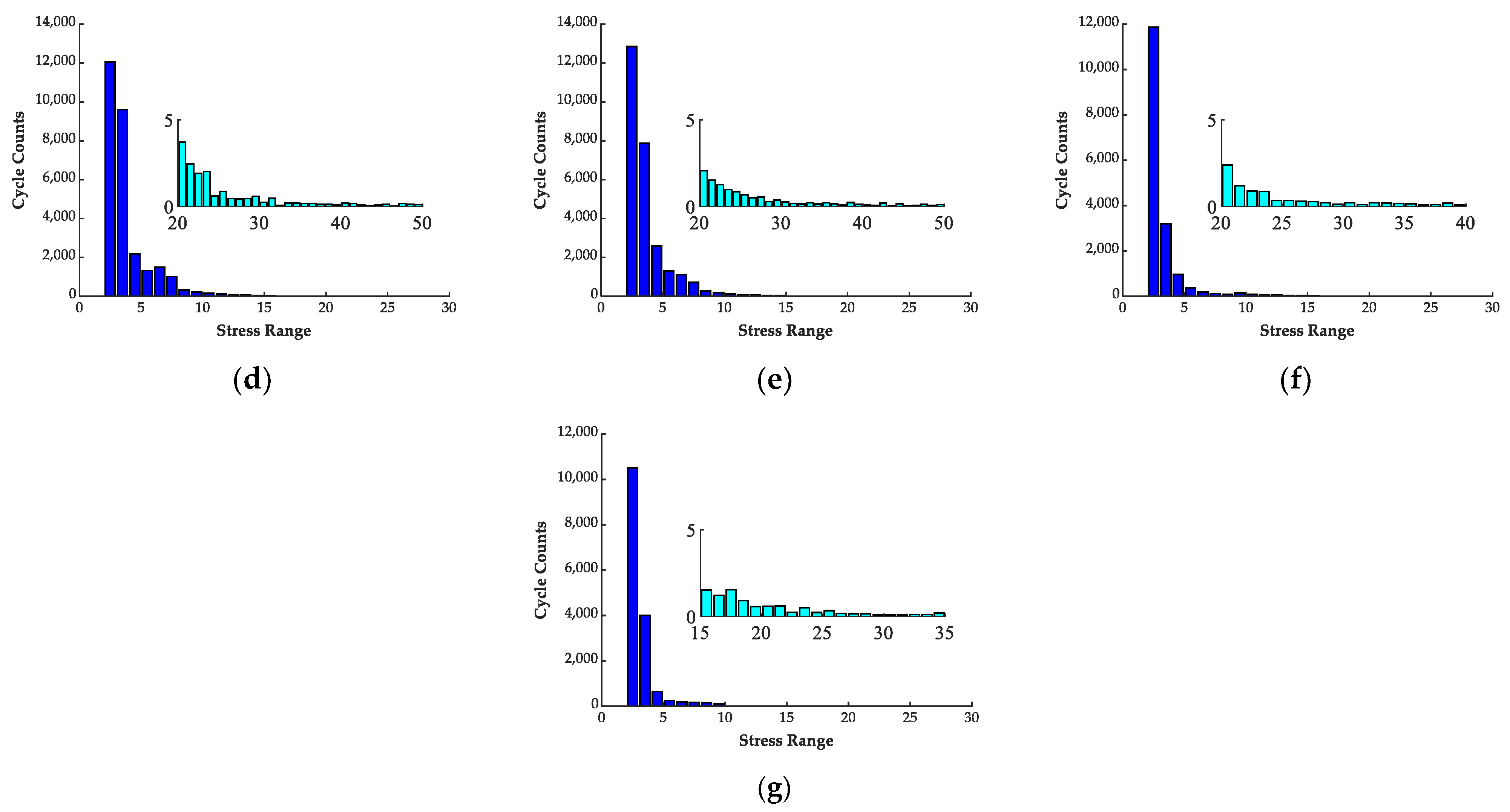
4. Statistical Analysis of Stress Spectrum
5. Fatigue Assessment
5.1. According to the Chinese Code for Design of Steel Structures
5.2. According to Eurocode 3
5.3. According to AASHTO
5.4. Consideration of the Growth of Traffic Volume
5.5. Assessment Results
6. Conclusions
- (i)
- The bending effect at the end zone of the hanger induces uneven axial stress in the key connecting weld lines. Simulation calculations have great significance in determining the monitoring location in stiff hangers. The EMD technique is applicable in the preprocessing of extensive SHM data.
- (ii)
- In average traffic service conditions, each involved hanger showed steady dynamic behavior during a continuous measuring duration of 159 days. The shortest hanger showed comparatively higher stress ranges in the statistical histogram.
- (iii)
- According to the estimated results based on three reference codes, the stipulation in AASHTO formulated a relatively higher cutoff stress range than the other two codes. Therefore, its calculated fatigue life was shorter. The fatigue damage assessed referring to GB50017-2017 and Eurocode 3 had a similar calculation progress since the S–N curves were different. When the contribution of low-stress amplitude to fatigue damage was considered, the fatigue life was significantly reduced when using AASHTO specifications. Moreover, the annual traffic load growth had a great influence on prospective fatigue life.
- (iv)
- Comparing the estimated fatigue life of all measured hangers, it was verified that the shortest hanger showed more severe fatigue damage than longer hangers. This is consistent with [30], which showed that the shortest hanger transferred relatively complicated stress as it was adjacent to the area where arch rib went through the girder to its skewback. Additionally, it suffered a more distinct dynamic effect as it was closer to the expansion joint compared with other hangers. However, the intrinsic reason for the difference between longer hangers is worthy of further research and investigation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, J.; Chen, W. Behavior of wires in parallel wire stayed cable under general corrosion effects. J. Constr. Steel Res. 2013, 85, 40–47. [Google Scholar] [CrossRef]
- Deng, Y.; Li, A.-Q.; Feng, D.-m.; Chen, X.; Zhang, M. Service life prediction for steel wires in hangers of a newly built suspension bridge considering corrosion fatigue and traffic growth. Struct. Control Health Monit. 2020, 27, e2642. [Google Scholar] [CrossRef]
- Zhou, Y.; Deng, N.; Yang, T. A Study on the Strength and Fatigue Properties of Seven-Wire Strands in Hangers under Lateral Bending. Appl. Sci. 2020, 10, 2160. [Google Scholar] [CrossRef] [Green Version]
- Lan, C.; Xu, Y.; Liu, C.; Li, H.; Spencer Jr, B. Fatigue life prediction for parallel-wire stay cables considering corrosion effects. Int. J. Fatigue 2018, 114, 81–91. [Google Scholar] [CrossRef]
- Manuel Garcia-Guerrero, J.; Jose Jorquera-Lucerga, J. Effect of Stiff Hangers on the Longitudinal Structural Behavior of Tied-Arch Bridges. Appl. Sci. 2018, 8, 258. [Google Scholar] [CrossRef] [Green Version]
- Zhong, W.; Ding, Y.-L.; Song, Y.-S.; Zhao, H.-W. Fatigue Behavior Evaluation of Full-Field Hangers in a Rigid Tied Arch High-Speed Railway Bridge: Case Study. J. Bridge Eng. 2018, 23, 05018003. [Google Scholar] [CrossRef]
- Song, Y.-S.; Ding, Y.-L.; Zhong, W.; Zhao, H. Reliable Fatigue-Life Assessment of Short Steel Hanger in a Rigid Tied Arch Bridge Integrating Multiple Factors. J. Perform. Constr. Facil. 2018, 32, 04018038. [Google Scholar] [CrossRef]
- Tochaei, E.N.; Fang, Z.; Taylor, T.; Babanajad, S.; Ansari, F. Structural monitoring and remaining fatigue life estimation of typical welded crack details in the Manhattan Bridge. Eng. Struct. 2021, 231, 111760. [Google Scholar] [CrossRef]
- Ni, Y.Q.; Chen, R. Strain monitoring based bridge reliability assessment using parametric Bayesian mixture model. Eng. Struct. 2021, 226, 111406. [Google Scholar] [CrossRef]
- Flanigan, K.A.; Lynch, J.P.; Ettouney, M. Probabilistic fatigue assessment of monitored railroad bridge components using long-term response data in a reliability framework. Struct. Health Monit. Int. J. 2020, 19, 2122–2142. [Google Scholar] [CrossRef]
- An, Y.; Guan, D.; Ding, Y.; Ou, J. Fast Warning Method for Rigid Hangers in a High-Speed Railway Arch Bridge Using Long-Term Monitoring Data. J. Perform. Constr. Facil. 2017, 31, 04017103. [Google Scholar] [CrossRef]
- Zhuang, M.; Miao, C.; Chen, R. Fatigue performance analysis and evaluation for steel box girder based on structural health monitoring system. Struct. Durab. Health Monit. 2020, 14, 51. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, M.; Feng, D.-M.; Li, A.-Q. Predicting fatigue damage of highway suspension bridge hangers using weigh-in-motion data and machine learning. Struct. Infrastruct. Eng. 2021, 17, 233–248. [Google Scholar] [CrossRef]
- Li, S.; Zhu, S.; Xu, Y.-L.; Chen, Z.-W.; Li, H. Long-term condition assessment of suspenders under traffic loads based on structural monitoring system: Application to the Tsing Ma Bridge. Struct. Control Health Monit. 2012, 19, 82–101. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, T.; Hebdon, M.H.; Zhang, Z. Corrosion fatigue analysis and reliability assessment of short suspenders in suspension and arch bridges. J. Perform. Constr. Facil. 2018, 32, 04018060. [Google Scholar] [CrossRef]
- Chen, B.; Li, X.; Xie, X.; Zhong, Z.; Lu, P. Fatigue Performance Assessment of Composite Arch Bridge Suspenders Based on Actual Vehicle Loads. Shock Vib. 2015, 2015, 659092. [Google Scholar] [CrossRef] [Green Version]
- Yu, Y.; Kurian, B.; Zhang, W.; Cai, C.; Liu, Y. Fatigue damage prognosis of steel bridges under traffic loading using a time-based crack growth method. Eng. Struct. 2021, 237, 112162. [Google Scholar] [CrossRef]
- Di, J.; Ruan, X.; Zhou, X.; Wang, J.; Peng, X. Fatigue assessment of orthotropic steel bridge decks based on strain monitoring data. Eng. Struct. 2021, 228, 111437. [Google Scholar] [CrossRef]
- Lei, J.; Zhou, Z.; Liu, T.; Wang, Z.; Zhang, W. Impact Behavior of Stiff Hangers in Arch Bridge Due to Moving Vehicles. Struct. Eng. Int. 2022, 2020, 1–10. [Google Scholar] [CrossRef]
- Deng, L.; Cai, C.S. Development of dynamic impact factor for performance evaluation of existing multi-girder concrete bridges. Eng. Struct. 2010, 32, 21–31. [Google Scholar] [CrossRef]
- Huang, D.Z.; Wang, T.L.; Shahawy, M. Impact Studies of Multigirder Concrete Bridges. J. Struct. Eng.Asce 1993, 119, 2387–2402. [Google Scholar] [CrossRef]
- Feng, D.; Scarangello, T.; Feng, M.Q.; Ye, Q. Cable tension force estimate using novel noncontact vision-based sensor. Measurement 2017, 99, 44–52. [Google Scholar] [CrossRef]
- Jie, W.U.; Xiamin, H.U.; Qiao, Y.; Teng, Y.U.; Zhu, S.; Jing, M.A. EMD-wavelet filtering based on cross-validation and its application in bridge dynamic monitoring. J. Vib. Shock 2017, 36, 212–217. [Google Scholar]
- Barbosh, M.; Singh, P.; Sadhu, A. Empirical mode decomposition and its variants: A review with applications in structural health monitoring. Smart Mater. Struct. 2020, 29, 093001. [Google Scholar] [CrossRef]
- Ding, H.; Shen, Q.; Du, S. Structural Condition Assessment of the Herringbone Middle Pylon of the Taizhou Bridge Using SHM Strain Data. J. Sens. 2017, 2017, 4269758. [Google Scholar] [CrossRef] [Green Version]
- Ye, X.W.; Ni, Y.Q.; Wong, K.Y.; Ko, J.M. Statistical analysis of stress spectra for fatigue life assessment of steel bridges with structural health monitoring data. Eng. Struct. 2012, 45, 166–176. [Google Scholar] [CrossRef]
- Nieslony, A. Determination of fragments of multiaxial service loading strongly influencing the fatigue of machine components. Mech. Syst. Signal Process. 2009, 23, 2712–2721. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, Y.; Feng, D.-M.; Li, A.-Q. Investigation of fatigue performance of welded details in long-span steel bridges using long-term monitoring strain data. Struct. Control Health Monit. 2015, 22, 1343–1358. [Google Scholar] [CrossRef]
- Kondoh, M.; Okuda, M.; Kawaguchi, K.; Yamazaki, T. Design Method of a Hanger System for Long-Span Suspension Bridge. J. Bridge Eng. 2001, 6, 176–182. [Google Scholar] [CrossRef]
- ZHANG, K.; YANG, J. Dynamic Response Analysis and Redesign on Short Suspenders of Bridge. J. Wuhan Univ. Technol. 2017, 41, 934–937, 942. [Google Scholar]
- BS5400-10; Steel, Concrete and Composite Bridges—Part 10: Code of Practice for Fatigu. British Standards Institution: London, UK, 2002.




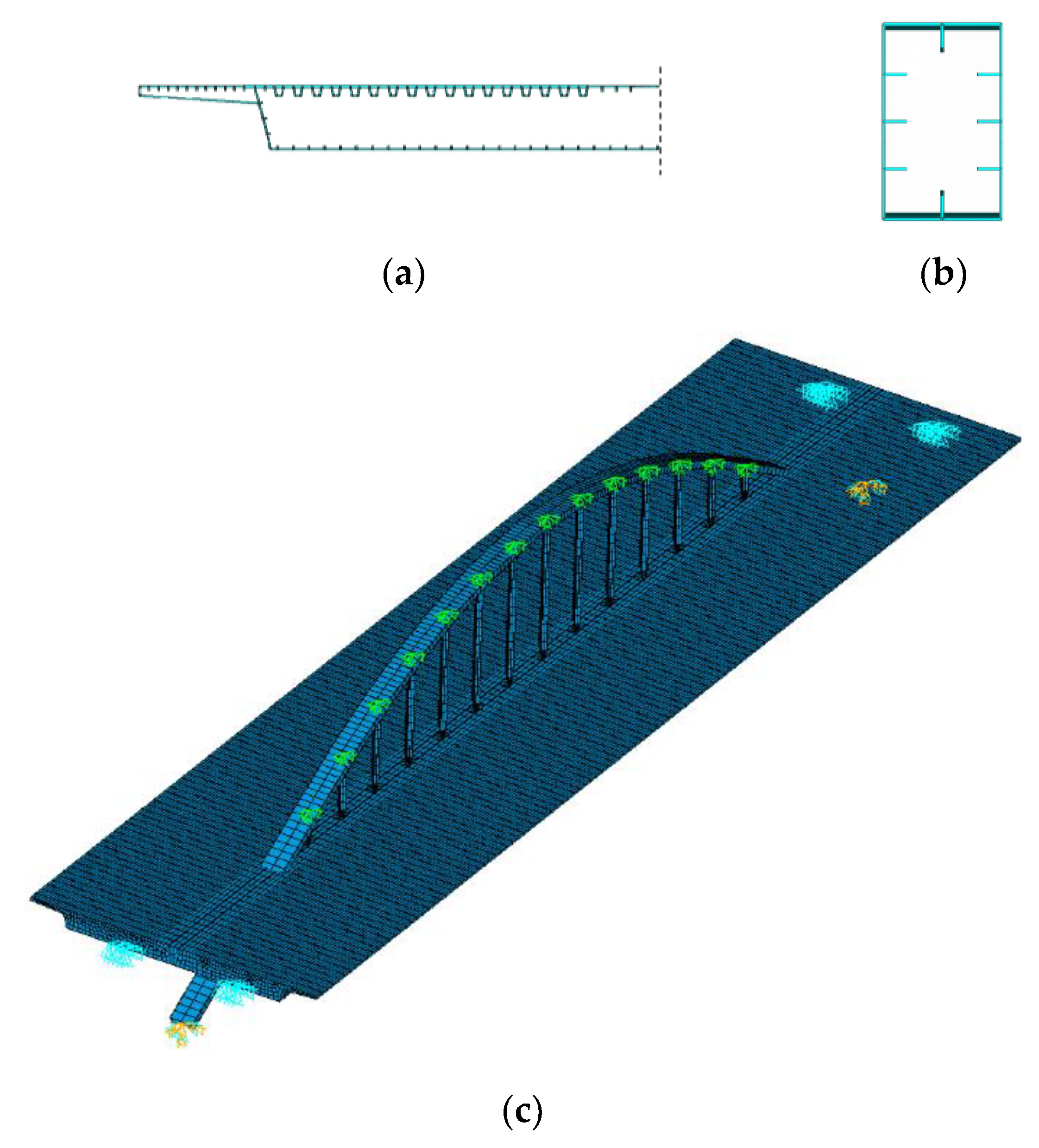
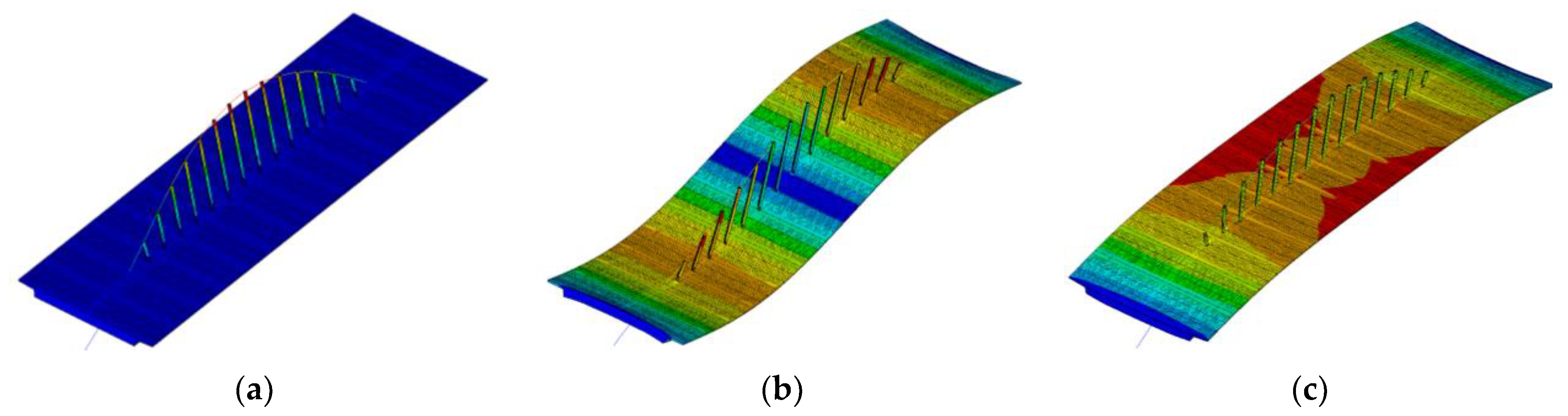
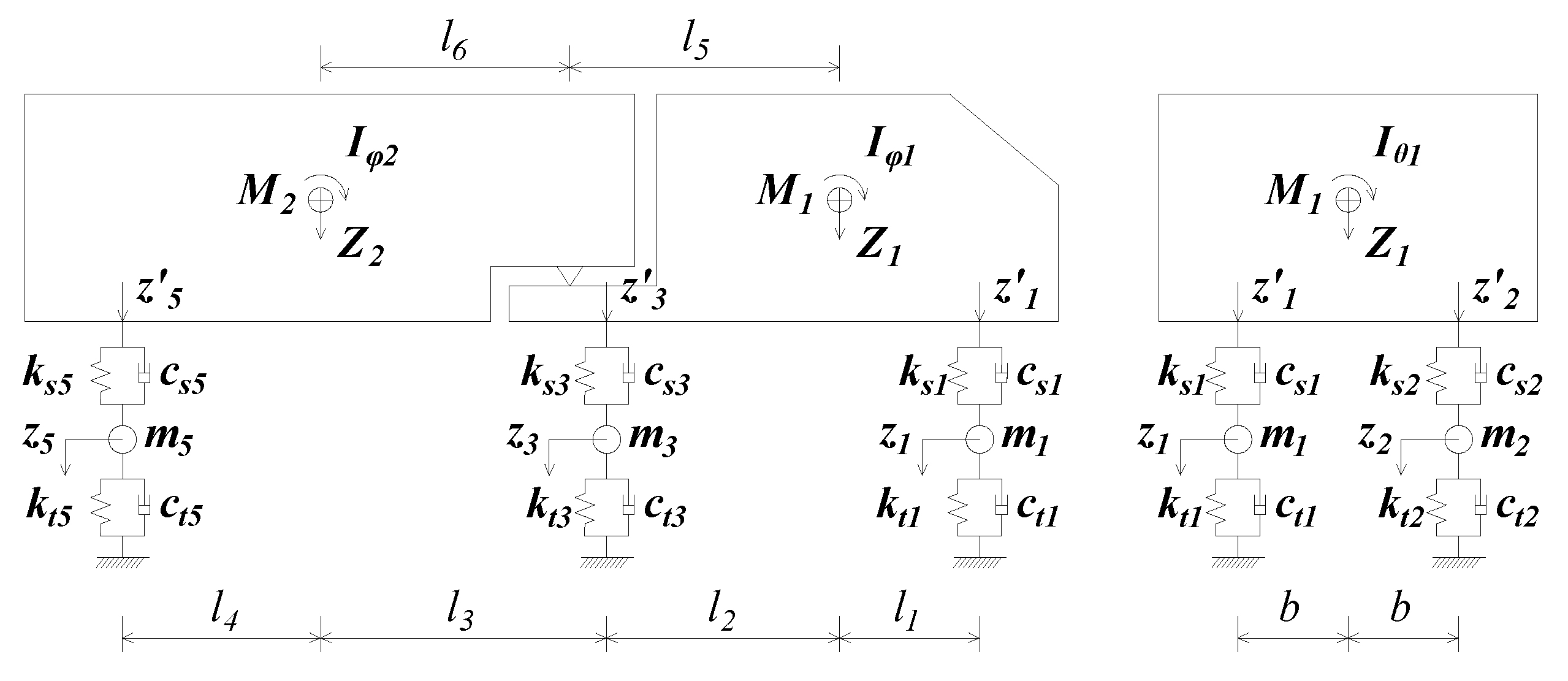
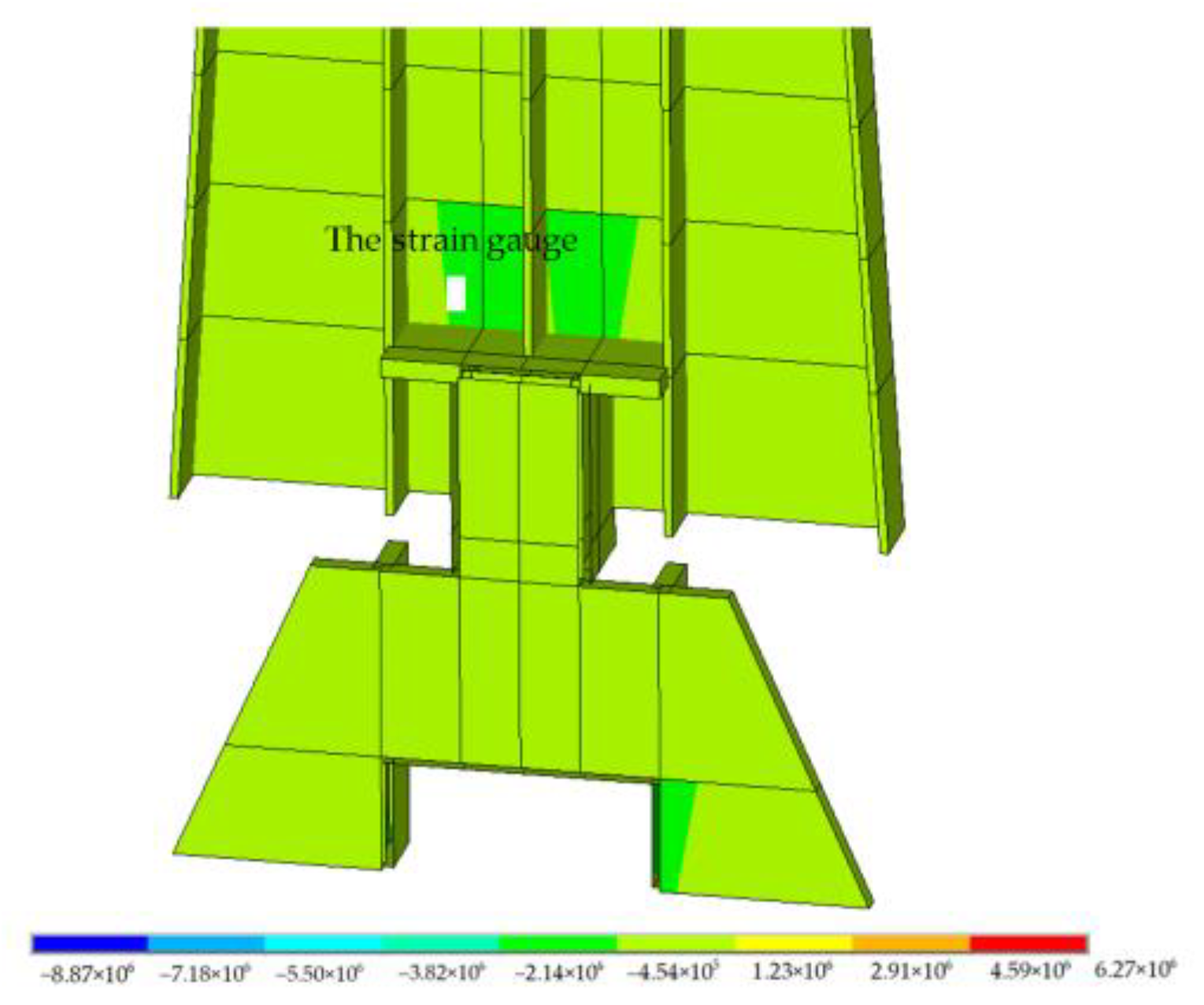
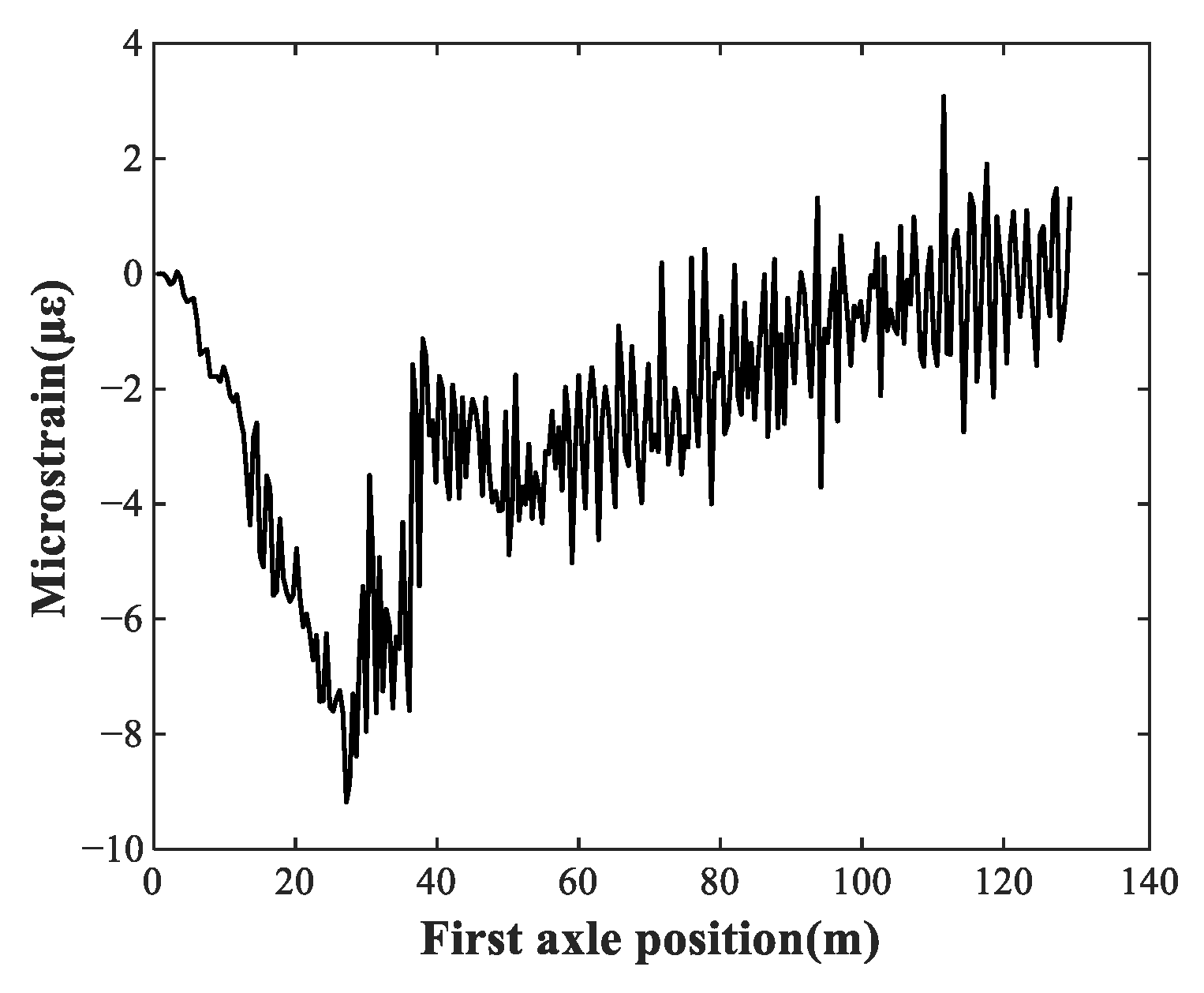
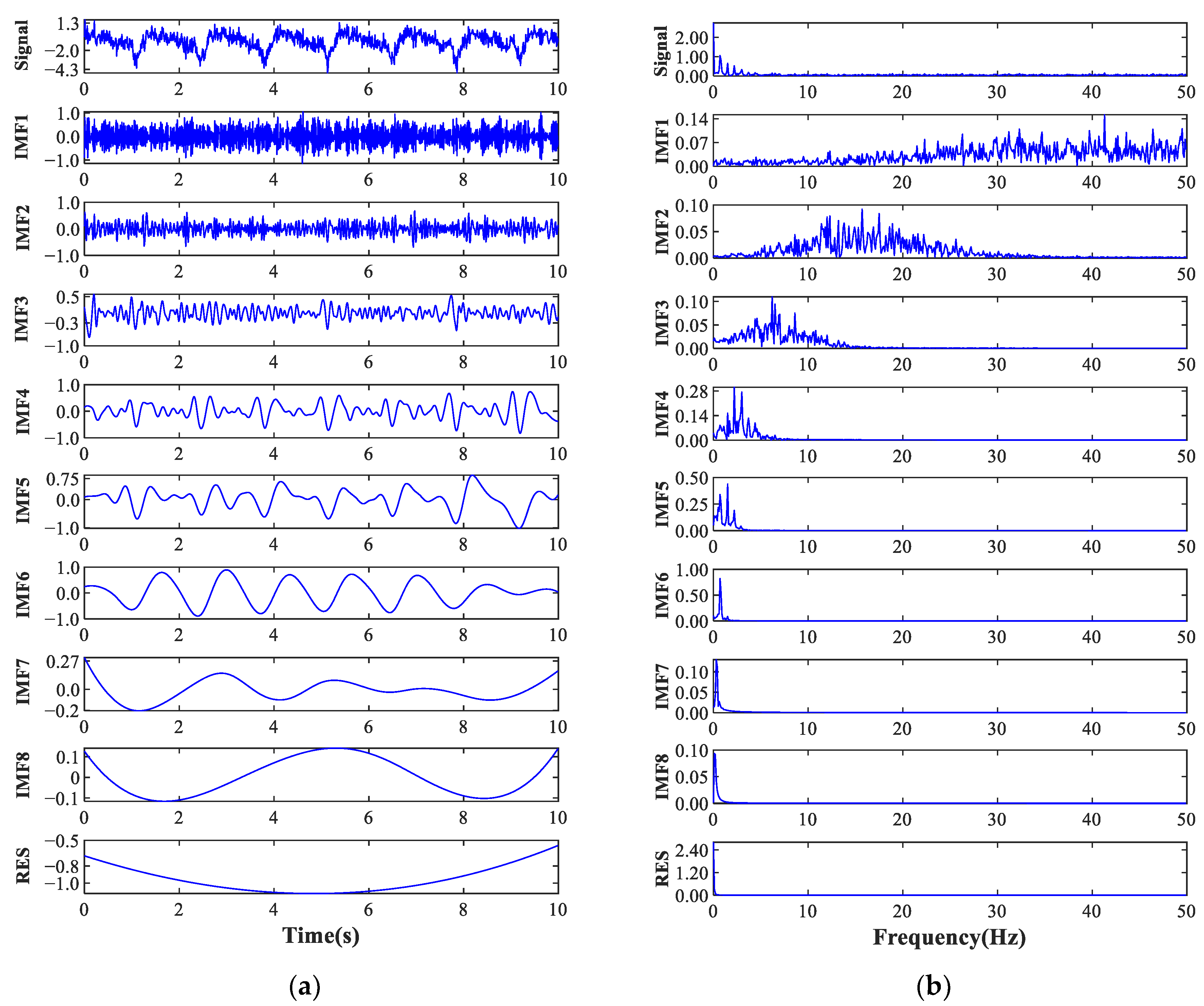
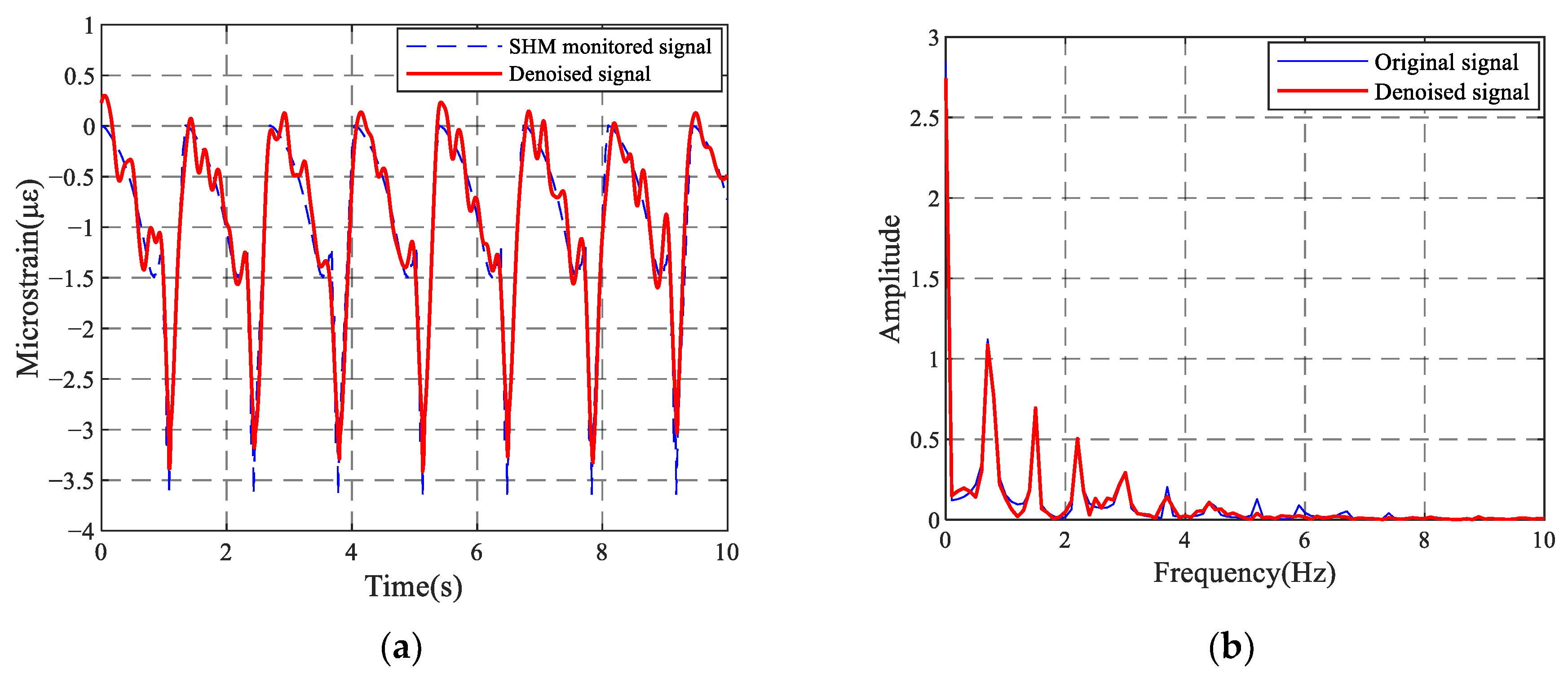


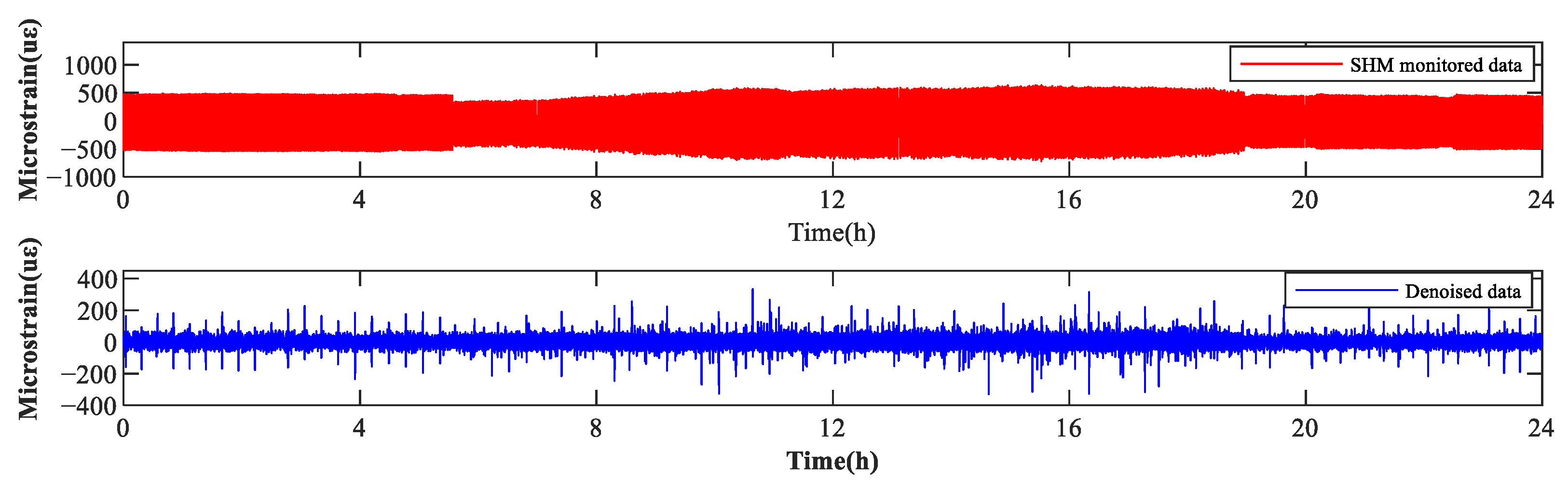


| Hanger ID | a (mm) | b (mm) | c (mm) | h (mm) |
|---|---|---|---|---|
| 1 | 700 | 1219 | 476 | 2643 |
| 2 | 979 | 1208 | 476 | 6042 |
| 3 | 1049 | 1206 | 476 | 8878 |
| 4 | 1080 | 1205 | 476 | 11,156 |
| 5 | 1096 | 1204 | 476 | 12,872 |
| 6 | 1105 | 1204 | 476 | 14,026 |
| 7 | 1108 | 1204 | 476 | 14,621 |
| Threshold | SNRin (%) | |||
|---|---|---|---|---|
| 4 dB | 7 dB | 10 dB | 13 dB | |
| 1 | 100.91 | 53.73 | 32.70 | 24.84 |
| 2 | 186.15 | 88.91 | 56.78 | 43.06 |
| 3 | 267.23 | 115.22 | 63.31 | 44.50 |
| 4 | 135.70 | 45.60 | 9.334 | −11.52 |
| Hanger Number | Stress Range (MPa) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0–2 | 2–10 | 11–20 | 21–30 | 31–40 | 41–50 | 51–60 | 61–70 | 71–80 | 81–90 | 91–100 | |
| 1 | 1,525,030 | 92,152.0 | 7861.8 | 672.5 | 151.6 | 46.8 | 17.4 | 7.3 | 3.2 | 2.2 | 1.3 |
| 2 | 1,641,476 | 44,229.2 | 1142.8 | 99.0 | 17.0 | 5.2 | 2.7 | 1.3 | 1.3 | 1.0 | 0.4 |
| 3 | 1,731,491 | 21,476.0 | 399.7 | 16.7 | 3.3 | 1.4 | 0.9 | 0.4 | 0.4 | 0.3 | 0.2 |
| 4 | 1,722,854 | 28,229.3 | 504.2 | 13.6 | 1.9 | 1.2 | 0.6 | 0.2 | 0.2 | 0.2 | 0.1 |
| 5 | 1,655,334 | 26,888.2 | 403.6 | 9.1 | 1.8 | 1.0 | 0.7 | 0.3 | 0.2 | 0.1 | 0.1 |
| 6 | 1,657,919 | 13,131.8 | 27.6 | 2.3 | 0.4 | 0.2 | 0.1 | 0.1 | 0.0 | 0.1 | 0.0 |
| 7 | 1,684,762 | 16,863.7 | 129.6 | 2.4 | 0.3 | 0.2 | 0.1 | 0.1 | 0.0 | 0.0 | 0.0 |
| Hanger Number | GB50017-2017 | Eurocode 3 | AASHTO | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0% | 2% | 5% | 0% | 2% | 5% | 0% | 2% | 5% | |
| 1 | 669 | 212 | 145 | 657 | 211 | 143 | 447 | 167 | 115 |
| 2 | 2525 | 455 | 298 | 2505 | 453 | 297 | 2006 | 401 | 264 |
| 3 | 7566 | 821 | 531 | 7531 | 819 | 529 | 6157 | 736 | 477 |
| 4 | 14,094 | 1138 | 731 | 13,922 | 1131 | 724 | 10,856 | 993 | 639 |
| 5 | 13,677 | 1121 | 720 | 13,559 | 1115 | 717 | 10,523 | 977 | 629 |
| 6 | 55,197 | 2299 | 1466 | 55,018 | 2296 | 1464 | 44,400 | 2058 | 1313 |
| 7 | 77,840 | 2740 | 1745 | 76,200 | 2711 | 1726 | 62,348 | 2447 | 1559 |
| Code | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0% | 2% | 5% | 0% | 2% | 5% | 0% | 2% | 5% | |
| GB50017-2017 | 669 | 212 | 145 | 512 | 182 | 125 | 474 | 173 | 119 |
| Eurocode 3 | 657 | 211 | 143 | 509 | 181 | 124 | 472 | 173 | 119 |
| AASHTO | 447 | 167 | 115 | 203 | 101 | 72 | 91 | 58 | 44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, J.; Kong, Q.; Wang, X.; Zhan, K. Strain Monitoring-Based Fatigue Assessment and Remaining Life Prediction of Stiff Hangers in Highway Arch Bridge. Symmetry 2022, 14, 2501. https://doi.org/10.3390/sym14122501
Lei J, Kong Q, Wang X, Zhan K. Strain Monitoring-Based Fatigue Assessment and Remaining Life Prediction of Stiff Hangers in Highway Arch Bridge. Symmetry. 2022; 14(12):2501. https://doi.org/10.3390/sym14122501
Chicago/Turabian StyleLei, Jiayan, Qinghui Kong, Xinhong Wang, and Kaizhen Zhan. 2022. "Strain Monitoring-Based Fatigue Assessment and Remaining Life Prediction of Stiff Hangers in Highway Arch Bridge" Symmetry 14, no. 12: 2501. https://doi.org/10.3390/sym14122501
APA StyleLei, J., Kong, Q., Wang, X., & Zhan, K. (2022). Strain Monitoring-Based Fatigue Assessment and Remaining Life Prediction of Stiff Hangers in Highway Arch Bridge. Symmetry, 14(12), 2501. https://doi.org/10.3390/sym14122501





