Fully Heavy Tetraquark Spectroscopy in the Relativistic Quark Model
Abstract
:1. Introduction
2. Model Description of Fully Heavy Tetraquarks
3. Relativistic Diquark–Antidiquark Model
4. Masses of Fully Heavy Tetraquarks
5. Threshold Analysis
| State | S | |||||
|---|---|---|---|---|---|---|
| 1S | 0 | 6190 | 12,838 | 19,314 | ||
| 1 | 6271 | 12,855 | 19,320 | |||
| 2 | 6367 | 12,883 | 19,330 | |||
| 1P | 0 | 6631 | 13,103 | 19,536 | ||
| 1 | 6628 | 13,100 | 19,533 | |||
| 6634 | 13,103 | 19,535 | ||||
| 6644 | 13,108 | 19,539 | ||||
| 2 | 6635 | 13,103 | 19,534 | |||
| 6648 | 13,109 | 19,538 | ||||
| 6664 | 13,116 | 19,545 | ||||
| 2S | 0 | 6782 | 13,247 | 19,680 | ||
| 1 | 6816 | 13,256 | 19,682 | |||
| 2 | 6868 | 13,272 | 19,687 | |||
| 1D | 0 | 6921 | 13,306 | 19,715 | ||
| 1 | 6909 | 13,299 | 19,710 | |||
| 6920 | 13,304 | 19,714 | ||||
| 6932 | 13,311 | 19,720 | ||||
| 2 | 6899 | 13,293 | 19,705 | |||
| 6904 | 13,296 | 19,707 | ||||
| 6915 | 13,301 | 19,711 | ||||
| 6929 | 13,308 | 19,717 | ||||
| 6945 | 13,317 | 19,724 | ||||
| 2P | 0 | 7091 | 13,428 | 19,820 | ||
| 1 | 7100 | 13,431 | 19,821 | |||
| 7099 | 13,431 | 19,821 | ||||
| 7098 | 13,431 | 19,822 | ||||
| 2 | 7113 | 13,434 | 19,823 | |||
| 7113 | 13,435 | 19,823 | ||||
| 7112 | 13,436 | 19,824 | ||||
| 3S | 0 | 7259 | 13,558 | 19,941 | ||
| 1 | 7287 | 13,566 | 19,943 | |||
| 2 | 7333 | 13,580 | 19,947 | |||
| 1S | 1 | 12,863 | ||||
| 1P | 13,096 | |||||
| 13,099 | ||||||
| 13,104 | ||||||
| 2S | 13,257 | |||||
| 1D | 13,293 | |||||
| 13,298 | ||||||
| 13,305 | ||||||
| 2P | 13,426 | |||||
| 13,426 | ||||||
| 13,427 | ||||||
| 3S | 13,566 | |||||
| 1S | 0 | 12,856 | ||||
| 1P | 13,095 | |||||
| 2S | 13,250 | |||||
| 1D | 13,293 | |||||
| 2P | 13,420 | |||||
| 3S | 13,559 |
| State | Meson Pair | |||||||
| 1S | 0 | 5968 | 222 | |||||
| 1 | 6271 | 6081 | 190 | |||||
| 2 | ||||||||
| 1P | 0 | 6631 | 6509 | 122 | ||||
| 6512 | 119 | |||||||
| 6608 | 23 | |||||||
| 1 | 6628 | 6399 | 229 | |||||
| 6622 | 6 | |||||||
| 6634 | 6495 | 139 | ||||||
| 6622 | 12 | |||||||
| 6644 | 6540 | 104 | ||||||
| 6622 | 22 | |||||||
| 2 | 6635 | 6509 | 126 | |||||
| 6512 | 123 | |||||||
| 6608 | 27 | |||||||
| 6653 | −18 | |||||||
| 6648 | 6608 | 40 | ||||||
| 6653 | −5 | |||||||
| 6664 | 6653 | 11 | ||||||
| 2S | 0 | 1 | 5968 | 814 | ||||
| 1 | 6816 | 6081 | 735 | |||||
| 2 | ||||||||
| 1D | 0 | |||||||
| 1 | 6909 | 6081 | 828 | |||||
| 6920 | 6808 | 112 | ||||||
| 6932 | 6827 | 105 | ||||||
| 2 | 5968 | 931 | ||||||
| 6929 | 6921 | 8 | ||||||
| 6940 | 19 | |||||||
| 6945 | 6940 | 5 | ||||||
| 2P | 0 | 7091 | 6509 | 582 | ||||
| 1 | 7100 | 6399 | 701 | |||||
| 7099 | 6495 | 604 | ||||||
| 7098 | 6540 | 558 | ||||||
| 2 | 7113 | 6509 | 604 | |||||
| 7113 | 6608 | 505 | ||||||
| 7112 | 6653 | 459 | ||||||
| 3S | 0 | 5968 | 1291 | |||||
| 1 | 7287 | 6081 | 1206 | |||||
| 2 | 2 |
| State | Meson Pair | |||||||
| 1S | 0 | 12,838 | 12,383 | 455 | ||||
| 1 | 12,855 | 12,444 | 411 | |||||
| 2 | 12,883 | 12,557 | 326 | |||||
| 1P | 0 | 13,103 | 12,875 | 228 | ||||
| 12,883 | 220 | |||||||
| 12,924 | 179 | |||||||
| 12,956 | 147 | |||||||
| 12,971 | 132 | |||||||
| 12,990 | 113 | |||||||
| 13,009 | 94 | |||||||
| 13,016 | 87 | |||||||
| 1 | 13,100 | 12,813 | 287 | |||||
| 12,843 | 257 | |||||||
| 12,986 | 114 | |||||||
| 12,996 | 104 | |||||||
| 13,103 | 12,877 | 226 | ||||||
| 12,909 | 194 | |||||||
| 12,986 | 117 | |||||||
| 12,996 | 107 | |||||||
| 13,108 | 12,896 | 212 | ||||||
| 12,955 | 153 | |||||||
| 12,986 | 122 | |||||||
| 12,996 | 112 | |||||||
| 1P | 2 | 13,103 | 12,875 | 228 | ||||
| 12,883 | 220 | |||||||
| 12,924 | 179 | |||||||
| 12,956 | 147 | |||||||
| 12,971 | 132 | |||||||
| 12,990 | 113 | |||||||
| 13,009 | 94 | |||||||
| 13,016 | 87 | |||||||
| 13,109 | 12,971 | 138 | ||||||
| 12,990 | 119 | |||||||
| 13,009 | 100 | |||||||
| 13,016 | 93 | |||||||
| 13,116 | 13,009 | 107 | ||||||
| 13,016 | 100 | |||||||
| 2S | 0 | 13,247 | 12,383 | 864 | ||||
| 1 | 13,256 | 12,444 | 812 | |||||
| 2 | 13,272 | 12,557 | 715 | |||||
| 1D | 0 | 13,306 | 12,557 | 749 | ||||
| 1 | 13,299 | 12,444 | 855 | |||||
| 13,304 | 13,148 | 156 | ||||||
| 13,222 | 82 | |||||||
| 13,311 | 13,241 | 70 | ||||||
| 2 | 13,293 | 12,383 | 910 | |||||
| 13,296 | 12,557 | 739 | ||||||
| 13,301 | 12,557 | 744 | ||||||
| 13,308 | 13,261 | 47 | ||||||
| 13,284 | 24 | |||||||
| 13,303 | 5 | |||||||
| 13,317 | 13,303 | 14 | ||||||
| 2P | 0 | 13,428 | 12,875 | 553 | ||||
| 1 | 13,431 | 12,813 | 618 | |||||
| 13,431 | 12,877 | 554 | ||||||
| 13,431 | 12,896 | 535 | ||||||
| 2 | 13,434 | 12,875 | 559 | |||||
| 13,435 | 12,971 | 464 | ||||||
| 13,436 | 13,009 | 427 | ||||||
| 3S | 0 | 13,558 | 12,383 | 1175 | ||||
| 1 | 13,566 | 12,444 | 1122 | |||||
| 2 | 13,580 | 12,557 | 1023 |
| State | S | M | Meson Pair | |||||
|---|---|---|---|---|---|---|---|---|
| 1S | 1 | 12,863 | 12,557 | 306 | ||||
| 12,444 | 419 | |||||||
| 1P | 13,096 | 12,813 | 283 | |||||
| 12,843 | 253 | |||||||
| 12,986 | 110 | |||||||
| 12,996 | 100 | |||||||
| 12,971 | 125 | |||||||
| 12,990 | 106 | |||||||
| 13,099 | 12,877 | 222 | ||||||
| 12,909 | 190 | |||||||
| 12,986 | 113 | |||||||
| 12,996 | 103 | |||||||
| 12,875 | 224 | |||||||
| 12,883 | 216 | |||||||
| 12,924 | 175 | |||||||
| 12,956 | 143 | |||||||
| 12,971 | 128 | |||||||
| 12,990 | 109 | |||||||
| 13,009 | 90 | |||||||
| 13,016 | 83 | |||||||
| 13,104 | 12,896 | 208 | ||||||
| 12,955 | 149 | |||||||
| 12,986 | 118 | |||||||
| 12,996 | 108 | |||||||
| 12,971 | 133 | |||||||
| 12,990 | 114 | |||||||
| 13,009 | 114 | |||||||
| 13,016 | 114 | |||||||
| 2S | 13,257 | 12,557 | 700 | |||||
| 12,444 | 813 | |||||||
| 1D | 13,293 | 12,557 | 736 | |||||
| 12,444 | 849 | |||||||
| 13,298 | 12,557 | 741 | ||||||
| 13,148 | 150 | |||||||
| 13,222 | 76 | |||||||
| 13,305 | 13,261 | 44 | ||||||
| 13,284 | 21 | |||||||
| 13,303 | 2 | |||||||
| 13,241 | 64 | |||||||
| 2P | 13,426 | 12,813 | 613 | |||||
| 12,971 | 455 | |||||||
| 13,426 | 12,877 | 549 | ||||||
| 12,875 | 551 | |||||||
| 13,427 | 12896 | 531 | ||||||
| 12,971 | 456 | |||||||
| 3S | 13,566 | 12,557 | 1009 | |||||
| 12,444 | 1122 |
| State | S | M | Meson Pair | |||||
|---|---|---|---|---|---|---|---|---|
| 1S | 0 | 12,856 | 12,383 | 473 | ||||
| 1P | 13,095 | 12,875 | 220 | |||||
| 12,883 | 212 | |||||||
| 12,924 | 171 | |||||||
| 12,956 | 139 | |||||||
| 12,971 | 124 | |||||||
| 12,990 | 105 | |||||||
| 13,009 | 86 | |||||||
| 13,016 | 79 | |||||||
| 2S | 13,250 | 12,383 | 867 | |||||
| 1D | 13,293 | 12,557 | 736 | |||||
| 2P | 13,420 | 12,875 | 545 | |||||
| 3S | 13,559 | 12,383 | 1176 |
| State | S | M | Meson Pair | |||||
|---|---|---|---|---|---|---|---|---|
| 1S | 0 | 18,798 | 516 | |||||
| 1 | 19,320 | 18,859 | 461 | |||||
| 2 | ||||||||
| 1P | 0 | 19,536 | 19,298 | 238 | ||||
| 19,320 | 216 | |||||||
| 19,353 | 183 | |||||||
| 19,373 | 163 | |||||||
| 1 | 19,533 | 19,258 | 275 | |||||
| 19,360 | 173 | |||||||
| 19,535 | 19,291 | 244 | ||||||
| 19,360 | 175 | |||||||
| 19,539 | 19,311 | 228 | ||||||
| 19,360 | 179 | |||||||
| 2 | 19,534 | 19,298 | 236 | |||||
| 19,320 | 214 | |||||||
| 19,353 | 181 | |||||||
| 19,373 | 161 | |||||||
| 19,538 | 19,353 | 185 | ||||||
| 19,373 | 165 | |||||||
| 19,545 | 19,373 | 172 | ||||||
| 2S | 0 | 18,798 | 882 | |||||
| 1 | 19,682 | 18,859 | 823 | |||||
| 2 | ||||||||
| 1D | 0 | |||||||
| 1 | 19,710 | 18,859 | 851 | |||||
| 19,714 | 19,562 | 152 | ||||||
| 19,720 | 19,812 | -92 | ||||||
| 2 | 18,798 | 907 | ||||||
| 19,717 | 19,624 | 93 | ||||||
| 19,724 | 19,824 | -100 | ||||||
| 2P | 0 | 19,820 | 19,298 | 522 | ||||
| 1 | 19,821 | 19,258 | 563 | |||||
| 19,821 | 19,291 | 530 | ||||||
| 19,822 | 19,311 | 511 | ||||||
| 2 | 19,823 | 19,298 | 525 | |||||
| 19,823 | 19,353 | 470 | ||||||
| 19,824 | 19,373 | 451 | ||||||
| 3S | 0 | 18,798 | 1143 | |||||
| 1 | 19,943 | 18,859 | 1084 | |||||
| 2 |
6. Theoretical Predictions
- DA, MM, mix—diquark–antidiquark, meson–meson models and their mixing;
- (I-III)—different sets of variable parameter values (quark masses, potential parameters, constants, etc.).
- SpB, OscI,II [39]—spherical bag model and oscillating potential model;
- QDCSM, ChQM [40]—quark delocalization color screening model and chiral quark model;
- RSM [41]—real scaling method;
- CQM, CMIM, MCFTM [45]—constituent quark model, color-magnetic interaction model and multiquark color flux-tube model;
- NR, Rel [48]—non-relativistic and relativistic considerations, respectively;
- Bt, Fl [49]—“butterfly” and “flip-flop” potentials.
- In many papers using the diquark–antidiquark picture, the cases of color antitriplet-diquark–triplet-antidiquark and color sextet-diquark–antisextet-antidiquark were considered. As we discussed in Section 2, in the color sextet (anti)diquark, the interaction potential between (anti)quarks within the (anti)diquark is repulsive, and thus a corresponding diquark cannot be a bound state, which we consider inappropriate for our problem. Therefore, in Table 10, Table 11, Table 12, Table 13, Table 14, Table 15, Table 16, Table 17, Table 18, Table 19, Table 20, Table 21, Table 22, Table 23, Table 24, Table 25, Table 26, Table 27, Table 28, Table 29 and Table 30, we give theoretical predictions for the masses calculated only for the configuration. If the results were a mixture of two configurations, we chose those masses that contain more of the triplet state in percentage. We note a general trend: in almost all cases, the calculated masses of sextet configurations turned out to be approximately MeV higher than their triplet counterparts.
- * in [39] for model 1, corrections were calculated only for all 1S states and for the two lowest 1P states; corrections for all other states were not calculated.
- ** Two cases were considered in [51]: the presence and absence of the heavy -meson exchange. The results only for the case without such an exchange are given.
- *** in [42], LO results were also obtained, but they are quite similar to NLO⊕G3, so we do not present them.
- **** in [44], all results were obtained in two mass schemes: in the -scheme and on-Shell-scheme. In view of the already colossal number of results of this study, we took the masses only in the -scheme.
| State | 1S | ||
| 0 | 1 | 2 | |
| Our | 6190 | 6271 | 6367 |
| [52] | 6200 | ||
| [39] | 6276 (DA, SpB); 6426 (DA, OscI); 6450 (DA, OscII); 6221, 6260 (MM, SpB) | 6276 (DA, SpB); 6440 (DA, OscI); 6450 (DA, OscII); 6221, 6260 (MM, SpB) | 6276 (DA, SpB); 6469 (DA, OscI); 6450 (DA, OscII); 6221, 6260 (MM, SpB) |
| [53] | 6477 | 6528 | 6573 |
| [54] | 6038∼6115 | 6101∼6176 | 6172∼6216 |
| [55] | 5970 | 6050 | 6220 |
| [56] | 5966 | 6051 | 6223 |
| [57] | |||
| [58] | |||
| [59] | |||
| [60,61] | , | ||
| [62] | 7016 | 6899 | 6956 |
| [48] | |||
| [63,64] | 5969 | 6021 | 6115 |
| [65] | 6487 | 6500 | 6524 |
| [66] | |||
| [67] | |||
| [68] | 6425 (Id); 6483 (IId) | 6425 (Id); 6450 (IId) | 6432 (Id); 6479 (IId) |
| [69] | 5883 | 6120 | 6246 |
| [70] | |||
| [40] | 6128, 6270, 6358 (DA, QDCSM (I-III)); 6466, 6482, 6493 (DA, ChQM (I-III)); 5961∼6206 (MM, QDCSM (I-III)); 5961∼6701 (MM, ChQM (I-III)) | 6149, 6285, 6375 (DA, QDCSM (I-III)); 6479, 6488, 6495 (DA, ChQM (I-III)); 6079∼6088 (MM, QDCSM (I-III)); 6079∼6575 (MM, ChQM (I-III)) | 6197, 6314, 6407 (DA, QDCSM (I-III)); 6498, 6499, 6505 (DA, ChQM (I-III)); 6197∼6207 (MM, QDCSM (I-III)); 6197∼6602 (MM, ChQM (I-III)) |
| [71] | 6542 | 6515 | 6543 |
| [50] | 6455 | 6500 | 6524 |
| [41] | 6360 (DA); 5973 (MM); 5973 (mix); 6510 (RSM) | 6398 (DA); 6084 (MM); 6084 (mix); 6600 (RSM) | 6410 (DA); 6194 (MM); 6194 (mix); 6708 (RSM) |
| [72] | 5960 (Id); 6198 (IId) | 6009 (Id); 6246 (IId) | 6100 (Id); 6323 (IId) |
| [42,43] | (DA, Cur, NLO⊕G3); (DA, Op, NLO⊕G3); , , , (MM) | ||
| [73] | 6469 (DA); 6536, 6657 (MM); 6423, 6650 (mix) | 6674 (DA); 6671 (MM); 6627 (mix) | 7026 (DA); 7030 (MM); 7014 (mix) |
| [74] | 6351 | 6441 | 6471 |
| [75] | 6476 | 6441 | 6475 |
| [45] | 6573 (CQM); 6035 (CMIM); 6454 (MCFTM) | 6580 (CQM); 6139 (CMIM); 6463 (MCFTM) | 6607 (CQM); 6194 (CMIM); 6486 (MCFTM) |
| [76] | |||
| [77] | 6200 | ||
| [78] | |||
| [79] | 6419 (Id); 6390 (IId); 6415 (IIId) | 6456 (Id); 6419 (IId); 6454 (IIId) | 6516 (Id); 6476 (IId); 6514 (IIId) |
| [80] | 6196 | ||
| [81] | , , , | - | |
| [82] | 6271 | 6231 | 6287 |
| [46,47] | 6421 (DA); 5936, 6268 (MM); 6150, 6340 (K) | 6439 (DA); 6070, 6325 (MM); 6271, 6436 (K) | 6472 (DA); 6204, 6338 (MM); 6358, 6473 (K) |
| [83] | 5939 | 5986 | 6079 |
| [84] | 6498 | 6481 | 6502 |
| [85] | 6466 | 6494 | 6551 |
| [86] | 6906 | 5955 (Id); 6896 (IId) | 5960 |
| [87] | 6322 | 6354 | 6385 |
| [88] | , | ||
| [89] | 6270 (Id); 6271 (IId); 6201 (IIId) | 6424 (Id); 6435 (IId); 6396 (IIId) | 6424 (Id); 6435 (IId); 6391 (IIId) |
| [90] | |||
| [91] | 7438-7542 | ||
| [49] | 6874 (Bt); 6850 (FL); 6822 (mix) | 6913 (Bt); 6870 (FL); 6822 (mix) | 6990 (Bt); 6913 (FL); 6822 (mix) |
| [92] | 5978 | 6155 | 6263 |
| [44] | , (DA, LO); , (DA, NLO); (MM, LO); (MM, NLO) | (DA, LO); (DA, NLO); (MM, LO); (MM, NLO) | , (DA, LO); , (DA, NLO); (MM, LO); (MM, NLO) |
| [93] | |||
| [94] | 7035, 7202 | 7050, 7274 | 7069, 7281 |
| [95] | 6384 | 6452 | 6483 |
| [96] | 6035 | 6137 | 6194 |
| State | 1P | ||||||
|---|---|---|---|---|---|---|---|
| S | 0 | 1 | 2 | ||||
| Our | 6631 | 6628 | 6634 | 6644 | 6635 | 6648 | 6664 |
| [97] | 6550 | 6550 | 6550 | 6550 | 6550 | 6550 | 6550 |
| [39] | 6694 (OscI); 6714 (OscII) | 6695 (OscI); 6714 (OscII) | 6718 (OscI); 6714 (OscII) | 6718 (OscI); 6714 (OscII) | 6718 (OscI); 6714 (OscII) | 6718 (OscI); 6714 (OscII) | 6718 (OscI); 6714 (OscII) |
| [53] | 7004 | 6969 | 7013 | 7033 | |||
| [54] | 6998∼7052 | 6993∼7051 | 7275∼7363 | 7002∼7055 | 7278∼7357 | ||
| [98] | (DA); (MM) | ||||||
| [60,61] | |||||||
| [63,64] | 6577 | 6480 | 6577 | 6610 | 6495 | 6600 | 6641 |
| [67] | |||||||
| [69] | 6580 | 6596 | 6584 | ||||
| [50] | 6636 | 6681 | 6676 | 6667 | 6768 | 6630 | 6801 |
| [83] | 6553 | 6460 | 6554 | 6587 | 6459 | 6577 | 6623 |
| [84] | 6740 | 6723 | 6743 | 6752 | 6740 | 6739 | 6753 |
| [86] | 6060 (Id); 6999 (IId) | 6054 (Id); 6995 (IId) | 6054 (Id); 6995 (IId) | 6054 (Id); 6995 (IId) | 6056 (Id); 6996 (IId) | 6056 (Id); 6996 (IId) | 6056 (Id); 6996 (IId) |
| [88] | , | , | , | ||||
| [44] | (DA, LO); (DA, NLO); (MM, LO); (MM, NLO) | (DA, LO); (DA, NLO); (MM, LO); (MM, NLO) | (DA, LO); (DA, NLO); (MM, LO); (MM, NLO) | ||||
| [93] | |||||||
| State | 2S | ||
|---|---|---|---|
| S | 0 | 1 | 2 |
| Our | 6782 | 6816 | 6868 |
| [63,64] | 6663 | 6675 | 6698 |
| [68] | 6856 (Id); 6894 (IId) | 6864 (Id); 6919 (IId) | |
| [69] | 6573 | 6669 | 6739 |
| [70] | |||
| [40] | 6950, 6975 (DA, QDCSM (I-III)); 6825, 6900, 6910 (DA, ChQM (I-III)) | 7250, 7280 (DA, QDCSM (I-III)); 7250, 7275, 7280 (DA, ChQM (I-III)) | |
| [71] | 6940 | 6928 | 6948 |
| [75] | 6908 | 6896 | 6921 |
| [99] | |||
| [79] | 6916 (Id); 6773 (IId); 6924 (IIId) | 6957 (Id); 6792 (IId); 6966 (IIId) | 7001 (Id); 6843 (IId); 7011 (IIId) |
| [83] | 6642 | 6654 | 6676 |
| [84] | 7007 | 6954 | 6917 |
| [85] | 6883 | 6911 | 6968 |
| [86] | 7073 (Id); 8095 (IId) | 7025 (Id); 8060 (IId) | 7041 (Id); 8072 (IId) |
| [87] | 6575 | 6609 | 6639 |
| [89] | 6393 (Id); 6411 (IId); 6575 (IIId) | 6458 (Id); 6502 (IId); 6799 (IIId) | 6458 (Id); 6502 (IId); 6794 (IIId) |
| [90] | |||
| [100] | 6908 | 6919 | 6927 |
| [93] | |||
| State | 1D | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| S | 0 | 1 | 2 | ||||||
| Our | 6921 | 6909 | 6920 | 6932 | 6899 | 6904 | 6915 | 6929 | 6945 |
| [97] | 6780 | 6780 | 6780 | 6780 | 6780 | 6780 | 6780 | 6780 | 6780 |
| [54] | 6586∼6648 | 6530∼6609 | |||||||
| [60,61] | |||||||||
| [69] | 6827 | 6829 | 6827 | 6827 | 6827 | ||||
| [40] | 7140, 7150, 7170 (DA, QDCSM (I-III)); 7150, 7160 (DA, ChQM (I-III)) | ||||||||
| [100] | 6832 | 6833 | 6835 | 6844 | 6848 | 6851 | 6857 | 6863 | 6870 |
| [44] | (DA, LO); (DA, NLO); (MM, LO); (MM, NLO) | ||||||||
| State | 2P | ||||||
|---|---|---|---|---|---|---|---|
| S | 0 | 1 | 2 | ||||
| Our | 7091 | 7100 | 7099 | 7098 | 7113 | 7113 | 7112 |
| [63,64] | 6944 | 6867 | 6944 | 6970 | 6876 | 6962 | 6997 |
| [69] | 6940 | 6953 | 6943 | ||||
| [99] | |||||||
| [83] | 6925 | 6851 | 6926 | 6951 | 6849 | 6944 | 6982 |
| [86] | 7143 (Id); 8174 (IId) | 7130 (Id); 8162 (IId) | 7130 (Id); 8162 (IId) | 7130 (Id); 8162 (IId) | 7134 (Id); 8166 (IId) | 7134 (Id); 8166 (IId) | 7134 (Id); 8166 (IId) |
| [93] | |||||||
| State | 3S | ||
|---|---|---|---|
| S | 0 | 1 | 2 |
| Our | 7259 | 7287 | 7333 |
| [68] | 6915 (Id); 7036 (IId) | 6919 (Id); 7058 (IId) | |
| [69] | 6948 | 7016 | 7071 |
| [40] | 7225, 7250 (DA, QDCSM (I-III)); 7210, 7250, 7260 (DA, ChQM (I-III)) | ||
| [71] | 7063 | 7052 | 7064 |
| [75] | 7296 | 7300 | 7320 |
| [99] | |||
| [79] | 7224 (Id); 7054 (IId); 7229 (IIId) | 7263 (Id); 7066 (IId); 7268 (IIId) | 7257 (Id); 7097 (IId); 7258 (IIId) |
| [83] | 7010 | 7017 | 7032 |
| [84] | 7024 | 7030 | |
| [85] | 7225 | 7253 | 7310 |
| [87] | 6782 | 6814 | 6842 |
| [89] | 6441 (Id); 6477 (IId); 6897 (IIId) | 6464 (Id); 6536 (IId); 7148 (IIId) | 6464 (Id); 6536 (IId); 7148 (IIId) |
| [90] | |||
| [100] | 7240 | 7243 | 7248 |
| [93] | |||
| State | 1S | ||
|---|---|---|---|
| S | 0 | 1 | 2 |
| Our | 12,838 | 12,855 | 12,883 |
| [56] | 12,471 | 12,488 | 12,566 |
| [62] | 13,483 | 13,592 | 13,590 |
| [48] | |||
| [65] | 12,864 | 12,864 | 12,884 |
| [101] | 12,746 (DA); 12,322, 12,684 (MM); 12,322 (mix) | 12,776 (DA); 12,432, 12,737 (MM); 12,432 (mix) | 12,809 (DA); 12,561, 12,791 (MM); 12,561 (mix) |
| [69] | 12,374 | 12,491 | 12,576 |
| [74] | 12,534 | 12,510 | 12,582 |
| [45] | 13,043 (CQM); 12,354 (CMIM); 12,955 (MCFTM) | 13,052 (CQM); 12,436 (CMIM); 12,955 (MCFTM) | 13,084 (CQM); 12,548 (CMIM); 12,984 (MCFTM) |
| [81] | , , , | - | |
| [82] | 12,682 | 12,720 | 12,755 |
| [46,47] | 12,861 (DA); 12,369, 12,809 (MM); 12,599, 12,717 (K) | 12,888 (DA); 12,431, 12,843 (MM); 12,635, 12,768 (K) | 12,926 (DA); 12,565, 12,885 (MM); 12,771, 12,844 (K) |
| [102] | |||
| [90] | |||
| [92] | 12,503 | 12,016 | 12,897 |
| [95] | 12,759 | 12,797 | 12,882 |
| [96] | 12,595 | 12,573 | 12,597 |
| State | 1P | ||||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | |||||
| Our | 13,103 | 13,100 | 13,103 | 13,108 | 13,103 | 13,109 | 13,116 |
| [69] | 12,934 | 12,943 | 12,944 | ||||
| State | 2S | ||
|---|---|---|---|
| S | 0 | 1 | 2 |
| Our | 13,247 | 13,256 | 13,272 |
| [69] | 12,975 | 13,022 | 13,063 |
| [90] | |||
| State | 1D | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| S | 0 | 1 | 2 | ||||||
| Our | 13,306 | 13,299 | 13,304 | 13,311 | 13,293 | 13,296 | 13,301 | 13,308 | 13,317 |
| [69] | 13,166 | 13,167 | 13,170 | 13,168 | 13,166 | ||||
| State | 2P | ||||||
|---|---|---|---|---|---|---|---|
| S | 0 | 1 | 2 | ||||
| Our | 13,428 | 13,431 | 13,431 | 13,431 | 13,434 | 13,435 | 13,436 |
| [69] | 13,262 | 13,269 | 13,269 | ||||
| State | 3S | ||
|---|---|---|---|
| S | 0 | 1 | 2 |
| Our | 13,558 | 13,566 | 13,580 |
| [69] | 13,301 | 13,335 | 13,365 |
| [90] | |||
| State | 1S | 1P | 2S | ||
|---|---|---|---|---|---|
| S | 1 | ||||
| Our | 12,863 | 13,096 | 13,099 | 13,104 | 13,257 |
| [56] | 12,485 (+); 12,424 (−) | ||||
| [62] | 13,599 (+); 13,555 (−) | ||||
| [65] | 12,870 (+); 12,852 (−) | ||||
| [101] | 12,804 (DA); 12,561, 12,737 (MM); 12,561 (mix) (+) | ||||
| [69] | 12,533 | 12,922 | 12,922 (−) | 13,036 | |
| [74] | 12,569 (+); 12,510 (−) | ||||
| [82] | 12,703 (+); 12,744 (−) | ||||
| [46,47] | 12,903 (DA); 12,431, 12,843 (MM); 12,635, 12,768 (K) (+) | ||||
| [102] | (+); (−) | ||||
| [92] | 12,155 (+); 12,896 (−) | ||||
| [95] | 12,857 (+) | ||||
| [96] | 12,538 (+); 12,339 (−) | ||||
| State | 1D | 2P | 3S | ||||
|---|---|---|---|---|---|---|---|
| S | 1 | ||||||
| Our | 13,293 | 13,298 | 13,305 | 13,426 | 13,426 | 13,427 | 13,566 |
| [69] | 13,154 | 13,250 | 13,250 (−) | 13,342 | |||
| State | 1S | 1P | 2S | 1D | 2P | 3S |
|---|---|---|---|---|---|---|
| S | 0 | |||||
| Our | 12,856 | 13,095 | 13,250 | 13,293 | 13,420 | 13,559 |
| [56] | 12,359 | |||||
| [62] | 13,553 | |||||
| [65] | 12,835 | |||||
| [69] | 12,521 | 12,910 | 13,024 | 13,143 | 13,238 | 13,330 |
| [74] | 12,534 | |||||
| [82] | 12,747 | |||||
| [46,47] | 12,892 (DA); 12,369, 12,809 (MM); 12,599, 12,717 (K) | |||||
| [102] | ||||||
| [92] | 12,359 | |||||
| [96] | 12,431 | |||||
| State | 1S | ||
| 0 | 1 | 2 | |
| Our | 19,314 | 19,320 | 19,330 |
| [56] | 18,754 | 18,808 | 18,916 |
| [58] | |||
| [59] | |||
| [60,61] | , | ||
| [103] | 18,800 | ||
| [62] | 20,275 | 20,212 | 20,243 |
| [48] | (NR, MM); (Rel, DA); | ||
| [38] | |||
| [65] | 19,322 | 19,329 | 19,341 |
| [51] | 19,191, 19,221 (DA); 18,670, 18,928, 19,195, 19,205 (MM); 18,670 (mix) | 19,227 (DA); 18,799, 19,179 (MM); 18,799 (mix) | 19,238 (DA); 18,928, 19,195 (MM); 18,928 (mix) |
| [66] | |||
| [67] | |||
| [68] | 19,247 (Id); 19,305 (IId) | 19,247 (Id); 19,311 (IId) | 19,249 (Id); 19,325 (IId) |
| [69] | 18,748 | 18,828 | 18,900 |
| [70] | |||
| [40] | 19,165, 19,256, 19,344 (DA, QDCSM (I-III)); 19,313, 19,456, 19,466 (DA, ChQM (I-III)); 18,800∼18,925 (MM, QDCSM (I-III)); 18,800∼20,041 (MM, ChQM (I-III)) | 19,184, 19,264, 19,354 (DA, QDCSM (I-III)); 19,323, 19,461, 19,467 (DA, ChQM (I-III)); 18,860∼18,864 (MM, QDCSM (I-III)); 18,860∼19,927 (MM, ChQM (I-III)) | 19,236, 19,279, 19,374 (DA, QDCSM (I-III)); 19,344, 19,471 (DA, ChQM (I-III)); 18,921∼18,925 (MM, QDCSM (I-III)); 18,921∼19,933 (MM, ChQM (I-III)) |
| [71] | 19,255 | 19,251 | 19,262 |
| [50] | 19,306 | 19,329 | 19,341 |
| [72] | 18,723 (Id); 18,754 (IId) | 18,738 (Id); 18,768 (IId) | 18,768 (Id); 18,797 (IId) |
| [42,43] | (DA, Cur, NLO⊕G3); (DA, Op, NLO⊕G3); , , , (MM) | ||
| [73] | 17,975, 19,033 (DA); 17,999, 18,038, 19,036, 19,069 (MM); 17,917, 18,010, 19,280 (mix) | 18065, 19,093 (DA); 18,062, 19,087 (MM); 18,009, 19,338, 19,627 (mix) | 18,241, 19,211 (DA); 18,238, 19,207 (MM); 18,189, 19,451, 19,708 (mix) |
| [74] | 19,199 | 19,276 | 19,289 |
| [75] | 19,226 | 19,214 | 19,232 |
| [45] | 19,417 (CQM); 18,834 (CMIM); 19,377 (MCFTM) | 19,413 (CQM); 18,890 (CMIM); 19,373 (MCFTM) | 19,429 (CQM); 18,921 (CMIM); 19,387 (MCFTM) |
| [104] | 19,650, 20,110, 21,470 (Id); 22,310, 22,660, 23,720 (IId) | ||
| [79] | 19,205 (Id); 19,187 (IId); 19,209 (IIId) | 19,221 (Id); 19,202 (IId); 19,225 (IIId) | 19,253 (Id); 19,234 (IId); 19,257 (IIId) |
| [80] | 18,572 | ||
| [81] | , , , | - | |
| [82] | 18,981 | 18,969 | 19,000 |
| [46,47] | 19,196 (DA); 18,802, 19,144 (MM); 18,977, 19,143 (K) | 19,205 (DA); 18,864, 19,126 (MM); 19,053, 19,206 (K) | 19,223 (DA); 18,926, 19,197 (MM); 19,093, 19,225 (K) |
| [105] | 18,719 (Id); 18,749 (IId) | 18,734 (Id); 18,764 (IId) | 18,764 (Id); 18,792 (IId) |
| [87] | 19,666 | 19,673 | 19,680 |
| [88] | , | ||
| [89] | 19,429 (Id); 19,428 (IId); 19,302 (IIId) | 19,557 (Id); 19,558 (IId); 19,409 (IIId) | 19,557 (Id); 19,558 (IId); 19,409 (IIId) |
| [90] | |||
| [49] | 18,444 (Bt); 18,440 (FL); 18,440 (mix) | 18,444 (Bt); 18,440 (FL); 18,440 (mix) | 18,444 (Bt); 18,440 (FL); 18,440 (mix) |
| [92] | 18,752 | 18,805 | 18,920 |
| [44] | , (DA, LO); (DA, NLO); (MM, LO); (MM, NLO) | (DA, LO); (DA, NLO); (MM, LO); (MM, NLO) | (DA, LO); , (DA, NLO); (MM, LO); (MM, NLO) |
| [95] | 19,240 | 19,304 | 19,328 |
| [96] | 18,834 | 18,890 | 18,921 |
| State | 1P | ||||||
|---|---|---|---|---|---|---|---|
| S | 0 | 1 | 2 | ||||
| Our | 19,536 | 19,533 | 19,535 | 19,539 | 19,534 | 19,538 | 19,545 |
| [60,61] | |||||||
| [67] | |||||||
| [69] | 19,281 | 19,288 | 19,288 | ||||
| [50] | 19,479 | 19,500 | 19,496 | 19,492 | 19,603 | 19,476 | 19,617 |
| [105] | 19,381 (Id); 19,361 (IId) | 19,340 (Id); 19,327 (IId) | 19,380 (Id); 19,361 (IId) | 19,395 (Id); 19,373 (IId) | 19,338 (Id); 19,325 (IId) | 19,390 (Id); 19,369 (IId) | 19,412 (Id); 19,388 (IId) |
| [88] | , | , | |||||
| [44] | (DA, LO); (DA, NLO); (MM, LO); (MM, NLO) | (DA, LO); (DA, NLO); (MM, LO); (MM, NLO) | (DA, LO); (DA, NLO); (MM, LO); (MM, NLO) | ||||
| State | 2S | ||
|---|---|---|---|
| S | 0 | 1 | 2 |
| Our | 19,680 | 19,682 | 19,687 |
| [68] | 19,594 (Id); 19,813 (IId) | 19,596 (Id); 19,823 (IId) | |
| [69] | 19,335 | 19,366 | 19,398 |
| [70] | |||
| [71] | 19,625 | 19,625 | 19,633 |
| [75] | 19,583 | 19,582 | 19,594 |
| [79] | 19,636 (Id); 19,544 (IId); 19,646 (IIId) | 19,662 (Id); 19565 (IId); 19,671 (IIId) | 19,684 (Id); 19,591 (IId); 19,694 (IIId) |
| [105] | 19,441 (Id); 19,414 (IId) | 19,443 (Id); 19,416 (IId) | 19,448 (Id); 19,421 (IId) |
| [87] | 19,841 | 19,849 | 19,855 |
| [89] | 19,512 (Id); 19,515 (IId); 19,591 (IIId) | 19,587 (Id); 19,597 (IId); 19,728 (IIId) | 19,587 (Id); 19,597 (IId); 19,728 (IIId) |
| [90] | |||
| [100] | 19,719 | 19,722 | 19,726 |
| State | 1D | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| S | 0 | 1 | 2 | ||||||
| Our | 19,715 | 19,710 | 19,714 | 19,720 | 19,705 | 19,707 | 19,711 | 19,717 | 19,724 |
| [60,61] | |||||||||
| [69] | 19,510 | 19,511 | 19,513 | 19,512 | 19,510 | ||||
| [100] | 19,669 | 19,671 | 19,672 | 19,675 | 19,677 | 19,678 | 19,680 | 19,684 | 19,686 |
| [44] | (DA, LO); (DA, NLO); (MM, LO); (MM, NLO) | ||||||||
| State | 2P | ||||||
|---|---|---|---|---|---|---|---|
| S | 0 | 1 | 2 | ||||
| Our | 19,820 | 19,821 | 19,821 | 19,822 | 19,823 | 19,823 | 19,824 |
| [69] | 19,597 | 19,602 | 19,602 | ||||
| State | 3S | ||
|---|---|---|---|
| S | 0 | 1 | 2 |
| Our | 19,941 | 19,943 | 19,947 |
| [68] | 19,681 (Id); 20,065 (IId) | 19,682 (Id); 20,077 (IID) | |
| [69] | 19,644 | 19,665 | 19,688 |
| [71] | 19,726 | 19,733 | 19,736 |
| [75] | 19,887 | 19,889 | 19,898 |
| [79] | 19,907 (Id); 19,795 (IId); 19,913 (IIId) | 19,930 (Id); 19,815(IId); 19,936 (IIId) | 19,926 (Id); 19,822 (IId); 19,930 (IIId) |
| [105] | 19,759 (Id); 19,701 (IId) | 19,760 (Id); 19,703 (IId) | 19,764 (Id); 19,706 (IId) |
| [87] | 20,001 | 20,012 | 20,021 |
| [89] | 19,557 (Id); 19,565 (IId); 19,845 (IIId) | 19,597 (Id); 19,615 (IId); 20,016 (IIId) | 19,597 (Id); 19,615 (IId); 20,016 (IIId) |
| [90] | |||
| [100] | 19,979 | 19,980 | 19,982 |
- For the tetraquark:
- -
- -
- For the tetraquark:
- -
- -
- For the tetraquark:
- -
- -
- For the tetraquark, our results are generally median: there are many results giving both heavier and lighter masses;
- For the tetraquark masses, our results exceed those of other scientific groups for all diquark spins and excitations;
- For the tetraquark masses, our results are slightly higher than those of most other scientific groups.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Choi, S.K.; Olsen, S.L.; Abe, K.; Abe, T.; Adachi, I.; Ahn, B.S.; Aihara, H.; Akai, K.; Akatsu, M.; Akemoto, M.; et al. Observation of a Narrow Charmoniumlike State in Exclusive B±→K±π+π-J/ψ Decays. Phys. Rev. Lett. 2003, 91, 262001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Workman, R.L.; Burkert, V.D.; Crede, V.; Klempt, E.; Thoma, U.; Tiator, L.; Agashe, K.; Aielli, G.; Allanach, B.C.; Amsler, C.; et al. Review of Particle Physics. Prog. Theor. Exp. Phys. 2022, 2022, 083C01. [Google Scholar] [CrossRef]
- Tornqvist, N.A. Isospin breaking of the narrow charmonium state of Belle at 3872 MeV as a deuson. Phys. Lett. B 2004, 590, 209–215. [Google Scholar] [CrossRef] [Green Version]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; Alkhazov, G.; et al. Observation of the Resonant Character of the Z(4430)- State. Phys. Rev. Lett. 2014, 112, 222002. [Google Scholar] [CrossRef] [Green Version]
- Aaij, R.; Abellán Beteta, C.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Afsharnia, H.; Aidala, C.A.; Aiola, S.; Ajaltouni, Z.; Akar, S.; et al. Observation of structure in the J/ψ-pair mass spectrum. Sci. Bull. 2020, 65, 1983–1993. [Google Scholar] [CrossRef]
- The CMS Collaboration. Observation of New Structures in the J/ψJ/ψ Mass Spectrum in pp Collisions at s=13 TeV, CMS-PAS-BPH-21-003; Technical report; CERN: Geneva, Switzerland, 2022. [Google Scholar]
- The ATLAS Collaboration. Observation of an Excess of Di-Charmonium Eventsin the Four-Muon Final State with the ATLAS Detector, ATLAS-CONF-2022-040; Technical report; CERN: Geneva, Switzerland, 2022. [Google Scholar]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; et al. Observation of J/ψp Resonances Consistent with Pentaquark States in Λb0→J/ψK-p Decays. Phys. Rev. Lett. 2015, 115, 072001. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.X.; Chen, W.; Liu, X.; Liu, Y.R.; Zhu, S.L. An updated review of the new hadron states. arXiv 2022, arXiv:2204.02649. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Aidala, C.A.; Ajaltouni, Z.; Akar, S.; Albicocco, P.; Albrecht, J.; Alessio, F.; Alexander, M.; et al. Search for beautiful tetraquarks in the Υ(1S)μ+μ- invariant-mass spectrum. J. High Energy Phys. 2018, 2018, 086. [Google Scholar] [CrossRef] [Green Version]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Erö, J.; et al. Observation of Υ(1S) pair production in proton-proton collisions at s=8 TeV. J. High Energy Phys. 2017, 05, 013. [Google Scholar] [CrossRef] [Green Version]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Bergauer, T.; Dragicevic, M.; Erö, J.; Escalante Del Valle, A.; Flechl, M.; Frühwirth, R.; et al. Measurement of the Υ(1S) pair production cross section and search for resonances decaying to Υ(1S)μ+μ- in proton-proton collisions at s=13 TeV. Phys. Lett. B 2020, 808, 135578. [Google Scholar] [CrossRef]
- Bigi, I.; Dokshitzer, Y.; Khoze, V.; Kühn, J.; Zerwas, P. Production and decay properties of ultra-heavy quarks. Phys. Lett. B 1986, 181, 157–163. [Google Scholar] [CrossRef] [Green Version]
- Faustov, R.N.; Galkin, V.O.; Savchenko, E.M. Masses of the QQQ¯Q¯ tetraquarks in the relativistic diquark-antidiquark picture. Phys. Rev. D 2020, 102, 114030. [Google Scholar] [CrossRef]
- Faustov, R.N.; Galkin, V.O.; Savchenko, E.M. Heavy Tetraquarks in the Relativistic Quark Model. Universe 2021, 7, 94. [Google Scholar] [CrossRef]
- Ebert, D.; Faustov, R.N.; Galkin, V.O. Masses of heavy baryons in the relativistic quark model. Phys. Rev. D 2005, 72, 034026. [Google Scholar] [CrossRef] [Green Version]
- Ebert, D.; Faustov, R.N.; Galkin, V.O. Spectroscopy and Regge trajectories of heavy baryons in the relativistic quark-diquark picture. Phys. Rev. D 2011, 84, 014025. [Google Scholar] [CrossRef] [Green Version]
- Logunov, A.A.; Tavkhelidze, A.N. Quasi-Optical Approach in Quantum Field Theory. Nuovo Cim. 1963, 29, 380–399. [Google Scholar] [CrossRef]
- Martynenko, A.P.; Faustov, R.N. Relativistic reduced mass and quasipotential equation. Theor. Math. Phys. 1985, 64, 765–770. [Google Scholar] [CrossRef]
- Galkin, V.O.; Faustov, R.N. Some properties of the solutions of a quasipotential equation. Theor. Math. Phys. 1990, 85, 1119–1123. [Google Scholar] [CrossRef]
- Ebert, D.; Faustov, R.N.; Galkin, V.O.; Martynenko, A.P. Mass spectra of doubly heavy baryons in the relativistic quark model. Phys. Rev. D 2002, 66, 014008. [Google Scholar] [CrossRef] [Green Version]
- Ebert, D.; Faustov, R.N.; Galkin, V.O. Masses of heavy tetraquarks in the relativistic quark model. Phys. Lett. B 2006, 634, 214–219. [Google Scholar] [CrossRef]
- Simonov, Y.A. Perturbation theory in the nonperturbative QCD vacuum. Phys. Atom. Nucl. 1995, 58, 107–123. [Google Scholar] [CrossRef]
- Badalian, A.M.; Veselov, A.I.; Bakker, B.L.G. Restriction on the strong coupling constant in the IR region from the 1D-1P splitting in bottomonium. Phys. Rev. D 2004, 70, 016007. [Google Scholar] [CrossRef] [Green Version]
- Galkin, V.O.; Mishurov, A.Y.; Faustov, R.N. Meson masses in the relativistic quark model. Sov. J. Nucl. Phys. 1992, 55, 1207–1213. [Google Scholar]
- Ebert, D.; Faustov, R.N.; Galkin, V.O.; Lucha, W. Masses of tetraquarks with two heavy quarks in the relativistic quark model. Phys. Rev. D 2007, 76, 114015. [Google Scholar] [CrossRef] [Green Version]
- Faustov, R. Magnetic Moment of the Relativistic Composite System. Nuovo Cim. A 1970, 69, 37–46. [Google Scholar] [CrossRef]
- Faustov, R.N. Relativistic Wawefunction and Form Factors of the Bound System. Ann. Phys. 1973, 78, 176–189. [Google Scholar] [CrossRef]
- Galkin, V.O.; Faustov, R.N. Relativistic corrections to radiative decay widths of vector mesons. Sov. J. Nucl. Phys. 1986, 44, 1575–1581. [Google Scholar]
- Galkin, V.O.; Mishurov, A.Y.; Faustov, R.N. Radiative E1 decays of quarkonium in the framework of relativistic quark model. Sov. J. Nucl. Phys. 1990, 51, 705–710. [Google Scholar]
- Faustov, R.N.; Galkin, V.O. Heavy quark 1/mQ expansion of meson weak decay form-factors in the relativistic quark model. Z Phys. C 1995, 66, 119–127. [Google Scholar] [CrossRef]
- Bugg, D.V. How resonances can synchronise with thresholds. J. Phys. G: Nucl. Part. Phys. 2008, 35, 075005. [Google Scholar] [CrossRef] [Green Version]
- Gasser, J.; Lyubovitskij, V.E.; Rusetsky, A. Hadronic atoms in QCD + QED. Phys. Rep. 2008, 456, 167–251. [Google Scholar] [CrossRef]
- Vijande, J.; Barnea, N.; Valcarce, A. Hyperspherical harmonic study of identical-flavor four-quark systems. Nucl. Phys. A 2007, 790, 542–545. [Google Scholar] [CrossRef] [Green Version]
- Richard, J.M.; Valcarce, A.; Vijande, J. String dynamics and metastability of all-heavy tetraquarks. Phys. Rev. D 2017, 95, 054019. [Google Scholar] [CrossRef]
- Richard, J.M.; Valcarce, A.; Vijande, J. Hall-Post inequalities: Review and application to molecules and tetraquarks. Ann. Phys. 2020, 412, 168009. [Google Scholar] [CrossRef]
- Dong, X.K.; Baru, V.; Guo, F.K.; Hanhart, C.; Nefediev, A. Coupled-Channel Interpretation of the LHCb Double-J/ψ Spectrum and Hints of a New State Near the J/ψJ/ψ Threshold. Phys. Rev. Lett. 2021, 126, 132001, Erratum in Phys. Rev. Lett. 2021, 127, 119901.. [Google Scholar] [CrossRef] [PubMed]
- Hughes, C.; Eichten, E.; Davies, C.T.H. Searching for beauty-fully bound tetraquarks using lattice nonrelativistic QCD. Phys. Rev. D 2018, 97, 054505. [Google Scholar] [CrossRef] [Green Version]
- Ader, J.P.; Richard, J.M.; Taxil, P. Do narrow heavy multiquark states exist? Phys. Rev. D 1982, 25, 2370. [Google Scholar] [CrossRef] [Green Version]
- Jin, X.; Xue, Y.; Huang, H.; Ping, J. Full-heavy tetraquarks in constituent quark models. Eur. Phys. J. C 2020, 80, 1083. [Google Scholar] [CrossRef]
- Chen, X. Fully-charm tetraquarks: ccc¯c¯. arXiv 2020, arXiv:2001.06755. [Google Scholar]
- Albuquerque, R.M.; Narison, S.; Rabemananjara, A.; Rabetiarivony, D.; Randriamanatrika, G. Doubly-hidden scalar heavy molecules and tetraquarks states from QCD at NLO. Phys. Rev. D 2020, 102, 094001. [Google Scholar] [CrossRef]
- Albuquerque, R.M.; Narison, S.; Rabetiarivony, D.; Randriamanatrika, G. Doubly hidden 0++ molecules and tetraquarks states from QCD at NLO. Nucl. Part. Phys. Proc. 2021, 312, 15289. [Google Scholar] [CrossRef]
- Wu, R.H.; Zuo, Y.S.; Wang, C.Y.; Meng, C.; Ma, Y.Q.; Chao, K.T. NLO results with operator mixing for fully heavy tetraquarks in QCD sum rules. arXiv 2022, arXiv:2201.11714. [Google Scholar] [CrossRef]
- Deng, C.; Chen, H.; Ping, J. Towards the understanding of fully-heavy tetraquark states from various models. Phys. Rev. D 2021, 103, 014001. [Google Scholar] [CrossRef]
- Yang, G.; Ping, J.; Segovia, J. Exotic resonances of fully-heavy tetraquarks in a lattice-QCD insipired quark model. Phys. Rev. D 2021, 104, 014006. [Google Scholar] [CrossRef]
- Yang, G.; Ping, J.; He, L.; Wang, Q. Potential model prediction of fully-heavy tetraquarks QQQ¯Q¯ (Q=c,b). arXiv 2021, arXiv:2006.13756. [Google Scholar]
- Anwar, M.N.; Ferretti, J.; Guo, F.K.; Santopinto, E.; Zou, B.S. Spectroscopy and decays of the fully-heavy tetraquarks. Eur. Phys. J. C 2018, 78, 647. [Google Scholar] [CrossRef] [Green Version]
- Asadi, Z.; Boroun, G.R. Masses of fully heavy tetraquark states from a four-quark static potential model. Phys. Rev. D 2022, 105, 014006. [Google Scholar] [CrossRef]
- Liu, M.S.; Liu, F.X.; Zhong, X.H.; Zhao, Q. Full-heavy tetraquark states and their evidences in the LHCb di-J/ψ spectrum. arXiv 2020, arXiv:2006.11952. [Google Scholar]
- Chen, X. Analysis of hidden-bottom bbb¯b¯ states. Eur. Phys. J. A 2019, 55, 106. [Google Scholar] [CrossRef]
- Iwasaki, Y. A Possible Model for New Resonances – Exotics and Hidden Charm. Prog. Theor. Phys. 1975, 54, 492. [Google Scholar] [CrossRef] [Green Version]
- Lloyd, R.J.; Vary, J.P. All-charm tetraquarks. Phys. Rev. D 2004, 70, 014009. [Google Scholar] [CrossRef] [Green Version]
- Barnea, N.; Vijande, J.; Valcarce, A. Four-quark spectroscopy within the hyperspherical formalism. Phys. Rev. D 2006, 73, 054004. [Google Scholar] [CrossRef] [Green Version]
- Berezhnoy, A.V.; Likhoded, A.K.; Luchinsky, A.V.; Novoselov, A.A. Production of J/ψ-meson pairs and 4c tetraquark at the LHC. Phys. Rev. D 2011, 84, 094023. [Google Scholar] [CrossRef] [Green Version]
- Berezhnoy, A.V.; Luchinsky, A.V.; Novoselov, A.A. Heavy tetraquarks production at the LHC. Phys. Rev. D 2012, 86, 034004. [Google Scholar] [CrossRef] [Green Version]
- Heupel, W.; Eichmann, G.; Fischer, C.S. Tetraquark bound states in a Bethe–Salpeter approach. Phys. Lett. B 2012, 718, 545–549. [Google Scholar] [CrossRef]
- Karliner, M.; Nussinov, S.; Rosner, J.L. QQQ¯Q¯ states: Masses, production, and decays. Phys. Rev. D 2017, 95, 034011. [Google Scholar] [CrossRef]
- Wang, Z.G. Analysis of the QQQ¯Q¯ tetraquark states with QCD sum rules. Eur. Phys. J. C 2017, 77, 432. [Google Scholar] [CrossRef]
- Chen, W.; Chen, H.X.; Liu, X.; Steele, T.G.; Zhu, S.L. Hunting for exotic doubly hidden-charm/bottom tetraquark states. Phys. Lett. B 2017, 773, 247–251. [Google Scholar] [CrossRef]
- Chen, W.; Chen, H.X.; Liu, X.; Steele, T.G.; Zhu, S.L. Doubly hidden-charm/bottom QQQ¯Q¯ tetraquark states. EPJ Web Conf. 2018, 182, 02028. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Liu, Y.R.; Chen, K.; Liu, X.; Zhu, S.L. Heavy-flavored tetraquark states with the QQQ¯Q¯ configuration. Phys. Rev. D 2018, 97, 094015. [Google Scholar] [CrossRef] [Green Version]
- Debastiani, V.R.; Navarra, F.S. Spectroscopy of the All-Charm Tetraquark. In Proceedings of the XVII International Conference on Hadron Spectroscopy and Structure — PoS(Hadron2017), Salamanca, Spain, 27–29 September 2018; Volume 310, p. 238. [Google Scholar] [CrossRef] [Green Version]
- Debastiani, V.R.; Navarra, F.S. A non-relativistic model for the [cc][c¯c¯] tetraquark. Chinese Phys. C 2019, 43, 013105. [Google Scholar] [CrossRef]
- Liu, M.S.; Lü, Q.F.; Zhong, X.H.; Zhao, Q. All-heavy tetraquarks. Phys. Rev. D 2019, 100, 016006. [Google Scholar] [CrossRef] [Green Version]
- Bai, Y.; Lu, S.; Osborne, J. Beauty-full tetraquarks. Phys. Lett. B 2019, 798, 134930. [Google Scholar] [CrossRef]
- Wang, Z.G.; Di, Z.Y. Analysis of the Vector and Axialvector QQQ¯Q¯ Tetraquark States with QCD Sum Rules. Acta Phys. Polon. B 2019, 50, 1335. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.J.; Meng, L.; Zhu, S.L. Spectrum of the fully-heavy tetraquark state QQQ¯′Q¯′. Phys. Rev. D 2019, 100, 096013. [Google Scholar] [CrossRef]
- Bedolla, M.A.; Ferretti, J.; Roberts, C.D.; Santopinto, E. Spectrum of fully-heavy tetraquarks from a diquark+antidiquark perspective. Eur. Phys. J. C 2020, 80, 1004. [Google Scholar] [CrossRef]
- Karliner, M.; Rosner, J.L. Interpretation of structure in the di-J/ψ spectrum. Phys. Rev. D 2020, 102, 114039. [Google Scholar] [CrossRef]
- Lü, Q.F.; Chen, D.Y.; Dong, Y.B. Masses of fully heavy tetraquarks QQQ¯Q¯ in an extended relativized quark model. Eur. Phys. J. C 2020, 80, 871. [Google Scholar] [CrossRef]
- Lundhammar, P.; Ohlsson, T. Nonrelativistic model of tetraquarks and predictions for their masses from fits to charmed and bottom meson data. Phys. Rev. D 2020, 102, 054018. [Google Scholar] [CrossRef]
- Yang, G.; Ping, J.; Segovia, J. Tetra- and Penta-Quark Structures in the Constituent Quark Model. Symmetry 2020, 12, 1869. [Google Scholar] [CrossRef]
- Gordillo, M.C.; De Soto, F.; Segovia, J. Diffusion Monte Carlo calculations of fully-heavy multiquark bound states. Phys. Rev. D 2020, 102, 114007. [Google Scholar] [CrossRef]
- Zhao, J.; Shi, S.; Zhuang, P. Fully-heavy tetraquarks in a strongly interacting medium. Phys. Rev. D 2020, 102, 114001. [Google Scholar] [CrossRef]
- Zhang, J.R. 0+ fully-charmed tetraquark states. Phys. Rev. D 2021, 103, 014018. [Google Scholar] [CrossRef]
- Obikhod, T.V. Application of the triangulated category to the explanation of fully-charm tetraquark mass. arXiv 2021, arXiv:2103.08449. [Google Scholar] [CrossRef]
- Wang, Z.G. Revisit the tetraquark candidates in the J/ψJ/ψ mass spectrum. Int. J. Mod. Phys. A 2021, 36, 2150014. [Google Scholar] [CrossRef]
- Li, Q.; Chang, C.H.; Wang, G.L.; Wang, T. Mass spectra and wave functions of TQQQ¯Q¯ tetraquarks. Phys. Rev. D 2021, 104, 014018. [Google Scholar] [CrossRef]
- Nefediev, A.V. X(6200) as a compact tetraquark in the QCD string model. Eur. Phys. J. C 2021, 81, 692. [Google Scholar] [CrossRef]
- Yang, B.C.; Tang, L.; Qiao, C.F. Scalar fully-heavy tetraquark states QQ′Q¯Q¯′ in QCD sum rules. Eur. Phys. J. C 2021, 81, 324. [Google Scholar] [CrossRef]
- Weng, X.Z.; Chen, X.L.; Deng, W.Z.; Zhu, S.L. Systematics of fully heavy tetraquarks. Phys. Rev. D 2021, 103, 034001. [Google Scholar] [CrossRef]
- Tiwari, R.; Rathaud, D.P.; Rai, A.K. Spectroscopy of all charm tetraquark states. Indian J. Phys. 2022. [Google Scholar] [CrossRef]
- Wang, G.J.; Meng, L.; Oka, M.; Zhu, S.L. Higher fully charmed tetraquarks: Radial excitations and P-wave states. Phys. Rev. D 2021, 104, 036016. [Google Scholar] [CrossRef]
- Zhao, Z.; Xu, K.; Kaewsnod, A.; Liu, X.; Limphirat, A.; Yan, Y. Study of charmoniumlike and fully-charm tetraquark spectroscopy. Phys. Rev. D 2021, 103, 116027. [Google Scholar] [CrossRef]
- Lesteiro-Tejeda, J.A.; Ramírez-Zaldívar, D.A.; Gracía-Trápaga, C.E.; Guzmán-Martínez, F. Spectroscopy of the tetraquark cc¯-cc¯ in a non-relativistic approach using a phenomenological QCD model. arXiv 2021, arXiv:2101.03192. [Google Scholar]
- Mutuk, H. Nonrelativistic treatment of fully-heavy tetraquarks as diquark-antidiquark states. Eur. Phys. J. C 2021, 81, 367. [Google Scholar] [CrossRef]
- Wang, Q.N.; Yang, Z.Y.; Chen, W. Exotic fully heavy QQQ¯Q¯ tetraquark states in 8[QQ¯]⨂8[QQ¯] color configuration. Phys. Rev. D 2021, 104, 114037. [Google Scholar] [CrossRef]
- Ke, H.W.; Han, X.; Liu, X.H.; Shi, Y.L. Tetraquark state X(6900) and the interaction between diquark and antidiquark. Eur. Phys. J. C 2021, 81, 427. [Google Scholar] [CrossRef]
- Zhu, R. Fully-heavy tetraquark spectra and production at hadron colliders. Nucl. Phys. B 2021, 966, 115393. [Google Scholar] [CrossRef]
- Kuang, Z.; Serafin, K.; Zhao, X.; Vary, J.P. All-charm tetraquark in front form dynamics. Phys. Rev. D 2022, 105, 094028. [Google Scholar] [CrossRef]
- Majarshin, A.J.; Luo, Y.A.; Pan, F.; Segovia, J. Bosonic algebraic approach applied to the [QQ][Q¯Q¯] tetraquarks. Phys. Rev. D 2022, 105, 054024. [Google Scholar] [CrossRef]
- Wang, Z.G. Analysis of the X(6600), X(6900), X(7300) and related tetraquark states with the QCD sum rules. arXiv 2022, arXiv:2207.08059. [Google Scholar] [CrossRef]
- Wang, G.J.; Meng, Q.; Oka, M. The S-wave fully-charmed tetraquark resonant states. arXiv 2022, arXiv:2208.07292. [Google Scholar] [CrossRef]
- An, H.T.; Luo, S.Q.; Liu, Z.W.; Liu, X. Systematic search of fully heavy tetraquark states. empharXiv 2022, arXiv:2208.03899. [Google Scholar]
- Zhuang, Z.; Zhang, Y.; Ma, Y.; Wang, Q. Lineshape of the compact fully heavy tetraquark. Phys. Rev. D 2022, 105, 054026. [Google Scholar] [CrossRef]
- Chao, K.T. The (cc)-(c¯c¯) (Diquark - Antidiquark) States in e+e- Annihilation. Z. Phys. C 1981, 7, 317. [Google Scholar] [CrossRef]
- Chiu, T.W.; Hsieh, T.H. Y(4260) on the lattice. Phys. Rev. D 2006, 73, 094510. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.G. Tetraquark candidates in LHCb’s di-J/ψ mass spectrum. Chinese Phys. C 2020, 44, 113106. [Google Scholar] [CrossRef]
- Liu, F.X.; Liu, M.S.; Zhong, X.H.; Zhao, Q. Higher mass spectra of the fully-charmed and fully-bottom tetraquarks. Phys. Rev. D 2021, 104, 116029. [Google Scholar] [CrossRef]
- Chen, X. Fully-heavy tetraquarks: bbc¯c¯ and bcb¯c¯. Phys. Rev. D 2019, 100, 094009. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.Y.; Wang, Q.N.; Chen, W.; Chen, H.X. Investigation of the stability for fully-heavy bcb¯c¯ tetraquark states. Phys. Rev. D 2021, 104, 014003. [Google Scholar] [CrossRef]
- Esposito, A.; Polosa, A.D. A bbb¯b¯ di-bottomonium at the LHC? Eur. Phys. J. C 2018, 78, 782. [Google Scholar] [CrossRef]
- Vogt, R.; Angerami, A. Bottom tetraquark production at RHIC? Phys. Rev. D 2021, 104, 094025. [Google Scholar] [CrossRef]
- Tiwari, R.; Rathaud, D.P.; Rai, A.K. Mass-spectroscopy of [bb][b¯b¯] and [bq][b¯q¯] tetraquark states in a diquark–antidiquark formalism. Eur. Phys. J. A 2021, 57. [Google Scholar] [CrossRef]
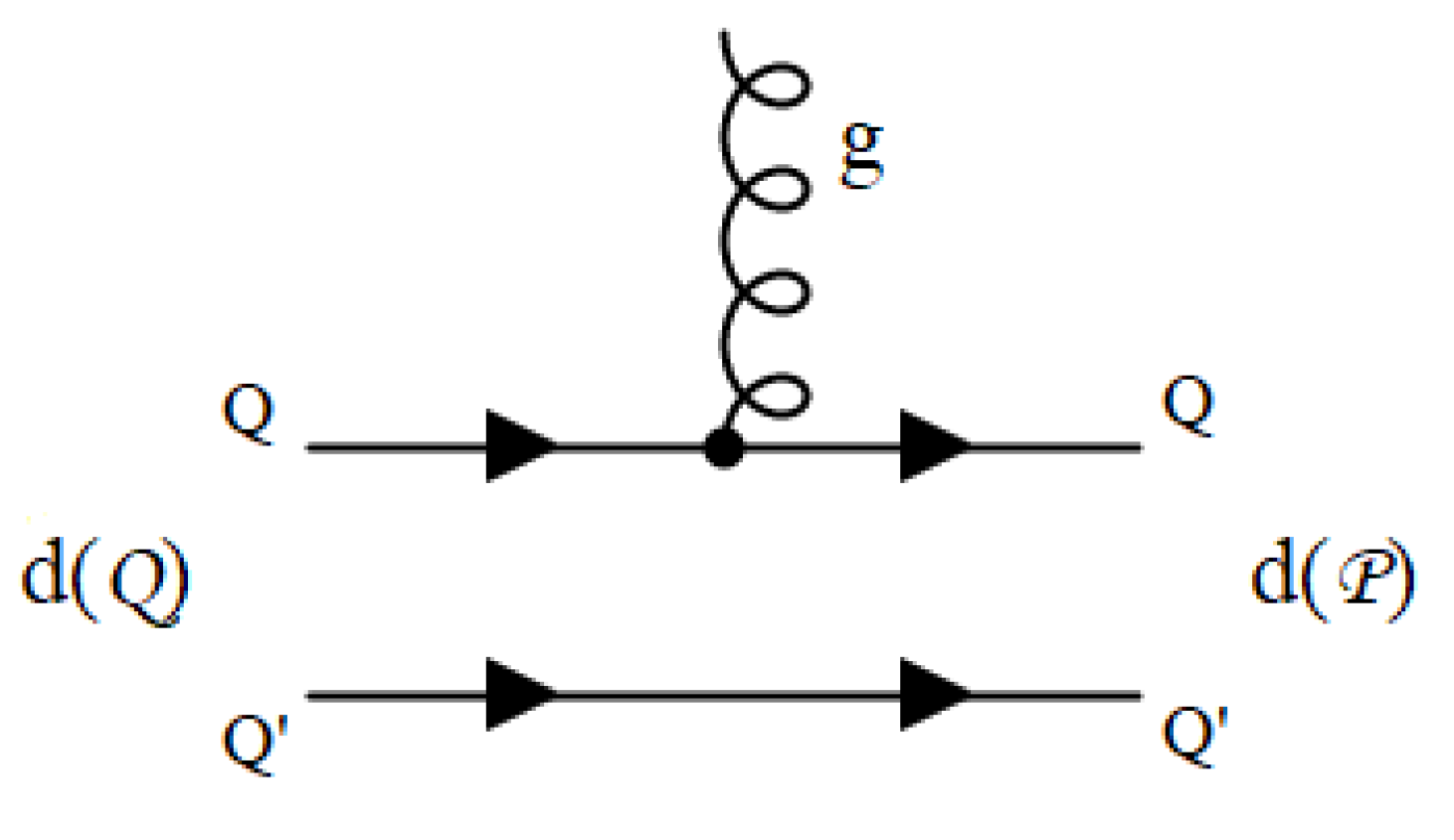
| d | |||||||
|---|---|---|---|---|---|---|---|
| , MeV | , GeV | , GeV | , MeV | , GeV | , GeV | ||
| S | 6519 | 1.50 | 0.59 | ||||
| A | 3226 | 1.30 | 0.42 | 6526 | 1.50 | 0.59 | |
| A | 6526 | 1.50 | 0.59 | 9778 | 1.30 | 1.60 | |
| Collaboration | State | Mass | Width | Our Candidates | |||
|---|---|---|---|---|---|---|---|
| State | S | Mass | |||||
| ATLAS | X(6200) | 1S | 0 | 6190 | |||
| LHCb | X(6400) | ≈ 6400 | 1S | 2 | 6367 | ||
| CMS | X(6600) | 1S 2S | 2 0 | 6367 6782 | |||
| ATLAS | |||||||
| LHCb | X(6900) | 2S 1D 1D 1D 1D | 2 0 2 2 2 | 6868 6921 6899 6904 6915 | |||
| CMS | |||||||
| ATLAS | |||||||
| LHCb | X(7200) | ≈ 7200 | 3S | 0 | 7259 | ||
| ATLAS | |||||||
| CMS | X(7300) | 3S 3S | 0 2 | 7259 7333 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faustov, R.N.; Galkin, V.O.; Savchenko, E.M. Fully Heavy Tetraquark Spectroscopy in the Relativistic Quark Model. Symmetry 2022, 14, 2504. https://doi.org/10.3390/sym14122504
Faustov RN, Galkin VO, Savchenko EM. Fully Heavy Tetraquark Spectroscopy in the Relativistic Quark Model. Symmetry. 2022; 14(12):2504. https://doi.org/10.3390/sym14122504
Chicago/Turabian StyleFaustov, Rudolf N., Vladimir O. Galkin, and Elena M. Savchenko. 2022. "Fully Heavy Tetraquark Spectroscopy in the Relativistic Quark Model" Symmetry 14, no. 12: 2504. https://doi.org/10.3390/sym14122504
APA StyleFaustov, R. N., Galkin, V. O., & Savchenko, E. M. (2022). Fully Heavy Tetraquark Spectroscopy in the Relativistic Quark Model. Symmetry, 14(12), 2504. https://doi.org/10.3390/sym14122504






