A Stochastic Mathematical Model for Understanding the COVID-19 Infection Using Real Data
Abstract
:1. Introduction
2. Model Formulation
3. Dynamics of the Deterministic Model
3.1. Existence and Uniqueness
3.2. Equilibrium Points Analysis
3.3. Endemic Equilibria
3.4. Global Stability Disease Free Case
4. Dynamics of the Stochastic Model
4.1. Preliminaries
4.2. Existence of the Positive Unique Global Solution
4.3. Extinction for the Proposed Model
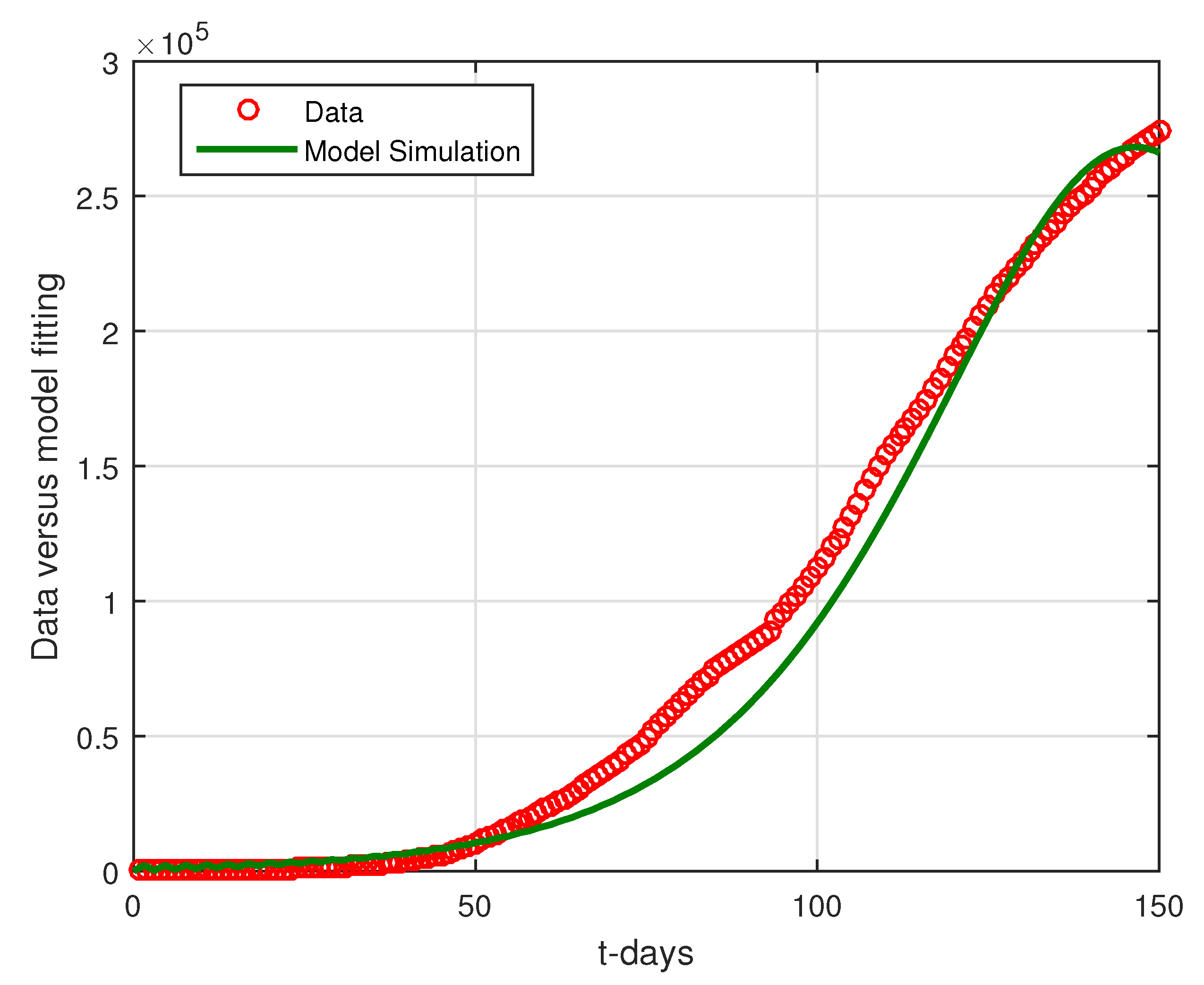
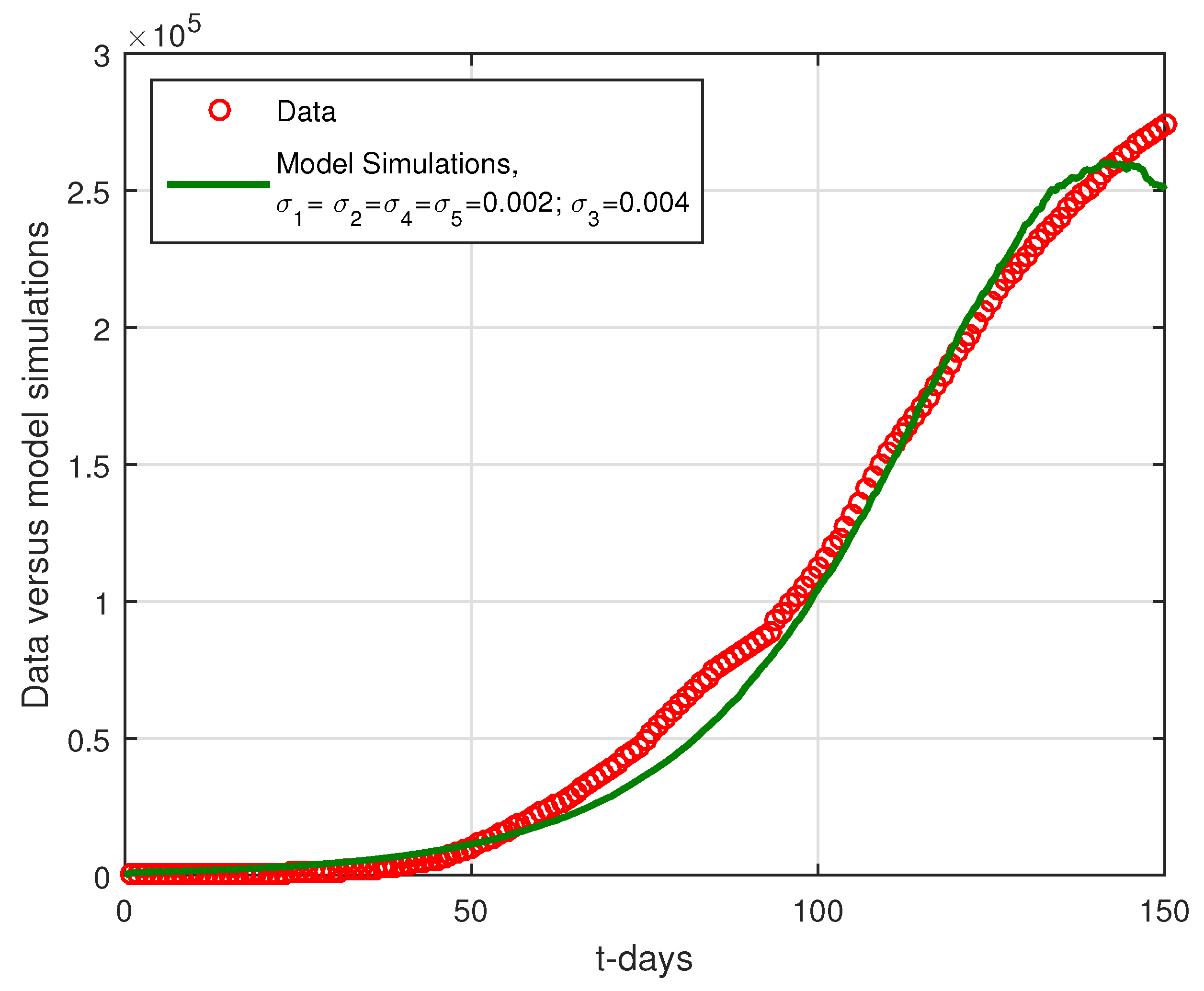
5. Parameters Estimation
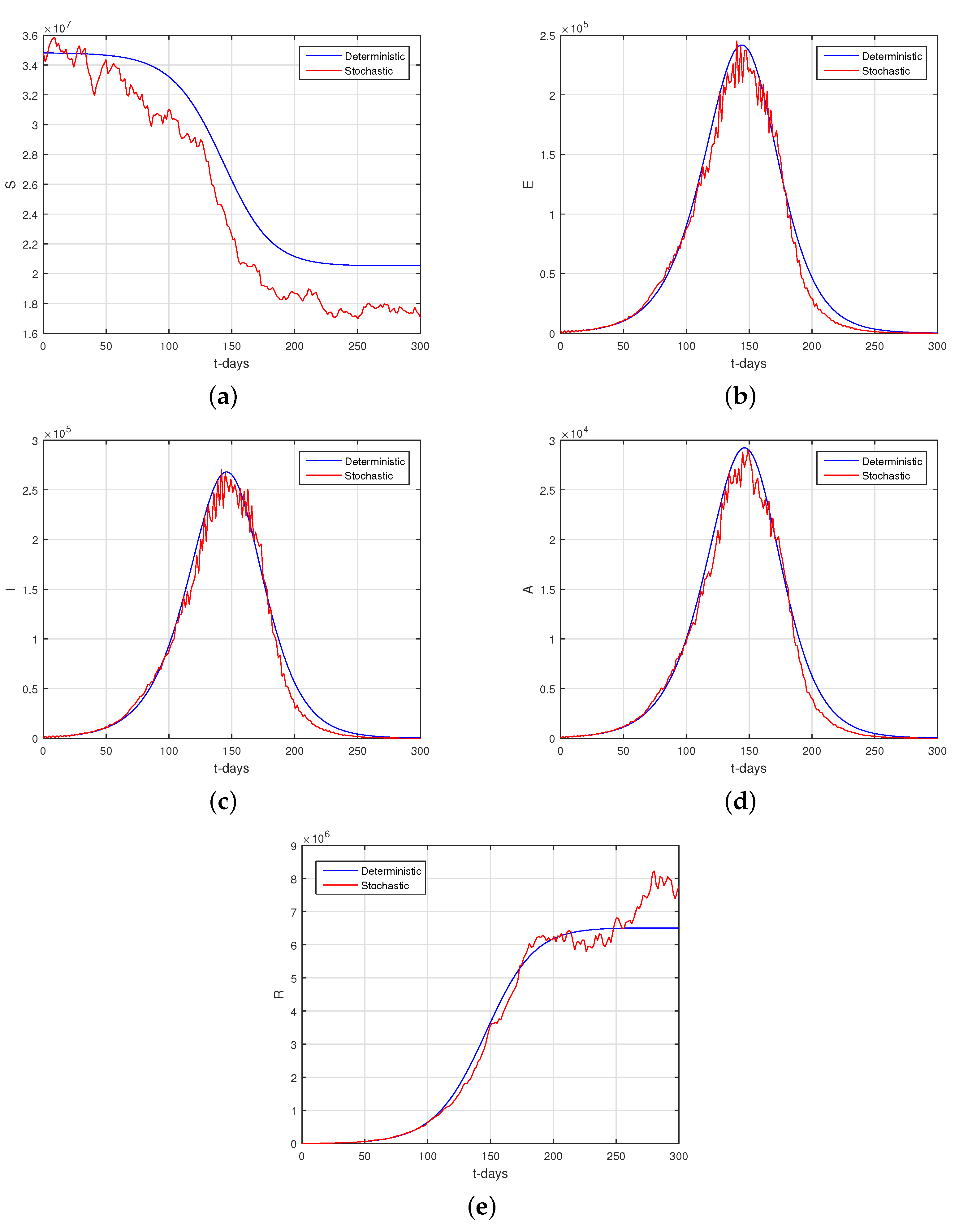
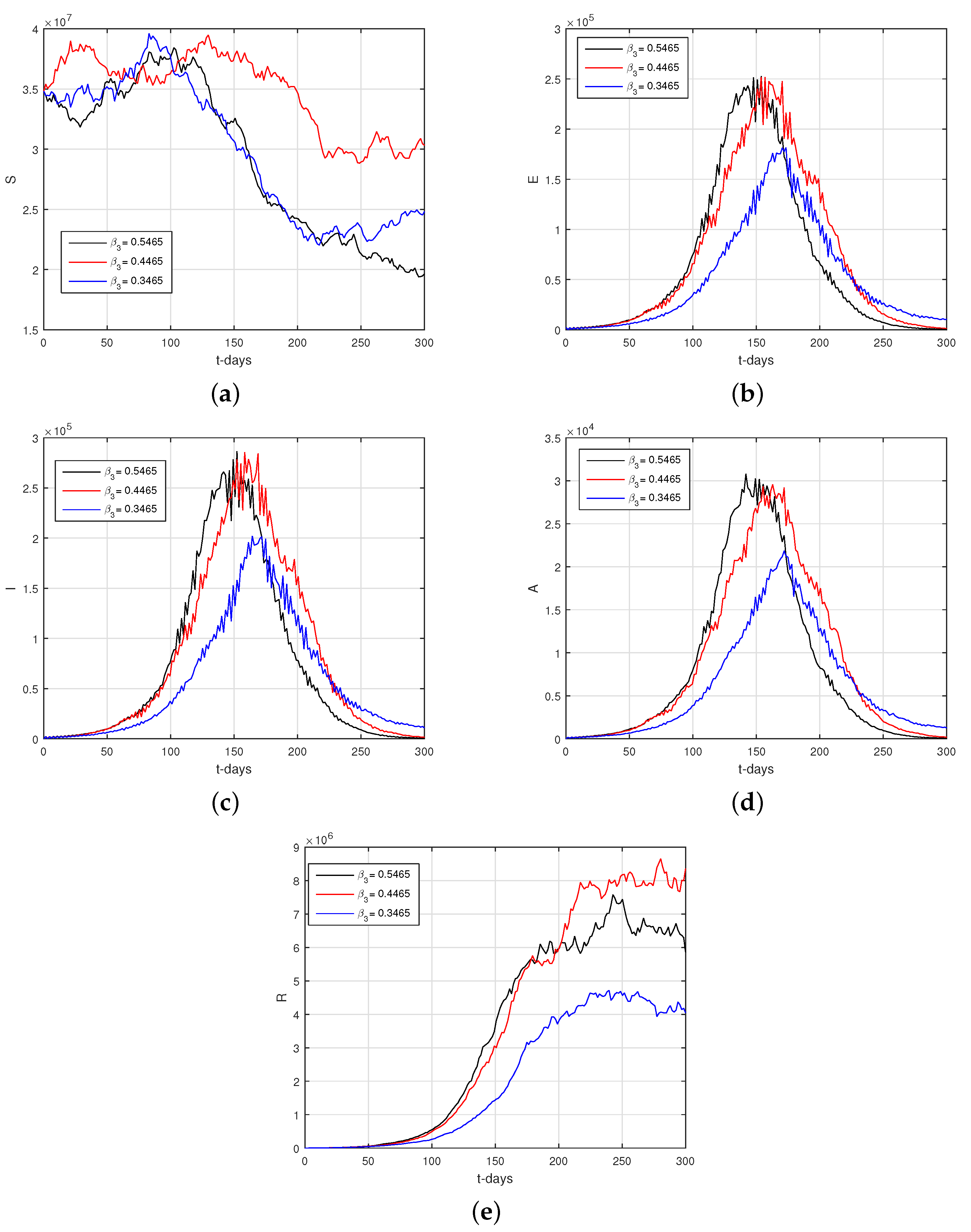
6. Numerical Results
6.1. Numerical Scheme
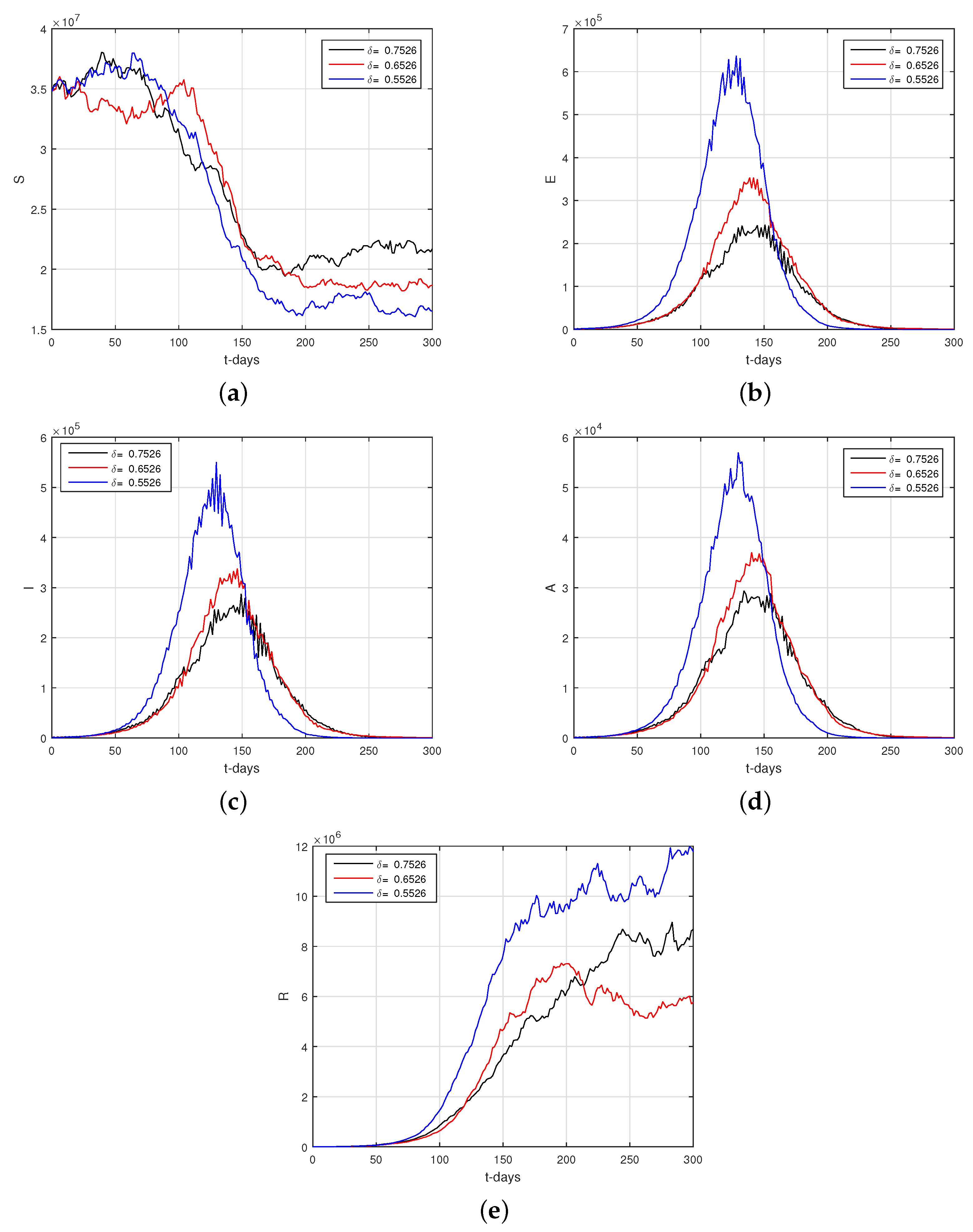
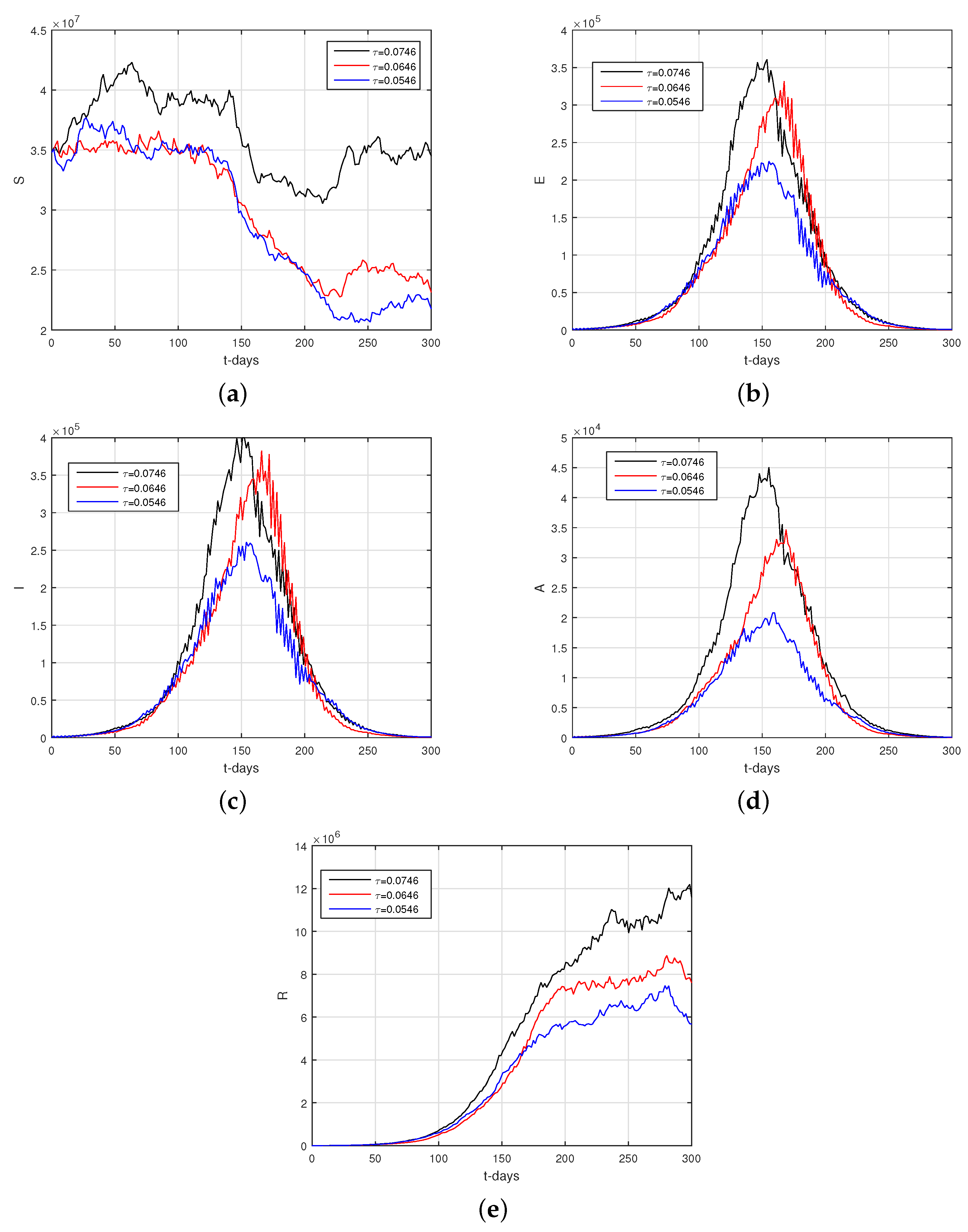
6.2. Results
6.3. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khan, M.A.; Atangana, A. Modeling the dynamics of novel coronavirus (2019-nCov) with fractional derivative. Alex. Eng. J. 2020, 59, 2379–2389. [Google Scholar] [CrossRef]
- Khan, M.A.; Atangana, A.; Alzahrani, E.; Fatmawati. The dynamics of COVID-19 with quarantined and isolation. Adv. Differ. Equ. 2020, 2020, 425. [Google Scholar] [CrossRef]
- Oud, M.A.A.; Ali, A.; Alrabaiah, H.; Ullah, S.; Khan, M.A.; Islam, S. A fractional order mathematical model for COVID-19 dynamics with quarantine, isolation, and environmental viral load. Adv. Differ. Equ. 2021, 2021, 106. [Google Scholar] [CrossRef]
- Rihan, F.; Alsakaji, H. Dynamics of a stochastic delay differential model for COVID-19 infection with asymptomatic infected and interacting people: Case study in the UAE. Results Phys. 2021, 28, 104658. [Google Scholar] [CrossRef] [PubMed]
- Anggriani, N.; Ndii, M.Z.; Amelia, R.; Suryaningrat, W.; Pratama, M.A.A. A mathematical COVID-19 model considering asymptomatic and symptomatic classes with waning immunity. Alex. Eng. J. 2022, 61, 113–124. [Google Scholar] [CrossRef]
- Masandawa, L.; Mirau, S.S.; Mbalawata, I.S. Mathematical modeling of COVID-19 transmission dynamics between healthcare workers and community. Results Phys. 2021, 29, 104731. [Google Scholar] [CrossRef] [PubMed]
- Rwezaura, H.; Tchoumi, S.; Tchuenche, J. Impact of environmental transmission and contact rates on Covid-19 dynamics: A simulation study. Informatics Med. Unlocked 2021, 27, 100807. [Google Scholar] [CrossRef]
- Liu, X.; Ullah, S.; Alshehri, A.; Altanji, M. Mathematical assessment of the dynamics of novel coronavirus infection with treatment: A fractional study. Chaos Solitons Fractals 2021, 153, 111534. [Google Scholar] [CrossRef]
- Beigi, A.; Yousefpour, A.; Yasami, A.; Gómez-Aguilar, J.; Bekiros, S.; Jahanshahi, H. Application of reinforcement learning for effective vaccination strategies of coronavirus disease 2019 (COVID-19). Eur. Phys. J. Plus 2021, 136, 609. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Guerra, R.; Flores-Flores, J.P. An algorithm for the robust estimation of the COVID-19 pandemics population by considering undetected individuals. Appl. Math. Comput. 2021, 405, 126273. [Google Scholar] [PubMed]
- Riyapan, P.; Shuaib, S.E.; Intarasit, A. A Mathematical model of COVID-19 Pandemic: A case study of Bangkok, Thailand. Comput. Math. Methods Med. 2021, 2021, 6664483. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.A.; Ullah, S.; Kumar, S. A robust study on 2019-nCOV outbreaks through non-singular derivative. Eur. Phys. J. Plus 2021, 136, 168. [Google Scholar] [CrossRef]
- Bock, W.; Jayathunga, Y.; Götz, T.; Rockenfeller, R. Are the upper bounds for new SARS-CoV-2 infections in Germany useful? Comput. Math. Biophys. 2021, 9, 242–260. [Google Scholar] [CrossRef]
- Khan, M.A.; Atangana, A. Mathematical modeling and analysis of COVID-19: A study of new variant Omicron. Phys. A Stat. Mech. Its Appl. 2022, 599, 127452. [Google Scholar] [CrossRef] [PubMed]
- Muniyappan, A.; Sundarappan, B.; Manoharan, P.; Hamdi, M.; Raahemifar, K.; Bourouis, S.; Varadarajan, V. Stability and numerical solutions of second wave mathematical modeling on covid-19 and omicron outbreak strategy of pandemic: Analytical and error analysis of approximate series solutions by using hpm. Mathematics 2022, 10, 343. [Google Scholar] [CrossRef]
- Pandey, P.; Gómez-Aguilar, J.; Kaabar, M.K.; Siri, Z.; Abd Allah, A.M. Mathematical modeling of COVID-19 pandemic in India using Caputo-Fabrizio fractional derivative. Comput. Biol. Med. 2022, 145, 105518. [Google Scholar] [CrossRef] [PubMed]
- Asamoah, J.K.K.; Okyere, E.; Abidemi, A.; Moore, S.E.; Sun, G.Q.; Jin, Z.; Acheampong, E.; Gordon, J.F. Optimal control and comprehensive cost-effectiveness analysis for COVID-19. Results Phys. 2022, 33, 105177. [Google Scholar] [CrossRef]
- Khajanchi, S.; Sarkar, K.; Banerjee, S. Modeling the dynamics of COVID-19 pandemic with implementation of intervention strategies. Eur. Phys. J. Plus 2022, 137, 129. [Google Scholar] [CrossRef]
- Ullah, M.S.; Higazy, M.; Kabir, K.A. Modeling the epidemic control measures in overcoming COVID-19 outbreaks: A fractional-order derivative approach. Chaos Solitons Fractals 2022, 155, 111636. [Google Scholar] [CrossRef] [PubMed]
- Tesfaye, A.W.; Satana, T.S. Stochastic model of the transmission dynamics of COVID-19 pandemic. Adv. Differ. Equ. 2021, 2021, 457. [Google Scholar] [CrossRef] [PubMed]
- Rihan, F.A.; Alsakaji, H.J.; Rajivganthi, C. Stochastic SIRC epidemic model with time-delay for COVID-19. Adv. Differ. Equ. 2020, 2020, 502. [Google Scholar] [CrossRef] [PubMed]
- Niño-Torres, D.; Ríos-Gutiérrez, A.; Arunachalam, V.; Ohajunwa, C.; Seshaiyer, P. Stochastic modeling, analysis, and simulation of the COVID-19 pandemic with explicit behavioral changes in Bogotá: A case study. Infect. Dis. Model. 2022, 7, 199–211. [Google Scholar] [CrossRef] [PubMed]
- Tesfay, A.; Saeed, T.; Zeb, A.; Tesfay, D.; Khalaf, A.; Brannan, J. Dynamics of a stochastic COVID-19 epidemic model with jump-diffusion. Adv. Differ. Equ. 2021, 2021, 228. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Gupta, A.; Sampat, A.; Zhai, C. A stochastic contact network model for assessing outbreak risk of COVID-19 in workplaces. PLoS ONE 2022, 17, e0262316. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.J. A primer on stochastic epidemic models: Formulation, numerical simulation, and analysis. Infect. Dis. Model. 2017, 2, 128–142. [Google Scholar] [CrossRef] [PubMed]
- Zhong, H.; Wang, W. Mathematical analysis for COVID-19 resurgence in the contaminated environment. Math. Biosci. Eng. 2020, 17, 6909–6927. [Google Scholar] [CrossRef]
- Li, S.; Ying, S. Latest Research Advances on Novel Coronavirus Pneumonia. 2020, SciFinder; 2020. Preprint|SciFinder|ID: Ppcovidwho-4385. Available online: https://pesquisa.bvsalud.org/global-literature-on-novel-coronavirus-2019-ncov/resource/pt/ppcovidwho-4385 (accessed on 20 September 2022).
- Chen, Y.; Wang, A.; Yi, B.; Ding, K.; Wang, H.; Wang, J.; Shi, H.; Wang, S.; Xu, G. Epidemiological characteristics of infection in COVID-19 close contacts in Ningbo city. Zhonghua Liu Xing Bing Xue Zhi Zhonghua Liuxingbingxue Zazhi 2020, 41, 667–671. [Google Scholar]
- Heilongjiang Provincial Health Committee. Available online: http://wsjkw.hlj.gov.cn/ (accessed on 10 July 2022).
- Xiong, C. A detailed explanation of survival time for COVID-19 virus in the environment. China Food Safty Mag. 2020, 5, 22–25. [Google Scholar]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Mao, X. Stochastic Differential Equations and their Applications; Horwood Publ.: Chichester, UK, 1997. [Google Scholar]
- Zhang, Q.; Zhou, K. Stationary distribution and extinction of a stochastic SIQR model with saturated incidence rate. Math. Probl. Eng. 2019, 2019, 3575410. [Google Scholar] [CrossRef]
- Din, A.; Liang, J.; Zhou, T. Detecting critical transitions in the case of moderate or strong noise by binomial moments. Phys. Rev. E 2018, 98, 012114. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Jiang, D. The threshold of a stochastic SIRS epidemic model with saturated incidence. Appl. Math. Lett. 2014, 34, 90–93. [Google Scholar] [CrossRef]
- Zhao, Y.; Jiang, D. The threshold of a stochastic SIS epidemic model with vaccination. Appl. Math. Comput. 2014, 243, 718–727. [Google Scholar] [CrossRef]
- World/Countries/Saudi Arabia. Available online: https://www.worldometers.info/coronavirus/country/saudi-arabia/ (accessed on 20 September 2022).
- Daily New Cases in Saudi Arabia. Available online: https://www.worldometers.info/coronavirus/country/saudi-arabia/ (accessed on 20 September 2022).
- Saudi Arabia Population. Available online: https://www.worldometers.info/world-population/saudi-arabia-population/ (accessed on 20 September 2022).
- Life Expectancy at Birth, Total (Years)—Saudi Arabia. Available online: https://data.worldbank.org/indicator/SP.DYN.LE00.IN?locations=SA (accessed on 20 September 2022).
- Higham, D.J. An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Yezli, S.; Khan, A. COVID-19 social distancing in the Kingdom of Saudi Arabia: Bold measures in the face of political, economic, social and religious challenges. Travel Med. Infect. Dis. 2020, 37, 101692. [Google Scholar] [CrossRef] [PubMed]
- Al-Harbi, S.K.; Al-Tuwairqi, S.M. Modeling the effect of lockdown and social distancing on the spread of COVID-19 in Saudi Arabia. PLoS ONE 2022, 17, e0265779. [Google Scholar] [CrossRef] [PubMed]



| Parameter | Description | Value | Source |
|---|---|---|---|
| Birth rate | 1273.94 | Estimated | |
| d | Natural death rate | Estimated | |
| Contact rate among E and S | 0.1321 | Fitted | |
| Contact rate among I and S | 0.5926 | Fitted | |
| Contact rate among A and S | 0.5465 | Fitted | |
| Incubation period | 0.7526 | Fitted | |
| Incubation period | 0.0746 | Fitted | |
| Natural mortality due to disease | 0.3691 | Fitted | |
| Recovery from I | 0.2588 | Fitted | |
| Recovery from A | 0.4639 | Fitted |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshammari, F.S.; Akyildiz, F.T.; Khan, M.A.; Din, A.; Sunthrayuth, P. A Stochastic Mathematical Model for Understanding the COVID-19 Infection Using Real Data. Symmetry 2022, 14, 2521. https://doi.org/10.3390/sym14122521
Alshammari FS, Akyildiz FT, Khan MA, Din A, Sunthrayuth P. A Stochastic Mathematical Model for Understanding the COVID-19 Infection Using Real Data. Symmetry. 2022; 14(12):2521. https://doi.org/10.3390/sym14122521
Chicago/Turabian StyleAlshammari, Fehaid Salem, Fahir Talay Akyildiz, Muhammad Altaf Khan, Anwarud Din, and Pongsakorn Sunthrayuth. 2022. "A Stochastic Mathematical Model for Understanding the COVID-19 Infection Using Real Data" Symmetry 14, no. 12: 2521. https://doi.org/10.3390/sym14122521
APA StyleAlshammari, F. S., Akyildiz, F. T., Khan, M. A., Din, A., & Sunthrayuth, P. (2022). A Stochastic Mathematical Model for Understanding the COVID-19 Infection Using Real Data. Symmetry, 14(12), 2521. https://doi.org/10.3390/sym14122521







