Abstract
This article presents the performance analysis and comparison of turbo codes for several interleavers with short blockchains. According to the symmetry concept, turbo codes consist of two symmetric convolutional codes preceded by an interleaver. Some interleavers can be described by symmetric 3 × 3 generator matrices, whereas others are represented through symmetric matrices in which the nonzero terms in the matrix are monomials. Interest in short blockchains has grown over the years because of their use in emerging applications that require the transmission of data units in the order of hundred bits. In this research, interleavers used are random interleaver, semi-random interleaver, quadratic polynomial permutation (QPP) interleaver, and chaotic Lozi map interleaver. For each interleaver, the turbo code is assessed with at least two short data distances; then, the interleavers are compared against each other. The performance of turbo codes is assessed based on bit error rate, particularly with lengths between 64 and 512 bits. Additionally, an interleaver based on Duffing chaotic maps is proposed, whose deterministic nature provides an advantage, and the performance results are presented, achieving excellent BER values for 64 bits. With these results, the effect of the interleaver on turbo codes and particularly on short block length interleavers, is studied.
1. Introduction
Convolutional codes concatenated in parallel are used for error detection and correction, as well as denominated turbo codes created by Claude Berrou, Alain Glavieux, and Punya Thitimajshima in 1993 [1]. In terms of bit error rate, the performance of convolutional codes concatenated in parallel is close to Shannon’s limit. Shannon’s channel capacity is a superior quota that establishes the maximum quantity of digital data that can be transmitted without error over a communication link that has a specific bandwidth and is subject to noise interference. This outstanding characteristic has allowed for the incorporation of turbo codes in communication standards such as 3G Long Term Evolution (LTE) [2], LTE/LTE-A for 4G mobile communication systems [3], and 5G communications [4]. For the 5G communication standard, its application considers diverse scenarios and would not be restricted to the coverage of large areas but would also be employed in machine-to-machine, vehicle-to-vehicle, indoor, and outdoor communications, among others [5]. Undoubtedly, the 5G network will present a significant change in the industry, businesses, and daily life in general. The coverage, data performance, latency, and energy efficiency will improve compared with the current fifth-generation system [6]. However, the diversity of application scenarios indicates that there will be multiple 5G technologies, which would not be represented by one dominant technology as they would coexist with some previous technologies from 1G to 4G systems.
Currently, applications such as machine communication, real-time communication, the Internet of Things, wireless sensor networks, smart metering networks, satellite uplink, messenger services, and remote command links [7,8,9,10] require short and medium data lengths, i.e., in the order of 50 to 1000 bits, in the communication [11]. Because of some emerging applications, interest in short and medium blockchain turbo codes has increased [12,13,14]. The applications above are characterized by having specific requirements such as low-latency and high-reliability transmitters. The use of short packages is considered a key element in complying with these requirements [15].
Other codes, such as the low-density parity check (LDPC) presented in [16] and the polar code, have similar error correction capacities [17]. Nevertheless, the computing complexity of both LPDC and polar decoders is lower for most codification rates, as opposed to the high complexity required in turbo codes [18]. Turbo, LDPC, and polar codes admit different block lengths L and coding rates R, which are given by their structures. In experimental coder tests for short lengths (64 and 128 bits), the turbo code performs better than the LDPC code [11].
The design of long channel codes for iterative decoding is well established and based on a set of performance metrics, such as the iterative decoding threshold [19] or the ensemble typical minimum distance [20]. For larger blocks, modern channel codes such as turbo codes [9] have an excellent performance in several communication channels. However, nowadays, performance degradation associated with short block length turbo codes has restricted their use to applications that employ communications with short block-length codewords [10].
Most classic tools developed for turbo code design are not applicable to the design of short blocks that can be decoded iteratively because of their extremely low performance [11]. In connection, if the performance of turbo codes is correlated with the code’s distance spectrum, an “error floor” is obtained, which is a consequence of the relatively small free distance of the code [21]. The design of an algorithm for decoding short blocks with optimal performance in terms of error correction and computational complexity continues to be an unsolved problem [10].
The error floor that may appear in these cases, which varies according to the distribution of code words with low weight, can be reduced through an increase in the free distance or a reduction in the number of code words [21]. Commonly, this can be achieved after an improvement in the design of the interleaver [22]. However, this topic is still a new field of research at both the theory and technology levels [11], despite the significant advances in the design and analysis codes for correcting errors in short blocks made by the academy and the industry [23].
A review of the main studies on interleavers for turbo codes with short and medium block lengths is presented below. In [22], the design of parallel turbo codes with short block lengths in the order of 64 to 128 bits is dealt with. This work methodically describes how to build turbo codes with a large minimum distance for short block lengths and arbitrary rates. The interleaver parameters were adequately selected to maximize the minimum distance of the turbo code, such that the error floor is considerably reduced, and better performance is obtained in the waterfall region. However, the decoding algorithms designed are too complex for many applications.
Quadratic permutation polynomial (QPP) interleavers have been widely researched since 2005. In [23], a study on permutation polynomial (PP) interleavers, which are deterministic interleavers for turbo codes, is conducted, and a degree 3, 4, and 5 PP is designed, which has optimal minimum distances and lowest corresponding codeword multiplicities for turbo codes with recursive convolutional component codes from LTE standard. The short and medium lengths used range from 40 to 512 bits.
In [24], a new method for designing efficient puncture-constrained interleavers for turbo codes is created. The interleaver function is defined through a layered design process that considers several criteria, such as minimum span, correlation girth, and puncturing constraints. This new design method enables the resulting turbo codes to profit from a joint optimization of the puncturing pattern, so the interleaver achieves an improved error rate performance. The tests consider data blocks with 1504 bits. Their bit error rate (BER) is assessed on the basis of Eb/N0 (bit signal-to-noise ratio (SNR)), and the Es/N0 (symbol SNR) relation as a function of data between 100 and 1000 bits. Additionally, significant improvements are achieved in the waterfall and error floor regions thanks to the incorporation of puncturing constraints into the interleaver design.
In [25], a modified interleaver design is shown, which takes advantage of the coder structure and improves the performance of the turbo code with a short block length. The applied criterion leads to the introduction of the subvector interleaver and of the S-random interleaver constrained by a subvector. The tests conducted use the 140- and 224-bit lengths and implement the corresponding turbo code in the 3GPP LTE encoder with the proposed interleaver in the GNU radio platform.
In [11], a comparison of the codes for short block lengths is presented. In addition, some of the most promising code buildings, which are aimed at the short block regimes, are introduced and compared with the performance limits for finite length as well as with the coding schemes for classic errors. The codes analyzed are turbo, LDPC, and polar codes, among others, which have block lengths of 512 and 256 bits with a one-half rate. From this analysis, it is concluded that the design of block codes for short data blocks is an unsolved research problem.
In [26], the turbo codes of the LTE standard are considered. These codes have short and medium interleaver lengths with 16Ψ or 48Ψ forms, where Ψ is a product between different prime numbers bigger than 3. The analyzed interleavers are Cubic Permutation Polynomials (CPP), for which the minimum distance is constrained by the 38, 36, and 28 values for three different classes of polynomial coefficients. The error correction performance obtained with the CPP interleavers is better than that of the Fourth-Degree Permutation Polynomial (4-PP) and QPP interleavers.
Meanwhile, studies of chaotic maps have been conducted. In [27], a chaotic interleaver is introduced to substitute the random interleaver generally used in conventional turbo codes. The results of computer simulations reveal that the scheme proposed delivers better BER performance compared with conventional block interleaving.
In [28], a new chaotic interleaver is proposed for correcting burst errors in an effective way. The results of computer simulations are shown in terms of the optimal solution observed, together with the value of BER against Eb/N0. In the cases simulated, a good performance is obtained with the chaotic golden interleaver when transmitting data both in short block (L = 400 bits) and long block lengths (L = 1024).
In [29], a chaotic interleaver has been used over a low-density parity-check code and applied to a power line communication (PLC), thereby proposing a new interleaver scheme based on the chaotic baker map. Images transmitted via computer simulations demonstrate that the proposed algorithms work well in the PLC channel.
From these recent studies on interleavers for turbo codes, it is noticed that new improvements for turbo codes continue to be proposed. However, the analysis and comparison of turbo code performance are still necessary for diverse interleavers with short block lengths. This is the motivation of this work, in which such an analysis and comparison is conducted from the perspective of the interleaver’s action. BER versus the SNR is assessed while maintaining the iterative coder and decoder features. Additionally, the performance results for the parallel turbo code for short block lengths are reviewed, particularly for lengths between 64 bits and 512 bits, and a new interleaver based on Duffing map is proposed.
2. Parallel Concatenated Convolutional Codes
In 1993, Berrou et al. [1] introduced the parallel concatenated convolutional codes (PCCC) with interleaver and named them turbo codes. These codes are based on two recursive systematic convolutional (RSC) encoders in parallel, but an interleaver precedes the second RSC. The binary information sequence of L length is expressed by ) in the first coder input, while describes the permuted version of the same sequence in the second coder input. Meanwhile, ) and ) are code words from the first and second components codes of the turbo code, respectively. The length of the codeword for the first and second component code is N1 and N2, respectively.
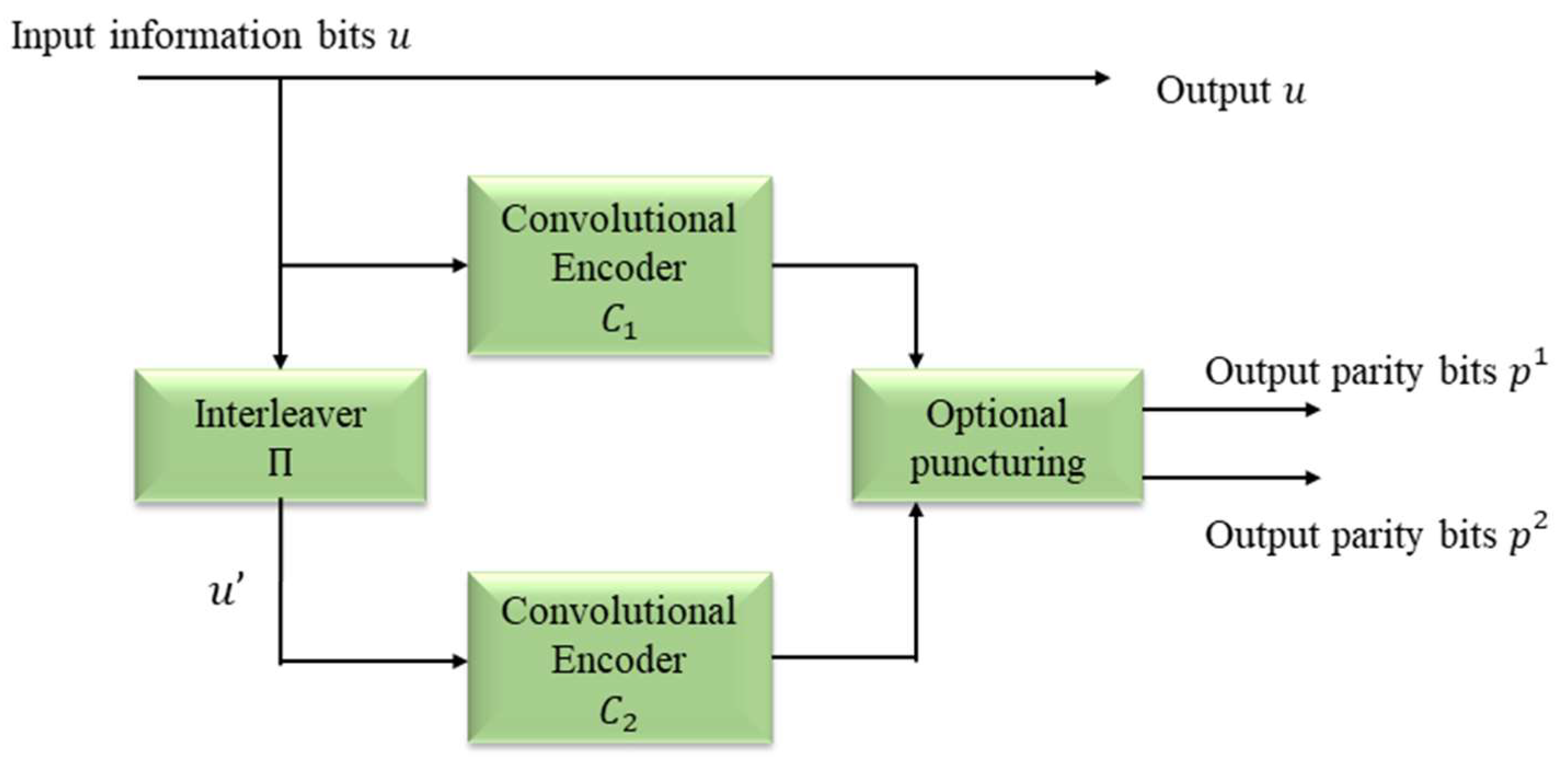
Figure 1 presents the formation of the output code word c based on the concatenation in Equation (1), omitting the permuted information symbols u′.
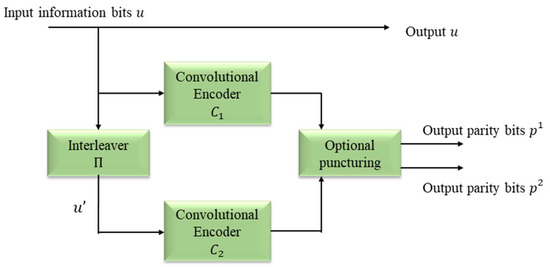
Figure 1.
Scheme for parallel concatenated turbo code.
The rate of the resulting code R is given by Equation (2).
The concatenation rule of the interleaver π is defined by Equation (3):
where π(i), corresponds to the indexes.
The relation between ui and u′i is given by Equation (4):
2.1. Selected Turbo Encoder Scheme
A coding scheme with a parallel concatenation is used by the selected turbo codes to encode a binary input. Specifically, this scheme employs an interleaver and two convolutional codes. A vector with tail bits on its end is generated by each encoder; the flows of systematic bits, together with the parity bit flows of the first and second encoder, form the output of these tail bits, while a block links these three flows and multiplexes their tail bits.
In turn, the encoder receives an input signal corresponding to a column vector of the L x 1 order and generates an output signal corresponding to the column vector of the M x 1 order. For a given trellis, the M and L lengths are given by Equations (5) and (6).
where
- L is the encoder input length;
- M is the encoder output length;
- n = log2(Tnos);
- Tnos is the number of output symbols for the trellis;
- NumTails = log2(Tns)·n
- Tns is the trellis status number;
- v is the memory of the convolutional component codes.
The trellis diagram corresponds to the mapping in the sense that all valid mapper configurations correspond to a path in the trellis diagram. The number of states is the number of binary combinations considered as inputs in the trellis diagram. The number of output symbols for the trellis is the number of elements obtained as a result of the trellis path. The post interleaver trellis termination is used, and the termination bits for the second component code are transmitted.
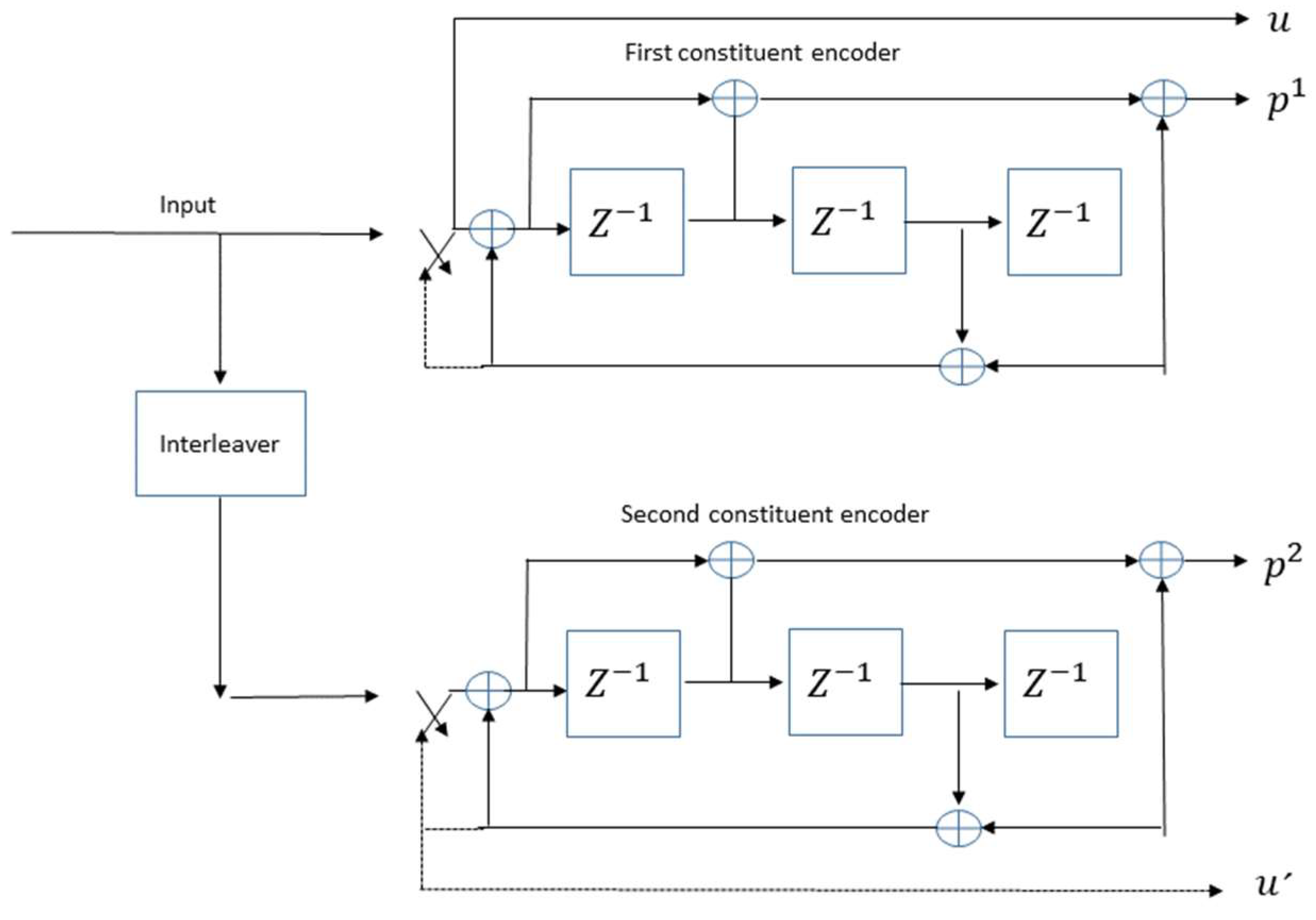
The configuration of the encoder for a trellis is presented in Figure 2. The trellis structure has the following parameters: a length constraint with a value of 4, a component code with the generator matrix in octal form. Three L-bit interlaced length flows compose the output, namely the systematic bits streams (u) and the parity bits (p1) and (p2) of the first encoder and second encoder, respectively. The last three parity bits in the streams p1 and p2 correspond to the tail bits of the two encoders, obtained at the outputs of the discontinuous lines when the switches are in the lower position.
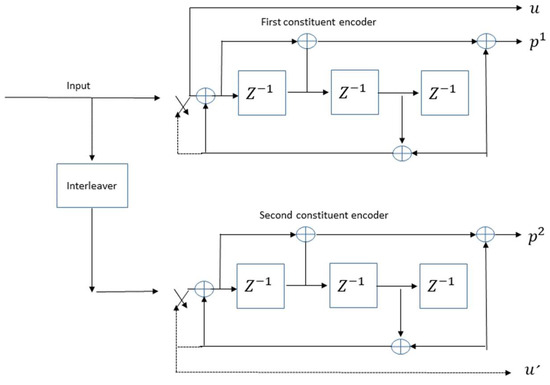
Figure 2.
Selected turbo encoder scheme for one-third rate.
2.2. Quality Scale for Bit Error Rate
The performance of turbo codes is first analyzed and then compared using BER based on the SNR. Four types of interleavers are employed in turbo codes with different short blockchains. BER is assessed through a comparison with the quality scale of the International Telecommunication Union (ITU), shown in Table 1 [30].

Table 1.
ITU quality scale in terms of the BER.
3. Interleaver
Interleavers play an important role in the minimum distance of turbo codes and also in the performance of the error floor. Interleavers are classified into the block and convolutional interleavers [31]. Some interleavers of interest applied to turbo codes are reviewed below.
3.1. Block Interleaver
A basic type of interleaver is described through a finite permutation over the numbers in Equation (7), where L is a period
An interleaver is described through the finite set of Equation (8)
where the range of the πi numbers corresponds to the number of elements in the set of Equation (9). This type of interleaver is denominated block permutation interleaver.
A permutation matrix provides an alternate description for a block permutation interleaver. For example, some interleavers can be described by symmetric 3 × 3 generator matrices, such as:
However, other interleavers are described by symmetric matrices where the nonzero terms in the matrix are monomials in the variable Dn, where n is an integer; in this way, the multiplexed interleaver has as its generator a symmetric diagonal matrix such as the one below:
3.2. Classical Block Interleaver
Classic block interleavers have an L period and are represented by Equation (12).
The interleavers are described in terms of a matrix of I × J order. These interleavers are characterized through processes in which their data inputs are written in the rows of a memory matrix and read along the columns. There are four basic variations of classic block interleavers with an L period: the schemes vary according to the order in which the columns are read (from left to right or from right to left) and the order in which the rows are read (from top to bottom and from the bottom to the top) [31]. These schemes allow for obtaining a permuted output matrix.
3.3. Random Interleaver
Random interleavers are based on the permutation that originates from the sequence described by a random generator. A random generator forms a noise vector with length L in which the order of the sequence to be permuted is imprinted. This random noise vector can be built by a pseudorandom generator.
Regarding the use in a turbo code scheme, the interleaver plays an essential role in its operation since, in general terms, its error rate is considerably reduced if the length or the size of the interleaving increases. The reverse is true when the size of the interleaver is small. This problem is directly related to the applications of turbo codes since, although a size increase in the interleaver allows a turbo code to reduce its error rate significantly until converting it into one of the most efficient error control techniques known, this effect is harmful for the system operation because it produces a delay that is unacceptable in several applications [32].
3.4. Semi-Random Interleaver
The S-random interleaver guarantees that if two input bits at the interleaver π encounter within an S1 distance, a distance smaller than S2 cannot be assigned to the interleaver output; normally S1 = S2 = S is used. Therefore, two different indexes i and j are used, such that they satisfy equations 13 and 14:
where S is selected as:
and L is the length of the interleaver [33].
3.5. Chaotic Interleaver Based on the Lozi Map
The chaotic interleaver based on the Lozi map has been presented in [34]. The Lozi map is a two-dimensional map introduced by René Lozi via a direct modification of the Hénon map. Simply speaking, a quadratic term in the latter is replaced with a piecewise linear version in the former. The same procedure is conducted for the quadratic map to derive the skew tent map. The state or system equations for the Lozi map, expressed component-wise, are the following:
where n is the iteration number, and ) are the initial conditions. The system exhibits a chaotic behavior for the typical values a = 1.7 and b = 0.5.
The chaotic interleaver based on the Lozi map is performed as follows:
Step 1: the integer sequence is mapped to a real number sequence using Equations (16) and (17).
Step 2: is mapped to another integer sequence by designing s(n) as the position of index of x(n) in the sort ascending of .
Step 3: the chaotic interleaver indexes are given by: .
3.6. Quadratic Polynomial Permutation Interleaver
Equation (18) presents a QPP interleaver defined by the polynomial.
where:
- i is the position index of the bit before interleaving with 0 ≤ i ≤ L − 1;
- L corresponds to block size;
- π(i) is an interleaved position corresponding to the position i;
- f1 and f2 are the coefficients that define the permutation.
The conditions for f1 and f2 are defined in extenso in [35]. Table 2 presents the coefficients f1 and f2 for some L lengths.

Table 2.
Parameters for QPP interleaver [36].
3.7. Proposed Interleaver
3.7.1. Chaotic Map Utilized
The Duffing map is a two-dimensional map and a discrete version of the Duffing equation. This is a differential and nonlinear equation of the second order used to model certain damped and driven oscillators.
Duffing maps describe a dynamic system that exhibits chaotic behavior. From a point on the plane, a new point is assigned, which is given by
The map depends on the two constants a and b. In general, a = 2.6 and b = 0.8 are defined to produce a chaotic behavior. For the experimental tests, the initial point considered is x1 = 1 and y1 = 1.
3.7.2. Criteria for the Chaotic Interleaver
The interleaver is an important element in defining the minimum distance and the performance of the turbo code [20,37].
Two main properties that characterize any interleaver are dispersion (randomness), which is the length of the set of all possible spreading factors for that interleaver, and spreading, which is the distance between indexes that were close before being permuted by the interleaver. Good spreading improves the BER performance of the system [38]. However, if some criteria are incorporated, it is possible to ensure the characteristics of the interleaver.
3.7.3. Circular Minimum Spread Constraint Criterion
The concept of propagation in the field of turbo codes was defined by Crozier in [39]. The circular minimum spread constraint (CMSC) criterion was proposed in [22] and is defined through the following equations:
For an interleaver π, with length L, it will have a circular extension of S if and only if:
and is the Lee distance of the two indices , is defined as
For the S that satisfies Equation (23), an interleaver obtained ensures a minimum circular Spread Smin:
In this way, the minimum circular dispersion constraint is satisfied.
Where Smin is given by [33]:
3.7.4. Correlation Criterion
To decrease the correlation between the information from the first encoder and the information at the input of the second decoder, a circular displacement is applied at the output of the interleaver. Let j1 and j2 be the information data, and and be the locations obtained after interleaving so that the interleaver can ensure that if then > S. However, some input data may be addressed in the output vector, and the index mapping and could occur. This could be a valid mapping for the interleaver. However, this type of mapping worsens the performance of the iterative decoding of turbo codes [40].
The minimum distance is defined as
for a higher value Dmin the correlation between the extrinsic information of the decoders decreases. If the circular travel distance d is applied, which maximizes Dmin when a circular displacement is made, it is described by
The value d that maximizes Dmin is calculated as
and the attainable values are
3.7.5. Proposed Chaotic Interleaver
Chaotic consequences show similar behavior to random behavior but with a deterministic origin that improves both the randomness and propagation properties of the interleaver.
The chaotic interleaver is created based on the Duffing map by applying the following algorithm:
- Step 1: generate a sequence of integers.where , L is the length of the interleaver, and , .
- Step 2: generate a chaotic sequence of values based on a Duffing map (Equations (19) and (20)), obtaining the two sequences xn and , and considering the initial conditions of a and b to obtain a chaotic behavior.
- Step 3: the sequence xn is sorted in ascending order.
- Step 4: the change of positions derived from the ascending sorting is stored in a u′ vector that contains whole values i in the new position derived from the order.
- Step 5: apply the circular minimum spread constraint criterion and store the values that satisfy the criterion in the output vector.
- Step 6: if after reviewing the L elements given by the chaotic permutation, the output vector has not been filled, step 1 should be repeated with a new sequence of chaotic values.
- Step 7: for the output vector filled with values that satisfy the CMSC criterion, apply the circular displacement criterion.
- Step 8: the interleaver is obtained with the chaotic permutations that satisfy the two criteria.
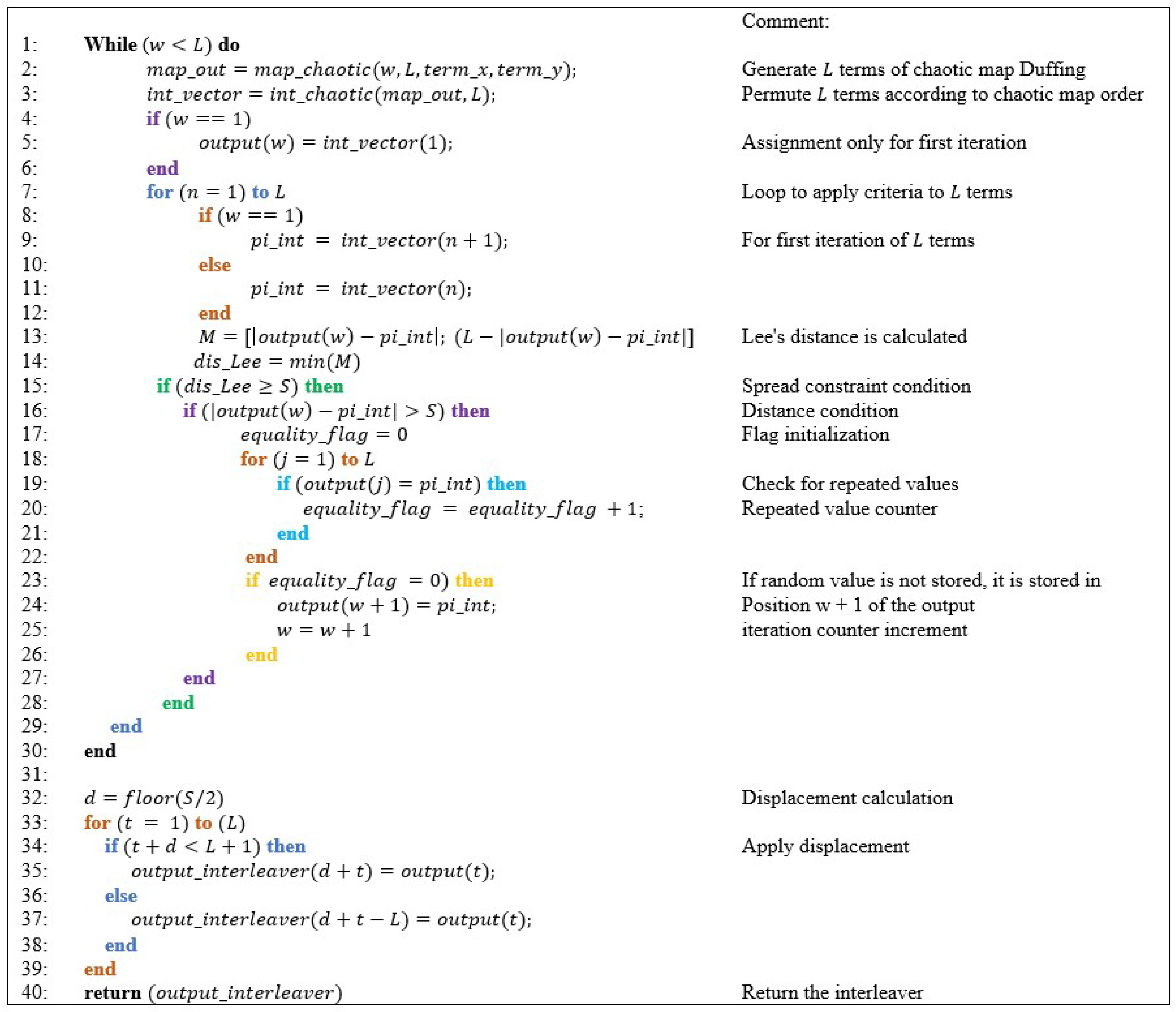
The pseudocode that describes the proposed interleaver employs two functions: one for obtaining the chaotic sequence (map_chaotic) and another function (int_chaotic) for linking the chaotic sequence to an integer vector, which has the permutation associated with the chaotic sequence.
First, the algorithm assesses the CMSC criterion. When a value satisfies the vector, it is saved in the output variable. If the value does not fill the vector, a new chaotic permutation is generated based on the last chaotic terms previously generated in the sequence; therefore, each chaotic sequence is different. The algorithm ends with the application of circular movement and generates an interleaver vector (output_interleaver), as shown in Figure 3.
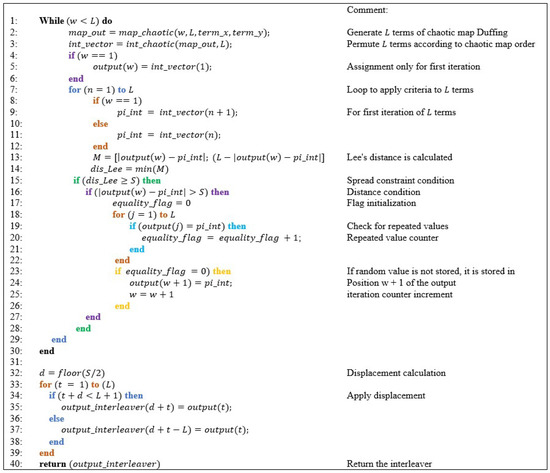
Figure 3.
Pseudocode for obtaining the interleaver.
- L is the length of the interleaver;
- term_x/term_y represent the initial values;
- w is the iteration counter;
- n, t, j are the iteration control variable;
- output is an auxiliary variable that stores values that satisfy CMSC criteria;
- pi_int is an auxiliary variable;
- S is the circular extension distance;
- equality_flag is a flag indicating if there are repeated values;
- d is the circular displacement;
- output_interleaver is a variable that stores the indices of the interleaver.
4. Empirical Tests in Software
4.1. Simulation of Communication System
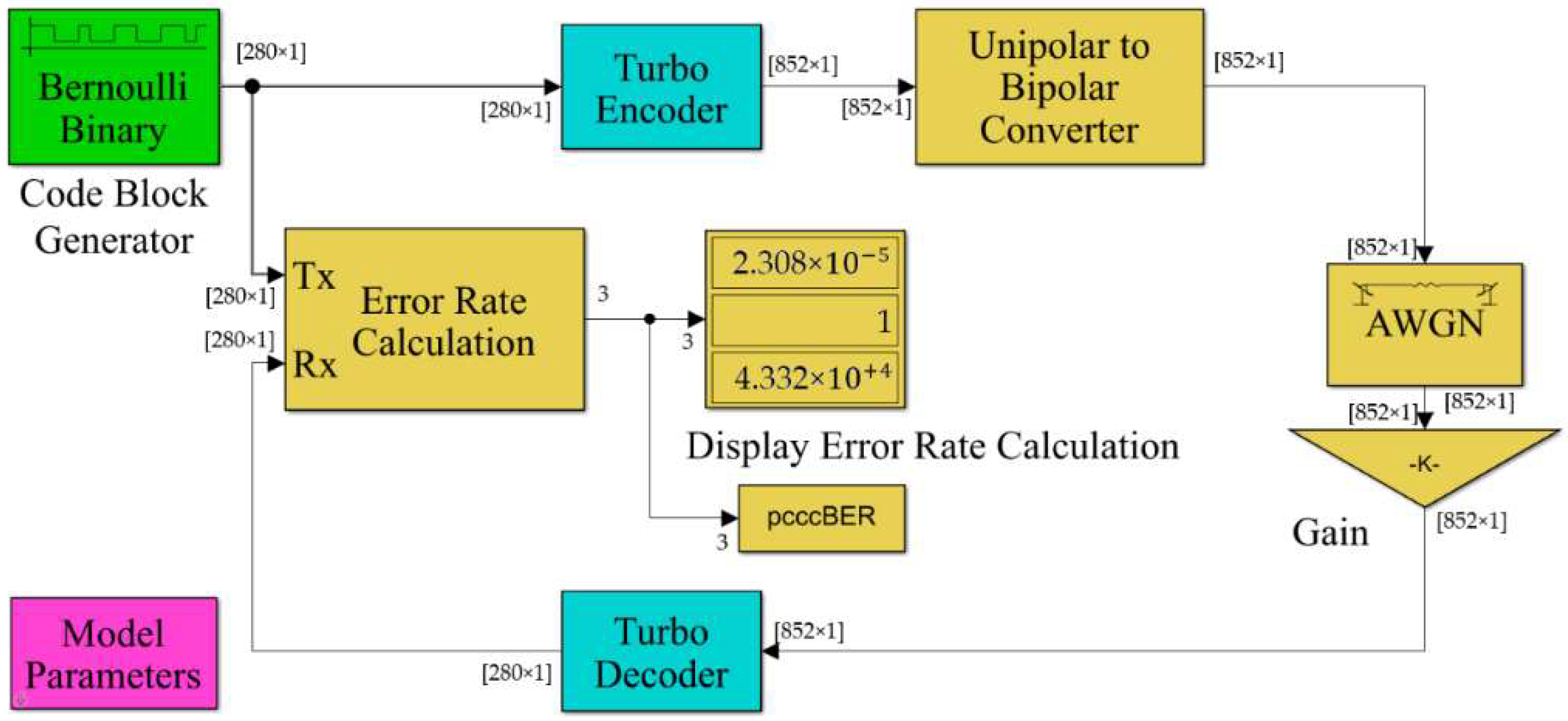
A communication system is simulated on the MatLab/Simulink software [41]. Figure 4 shows the implemented system, which comprises a turbo encoder and a decoder. A length constraint of four values and a generator are required for coding. Configurations are set up, so the system employs the following parameters: the interleaver indexes, code block length, number of decoding iterations, and the values of the Eb/N0 relation.
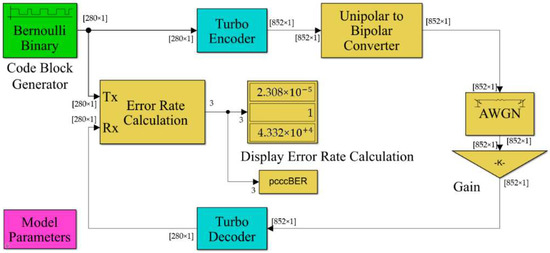
Figure 4.
Simulation for the communication system in Simulink.
The blocks used in the Simulink software corresponding to the communication system are described below:
- Bernoulli binary generator, which enables the generation of random binary numbers using Bernoulli’s distribution;
- Unipolar-to-bipolar converter, which enables the conversion of the unipolar signal input into a bipolar output signal;
- Additive white Gaussian noise (AWGN) channel, which allows for adding white Gaussian noise into a real or complex input signal;
- Error rate calculation, which compares input data from a transmitter with output data from a receiver while calculating error rate;
- Turbo encoder, which enables the coding of a binary input signal using the scheme of coding concatenated in parallel. This coding scheme uses two identical convolutional coders and an internal interleaver. This internal interleaver is modified through the application of the interleavers presented above;
- Turbo decode, which decodes input signals through concatenated decoding in parallel. The scheme of iterative decoding employs an a posteriori probability (APP) algorithm for this purpose. The same trellis structure and decoding algorithm are used by the two decoders;
- Model parameters that allow for specifying the execution parameters for the simulation, which are the SNR in decibels, the block length in bits, and the decoding iteration number.
4.2. Interleaver Implementation in MatLab/Simulink Software
The implementation of the interleaver in MatLab/Simulink is conducted on a script, where the instructions of the pseudocode presented in Figure 3 are programmed. With this purpose, the same functions described in Section 3.7.5 are employed, as well as the control routines and sentences that enable the application of the criteria. The result of this implementation, according to the described algorithm, generates a vector with permutated indexes, which is inserted in the turbo coder and decoder of the communication system simulation, as shown in Figure 4.
4.3. Test Results
To compare turbo code performances, four data lengths are considered, and the same encoder and decoder are maintained, substituting only the interleaver. The communication system shown in Figure 4 is simulated, and the tests assess the performance of BER versus the SNR. The tests have the objective of showing changes in the performance of the turbo code of each interleaver when the block length is modified.
For each interleaver, a vector is obtained that contains the indexes applied to the encoder and decoder in the turbo code simulation.
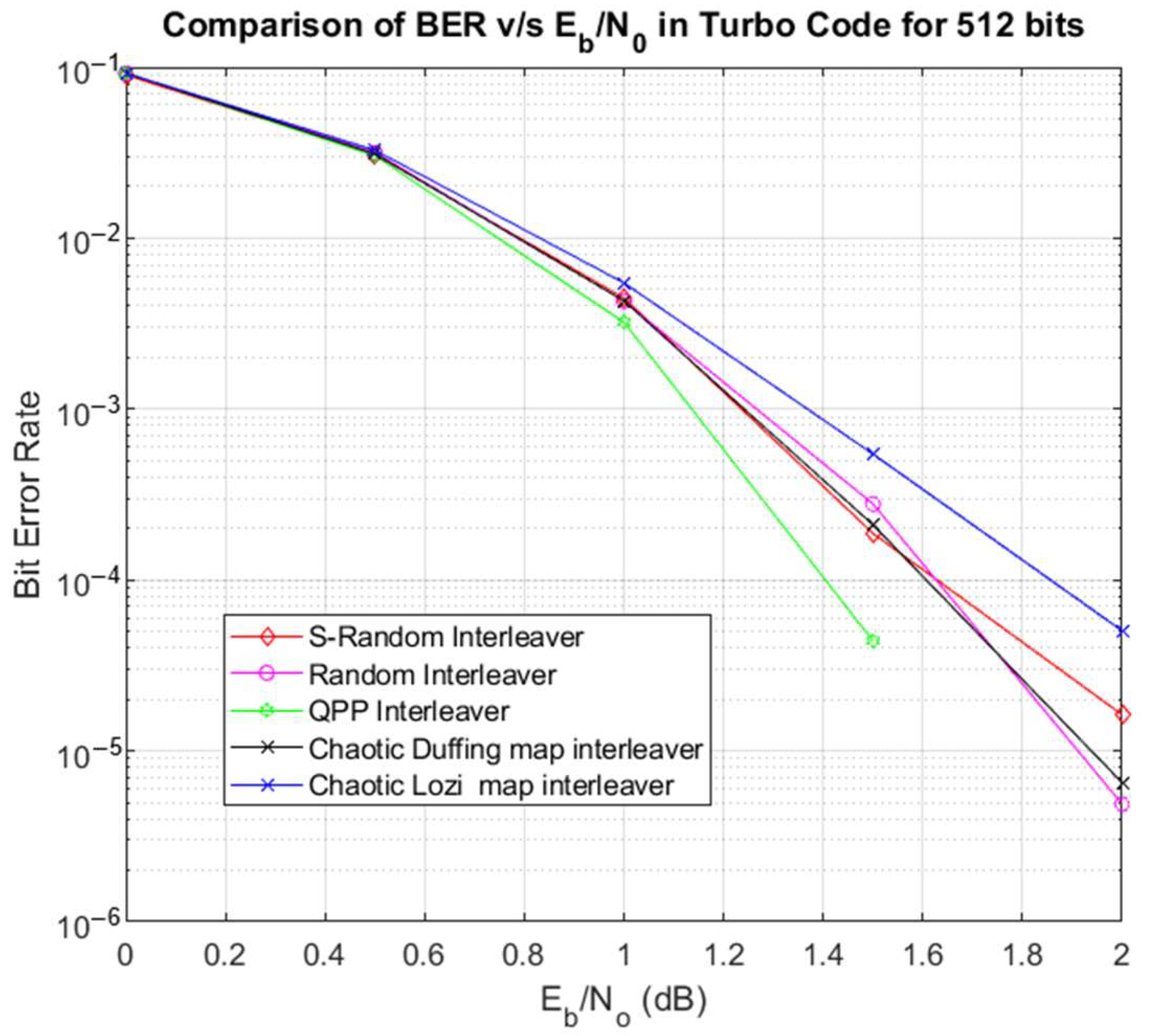
Since the main focus is a performance analysis on bits of short lengths, the results of the interleavers for shorter lengths are compared. Figure 5 shows these results for the 512-bit length of the random, S-random, QPP interleavers, and chaotic Lozi map, as well as the proposed chaotic interleaver.
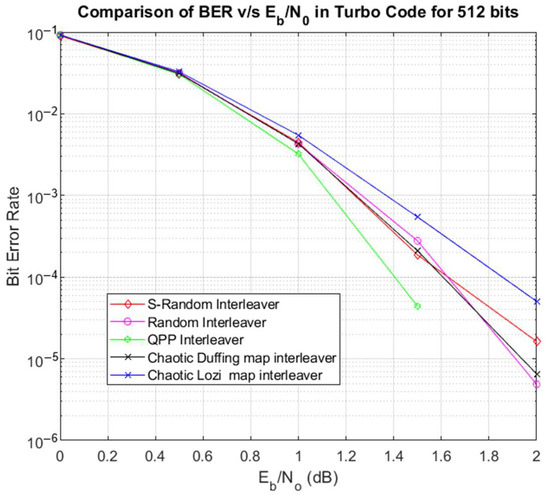
Figure 5.
BER v/s Eb/N0 comparison for 512 bits.
The comparison in Figure 5 shows that for a 512-bit length, the performance of the chaotic Duffing interleaver reaches an SNR of 2 dB, while BER has a curve similar to that of a random interleaver.
For an SNR of 2 dB, the BER of the random interleaver reaches the value of 4.8787 × 10−6, the result obtained by the S-random interleaver is a BER of 1.6262 × 10−5, the result of the Lozi chaotic interleaver is a BER of 5.0414 × 10−5, and of the proposed chaotic interleaver reached is a BER of 6.5050 × 10−6. These four cases present an excellent performance.
For the QPP interleaver, the result obtained for an SNR of 1 dB is a BER of 0.0032, while the result obtained for an SNR of 1.5 dB is a BER of 4.3909 × 10−5, achieving very poor and excellent performances, respectively. In both cases, BER is smaller than for other interleavers.
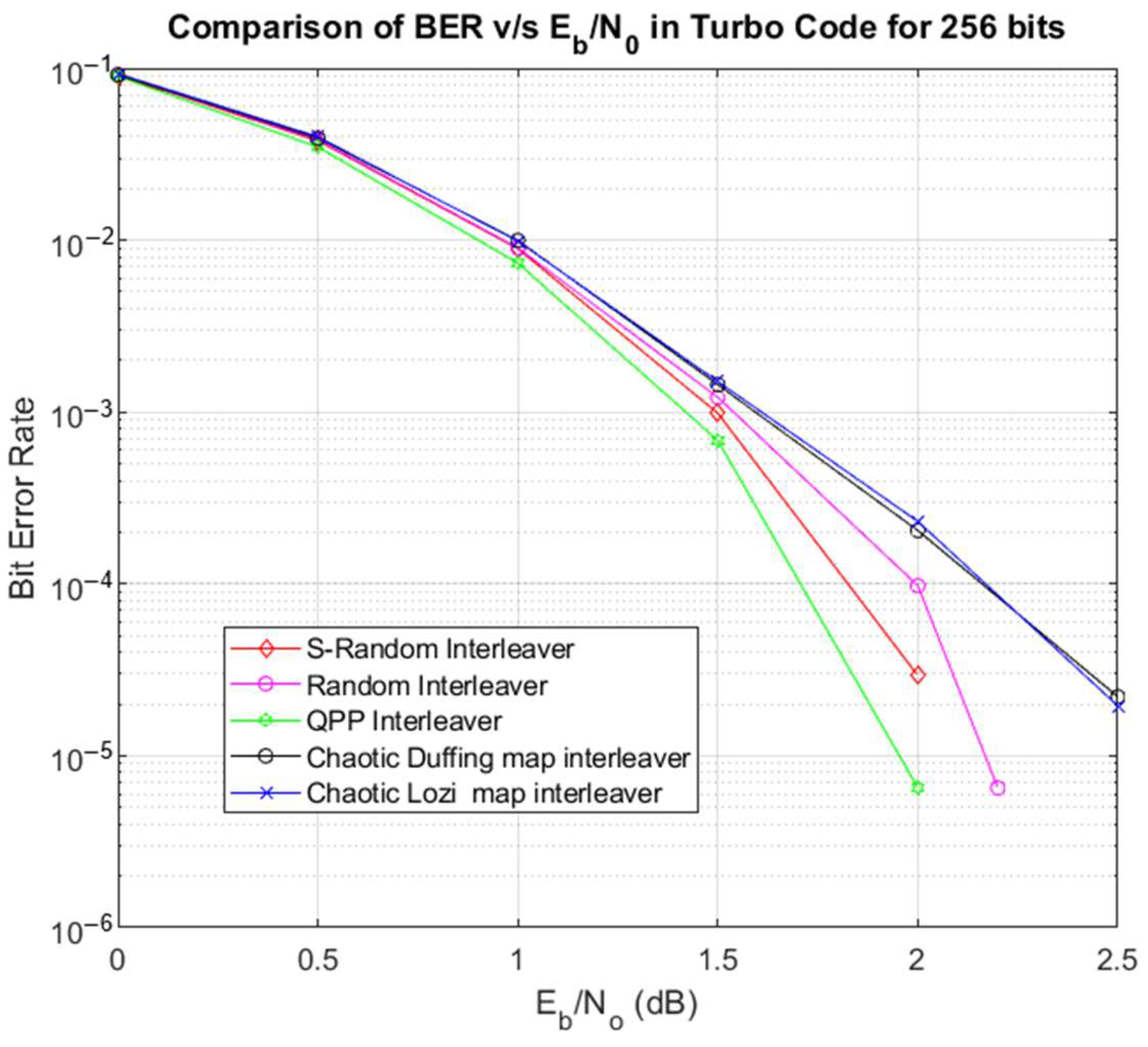
Figure 6 shows the comparison of the results for a 256-bit length.
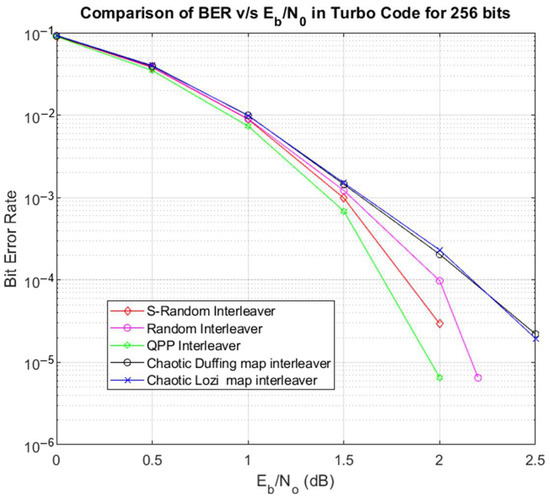
Figure 6.
BER v/s Eb/N0 comparison for 256 bits.
The comparison in Figure 6 shows that for a 256-bit length, the performance of the chaotic Duffing interleaver reaches an SNR of 2.5 dB, while BER exhibits a curve similar to that of the Lozi chaotic interleaver.
For an SNR of 2 dB, the BER of the random interleaver reaches the value of 9.7575 × 10−5, the result of the S-random interleaver is a BER of 2.9272 × 10−5, and of the QPP interleaver is a BER of 6.5050 × 10−6. These three cases present an excellent performance.
The Lozi chaotic interleaver achieved a BER of 2.3093 × 10−4, and the proposed chaotic interleaver reached a BER of 2.0442 × 10−4. Therefore, both have good performance.
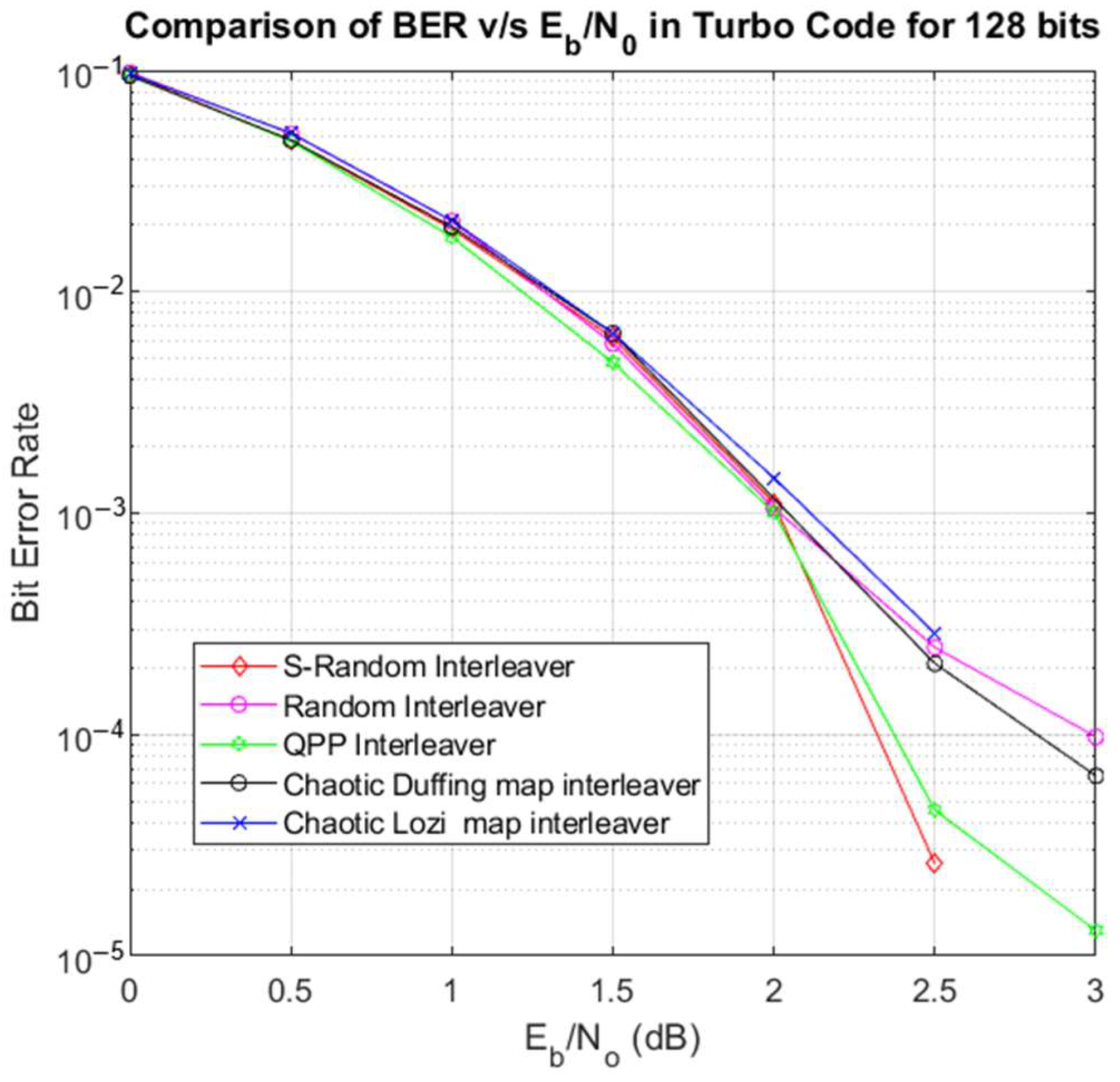
Figure 7 shows the comparison of the results for a 128-bit length.
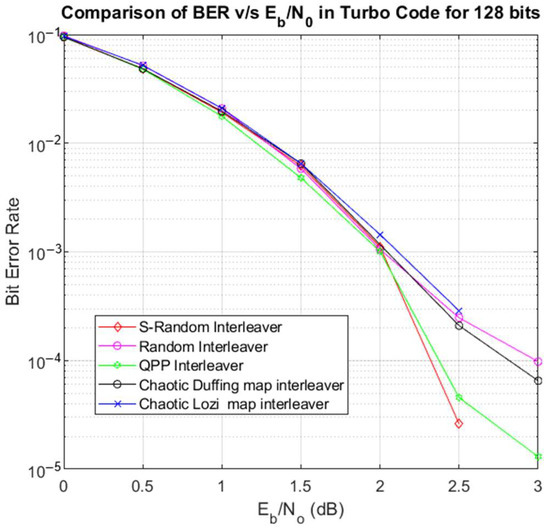
Figure 7.
BER v/s Eb/N0 comparison for 128 bits.
The comparison in Figure 7 shows that for a 128-bit length, the performance of the chaotic Duffing reaches an SNR of 3 dB, while BER exhibits a curve similar to that of the random interleaver until 2.5 dB, with a slightly lower BER.
For an SNR of 2.5 dB, the BER of the random interleaver reaches the value of 2.471 × 10−4, and the result obtained by the Lozi chaotic interleaver is a BER of 2.8622 × 10−4; in both cases, the performance is good.
The result obtained by the S-random interleaver is a BER of 2.6020 × 10−5, the result of the QPP interleaver is a BER of 4.5535 × 10−5, and of the proposed chaotic interleaver is a BER of 6.5050 × 10−5. In these three cases, the performance is excellent.
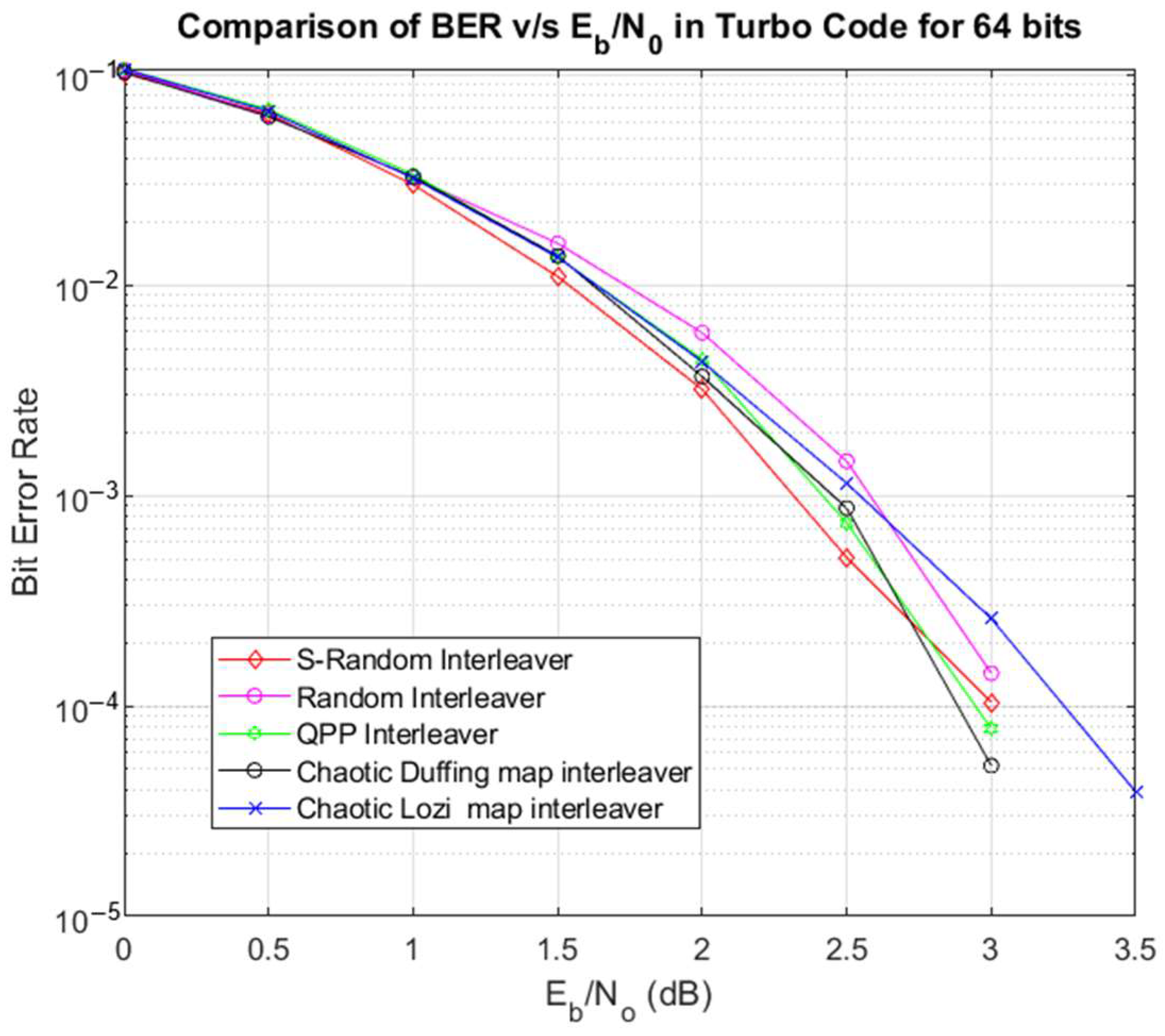
Figure 8 shows the comparison of the results for a 64-bit length.
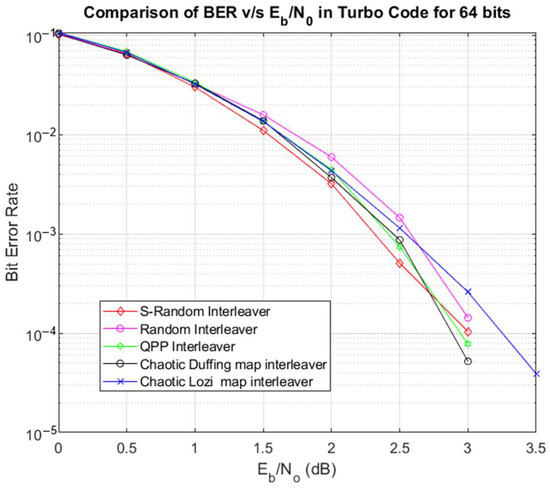
Figure 8.
BER v/s Eb/N0 comparison for 64 bits.
The main interest of this study is to evaluate the performance of the turbo code in terms of an interleaver for short lengths. Table 3 below shows the quality state of BER according to Table 1 for the performance of the 64-bit turbo code.

Table 3.
Comparison of BER for the performance of the 64-bit turbo code.
The comparison in Figure 8 shows that for a 64-bit length and an SNR of 2 dB, the BER of the random interleaver reaches the value of 1.4311 × 10−4, the result of the S-random interleaver is a BER of 1.0408 × 10−4, and of the Lozi chaotic interleaver is a BER of 2.6020 × 10−4. These three cases exhibit good performance. The result of the QPP interleaver is a BER of 7.8060 × 10−5, and that of the proposed chaotic interleaver reached 5.2040 × 10−5. This is an excellent performance for both interleavers.
5. Conclusions
This article presented the analysis and comparison of turbo code performance for diverse interleavers with short block lengths. A new deterministic interleaver with behavior based on the Duffing map model is presented. The interleaver uses the chaotic qualities of the Duffing map, CMSC criteria, and circular displacement to ensure distance and decorrelation. In a short-length communication of 64 bits, the proposed interleaver is advantageous as its BER is better than the performance obtained by other interleavers. In addition, the application of the criteria ensures a minimum dispersion and decorrelation that favors iterative decoding and TC performance. The chaotic interleaver proposed is deterministic, which allows for a simple implementation. The algorithm can be adapted to other lengths. The Duffing map requires two parameters a and b, as well as two initial conditions x1 and y1, which could influence the construction of the interleaver. After comparing this interleaver in short bit blocks, performance is similar to that of existing interleavers, with small differences between them. In the case of 64 bits, the BER obtained during the test that assesses the proposed chaotic interleaver is lower than that of other interleavers for SNRs of 3 dB. Regarding the 512-bit length, the BER results of the test with the chaotic interleaver are inferior to those of the random interleaver for SNRs of 0 dB, 0.5 dB, 1.5 dB, and 2 dB. Regarding the 128-, 256- and 512-bit lengths, despite performing similarly to the already existing interleavers, the proposed interleaver always performs better than the chaotic Lozi map interleaver. The proposed chaotic interleaver, based on a chaotic Duffing map, achieves a performance similar to that of the existing interleavers, reaching excellent levels in 64-bit lengths. In future work, the performance of the proposed chaotic interleaver could be improved by changing the initial conditions of the Duffing map.
Author Contributions
Conceptualization, C.U., J.K. and R.L.-E.; methodology, C.U., J.K. and R.L.-E.; software, C.U., J.K. and R.L.-E.; validation, C.U., J.K. and R.L.-E.; formal analysis, C.U., J.K. and R.L.-E.; investigation, C.U., J.K. and R.L.-E.; resources, C.U., J.K. and R.L.-E.; data curation, C.U., J.K. and R.L.-E.; writing—original draft preparation, C.U., J.K. and R.L.-E.; writing—review and editing, C.U.; visualization, C.U., J.K. and R.L.-E.; supervision, C.U.; project administration, C.U.; funding acquisition, C.U. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work was supported by the Faculty of Engineering of the University of Santiago of Chile, Chile. Ricardo López-Escobar completed his doctoral studies in Engineering Sciences, specializing in Automation, funded by CONICYT: CONICYT-PFCHA/Doctorado Nacional/2019.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Berrou, C.; Glavieux, A.; Thitimajshima, P. Near Shannon limit error-correcting coding and decoding: Turbo-codes. 1. In Proceedings of the ICC’93—IEEE International Conference on Communications, Geneva, Switzerland, 23–26 May 1993; IEEE: Piscataway, NJ, USA; Volume 2, pp. 1064–1070. [Google Scholar]
- 3GPP TS 36.212 V8.3.0 3rd Generation Partnership Project, Multiplexing and Channel Coding (Release 8). Available online: http://www.etsi.org (accessed on 8 October 2021).
- ETSI. E-UTRA Evolved Universal Terrestrial Radio Access (E-UTRA); Multiplexing and Channel Coding, Technical Specification; 3GPP TS 36.212 version 11.6.0. release 11; ETSI: Sophia Antipolis, France, 2012. [Google Scholar]
- Arora, K.; Singh, J.; Randhawa, Y.S. A survey on channel coding techniques for 5G wireless networks. Telecommun. Syst. 2019, 73, 637–663. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhu, L. Application scenarios and enabling technologies of 5G. China Commun. 2014, 11, 69–79. [Google Scholar] [CrossRef]
- De Almeida, I.B.F.; Mendes, L.L.; Rodrigues, J.J.P.C.; Da Cruz, M.A.A. 5G Waveforms for IoT Applications. IEEE Commun. Surv. Tutor. 2019, 21, 2554–2567. [Google Scholar] [CrossRef]
- Boccardi, F.; Heath, R.; Lozano, A.; Marzetta, T.L.; Popovski, P. Five disruptive technology directions for 5G. IEEE Commun. Mag. 2014, 52, 74–80. [Google Scholar] [CrossRef]
- Paolini, E.; Stefanović, Č.; Liva, G.; Popovski, P. Coded random access: Applying codes on graphs to design random access protocols. IEEE Commun. Mag. 2015, 53, 144–150. [Google Scholar] [CrossRef]
- Durisi, G.; Koch, T.; Popovski, P. Toward Massive, Ultrareliable, and Low-Latency Wireless Communication with Short Packets. Proc. IEEE 2016, 104, 1711–1726. [Google Scholar] [CrossRef]
- Salija, P.; Yamuna, B.; Padmanabhan, T.R.; Mishra, D. Performance Analysis of Reliability-Based Decoding Algorithm for Short Block Length Turbo Codes. IETE J. Res. 2019, 68, 1736–1747. [Google Scholar] [CrossRef]
- Coşkun, M.C.; Durisi, G.; Jerkovits, T.; Liva, G.; Ryan, W.; Stein, B.; Steiner, F. Efficient error-correcting codes in the short blocklength regime. Phys. Commun. 2019, 34, 66–79. [Google Scholar] [CrossRef]
- Oestman, J.; Durisi, G.; Stroem, E.G.; Li, J.; Sahlin, H.; Liva, G. Low-latency Ultra-Reliable 5G Communications: Finite-Blocklength Bounds and Coding Schemes. In Proceedings of the SCC 2017: 11th International ITG Conference on Systems, Communications and Coding, Hamburg, Germany, 6–9 February 2017; pp. 1–6. [Google Scholar]
- Shirvanimoghaddam, M.; Mohammadi, M.S.; Abbas, R.; Minja, A.; Yue, C.; Matuz, B.; Han, G.; Lin, Z.; Liu, W.; Li, Y.; et al. Short Block-Length Codes for Ultra-Reliable Low Latency Communications. IEEE Commun. Mag. 2019, 57, 130–137. [Google Scholar] [CrossRef]
- Van Wonterghem, J.; Alloum, A.; Moeneclaey, M.; Van Wonterghem, J.; Alloum, A.; Boutros, J.J.; Moeneclaey, M. On Performance and Complexity of OSD for Short Error Correcting Codes in 5G-NR. In Proceedings of the BalkanCom 2017: First International Balkan Conference on Communications and Networking, Tirana, Albania, 31 May–2 June 2017. [Google Scholar]
- Al Bechlawi, C.; Guilloud, F. Frame length reduction for massive-machine communications. In Proceedings of the IEEE 81st Vehicular Technology Conference, Glasgow, UK, 11–14 May 2015; IEEE: Piscataway, NJ, USA, 2015; Volume 2015. [Google Scholar]
- MacKay, D.J.C. Near Shannon limit performance of low density parity check codes. Comput. Sci. 1996, 33, 457–458. [Google Scholar] [CrossRef]
- Arikan, E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef]
- Maunder, R.G. The 5G Channel Code Contenders; ACCELERCOMM: Southampton, UK, 2016. [Google Scholar]
- Luby, M.G.; Mitzenmacher, M.; Shokrollahi, M.A.; Spielman, D.A. Improved low-density parity-check codes using irregular graphs. IEEE Trans. Inf. Theory 2001, 47, 585–598. [Google Scholar] [CrossRef]
- Trifina, L.; Tarniceriu, D.; Ryu, J.; Rotopanescu, A.M. Further upper bounds on the minimum distance for turbo codes using CPP interleavers. Phys. Commun. 2020, 43, 101212. [Google Scholar] [CrossRef]
- Ferez, L.C.; Seghers, J.; Costello, D.J. A distance spectrum interpretation of turbo codes. IEEE Trans. Inf. Theory 1996, 42, 1698–1709. [Google Scholar] [CrossRef]
- Jerkovits, T.; Matuz, B. Turbo code design for short blocks. In Proceedings of the 2016 8th Advanced Satellite Multimedia Systems Conference and 14th Signal Processing for Space Communications Workshop, ASMS/SPSC 2016, Palma de Mallorca, Spain, 5–7 September 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Trifina, L.; Ryu, J.; Tarniceriu, D. Up to five degree permutation polynomial interleavers for short length LTE turbo codes with optimum minimum distance. In Proceedings of the ISSCS 2017—International Symposium on Signals, Circuits and Systems, Iasi, Romania, 13–14 July 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Garzón Bohórquez, R.; Nour, C.A.; Douillard, C. Protograph-Based Interleavers for Punctured Turbo Codes. IEEE Trans. Commun. 2018, 66, 1833–1844. [Google Scholar] [CrossRef]
- Sreedevi, M.; Yamuna, B.; Salija, P. Design and implementation of interleaver in GNU radio for short block length turbo codes. In Proceedings of the 2019 9th International Conference on Advances in Computing and Communication, ICACC 2019, Kochi, India, 6–8 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 17–21. [Google Scholar]
- Trifina, L.; Tarniceriu, D.; Ryu, J.; Rotopanescu, A.M. Upper bounds on the minimum distance for turbo codes using CPP interleavers. Telecommun. Syst. 2021, 76, 423–447. [Google Scholar] [CrossRef]
- Himeur, Y.; Boukabou, A.; Senouci, A. Performance of turbo-coded chaotic interleaving and frequency-domain equalization scheme for high speed OFDM-based PLC systems. J. Franklin Inst. 2016, 353, 3799–3817. [Google Scholar] [CrossRef]
- Abderrahmane, L.H.; Bacha, M.; Mebrek, A. A new optimised interleaver structure for turbo coding. In Proceedings of the 2014 IEEE 27th Canadian Conference on Electrical and Computer Engineering (CCECE), Toronto, ON, Canada, 4–7 May 2014. [Google Scholar] [CrossRef]
- Shebl, S.; Soliman, N.F.; El-Fishawy, N.A.; Abou-El-Azm, A.E.; Alshebeili, S.A.; Abd El-Samie, F.E. Performance enhancement of power line communication systems with efficient low density parity-check codes, noise removal, equalization, and chaotic interleaving. Digit. Signal Process. 2013, 23, 1933–1944. [Google Scholar] [CrossRef]
- ITU-T. P Series: Telephone Transmission Quality; ITU-T.: Geneva, Switzerland, 1996. [Google Scholar]
- Heegard, C.; Wicker, S.B. Introduction. In Turbo Coding; Springer: Boston, MA, USA, 1999; pp. 1–10. [Google Scholar]
- Hanzo, L.; Liew, T.H.; Yeap, B.L.; Tee, R.Y.S.; Ng, S.X. Turbo Coding, Turbo Equalisation and Space-Time Coding: EXIT-Chart-Aided Near-Capacity Designs for Wireless Channels, 2nd ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2011; ISBN 9780470978481. [Google Scholar]
- Divsalar, D.; Pollara, F. Low-rate turbo codes for deep-space communications. In Proceedings of the Proceedings of 1995 IEEE International Symposium on Information Theory, Whistler, BC, Canada, 17–22 September 1995; IEEE: Piscataway, NJ, USA, 1995; p. 35. [Google Scholar]
- Sahnoune, A.; Berkani, D. On the performance of chaotic interleaver for turbo codes. SN Appl. Sci. 2021, 3, 106. [Google Scholar] [CrossRef]
- Sun, J.; Takeshita, O.Y. Interleavers for turbo codes using permutation polynomials over integer rings. IEEE Trans. Inf. Theory 2005, 51, 101–119. [Google Scholar] [CrossRef]
- ETSI. 3GPP TS 36.212 v8.0.0 Multiplexing and Channel Coding (FDD) (Release 8); ETSI: Sophia Antipolis, France, 2010. [Google Scholar]
- Trifina, L.; Tarniceriu, D.; Ryu, J.; Rotopanescu, A.M. Some lengths for which CPP interleavers have weaker minimum distances than QPP interleavers. J. Franklin Inst. 2020, 357, 3097–3112. [Google Scholar] [CrossRef]
- Sharma, S.; Sau, P.C.; Shukla, A. Performance analysis of S-Random interleaver for IDMA system using MRRC diversity scheme. In Proceedings of the 2014 7th International Conference on Contemporary Computing, IC3 2014, Noida, India, 7–9 August 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 248–253. [Google Scholar]
- Crozier, S. New high-spread high-distance interleavers for turbo-codes. In Proceedings of the 20th Biennial Symposium on Communications, Kingston, ON, Canada, 28–31 May 2000; pp. 3–7. [Google Scholar]
- Arif, M.; Sheikh, N.M.; Sheikh, A.U.H. Design of two step deterministic interleaver for turbo codes. Comput. Electr. Eng. 2008, 34, 368–377. [Google Scholar] [CrossRef]
- MathWorks MatLab Documentation. Available online: https://la.mathworks.com/help/matlab/ (accessed on 8 November 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).