Structure–Attribute Social Network Graph Data Publishing Satisfying Differential Privacy

Abstract

With the development of big data, data collection and publishing are symmetrical. The purpose of data collection is to better publish data. To better collect user data and promote data analysis, publishing massive amounts of data can better provide services for people’s lives. However, in the process of publishing data, the problem of low data availability caused by over protection is widespread. In addition, the attacker indirectly obtains the data of the target user by accessing the data of the user’s friends or neighbors, which leads to the disclosure of the user’s privacy. In order to solve these problems, a structure–attribute social network data publishing model is proposed. This model protects the privacy of user attribute data and prevents homogeneity attacks through attribute data perturbation. In addition, the model disrupts the structure of social networks by introducing uncertainty graphs into network partitions to generate published social network data. Our scheme has been tested on three public datasets, and the results show that our scheme can retain the social network structure as much as possible.

1. Introduction

During COVID-19, the social network [1] was regarded as an indispensable communication means and platform in people’s lives. Users communicate with each other, disseminate information on social networks [2], and hold online meetings [3]. In social networks, users usually have many attributes [4]. They also have a lot of information. Users usually have friend information, behavior information, content information, and attribute data [4]. For example, behavioral information can be a user’s favorite circle of friends, a user-commented movie, or a mobile application that users often open. The content information can be the user’s circle of friends, uploaded photos, microblog, etc. The attribute data includes the user’s gender, age, date of birth, religious beliefs, and promotion information. Some users choose to publish their personal information, life status, and friends’ photos on their friend’s circle, microblog, or dating website. However, some users choose not to disclose or provide some of their own data, such as various personal information. In general, social networks can be viewed as a combination of public and private data. Generally, when publishing social network data [1], the number of nodes in the social network and the relationship between users will be disturbed after anonymization [5].

For data platforms with massive data, such as social networks, attackers can obtain users’ privacy information through various means [6]. For example, attackers want to obtain user attribute information [4] and predict attacks against social network user attributes [7]. Attribute prediction [8] is a serious privacy and security attack faced by social network users [9]. In attribute prediction attacks, attackers can first collect public data about users on social networks and then use machine learning [10] and data mining [11] methods to predict the privacy attributes of target users. Attackers can be any person or organization interested in users, such as advertisers, hackers, etc. Advertisers can use the predicted attributes to provide targeted advertising, thereby increasing profits. When a hacker sends a malicious website to a user, he can describe the website as having information related to the user’s school, thus increasing the probability of users clicking on the malicious website. Data buyers can sell the predicted attribute data to advertisers, banks, insurance companies, etc. to obtain economic benefits. More seriously, attackers can use predicted attributes to associate user accounts in different social networks or even associate online data with offline data to form more comprehensive user data, thus causing greater privacy and security risks. For the edge relationship attack, the attacker knows the user’s friends through various channels and means and analyzes the user’s attributes through the friend’s attributes, thus leading to the disclosure of user privacy. Another problem is that, due to the need to protect users, the published data interfere too much with them, resulting in very low data availability, which also undermines the role of data publishing [12].

Aiming at the problems of low data availability, user attribute attacks [7], and user relationship attacks [13], a social network data publishing model based on structural attributes is proposed. This model protects the privacy of user attributes to the greatest extent and retains the structural information of social networks by proposing various attribute processing schemes and interfering with the graph structure.

The main contributions of this paper are as follows:

• A network protection model of attributes and structure is proposed. Information is added to social network data in the process of publishing a graphic structure to improve the availability of data. The continuous attributes are classified by the binary discrete method, which is convenient for attribute application and improves operation efficiency. In addition, the attribute structure of the social network publishing model can protect user attributes while resisting the community homogeneity attack caused by community division and protecting user privacy.
• The Louvain community partition algorithm is introduced and further optimized. The time efficiency of the optimized method is increased by 20%.
• In the process of implementing edge differential privacy protection for social networks, a tainted graph is introduced to improve the availability of published data. This method can effectively preserve the community structure.
• We propose an attribute–structure publishing model for social network data publishing, and we prove that the model satisfies differential privacy.

The organizational structure of this paper is as follows: Section 2 describes the related work. In Section 3, we introduce the relevant definitions of attribute social networks and differential privacy. In Section 4, the framework and process of the whole model are described. We describe the details of attribute protection and structure protection and prove their privacy in Section 5 and Section 6. In Section 7, we present and explain the experimental dataset and results. Section 8 gives relevant conclusions.

2. Related Works

2.1. Application of Differential Privacy

Cynthia Dwork [14] put forward the concept of differential privacy. By adding designed noise to anonymous data sets, attackers cannot restore user information. Hay et al. [15] applied differential privacy to histogram data publishing, and improve the accuracy of differential privacy histogram through consistency. Alexander et al. [16] applied differential privacy to the deep learning of medical imaging, achieving deep neural network training through a differential privacy random gradient descent algorithm and using differential privacy to protect the privacy information provided by patients. In June 2016, Apple announced that it would use differential privacy for the collection of some user data to ensure the privacy of user data [17]. Dong Jin Shuo et al. [18] proposed a new concept of differential privacy with more relaxed conditions and introduced this concept into a standard series of single-parameter privacy concepts called “Gaussian differential privacy”. Yang Meng Meng et al. [19] gave a comprehensive and structured overview of localized differential privacy technology. Hou Jun et al. [20] applied differential privacy to the construction of a random forest and optimized the differential privacy random forest algorithm, balancing the privacy and classification accuracy of the differential privacy-based random forest algorithm. Munib et al. [21] introduced differential privacy into the blockchain and used differential privacy technology at each layer of the blockchain and in some block chain-based scenarios. Nao Y et al. [22] introduced a general-population open-source differential privacy library for investigating, testing, and developing differential privacy applications in the Python programming language. Zhao Jing Wen et al. [23] studied the privacy disclosure problem in the deep learning model and discussed it from the perspectives of member reasoning, training data, and model extraction. Jiang Bin et al. [24] discussed the combination of differential privacy and industrial Internet of Things applications in view of the risk of privacy disclosure caused by the strong reliance on data collection in the deep learning model.

2.2. Data Publishing

Mark et al. [25] discussed the issue of privacy disclosure in track data by combining privacy protection and track data publishing. Song Jing Cheng et al. [26] proposed a privacy protection data aggregation scheme for data publishing in view of the large amount of data and data sensitivity faced by intelligent agriculture. Wang et al. [27] discussed real-time spatio-temporal data publishing in privacy-protected social networks for social network data publishing and used adaptive sampling, adaptive budget allocation, dynamic grouping, perturbation, and filtering methods to publish social network data, which improved the practicality of real-time data sharing and had strong privacy protection. Mina et al. [28] proposed an analysis algorithm based on the privacy needs of data providers for the analysis of data sharing among multiple data providers to realize the trade-off between privacy and accuracy. Qian Xu et al. [29] proposed a decentralized data publishing scheme with computing outsourcing and anti-concatenation based on attribute encryption and searchable encryption functions. Chen Ping et al., Wang Tian et al., and Xu Zheng et al. [30] proposed a data sharing framework to protect privacy by adopting differential privacy protection in view of the privacy challenges brought by data sharing. Li Boyu et al. [31] proposed a new technology of mutual coverage to achieve privacy protection during data publishing. Chen Rui et al. [32] studied the issue of relevant data publishing under differential privacy for different privacy needs and proposed a non-interactive data publishing scheme.

2.3. Social Network Clustering and Community Discovery

Kun He et al. [33] proposed a meta method to identify hidden community structures by analyzing complex networks containing different types of communities. Andreas et al. [34] studied community detection at the emotional level by analyzing vertex clustering and community detection in social networks. Mehdi et al. [35] analyzed community detection in social networks and conducted a comprehensive investigation into community detection in static and dynamic social networks. Su Xing et al. [36] designed a new classification method for community discovery based on a deep learning model of deep neural networks, deep non-negative matrix decomposition and deep sparse filtering. Zeng Xiangxiang et al. [37] put forward the concept of consensus community for community detection in dynamic networks, which can solve the problem that community structure is affected by assessment, renewal, and mutation events in the process of event evolution. Geng Junxian et al. [38] proposed an efficient Markov Monte Carlo algorithm to solve the problem of unequal clustering quality caused by the uncertainty of clustering quantity and estimated the number and structure of communities at the same time, avoiding the need to invert the number of clusters to Markov Monte Carlo. Li Chunlin et al. [39] proposed a community detection algorithm based on network topology and user interest. This algorithm detects the number of communities based on a hierarchical clustering algorithm and partition density to improve the accuracy of the community detection algorithm. Nate Werter et al. [40] proposed a new LambdaCC community detection framework based on association clustering analysis. Through clustering analysis parameters, the size and structure of clusters can be implicitly controlled, which can be applied to large-scale collaborative networks and social networks. Hu Lu et al. [41] proposed a new multi-core combination algorithm for community partition under the problem of community detection on social networks and studied several basic kernel matrices from the adjacency matrix of the network, which constitute community partition. Sarah Ahajim et al. [42] proposed a new scalable and deterministic method, the leader community detection method, which conducts community detection through leader retrieval and node similarity.

3. Preliminaries

3.1. Attributed Graph Model

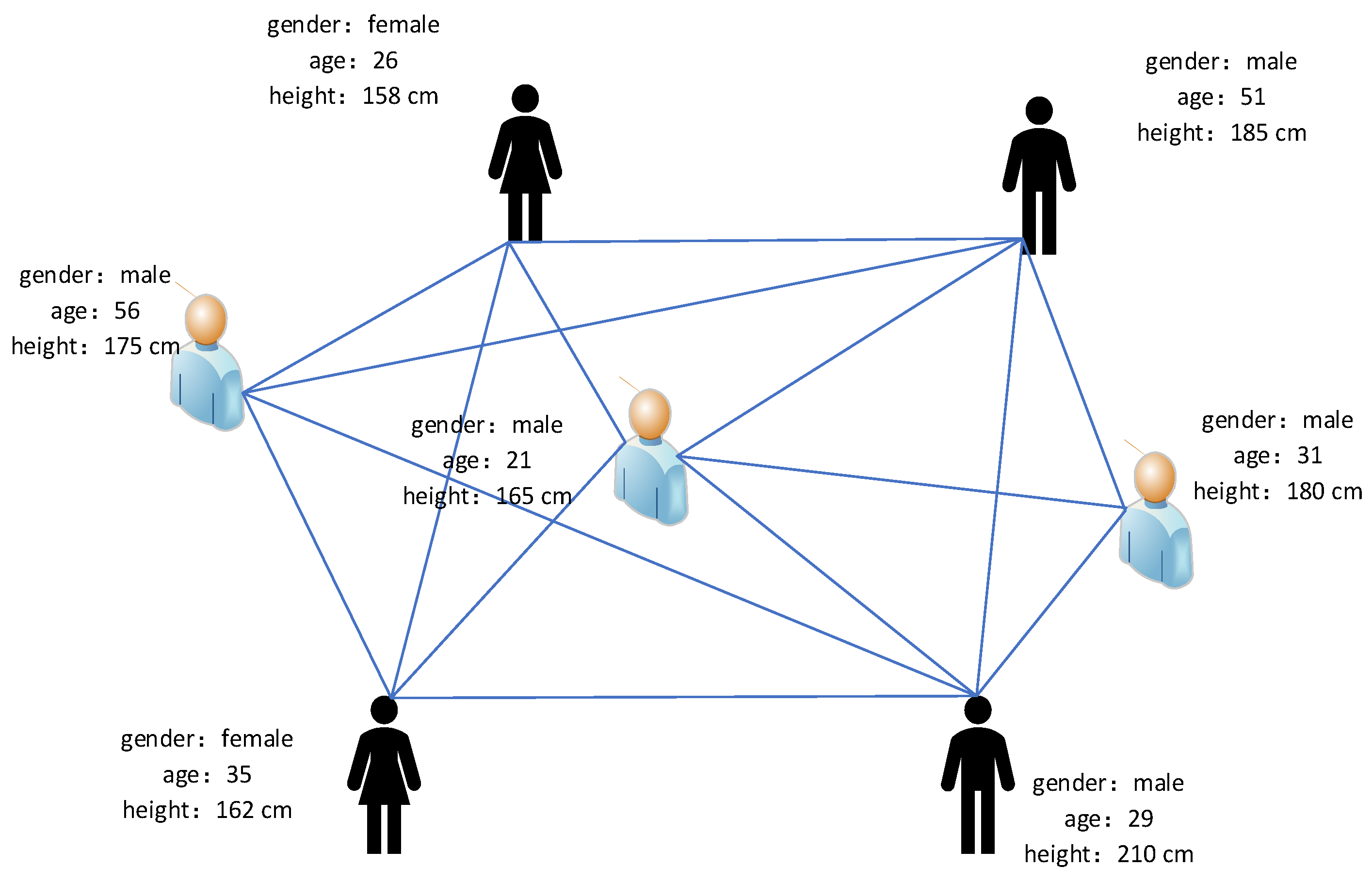
We model a social network as an undirected graph $G=\left(V,E\right)$, where $V$ represents users (nodes) and $E$ represents the relationship between nodes in $V$. In addition to relationships, each node is associated with a set of attributes, as shown in Figure 1, the attributes of each user include gender, age, height. For example, in SINA Weibo, the nodes are SINA Weibo users, and they represent the friendship between different users; you can extract age, gender, birthday, height, and other node attributes from user files.

We need to distinguish between attributes and attribute values. Each user has a limited number of attributes, such as gender, age, height, etc., and each attribute has a limited number of attribute values. For example, the attribute value of the user’s gender is either male or female. Let $m$ be the total number of different attribute values in the social network. Then, we can use an $m$-dimensional binary vector to represent the existence of attribute values for each node. More specifically, let $a_u$ be the attribute vector of node $u$. Then, the item equal to 1 in $a_u$ indicates that $u$ has the corresponding attribute value. Otherwise, it is 0. The attribute value of all nodes uses the matrix $U=\left[u_1,u_2,\cdots ,u_n\right]$, where n is the total number of social nodes, and $u1=\left[a_1,a_2,a_3,\cdots ,a_m\right]$, where m is the number of attributes. In this paper, we use a structure attribute network $G=\left(V,E,B\right)$ to model a social network consisting of a social structure $G=\left(V,E\right)$ and an attribute matrix $B$.

3.2. Differential Privacy

Differential privacy is proposed to solve the problem of privacy disclosure caused by differential attacks; that is, when the attacker’s knowledge background is the largest, it cannot determine whether one of the users exists in the database. For example, there is a database containing 10 people, among whom there are several patients with COVID-19. Later, the next user entered into the database is a patient with COVID-19. After we publish the data, the attacker cannot distinguish whether the last patient added has COVID-19 or not, even though he knows the information of all patients except for the last newly added patient. Differential privacy mainly uses random noise to ensure that the results of the query request for public visible information will not disclose individual privacy information, that is, to provide a way to maximize the accuracy of data queries when querying from the statistical database while minimizing the opportunity to identify its records. In other words, remove individual features to protect user privacy while retaining statistical features.

A related concept in differential privacy is adjacent datasets. Assuming that two datasets $D$ and $D^{\prime }$ are given, if they have only one piece of data that is different, then these two datasets are called adjacent datasets [14]. Then, if a random algorithm A acts on two adjacent datasets to obtain two output distributions that are difficult to distinguish, the algorithm is considered to achieve differential privacy. For a random algorithm $A$, for input $D$ and $D^{\prime }$, the possible output field $O$ is not a fixed value but data satisfying a certain distribution, as defined below.

Definition 1.

(Differential privacy [14]) A random algorithm $A$ satisfies differential privacy if and only if for any two adjacent datasets $D$, $D^{\prime }$, the output field $O$ satisfies

$$\mathrm{Pr}\left(A\left(D\right)=O\right)\le e^{\epsilon }\times \mathrm{Pr}\left(A\left(D^{\prime }\right)=O\right)$$

(1)

This algorithm works with any adjacent dataset, and the probability of obtaining a specific output $O$ is almost the same. Thus, it is difficult for attackers to detect small changes in the dataset by observing the output results. In this way, privacy can be protected.

The implementation mechanism of differential privacy is mainly to add randomiza tion noise to the input or output: Laplace noise [14], Gaussian noise [14], exponential mechanism [14], etc.

Definition 2.

(Neighboring databases [15]) As for a randomized community $C_i=\left(V_i,E_i\right)$ in a graph $G$, two community graphs, $C_i=\left(V_i,E_i\right)$ and $C_i{}^{\prime }=\left(V_i{}^{\prime },E_i{}^{\prime }\right)$, are randomized; if $V_i=V_i{}^{\prime }$, $E_i\in E_i{}^{\prime }$, and |Ei| ± 1 = |E_i’|, we consider that $C_i$ and $C_i^{\prime }$ are neighboring community graphs.

Definition 3.

(Sensitivity [14]) As for randomized neighboring graphs $C_i$, $C^{\prime }{}_i$, the definition of the sensitivity of the function $f_{C_i}:C_i\to R^d$ is:

$$\Delta f_{C_i}=\underset{C_i{C}^{\prime }{}_i}{\max \parallel f\left(C_i\right)-f\left(C^{\prime }{}_i\right){\parallel }_1}$$

(2)

Theorem 1.

(Laplace mechanism [15]) For any function $f:G\to R^d$, the mechanism satisfied with the $\epsilon$-differential privacy,

$$A\left(G\right)=f\left(G\right)+\langle La{p}_1\left(\frac{\Delta f}{\epsilon }\right),\cdots ,La{p}_d\left(\frac{\Delta f}{\epsilon }\right)\rangle$$

(3)

where $La{p}_i\left(\frac{\Delta f}{\epsilon }\right)$ is the Laplace variables, and the parameter is $\frac{\Delta f}{\epsilon }$.

Definition 4.

(Social network community) As for a social network $G=\left(V,E\right)$, the collection of a community is $C=\left\{C_1,C_2,\cdots ,C_m\right\}$, where $C_i\cap C_j=\varnothing$ $\left(1\le i\ne j\le m\right)$. For any node $v\in C$, if the density of internal connections in community $C$ is higher than that of external connections between communities, $C$ is called a community.

This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, and the experimental conclusions that can be drawn.

4. Structure–Attribute Social Network Graph Publishing Model

4.1. Design Motivation

At present, the types of attacks that social network users have are mainly divided into two categories: one is from the user attributes and the other is from the relationship between users and friends. User attribute attacks involve user attributes include gender, age, height, etc. There is a correlation between attributes. If we obtain the true information for one attribute, we can speculate on the information for another attribute. For example, if a person likes spicy food, the attacker may speculate that he is from Sichuan or Chongqing and recommend some spicy products to users, or the hacker may send a connection of spicy food to users, which is a virus connection. A structural attack refers to the protection of the relationship between users. In social networks, it is expressed as the existence of edges. Attackers can judge the relationship between two people by the number of mutual friends or infer the relevant information of users by obtaining the attribute information of friends. It is necessary to protect user attributes and structures. Differential privacy can protect user information by disturbing the data. On the premise of ensuring that the attacker has the maximum background knowledge, specific user information cannot be inferred, and the published data can be used for data statistics.

Problems:

• In practice, social network data are usually anonymous before publishing, generating anonymous graphs. Attackers can obtain additional information in many ways, such as data mining, cooperative information systems, and attacks on knowledge or data, which still cause the disclosure of user privacy.
• Social network data publishing usually only goes through clustering and structural perturbation, which will lead to the risk of homogeneous privacy disclosure in the publishing community.
• The current social network protection scheme lacks the protection of attributes in formation, causing user privacy to be attacked.

4.2. Model Overview

The main steps of structure-attribute social network graph publishing model are: (1) to protect the user’s binary attribute information—specifically, to use the binary discretization method for continuous attributes and to divide the attribute values into two categories to improve the operation efficiency; (2) to improve the operation efficiency, we optimized the Louvain community division algorithm, which divides communities according to map data; (3) to improve the availability of data and reduce the addition of noise, we introduced the community partition algorithm and carried out further optimization; (4) to preserve as much of the graph structure as possible, we introduce an uncertainty graph and build a composite social network graph using structure and attribute information.

We have designed an overall model diagram. The overall overview of the model is shown in Figure 2.

Phase 1 (Protection of social network user attributes): This stage is to protect the user’s attribute information. The data collector converts continuous attributes into binary attributes by using the discrete binary method for the user’s continuous attributes, uses p-flip probability flipping for all binary attributes, and corrects statistical attribute information for unbiased estimation. Following iterations with prior probability, flipping probability, conditional probability, and the Bayesian formula, the joint attribute distribution is generated.

Phase 2 (Social network structure protection): This stage is a disturbance to the data-side relationship of social networks. In order to reduce the impact of disturbances on the data structure of social network graphs, we propose the uncertainty graph. First of all, we use the Louvain community division algorithm to divide the social network graph data into communities. The Louvain algorithm is an algorithm specially used for the community discovery of graph data. In order to improve the operation efficiency, we have further optimized the Louvain algorithm. Secondly, we introduce an uncertainty graph, generate social network edges with probability, and use differential privacy protection for the published uncertainty graph. Finally, we calculate the similarity of node attributes, build the edges between different communities, and generate a composite social network graph for publishing.

5. Protection of User Attributes

Before operating the user attribute information, we should preprocess the data first, mainly to discretize the continuous data. The process of mapping finite individuals in an infinite space to a finite space is known as discretization. The data discretization operation is mainly performed on continuous data. After processing, the data range distribution will be changed from a continuous attribute to a discrete attribute. This property usually contains two or more value ranges. The advantages of discretization include: (1) saving computing resources and improving computing efficiency; and (2) computing requirements of computing models. Although some methods can support the input of continuous data, they first discretize the continuous data and then further operate, such as the decision tree model. Although they support continuous data, the decision tree itself will first convert the continuous data into discrete data, so the discretization conversion is an indispensable step.

Collect information from users and convert the collected attribute information into binary attributes. We use the binary discretization method to set a threshold value, which is set to 1 if it is greater than the threshold value and to 0 if it is less than the threshold value, and then obtain a binary dataset with only two value fields. For example, gender (male and female) is a binary attribute, so there is no need to divide them. For age, use the binary discretization method to set the attribute value greater than the average age to 1 and the attribute value less than the average age to 0.

First, the data collector preprocesses the collected user attribute information and judges the attribute information. If it is a binary attribute, it will not be processed. If it is other attributes, we use the binary discretization method to cluster the attribute values into two categories, which are represented by 0,1. Generate an attribute matrix from the processed attribute values of each user. Each row represents a user, and each column represents the value of an attribute. We use the probability $P=\frac{1}{1+e^{\epsilon }}$ to flip the attribute values of each user to generate a disturbance matrix. We count the frequency of 1 for each attribute $f_{ai}=\frac{{\displaystyle \sum _{i=1}^n{u}_{a_i}}}{n}$ and use the formula for this frequency $f^{\prime }=\frac{p-1+f}{2p-1}$ to rectify and obtain unbiased estimates. Then, the conditional probability is obtained according to the prior probability of the attribute and the flipping probability of the attribute. The posterior probability is obtained according to the Bayesian formula, and the average value of the posterior probability is also obtained. The prior probability is iterated, and then the posterior probability is iterated. Until the difference between two adjacent posterior probabilities is less than the given threshold, we stop iterating to obtain the joint distribution of the attribute.

It is proved that the perturbation algorithm satisfies the differential privacy,

Given the attribute list $A=\left(a_1,a_2,a_3,\cdots ,a_m\right)$ and $A^{\prime }=\left(a_1{}^{\prime },a_2{}^{\prime },a_3{}^{\prime },\cdots ,a_m{}^{\prime }\right)$ and the mechanism $M$, the output of $M$ is $O=\left(o_1,o_2,o_3,\cdots ,o_m\right)$:

$$\begin{array}{l}\frac{P\left[M\left(A\right)=O\right]}{P\left[M\left(A^{\prime }\right)=O\right]}=\frac{P[a_1\to o_1],\cdots ,P[a_m\to o_m]}{P[a_1{}^{\prime }\to o_1],\cdots ,P[a_m{}^{\prime }\to o_m]}\\ =\frac{P[a_1\to o_1]}{P[a_1{}^{\prime }\to o_1]}\\ <\frac{1-p}{p}=e^{\epsilon }\end{array}$$

(4)

6. Protecting the Structure of the Social Network (Social Network Graph Publish Method—SNGPM)

6.1. Optimization of Community Partition Algorithm

The Louvain algorithm is a community detection algorithm based on modular computing. It is an iterative process of clustering vertices with the goal of maximizing modular computing. It can calculate satisfactory community recognition results with a high efficiency. The weight is calculated by considering the weight on the edge. In this paper, the weight of all the edges is set as 1. The modular definition of social networks is as follows:

$$Q={\displaystyle \sum _C[\frac{{\displaystyle {\sum }_{in}^c}}{2m}-{\left(\frac{{\displaystyle {\sum }_{tot}^c}}{2m}\right)}^2]}$$

(5)

where $m$ is the weight value of the graph; this paper sets the weight of each edge to 1. $C$ is any community in the graph. ${\displaystyle {\sum }_{in}^c}$ is the weight value within any community. ${\displaystyle {\sum }_{tot}^c}$ is the weight value of the whole community.

In our optimization scheme, in the first round of iteration, we find the nodes with a degree of 0 and remove them from the iteration graph. The points with a degree of 0 (isolated points) have a negative value for any other community or node. When moving into other communities, the number of iteration rounds and the time complexity can be reduced by removing the isolated points. At the same time, we first regard the node with a degree of 1 and its neighbors as a whole. The node with a degree of 1 needs to iterate with all communities and calculate the modularity ($Q$) value. After multiple iterations, it is finally divided with the community where its neighbor node resides. Before starting the iteration, the node with a degree of 1 and its neighbor node are first regarded as a node, which can reduce the number of iterations and reduce the time complexity.

6.2. Algorithm Details

This section describes our solution in detail, including three steps:

• Attribute perturbation algorithm (Algorithm 1)
• Optimized Leuven community discovery (Algorithm 2)
• Adding disturbance to generate an uncertainty graph (Algorithm 3)
• Post-processing edge reconstruction (Algorithm 4)

In Algorithm 1, we use the binary discretization method (line 5–9) to discrete disturb and process user attributes (line 11–22). In Algorithm 2, we optimized the Leuven community discovery algorithm, input a social network graph $G$, and output a graph $G1$ with a community structure. First, each node is regarded as a community, and the independent node is first established as a community and does not participate in the community division iteration (lines 2–5). A node with a degree of 1 finally enters its neighbor’s community and binds it to the neighbor node (line 7). Calculate whether each point can find a community where its neighbors live. If this point can be allocated in the past to generate the largest and most positive community, and if it can be found, adjust the node to a new community; use the same method to calculate and adjust the next point. After all points have been calculated and adjusted, the next iteration is started. This stage iterates according to this rule until no points can be reallocated (lines 12–17). The runtime of our algorithm is $O(n\ast n)$.

Algorithm 1. Attribute perturbation algorithm

Input: user collection $U\left(u_1,u_2,u_3,\cdots ,u_n\right)$ ($n$ is the number of users)

Attribute collection A(a1,a2,a3,…am) ($m$ is the number of attribute),

Threshold t, flip probability $P_{flip}$,

Output: joint distribution of user attributes $P_u$

Start

1: get property information $A$

2: if $A$ is a binary attribute

3:    Continue

4: Else

5:    //binary discretization method, with attribute value marked as 0,1

6:    If attribute value > the average value of this attribute,

7:     set the attribute value to 1,

8:    Else

9:     set the property value to 0

10: For the attribute values of every user is $a_i$,

11:   With probability $P_{flip}$ flip attribute values per user//disturbance attribute list of each user $u_i\to u_i{}^{\prime }$

12:   count the frequency of attribute values of each user $f_{ai}=\frac{{\displaystyle \sum _{i=1}^n{u}_{ai}}}{n}$//Frequency per attribute $\left(f_{a1},f_{a2},f_{a3},\cdots ,f_{am}\right)$

13:   user $f^{\prime }=\frac{p-1+f}{2p-1}$ to corrected, obtain unbiased estimates

14: End for

15: get the prior probability of each attribute of each user $P_{former}=P\left(u_1=a_1,u_2=a_2,u_3=a_3,\cdots ,u_m=a_m\right)$ and $P_{flip}$

16: get conditional probability $P\left(u^{\prime }{}_i|a_i\right)={{\displaystyle \prod _{j=1}^m\left(1-P_{flip}\right)}}^{|u_i{}^{\prime }\left[j\right]-a_i\left[j\right]|}\times P_{flip}{}^{1-|u_i{}^{\prime }\left[j\right]-a_i\left[j\right]|}$

17: according to Bayesian formula $P_t\left(a_i|u_i{}^{\prime }\right)=\frac{P_t\left(u_i=a_i\right)P\left(u_i{}^{\prime }|u_i=a_i\right)}{{\displaystyle \sum _{a_i}{P}_t\left(a_i\right)P\left(u_i{}^{\prime }|u_i=a_i\right)}}$

18: obtain a posterior probability $P_{latter}$,

19: If $P_{latter}\left(t\right)-P_{latter}\left(t-1\right)\ge t$

20: calculated and get $P_{latter}\left(ave\right)$, use it to repeat iteration for prior probability

21: Else

22:   Return $P_u=P_{latter}\left(t\right)$

End

Algorithm 2. Optimization of the Louvain community (OLC)

Input: Social network graph, $G$

Output: The graph $G1$ with community, community collection $C$

Start

1:  initialization, create $G1,V1,E1$ //node set, edge set

2: $G1$.nodes = $G$.nodes, $G1$.edges = $G$.edges

3: For all nodes do

4:   If $d_i$ == 0 do

5:    $d_i$ is a community

6:   Elseif $d_i$ == 1 do

7:     Consider $d_i$ and $d_i{}^{\prime }$s neighbor node as a super node

8:  end

9: While $G$ is a connected graph do

10:   for all nodes do

11:     If node $I$ has neighbor node

12:        Put node $I$ into a community $C_i$ where node $I$’s neighbor in it

13:        Calculate $\Delta Q$ //$\Delta Q$ is the value that before and after the node is placed

14:        If $\Delta Q$ > 0

15:          Merge this node into the neighborhood community

16:        Else

17:        Keep it as it is

18:     Else remove the node from node set and no longer participates in traversal

19:   End for

20: End while

End

Algorithm 3. Algorithm for generating the uncertainty graph

Input: A graph $G1$ with community, privacy budget $\epsilon$

Output: uncertainty graph $G2$

Start

1: for traverse every community do

2:     Calculate the total degree of all nodes in the community ${\displaystyle {\sum }_{V_i\in C}{d}_{V_i}}$

3:   If this community has only one node

Continue

4:   End if

5: end

6:   For traverse every side in the community $E_{i,j}$ do

7:     calculate the degree of node $i,j$, as $d_i,d_j$

8:      $P_{e_{i,j}}=\left(d_{{}_i}+d_j\right)$ //the sum of degree

9:       calculate community sensitivity Δf, injection noise $P^{\prime }{}_{d_{i,j}}=P_{e_{i,j}}+Lap\left(\Delta f/\epsilon \right)$

10:   End for

11: Return $G2$

End

Algorithm 3 realizes the privacy of a network graph through an uncertainty graph. The input is the network graph $G1$ with a community structure and the privacy budget e, and the output is the uncertain social network with Laplace disturbance. First, calculate the sum of degrees of all nodes in each community and the probabilities of all edges (lines 2–7). In addition, we do not calculate the community with just one node. Then, calculate the sensitivity $\Delta f$ based on the edge probability, inject the Laplace noise, and generate the perturbation probability (line 8). The running time of the algorithm is $O\left(n\right)$.

Algorithm 4. Post-processing algorithm

Input: An uncertainty graph $G2$ with community

Output:$G^{\prime }$

Start

1: for all edges do

2:  If the two nodes $i$ and $j$ connected by this edge are in different communities

3:   Delete edge, save probability in variable $list$

4:    randomly select a node $i^{\prime },j^{\prime }$,

5:      If $d_i{}^{\prime }>d_{average}$ and $d_j{}^{\prime }>d_{average}$

6:        Create edge, $E_{i^{\prime },j^{\prime }}$, and $P_{E_{i^{\prime },j^{\prime }}}=list$

7:      End if

8:   End for

End

Algorithm 4 is post-processing. The input is an uncertainty graph $G2$ with a community structure, and the output is a finally released graph $G$. The first step is to traverse all the edges to determine whether the endpoint nodes are in different communities. If the conditions are met, delete the edge and save the probability values in the variable list (lines 2 and 3). Step 2: Choose nodes $i^{\prime }$ and $j^{\prime }$ at random. If the degree values of these two nodes are both greater than the average degree value, create an edge and assign the value of the list to the edge (lines 4–6). Finally, return to $G^{\prime }$. The operation time is $O\left(n\right)$. Nodes with higher degree values have a greater user influence and are easy to attack. An edge is established between nodes with higher degree values than the average degree to effectively protect user privacy.

6.3. Privacy Analysis

According to the definition of sensitivity, we can see that the global sensitivity of the algorithm is $\Delta f_G={\max }_{G,G^{\prime }}\parallel f\left(G\right)-f\left(G^{\prime }\right){\parallel }_1$, the dataset with the largest difference between datasets on the entire social network graph and adjacent graphs. Our algorithm reduces the global scope of an adjacent graph to the sensitivity of each adjacent community through community division $\Delta f_{C_i}={\max }_{C_i,C_i{}^{\prime }}\parallel f\left(C_i\right)-f\left(C_i{}^{\prime }\right){\parallel }_1$. The local sensitivity of adjacent communities is $\Delta f_{C_i}={\max }_{C_i}\left(P_{E_i}-P_{E_j}\right)\left(i,j\in V_{C_i}\right)$; reduce sensitivity and noise by dividing communities.

The proof of satisfying differential privacy is:

$$\begin{array}{c}\frac{\mathrm{Pr}[{\tilde{C}}_i=S]}{\mathrm{Pr}[{\tilde{C}}_i^{\prime }=S]}={\displaystyle \prod _{j=1}^{m^{*}}}\frac{\mathrm{Pr}[{\tilde{C}}_i[j]=S_j\mid S_1,\cdots ,S_{j-1}]}{\mathrm{Pr}[{\tilde{C}}_i^{\prime }[j]=S_j\mid S_1,\cdots ,S_{j-1}]}\\ {\displaystyle \prod _{j=1}^{m^{*}}}\frac{\mathrm{Pr}[{\tilde{C}}_i[j]=S_j\mid S_1,\cdots ,S_{j-1}]}{\mathrm{Pr}[{\tilde{C}}_i^{\prime }[j]=S_j\mid S_1,\cdots ,S_{j-1}]}\le {\displaystyle \prod _{j=1}^{m^{*}}}e\frac{\mid {\tilde{C}}_i[j]-\widetilde{{C\prime }_i[j]}\mid }{\sigma }\end{array}$$

(6)

$${\stackrel{\sim }{C}}_i=C_i+Lap{\left(\frac{\Delta f}{\epsilon }\right)}^{\left|C_i\right|}$$

(7)

$$\parallel C_i-C^{\prime }{}_i\parallel \le \Delta f$$

(8)

$$\begin{array}{l}{\displaystyle \prod _{j=1}^{m^{\ast }}e\frac{{}^{|{\stackrel{\sim }{C}}_i[j]-\stackrel{\sim }{C^{\prime }{}_i[j]}|}}{\sigma }}=e^{\frac{\parallel {\stackrel{\sim }{C}}_i-\stackrel{\sim }{C^{\prime }{}_i}{\parallel }_1}{\sigma }}\\ =e\frac{\parallel \stackrel{}{{\stackrel{\sim }{C}}_i+Lap\left(\frac{\Delta f}{\epsilon }\right)}-{\stackrel{\sim }{C^{\prime }}}_i-Lap\left(\frac{\Delta f}{\epsilon }\right){\parallel }_1}{\sigma }\\ =e^{\frac{\parallel C_i-C^{\prime }{}_i{\parallel }_1}{\sigma }}\\ \le e^{\epsilon }\end{array}$$

(9)

$C_i$ and $C_i{}^{\prime }$ are adjacent communities, $C_i[j]$ is the probability value of the corresponding edge in each community, and $m^{\ast }$ is the number of nodes in any community.

7. Experiment

7.1. Experimental Setup

The experimental environment of this paper is Windows 10, 2.50 GHz, 8.0 GB. All algorithms are implemented in Python, and the programming environment is version Python 3.6.0 was founded by Gudio van Rossum, a Dutchman, in Amsterdam, the Netherlands.

7.2. Experimental Data

The experimental data are from the Stanford official dataset and the network official dataset, as shown in

Table 1. Experimental datasets.

Datasets	The Number of Nodes	The Number of Edges
Train bombing	64	243
Jazz musicians	198	2743
Facebook	4039	88,234
Wiki-vote	7115	103,689

, which can be found at http://snap.stanford.edu/ (accessed on 4 March 2022) and http://konect.cc/networks/, respectively (accessed on 4 March 2022).

7.3. Time Comparison Experiment

The running time of the Louvain algorithm before and after optimization is tested on four different real datasets.

As shown in Figure 3, the comparison of time before and after the optimization of the Louvain community partition algorithm from four datasets of different sizes (Train Bombing, Jazz Musicians, Facebook, Wiki-vote) shows that there is no significant difference in smaller datasets (Train Bombing, Jazz Musicians). However, with the increase in datasets, the time advantage becomes more and more obvious. We divide a single node into a single community, which can effectively prevent this node and all other nodes from calculating the degree of modularity, reduce the number of traverses in the process of dividing the experimental community, and reduce the time complexity. In addition, we bind a node with a degree of one to the neighbor node of this node, which belongs to the community where the neighbor node resides. If not, the node with a degree of one will calculate the modularity with the community after each iteration, which is an order of magnitude of time consumption for large datasets. We have conducted thousands of experiments and found that when the social network is larger, the time saving of the optimization algorithm is more prominent, and the time efficiency of running on Facebook and Wiki-vote is improved by 20%.

7.4. Data Release Availability Measurement

We measure the availability of generated data through three experiments, namely, the number of edges, the local clustering coefficient, and the global clustering coefficient. We compare the DP and SNGPM algorithms for the three datasets in the original image with privacy budgets of 0.1, 0.2, 1, 5, 10, and 100.

Figure 4 shows the experimental data on the number of edges in different datasets (Train Bombing, Jazz Musicians, Facebook). The experiment shows that the SNGPM algorithm is closer to real data than the DP algorithm. From the two small and medium sized datasets, Train Bombing and Jazz Musicians, we can see that SNGPM is closer to the edge number of real data than DP and that its performance is stable under different privacy budgets. By introducing an uncertainty graph, our algorithm can retain the structure of the social network to the greatest extent and thus retain the structure and number of edges close to the original data. The experimental results on the Facebook dataset show that our algorithm has obvious advantages and performs better on large datasets. We compare the number of edges under different privacy budgets and quantitatively show the impact of algorithm perturbations on the number of edges in the graph. The results show that our algorithm is obviously superior to the DP algorithm. Our algorithm can better preserve the edge number and structure of the graph and effectively improve the availability of published graphs.

Figure 5 shows the distribution of local clustering coefficients in different datasets (Train Bombing, Jazz Musicians, Facebook) under different privacy budgets. The local clustering coefficient quantifies the degree to which adjacent nodes gather to form a complete graph. In 1998, Duncan J. Watts and Steven H. Strogatz applied this measurement method to determine whether a graph constitutes a small-world network. It is found that the network with the largest local clustering coefficient has a modular structure, and the average distance between different nodes is as small as possible. The experimental results show that our algorithm is more stable than the DP algorithm and closer to the local clustering coefficient of the original graph. After Louvain community division, our algorithm effectively reduces the sensitivity and reduces the introduction of noise. We can conduct less disturbance while maintaining the same differential privacy protection degree as DP, so we have less disturbance to the original graph and more structure retention in the social network. The results show that our algorithm can retain the structure of the original graph to the greatest extent.

Figure 6 shows the experimental results of global clustering coefficients for different datasets (Train Bombing, Jazz Musicians, and Facebook) under different privacy budgets (0.1, 0.2, 1, 5, 10, 100). The global clustering coefficient is based on the tripleness of nodes. A triplet is three nodes connected by two (open triples) or three (closed triples) undirected connections. The global clustering coefficient is the total number of triples divided by the number of closed triples. This metric summarizes clusters across the global network. In the process of community division, we connect closely connected users together to increase the tightness of the community. At the same time, the uncertainty graph algorithm we introduced can preserve the internal structure of the community as much as possible while maintaining user privacy. Our algorithm performs well on large datasets. Compared with the DP algorithm, our algorithm can better maintain the clustering of the social network graph and keep as many structures as possible in the whole social network graph. Experiments show that our algorithm performs better than the DP algorithm.

Figure 7 shows the correlation coefficient measurement under different graph generation models. $P\left(i,j\right)=\frac{e}{m}$ represents that the degrees of two endpoints of an edge randomly selected in the network are the probabilities of $i$ and $j$, respectively; $p\left(i\right)$ represents the probability that the degrees of a node randomly selected in the network and then a neighbor node randomly selected in the network are $i$. Similarly, $P\left(j\right)$. If $P\left(i,j\right)=P\left(i\right)\ast P\left(j\right)$, the network is said to have no degree correlation; otherwise, it has degree correlation. In a network with further degree correlation, if the nodes with a higher degree tend to the nodes with a higher degree of connectivity, then the network is said to be homogeneous; if the nodes with a higher degree tend to the nodes with a lower degree of connectivity, then the network is heterogeneous. We use ${\displaystyle \sum _{i,j\in V}P\left(i,j\right)-P\left(i\right)P\left(j\right)}$ to indicate the degree of the same match and different matches in the network. After normalization, we think that when the value is greater than zero, the network has the same match, and vice versa. Figure 7 shows the correlation coefficients under different graph generation models. It can be seen that our algorithm is the closest to the correlation coefficients of the original graph and does not change the properties of the graph. The ER algorithm does not change the properties of the graph but has a large difference from the correlation coefficients of the original graph. WS and BA also change the correlation coefficients greatly.

8. Conclusions

In this paper, we propose a social network data publishing model that combines node attributes and graph structure. This model protects social network data from both node attributes and network structure and uses the protected data for other research. First, we discretize the continuous attributes through binary attribute discretization to reduce the computational overhead. We protect the attributes of nodes by flipping the binary attributes so that the published attributes do not disclose user privacy on the premise of meeting availability. Secondly, we use the Louvain community partition algorithm to partition the entire social network, further reducing the sensitivity of the data and reducing the introduction of noise. Then, we introduce an uncertainty graph to maintain the community structure to the greatest extent possible. Our experiments show that our method maintains the structure of the whole network in terms of the number of edges, local clustering coefficients, and global clustering coefficients on three datasets of different sizes. We prove theoretically that our method satisfies differential privacy. In the process of analyzing social network structure disturbances, we optimized the Louvain community partition algorithm. Experiments on large datasets show that our method improves efficiency by 20%. In summary, our model not only improves efficiency but also ensures privacy.

In our future work, we will continue to study the following aspects in depth:

(1)

Further improve the operation time and efficiency of the community partition algorithm.

(2)

In conventional social network protection methods, node attribute information is combined, and further discussion is carried out, such as on the continuous numerical value, multi-category attribute, and text attribute. Different types of attributes are studied to improve the effectiveness of the published data.

(3)

In the attribute structure of the social network composite graph, we can use the association information of node attributes to generate the social network graph.