Stable Many-Body Resonances in Open Quantum Systems
Abstract
1. Introduction
2. The Model
The Bose–Hubbard Model
3. Open Quantum System Dynamics
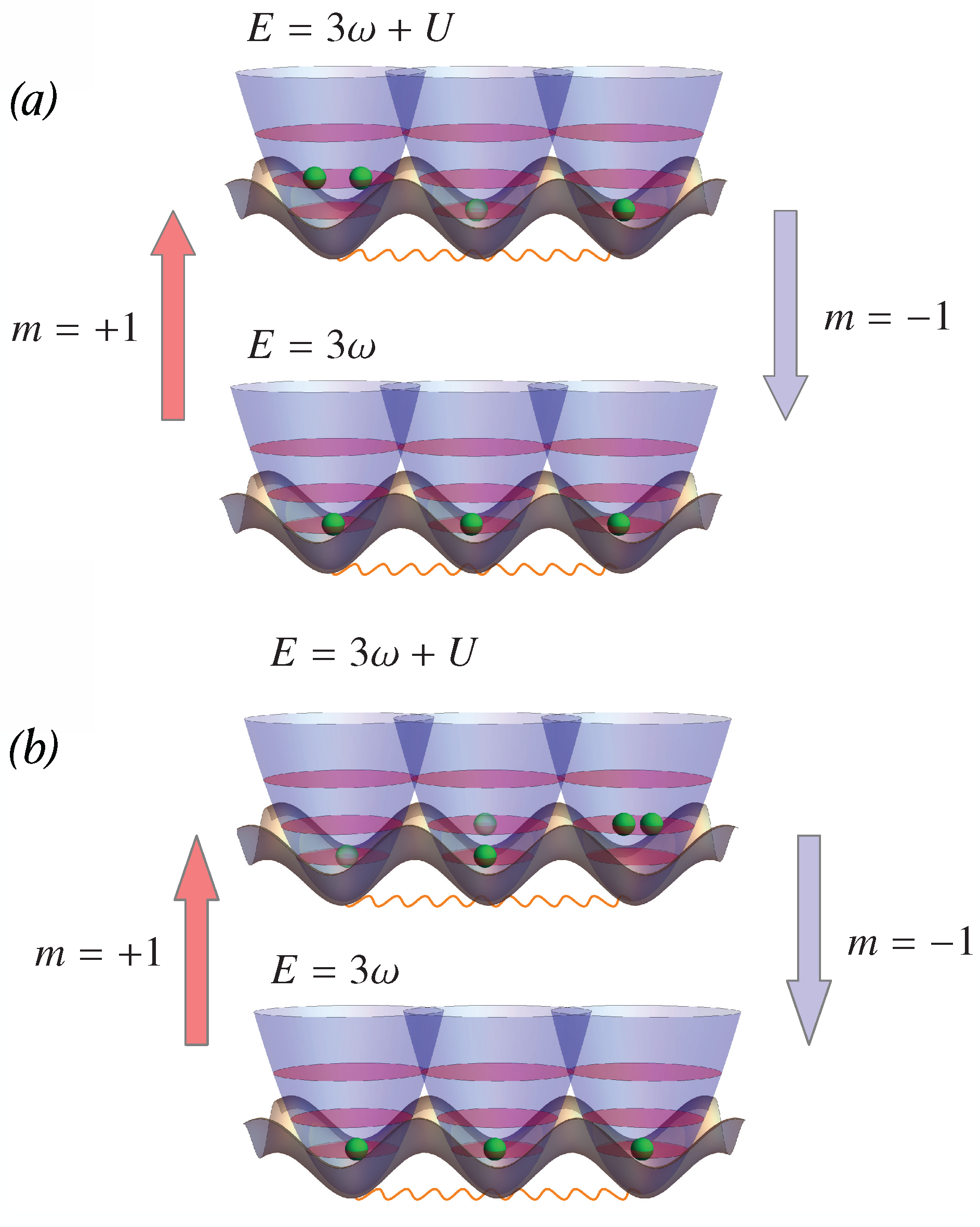
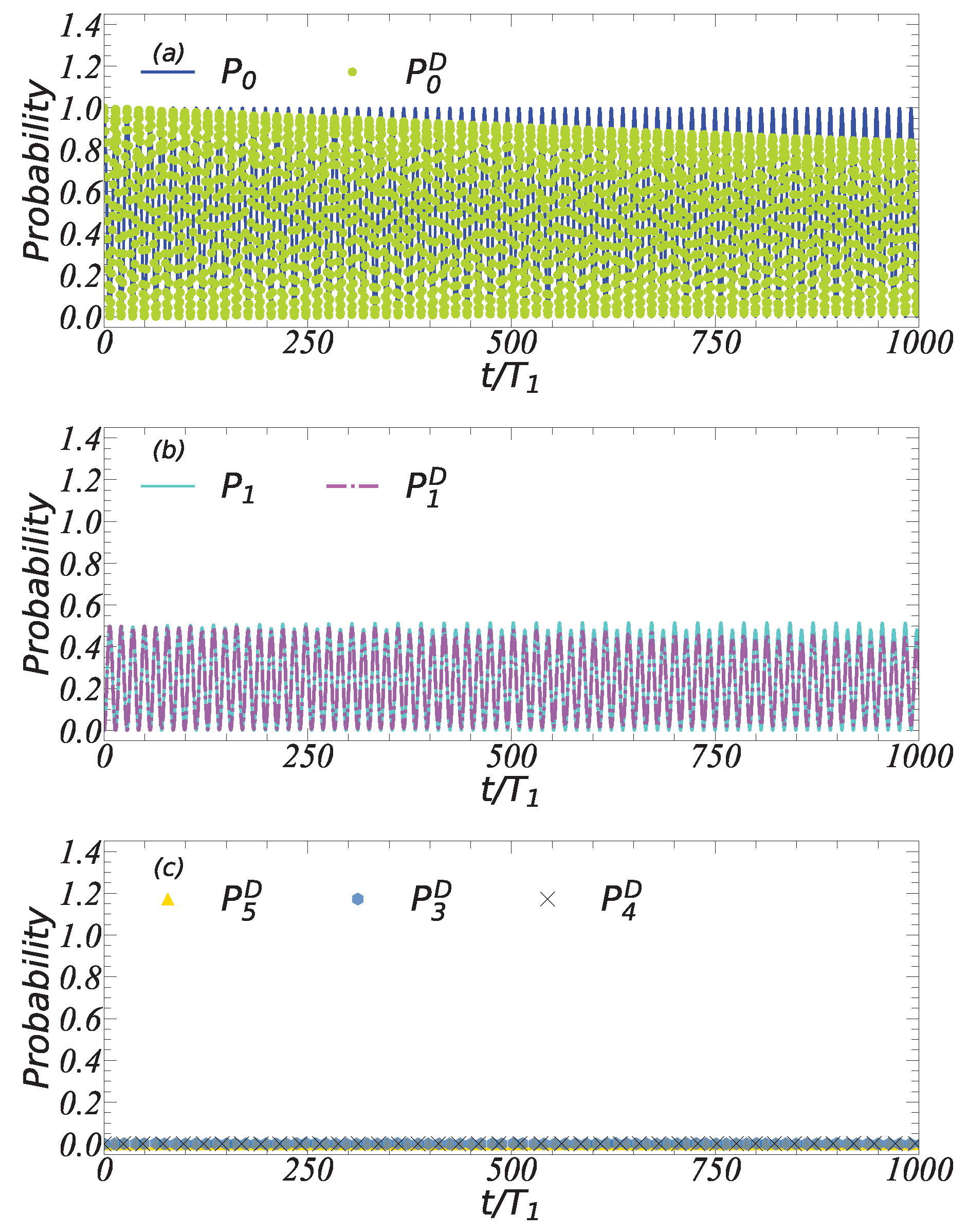
3.1. Three-Site Bose–Hubbard Lattice
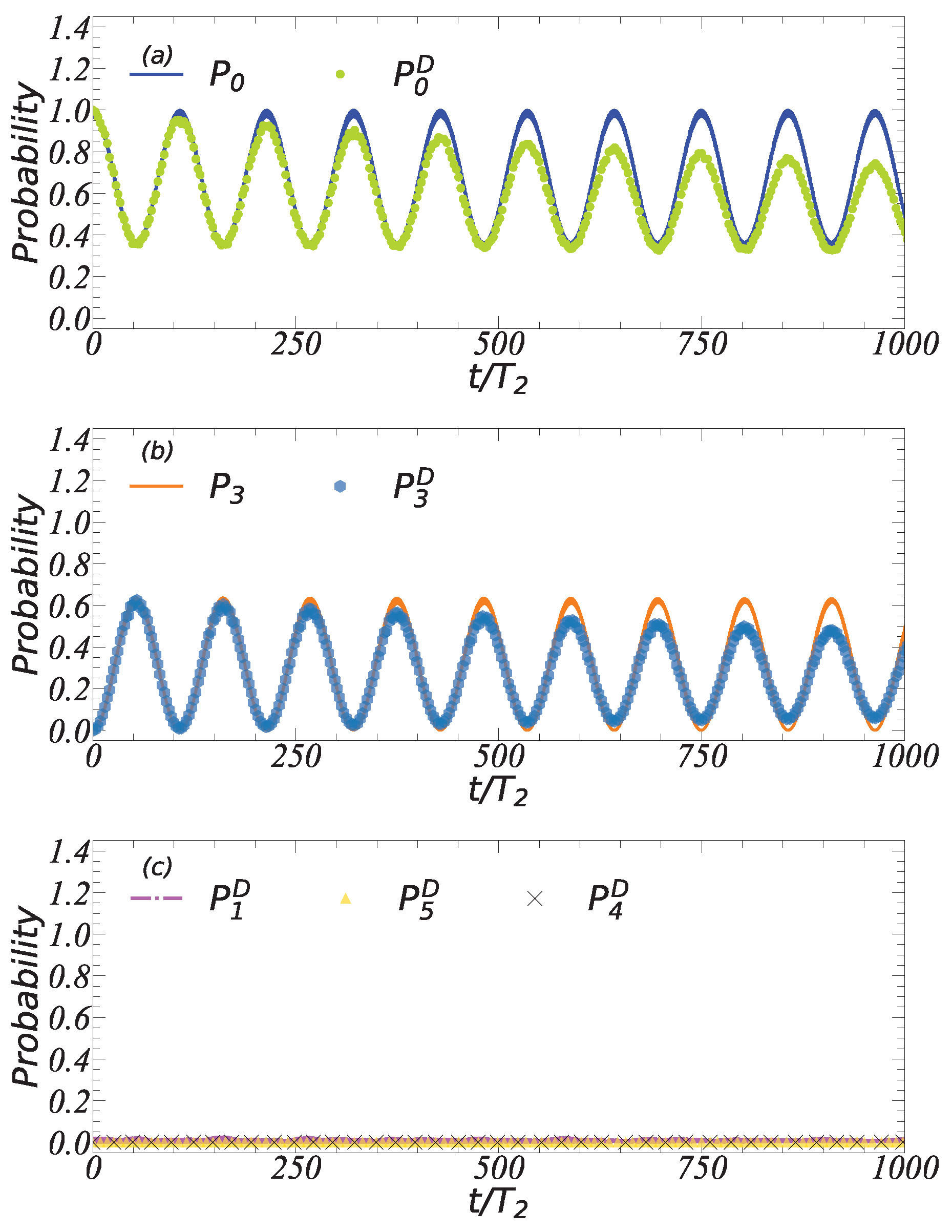
3.2. Four-Site Bose-Hubbard Lattice
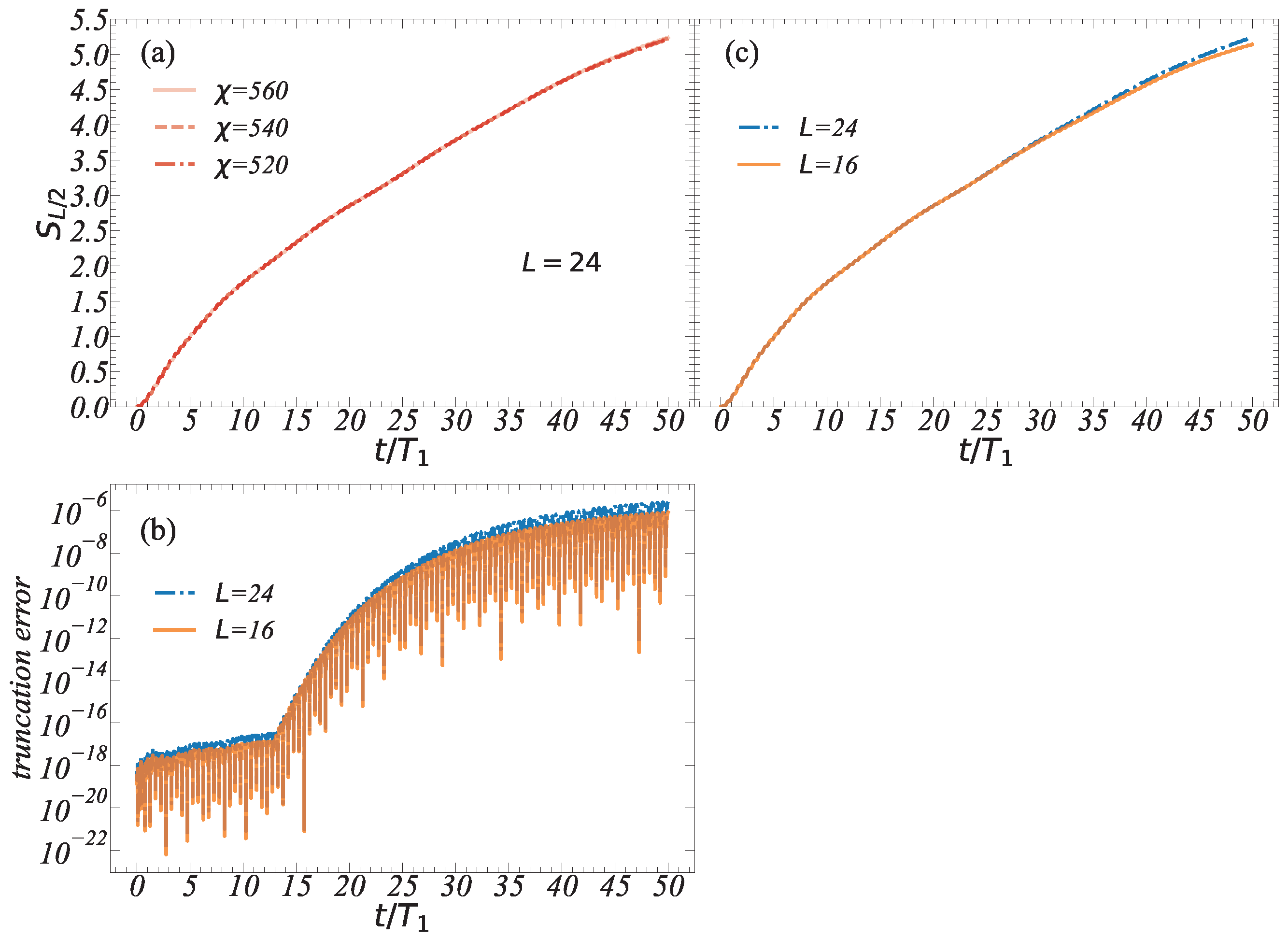
3.3. The Linear Entropy
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. [Stability of Integer Resonance]
References
- Altman, E.; Brown, K.R.; Carleo, G.; Carr, L.D.; Demler, E.; Chin, C.; DeMarco, B.; Economou, S.E.; Eriksson, M.A.; Fu, K.M.C.; et al. Quantum Simulators: Architectures and Opportunities. PRX Quantum 2021, 2, 017003. [Google Scholar] [CrossRef]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 885–964. [Google Scholar] [CrossRef]
- Cheneau, M.; Barmettler, P.; Poletti, D.; Endres, M.; Schauß, P.; Fukuhara, T.; Gross, C.; Bloch, I.; Kollath, C.; Kuhr, S. Light-cone-like spreading of correlations in a quantum many-body system. Nature 2012, 481, 484–487. [Google Scholar] [CrossRef] [PubMed]
- Bernien, H.; Schwartz, S.; Keesling, A.; Levine, H.; Omran, A.; Pichler, H.; Choi, S.; Zibrov, A.S.; Endres, M.; Greiner, M.; et al. Probing many-body dynamics on a 51-atom quantum simulator. Nature 2017, 551, 579. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.Y.; Hild, S.; Zeiher, J.; Schauß, P.; Rubio-Abadal, A.; Yefsah, T.; Khemani, V.; Huse, D.A.; Bloch, I.; Gross, C. Exploring the many-body localization transition in two dimensions. Science 2016, 352, 1547–1552. [Google Scholar] [CrossRef] [PubMed]
- Roushan, P.; Neill, C.; Tangpanitanon, J.; Bastidas, V.M.; Megrant, A.; Barends, R.; Chen, Y.; Chen, Z.; Chiaro, B.; Dunsworth, A.; et al. Spectroscopic signatures of localization with interacting photons in superconducting qubits. Science 2017, 358, 1175–1179. [Google Scholar] [CrossRef]
- Ma, R.; Saxberg, B.; Owens, C.; Leung, N.; Lu, Y.; Simon, J.; Schuster, D.I. A dissipatively stabilized Mott insulator of photons. Nature 2019, 566, 51–57. [Google Scholar] [CrossRef]
- Ye, Y.; Ge, Z.Y.; Wu, Y.; Wang, S.; Gong, M.; Zhang, Y.R.; Zhu, Q.; Yang, R.; Li, S.; Liang, F.; et al. Propagation and Localization of Collective Excitations on a 24-Qubit Superconducting Processor. Phys. Rev. Lett. 2019, 123, 050502. [Google Scholar] [CrossRef]
- Zha, C.; Bastidas, V.M.; Gong, M.; Wu, Y.; Rong, H.; Yang, R.; Ye, Y.; Li, S.; Zhu, Q.; Wang, S.; et al. Ergodic-Localized Junctions in a Periodically Driven Spin Chain. Phys. Rev. Lett. 2020, 125, 170503. [Google Scholar] [CrossRef]
- Gong, M.; de Moraes Neto, G.D.; Zha, C.; Wu, Y.; Rong, H.; Ye, Y.; Li, S.; Zhu, Q.; Wang, S.; Zhao, Y.; et al. Experimental characterization of the quantum many-body localization transition. Phys. Rev. Res. 2021, 3, 033043. [Google Scholar] [CrossRef]
- Neill, C.; Roushan, P.; Kechedzhi, K.; Boixo, S.; Isakov, S.V.; Smelyanskiy, V.; Megrant, A.; Chiaro, B.; Dunsworth, A.; Arya, K.; et al. A blueprint for demonstrating quantum supremacy with superconducting qubits. Science 2018, 360, 195–199. [Google Scholar] [CrossRef] [PubMed]
- Sacha, K. Modeling spontaneous breaking of time-translation symmetry. Phys. Rev. A 2015, 91, 033617. [Google Scholar] [CrossRef]
- Else, D.V.; Bauer, B.; Nayak, C. Floquet Time Crystals. Phys. Rev. Lett. 2016, 117, 090402. [Google Scholar] [CrossRef]
- Yao, N.Y.; Potter, A.C.; Potirniche, I.D.; Vishwanath, A. Discrete Time Crystals: Rigidity, Criticality, and Realizations. Phys. Rev. Lett. 2017, 118, 030401. [Google Scholar] [CrossRef] [PubMed]
- Sacha, K.; Zakrzewski, J. Time crystals: A review. Rep. Prog. Phys. 2017, 81, 016401. [Google Scholar] [CrossRef] [PubMed]
- Pizzi, A.; Knolle, J.; Nunnenkamp, A. Period-n Discrete Time Crystals and Quasicrystals with Ultracold Bosons. Phys. Rev. Lett. 2019, 123, 150601. [Google Scholar] [CrossRef]
- Sacha, K. Time Crystals, 1st ed.; Springer Series on Atomic, Optical, and Plasma Physics; Springer: Cham, Switzerland, 2020; Volume 114. [Google Scholar]
- Pizzi, A.; Knolle, J.; Nunnenkamp, A. Higher-order and fractional discrete time crystals in clean long-range interacting systems. Nat. Commun. 2021, 12, 2341. [Google Scholar] [CrossRef]
- Pizzi, A.; Nunnenkamp, A.; Knolle, J. Classical Prethermal Phases of Matter. Phys. Rev. Lett. 2021, 127, 140602. [Google Scholar] [CrossRef]
- Pizzi, A.; Nunnenkamp, A.; Knolle, J. Classical approaches to prethermal discrete time crystals in one, two, and three dimensions. Phys. Rev. B 2021, 104, 094308. [Google Scholar] [CrossRef]
- Ojeda Collado, H.P.; Usaj, G.; Balseiro, C.A.; Zanette, D.H.; Lorenzana, J. Emergent parametric resonances and time-crystal phases in driven Bardeen-Cooper-Schrieffer systems. Phys. Rev. Res. 2021, 3, L042023. [Google Scholar] [CrossRef]
- Abanin, D.A.; De Roeck, W.; Huveneers, F.m.c. Exponentially Slow Heating in Periodically Driven Many-Body Systems. Phys. Rev. Lett. 2015, 115, 256803. [Google Scholar] [CrossRef]
- Abanin, D.A.; De Roeck, W.; Ho, W.W.; Huveneers, F.m.c. Effective Hamiltonians, prethermalization, and slow energy absorption in periodically driven many-body systems. Phys. Rev. B 2017, 95, 014112. [Google Scholar] [CrossRef]
- Abanin, D.; De Roeck, W.; Ho, W.W.; Huveneers, F. A Rigorous Theory of Many-Body Prethermalization for Periodically Driven and Closed Quantum Systems. Commun. Math. Phys. 2017, 354, 809–827. [Google Scholar] [CrossRef]
- Mori, T.; Kuwahara, T.; Saito, K. Rigorous Bound on Energy Absorption and Generic Relaxation in Periodically Driven Quantum Systems. Phys. Rev. Lett. 2016, 116, 120401. [Google Scholar] [CrossRef]
- Kuwahara, T.; Mori, T.; Saito, K. Floquet–Magnus theory and generic transient dynamics in periodically driven many-body quantum systems. Ann. Phys. 2016, 367, 96–124. [Google Scholar] [CrossRef]
- Rubio-Abadal, A.; Ippoliti, M.; Hollerith, S.; Wei, D.; Rui, J.; Sondhi, S.L.; Khemani, V.; Gross, C.; Bloch, I. Floquet Prethermalization in a Bose-Hubbard System. Phys. Rev. X 2020, 10, 021044. [Google Scholar] [CrossRef]
- Ying, C.; Guo, Q.; Li, S.; Gong, M.; Deng, X.H.; Chen, F.; Zha, C.; Ye, Y.; Wang, C.; Zhu, Q.; et al. Floquet prethermal phase protected by U(1) symmetry on a superconducting quantum processor. Phys. Rev. A 2022, 105, 012418. [Google Scholar] [CrossRef]
- Torre, E.G.D.; Dentelski, D. Statistical Floquet prethermalization of the Bose-Hubbard model. SciPost Phys. 2021, 11, 40. [Google Scholar] [CrossRef]
- Dziarmaga, J. Dynamics of a quantum phase transition and relaxation to a steady state. Adv. Phys. 2010, 59, 1063–1189. [Google Scholar] [CrossRef]
- Polkovnikov, A.; Sengupta, K.; Silva, A.; Vengalattore, M. Colloquium: Nonequilibrium dynamics of closed interacting quantum systems. Rev. Mod. Phys. 2011, 83, 863–883. [Google Scholar] [CrossRef]
- Eisert, J.; Friesdorf, M.; Gogolin, C. Quantum many-body systems out of equilibrium. Nat. Phys. 2015, 11, 124–130. [Google Scholar] [CrossRef]
- Mitra, A. Quantum Quench Dynamics. Annu. Rev. Condens. Matter Phys. 2018, 9, 245–259. [Google Scholar] [CrossRef]
- Heyl, M. Dynamical quantum phase transitions: A review. Rep. Prog. Phys. 2018, 81, 054001. [Google Scholar] [CrossRef] [PubMed]
- Orús, R. Tensor networks for complex quantum systems. Nat. Rev. Phys. 2019, 1, 538–550. [Google Scholar] [CrossRef]
- Schollwöck, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 2011, 326, 96–192. [Google Scholar] [CrossRef]
- Silvi, P.; Tschirsich, F.; Gerster, M.; Jünemann, J.; Jaschke, D.; Rizzi, M.; Montangero, S. The Tensor Networks Anthology: Simulation techniques for many-body quantum lattice systems. SciPost Phys. Lect. Notes 2019, 8. [Google Scholar] [CrossRef]
- Peña, R.; Bastidas, V.M.; Torres, F.; Munro, W.J.; Romero, G. Fractional resonances and prethermal states in Floquet systems. Phys. Rev. B 2022, 106, 064307. [Google Scholar] [CrossRef]
- Fisher, M.P.A.; Weichman, P.B.; Grinstein, G.; Fisher, D.S. Boson localization and the superfluid-insulator transition. Phys. Rev. B 1989, 40, 546–570. [Google Scholar] [CrossRef]
- Jaksch, D.; Bruder, C.; Cirac, J.I.; Gardiner, C.W.; Zoller, P. Cold Bosonic Atoms in Optical Lattices. Phys. Rev. Lett. 1998, 81, 3108–3111. [Google Scholar] [CrossRef]
- Chen, W.; Hida, K.; Sanctuary, B.C. Ground-state phase diagram of S = 1 XXZ chains with uniaxial single-ion-type anisotropy. Phys. Rev. B 2003, 67, 104401. [Google Scholar] [CrossRef]
- Chung, W.C.; de Hond, J.; Xiang, J.; Cruz-Colón, E.; Ketterle, W. Tunable Single-Ion Anisotropy in Spin-1 Models Realized with Ultracold Atoms. Phys. Rev. Lett. 2021, 126, 163203. [Google Scholar] [CrossRef] [PubMed]
- Greentree, A.D.; Tahan, C.; Cole, J.H.; Hollenberg, L.C.L. Quantum phase transitions of light. Nat. Phys. 2006, 2, 856–861. [Google Scholar] [CrossRef]
- Hartmann, M.J.; Brandao, F.G.S.L.; Plenio, M.B. Strongly interacting polaritons in coupled arrays of cavities. Nat. Phys. 2006, 2, 849–855. [Google Scholar] [CrossRef]
- Angelakis, D.G.; Santos, M.F.; Bose, S. Photon-blockade-induced Mott transitions and XY spin models in coupled cavity arrays. Phys. Rev. A 2007, 76, 031805. [Google Scholar] [CrossRef]
- Van Nieuwenburg, E.; Baum, Y.; Refael, G. From Bloch oscillations to many-body localization in clean interacting systems. Proc. Natl. Acad. Sci. USA 2019, 116, 9269–9274. [Google Scholar] [CrossRef]
- Mishra, U.; Bayat, A. Driving Enhanced Quantum Sensing in Partially Accessible Many-Body Systems. Phys. Rev. Lett. 2021, 127, 080504. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Wittek, P. Quantum Machine Learning: What Quantum Computing Means to Data Mining; Academic Press: Cambridge, MA, USA, 2014; p. 176. [Google Scholar]
- Carleo, G.; Cirac, I.; Cranmer, K.; Daudet, L.; Schuld, M.; Tishby, N.; Vogt-Maranto, L.; Zdeborová, L. Machine learning and the physical sciences. Rev. Mod. Phys. 2019, 91, 045002. [Google Scholar] [CrossRef]
- Schuld, M.; Petruccione, F. Machine Learning with Quantum Computers; Quantum Science and Technology; Springer International Publishing: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Shor, P. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar] [CrossRef]
- Aspuru-Guzik, A.; Dutoi, A.D.; Love, P.J.; Head-Gordon, M. Simulated Quantum Computation of Molecular Energies. Science 2005, 309, 1704–1707. [Google Scholar] [CrossRef]
- Georgescu, I.M.; Ashhab, S.; Nori, F. Quantum simulation. Rev. Mod. Phys. 2014, 86, 153–185. [Google Scholar] [CrossRef]
- Cao, Y.; Romero, J.; Olson, J.P.; Degroote, M.; Johnson, P.D.; Kieferová, M.; Kivlichan, I.D.; Menke, T.; Peropadre, B.; Sawaya, N.P.D.; et al. Quantum Chemistry in the Age of Quantum Computing. Chem. Rev. 2019, 119, 10856–10915. [Google Scholar] [CrossRef]
- McArdle, S.; Endo, S.; Aspuru-Guzik, A.; Benjamin, S.C.; Yuan, X. Quantum computational chemistry. Rev. Mod. Phys. 2020, 92, 015003. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.S.L.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Zhong, H.S.; Wang, H.; Deng, Y.H.; Chen, M.C.; Peng, L.C.; Luo, Y.H.; Qin, J.; Wu, D.; Ding, X.; Hu, Y.; et al. Quantum computational advantage using photons. Science 2020, 370, 1460–1463. [Google Scholar] [CrossRef]
- Wu, Y.; Bao, W.S.; Cao, S.; Chen, F.; Chen, M.C.; Chen, X.; Chung, T.H.; Deng, H.; Du, Y.; Fan, D.; et al. Strong Quantum Computational Advantage Using a Superconducting Quantum Processor. Phys. Rev. Lett. 2021, 127, 180501. [Google Scholar] [CrossRef]
- Madsen, L.S.; Laudenbach, F.; Askarani, M.F.; Rortais, F.; Vincent, T.; Bulmer, J.F.F.; Miatto, F.M.; Neuhaus, L.; Helt, L.G.; Collins, M.J.; et al. Quantum computational advantage with a programmable photonic processor. Nature 2022, 606, 75–81. [Google Scholar] [CrossRef]
- Bharti, K.; Cervera-Lierta, A.; Kyaw, T.H.; Haug, T.; Alperin-Lea, S.; Anand, A.; Degroote, M.; Heimonen, H.; Kottmann, J.S.; Menke, T.; et al. Noisy intermediate-scale quantum algorithms. Rev. Mod. Phys. 2022, 94, 015004. [Google Scholar] [CrossRef]
- Chen, S.; Cotler, J.; Huang, H.Y.; Li, J. Exponential separations between learning with and without quantum memory. arXiv 2021, arXiv:arXiv2111.05881. [Google Scholar]
- Huang, H.Y.; Broughton, M.; Cotler, J.; Chen, S.; Li, J.; Mohseni, M.; Neven, H.; Babbush, R.; Kueng, R.; Preskill, J.; et al. Quantum advantage in learning from experiments. arXiv 2021, arXiv:arXiv2112.00778. [Google Scholar] [CrossRef]
- Aharonov, D.; Cotler, J.; Qi, X.L. Quantum algorithmic measurement. Nat. Commun. 2022, 13, 887. [Google Scholar] [CrossRef]
- Harrow, A.W.; Hassidim, A.; Lloyd, S. Quantum Algorithm for Linear Systems of Equations. Phys. Rev. Lett. 2009, 103, 150502. [Google Scholar] [CrossRef]
- Lloyd, S.; Mohseni, M.; Rebentrost, P. Quantum principal component analysis. Nat. Phys. 2014, 10, 631–633. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum Random Access Memory. Phys. Rev. Lett. 2008, 100, 160501. [Google Scholar] [CrossRef]
- Kyaw, T.H.; Felicetti, S.; Romero, G.; Solano, E.; Kwek, L.C. Scalable quantum memory in the ultrastrong coupling regime. Sci. Rep. 2015, 5, 8621. [Google Scholar] [CrossRef]
- Nandkishore, R.; Huse, D.A. Many-Body Localization and Thermalization in Quantum Statistical Mechanics. Annu. Rev. Condens. Matter Phys. 2015, 6, 15–38. [Google Scholar] [CrossRef]
- Abanin, D.A.; Altman, E.; Bloch, I.; Serbyn, M. Colloquium: Many-body localization, thermalization, and entanglement. Rev. Mod. Phys. 2019, 91, 021001. [Google Scholar] [CrossRef]
- Alet, F.; Laflorencie, N. Many-body localization: An introduction and selected topics. C. R. Phys. 2018, 19, 498–525, Quantum simulation/Simulation quantique. [Google Scholar] [CrossRef]
- Nico-Katz, A.; Bayat, A.; Bose, S. Information-theoretic memory scaling in the many-body localization transition. Phys. Rev. B 2022, 105, 205133. [Google Scholar] [CrossRef]
- Chirikov, B.V. A universal instability of many-dimensional oscillator systems. Phys. Rep. 1979, 52, 263–379. [Google Scholar] [CrossRef]
- Moessner, R.; Sondhi, S.L. Equilibration and order in quantum Floquet matter. Nat. Phys. 2017, 13, 424–428. [Google Scholar] [CrossRef]
- Bukov, M.; D’Alessio, L.; Polkovnikov, A. Universal high-frequency behavior of periodically driven systems: From dynamical stabilization to Floquet engineering. Adv. Phys. 2015, 64, 139–226. [Google Scholar] [CrossRef]
- Blanes, S.; Casas, F.; Oteo, J.A.; Ros, J. A pedagogical approach to the Magnus expansion. Eur. J. Phys. 2010, 31, 907–918. [Google Scholar] [CrossRef]
- Kühner, T.D.; White, S.R.; Monien, H. One-dimensional Bose-Hubbard model with nearest-neighbor interaction. Phys. Rev. B 2000, 61, 12474–12489. [Google Scholar] [CrossRef]
- Raftery, J.; Sadri, D.; Schmidt, S.; Türeci, H.E.; Houck, A.A. Observation of a Dissipation-Induced Classical to Quantum Transition. Phys. Rev. X 2014, 4, 031043. [Google Scholar] [CrossRef]
- Underwood, D.L.; Shanks, W.E.; Li, A.C.Y.; Ateshian, L.; Koch, J.; Houck, A.A. Imaging Photon Lattice States by Scanning Defect Microscopy. Phys. Rev. X 2016, 6, 021044. [Google Scholar] [CrossRef]
- Fitzpatrick, M.; Sundaresan, N.M.; Li, A.C.Y.; Koch, J.; Houck, A.A. Observation of a Dissipative Phase Transition in a One-Dimensional Circuit QED Lattice. Phys. Rev. X 2017, 7, 011016. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2007. [Google Scholar] [CrossRef]
- Peterer, M.J.; Bader, S.J.; Jin, X.; Yan, F.; Kamal, A.; Gudmundsen, T.J.; Leek, P.J.; Orlando, T.P.; Oliver, W.D.; Gustavsson, S. Coherence and Decay of Higher Energy Levels of a Superconducting Transmon Qubit. Phys. Rev. Lett. 2015, 114, 010501. [Google Scholar] [CrossRef]
- Vidal, G. Efficient Simulation of One-Dimensional Quantum Many-Body Systems. Phys. Rev. Lett. 2004, 93, 040502. [Google Scholar] [CrossRef]
- Hauschild, J.; Pollmann, F. Efficient numerical simulations with Tensor Networks: Tensor Network Python (TeNPy). SciPost Phys. Lect. Notes 2018, 5. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peña, R.; Kyaw, T.H.; Romero, G. Stable Many-Body Resonances in Open Quantum Systems. Symmetry 2022, 14, 2562. https://doi.org/10.3390/sym14122562
Peña R, Kyaw TH, Romero G. Stable Many-Body Resonances in Open Quantum Systems. Symmetry. 2022; 14(12):2562. https://doi.org/10.3390/sym14122562
Chicago/Turabian StylePeña, Rubén, Thi Ha Kyaw, and Guillermo Romero. 2022. "Stable Many-Body Resonances in Open Quantum Systems" Symmetry 14, no. 12: 2562. https://doi.org/10.3390/sym14122562
APA StylePeña, R., Kyaw, T. H., & Romero, G. (2022). Stable Many-Body Resonances in Open Quantum Systems. Symmetry, 14(12), 2562. https://doi.org/10.3390/sym14122562







