Shape Phase Transitions in Even–Even 176–198Pt: Higher-Order Interactions in the Interacting Boson Model †
Abstract
:1. Introduction
2. The CQ Formalism and Its Extension
3. The Modified Soft Rotor Model
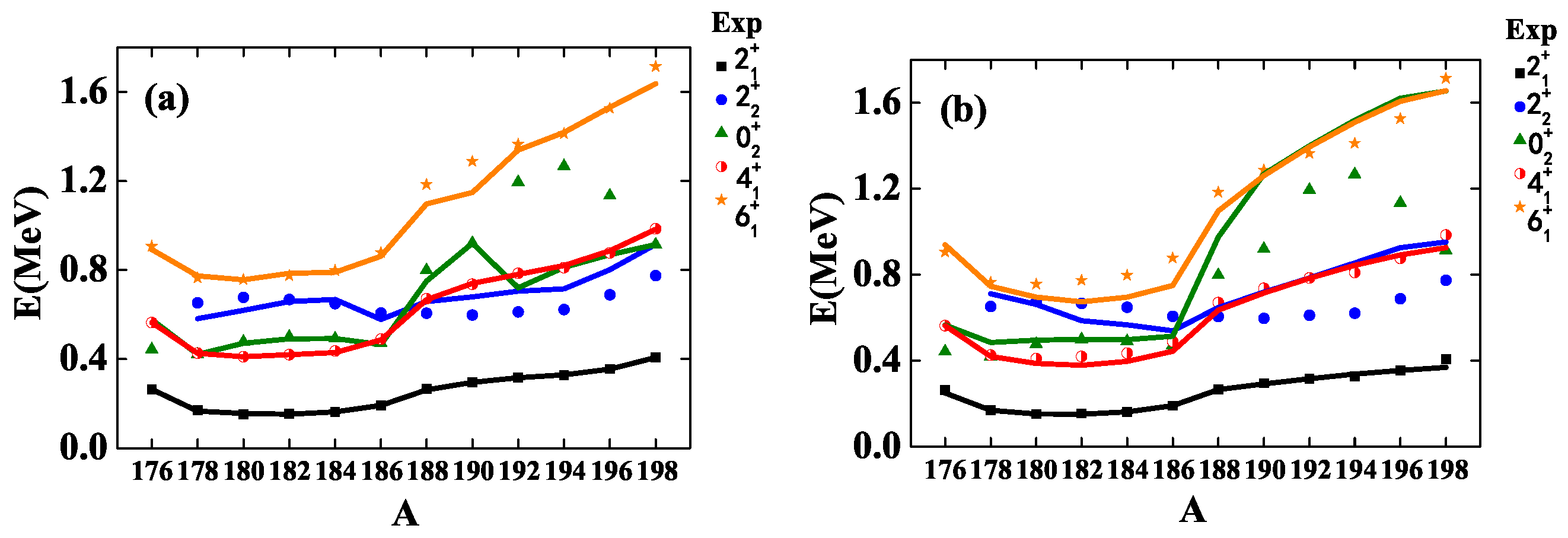
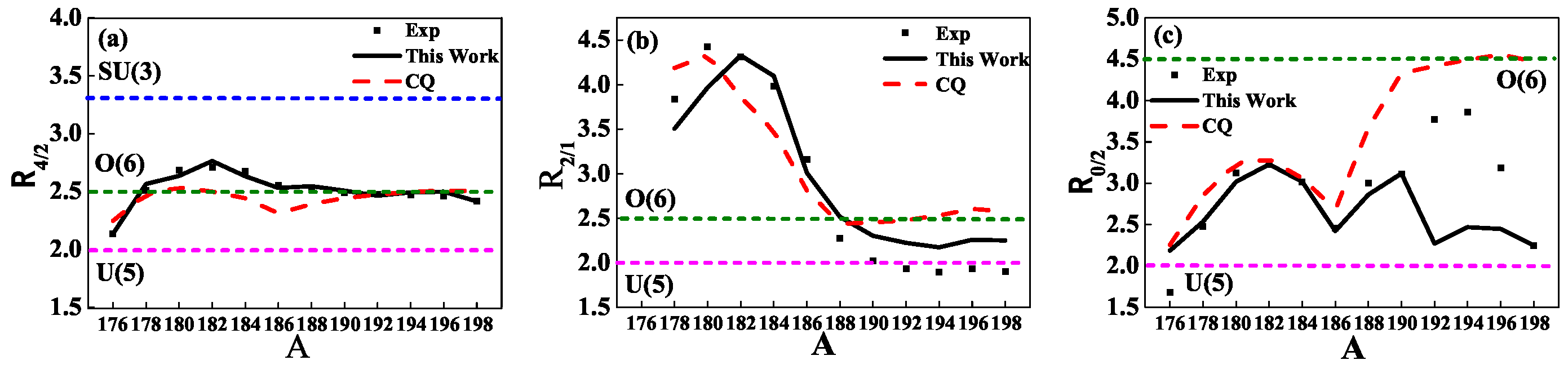
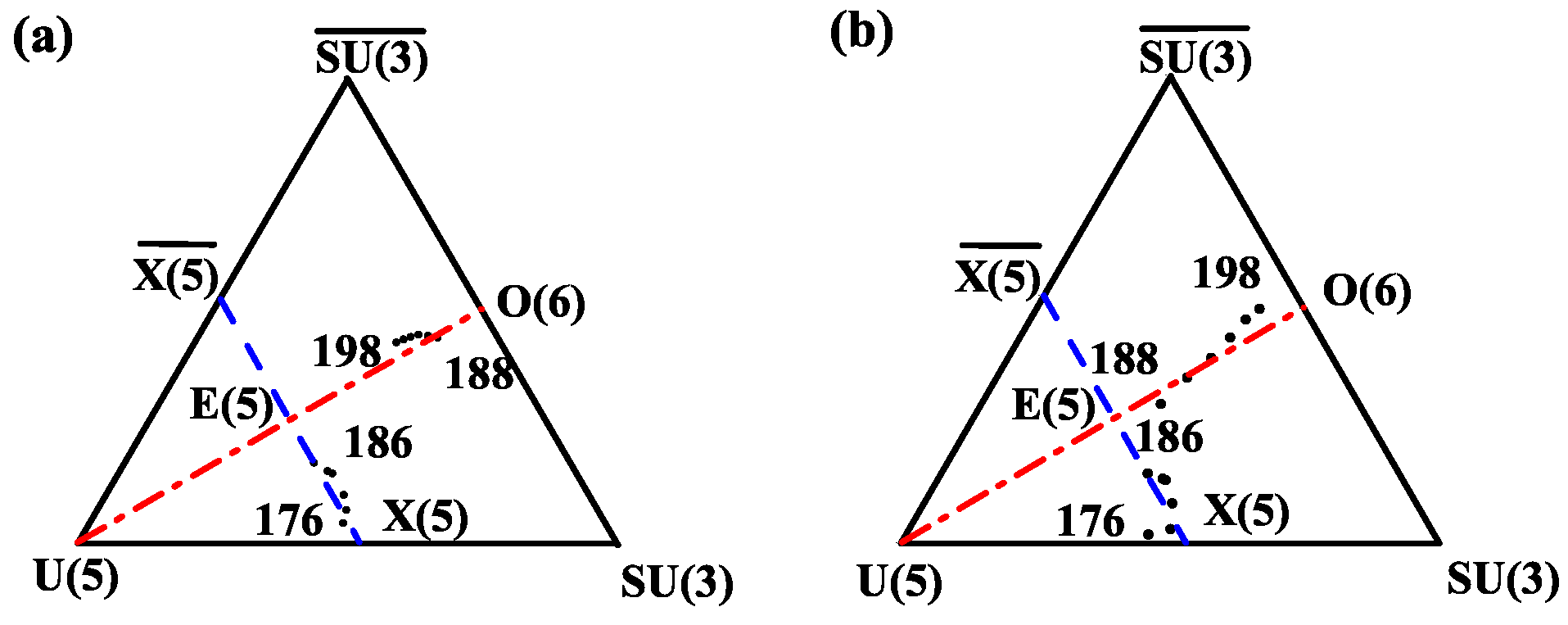
4. Shape Phase Transition in Pt
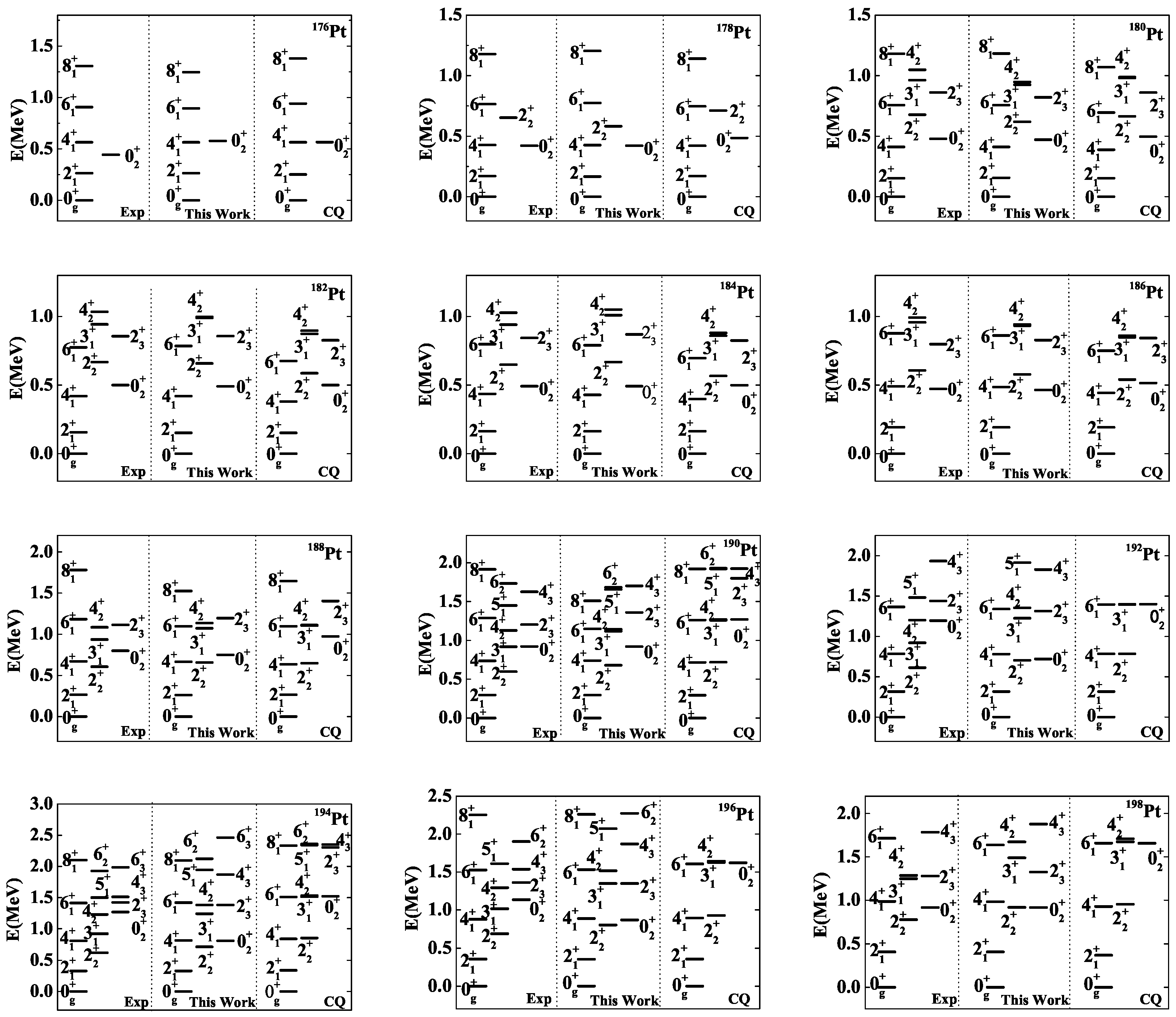
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Arima, A.; Iachello, F. Collectiven nuclear states as representations of a SU(6) group. Phys. Rev. Lett. 1975, 35, 1069–1072. [Google Scholar] [CrossRef]
- Arima, A.; Iachello, F. Interacting boson model of collective states I. The vibrational Limit. Ann. Phys. 1976, 99, 253–317. [Google Scholar] [CrossRef]
- Arima, A.; Iachello, F. Interacting boson model of collective states II. The rotational limit. Ann. Phys. 1978, 111, 201–238. [Google Scholar] [CrossRef]
- Arima, A.; Iachello, F. Interacting boson model of collective states III. The transition from SU(5) to SU(3). Ann. Phys. 1978, 115, 325–366. [Google Scholar] [CrossRef]
- Arima, A.; Iachello, F. Interacting boson model of collective states IV. The O(6) limit. Ann. Phys. 1979, 123, 468–492. [Google Scholar] [CrossRef]
- Iachello, F.; Arima, A. The Interacting Boson Model; Cambridge University: Cambridge, UK, 1987. [Google Scholar]
- Casten, R.F.; Warner, D.D. The ineracting boson approximation. Rev. Mod. Phys. 1988, 60, 389–469. [Google Scholar] [CrossRef]
- Casten, R.F. Quantum phase transitions and structural evolution in nuclei. Prog. Part. Nucl. Phys. 2009, 62, 183–209. [Google Scholar] [CrossRef]
- Cejnar, P.; Jolie, J.; Casten, R.F. Quantum phase transitions in the shapes of atomic nuclei. Rev. Mod. Phys. 2010, 82, 2155–2212. [Google Scholar] [CrossRef]
- Fortunato, L. Quantum phase transitions in algebraic and collective models of nuclear structure. Prog. Part. Nucl. Phys. 2021, 121, 103891. [Google Scholar] [CrossRef]
- Böyükata, M.; Alonso, C.E.; Arias, J.M.; Fortunato, L.; Vitturi, A. Review of shape phase transition studies for Bose-Fermi systems, The effect of the odd-particle on the bosonic core. Symmetry 2021, 13, 215. [Google Scholar] [CrossRef]
- Parker, M.C.; Jeynes, C.; Catford, W.N. Halo properties in helium nuclei from the perspective of geometrical thermodynamics. Ann. Phys. 2022, 534, 2100278. [Google Scholar] [CrossRef]
- Chen, J.Q. Nucleon-pair shell model, Formalism and special cases. Nucl. Phys. A 1997, 626, 686–714. [Google Scholar] [CrossRef]
- McCutchan, E.A.; Casten, R.F.; Zamfir, N.V. Simple interpretation of shape evolution in Pt isotopes without intruder states. Phys. Rev. C 2005, 71, 061301(R). [Google Scholar] [CrossRef]
- Pan, F.; Wang, T.; Huo, Y.-S.; Draayer, J.P. Quantum phase transitions in the consistent-Q Hamiltonian of the interacting boson model. J. Phys. G, Nucl. Part. Phys. 2008, 35, 125105. [Google Scholar] [CrossRef] [Green Version]
- Tobin, G.K.; Ferriss, M.C.; Launey, K.D.; Draayer, J.P.; Drefuss, A.C.; Bahri, C. Symplectic no-core shell-model approach to intermediate-mass nuclei. Phys. Rev. C 2014, 89, 034312. [Google Scholar] [CrossRef] [Green Version]
- Pan, F.; Yuan, S.L.; Qiao, Z.; Bai, J.C.; Zhang, Y.; Draayer, J.P. γ-soft rotor with configurationg mixing in the O(6) limit of the interavting boson model. Phys. Rev. C 2018, 97, 034326. [Google Scholar] [CrossRef] [Green Version]
- Smirnov, Y.F.; Smirnova, N.A.; Van Isacker, P. SU(3) realization of the rigid asymmetric rotor within the interacting boson model. Phy. Rev. C 2000, 61, 041302. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Pan, F.; Dai, L.R.; Draayer, J.P. Triaxial rotor in the SU(3) limit of the interacting boson model. Phys. Rev. C 2014, 90, 044310. [Google Scholar] [CrossRef]
- Warner, D.D.; Casten, R.F.D. Revised formulation of the phenomenological interacting boson approximation. Phys. Rev. Lett. 1982, 48, 1385–1389. [Google Scholar] [CrossRef]
- Warner, D.D.; Casten, R.F. Predictions of the interacting boson approximation in a consistent Q framework. Phys. Rev. C 1983, 28, 1798–1806. [Google Scholar] [CrossRef]
- Jolie, J.; Cejnar, P.; Casten, R.F.; Heinze, S.; Linnemann, A.; Werner, V. Triple point of nuclear deformations. Phys. Rev. Lett. 2002, 89, 182502. [Google Scholar] [CrossRef] [PubMed]
- Bohr, A.; Mottelson, B.R. Nuclear Structure II; World Scientific Publishing Company: Singapore, 1998. [Google Scholar]
- Ginocchio, J.N.; Kirson, M.W. Relationship between the Bohr Collective Hamiltonian and the Interacting-Boson Model. Phys. Rev. Lett. 1980, 44, 1744–1747. [Google Scholar] [CrossRef]
- Dieperink, A.E.L.; Scholten, O.; Iachello, F. Classical limit of the Interacting-Boson Model. Phys. Rev. Lett. 1980, 44, 1747–1750. [Google Scholar] [CrossRef]
- Zhang, Y.; Zuo, Y.; Pan, F.; Draayer, J.P. Excited-state quantum phase transitions in the interacting boson model, Spectral characteristics of 0+ states and effective order parameter. Phys. Rev. C 2016, 93, 044302. [Google Scholar] [CrossRef] [Green Version]
- Iachello, F. Dynamic symmetries at the critical point. Phys. Rev. Lett. 2000, 85, 3580–3584. [Google Scholar] [CrossRef] [PubMed]
- Iachello, F. Analytic description of critical point nuclei in a spherical-axially deformed shape phase transition. Phys. Rev. Lett. 2001, 87, 052502. [Google Scholar] [CrossRef]
- Van Isacker, P.; Chen, J.Q. Classical limit of the interacting boson Hamiltonian. Phys. Rev. C 1981, 24, 684–689. [Google Scholar] [CrossRef]
- Heyde, K.; Van Isacker, P.; Waroquier, M.; Moreau, J. Triaxial shapes in the interacting boson model. Phys. Rev. C 1984, 29, 1420–1427. [Google Scholar] [CrossRef]
- Garcia-Ramos, J.E.; Alonso, C.E.; Arias, J.M.; Van Isacker, P. Anharmonic double-γ vibrations in nuclei and their description in the interacting boson model. Phys. Rev. C 2000, 61, 047305. [Google Scholar] [CrossRef]
- Loewenich, K.; Zell, K.O.; Dewald, A.; Gast, W.; Gelberg, A.; Lieberz, W.; Von Brentano, P.; Van Isacker, P. In-beam spectroscopy of 120Xe. Nucl. Phys. A 1986, 468, 361–372. [Google Scholar] [CrossRef]
- Sorgunlu, B.; Van Isacker, P. Triaxiality in the interacting boson model. Nucl. Phys. A 2008, 808, 27–46. [Google Scholar] [CrossRef] [Green Version]
- Vanthournout, J.; De Meyer, H.; Vanden Berghe, G. Symmetry-preserving higher-order terms in the O(6) limit of the interacting boson model. Phys. Rev. C 1988, 38, 414–418. [Google Scholar] [CrossRef] [PubMed]
- Vanthournout, J. Influence of symmetry-conserving higher order interactions in the interacting boson model on the first β and γ band in rotational nuclei. Phys. Rev. C 1990, 41, 2380–2385. [Google Scholar] [CrossRef] [PubMed]
- Van Isacker, P. Dynamical symmetry and higher-order interactions. Phys. Rev. Lett. 1999, 83, 4269–4272. [Google Scholar] [CrossRef] [Green Version]
- Rowe, D.J.; Thiamova, G. The many relationships between the IBM and the Bohr model. Nucl. Phys. A 2005, 760, 59–81. [Google Scholar] [CrossRef]
- Thiamova, G.; Cejnar, P. Prolate-oblate shape-phase transition in the O(6) description of nuclear rotation. Nucl. Phys. A 2006, 765, 97–111. [Google Scholar] [CrossRef]
- Leschber, Y.; Draayer, J.P. Algebraic realization of rotational dynamics. Phys. Lett. B 1987, 190, 1–6. [Google Scholar] [CrossRef]
- Castaños, O.; Draayer, J.P.; Leschbe, Y. Shape variables and the shell model. Z. Phys. A 1988, 329, 33–43. [Google Scholar] [CrossRef]
- Fortunato, L.; Alonso, C.E.; Arias, J.M.; García-Ramos, J.E.; Vitturi, A. Phase diagram for a cubic-Q interacting boson model Hamiltonian: Signs of triaxiality. Phys. Rev. C 2011, 84, 014326. [Google Scholar] [CrossRef]
- Wang, T. New γ-soft rotation in the interacting boson model with SU(3) higher-order interactions. Chin. Phys. C 2022, 46, 074101. [Google Scholar] [CrossRef]
- Wang, T. A collective description of the unusually low ratio B4/2 = B(E2;41+ → 21+)/B(E2;21+ → 11+). EPL 2020, 129, 52001. [Google Scholar] [CrossRef]
- Zhang, Y.; He, Y.W.; Karlsson, D.; Qi, C.; Pan, F.; Draayer, J.P. A theoretical interpretation of the anomalous reduced E2 transition probabilities along the yrast line of neutron-deficient nuclei. Phys. Lett. B 2022, 834, 137443. [Google Scholar] [CrossRef]
- Rosensteel, G. Analytic formulae for interacting boson model matrix elements in the SU(3) basis. Phys. Rev. C 1990, 41, 730–735. [Google Scholar] [CrossRef]
- Akiyama, Y.; Draayer, J.P. A user’s guide to fortran programs for Wigner and Racah coefficients of SU(3). Comput. Phys. Commun. 1973, 5, 405–406. [Google Scholar] [CrossRef] [Green Version]
- McCutchan, E.A.; Zamfir, N.V. Simple description of light W, Os, and Pt nuclei in the interacting boson model. Phys. Rev. C 2005, 71, 054306. [Google Scholar] [CrossRef]
- Bijker, R.; Dieperink, A.E.L.; Scholten, O.; Spanhoff, R. Description of the Pt and Os isotopes in the interacting boson model. Nucl. Phys. A 1980, 344, 207–232. [Google Scholar] [CrossRef]
- García-Ramos, J.E.; Heyde, K. The Pt isotopes, Comparing the Interacting Boson Model with configuration mixing and the extended consistent-Q formalism. Nucl. Phys. A 2009, 825, 39–70. [Google Scholar] [CrossRef] [Green Version]
- Thiamova, G. The IBM description of triaxial nuclei. Eur. Phys. J. A 2010, 45, 81–90. [Google Scholar] [CrossRef]
- Gladnishki, K.A.; Petkov, P.; Dewald, A.; Fransen, C.; Hackstein, M.; Jolie, J.; Pissulla, T.; Rother, W.; Zell, K.O. Yrast electromagnetic transition strengths and shape coexistence in 186Pt. Nucl. Phys. A 2012, 877, 19–34. [Google Scholar] [CrossRef]
- Delion, D.S.; Florescu, A.; Huyse, M.; Wauters, J.; Van Duppen, P.; Insolia, A.; Liotta, R.J. Microscopic description of alpha decay to intruder 02+ states in Pb, Po, Hg, and Pt isotopes. Phys. Rev. Lett. 1995, 74, 3939–3942. [Google Scholar] [CrossRef]
- Garg, U.; Chaudhury, A.; Drigert, M.W.; Funk, E.G.; Mihelich, J.W.; Radford, D.C.; Helppi, H.; Holzmann, R.; Janssens, R.V.F.; Khoo, T.L.; et al. Life time measurements in 184Pt and the shape coexistence picture. Phys. Lett. B 1986, 180, 319–323. [Google Scholar] [CrossRef]
- Hebbinghaus, G.; Kutsarova, T.; Gast, W.; Krämer-Flecken, A.; Lieder, R.M.; Urban, W. Study of band structures in the γ-unstable nucleus 186Pt. Nucl. Phys. A 1990, 514, 225–251. [Google Scholar] [CrossRef]
- Basunia, M.S. Nuclear Data Sheets for A = 176. Nucl. Data Sheets 2006, 107, 791–1026. [Google Scholar] [CrossRef]
- Achterberg, E.; Capurro, O.A.; Marti, G.V. Nuclear Data Sheets for A = 178. Nucl. Data Sheets 2009, 110, 1473–1688. [Google Scholar] [CrossRef]
- McCutchan, E.A. Nuclear Data Sheets for A = 180. Nucl. Data Sheets 2015, 126, 151–372. [Google Scholar] [CrossRef] [Green Version]
- Singh, B.; Roediger, J.C. Nuclear Data Sheets for A = 182. Nucl. Data Sheets 2010, 111, 2081–2330. [Google Scholar] [CrossRef]
- Baglin, C.M. Nuclear Data Sheets for A = 184. Nucl. Data Sheets 2010, 111, 275–523. [Google Scholar] [CrossRef]
- Firestone, R.B. Nuclear Data Sheets for A = 186. Nucl. Data Sheets 1988, 55, 585–664. [Google Scholar] [CrossRef]
- Kondev, F.G.; Juutinen, S.; Hartley, D.J. Nuclear Data Sheets for A = 188. Nucl. Data Sheets 2018, 150, 1–364. [Google Scholar] [CrossRef]
- Singh, B.; Chen, J. Nuclear Data Sheets for A = 190. Nucl. Data Sheets 2020, 169, 1–390. [Google Scholar] [CrossRef]
- Baglin, C.M. Nuclear Data Sheets for A = 192. Nucl. Data Sheets 2012, 113, 1871–2111. [Google Scholar] [CrossRef]
- Singh, B. Nuclear Data Sheets for A = 194. Nucl. Data Sheets 2006, 107, 1531–1746. [Google Scholar] [CrossRef]
- Huang, X. Nuclear Data Sheets for A = 196. Nucl. Data Sheets 2007, 108, 1093–1286. [Google Scholar] [CrossRef]
- Huang, X. Nuclear Data Sheets for A = 198. Nucl. Data Sheets 2009, 110, 2533–2688. [Google Scholar] [CrossRef]
- Available online: https://www.nndc.bnl.gov/ensdf/ (accessed on 1 January 2020).
- Morinaga, H.; Yamazaki, T. In-Beam Gamma-Ray Spectroscopy; North Holland Publishing Company: Amsterdam, The Netherlands, 1976; Volume 54, Available online: https://inis.iaea.org/search/search.aspx?orig_q=RN:8314742 (accessed on 1 January 2020).
- Fossan, D.B.; Herskind, B. Half-lives of first 2+ states (150 < A < 190). Nucl. Phys. A 1963, 40, 24–33. [Google Scholar]
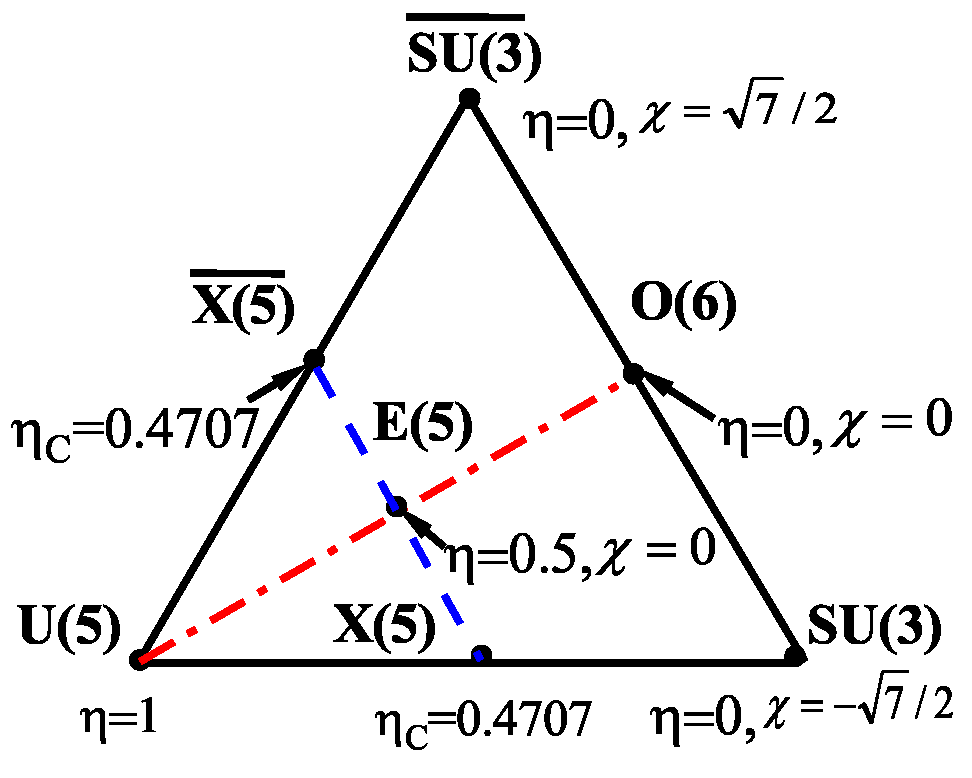


| Nucleus | (MeV) | N | ||||||
|---|---|---|---|---|---|---|---|---|
| Pt | −0.008 | 0.6216 | 0.4795 | 0 | 0 | 0.1287 | −1.1218 | 10 |
| Pt | 0 | 0.8363 | 0.4594 | 0 | 0 | 0.1841 | −1.0001 | 11 |
| Pt | 0.0002 | 0.9624 | 0.4483 | −0.0449 | 0 | 0.0499 | −0.8625 | 12 |
| Pt | 0.0006 | 0.9996 | 0.4462 | 0 | −0.1648 | 0 | −0.6456 | 13 |
| Pt | 0.0007 | 0.9481 | 0.4530 | 0.1747 | −0.0775 | 0.2886 | −0.6085 | 12 |
| Pt | 0.001 | 0.8079 | 0.4690 | 0 | −0.2471 | 0 | −0.4868 | 11 |
| Pt | 0.0011 | 1.0696 | 0.1061 | −0.2197 | −0.5142 | 0 | −0.0159 | 10 |
| Pt | 0.00201 | 1.0708 | 0.1225 | −0.3707 | −0.2638 | 0.1009 | 0.0265 | 9 |
| Pt | 0.0009 | 1.0514 | 0.1389 | −0.2587 | −0.4614 | 0.2395 | 0.0635 | 8 |
| Pt | 0.0014 | 1.0113 | 0.1553 | −0.2083 | −0.3281 | 0.2547 | 0.0741 | 7 |
| Pt | 0.001 | 0.9507 | 0.1717 | −0.2007 | −0.3380 | 0.2777 | 0.0846 | 6 |
| Pt | 0.00148 | 0.8694 | 0.1882 | −0.2085 | −0.3810 | 0.2553 | 0.0953 | 5 |
| Nucleus | c (MeV) | N | ||
|---|---|---|---|---|
| Pt | 0.9814 | 0.5240 | −1.2382 | 10 |
| Pt | 1.0296 | 0.4761 | −1.1959 | 11 |
| Pt | 1.0402 | 0.4457 | −0.9631 | 12 |
| Pt | 1.0133 | 0.4329 | −0.7461 | 13 |
| Pt | 0.9490 | 0.4376 | −0.7302 | 12 |
| Pt | 0.8471 | 0.4598 | −0.6456 | 11 |
| Pt | 1.3784 | 0.3609 | −0.1058 | 10 |
| Pt | 1.7264 | 0.2848 | −0.0212 | 9 |
| Pt | 1.9379 | 0.2182 | 0.0159 | 8 |
| Pt | 2.0130 | 0.1612 | 0.0688 | 7 |
| Pt | 1.9515 | 0.1138 | 0.1111 | 6 |
| Pt | 1.7535 | 0.0759 | 0.1217 | 5 |
| 87(8) | 87.011 | 87.008 | 76 | 130.180 | 130.184 | ||
| 163(15) | 148.646 | 159.366 | 22.2 | 40.214 | 37.509 | ||
| 174(16) | 191.204 | 197.981 | 11.2 | 16.237 | 15.681 | ||
| 192(25) | 217.843 | 215.919 | 4.7 | 6.512 | 6.570 | ||
| 195(17) | 195.068 | 195.009 | 37.5 | 65.430 | 65.450 | ||
| 186(14) | 231.816 | 232.173 | 10.9 | 13.993 | 13.971 | ||
| 206(23) | 248.684 | 249.205 | – | 4.789 | 4.779 | ||
| 154(15) | 154.051 | 154.027 | 374 | 1091.599 | 1091.769 | ||
| (4) | 247.620 | 251.145 | 22.9 | 49.808 | 49.109 | ||
| ≥50 | 290.043 | 296.687 | ≤35 | 9.662 | 9.446 | ||
| 114(8) | 114.002 | 114.004 | 479 | 1361.953 | 1361.929 | ||
| 192(12) | 176.723 | 184.507 | 32.5 | 61.294 | 58.708 | ||
| 292(20) | 203.217 | 219.257 | 5.28 | 12.124 | 11.237 | ||
| 127(5) | 127.009 | 127.014 | 360 | 936.807 | 936.770 | ||
| > | 2.960 | 1.385 | ≤ | 10.800 | 23.081 | ||
| > | 47.809 | 74.740 | ≤ | 52.991 | 33.897 | ||
| 210(8) | 202.506 | 207.042 | 25.3 | 44.583 | 43.606 | ||
| 226(12) | 236.014 | 246.825 | 6.1 | 9.331 | 8.923 | ||
| 271(18) | 251.128 | 267.136 | 2.15 | 3.623 | 3.406 | ||
| 94(5) | 94.010 | 94.426 | 240 | 550.146 | 547.722 | ||
| 89(4) | 89.167 | 89.014 | 66 | 112.028 | 112.220 | ||
| 150(+4-5) | 117.39 | 129.247 | 5.1 | 10.400 | 9.446 | ||
| 158(15) | 132.752 | 148.733 | 1.53 | 2.820 | 2.517 | ||
| 118(17) | 137.830 | 155.836 | 0.97 | 1.262 | 1.116 | ||
| 56(3) | 56.010 | 56.018 | 62.3 | 103.070 | 103.055 | ||
| 57.2(12) | 57.199 | 57.198 | 43.7 | 70.653 | 70.654 | ||
| 0.55(4) | 1.911 | 0.004 | 26.5 | 78.849 | 37,670.042 | ||
| 109(7) | 69.760 | 77.975 | 26.5 | 81.611 | 73.013 | ||
| 89(5) | 77.345 | 78.108 | 4.2 | 7.450 | 7.377 | ||
| 0.68(7) | 1.525 | 0.007 | 21.3 | 105.526 | 22,989.550 | ||
| 102(10) | 46.093 | 60.795 | 21.3 | 101.257 | 76.770 | ||
| 70(30) | 84.382 | 84.901 | 1.8 | 2.316 | 2.302 | ||
| 38(10) | 26.257 | 24.342 | 21.3 | 10,589.454 | 11,422.533 |
| 49.2(8) | 41.7 | 68.261 | 68.274 | ||||
| 0.29(4) | 1.008 | 0.137 | 35 | 135.900 | 999.908 | ||
| 89(11) | 62.116 | 63.507 | 35 | 93.474 | 91.427 | ||
| 85(5) | 65.238 | 66.106 | 3.7 | 7.437 | 7.339 | ||
| 0.36(7) | 1.279 | 0.0003 | 3.8 | 16.793 | 71,595.730 | ||
| 21(4) | 36.687 | 36.299 | 3.8 | 4.219 | 4.229 | ||
| 14 | 24.721 | 31.944 | 3.8 | 40.428 | 31.287 | ||
| 0.63(14) | 3.269 | 0.396 | 6.1 | 5.344 | 44.117 | ||
| 8.4(19) | 87.311 | 67.085 | 6.1 | 1.308 | 1.703 | ||
| <75 | 21.289 | 19.870 | – | 35,551.848 | 38,090.754 | ||
| 100 | 42.538 | 50.148 | – | 121.345 | 102.931 | ||
| < | 0.766 | 0.190 | – | 225.150 | 907.709 | ||
| 67(21) | 69.313 | 69.965 | 1.6 | 2.347 | 2.325 | ||
| 50(14) | 64.454 | 66.068 | 1.1 | 1.284 | 1.252 | ||
| 53(10) | 40.362 | 42.628 | 0.61 | 1.222 | 1.157 | ||
| 40.60(20) | 34.15 | 54.244 | 54.248 | ||||
| (4) | 1.373 | 0.309 | 33.8 | 59.081 | 262.519 | ||
| 5(5) | 0.003 | 11.079 | – | 7,121,171.886 | 1928.289 | ||
| 0.0025(24) | 0.064 | 0.033 | – | 42.145 | 81.735 | ||
| 18(10) | 69.587 | 51.888 | 4.2 | 10.143 | 13.602 | ||
| 2.8(15) | 3.072 | 0.545 | 4.2 | 14.201 | 80.047 | ||
| < | 1.046 | 0.380 | 1.6 | 9.571 | 26.345 | ||
| < | 0.009 | 1.218 | 1.6 | 7541.910 | 55.728 | ||
| 54(+11-12) | 45.337 | 50.195 | 33.8 | 31.224 | 28.203 | ||
| 0.26(23) | 0.277 | 0.086 | – | 329.352 | 1060.819 | ||
| 60.0(9) | 53.551 | 53.566 | 3.55 | 6.127 | 6.125 | ||
| 29(+6-29) | 28.837 | 28.323 | 2.6 | 5.389 | 5.487 | ||
| 0.56(+12-17) | 0.691 | 0.002 | 2.6 | 25.103 | 8673.028 | ||
| 0.13(12) | 0.600 | 0.370 | – | 782.267 | 1268.541 | ||
| 17(6) | 18.093 | 23.829 | 2.6 | 55.878 | 42.427 | ||
| 73(+4-73) | 54.709 | 54.661 | 0.98 | 2.000 | 2.001 | ||
| 0.48(14) | 0.029 | 0.0003 | 0.77 | 234.695 | 22,687.186 | ||
| 49(13) | 0.036 | 0.008 | 0.77 | 1885.478 | 8484.649 | ||
| 16(5) | 0.007 | 0.020 | 0.77 | 69,886.211 | 24,460.174 | ||
| 78(+10-78) | 47.562 | 48.542 | 0.42 | 1.304 | 1.278 | ||
| 31.81(22) | 22.25 | 34.950 | 34.945 | ||||
| 0.038(12) | 1.035 | 0.148 | 27 | 42.912 | 300.093 | ||
| 0.05(3) | 0.066 | 0.009 | 9.7 | 54.756 | 401.545 | ||
| 0.6(4) | 0.003 | 0.0001 | 9.7 | 8209.613 | 246,288.402 | ||
| 2.2(15) | 0.469 | 0.060 | 9.7 | 806.114 | 6301.127 | ||
| 37(7) | 34.484 | 37.277 | 27 | 54.085 | 50.033 | ||
| 26(7) | 2.225 | 0.302 | – | 166.593 | 1227.382 | ||
| 38(4) | 40.519 | 40.567 | 3.3 | 4.750 | 4.745 | ||
| >57 | 38.899 | 39.092 | 1.550 | 1.543 |
| Experiment | This Work | CQ | ||
|---|---|---|---|---|
| +0.55(21) | +0.478 | +0.051 | ||
| +0.409 | +0.348 | +0.267 | ||
| −0.303 | −0.322 | −0.249 | ||
| +0.752 | +0.624 | +0.268 | ||
| −0.06(11) | +0.111 | −0.106 | ||
| +0.195 | +0.794 | +0.263 | ||
| −0.06, 0.28 | +0.908 | +0.262 | ||
| +0.62 | +0.503 | +0.399 | ||
| −0.39 | −0.474 | −0.372 | ||
| +1.03 | +0.662 | +0.397 | ||
| −0.18 | +0.762 | +0.380 | ||
| +0.42(12), 0.54(12) | +0.431 | +0.305 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Wang, T.; Pan, F. Shape Phase Transitions in Even–Even 176–198Pt: Higher-Order Interactions in the Interacting Boson Model. Symmetry 2022, 14, 2610. https://doi.org/10.3390/sym14122610
Li D, Wang T, Pan F. Shape Phase Transitions in Even–Even 176–198Pt: Higher-Order Interactions in the Interacting Boson Model. Symmetry. 2022; 14(12):2610. https://doi.org/10.3390/sym14122610
Chicago/Turabian StyleLi, Dongkang, Tao Wang, and Feng Pan. 2022. "Shape Phase Transitions in Even–Even 176–198Pt: Higher-Order Interactions in the Interacting Boson Model" Symmetry 14, no. 12: 2610. https://doi.org/10.3390/sym14122610





