A Fractional Atmospheric Circulation System under the Influence of a Sliding Mode Controller

Abstract

The earth’s surface is heated by the large-scale movement of air known as atmospheric circulation, which works in conjunction with ocean circulation. More than ${10}^5$ variables are involved in the complexity of the weather system. In this work, we analyze the dynamical behavior and chaos control of an atmospheric circulation model known as the Hadley circulation model, in the frame of Caputo and Caputo–Fabrizio fractional derivatives. The fundamental novelty of this paper is the application of the Caputo derivative with equal dimensionality to models that includes memory. A sliding mode controller (SMC) is developed to control chaos in this fractional-order atmospheric circulation system with uncertain dynamics. The proposed controller is applied to both commensurate and non-commensurate fractional-order systems. To demonstrate the intricacy of the models, we plot some graphs of various fractional orders with appropriate parameter values. We have observed the influence of thermal forcing on the dynamics of the system. The outcome of the analytical exercises is validated using numerical simulations.

1. Introduction

Chaos has evolved into the focal point of crucial interdisciplinary and multidisciplinary research because of its extensiveness in nature and its distinctive qualities. This has led to a better understanding of the underlying dynamics responsible for many interesting behaviors of some natural and artificial systems. As a result, it has attracted many researchers in various scientific disciplines, such as biology [1], power system [2], circuits [3], medicine [4], chemical reactors [5] and some others. In the literature, some dynamical systems such as Lorenz system [6], Newton–Leipnik system [7], Chen system [8] and Lu system [9] show an attractive chaotic nature. For the last decade, the control of chaotic systems has fascinated the investigation of many researchers. For example, in [10], the sliding mode control approach is used to stabilize chaotic systems. The authors in [11] analyze the chaotic system of unstable periodic orbits with a fuzzy adaptive SMC. In [12], the class of chaotic systems is studied under the effect of an adaptive SMC. Yassen studied the chaotic system with backstepping design in [13] and some others as seen in [14,15]. The symmetric properties associated with physical and other related problems are attracted working in fractional calculus to illustrate and predict the future consequences of fractional calculus [16,17].

Even though fractional derivatives have more than 300 years of historical background, they have secured significant attention since 1967 and have several different definitions. By way of illustration, Riemann and Liouville introduced the idea of fractional order differentiation with a power-law in [18,19]. Over the last decade, the research community has paid particular attention to Riemann–Liouville and Caputo fractional derivatives. With the Riemann–Liouville fractional derivative at the origin, an arbitrary function’s continuity and differentiability are not required. The concept of fractional calculus with fundamental theory is proven to be an efficient tool with both integral and differential operators to capture exciting and essential consequences associated with real-world problems to predict future consequences. Even though we have diverse fractional differential operators, we used only a few operators due to their ability and applicability.

The Caputo fractional derivative has the advantage of enabling common initial and boundary conditions in the model formulation [20]. Furthermore, the derivative value of the constant under the Caputo fractional derivative is zero. Even while these fractional derivatives have many benefits, not all situations lend themselves to their usage. In [21], a novel fractional-order derivative based on the exponential-law was introduced by Caputo and Fabrizio in [22], Atangana and Baleanu proposed a different fractional-order derivative that makes use of the generalized Mittag–Leffler function with strong memory as a non-local and nonsingular kernel.

Recent research has shown that fractional differential equations are a useful and efficient modeling tool in a variety of scientific and engineering fields [23,24]. Indeed, significant applications of fractional derivatives can be observed in areas such as viscoelasticity, regular variation in thermodynamics, biophysics, blood flow phenomena, aerodynamics, Bode analysis of feedback amplifiers, capacitor theory, electrical circuits, electro-analytical chemistry, biology, control theory and more [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45]. It has been noted that fractional-order differential systems such as the fractional-order Lorenz system [46,47] and the fractional-order Chen system [48,49] operate in a chaotic or hyper-chaotic manner.

In recent years, one of the most fascinating areas of study, where a lot of academics have made significant contributions, is the control and synchronization of fractional-order chaotic systems [50]. A variety of fractional-order chaotic systems have been controlled using various techniques. One of the most importantly used techniques is SMC [51,52,53]. The primary function of the SMC is to change the control law to drive the system’s states away from their beginning states and onto a predetermined sliding surface. Desirable characteristics of the system on the sliding surface are stability, the ability to reject disturbances, and tracking. In [54], the authors analyze the chaos synchronization of fractional order unified systems theoretically and numerically by using the one-way coupling method. Matouk’s study on the fractional-order modified autonomous van der Pol-Duffing system is subjected to fractional Routh–Hurwitz conditions to bring the chaos under control [55]. A nonlinear system is explored with intelligent, robust fractional surface sliding mode control in [56]. In [57], it discusses optimal controls in $\alpha$−norms and the presence of a moderate solution for modified semilinear fractional equations. Maphou examines the classical control theory to a fractional diffusion equation used in a bounded domain in [58]. The authors of [59] provided a concrete analysis of the chaotic behavior of the fractional-order revised coupled dynamical system and essential that would suppress chaos to distracted points of equilibrium, employed the fractional-order revised coupled dynamical system’s feedback control approach to manage the chaos. In [60], authors propose the use of the generalized T-S fuzzy model and adaptive mechanism as an easy but effective approach to restrain fractional-order chaotic structure.

In the present work, we have studied a chaotic atmospheric circulation system in the frame of the Caputo and Caputo–Fabrizio (CF) fractional derivative. By heating the air close to the earth’s surface, warm air rises, cool air descends and in this process, a general circulation pattern is generated in the atmosphere. Air rises towards the equator, travels north and south away from the equator at a greater height, dips down near the poles and finally flows back along the surface from both poles to the equator [61]. This flow is named Hadley circulation in honor of George Hadley [62]. This model has three nonlinear differential equations and is described as,

$$\begin{array}{cc}\hfill \frac{du}{dt}=& -v^2-w^2-au+a\delta ,\hfill \\ \hfill \frac{dv}{dt}=& uv-buw-v+\rho ,\hfill \\ \hfill \frac{dw}{dt}=& buv+uw-w,\hfill \end{array}$$

(1)

where u is the intensity of the westerly current on a global scale and v and w represent the cosine and sine phases of a series of superposed wave’s strength. For the determination of the timing of the events, in this paper, we have considered that the unit of time corresponds to the wave’s damping time, which is approximated to be five days. Here, $\delta$ is the cross latitude external heating contrast and $\rho$ is the heating contrast between ocean and continent. b is the force of the wave advection caused by the westerly current.

At around 30 degrees latitude, the majority of the planet’s arid and driest regions are found and they are in the zone just beneath the Hadley circulation’s descending branches. Experiments using both idealized and many realistic climate models reveal that the Hadley circulation extends as the average global temperature rises and this can result in significant variations in rainfall in the latitudes at the boundary of the cells [63]. Scientists worry that the deep tropics’ ecosystems could alter as a result of continuous global warming and that the deserts would grow drier and drier [64]. Atmosphere projection is a concern that is closely related to the national economy and people’s day-to-day life. Analysis of this is a difficult task, because of the complexity of the atmospheric progression. Numerical forecasting models, which cover all processes deemed to be significant, are the foundation of the widely accepted approaches for analyzing the dynamics of the atmosphere and climate. Borer et al. used seasonal forcing to explore the bifurcations and odd attractors in the Lorenz-84 system [65]. Yu examines the low-order Hadley circulation model in [66]. The authors of [67], analyzed the Lorenz-84 atmospheric model with seasonal forcing for stability and chaos. The dynamical actions of a low-order coupled ocean–atmospheric mode were studied by Roebber [68]. The main aim of this study is to use analytical techniques and numerical simulations to carry out a detailed analysis of the chaos with fractional order commensurate and non-commensurate derivatives of the Caputo and the CF sense. The model representation in the Caputo fractional order sense is

$$\begin{array}{cc}\hfill {}^C{D}_t^{{\beta }_1}u\left(t\right)=& -v^2-w^2-au+a\delta ,\hfill \\ \hfill {}^C{D}_t^{{\beta }_2}v\left(t\right)=& uv-buw-v+\rho ,\hfill \\ \hfill {}^C{D}_t^{{\beta }_3}w\left(t\right)=& buv+uw-w,\hfill \end{array}$$

(2)

and the model representation in CF sense is

$$\begin{array}{cc}\hfill {}^{CF}{D}_t^{{\beta }_1}u\left(t\right)=& -v^2-w^2-au+a\delta ,\hfill \\ \hfill {}^{CF}{D}_t^{{\beta }_2}v\left(t\right)=& uv-buw-v+\rho ,\hfill \\ \hfill {}^{CF}{D}_t^{{\beta }_3}w\left(t\right)=& buv+uw-w.\hfill \end{array}$$

(3)

We have designed an SMC with and without uncertainty and external disturbance. This controller is employed in the Hadley system in the presence of both Caputo and CF derivatives and their dynamics are analyzed. This work aims at investigating the effect of fractional derivatives and SMC in controlling the underlying chaos in the Hadley system. We have observed this both for commensurate and non-commensurate derivatives. Furthermore, we aim to notice the differences in the effectiveness of the Caputo and the Caputo–Fabrizio derivatives on the chaotic system. Since the heating contrast parameter has a significant influence on westerly current, we intend to observe the effect of cross-latitude external heating contrast and heating contrast between the ocean and continent on the dynamics of the system. This paper is organized as follows in the remaining section.

Some definitions relating to Caputo and the CF fractional order system are provided in Section 2. Existence, uniqueness and boundedness of the solution of the proposed system is demonstrated is the Section 3. The dynamical study of the atmospheric circulation system with fractional order is provided in Section 4. In Section 5, an atmospheric circulation system with chaotic fractional order is controlled by an SMC. Numerical simulations are expected in Section 6. The conclusion of the overall work is presented in Section 7.

2. Preliminaries

Here, we provide a few fundamental results that will be applied to the manuscript’s primary conclusions.

Definition 1

([19]). (Caputo fractional derivative) Assume that $h\left(t\right)$ is n times continuously differentiable function and $h^n\left(t\right)$ is integrable in $[t_0,t].$ Then, the Caputo fractional derivative of order β for a function $h\left(t\right)$ is defined as:

$${}_{t_0}^C{D}_t^{\beta }h\left(t\right)=\frac{1}{\Gamma (n-\beta )}{\int }_{t_0}^t\frac{h^n\left(\zeta \right)}{{(t-\zeta )}^{\beta +1-n}}d\zeta ,$$

where $\Gamma (·)$ refers to Gamma function, $t>a$ and n is a non-negative integer such that $n-1<\beta <n.$

Definition 2

([19]). The Riemann–Liouville fractional order integral operator is defined by

$$J_t^{\beta }g\left(x\right)=\frac{1}{\Gamma \left(\beta \right)}{\int }_0^t\frac{g\left(\zeta \right)}{{(t-\zeta )}^{\beta -1}}d\zeta ,\beta >0.$$

Definition 3

([21]). For $x\in {\mathbb{H}}^1(0, T), \beta \in (0, 1), T>0.$ The Caputo–Fabrizio fractional derivative is given by

$${}_{t_0}^{CF}{D}_t^{\beta }g\left(t\right)=\frac{B\left(\beta \right)}{1-\beta }{\int }_{t_0}^t{g}^{\prime }\left(\xi \right)exp\left(\frac{-\beta }{1-\beta }(t-\zeta )\right)d\zeta ,0<\beta <1,$$

where the smooth function $B\left(\beta \right)>0,$ satisfies the condition $B\left(0\right)=B\left(1\right)=1.$

Lemma 1

([69]). We assume that $g\left(\mathfrak{t}\right)$ is a continuous function on $[{\mathfrak{t}}_0,+\infty ),$ which satisfies

$$D_{\mathfrak{t}}^{\beta }\mathfrak{0}g\left(\mathfrak{t}\right)\le -\lambda g\left(\mathfrak{t}\right)+\xi ,g\left({\mathfrak{t}}_0\right)=f_{{\mathfrak{t}}_0},$$

here $0<\beta \le 1,(\lambda ,\xi )\in {\mathbb{R}}^2$ and $\lambda \ne 0$ and consider ${\mathfrak{t}}_0\ge 0$ as the initial time. Now,

$$g\left(\mathfrak{t}\right)\le (g\left({\mathfrak{t}}_0\right)-\frac{\xi }{\lambda })E_{\beta }[-\lambda {(\mathfrak{t}-{\mathfrak{t}}_0)}^{\beta }]+\frac{\xi }{\lambda }.$$

3. Existence, Uniqueness and Boundedness of the Solution

The Banach Fixed-Point theorem is used in this section to prove the existence and uniqueness of the solution to the model (2). There are no precise techniques or strategies for evaluating precise solutions due to the model’s complexity and non-locality. The existence of a solution is guaranteed, nevertheless, if certain requirements are met. Furthermore, we have proved the boundedness of the solution of the model (2). System (2) can be rewritten as follows:

$$\begin{array}{ccc}\hfill {}^C{D}^{{\beta }_1}\left[u\left(t\right)\right]& =& {\xi }_1(t,u),\hfill \\ \hfill {}^C{D}^{{\beta }_2}\left[v\left(t\right)\right]& =& {\xi }_2(t,v),\hfill \\ \hfill {}^C{D}^{{\beta }_3}\left[w\left(t\right)\right]& =& {\xi }_3(t,w).\hfill \end{array}$$

(4)

The Volterra integral equation corresponding to the above equation is:

$$\begin{array}{ccc}\hfill u\left(t\right)-u\left(t_0\right)& =& \frac{1}{\Gamma \left({\beta }_1\right)}{\int }_0^t{\xi }_1(\tau ,u\left(\tau \right)){(t-\tau )}^{{\beta }_1-1}d\tau ,\hfill \\ \hfill v\left(t\right)-v\left(t_0\right)& =& \frac{1}{\Gamma \left({\beta }_2\right)}{\int }_0^t{\xi }_2(\tau ,v\left(\tau \right)){(t-\tau )}^{{\beta }_2-1}d\tau ,\hfill \\ \hfill w\left(t\right)-w\left(t_0\right)& =& \frac{1}{\Gamma \left({\beta }_3\right)}{\int }_0^t{\xi }_3(\tau ,w\left(\tau \right)){(t-\tau )}^{{\beta }_3-1}d\tau .\hfill \end{array}$$

(5)

Theorem 1.

In the region $\Psi \times [t_0,T]$, where $\Psi =\left\{(u,v,w)\in {\mathbb{R}}^3:\left|u\right|\le {\varphi }_1,\left|v\right|\le {\varphi }_2,\left|w\right|\le {\varphi }_3\right\}$ and $T\le +\infty$, the Lipschitz condition is satisfied and contraction occurs by the kernel ${\xi }_1$ if $0\le a<1$ is held true.

Proof. 

Consider the two functions u and $\overline{u}$ such that

$$\begin{array}{ccc}\hfill \left|\right|{\xi }_1(t,u)-{\xi }_1(t,\overline{u})\left|\right|& =& \left|\right|-v^2-w^2-au+a\delta -(-v^2-w^2-au+a\delta )\left|\right|\hfill \\ & \le & a\left|\right|u-\overline{u}\left|\right|.\hfill \end{array}$$

(6)

The Lipschitz condition is met for ${\xi }_1$ and if $0\le a<1$, then ${\xi }_1$ follows contraction. Similarly, it can be exhibited and demonstrated in the other equations as follows:

$$\begin{array}{ccc}\hfill \left|\right|{\xi }_2(t,v)-{\xi }_2(t,\overline{v})\left|\right|& \le & |({\varphi }_1-1)\left|\right||v-\overline{v}\left|\right|,\hfill \\ \hfill \left|\right|{\xi }_3(t,w)-{\xi }_3(t,\overline{w})\left|\right|& \le & |({\varphi }_1-1)\left|\right||w-\overline{w}\left|\right|,\hfill \end{array}$$

(7)

Hence, ${\xi }_i,$$i=2,3$ are the contractions if $1<{\varphi }_1<2.$ Let, $\left|\right({\varphi }_1-1\left)\right|=\sigma .$ □

Theorem 2.

The solution of the fractional model (2) exists and will be unique, if we acquire some $t_{{\beta }_i},\mathrm{for}i=1,2,3$ such that $\frac{1}{\Gamma \left({\beta }_1\right)}a{t}_{{\beta }_1}<1,\frac{1}{\Gamma \left({\beta }_2\right)}\sigma t_{{\beta }_2}<1,\frac{1}{\Gamma \left({\beta }_3\right)}\sigma t_{{\beta }_3}<1.$

Proof. 

The proof of this theorem is illustrated in three steps.

• From system (5), the recurrent form can be written as follows:

  $$\begin{array}{ccc}\hfill F_{1,n}\left(t\right)& =& u_n\left(t\right)-u_{n-1}\left(t\right)=\frac{1}{\Gamma \left({\beta }_1\right)}{\int }_0^t({\xi }_1(\tau ,u_{n-1})-{\xi }_1(\tau ,u_{n-2})){(t-\tau )}^{{\beta }_1-1}d\tau ,\hfill \\ \hfill F_{2,n}\left(t\right)& =& v_n\left(t\right)-v_{n-1}\left(t\right)=\frac{1}{\Gamma \left({\beta }_2\right)}{\int }_0^t({\xi }_2(\tau ,v_{n-1})-{\xi }_2(\tau ,v_{n-2})){(t-\tau )}^{{\beta }_2-1}d\tau ,\hfill \\ \hfill F_{3,n}\left(t\right)& =& w_n\left(t\right)-w_{n-1}\left(t\right)=\frac{1}{\Gamma \left({\beta }_3\right)}{\int }_0^t({\xi }_3(\tau ,w_{n-1})-{\xi }_3(\tau ,w_{n-2})){(t-\tau )}^{{\beta }_3-1}d\tau .\hfill \end{array}$$

  (8)
  The conditions are: $u_0\left(t\right)=u\left(0\right)$, $v_0\left(t\right)=v\left(0\right)$, $w_0\left(t\right)=w\left(0\right)$. By applying the norm to the Equation (8), we get

  $$\begin{array}{ccc}\hfill \left|\right|F_{1,n}\left|\right|& =& \left|\right|u_n\left(t\right)-u_{n-1}\left(t\right)\left|\right|\hfill \\ & =& ∥\frac{1}{\Gamma \left({\beta }_1\right)}{\int }_0^t({\xi }_1(\tau ,u_{n-1})-{\xi }_1(\tau ,u_{n-2})){(t-\tau )}^{{\beta }_1-1}d\tau ∥\hfill \\ & \le & \frac{1}{\Gamma \left({\beta }_1\right)}{\int }_0^t\left|\right|({\xi }_1(\tau ,u_{n-1})-{\xi }_1(\tau ,u_{n-2})){(t-\tau )}^{{\beta }_1-1}d\tau \left|\right|.\hfill \end{array}$$

  (9)
  Using the Lipchitz condition in Equation (1), we get:

  $$\begin{array}{ccc}\hfill \left|\right|F_{1,n}\left(t\right)\left|\right|& \le & \frac{1}{\Gamma \left({\beta }_1\right)}a{\int }_0^t\left|\right|F_{1,n-1}\left(\tau \right)d\tau \left|\right|.\hfill \end{array}$$

  (10)
  Subsequently we have,

  $$\begin{array}{ccc}\hfill \left|\right|F_{2,n}\left(t\right)\left|\right|& \le & \frac{1}{\Gamma \left({\beta }_2\right)}\sigma {\int }_0^t\left|\right|F_{2,n-1}\left(\tau \right)d\tau \left|\right|,\hfill \\ \hfill \left|\right|F_{3,n}\left(t\right)\left|\right|& \le & \frac{1}{\Gamma \left({\beta }_3\right)}\sigma {\int }_0^t\left|\right|F_{3,n-1}\left(\tau \right)d\tau \left|\right|.\hfill \end{array}$$

  (11)
  Which implies that it can be written as:
  $u_n\left(t\right)={\sum }_{i=1}^n{F}_{1,i}$, $v_n\left(t\right)={\sum }_{i=1}^n{F}_{2,i}$, $w_n\left(t\right)={\sum }_{i=1}^n{F}_{3,i}$. Applying Equations (10) and (11) recursively, we have:

  $$\begin{array}{ccc}\hfill \left|\right|F_{1,i}\left(t\right)\left|\right|& \le & \left|\right|u_n\left(t_0\right)\left|\right|{\left[\frac{1}{\Gamma \left({\beta }_1\right)}at\right]}^n,\hfill \\ \hfill \left|\right|F_{2,i}\left(t\right)\left|\right|& \le & \left|\right|v_n\left(t_0\right)\left|\right|{\left[\frac{1}{\Gamma \left({\beta }_2\right)}\sigma t\right]}^n,\hfill \\ \hfill \left|\right|F_{3,i}\left(t\right)\left|\right|& \le & \left|\right|w_n\left(t_0\right)\left|\right|{\left[\frac{1}{\Gamma \left({\beta }_3\right)}\sigma t\right]}^n.\hfill \end{array}$$

  (12)
  As a consequence, the existence and continuity are demonstrated.
• To show that the associated Equations (11) and (12) work out the solutions for Equation (2), we review the following:

  $$\begin{array}{ccc}\hfill u\left(t\right)-u\left(t_0\right)& =& u_n\left(t\right)-{\eta }_{1n}\left(t\right),\hfill \\ \hfill v\left(t\right)-v\left(t_0\right)& =& v_n\left(t\right)-{\eta }_{2n}\left(t\right),\hfill \\ \hfill w\left(t\right)-w\left(t_0\right)& =& w_n\left(t\right)-{\eta }_{3n}\left(t\right).\hfill \end{array}$$

  (13)
  In order to execute the desired results, we set

  $$\begin{array}{ccc}\hfill \left|\right|{\eta }_{1n}\left(t\right)\left|\right|& =& ∥\frac{1}{\Gamma \left({\beta }_1\right)}{\int }_0^t({\xi }_1(\tau ,u)-{\xi }_1(\tau ,u_{n-1}))d\tau ∥\hfill \\ & \le & \frac{1}{\Gamma \left({\beta }_1\right)}a{\int }_0^t\left|\right|{\xi }_1(\tau ,u)-{\xi }_1(\tau ,u_{n-1})\left|\right|d\tau \hfill \\ & \le & \frac{1}{\Gamma \left({\beta }_1\right)}a\left|\right|u-u_{n-1}\left|\right|t.\hfill \end{array}$$

  (14)
  Continuing the same procedure recursively, we get

  $$\begin{array}{ccc}\hfill \left|\right|{\eta }_{1n}\left(t\right)\left|\right|& \le & {\left(\frac{1}{\Gamma \left({\beta }_1\right)}at\right)}^{n+1}{\varphi }_1.\hfill \end{array}$$

  (15)
  At $t_{{\beta }_1}$, we have

  $$\begin{array}{ccc}\hfill \left|\right|{\eta }_{1n}\left(t\right)\left|\right|& \le & {\left(\frac{1}{\Gamma \left({\beta }_1\right)}a{t}_{{\beta }_1}\right)}^{n+1}{\varphi }_1.\hfill \end{array}$$

  (16)
  From Equation (16), as we can observe that as n tends to ∞, $\left|\right|{\eta }_{1n}\left|\right|$ approaches $0.$ Similarly, it may be prove that $\left|\right|{\eta }_{2n}\left|\right|$, $\left|\right|{\eta }_{3n}\left|\right|$ tends to $0.$
• To establish the uniqueness for solution of the system (2).
  Consider a different set of solutions for the system (2), say $\tilde{u},\tilde{v},\tilde{w}$. Then, as an outcome of the first Equation of (5) we write:

  $$u\left(t\right)-\tilde{u}\left(t\right)=\frac{1}{\Gamma \left({\beta }_1\right)}{\int }_0^t({\xi }_1(t,u)-{\xi }_1(t,\tilde{u}))d\tau .$$
  Using the norm, the above equation becomes

  $$\begin{array}{ccc}\hfill \left|\right|u\left(t\right)-\tilde{u}\left(t\right)\left|\right|& =& \frac{1}{\Gamma \left({\beta }_1\right)}{\int }_0^t\left|\right|({\xi }_1(t,u)-{\xi }_1(t,\tilde{u}))d\tau \left|\right|.\hfill \end{array}$$

  (17)
  By applying the Lipchitz condition we get

  $$\left|\right|u\left(t\right)-\tilde{u}\left(t\right)\left|\right|\le \frac{1}{\Gamma \left({\beta }_1\right)}at\left|\right|u-\tilde{u}\left|\right|.$$

  At some $t_{{\beta }_1}$ this result yields

  $$\left|\right|u\left(t\right)-\tilde{u}\left(t\right)\left|\right|\left(1-\frac{1}{\Gamma \left({\beta }_1\right)}a{t}_{{\beta }_1}\right)\le 0.$$

  Since $\left(1-\frac{1}{\Gamma \left({\beta }_1\right)}a{t}_{{\beta }_1}\right)>0$, we have $\left|\right|u\left(t\right)-\tilde{u}\left(t\right)\left|\right|=0$. Hence, $u\left(t\right)=\tilde{u}\left(t\right).$

□

Theorem 3.

All the solutions of the system (2) that initiate in Ψ are bounded.

Proof. 

Let us define the function $\kappa \left(t\right)=u\left(t\right)+v\left(t\right)+v\left(t\right).$

On applying the Caputo fractional derivative, we have

$$\begin{array}{ccc}\hfill {}^C{D}^{\beta }\kappa \left(t\right)+\kappa \left(t\right)& =& {}^C{D}^{\beta }u\left(t\right){+}^C{D}^{\beta }v\left(t\right){+}^C{D}^{\beta }w\left(t\right)+(u\left(t\right)+v\left(t\right)+w\left(t\right)),\hfill \\ & =& (-v^2-w^2-au+a\delta )+(uv-buw-v+\rho )+(buv+uw-w)\hfill \\ & & +(u+v+w),\hfill \\ & \le & -v^2-w^2-au+a\delta +uv-buw+\rho +buv+uw+u,\hfill \\ & \le & u(1+v+bv+w)+a\delta +\rho .\hfill \end{array}$$

(18)

The solution exists and is unique in $\Psi =\left\{(u,v,w)\in {\mathbb{R}}^3:\left|u\right|\le {\varphi }_1,\left|v\right|\le {\varphi }_2,\left|w\right|\le {\varphi }_3\right\}.$ The above inequality submits:

$$\begin{array}{ccc}\hfill {}^C{D}^{\beta }\kappa \left(t\right)+\kappa \left(t\right)& \le & {\varphi }_1(1+{\varphi }_2+b{\varphi }_2+{\varphi }_3)+a\delta +\rho .\hfill \end{array}$$

(19)

By Lemma 1, we have

$$\begin{array}{ccc}\hfill {}^C{D}^{\beta }\kappa \left(t\right)& \le & \left(\kappa \left(t_0\right)-{\varphi }_1(1+{\varphi }_2+b{\varphi }_2+{\varphi }_3)+a\delta +\rho \right)E_{\beta }[-{(t-t_0)}^{\beta }]\hfill \\ & & +{\varphi }_1(1+{\varphi }_2+b{\varphi }_2+{\varphi }_3)+a\delta +\rho \hfill \\ & & \to {\varphi }_1(1+{\varphi }_2+b{\varphi }_2+{\varphi }_3)+a\delta +\rho ,ast\to \infty .\hfill \end{array}$$

Hence, all the solutions of system (2) that initiate in $\Psi$ remain bounded in

$$\Delta =\left\{(u,v,w)\in \Psi |\kappa \left(t\right)\le {\varphi }_1(1+{\varphi }_1+b{\varphi }_2+{\varphi }_3)+a\delta +\rho +ϵ,ϵ>0\right\}.$$

□

4. Dynamics of the System

If ${\beta }_1={\beta }_2={\beta }_3,$ then the system (2) and (3) are called a commensurate fractional-order system, otherwise, they are known as a non-commensurate fractional order system [70]. The Jacobian matrix of the system (2) and (3) is as follows:

$$J=\left(\begin{array}{ccc}-a& -2v& -2w\\ v-bw& -1+u& -bu\\ bv+w& bu& -1+u\end{array}\right).$$

(20)

An equilibrium point E of a non-commensurate fractional order system, that is, a fractional order system whose derivation orders are not identical, is asymptotically stable provided the following criteria are met.

$$|arg(\Lambda )|>\frac{\pi }{2B},$$

(21)

is holds for all roots $\Lambda$ of the below equation:

$$\begin{array}{c}\hfill det\left(\mathrm{diag}\left([{\Lambda }^{L_{{\beta }_1}},{\Lambda }^{L_{{\beta }_2}},\cdots ,{\Lambda }^{L_{{\beta }_n}}]\right)\right)=0,\end{array}$$

(22)

where L indicates the Least Common Multiple (LCM) of the denominators $z_i^{\prime }$s of ${\beta }_i^{\prime }$s where ${\beta }_i=\frac{z_i}{y_i},z_i$ and $y_i\in {\mathit{Z}}_{+},$ for $i=1,2,\cdots ,n.$ The constraint Equation (21) can be revised as follows:

$$\frac{\pi }{2L}-min|arg(\Lambda \left)\right|<0.$$

(23)

An equilibrium point E is asymptotically stable if its roots satisfy the requirement given in Section 5. As the instability measure for points of equilibrium in fractional order systems, the expression $\frac{\pi }{2L}-min|arg(\Lambda )|$ is well known. This condition must be met for chaos to occur in a fractional order system, but it is not enough [70].

Theorem 4.

The axial equilibrium point $E_0=(0,0,0)$ always exits and is stable.

Proof. 

The eigenvalues of the Jacobian matrix at $E_0$ are:

${\lambda }_{11}=-1,{\lambda }_{12}=-1,{\lambda }_{13}=-a.$

Clearly it is noticed that $E_0$ is stable. □

Theorem 5.

When $b=0$ and $\rho \ne 0$ in system (2), there exists at least one equilibrium point $E_1=(u_1,v_1,0)=\left(u_1,\frac{\rho }{1-u_1},0\right).$

• $E_1$ is stable if $a>0$ and the equation $a(\delta -u){(1-u)}^2={\rho }^2$ has solution $u_1<1.$
• $E_1$ is unstable if $u_1>1.$

Proof. 

The Jacobian matrix at $E_1$ is

$$J=\left(\begin{array}{ccc}-a& -2v_1& 0\\ v_1& u_1-1& 0\\ 0& 0& u_1-1\end{array}\right).$$

Its characteristic equation is

$$(u_1-1-\lambda )({\lambda }^2+\lambda (1+a-u_1)-a(u_1-1)+2v_1^2)=0.$$

The eigenvalues are given by:

${\lambda }_{21}=u_1-1$,

${\lambda }_{22}=\frac{-(a+1-u_1)-\sqrt{{(a-1+u_1)}^2-\frac{8{\rho }^2}{{(1-u_1)}^2}}}{2}$,

${\lambda }_{32}=\frac{-(a+1-u_1)+\sqrt{{(a-1+u_1)}^2-\frac{8{\rho }^2}{{(1-u_1)}^2}}}{2}$.

For $b=0,$ the system of Equation (2) reduces to $a(\delta -u_1){(1-u_1)}^2={\rho }^2.$

• If $a>0$ and the equation $a(\delta -u_1){(1-u_1)}^2={\rho }^2$ has solution $u_1<1$, then ${\lambda }_{21}<0.$ Again, since $\frac{8{\rho }^2}{{(1-u_1)}^1}>0$ and ${(a+1-u_1)}^2-{(a-1+u_1)}^2=4(1-u_1)a>0,$ it is clear that $Re\left({\lambda }_{22}\right)<0$ and $Re\left({\lambda }_{23}\right)<0.$ Hence, the equilibrium point $E_1$ is stable.
• If $u_1>1,$ then ${\lambda }_{21}>0$ and hence the the equilibrium point $E_1$ is unstable.

□

Theorem 6.

Coexistence equilibrium point exists.

Proof. 

The coexistence equilibrium point is $E_2=(u^{*},v^{*},w^{*}),$ where $u^{*},v^{*}$ and $w^{*}$ are the solutions of the system:

$$\begin{array}{ccc}\hfill -v^2-w^2-au+a\delta & =& 0,\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill uv-buw-v+\rho & =& 0,\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill buv+uw-w& =& 0.\hfill \end{array}$$

(26)

It can be shown that:

$$\begin{array}{ccc}\hfill v^{*}& =& \frac{-\rho (u^{*}-1)}{{u^{*}}^2(1-b^2)-2u^{*}+1},\hfill \\ \hfill w^{*}& =& \frac{-\rho b{u}^{*}}{{u^{*}}^2(1-b^2)-2u^{*}+1}.\hfill \end{array}$$

(27)

Substituting the above values in Equation (24), we get:

$$\begin{array}{c}\hfill L_1{u^{*}}^3+L_2{u^{*}}^2+L_3{u}^{*}+L_4=0,\end{array}$$

(28)

where

$$\begin{array}{c}\hfill L_1=a(1+b^2),L_2=-a(2+\delta (1+b^2)),L_3=a(1+2\delta ),L_4=-(\delta a-{\rho }^2).\end{array}$$

Since, $L_1>0,L_2<0,L_3>0,$ by Descartes’ rule of signs the system has two real roots if $\delta a<{\rho }^2$ and three real roots if $\delta a>{\rho }^2.$ Therefore, the coexistence point of the equilibrium point exists. □

5. Design of Sliding Mode Controller

The core idea behind the sliding mode control law is to use a discontinuous control to direct the system’s state orientation toward a predetermined sliding surface. The sliding mode control theory states that we must implement two steps to build a sliding controller.

• Create a sliding surface that depicts the desired system dynamics.
• Creating a switching control law to push any state outside the sliding surface to reach it in a finite time and make sliding modes available on all points in the sliding surface [52].

Assuming that $P\left(t\right)$ is a control input to be applied as follows to the level of the second state equation of the fractional order system (2) and (3). While designing the controller we have not differentiated between the Caputo and the CF derivatives and hence use the symbol $D_t^{{\beta }_i},(i=1,2,3)$

$$\begin{array}{cc}\hfill D_t^{{\beta }_1}u=& -v^2-w^2-au+a\delta ,\hfill \\ \hfill D_t^{{\beta }_2}v=& uv-buw-v+\rho +P\left(t\right),\hfill \\ \hfill D_t^{{\beta }_3}w=& buv+uw-w.\hfill \end{array}$$

(29)

We offer the following possibility for the sliding surface

$$\alpha \left(t\right)=D_t^{{\beta }_1-1}v\left(t\right)+D^{-1}\Phi \left(\zeta \right)d\zeta ,$$

(30)

where $\Phi \left(t\right)$ is a function defined as

$$\Phi \left(t\right)=v-uv-w^2.$$

(31)

Sliding surfaces and their derivatives must satisfy certain requirements for the sliding mode technique

$$\alpha \left(t\right)=0,\frac{d}{dt}\alpha \left(t\right)=0.$$

(32)

Hence, from Equations (30) and (32), we have

$$D_t^{{\beta }_2}v\left(t\right)=-\Phi \left(t\right)=-(v-w^2-uv).$$

(33)

Therefore, utilizing the second equation of the system of (29) and (33), and the sliding mode control theory, the corresponding control law is determined to be:

$$\begin{array}{cc}\hfill P_{eq}\left(t\right)=& D_t^{{\beta }_2}v\left(t\right)-uv+buw+v-\rho ,\hfill \\ \hfill =& -v+uv+w^2-uv+buw+v-\rho ,\hfill \\ \hfill =& w^2+buw-\rho .\hfill \end{array}$$

(34)

To hold the sliding condition, the disconnected reaching law is chosen as:

$$P_r=K_r\mathrm{sign}\left(\alpha \right),$$

(35)

where

$$\begin{array}{c}\hfill \mathrm{sign}\left(\alpha \right)=\left\{\begin{array}{cc}+1,\hfill & \mathrm{if}\alpha >0,\hfill \\ 0,\hfill & \mathrm{if}\alpha =0,\hfill \\ -1,\hfill & \mathrm{if}\alpha <0,\hfill \end{array}\right.\end{array}$$

and Gain for the controller is denoted by $K_r.$ Finally, the following definition of the total control law is possible:

$$P\left(t\right)=P_{eq}+P_r=w^2+buw-\rho +K_r\mathrm{sign}\left(\alpha \right).$$

(36)

Theorem 7.

If the controller gain $K_r<0,$ the system (29) with control rule Equation (36) is globally asymptotically stable.

Proof. 

Let us consider the Lyapunov function as:

$$Y=\frac{1}{2}{\alpha }^2.$$

(37)

Its derivative is

$$\begin{array}{cc}\hfill \dot{Y}=& \alpha \dot{\alpha }=\alpha [D^{{\beta }_2}v+v-w^2-uv]\hfill \\ \hfill =& \alpha [-buw+\rho +P-w^2]\hfill \\ \hfill =& \alpha [-buw+\rho -w^2+w^2+buw-\rho +K_r\mathrm{sign}\left(\alpha \right)]\hfill \\ \hfill =& K_r\left|\alpha \right|<0.\hfill \end{array}$$

(38)

This shows that, the defined Lyapunov function meets the requirements of the Lyapunov theorem, that is $Y>0$ and $\dot{Y}<0.$ Hence, the system (29) with the sliding mode control rule Equation (36) exhibits global asymptotic stability. □

Theorem 8.

Assume that an external disturbance and uncertainty perturb the system Equation (29). The system then takes the form:

$$\begin{array}{cc}\hfill D_t^{{\beta }_1}u=& -v^2-w^2-au+a\delta ,\hfill \\ \hfill D_t^{{\beta }_2}v=& uv-buw-v+\rho +P\left(t\right)+\Delta h(u,v,w)+q\left(t\right),\hfill \\ \hfill D_t^{{\beta }_3}w=& buv+uw-w,\hfill \end{array}$$

(39)

where $\Delta h(u,v,w)$ and $q\left(t\right)$ are suppose to be bounded, that means $\Delta h(u,v,w)<{\xi }_1$ and $q\left(t\right)<{\xi }_2,$ where ${\xi }_1$ and ${\xi }_2$ are non-negative constants. If $K_r<-({\xi }_1+{\xi }_2),$ then system (39) with sliding mode control rule Equation (36) is globally asymptotically stable.

Proof. 

Let us define a Lyapunov function as:

$$Y=\frac{1}{2}{\alpha }^2,$$

we have

$$\begin{array}{cc}\hfill \dot{Y}=& \alpha \dot{\alpha }=\alpha [D^{{\beta }_2}v\left(t\right)+v-w^2-uv]\hfill \\ \hfill =& \alpha [-buw+\rho +\Delta h+q\left(t\right)+P\left(t\right)-w^2]\hfill \\ \hfill =& \alpha [\Delta h+q\left(t\right)+K_{r}sign\left(\alpha \right)]\hfill \\ \hfill \le & (K_r+{\xi }_1+{\xi }_2)\left|\alpha \right|.\hfill \end{array}$$

(40)

Hence, $\dot{Y}<0$ and $K_r<-({\xi }_1+{\xi }_2).$ □

6. Numerical Simulation

In this section, we have analyzed the dynamics of the model in Equation (2) using the Adams–Bashforth–Moulton predictor-corrector [71,72]. While analyzing the model in Equation (3), we have modified the single step Adams–Bashforth–Moulton method to make it compatible to solve CF fractional differential equation. The modified method is presented below. If $0<\beta <1,$ then the unique solution of the following initial value problem is

$$\begin{array}{cc}\hfill {}^{CF}{D}_t^{\beta }g\left(t\right)=& f(t,g(t\left)\right)=z\left(t\right),t\ge 0,\hfill \\ \hfill g\left(0\right)=& g_0.\hfill \end{array}$$

(41)

Taking the Laplace transform on both sides of Equation (41), we get

$$G\left[s\right]=\frac{1}{s}g\left(0\right)+\frac{1-\beta }{B\left(\beta \right)}Z\left[s\right]+\frac{\beta }{B\left(\beta \right)}\frac{1}{s}Z\left[s\right].$$

(42)

Taking inverse Laplace transform on Equation (42), we get

$$g\left(t\right)=g\left(0\right)+\frac{1-\beta }{B\left(\beta \right)}z\left(t\right)+\frac{\beta }{B\left(\beta \right)}{\int }_0^{t}z\left(x\right)dx.$$

(43)

We set the time interval $[0,t]$ in the initiative of h and acquire the sequence $t_0=0,t_{k+1}=t_k+h,k=0,1,2,\cdots ,n-1,t_n=t.$ From Equation (43), we can establish the following recursive formulas

$$g\left(t_{k+1}\right)=g\left(0\right)+\frac{1-\beta }{B\left(\beta \right)}z\left(t_k\right)+\frac{\beta }{B\left(\beta \right)}{\int }_0^{t_{k+1}}{\overline{z}}_{k+1}\left(x\right)dx.$$

(44)

The integrand is approached as ${\overline{z}}_{k+1}\left(t\right)=z\left(t_i\right),0\le i\le k$ and we get the explicit predictor formula as:

$$\begin{array}{ccc}\hfill g_{k+1}^p& =& g\left(0\right)+\frac{1-\beta }{B\left(\beta \right)}z\left(t_k\right)+\frac{\beta h}{B\left(\beta \right)}\left({\int }_0^{t_1}{\overline{z}}_0\left(x\right)dx+{\int }_0^{t_2}{\overline{z}}_1\left(x\right)dx+\cdots +{\int }_0^{t_{k+1}}{\overline{z}}_k\left(x\right)dx\right)\hfill \\ & =& g\left(0\right)+\frac{1-\beta }{B\left(\beta \right)}z\left(t_k\right)+\frac{\beta h}{B\left(\beta \right)}\sum _{i=0}^{k}z\left(t_i\right).\hfill \end{array}$$

(45)

If we approach the integrand in Equation (44) as ${\overline{z}}_{k+1}\left(t\right)=\frac{t_{i+1}-t}{h}z\left(t_i\right)+\frac{t-t_i}{h}z\left(t_{i+1}\right),$ we get the corrector formula as:

$$g_{k+1}=g\left(0\right)+\frac{1-\beta }{B\left(\beta \right)}f(x_k,g_k)+\frac{\beta h}{2B\left(\beta \right)}\left(\sum _{i=0}^{k}f(x_i,f\left(x_i\right))+f(x_{k+1},g^P\left(x_{k+1}\right))\right).$$

(46)

Applying the predictor-corrector method defined in Equations (45) and (46), the numerical simulation for the system of Equation (3) are executed. We have consider the parameter values as $a=0.2,\delta =8,\rho =1,b=4,$ and $K_r=-2$ to evaluate the nature of the systems (2) and (3) under the influence of CF and Caputo fractional derivatives. Throughout this simulation we have considered $\delta =8,$ which reflect a winter condition. With these parameter values, the points of equilibrium of the present system are $E_0=(0,0,0)$, $E_1=(7.995334,-0.006527,0.0298406)$ and the eigen values of the Jacobian matrix at them are $E_0:(-1,-1,-0.2)$ and $E_1:(6.99522+31.9813i,6.99522-31.9813i,-0.19976).$ We noticed that the trivial equilibrium point $E_0$ is stable and the co-existence equilibrium point $E_1$ is the saddle point. In the following section, we have presented the dynamics of the system (2) and (3) numerically.

1.

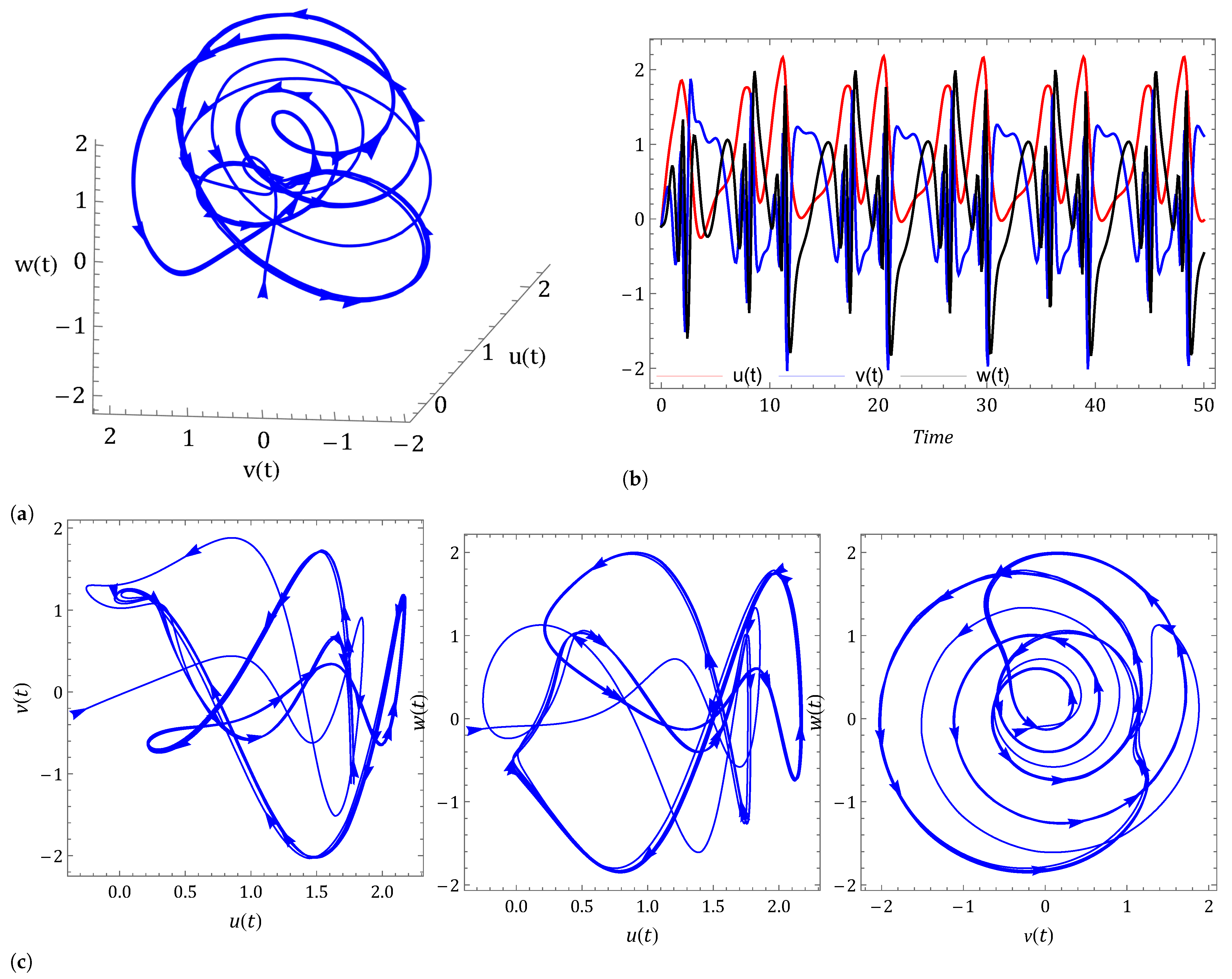
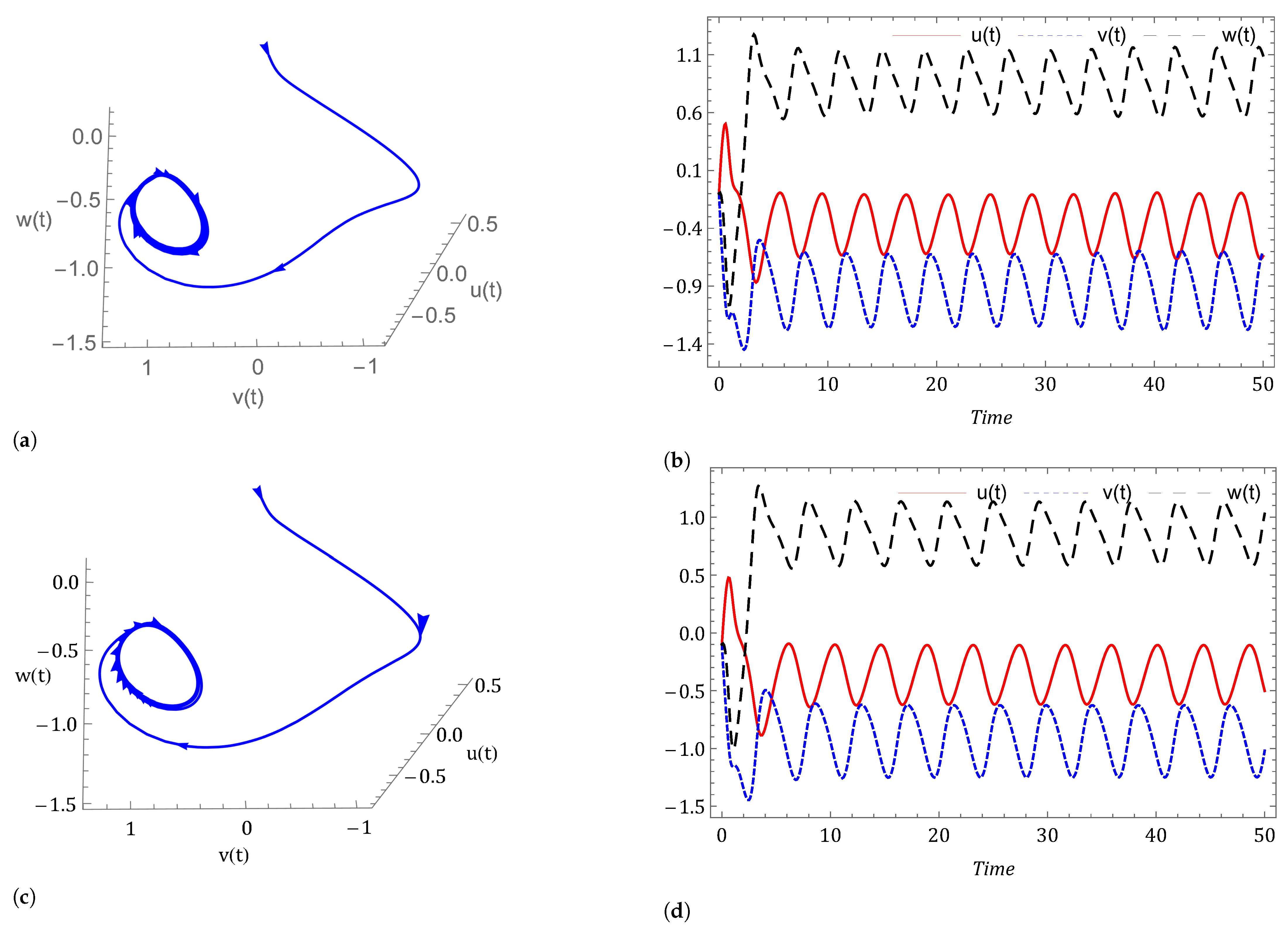
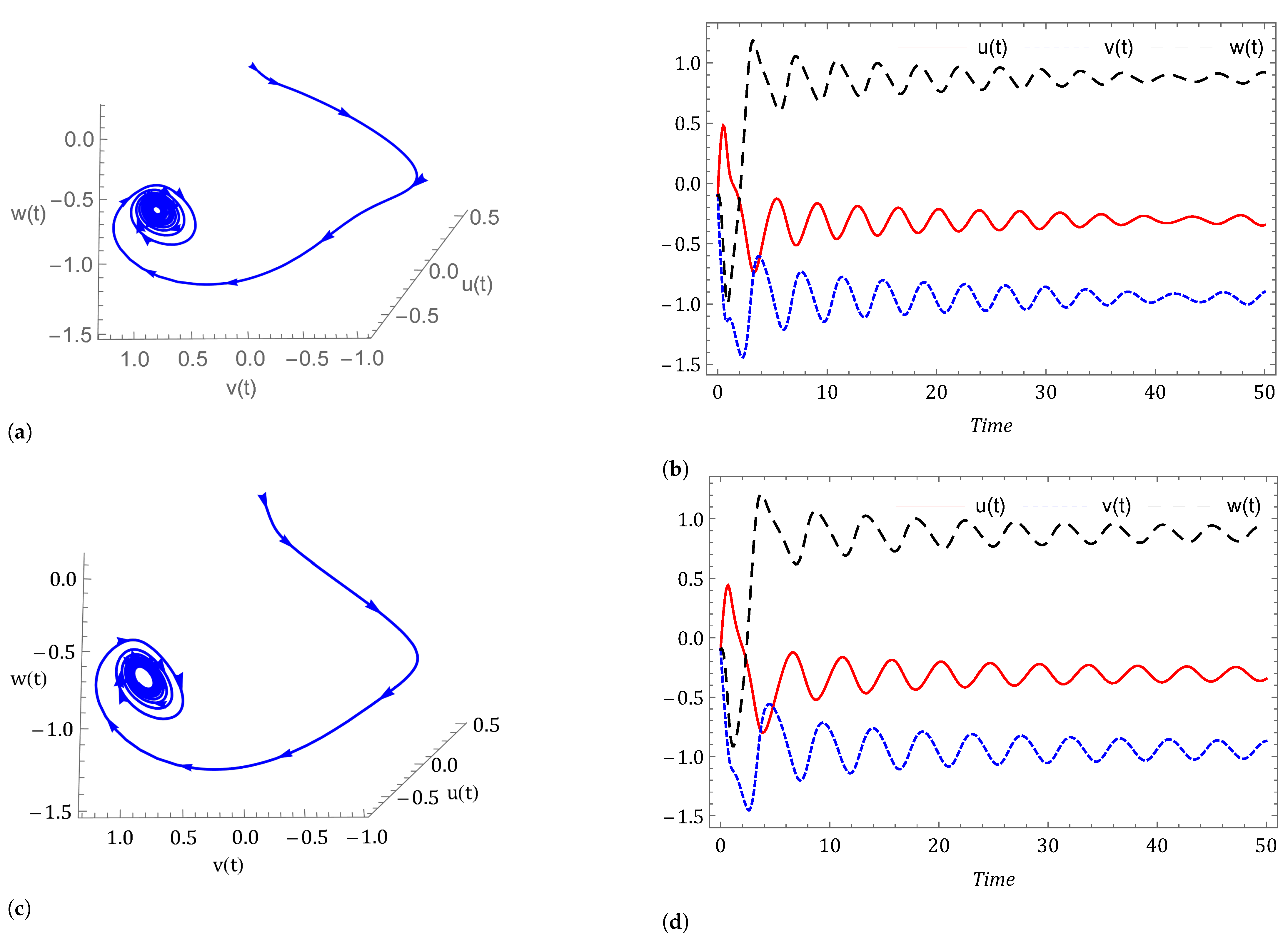
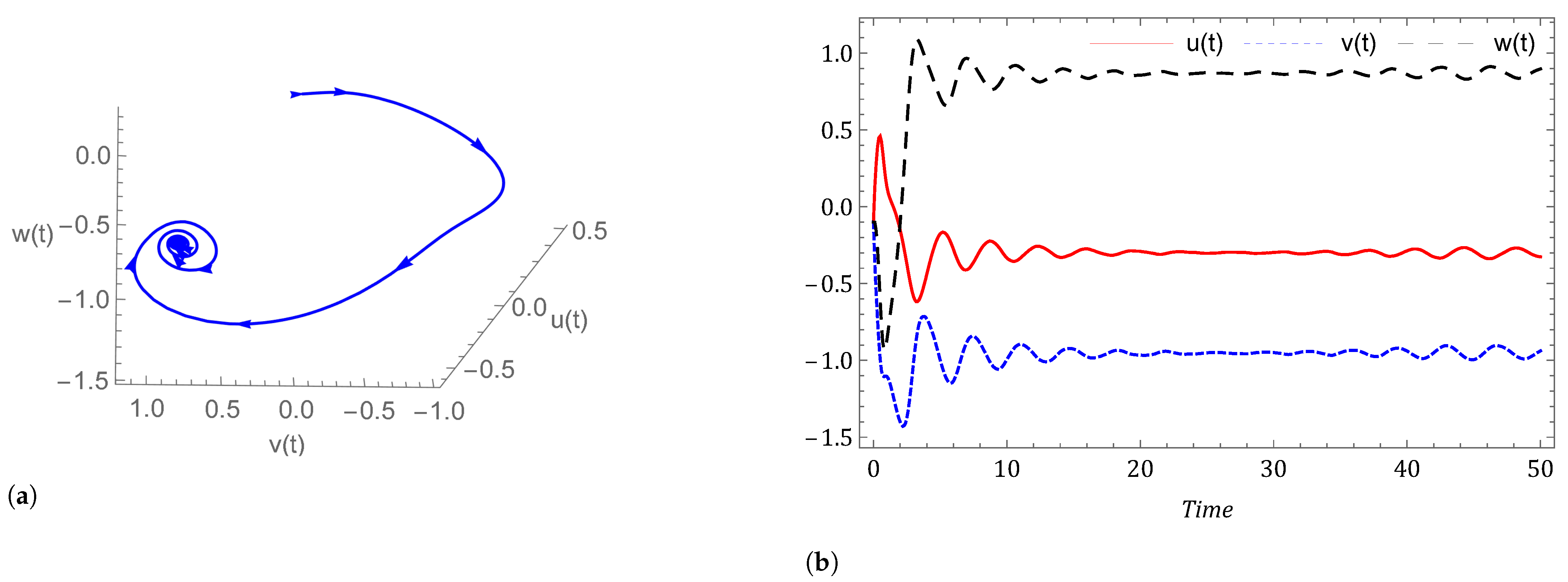
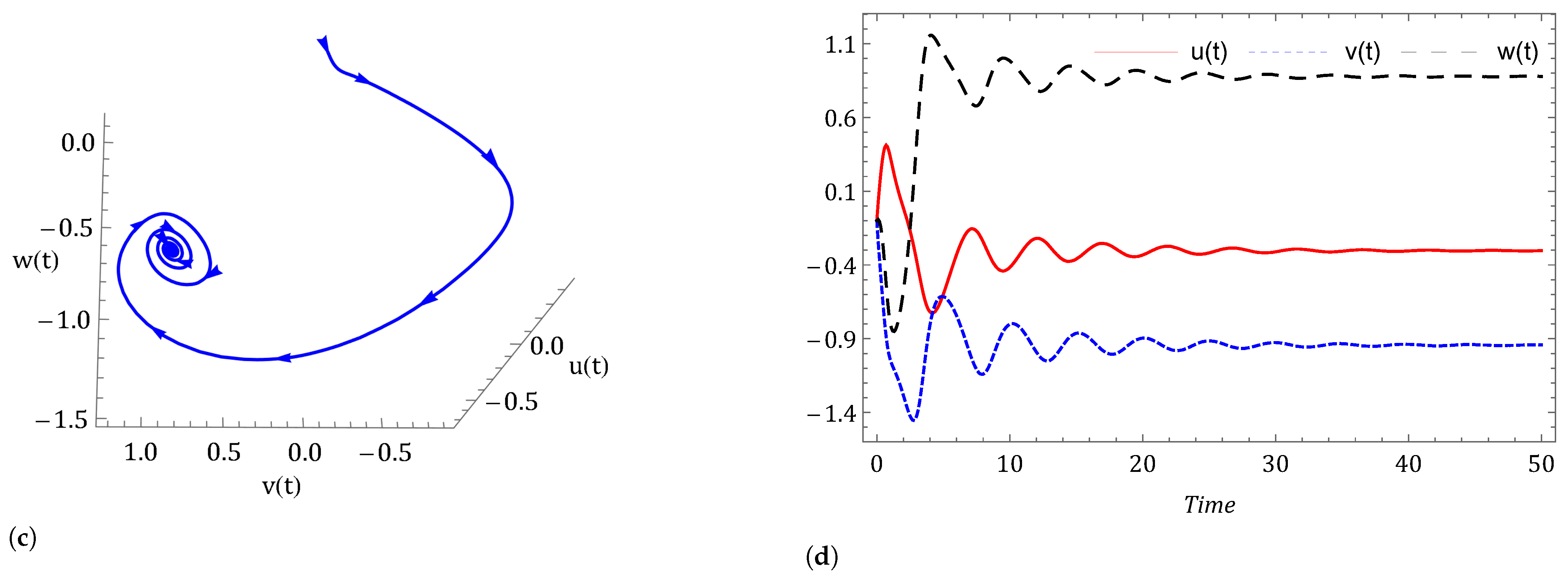
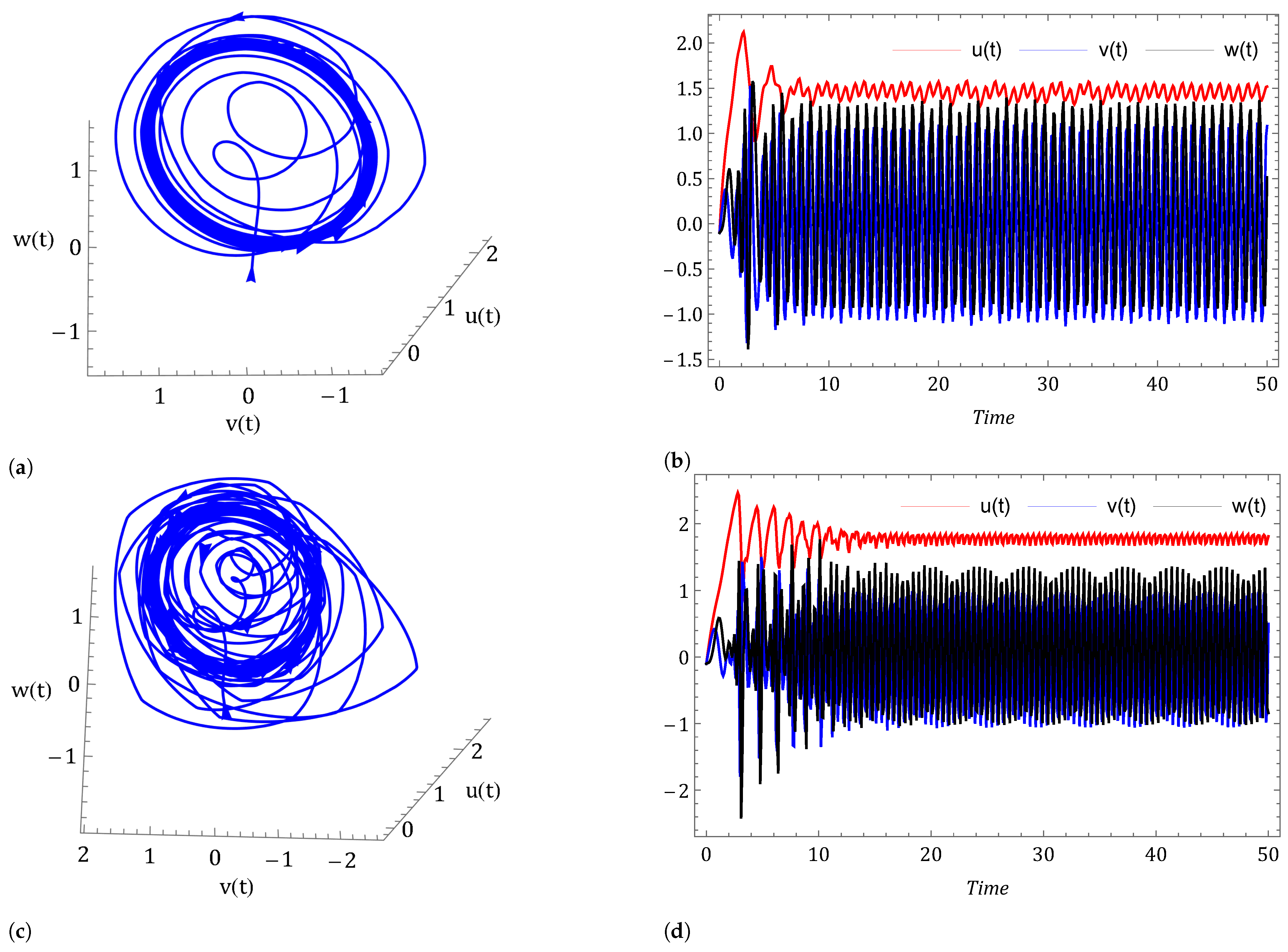
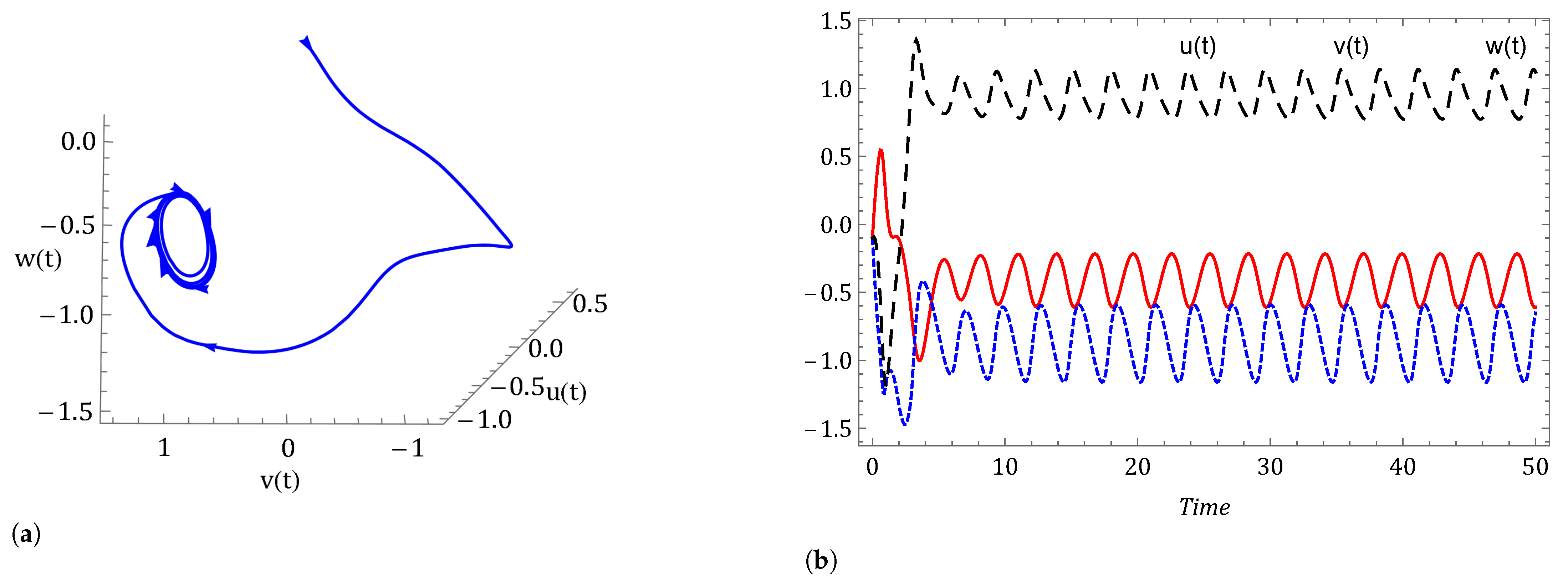
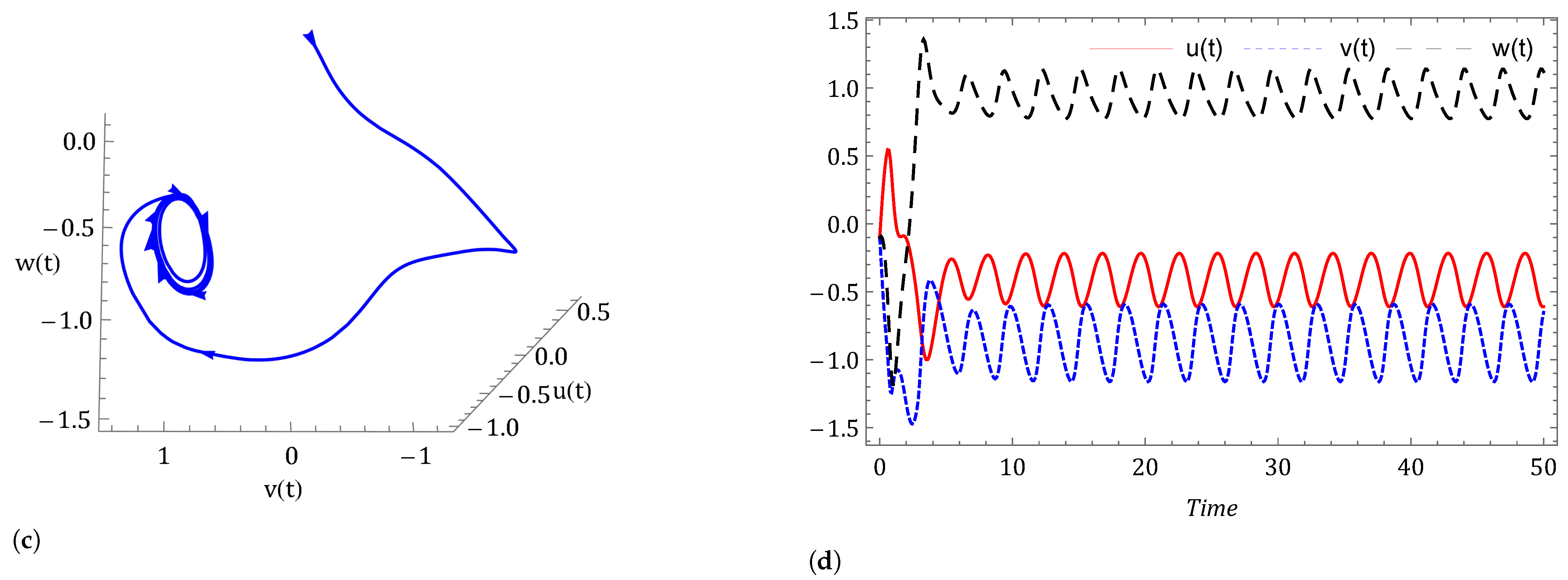
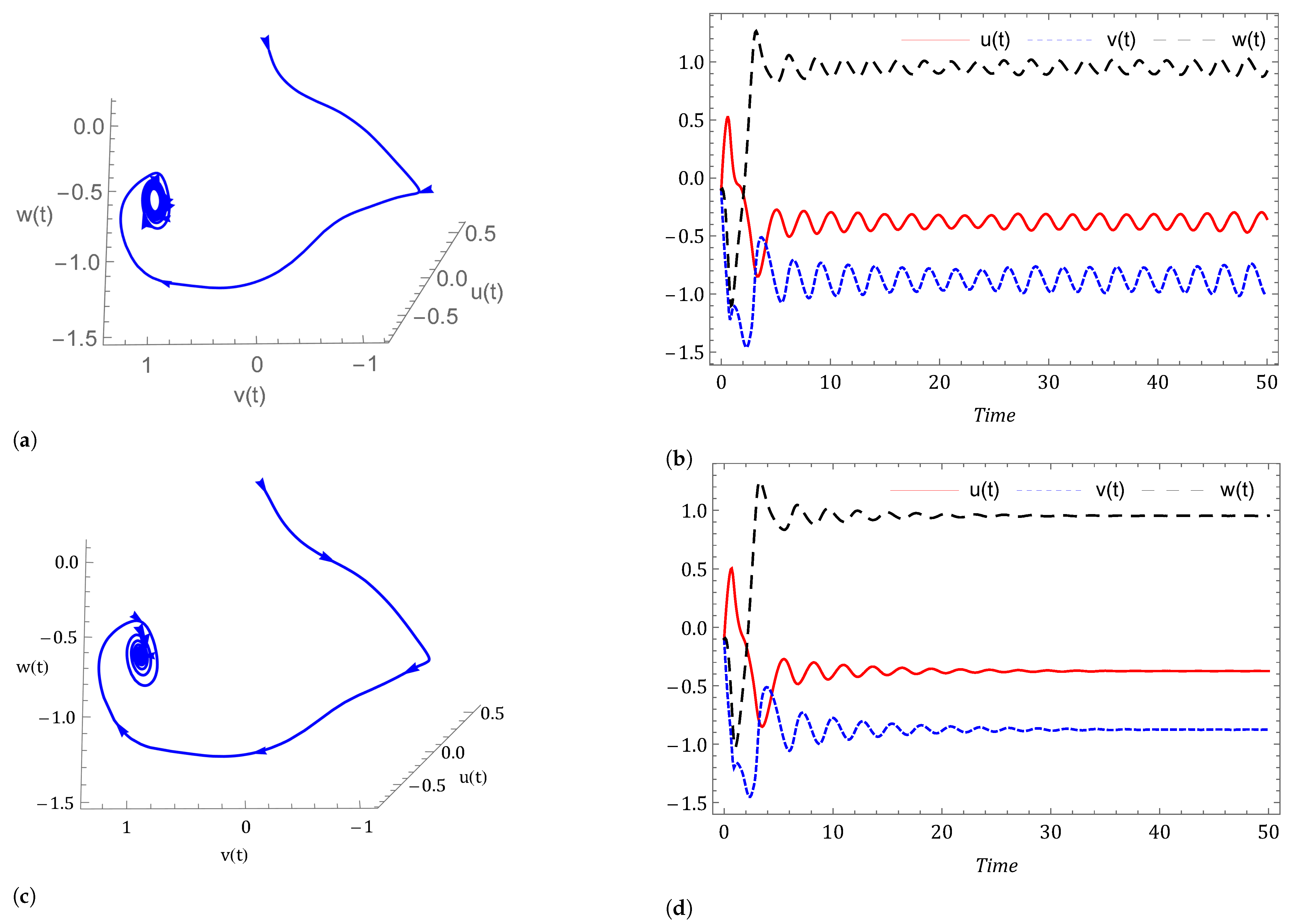
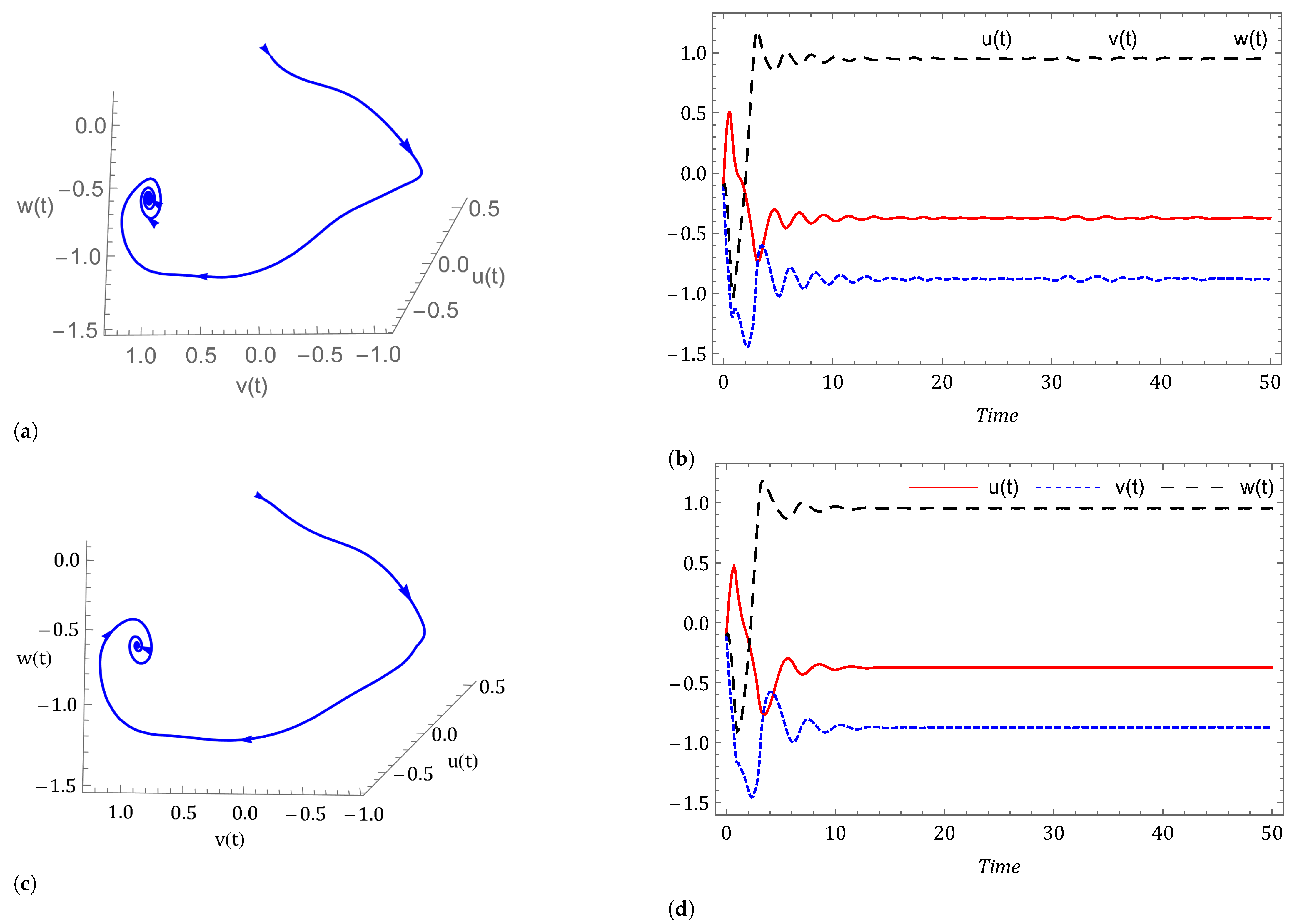
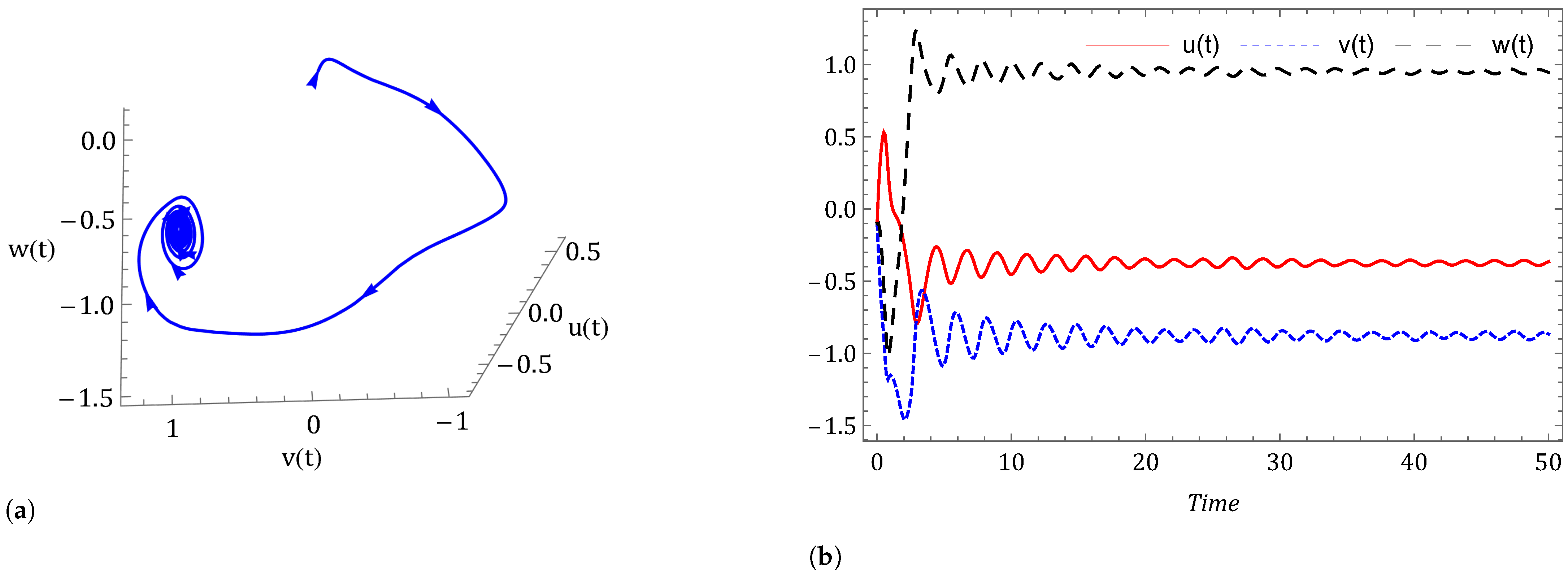
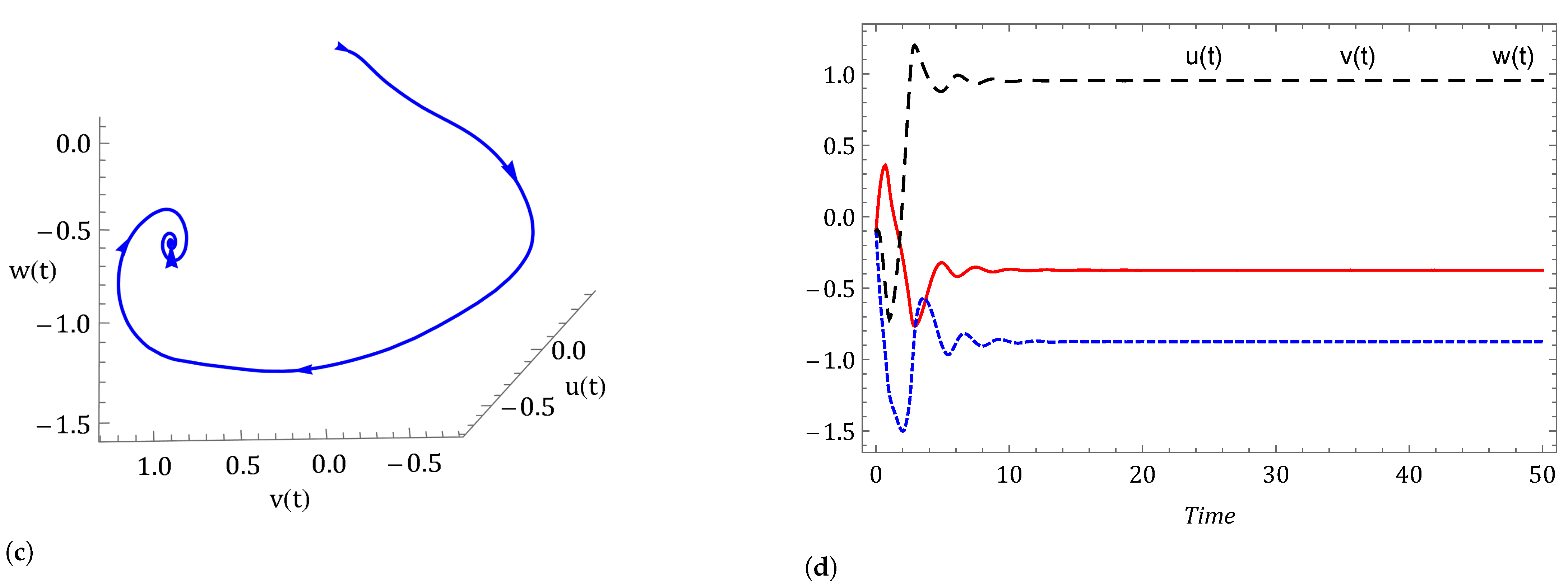
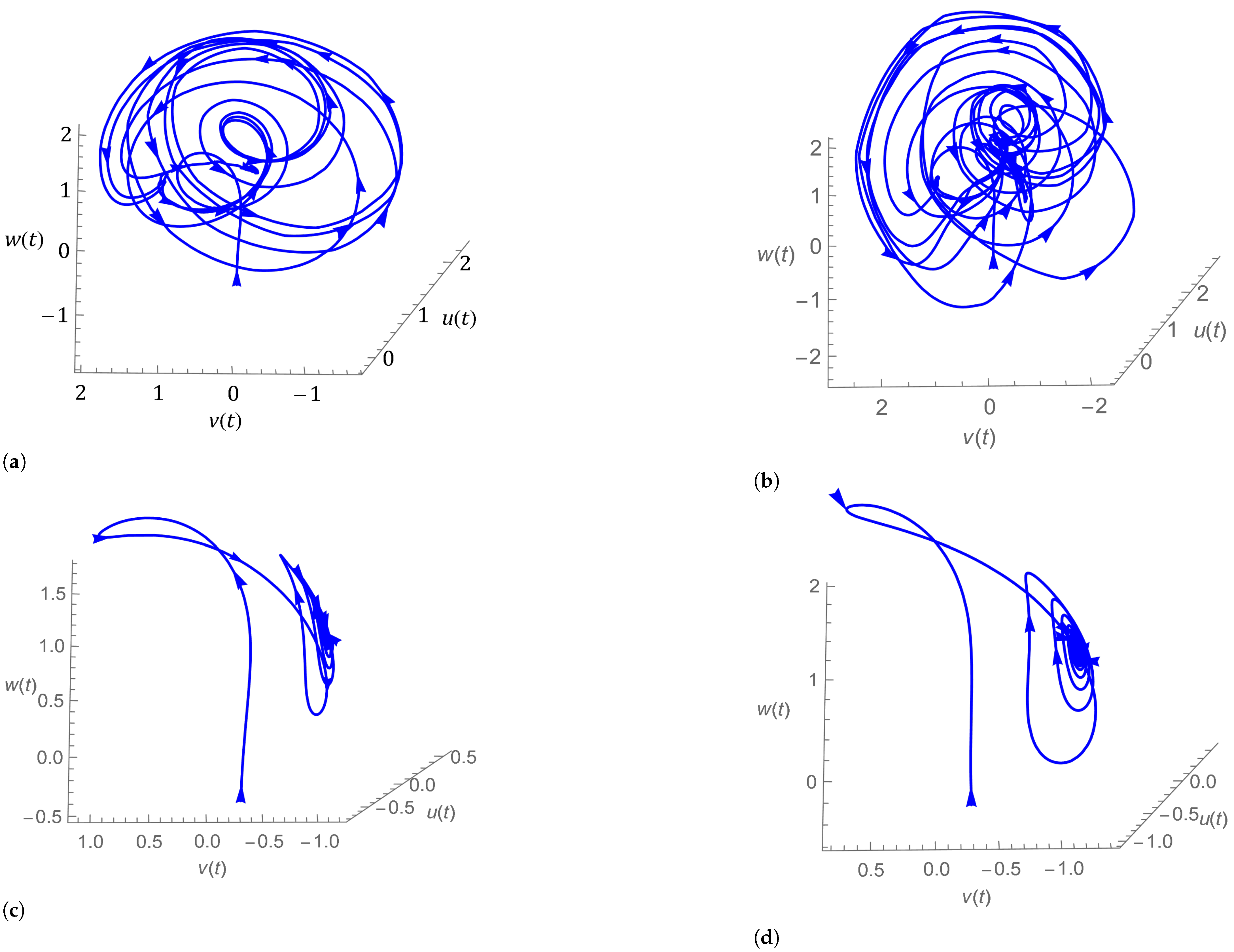
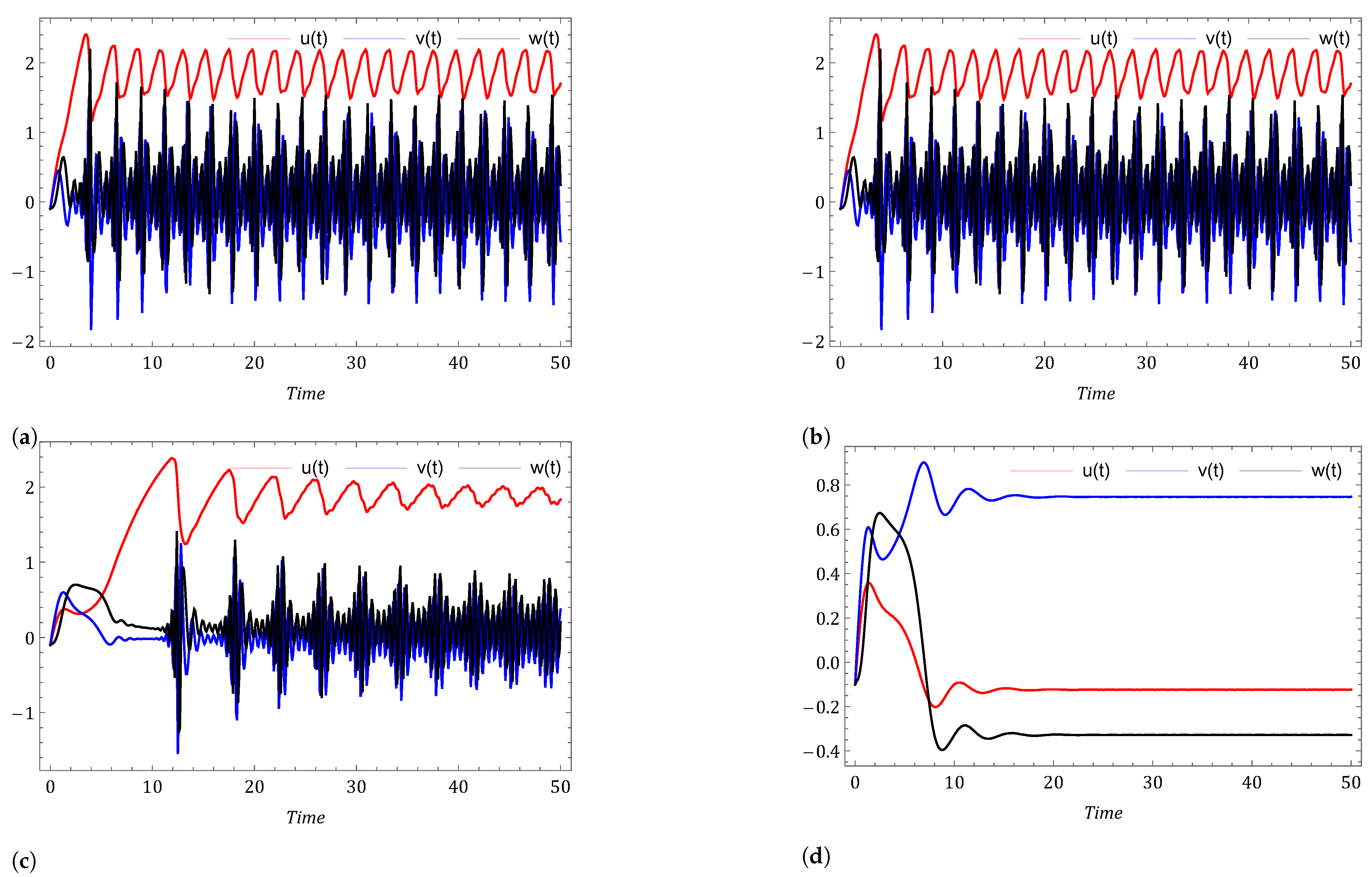
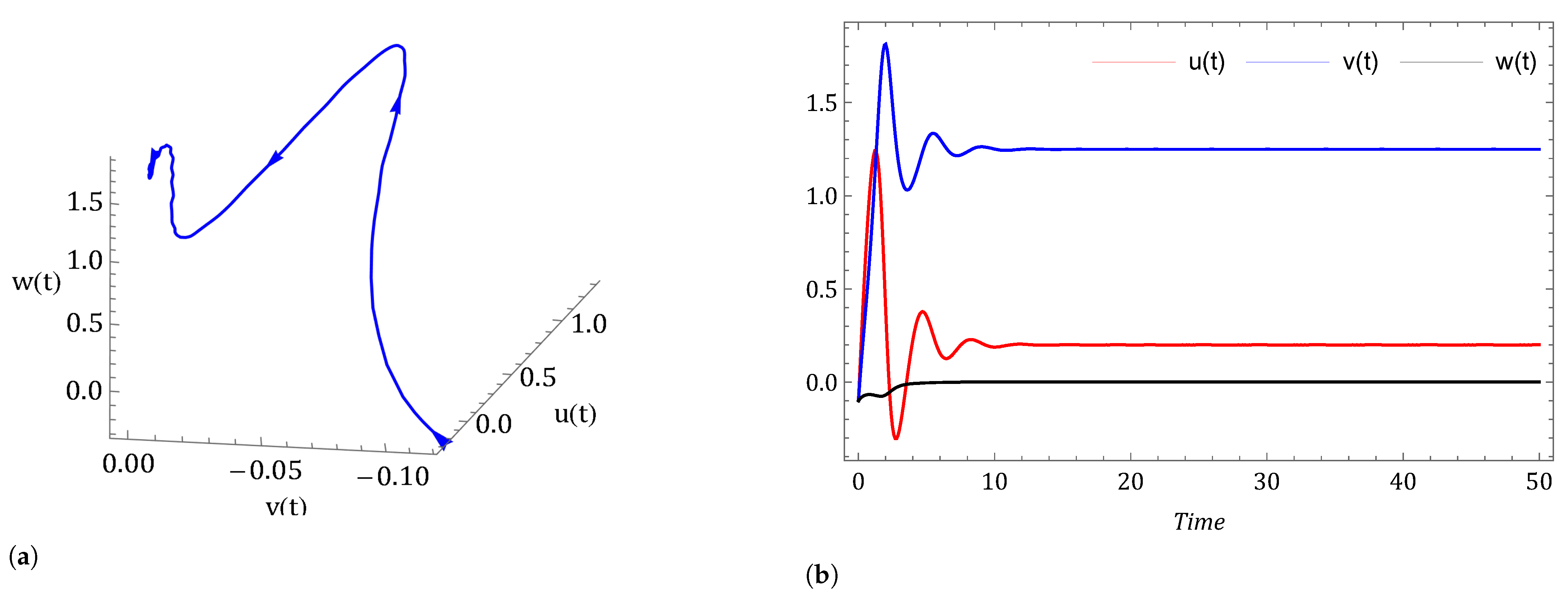
Case I: Commensurate order.

For a commensurate system, we consider ${\beta }_1={\beta }_2={\beta }_3=\beta .$ Figure 1a,b, represent the dynamics of the commensurate system (2) or (3) with initial conditions $(-0.1,-0.1,-0.1)$ for ${\beta }_1={\beta }_2={\beta }_3=1$. We observe the weak periodic oscillations or irreflexive chaotic behavior in winter due to low pressure over the pole. This means the system’s solution diverges, and as a result the variables seem to vary chaotically in Figure 1. A strong intransitive chaotic behavior is noticed from Figure 2, Figure 3 and Figure 4 for reduced values of $\beta$. From Figure 2, Figure 3 and Figure 4 we notice that the system under the Caputo derivative is less chaotic than the system under the CF derivative. Figure 5, Figure 6, Figure 7 and Figure 8 present the nature of the system (29) with the SMC Equation (36) under the influence of the Caputo and CF fractional derivative. The strength of the westerlies in winter decreases by the influence of SMC, so that the system demonstrate non-chaotic behavior. This is seen in Figure 5 and Figure 6. Further on reducing the value of $\beta ,$ the system converges towards stability in Figure 7 and Figure 8. Graphical representations exhibit that the SMC have a stabilizing effect on the systems (2) and (3). In addition to the effect of controller, it is noticed that Caputo fractional derivative makes the stabilizing effect faster than the CF derivative.

2.

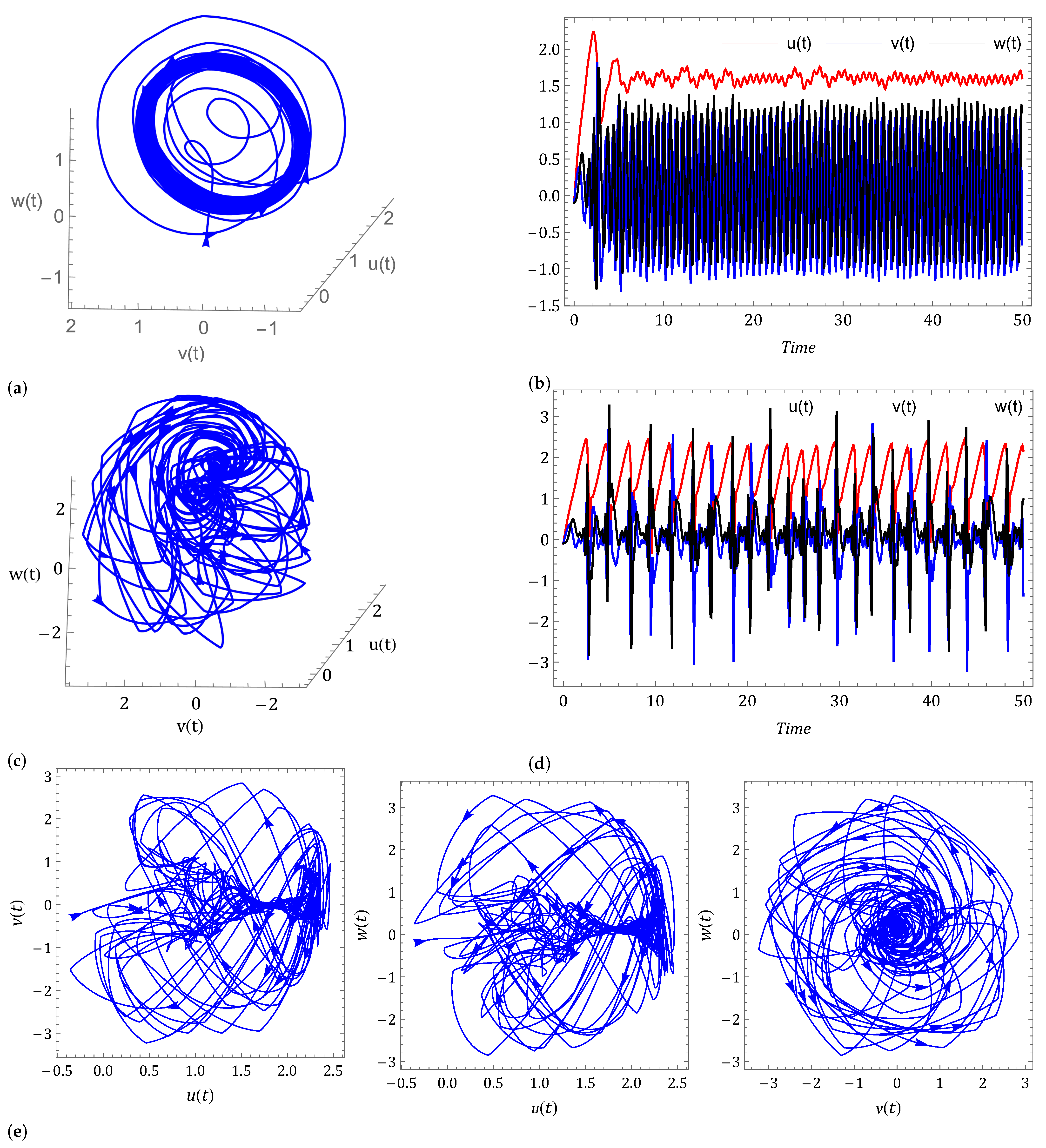
Case II: Non-commensurate order.

In Figure 9 and Figure 10 we have shown the nature of the non-commensurate system (2) and (3) with ${\beta }_1=0.85,{\beta }_2=0.95,{\beta }_3=0.9.$ In Figure 9, we observe the strong chaotic behavior of the non-commensurate system (2) and (3) due to low pressure over the poles in winter. The influence of the Caputo and CF fractional derivative on the system (29) with controller Equation (36) can be shown in Figure 10. We have observed that the system under the CF fractional derivative response more effectively toward the controller than the system under Caputo fractional derivative.

3.

Case III: Commensurate and non-commensurate order with uncertainty and external disturbance.

We have disturbed the fractional order system (29) by an uncertainty $\Delta h(u,v,w)=0.45sin\left(\pi u\right)cos\left(\pi v\right)sin\left(2\pi w\right)$ and an external disturbance $q\left(t\right)=0.5sin\left(\pi t\right)$ where $|\Delta h(u,v,w)|\le {\zeta }_1=0.45$ and $q\left(t\right)\le {\zeta }_2=0.5$ and we get the system (39). The disturbed system with controller response can be seen in Figure 11, Figure 12, Figure 13 and Figure 14. It is observed that on applying the external disturbance and uncertainty, the strong prevailing westerlies remain in control. We can see this in Figure 11 for $\beta =1$. The powerful westerlies weaken as pressure over the poles rises, which causes the system to converge toward stability. This can be seen in Figure 12, Figure 13 and Figure 14. It has been noticed that the system’s controller Equation (36) keeps the chaos under control even in the presence of uncertainty and external disturbance in the system (2) and (3).

4.

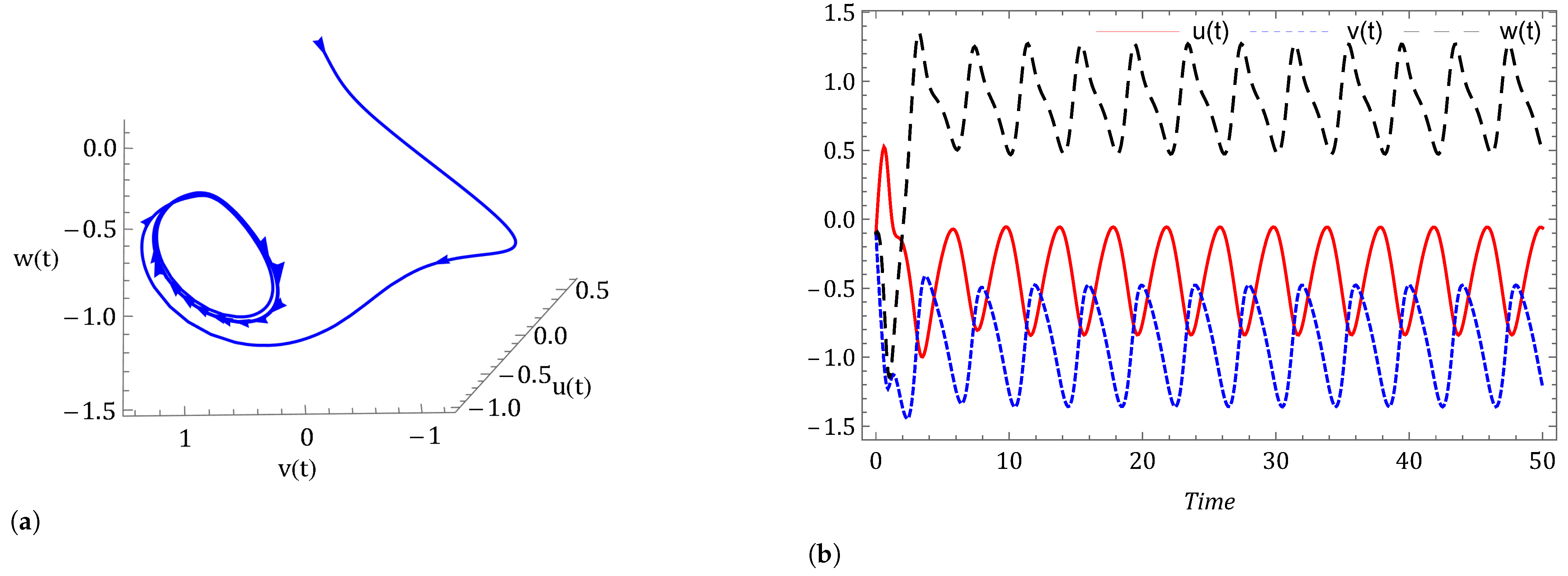
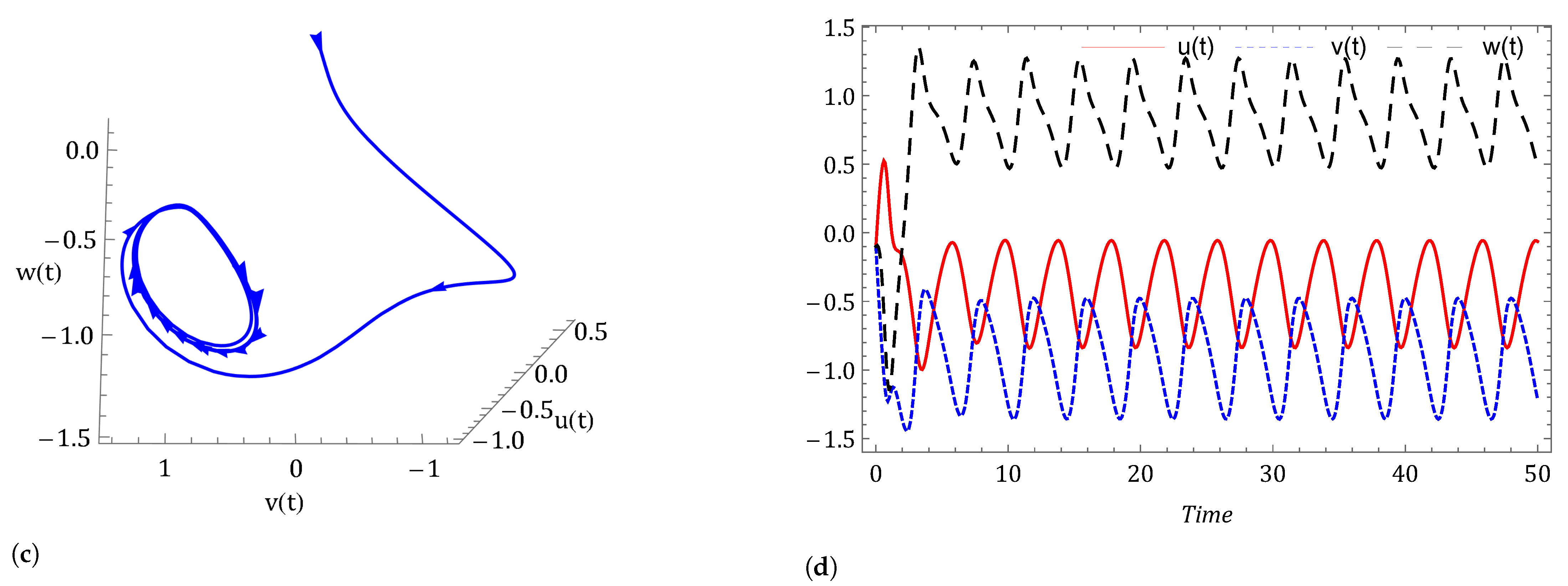
Investigating the impact of other factors The effect of increasing thermal forcing term $\rho$ on system (2) under the Caputo fractional derivative is shown in Figure 15. We observed that the system is chaotic for $\rho =1.5$ and $\rho =2.$ This happens due to less heating contrast polarity between oceans and continents ($\rho$). However, when we increase the value of $\rho$ logically, the system advances toward stability. The dynamical behavior of the system (3) is examined with decreasing cross-latitude external heating contrast $\delta$ in Figure 16. The number of oscillations decreases with decreasing polarity of cross-latitude heating because increasing temperature decreases the strength of the westerlies. In support of Theorem 5, Figure 17 shows that when we set the force of wave advection caused by the westerly current zero ($b=0$), we arrived at a stable point of equilibrium. When $b=0$ and $\rho \ne 0,$ the equilibrium point is $E_1=(0.199390,1.249048,0)$ and the eigenvalues of the Jacobian matrix at $E_1$ is $(-0.500305+1.74071i,-0.500305-1.74071i,-0.800609).$ Hence, $E_1$ is stable.

Figure 1. Chaotic nature of the systems (2) and (3) through (a) 3D parametric graph, (b) time graph, (c) 2D parametric graph for $\beta =1$.

Figure 1. Chaotic nature of the systems (2) and (3) through (a) 3D parametric graph, (b) time graph, (c) 2D parametric graph for $\beta =1$.

Figure 2. (a,b) The dynamics of the system (2) and (c,d) represent dynamics of the system (3) (e) parametric relation of the variable for the system (2) for $\beta =0.95$.

Figure 2. (a,b) The dynamics of the system (2) and (c,d) represent dynamics of the system (3) (e) parametric relation of the variable for the system (2) for $\beta =0.95$.

Figure 3. (a,b) The dynamics of the system (2) and (c,d) represent dynamics of the system (3) (e) parametric relation of the variable for the system (3) for $\beta =0.9$.

Figure 3. (a,b) The dynamics of the system (2) and (c,d) represent dynamics of the system (3) (e) parametric relation of the variable for the system (3) for $\beta =0.9$.

Figure 4. (a,b) The dynamics of the system (2) and (c,d) represent dynamics of the system (3) for $\beta =0.85$.

Figure 4. (a,b) The dynamics of the system (2) and (c,d) represent dynamics of the system (3) for $\beta =0.85$.

Figure 5. (a,b) The dynamics of the controlled system (29) with the Caputo derivative and (c,d) represent dynamics of the controlled system (29) with CF Fractional derivative for $\beta =1$.

Figure 5. (a,b) The dynamics of the controlled system (29) with the Caputo derivative and (c,d) represent dynamics of the controlled system (29) with CF Fractional derivative for $\beta =1$.

Figure 6. (a,b) The dynamics of the controlled system (29) with the Caputo derivative and (c,d) represent dynamics of the controlled system (29) with CF Fractional derivative for $\beta =0.95$.

Figure 6. (a,b) The dynamics of the controlled system (29) with the Caputo derivative and (c,d) represent dynamics of the controlled system (29) with CF Fractional derivative for $\beta =0.95$.

Figure 7. (a,b) The dynamics of the controlled system (29) with the Caputo derivative and (c,d) represent dynamics of the controlled system (29) with CF Fractional derivative for $\beta =0.9$.

Figure 7. (a,b) The dynamics of the controlled system (29) with the Caputo derivative and (c,d) represent dynamics of the controlled system (29) with CF Fractional derivative for $\beta =0.9$.

Figure 8. (a,b) The dynamics of the controlled system (29) with the Caputo derivative and (c,d) represent dynamics of the controlled system (29) with CF Fractional derivative for $\beta =0.85$.

Figure 8. (a,b) The dynamics of the controlled system (29) with the Caputo derivative and (c,d) represent dynamics of the controlled system (29) with CF Fractional derivative for $\beta =0.85$.

Figure 9. (a,b) The dynamics of the system (29) with the Caputo derivative and (c,d) represent dynamics of the system (29) with CF Fractional derivative for ${\beta }_1=0.85,{\beta }_2=0.95,{\beta }_3=0.9$ without control.

Figure 9. (a,b) The dynamics of the system (29) with the Caputo derivative and (c,d) represent dynamics of the system (29) with CF Fractional derivative for ${\beta }_1=0.85,{\beta }_2=0.95,{\beta }_3=0.9$ without control.

Figure 10. (a,b) The dynamics of the controlled system (29) with the Caputo derivative and (c,d) represent dynamics of the controlled system (29) with CF Fractional derivative for ${\beta }_1=0.85,{\beta }_2=0.95,{\beta }_3=0.9$.

Figure 10. (a,b) The dynamics of the controlled system (29) with the Caputo derivative and (c,d) represent dynamics of the controlled system (29) with CF Fractional derivative for ${\beta }_1=0.85,{\beta }_2=0.95,{\beta }_3=0.9$.

Figure 11. (a,b) The dynamics of the controlled system (39) with the Caputo derivative and (c,d) represent dynamics of the controlled system (39) with CF Fractional derivative for $\beta =1$.

Figure 11. (a,b) The dynamics of the controlled system (39) with the Caputo derivative and (c,d) represent dynamics of the controlled system (39) with CF Fractional derivative for $\beta =1$.

Figure 12. Controlled commensurate system (39) for $\beta =0.95$ with uncertainty and external disturbance under the influence of (a,b) Caputo fractional derivative, (c,d) CF fractional derivative.

Figure 12. Controlled commensurate system (39) for $\beta =0.95$ with uncertainty and external disturbance under the influence of (a,b) Caputo fractional derivative, (c,d) CF fractional derivative.

Figure 13. Controlled commensurate system (39) for $\beta =0.9$ with uncertainty and external disturbance under the influence of (a,b) Caputo fractional derivative, (c,d) CF fractional derivative.

Figure 13. Controlled commensurate system (39) for $\beta =0.9$ with uncertainty and external disturbance under the influence of (a,b) Caputo fractional derivative, (c,d) CF fractional derivative.

Figure 14. (a,b) The dynamics of the controlled system (39) with the Caputo derivative and (c,d) represent dynamics of the controlled system (39) with CF Fractional derivative for ${\beta }_1=0.85,{\beta }_2=0.95,{\beta }_3=0.9$.

Figure 14. (a,b) The dynamics of the controlled system (39) with the Caputo derivative and (c,d) represent dynamics of the controlled system (39) with CF Fractional derivative for ${\beta }_1=0.85,{\beta }_2=0.95,{\beta }_3=0.9$.

Figure 15. Dynamics of the system (2) with increasing thermal forcing term (a) $\rho =1.5,$ (b) $\rho =2,$ (c) $\rho =2.5,$ and (d) $\rho =3$ under Caputo fractional derivative for $\beta =0.95$.

Figure 15. Dynamics of the system (2) with increasing thermal forcing term (a) $\rho =1.5,$ (b) $\rho =2,$ (c) $\rho =2.5,$ and (d) $\rho =3$ under Caputo fractional derivative for $\beta =0.95$.

Figure 16. Dynamics of the system (2) with changing cross-latitude external heating contrast $\delta$ (a) $\delta =6,$ (b) $\delta =4,$ (c) $\delta =3.3,$ and (d) $\delta =3.2$ under CF fractional derivative for $\beta =0.95$.

Figure 16. Dynamics of the system (2) with changing cross-latitude external heating contrast $\delta$ (a) $\delta =6,$ (b) $\delta =4,$ (c) $\delta =3.3,$ and (d) $\delta =3.2$ under CF fractional derivative for $\beta =0.95$.

Figure 17. Dynamics of the system (2) under Caputo fractional derivative for $b=0$ and $\beta =0.95$ through (a) 3D parametric graph, (b) time graph.

Figure 17. Dynamics of the system (2) under Caputo fractional derivative for $b=0$ and $\beta =0.95$ through (a) 3D parametric graph, (b) time graph.

7. Conclusions

In this work, we have analyzed a chaotic system representing the atmospheric circulation in the frame of the Caputo and the CF fractional derivative. To control chaos in the system, a sliding mode control law has been developed and its global stability is established using the Lyapunov stability theorem. The results achieved from the Caputo model are compared with that of the CF model. We have observed that as the order of the derivative reduces, the solution of the system exhibits a switch from chaotic behavior to a stable profile. Again, it is noticed that the states of the fractional-order system can be stabilized using the SMC approach. Even in the presence of uncertainty and external disruption, the SMC approach stabilizes the system. These observations are effectively validated by numerical simulations in this paper using the single-step predictor–corrector method. Therefore, we can conclude that fractional order along with the SMC can act as a strong stability control tool for a chaotic system. Moreover, we have noticed that SMC is more effective in the CF model as compared to the Caputo model. We have observed that the chaotic nature is inversely proportional to the thermal forcing.