Superpotential for Novel Symmetry in Real and Complex Space
Abstract
:1. Introduction
2. Supersymmetric Energy Conditions (SUSYEC) and Shape Invariance (SI) Relations
Shape Invariance Condition
3. A Few Deviated Superpotentials with SUSYEC Being Valid and SI Being Invalid
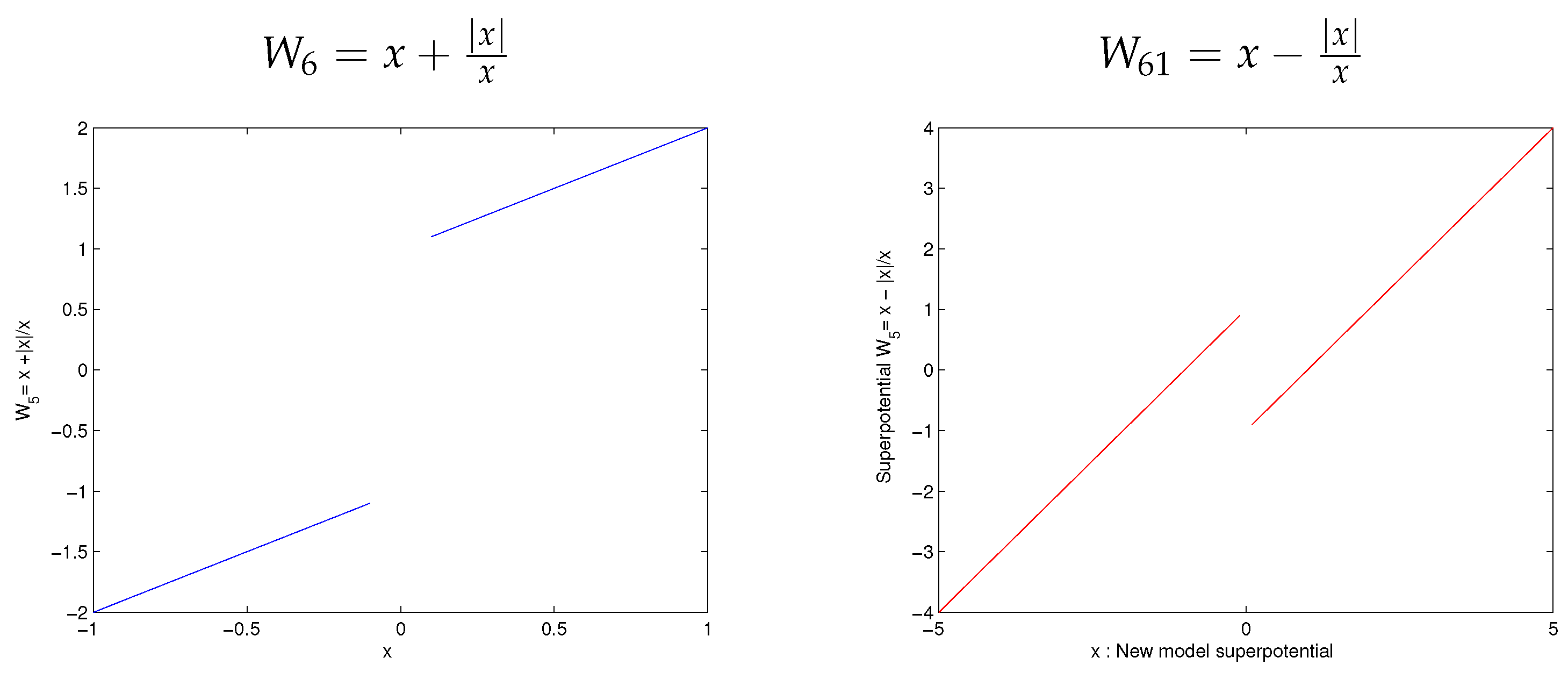
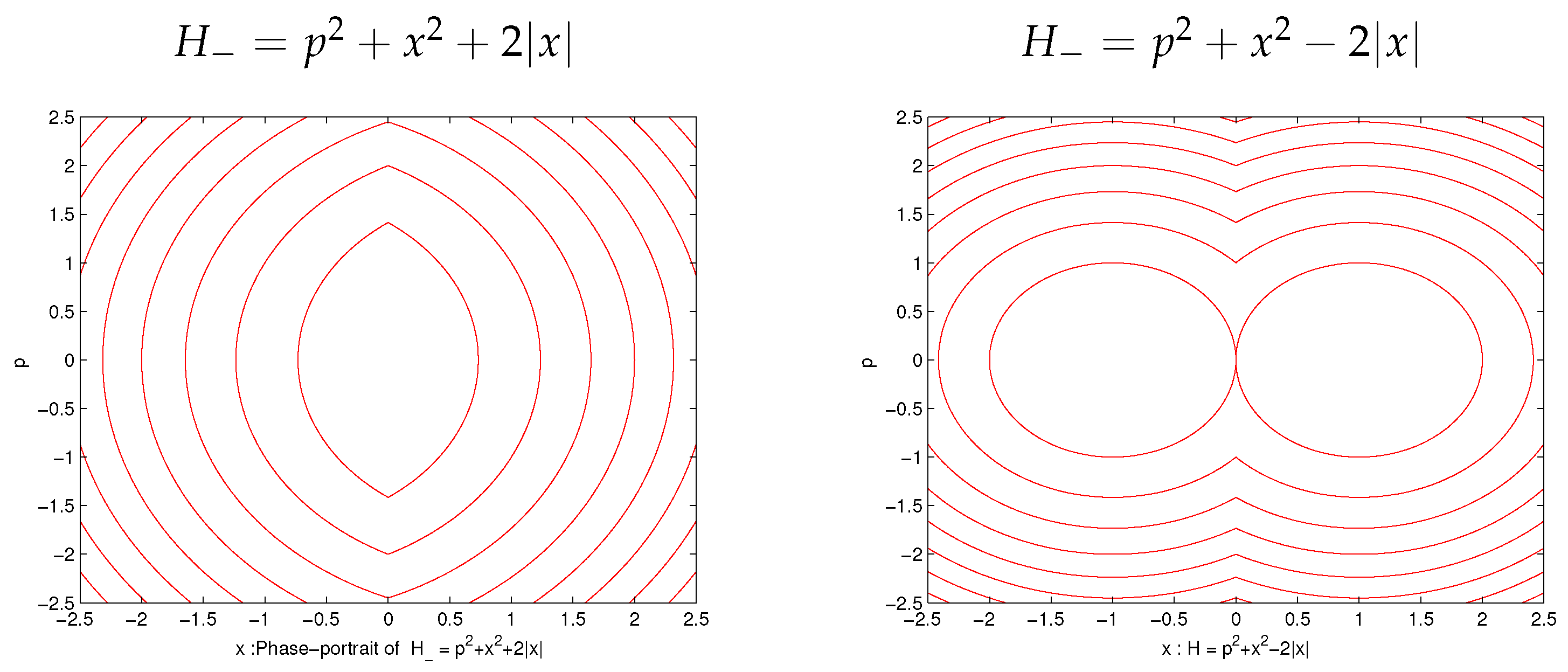
3.1. New Superpotential for Novel Symmetry in Real Space
3.2. Mathematical Proof of Novel Symmetry
4. New Superpotential in Complex Space: -Symmetry
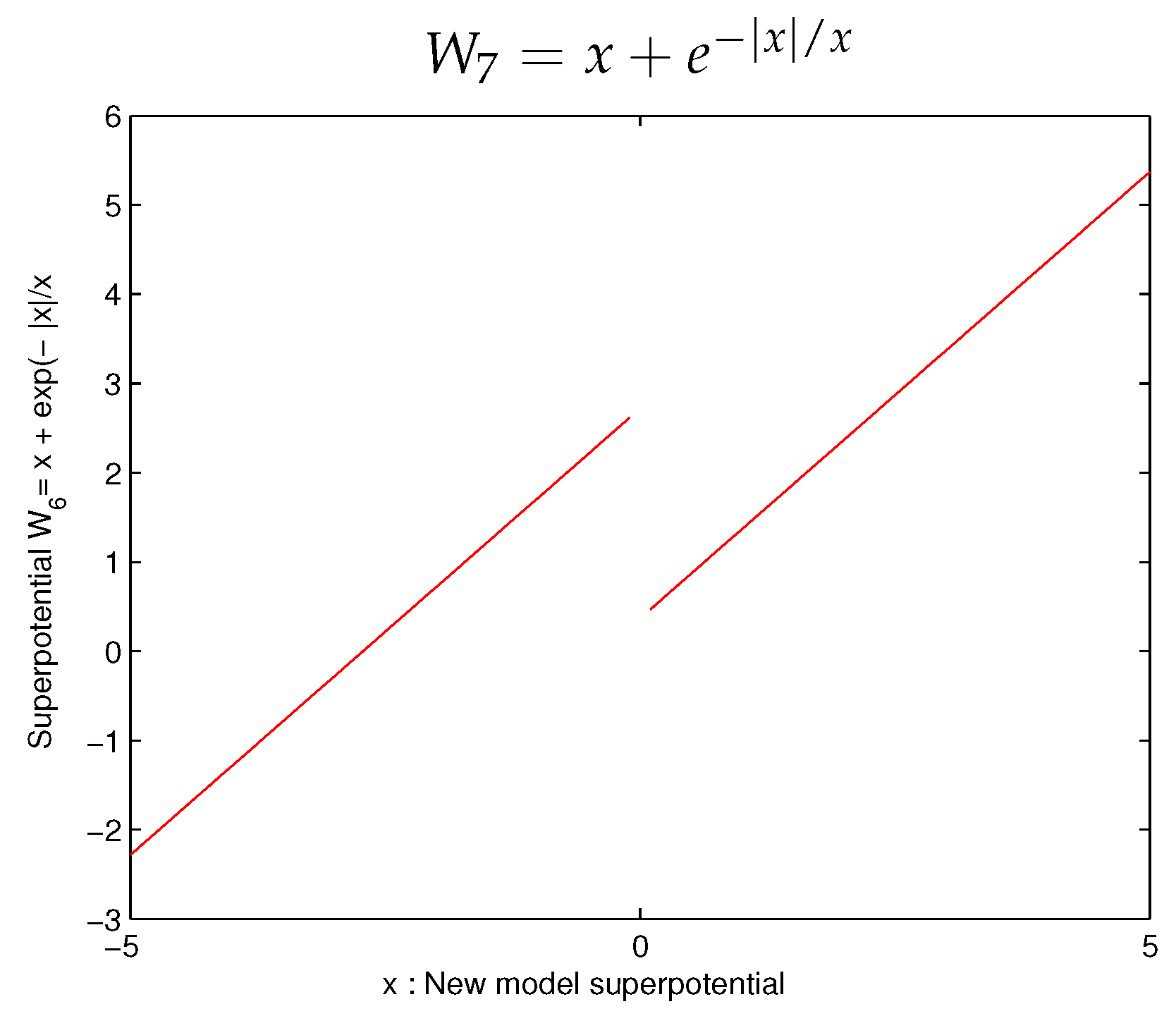
4.1. First Model in Complex Space Having -Symmetry Condition
4.2. Second Exponential Model in Complex Space Having a -Symmetry Condition
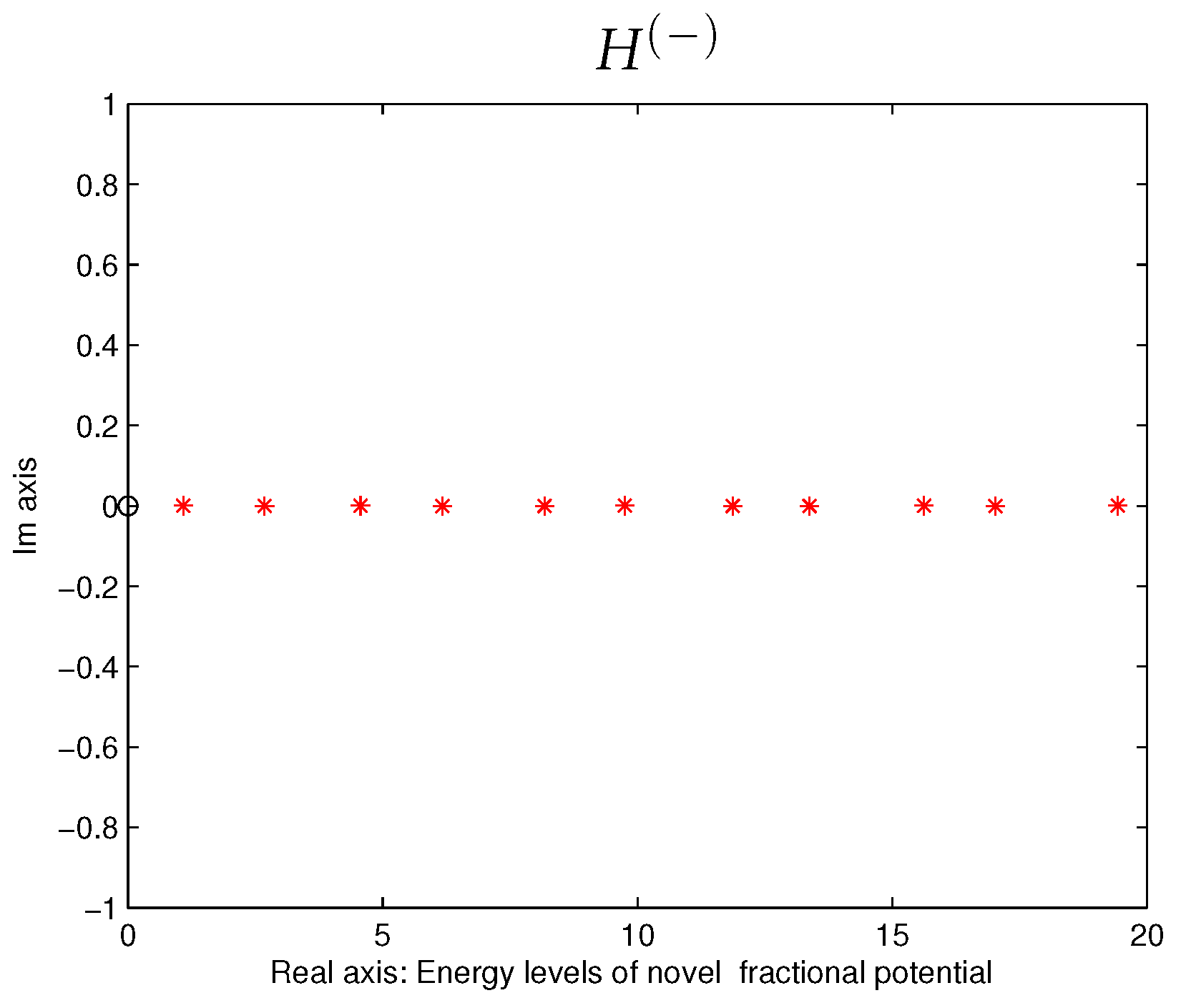
4.3. Third Fractional Model in Complex Space Having -Symmetry Condition
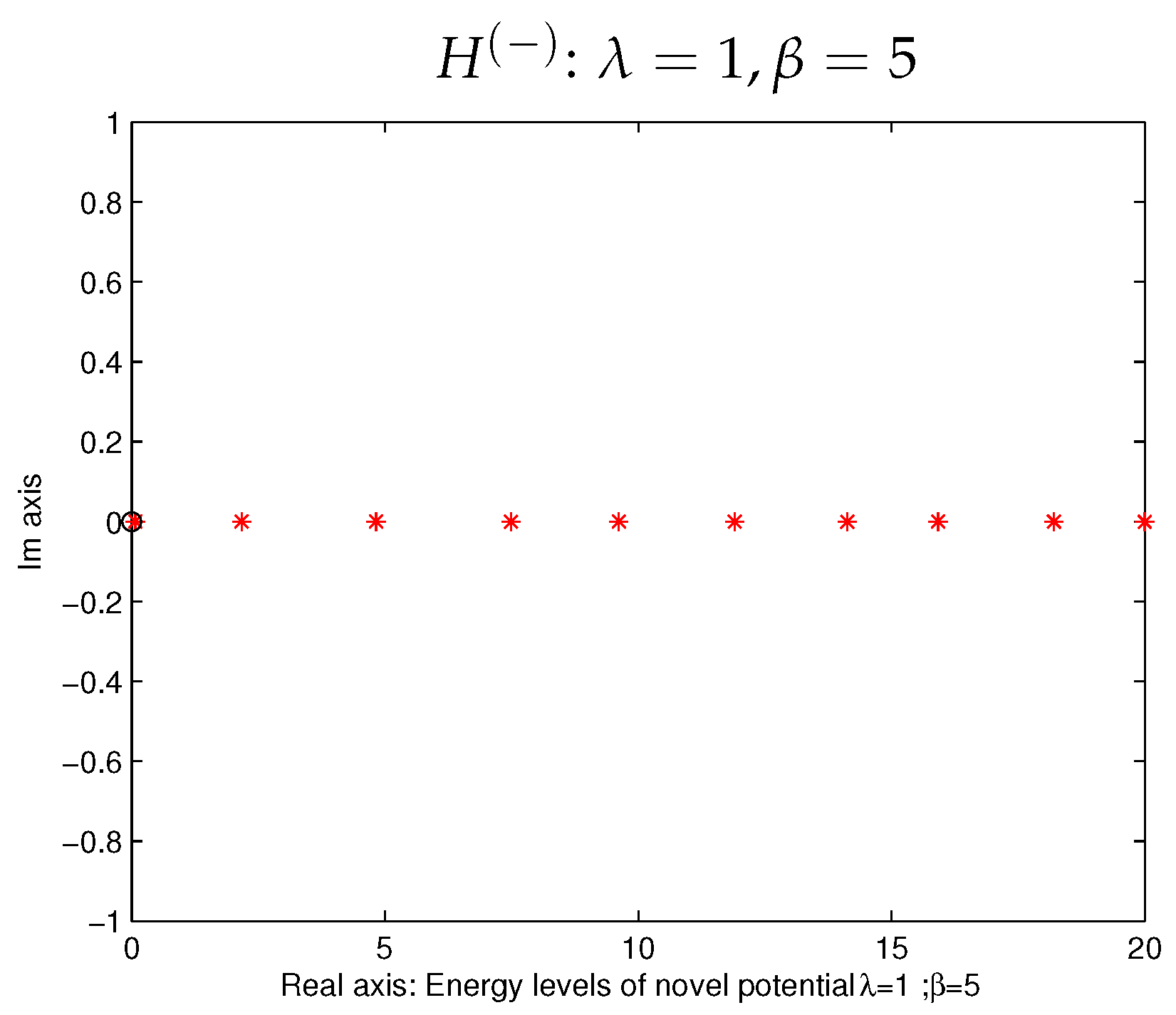
5. Method of Calculation
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Witten, E. Dynamical breaking on supersymmetry. Nucl. Phys. B 1981, 185, 513–554. [Google Scholar] [CrossRef]
- Witten, E. Constraints on supersymmetry breaking. Nucl. Phys. B 1982, 202, 253–316. [Google Scholar] [CrossRef]
- Wozor, C.; Wipf, A. Supersymmetry breaking in low dimensional models. arXiv 2011, arXiv:1107.3324v1. [Google Scholar] [CrossRef] [Green Version]
- Gies, H.; Synatschke, F.; Wipf, A. Supersymmetry breaking as a quantum phase transition. arXiv 2009, arXiv:0906.5492v2. [Google Scholar] [CrossRef] [Green Version]
- Intriligator, K.; Thomas, S. Dynamical Supersymmetry breaking on quantum moduli spaces. arXiv 1996, arXiv:9603158v1. [Google Scholar] [CrossRef] [Green Version]
- Flambaum, V.; Liu, X.; Samsonov, I.; Wu, L.; Zhu, B. Probing supersymmetry breaking scale with atomic clocks. arXiv 2022, arXiv:2209.03231v1. [Google Scholar]
- Peskin, M.E. The experimental invastigation on supersymmetry breaking. arXiv 1996, arXiv:9604339v1. [Google Scholar]
- Intriligator, K.; Seiberg, N. Lectures on supersymmetry breaking. arXiv 2007, arXiv:0702069v1. [Google Scholar] [CrossRef]
- Feldstein, B.; Yanagida, T.T. Why is the supersymmetry breaking scale unnaturally high? arXiv 2012, arXiv:1210:7578v2. [Google Scholar] [CrossRef] [Green Version]
- Cai, M.L.; Wu, Y.K.; Mei, Q.X.; Zhao, W.D.; Jiang, Y.; Yao, L.; He, L.; Zhou, Z.C.; Duan, L.M. Observation of supersymmetry and its spontaneous breaking in a trapped ion quantum simulator. Nat. Commun. 2022, 13, 3412. [Google Scholar] [CrossRef]
- Hirokawa, M. The Rabi model gives off a flavour of spontaneous SUSY breaking. Quant. Stud. Math. Found. 2015, 2, 379–388. [Google Scholar] [CrossRef] [Green Version]
- Mei, Q. Experimental realization of Rabi-Hubbard model with trapped ions. Phys. Rev. Lett. 2022, 128, 160504. [Google Scholar] [CrossRef] [PubMed]
- Gendeshtein, L.E. Derivation of exact spectra of the Schrödinger equation by means of supersymmetry. JETP Lett. 1983, 38, 356–358. [Google Scholar]
- Oikonomou, V.K. A relation between Z3-graded symmetry and shape invariant supersymmetric systems. J. Phys. A 2014, 47, 435304. [Google Scholar] [CrossRef] [Green Version]
- Junker, G. Supersymmetric Methods in Quantum and Statistical Physics; Springer: Berlin, Germany, 1996. [Google Scholar]
- Cooper, F.; Khare, A.; Sukhatme, U. Supersymmetry in Quantum Mechanics; World Scientific: Singapore, 2001. [Google Scholar]
- Bagchi, B.K. Supersymmetry in Quantum and Classical Mechanics; Hall CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Biswas, S.N. Quantum Mechanics; Books and Allied(P) Limited: Kolkatta, India, 2013. [Google Scholar]
- Marques, F.; Negrini, O.; da Silva, A.J. A new simple class of superpotentials on SUSY quantum mechanics. J. Phys. A 2012, 45, 115307. [Google Scholar] [CrossRef]
- Mallow, J.V.; Gangopadhya, A.; Bougie, J.; Rasinariu, C. Inter-relations between additive shape invariant superpotentials. Phys. Lett. A 2019, 384, 126129. [Google Scholar] [CrossRef] [Green Version]
- Bougie, J.; Gangopadhya, A.; Mallow, J.V. Generation of a completa set of additive shape invariant potentials from an Euler equation. Phys. Rev. Lett. 2010, 105, 210402. [Google Scholar] [CrossRef] [Green Version]
- Sree Ranjani, S.; Sandhya, R.; Kapoor, A.K. Shape invariant rational extensions and potentials related to exceptional polynomials. Int. J. Mod. Phys. A 2015, 30, 1550146. [Google Scholar] [CrossRef] [Green Version]
- Sandhya, R.; Ranjani, S.S.; Kapoor, A.K. Shape invariant potentials in higher dimensions. Ann. Phys. 2015, 359, 125–135. [Google Scholar] [CrossRef] [Green Version]
- Gangopadhya, A.; Mallow, J.V.; Rasinaru, C.; Bougie, J. Exacness of shape invariant potentials. Phys. Lett. A 2020, 384, 126722. [Google Scholar] [CrossRef]
- Roy, B.; Roy, P.; Roychoudhury, R. On solutions of Quantum Eigenvalue Problems: A supersymmetric approach. Fortschr. Phys. 1981, 89, 211–258. [Google Scholar] [CrossRef]
- Dong, S.H. Factorization Method in Quantum Mechanics; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Rath, B. A generalisation of supersymmetric energy condition (SUSY-EC) from Fokker-Plank equatio. Nuovo Cimento B 2009, 115, 1229–1234, Erratum in Nuovo Cimento B 2009, 124, 1. [Google Scholar]
- Panigrahi, P.K.; Sukhatme, U. Singular superpotentials in supersymmetric quantum mechanics. Phys. Lett. A 1993, 178, 251–257. [Google Scholar] [CrossRef]
- Fernandez, F.M. Accurate calculation of the eigenvalues of a new simple class of superpotentials in SUSY quantum mechanics. Cent. Eur. J. Phys. 2013, 11, 470–473. [Google Scholar] [CrossRef]
- Nieto, M.M. Relation between supersymmetry and the inverse method in quantum mechanics. Phys. Lett. B 1984, 145, 208–210. [Google Scholar] [CrossRef]
- Znojil, M.; Jakubsky, V. Supersymmetric quantum mechanics living on topologically non-trivial Riemann surfaces. Pramana. J. Phys. 2009, 73, 397–404. [Google Scholar] [CrossRef] [Green Version]
- Jafarizadeh, M.A.; Fakhri, M.A. Supersymmetry and shape invariance in differential equations of mathematical physics. Phys. Lett. A 1997, 230, 164–170. [Google Scholar] [CrossRef]
- Quense, C. Solvable rational potentials and exceptional orthogonal polynomials in supersymmetric quantum mechanics. SIGMA 2009, 5, 084. [Google Scholar]
- Miao, C.H.; Qian, S.-W. Variational supersymmetric WKB approximation. Phys. Rev. A 1997, 56, 2414–2612. [Google Scholar] [CrossRef]
- Amir, N.; Iqbal, S. Algebraic solutions of shape invariant position dependent effective mass systems. J. Math. Phys. 2016, 57, 062105. [Google Scholar] [CrossRef] [Green Version]
- Abhinav, K.; Panigrahi, P.K. Supersymmetry, PT-symmetry and spectral bifurcation. Ann. Phys. 2010, 325, 1198–1206. [Google Scholar] [CrossRef] [Green Version]
- Bender, C.M.; Boettecher, S. Real spectra in non-Hermitian Hamiltonians having PT-symmetry. Phys. Rev. Lett. 1997, 24, 5243–5246. [Google Scholar]
- Znojil, M. PT-symmetrized supersymmetric quantum mechanics. Czech. J. Phys. 2001, 51, 420–428. [Google Scholar] [CrossRef] [Green Version]
- Andrianov, A.A.; Loffe, M.V.; Cannata, F.; Dedonder, J.P. SUSY quantum mechanics with complex superpotentials and real energy spectra. Int. J. Mod. Phys. A 1999, 14, 2675–2688. [Google Scholar] [CrossRef] [Green Version]
- Bezia, D.; Das, A.; Lasano, L.; Greenhood, L. The structure of supersymmetry in PT-symmetric quantum mechanics. Phys. Lett. B 2009, 673, 283–287. [Google Scholar] [CrossRef] [Green Version]
- Rath, B.; Nanayakkara, A.; Mallick, P.; Samal, P.K. SUSY quantum mechanics for PT-symmetric systems. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2018, 88, 633–638. [Google Scholar] [CrossRef]
- Rath, B. Real spectra in some negative potentials: Linear and non-linear one-dimensional PT-invariant quantum systems. Eur. J. Phys. Plus 2021, 136, 493. [Google Scholar] [CrossRef]
- Bhosale, S.S.; Rath, B.; Panigrahi, P.K. On Bell’s inequality in PT-symmetric quantum systems. Quantum Rep. 2021, 3, 417–424. [Google Scholar] [CrossRef]
- Rath, B. Superpotential for novel symmetry in real and complex space. arXiv 2019, arXiv:1905.09724v4. [Google Scholar]
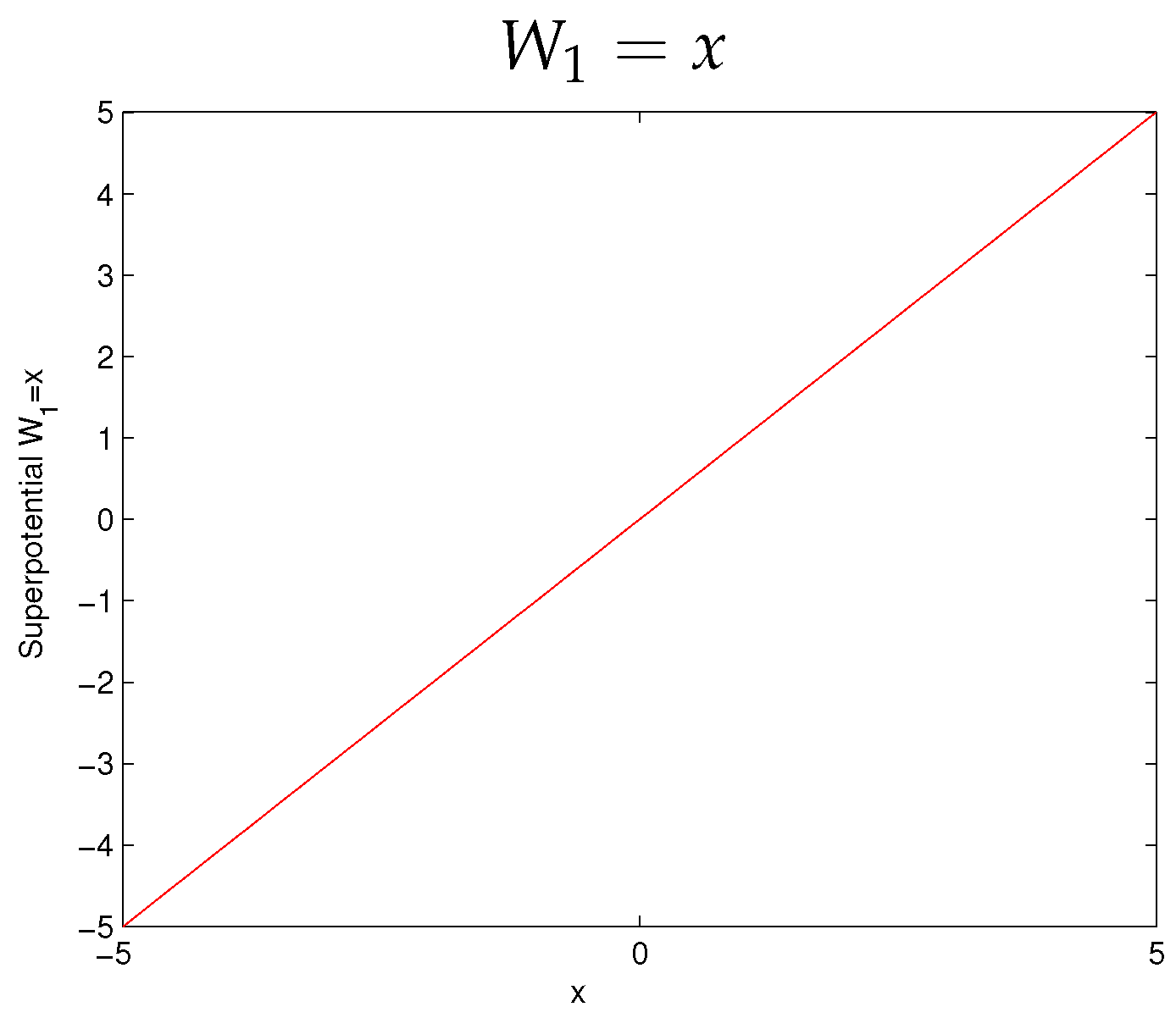

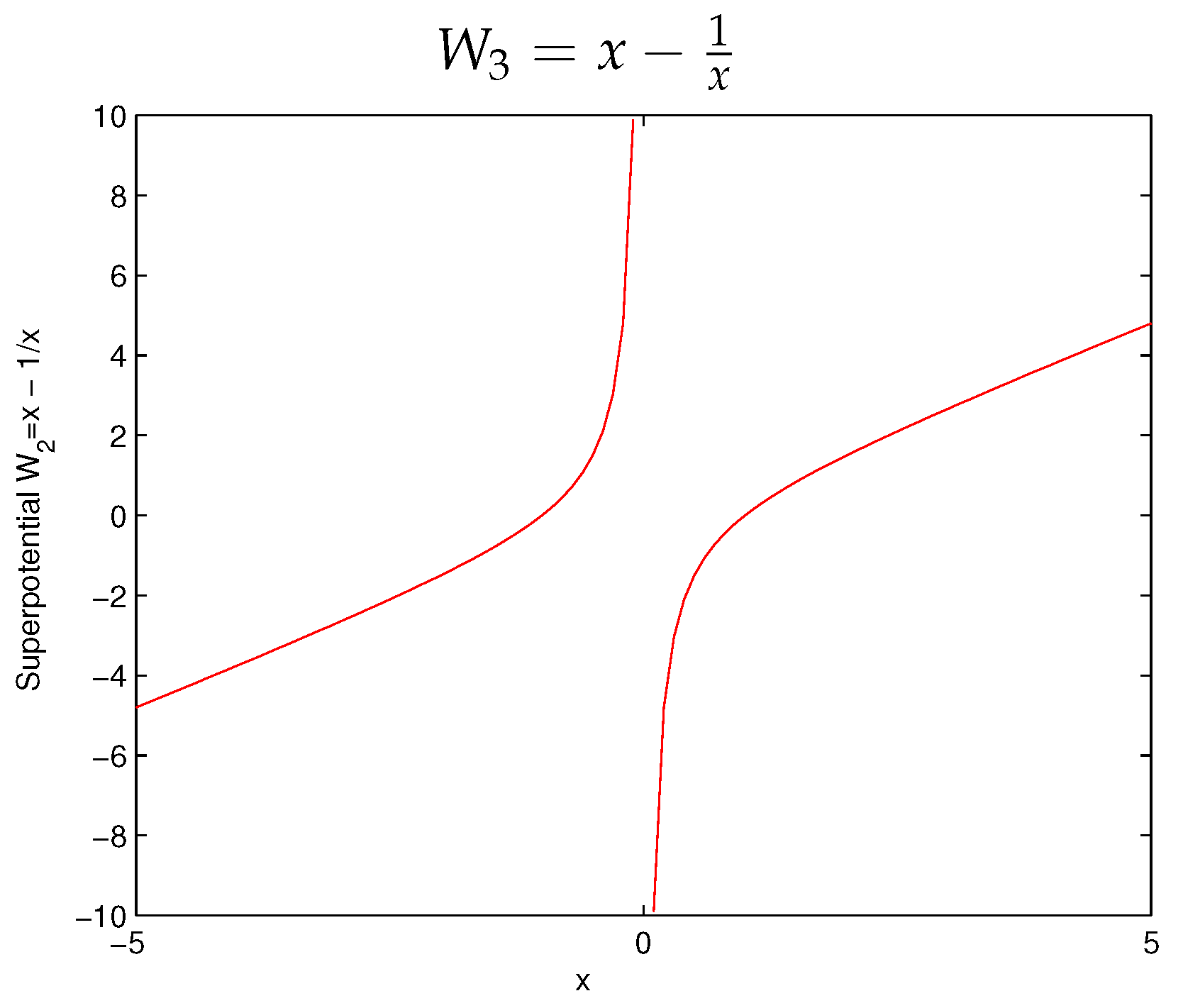
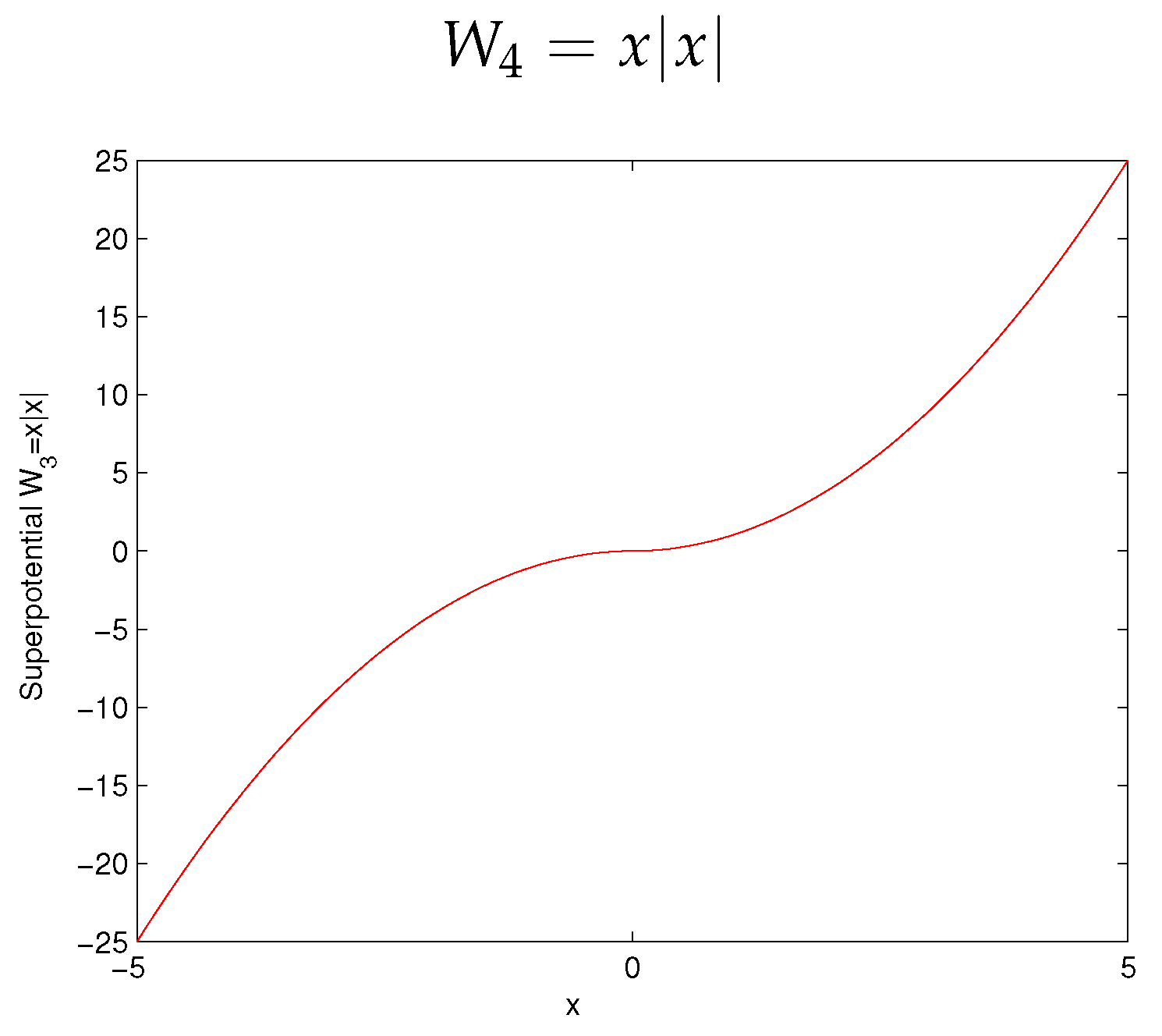
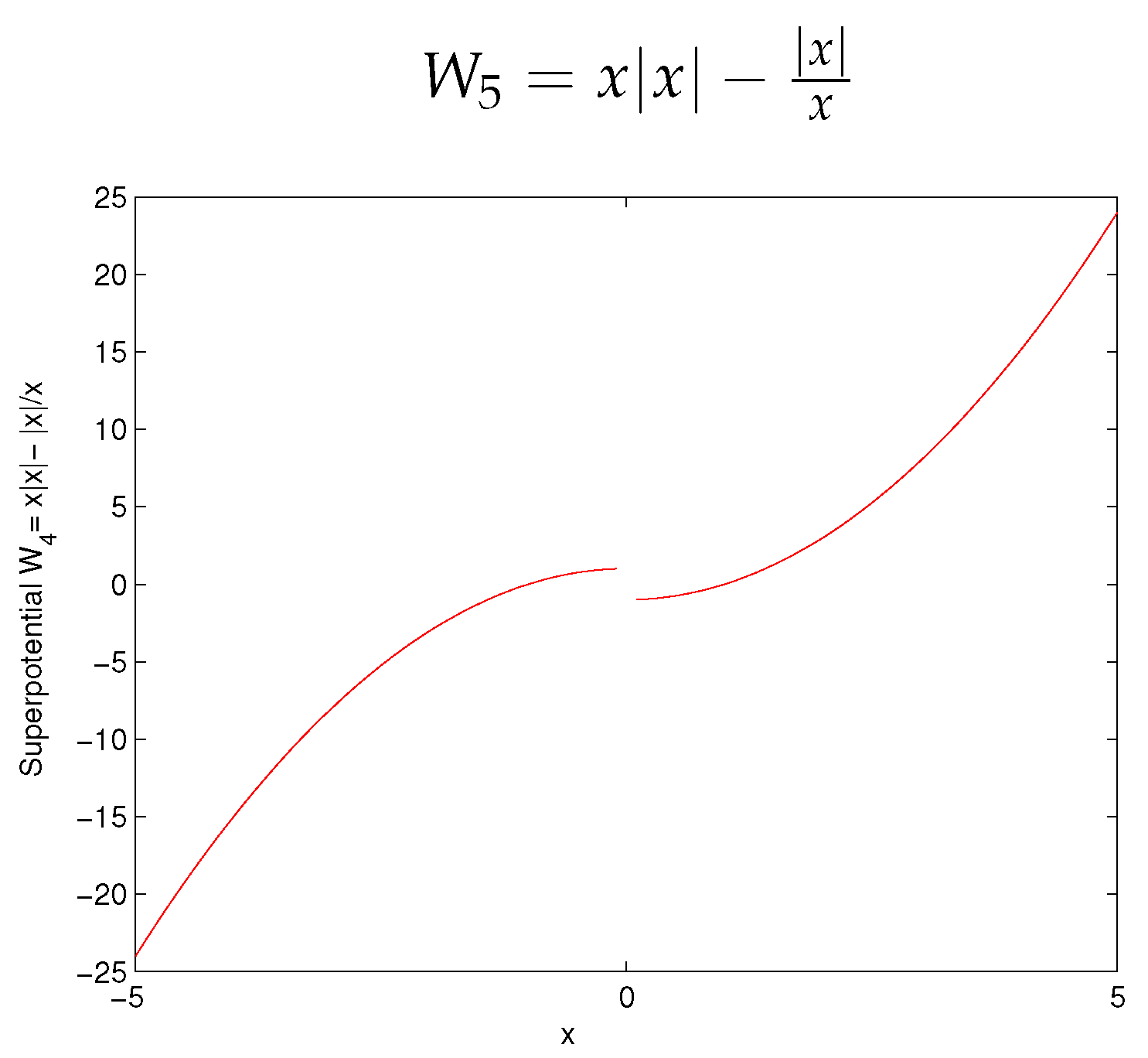

| −0.333 8 |
| 0.553 1 |
| 3.821 7 |
| 6.961 7 |
| 2.001 1 | −0.381 5 |
| 5.074 3 | 0.468 4 |
| 7.659 0 | 1.999 5 |
| 10.207 6 | 3.394 9 |
| −0.001 5 |
| 1.721 9 |
| 2.103 4 |
| 4.012 6 |
| 0.072 5 |
| 2.173 3 |
| 4.826 1 |
| 7.488 2 |
| −0.490 0 |
| 1.087 9 |
| 2.683 4 |
| 4.562 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rath, B. Superpotential for Novel Symmetry in Real and Complex Space. Symmetry 2022, 14, 2632. https://doi.org/10.3390/sym14122632
Rath B. Superpotential for Novel Symmetry in Real and Complex Space. Symmetry. 2022; 14(12):2632. https://doi.org/10.3390/sym14122632
Chicago/Turabian StyleRath, Biswanath. 2022. "Superpotential for Novel Symmetry in Real and Complex Space" Symmetry 14, no. 12: 2632. https://doi.org/10.3390/sym14122632
APA StyleRath, B. (2022). Superpotential for Novel Symmetry in Real and Complex Space. Symmetry, 14(12), 2632. https://doi.org/10.3390/sym14122632






