Hysteresis Response Loops in Stationary Vibrator Regimes for Elastomeric Insulators

Abstract

In order to raise the hysteresis loops in stationary dynamic regimes in the case of elastomeric insulators, specialized dynamic stands are used that may obtain both the necessary harmonic excitation by force as well as the modification of the angular arrangement discreetly variable from zero to 90 degrees. In this context, for the evaluation of the elastomeric insulators, a dynamic stand with an inertial vibrator was used, the frequency of which can be changed by continuous adjustment within the range of values from 2 Hz to 60 Hz. Forces and displacements can be measured with the appropriate sensors, and based on the recording of signals, the characteristics of rigidity, damping and the raise of hysteresis loops could be determined for three significant dynamic regimes: ante-resonance and post-resonance. Research on the dynamic stand, patented in Romania, has highlighted the fact that the parametric evaluation can be performed based on the lifting of the hysteretic loops in stationary harmonic regimes. Additionally, there are two situations specifically mentioned, one in which the significant inertial effect for the F-x loops leads to their positioning in quadrants II and IV, and the case of Q-x loops, where the inertial effect does not exist, and their positioning is only in quadrants I and III. From the analysis of the two cases, the most advantageous evaluation method for the test can be chosen. This article provides the calculation relationships established for the dynamic model with linear viscoelastic behaviour. The requirements of Voight–Kelvin modeling with a single degree of freedom is fully justified and ensured by the conditions of geometric and mass symmetry in the construction of the stand. The verification of the numerical results with the experimental ones was performed with the hysteresis loops corresponding to the previously defined three significant dynamic regimes, as well as according to the three positions of the elastomeric insulators for compression, compression-shear and shear.

1. Introduction

The analysis of the dynamic response for distinct positions of placing the elastomeric insulators showed that, depending on the dynamic ante-resonance or post-resonance regime, the dissipated energy, the force transmitted to the foundation, and the rigidity and damping characteristics are defining parameters in designing and/or optimizing an antivibration system [1,2,3,4,5,6]. Thus, in Romania, at ICECON Bucharest, dynamic test stands were developed for elastomeric insulators used in industry and construction [7].

The experiments on elastomeric insulators, either made in Romania or imported from companies in Europe and the USA, were performed on a dynamic stand patented in Romania and owned by ICECON Bucharest. In principle, the dynamic stand consists of three vertical columns and an inertial vibrator located at the top.

Each column consists of a two semi-cylindrical bodies system with central seats where the elastomer insulator is mounted. In the mounted system, a circular group with radial holes is formed so that it may be positioned at various angles, with a 15-degree angular pace. Thus, the angular position of placing the elastomeric insulator is defined by the angle α formed by the direction of the vertical perturbator force and the compression axis of the elastomeric device. Experimental tests were performed for all positions indexed with the 15° step, by performing simple or combined requirements such as: compression at α = 0°, compression + shear at α > 0 and shear at α = 90° [8,9,10,11,12,13].

On the analyzed dynamic stand, 628 tests were performed for elasatomeric anti-vibration devices that were analyzed and certified in the period 2015–2020, the manufacturers being from Romania, Italy, France, Austria and Spain. The experimental results were statistically processed, taking into account the uncertainty of the measurements [14,15].

2. Test Stand Constructive Scheme

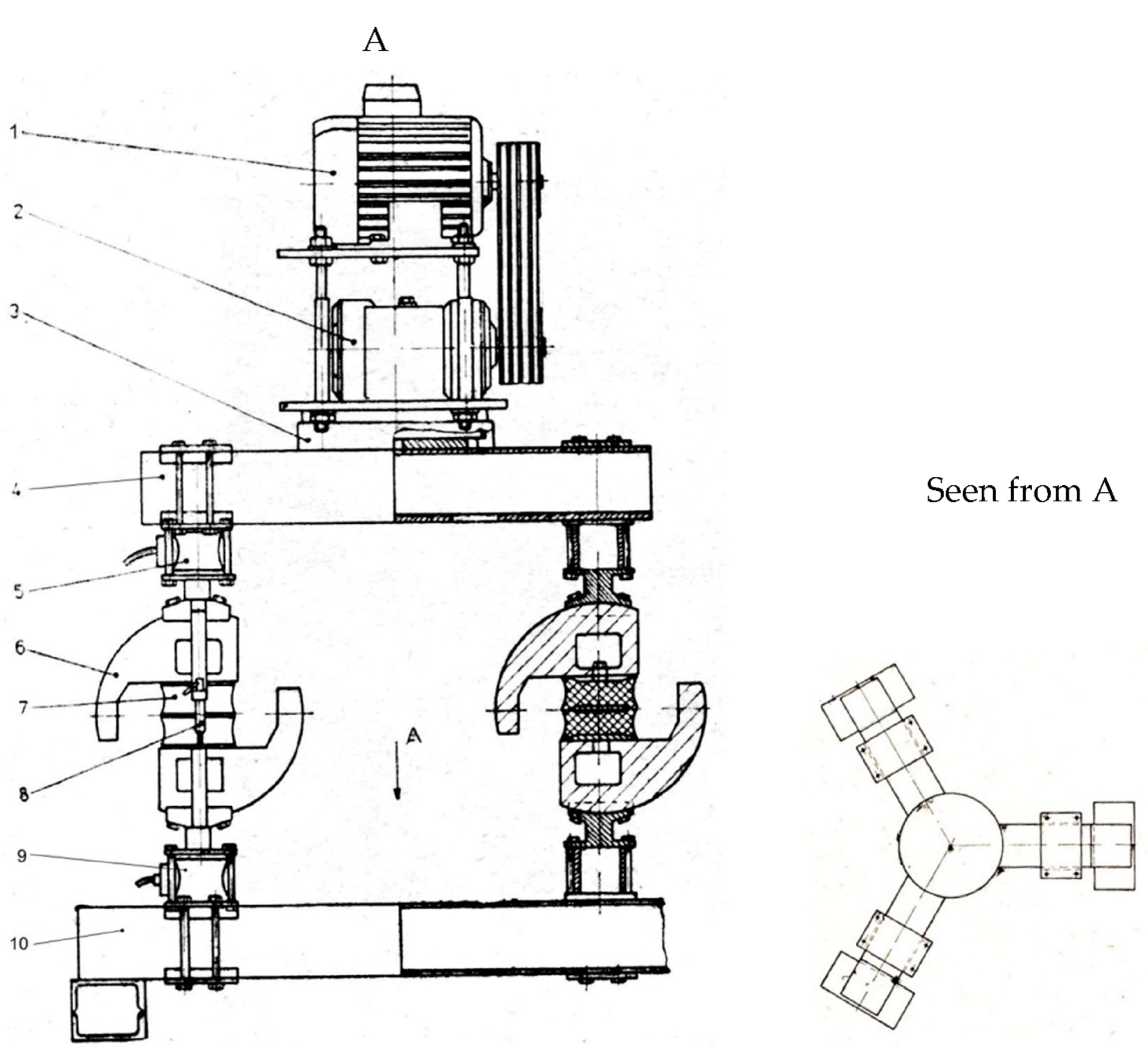
Figure 1 presents the construction solution of the stand with three test groups arranged at 120° so that the vertical excitation force may be applied equally to each elastomeric insulator. The following notations were used in Figure 1: 1—variable speed drive electric engine; 2—unidirectional vibrator; 3—adjustment and fixing support; 4—upper beam; 5—force transducer T_f; 6—semi-circular clamping device; 7—elastomeric insulator; 8—displacement transducer T_x; 9—force transducer T_q; 10—fixed base (frame) [16,17,18,19,20].

The inertial vibrator generates a vertical force, harmonic with parallel and symmetrical action direction in relation to the three elastomeric insulators connected in parallel. Transducer T_f measures the incident force on the elastomeric insulator, transducer T_q measures the emergent force, or the force transmitted at the base and transducer T_x measures the instantaneous displacement x = x(t) or the vertical deformation of the deformable assembly. Each column has its own system of transducers T_x si T_f.

The principle schematization of the stand in constructive solution is presented in Figure 2 where the following notations were used: 1—unidirectional vibrator mounted on upper structure; 2—force transducer (tensometric dose) input; 3—upper semi-circular guiding device and radial positional indexing; 4—upper device for holding the elastomeric insulator; 5—elastomeric insulator; 6—lower device for holding the elastomeric insulator; 7—lower semi-circular device for guiding and radial positional indexing; 8—force transducer (tensometric dose) output; 9—fixed base.

It is shown that the force transducer 5 and the displacement transducer 7 in Figure 1, are mounted and maintained in the initial mechanical state, regardless of any modifications of the angular position of group 6. This makes the initial calibration of the transducers uninfluenced by the subsequent states of the dynamic tests.

Figure 3 presents the schematic of the linear dynamic model, where x = x(t) is the instantaneous displacement; F = F(t) harmonic excitation force; m—mass of the mobile assembly; Q = Q(t)—the force transmitted to the base; k—stiffness of the insulator in the vertical direction; c—viscous damping; T_f—the incident force transducer which measures force F(t); T_q—the displacement transducer that measures the instantaneous displacement x = x(t).

The significant positions of the elastomeric insulator are presented in Figure 4 where the axes of the fixed system are Ox and O_y, and the moving axes O_c, for compression, and O_f, for shear, are connected to the elastomeric device. The three distinct positions are highlighted by the seating angle α. Thus, for compression α = 0, compression-shear α > 0 and α < 90, and for shear α = 90° [21,22].

3. Evaluation of Dissipated Energy

Highlighting the modality of variation of the dissipated energy, in some well specified cases, is a criterion for optimizing the dynamic system based on the stationary harmonic regime and of the linear viscoelastic characteristics of the elastomeric insulators (stiffness k and viscous damping c) [22]. In this case, for a dynamic regime with relative pulsation $\mathsf{\Omega } =\frac{\omega }{{\omega }_n}$, where ω is the excitation pulsation and ω_n is its own pulsation, the dissipated energy W_d may be expressed as:

$$W_d\left(\mathsf{\Omega }, \zeta \right)=2\pi {\left(\frac{m_{0}r}{m}\right)}^{2}k\zeta \frac{{\mathsf{\Omega }}^5}{{\left(1-{\mathsf{\Omega }}^2\right)}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2}$$

(1)

where $\zeta$ is damping rate or the fraction of the critical damping (where $\zeta =c/c_r$, where c—effective viscous damping, and c_r—critical viscous damping). Usually, $\zeta$ is under the value of 0.7;

k—system stiffness, N/m;

m₀r—static moment of the exciter with eccentric bodies in rotation motion, kg·m;

m—mobile mass of the stand, kg;

The maximum dissipated energy in the ante-resonance regime $W_{d,a}^{max}$ corresponds to a fraction of the critical damping ${\zeta }_a^0=\frac{1-{\mathsf{\Omega }}_a^2}{2{\mathsf{\Omega }}_a}$, so it may be written as:

$$W_{d,a}^{max}=2\pi {\left(\frac{m_{0}r}{m}\right)}^{2}k\frac{{\mathsf{\Omega }}_a^4}{4\left(1-{\mathsf{\Omega }}_a^2\right)}$$

(2)

where ${\mathsf{\Omega }}_a<1$ is the ante-resonance relative pulsation.

The maximum dissipated energy in the post-resonance regime $W_{d,p}^{max}$ corresponds to pulsation ${\mathsf{\Omega }}_p>1$ and to the fraction of the critical damping ${\zeta }_p^0=\frac{{\mathsf{\Omega }}_p^2-1}{2{\mathsf{\Omega }}_p}$, so that we have

$$W_{d,p}^{max}=2\pi {\left(\frac{m_{0}r}{m}\right)}^{2}k\frac{{\mathsf{\Omega }}_p^4}{4\left({\mathsf{\Omega }}_p^2-1\right)}$$

(3)

The dissipated energy in the resonance regime $W_d^{rez}$ corresponds to pulsation $\mathsf{\Omega } =1$ and to the fraction of the critical damping ${\zeta }_n=\frac{c}{2m{\omega }_n}$, so that we have

$$W_d^{rez}=2\pi {\left(\frac{m_{0}r}{m}\right)}^{2}k\frac{1}{4{\zeta }_n}$$

(4)

From Relations (2), (4) then from Relations (3) and (4), it emerges the following correlations

$$W_{d,a}^{max}=W_d^{rez}\frac{{\mathsf{\Omega }}_a^4}{1-{\mathsf{\Omega }}_a^2}{\zeta }_n$$

(5)

$$W_{d,p}^{max}=W_d^{rez}\frac{{\mathsf{\Omega }}_p^4}{1-{\mathsf{\Omega }}_p^2}{\zeta }_n$$

(6)

The correlation between $W_{d,a}^{max}$ and $W_{d,p}^{max}$ emerges from Relations (5) and (6) as

$$\frac{W_{d,p}^{max}}{W_{d,a}^{max}}={\left(\frac{{\mathsf{\Omega }}_a}{\mathrm{a}}\right)}^2\frac{1-{\mathsf{\Omega }}_a^2}{{\mathsf{\Omega }}_p^2-1}$$

(7)

3.1. Dissipated Energy as a Function of Damping

For the current variable $\zeta$ with $\mathsf{\Omega }\ne 1$ mentioned at constant value, we have the following situations, that is:

(a)

ante-resonance with Ω_a< 1 for which we have

$$W_{d,a}^{ciclu}\left(\zeta \right)=2\pi {\left(\frac{m_{0}r}{m}\right)}^{2}k\zeta \frac{{\mathsf{\Omega }}_a^5}{{\left(1-{\mathsf{\Omega }}^2\right)}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2}$$

(8)

with graphical representation in Figure 5 [23,24].

(b)

Post-resonance with Ω_p > 1 for which it is valid the relation

$$W_{d,p}^{ciclu}\left(\zeta \right)=2\pi {\left(\frac{m_{0}r}{m}\right)}^{2}k\zeta \frac{{\mathsf{\Omega }}_p^5}{{\left(1-{\mathsf{\Omega }}^2\right)}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2}$$

(9)

with graphical representation in Figure 6 [23,24].

The three curves in Figure 5 and Figure 6 correspond to the cases in which the elastomeric anti-vibration devices, required for compression with k_c, compression—shear k_α and shear k_f are characteristic of the ante-resonance regime ${\mathsf{\Omega }}_a=0.8, {\zeta }_a^0=0.225$ and, respectively, of the post-resonance regime ${\mathsf{\Omega }}_p=1.5, {\zeta }_p^0=0.41$ [23,24].

3.2. Dissipated Energy as a Function of Relative Pulsation

The energy dissipated per cycle W_d^ciclu(Ω) depending on the relative excitation pulsation $\mathsf{\Omega } =\frac{\omega }{{\omega }_n}$ for the given values of stiffness k and the fraction of the critical damping $\zeta$ is given by relation, with the parameter order i, so

$$W_d^{ciclu}\left(\mathsf{\Omega }\right)=2\pi {\left(\frac{m_{0}r}{m}\right)}^2{k}_i{\zeta }_i\frac{{\mathsf{\Omega }}^5}{{\left(1-{\mathsf{\Omega }}^2\right)}^2+{\left(2{\zeta }_i\mathsf{\Omega }\right)}^2}=E_i$$

(10)

where i = 1, 2, …, n represents the index of the parametric order $k_{i, }{\zeta }_i$ which describes a curve from the curve family with current variable Ω [23,24].

Figure 7 shows the curve family with discrete values $k_{i, }{\zeta }_i$ and the continuous variation of Ω.

The relative pulsation Ω_i can also be written as

$${\mathsf{\Omega }}_i=\omega \sqrt{\frac{m}{k_i}}$$

where, k_i is the stiffness for i = c, α, f, for the three situations corresponding to angle α = 0°, α = 60°, α = 90°, respectively, compression, compression—shear and shear.

As k_c > k_α > k_f, it emerges that the relative pulsations are in order Ω_c< Ω_α< Ω_f as shown in Figure 7.

The raised curves in Figure 5, Figure 6 and Figure 7 are obtained numerically, and the marked values are obtained experimentally in the stationary dynamic regime regulated and controlled especially for this purpose. The deviations of the experimental values in relation to those obtained numerically fall within the range −3–5%.

4. Hysteretic Loops

For the viscoelastic linear dynamic system, the hysteretic loops of elliptic shape can be represented for the dynamic excitation force F(t) in relation to deformation x = x(t) in coordinates F-x, as well as for the transmitted dynamic force Q = Q(t) depending on deformation x = x(t) in coordinates Q-x.

(a)

Hysteretic loops in F-x coordinates

The equation of the elliptical hysteretic loops in the coordinate system F-x is given by the relation parameterized by k and $\zeta$ discrete variable and x continuous variable, so that $x\in \left[-A,+A\right]$, the demonstration is given in the following papers [24,25].

Thus, we have

$$F\left(x, \mathsf{\Omega }\right)=k\left[\left(1-{\mathsf{\Omega }}^2\right)x\pm 2\zeta \mathsf{\Omega }\sqrt{A^2-x^2}\right]$$

(11)

where A = A (Ω) is the amplitude of instantaneous displacement (deformation) x = x(t).

$$A=A\left(\mathsf{\Omega }\right)=\frac{m_{0}r}{m}{\mathsf{\Omega }}^2\frac{1}{\sqrt{{\left(1-{\mathsf{\Omega }}^2\right)}^2+{\left(2{\zeta }_i\mathsf{\Omega }\right)}^2}}$$

(12)

Figure 8 for Ω_a= 0.8 in the ante-resonance regime presents the family of elliptical loops for the three significant cases of the viscoelastic system ${\alpha }_c=0^{\mathrm{o}}$, $\alpha ={60}^{\mathrm{o}}$ and ${\alpha }_f={90}^{\mathrm{o}}$ that is in situation $k_c, {\zeta }_c$, $k_{\alpha }, {\zeta }_{\alpha }$ and $k_f, {\zeta }_f$. It is specified that all ellipses are inclined in quadrants I and III [23,24].

Figure 9 for Ω_p = 1.5 in the post-resonance regime presents the family of elliptical loops for the three significant cases, with the specification that all ellipses are inclined in quadrant II and IV as effect of the influence of the resonance regime [23,24,25].

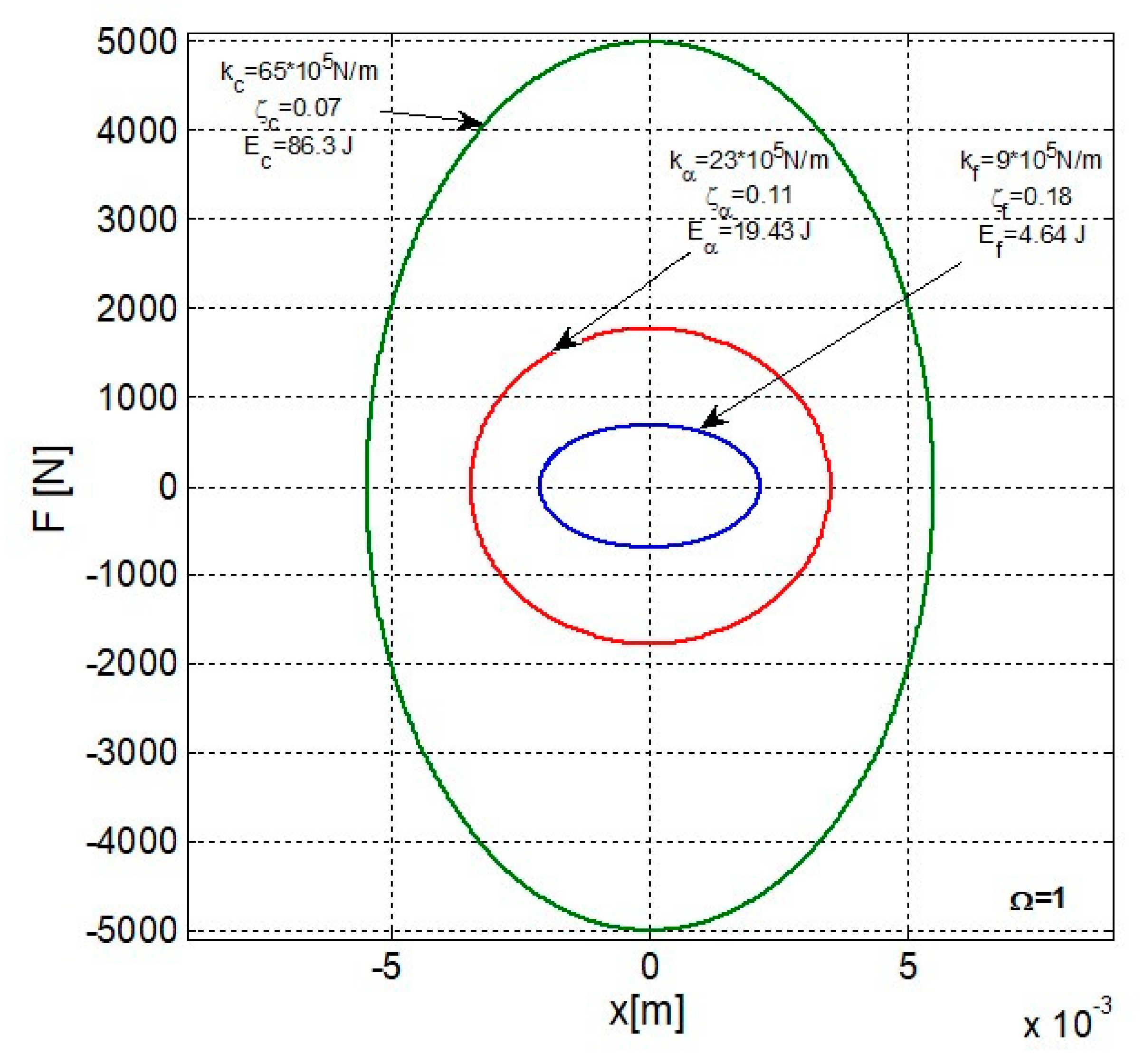
Figure 10 shows the elliptical hysteretic loops in resonance mode for the three significant cases.

It is found that the energy dissipated at resonance E_c, E_α and E_f with the values in Figure 10 coincides with the corresponding values in Figure 7.

Figure 8 and Figure 9 show the significant inertial effect in post-resonance with hysteretic loops in quadrants I and IV compared to the reduced inertial effect for pre-resonance with hysteretic loops found only in quadrants I and III.

(b)

Hysteretic loops in Q-x coordinates

The equation of the elliptical hysteretic loops in coordinates Q-x is given by the equation parameterized by k and $\zeta$ discrete variables and by the continuous variable $x\in \left[-A,+A\right]$. In this case we have

$$Q\left(x, \mathsf{\Omega }\right)=k\left[x\pm 2\zeta \mathsf{\Omega }\sqrt{A^2-x^2}\right]$$

(13)

where Ω is Ω_a < 1, Ω_p > 1 and Ω = 1 [23,24,25].

In Figure 11 at Ω_a = 0.8 in ante-resonance, for the three significant values and $k_c, {\zeta }_c$, $k_{\alpha }, {\zeta }_{\alpha }$ and $k_f, {\zeta }_f$ it is presented as the family of elliptical loops, all inclined in quadrants I and III.

Figure 12 at Ω_p = 1.5 in post-resonance, for the three sets of significant values $k_c, {\zeta }_c$, $k_{\alpha }, {\zeta }_{\alpha }$ and $k_f, {\zeta }_f$ there are presented the hysteretic loops in quadrants I and III.

Figure 13 for Ω = 1 at resonance presents the hysteretic loops for the three sets of significant data. It is found that the areas of the elliptical hysteretic loops are the same as the ones in Figure 10 in the F-x system at resonance.

5. Conclusions

Based on the analysis of the analytical relations established both for the dissipated energy as well as for the representation of the hysteretic loops specific to the linear viscoelastic system that models a dynamic stand for elastomeric anti-vibration devices, the following conclusions can be drawn:

(a)

The analytical expression of the dissipative energy offers the possibility of evaluation for two significant cases, namely:

-

The variation of the dissipated energy depending on the discrete change of the damping for the three dynamic regimes: ante-resonance, post-resonance and resonance;

-

The variation of the dissipated energy depending on the variation of Ω for discrete variable sets of values of k and $\zeta$;

(b)

The representation of the elliptical hysteretic loops in the F-x coordinate system for the three cases of the dynamic regimes, namely: ante-resonance, post-resonance and resonance. It was found that in post-resonance the inclination of the axes of the ellipses towards the ante-resonance regime changes due to the inertial effect of the mass, and in resonance, the ellipses are symmetrically centered in relation to the F-x axis system.

(c)

The elliptical hysteretic loops in the Q-x system are inclined only in quadrants I and III, regardless of the dynamic regime.

(d)

The areas of the ellipses represent the dissipated energy. The numerical results were verified by experimental lifting of hysteretic loops on the dynamic stand.

The experimental values were verified in accordance with those numerically determined by hysteretic loops with deviations of −3–5%.