A Chaotic Quadratic Oscillator with Only Squared Terms: Multistability, Impulsive Control, and Circuit Design
Abstract
1. Introduction
2. The Proposed Oscillator
3. Dynamical Properties
4. Impulsive Control
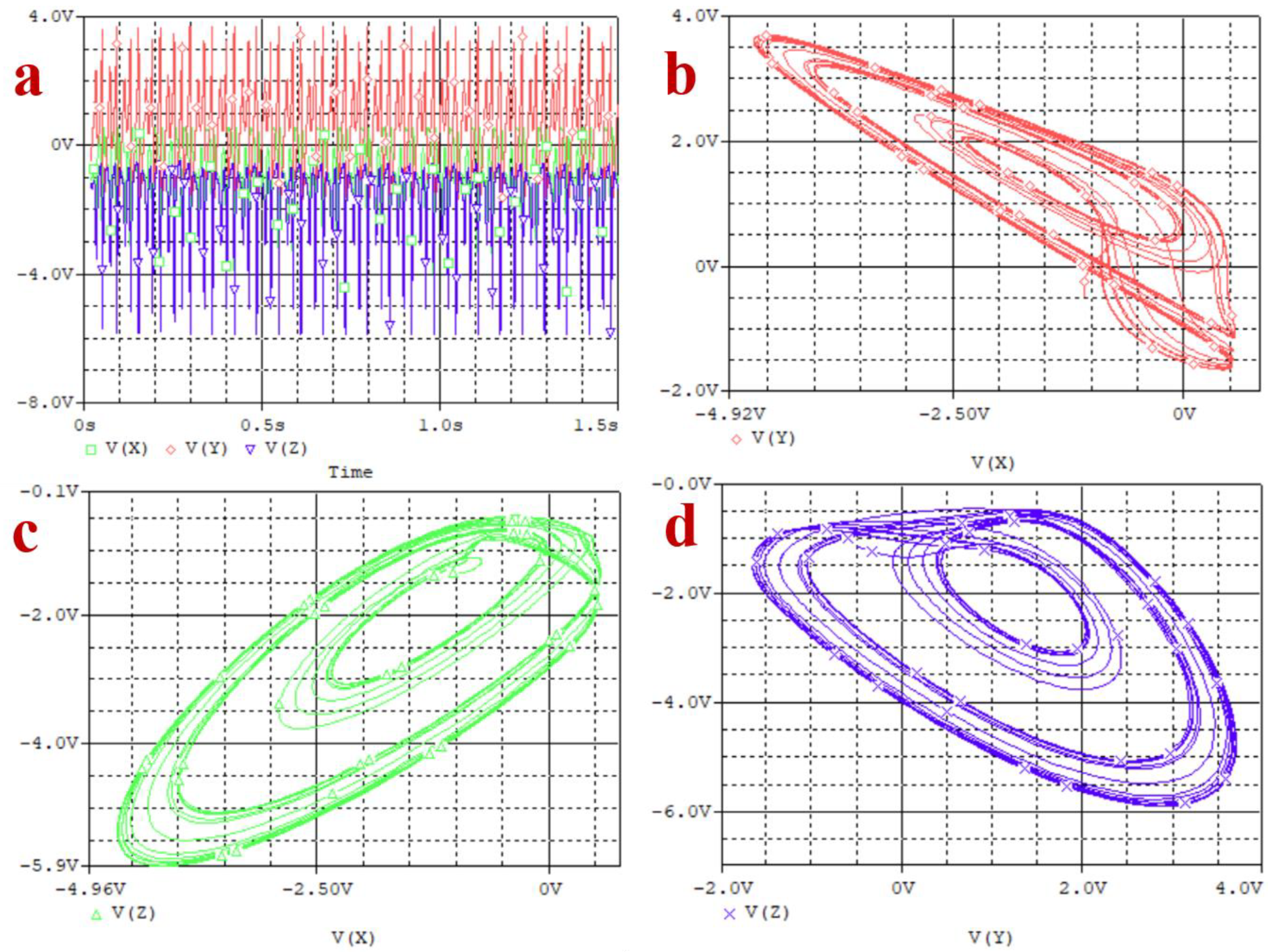
5. Circuit Design
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, C.; Yang, Y.; Du, J.; Chen, Z. A simple chaotic circuit with magnetic flux-controlled memristor. Eur. Phys. J. Spec. Top. 2021, 230, 1723–1736. [Google Scholar] [CrossRef]
- Kamal, F.; Elsonbaty, A.; Elsaid, A. A novel fractional nonautonomous chaotic circuit model and its application to image encryption. Chaos Solitons Fractals 2021, 144, 110686. [Google Scholar] [CrossRef]
- Ma, C.; Mou, J.; Xiong, L.; Banerjee, S.; Liu, T.; Han, X. Dynamical analysis of a new chaotic system: Asymmetric multistability, offset boosting control and circuit realization. Nonlinear Dyn. 2021, 103, 2867–2880. [Google Scholar] [CrossRef]
- Bonny, T. Chaotic or hyper-chaotic oscillator? Numerical solution, circuit design, MATLAB HDL-coder implementation, VHDL code, security analysis, and FPGA realization. Circuits Syst. Signal Process. 2021, 40, 1061–1088. [Google Scholar]
- Mathale, D.; Goufo, E.F.D.; Khumalo, M. Coexistence of multi-scroll chaotic attractors for a three-dimensional quadratic autonomous fractional system with non-local and non-singular kernel. Alex. Eng. J. 2021, 60, 3521–3538. [Google Scholar] [CrossRef]
- Mammeri, M. A 2-D Discrete Cubic Chaotic Mapping with Symmetry: Una cartografía caótica cúbica discreta con simetría. South Fla. J. Dev. 2021, 2, 5111–5121. [Google Scholar] [CrossRef]
- Chen, M.; Wang, Z.; Nazarimehr, F.; Jafari, S. A novel memristive chaotic system without any equilibrium point. Integration 2021, 79, 133–142. [Google Scholar] [CrossRef]
- Wei, Z. Dynamical behaviors of a chaotic system with no equilibria. Phys. Lett. A 2011, 376, 102–108. [Google Scholar] [CrossRef]
- Wang, X.; Chen, G. A chaotic system with only one stable equilibrium. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1264–1272. [Google Scholar] [CrossRef]
- Sambas, A.; Vaidyanathan, S.; Bonny, T.; Zhang, S.; Hidayat, Y.; Gundara, G.; Mamat, M. Mathematical Model and FPGA Realization of a Multi-Stable Chaotic Dynamical System with a Closed Butterfly-Like Curve of Equilibrium Points. Appl. Sci. 2021, 11, 788. [Google Scholar] [CrossRef]
- Sambas, A.; Vaidyanathan, S.; Tlelo-Cuautle, E.; Abd-El-Atty, B.; El-Latif, A.A.A.; Guillén-Fernández, O.; Hidayat, Y.; Gundara, G. A 3-D multi-stable system with a peanut-shaped equilibrium curve: Circuit design, FPGA realization, and an application to image encryption. IEEE Access 2020, 8, 137116–137132. [Google Scholar] [CrossRef]
- Rajagopal, K.; Duraisamy, P.; Tadesse, G.; Volos, C.; Nazarimehr, F.; Hussain, I. A fractional-order ship power system: Chaos and its dynamical properties. Int. J. Nonlinear Sci. Numer. Simul. 2021. [Google Scholar] [CrossRef]
- Nestor, T.; de Dieu, N.J.; Jacques, K.; Yves, E.J.; Iliyasu, A.M.; El-Latif, A.; Ahmed, A. A multidimensional hyperjerk oscillator: Dynamics analysis, analogue and embedded systems implementation, and its application as a cryptosystem. Sensors 2020, 20, 83. [Google Scholar] [CrossRef] [PubMed]
- Ali, A.M.; Ramadhan, S.M.; Tahir, F.R. A Novel 2D—Grid of Scroll Chaotic Attractor Generated by CNN. Symmetry 2019, 11, 99. [Google Scholar] [CrossRef]
- Lai, Q.; Chen, S. Generating multiple chaotic attractors from Sprott B system. Int. J. Bifurc. Chaos 2016, 26, 1650177. [Google Scholar] [CrossRef]
- Yu, F.; Shen, H.; Zhang, Z.; Huang, Y.; Cai, S.; Du, S. Dynamics analysis, hardware implementation and engineering applications of novel multi-style attractors in a neural network under electromagnetic radiation. Chaos Solitons Fractals 2021, 152, 111350. [Google Scholar] [CrossRef]
- Tsafack, N.; Sankar, S.; Abd-El-Atty, B.; Kengne, J.; Jithin, K.; Belazi, A.; Mehmood, I.; Bashir, A.K.; Song, O.-Y.; El-Latif, A.A.A. A new chaotic map with dynamic analysis and encryption application in internet of health things. IEEE Access 2020, 8, 137731–137744. [Google Scholar] [CrossRef]
- Amin, M.; Abd El-Latif, A.A. Efficient modified RC5 based on chaos adapted to image encryption. J. Electron. Imaging 2010, 19, 013012. [Google Scholar] [CrossRef]
- Abd El-Latif, A.A.; Yan, X.; Li, L.; Wang, N.; Peng, J.-L.; Niu, X. A new meaningful secret sharing scheme based on random grids, error diffusion and chaotic encryption. Opt. Laser Technol. 2013, 54, 389–400. [Google Scholar] [CrossRef]
- Li, L.; Abd-El-Atty, B.; El-Latif, A.A.A.; Ghoneim, A. Quantum color image encryption based on multiple discrete chaotic systems. In Proceedings of the 2017 Federated Conference on Computer Science and Information Systems (FedCSIS), Prague, Czech Republic, 3–6 September 2017. [Google Scholar]
- Abd el-Latif, A.A.; Abd-el-Atty, B.; Amin, M.; Iliyasu, A.M. Quantum-inspired cascaded discrete-time quantum walks with induced chaotic dynamics and cryptographic applications. Sci. Rep. 2020, 10, 1930. [Google Scholar] [CrossRef]
- Abd EL-Latif, A.A.; Abd-El-Atty, B.; Abou-Nassar, E.M.; Venegas-Andraca, S.E. Controlled alternate quantum walks based privacy preserving healthcare images in internet of things. Opt. Laser Technol. 2020, 124, 105942. [Google Scholar] [CrossRef]
- Zhang, R.; Yu, L.; Jiang, D.; Ding, W.; Song, J.; He, K.; Ding, Q. A Novel Plaintext-Related Color Image Encryption Scheme Based on Cellular Neural Network and Chen’s Chaotic System. Symmetry 2021, 13, 393. [Google Scholar] [CrossRef]
- Veeman, D.; Natiq, H.; Al-Saidi, N.M.; Rajagopal, K.; Jafari, S.; Hussain, I. A New Megastable Chaotic Oscillator with Blinking Oscillation terms. Complexity 2021, 2021, 5518633. [Google Scholar] [CrossRef]
- Ji’e, M.; Yan, D.; Wang, L.; Duan, S. Hidden Attractor and Multistability in a Novel Memristor-Based System Without Symmetry. Int. J. Bifurc. Chaos 2021, 31, 2150168. [Google Scholar] [CrossRef]
- Lai, Q. A Unified Chaotic System with Various Coexisting Attractors. Int. J. Bifurc. Chaos 2021, 31, 2150013. [Google Scholar] [CrossRef]
- Pisarchik, A.N.; Jaimes-Reátegui, R.; Rodríguez-Flores, C.; García-López, J.; Huerta-Cuéllar, G.; Martín-Pasquín, F. Secure chaotic communication based on extreme multistability. J. Frankl. Inst. 2021, 358, 2561–2575. [Google Scholar] [CrossRef]
- Chen, B.; Rajagopal, K.; Hamarash, I.I.; Karthikeyan, A.; Hussain, I. Simple megastable oscillators with different types of attractors; tori, chaotic and hyperchaotic ones. Eur. Phys. J. Spec. Top. 2020, 229, 1155–1161. [Google Scholar] [CrossRef]
- Meli, M.I.T.; Yemélé, D.; Leutcho, G.D. Dynamical analysis of series hybrid electric vehicle powertrain with torsional vibration: Antimonotonicity and coexisting attractors. Chaos Solitons Fractals 2021, 150, 111174. [Google Scholar] [CrossRef]
- Tametang Meli, M.I.; Leutcho, G.D.; Yemele, D. Multistability analysis and nonlinear vibration for generator set in series hybrid electric vehicle through electromechanical coupling. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 073126. [Google Scholar] [CrossRef]
- Chen, M.; Wang, C.; Bao, H.; Ren, X.; Bao, B.; Xu, Q. Reconstitution for interpreting hidden dynamics with stable equilibrium point. Chaos Solitons Fractals 2020, 140, 110188. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, K.; He, S. A fractional-order ship power system with extreme multistability. Nonlinear Dyn. 2021, 106, 1027–1040. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, G.; Kuznetsov, N.V.; Bao, H. Hidden attractors and multistability in a modified Chua’s circuit. Commun. Nonlinear Sci. Numer. Simul. 2021, 92, 105494. [Google Scholar] [CrossRef]
- Bao, H.; Hua, Z.; Li, H.; Chen, M.; Bao, B. Discrete Memristor Hyperchaotic Maps. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 4534–4544. [Google Scholar] [CrossRef]
- Bao, B.; Zhu, Y.; Ma, J.; Bao, H.; Wu, H.; Chen, M. Memristive neuron model with an adapting synapse and its hardware experiments. Sci. China Technol. Sci. 2021, 64, 1107–1117. [Google Scholar] [CrossRef]
- Hua, M.; Wu, H.; Xu, Q.; Chen, M.; Bao, B. Asymmetric memristive Chua’s chaotic circuits. Int. J. Electron. 2021, 108, 1106–1123. [Google Scholar] [CrossRef]
- Gu, J.; Li, C.; Lei, T.; He, S.; Min, F. A memristive chaotic system with flexible attractor growing. Eur. Phys. J. Spec. Top. 2021, 230, 1695–1708. [Google Scholar] [CrossRef]
- Peng, Y.; He, S.; Sun, K. Chaos in the discrete memristor-based system with fractional-order difference. Results Phys. 2021, 24, 104106. [Google Scholar] [CrossRef]
- Huang, L.-L.; Liu, S.; Xiang, J.-H.; Wang, L.-Y. Design and multistability analysis of five-value memristor-based chaotic system with hidden attractors. Chin. Phys. B 2021, 30, 100506. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, X.; Rao, R. Synchronization of nonidentical complex dynamical networks with unknown disturbances via observer-based sliding mode control. Neurocomputing 2021, 454, 441–447. [Google Scholar] [CrossRef]
- Zhou, Z.-X.; Grebogi, C.; Ren, H.-P. Parameter impulse control of chaos in crystal growth process. J. Cryst. Growth 2021, 563, 126079. [Google Scholar] [CrossRef]
- Mahmoud, E.E.; Higazy, M.; Althagafi, O.A. A novel strategy for complete and phase robust synchronizations of chaotic nonlinear systems. Symmetry 2020, 12, 1765. [Google Scholar] [CrossRef]
- Boccaletti, S.; Grebogi, C.; Lai, Y.-C.; Mancini, H.; Maza, D. The control of chaos: Theory and applications. Phys. Rep. 2000, 329, 103–197. [Google Scholar] [CrossRef]
- Yassen, M. Chaos control of Chen chaotic dynamical system. Chaos Solitons Fractals 2003, 15, 271–283. [Google Scholar] [CrossRef]
- Zhou, S.-S.; Jahanshahi, H.; Din, Q.; Bekiros, S.; Alcaraz, R.; Alassafi, M.O.; Alsaadi, F.E.; Chu, Y.-M. Discrete-time macroeconomic system: Bifurcation analysis and synchronization using fuzzy-based activation feedback control. Chaos Solitons Fractals 2021, 142, 110378. [Google Scholar] [CrossRef]
- Fu, S.; Liu, Y.; Ma, H.; Du, Y. Control chaos to different stable states for a piecewise linear circuit system by a simple linear control. Chaos Solitons Fractals 2020, 130, 109431. [Google Scholar] [CrossRef]
- Pham, V.-T.; Vaidyanathan, S.; Volos, C.; Jafari, S.; Alsaadi, F.E.; Alsaadi, F.E. Chaos in a simple snap system with only one nonlinearity, its adaptive control and real circuit design. Arch. Control. Sci. 2019, 29, 73–96. [Google Scholar]
- Pyragas, K. Delayed feedback control of chaos. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 2309–2334. [Google Scholar] [CrossRef]
- Wu, S.; Li, X.; Ding, Y. Saturated impulsive control for synchronization of coupled delayed neural networks. Neural Netw. 2021, 141, 261–269. [Google Scholar] [CrossRef]
- Peng, D.; Li, X.; Rakkiyappan, R.; Ding, Y. Stabilization of stochastic delayed systems: Event-triggered impulsive control. Appl. Math. Comput. 2021, 401, 126054. [Google Scholar] [CrossRef]
- Wang, M.; Wu, S.; Li, X. Event-triggered delayed impulsive control for nonlinear systems with applications. J. Frankl. Inst. 2021, 358, 4277–4291. [Google Scholar] [CrossRef]
- Li, X.; Li, P. Input-to-state stability of nonlinear systems: Event-triggered impulsive control. IEEE Trans. Autom. Control 2021, 1–7. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.; Han, X. Design of hybrid controller for synchronization control of Chen chaotic system. J. Nonlinear Sci. Appl. 2017, 10, 3320–3327. [Google Scholar] [CrossRef][Green Version]
- Li, X.; Rakkiyappan, R. Impulsive controller design for exponential synchronization of chaotic neural networks with mixed delays. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 1515–1523. [Google Scholar] [CrossRef]
- Leutcho, G.D.; Kengne, J.; Kengne, L.K.; Akgul, A.; Pham, V.-T.; Jafari, S. A novel chaotic hyperjerk circuit with bubbles of bifurcation: Mixed-mode bursting oscillations, multistability, and circuit realization. Phys. Scr. 2020, 95, 075216. [Google Scholar] [CrossRef]
- Yu, F.; Shen, H.; Liu, L.; Zhang, Z.; Huang, Y.; He, B.; Cai, S.; Song, Y.; Yin, B.; Du, S. CCII and FPGA realization: A multistable modified fourth-order autonomous Chua’s chaotic system with coexisting multiple attractors. Complexity 2020, 2020, 5212601. [Google Scholar] [CrossRef]
- Li, C.; Wei, Z.; Zhang, W. Periodic solutions and circuit design of chaos in a unified stretch-twist-fold flow. Eur. Phys. J. Spec. Top. 2021, 230, 1971–1978. [Google Scholar] [CrossRef]
- Kengne, J.; Kengne, L.K.; Chedjou, J.C.; Nosirov, K. A simple anti-parallel diodes based chaotic jerk circuit with arcsinh function: Theoretical analysis and experimental verification. Analog Integr. Circuits Signal Process. 2021, 108, 597–623. [Google Scholar] [CrossRef]
- Hu, H.; Cao, Y.; Xu, J.; Ma, C.; Yan, H. An image compression and encryption algorithm based on the fractional-order simplest chaotic circuit. IEEE Access 2021, 9, 22141–22155. [Google Scholar] [CrossRef]
- Wan, Q.; Zhou, Z.; Ji, W.; Wang, C.; Yu, F. Dynamic analysis and circuit realization of a novel no-equilibrium 5D memristive hyperchaotic system with hidden extreme multistability. Complexity 2020, 2020, 7106861. [Google Scholar] [CrossRef]
- Lai, Q.; Kuate, P.D.K.; Liu, F.; Iu, H.H.-C. An extremely simple chaotic system with infinitely many coexisting attractors. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 1129–1133. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kengne, L.K.; Kuate, P.D.K.; Chen, C. Two-memristor-based chaotic system with infinite coexisting attractors. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 2197–2201. [Google Scholar] [CrossRef]
- Yu, F.; Shen, H.; Zhang, Z.; Huang, Y.; Cai, S.; Du, S. A new multi-scroll Chua’s circuit with composite hyperbolic tangent-cubic nonlinearity: Complex dynamics, Hardware implementation and Image encryption application. Integration 2021, 81, 71–83. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kuate, P.D.K. Modelling and circuit realisation of a new no-equilibrium chaotic system with hidden attractor and coexisting attractors. Electron. Lett. 2020, 56, 1044–1046. [Google Scholar] [CrossRef]
- Li, C.; Lei, T.; Wang, X.; Chen, G. Dynamics editing based on offset boosting. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 063124. [Google Scholar] [CrossRef]
- Li, C.; Wang, X.; Chen, G. Diagnosing multistability by offset boosting. Nonlinear Dyn. 2017, 90, 1335–1341. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, Y. Impulsive control of Lorenz systems. In Proceedings of the Fifth World Congress on Intelligent Control and Automation (IEEE Cat. No. 04EX788), Hangzhou, China, 15–19 June 2004. [Google Scholar]
- Zhang, Y.; Sun, J. Controlling chaotic Lu systems using impulsive control. Phys. Lett. A 2005, 342, 256–262. [Google Scholar] [CrossRef]




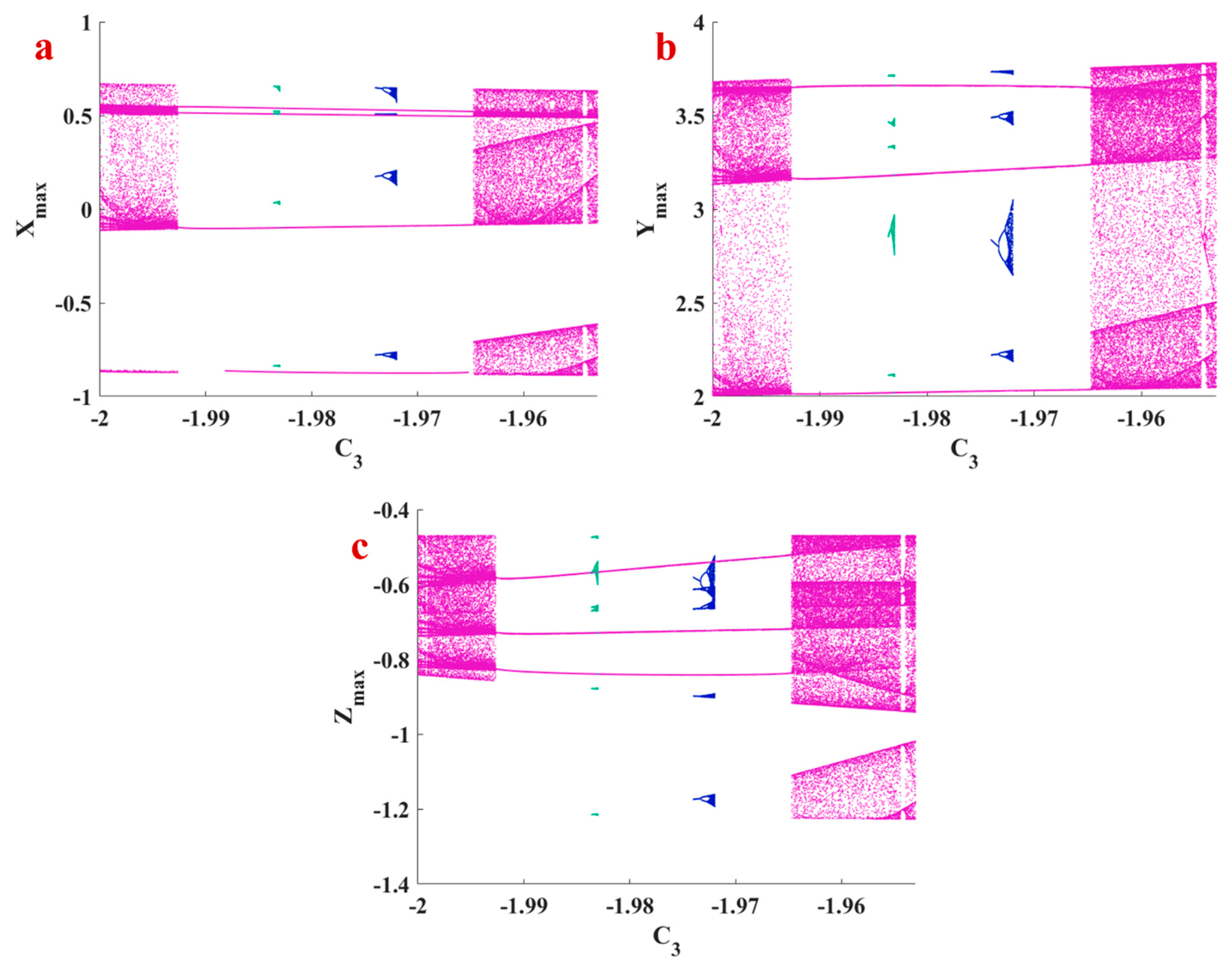

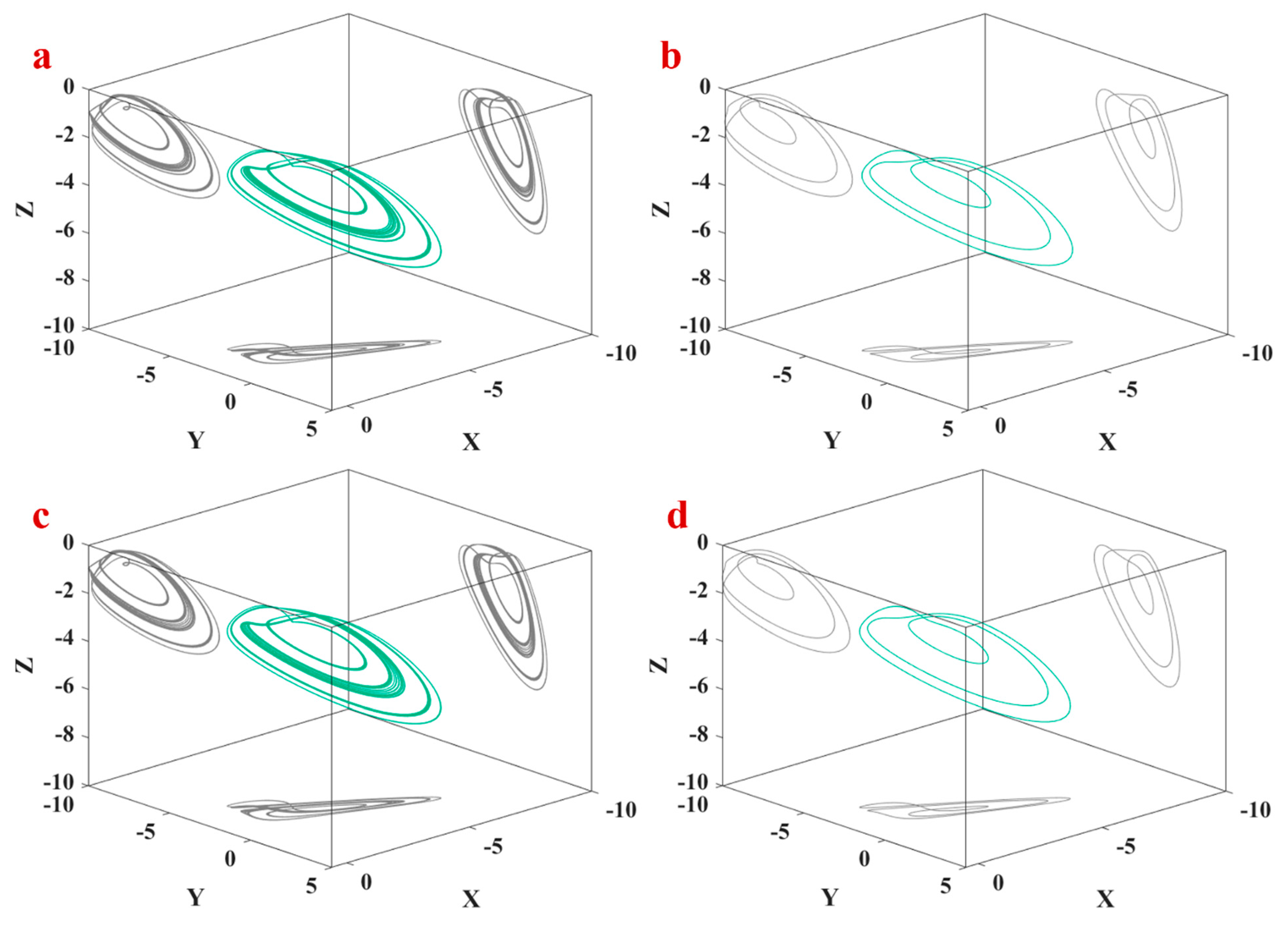
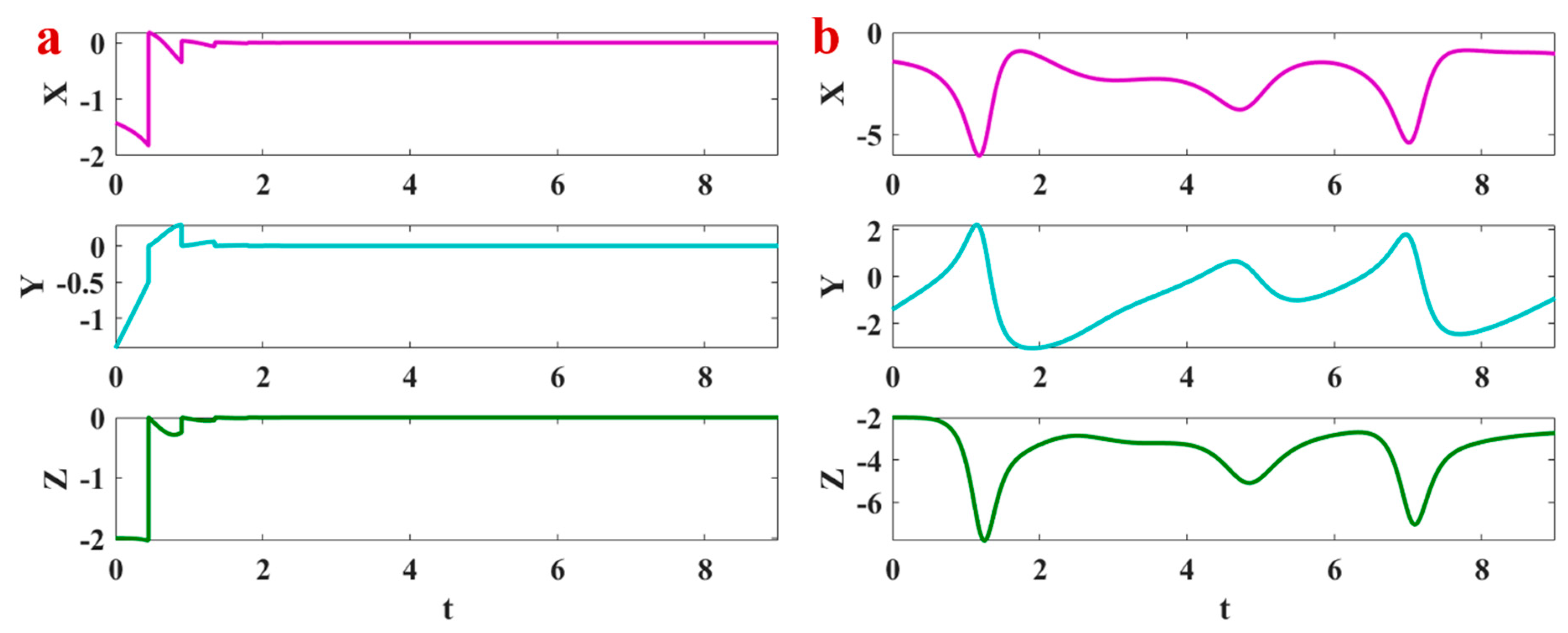
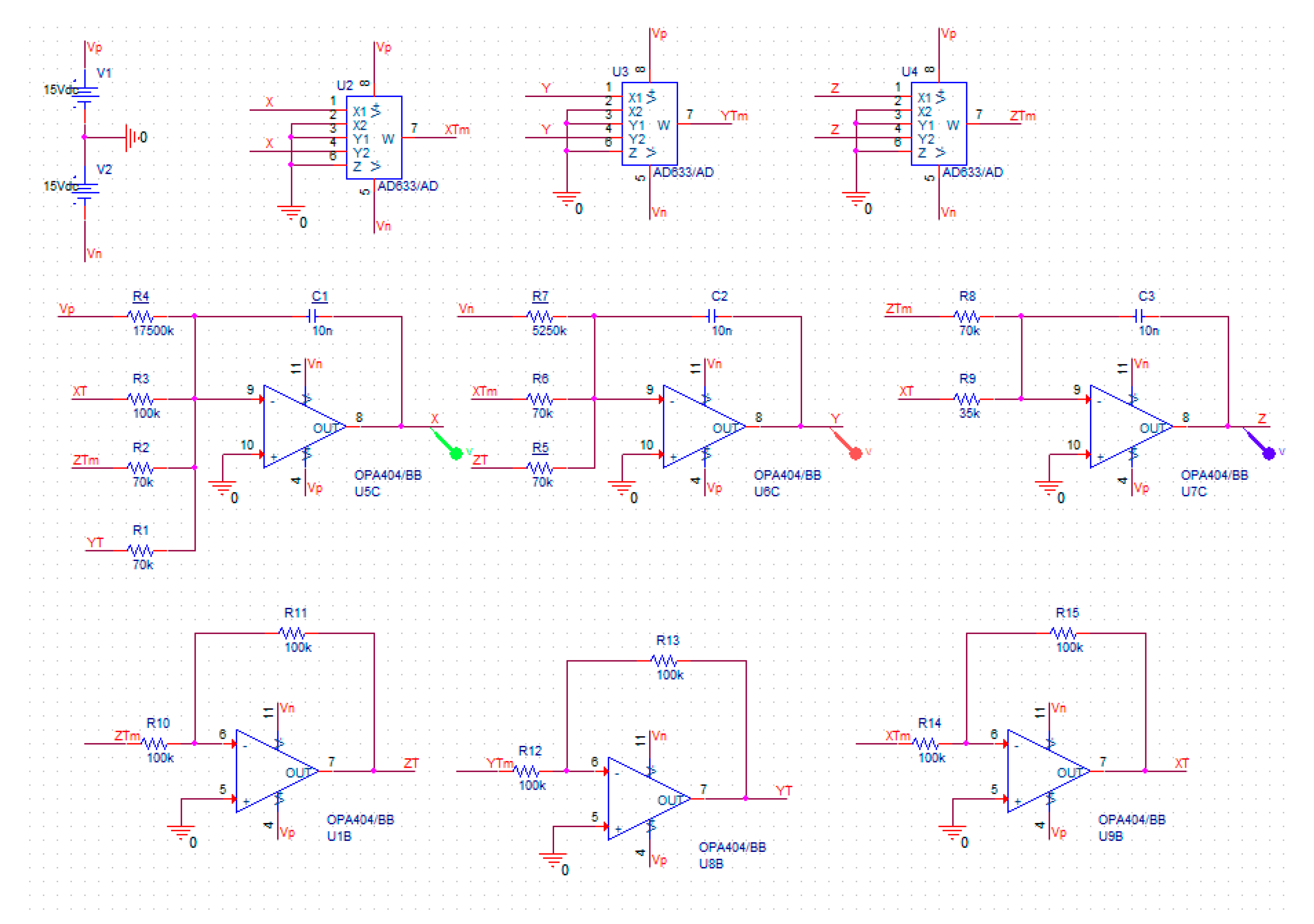
| Ref. | Dimension | Type of Terms | Number of Terms | Number of Equilibrium Points | Multistability | Circuit |
|---|---|---|---|---|---|---|
| [62] | 4 | Cubic | 9 | Infinite | ✓ | ✓ |
| [63] | 3 | Cubic & tanh(.) | 7 | 5 | ✓ | ✓ |
| [64] | 4 | Quadratic | 9 | 0 | ✓ | ✓ |
| [16] | 3 | Linear & Tanh | 10 | 3–7 | ✓ | ✓ |
| This work | 3 | Quadratic with only squared terms | 9 | 8 | ✓ | ✓ |
| # | Equilibrium | Eigenvalues |
|---|---|---|
| E1 | ||
| E2 | ||
| E3 | ||
| E4 | ||
| E5 | ||
| E6 | ||
| E7 | ||
| E8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veeman, D.; Alanezi, A.; Natiq, H.; Jafari, S.; Abd El-Latif, A.A. A Chaotic Quadratic Oscillator with Only Squared Terms: Multistability, Impulsive Control, and Circuit Design. Symmetry 2022, 14, 259. https://doi.org/10.3390/sym14020259
Veeman D, Alanezi A, Natiq H, Jafari S, Abd El-Latif AA. A Chaotic Quadratic Oscillator with Only Squared Terms: Multistability, Impulsive Control, and Circuit Design. Symmetry. 2022; 14(2):259. https://doi.org/10.3390/sym14020259
Chicago/Turabian StyleVeeman, Dhinakaran, Ahmad Alanezi, Hayder Natiq, Sajad Jafari, and Ahmed A. Abd El-Latif. 2022. "A Chaotic Quadratic Oscillator with Only Squared Terms: Multistability, Impulsive Control, and Circuit Design" Symmetry 14, no. 2: 259. https://doi.org/10.3390/sym14020259
APA StyleVeeman, D., Alanezi, A., Natiq, H., Jafari, S., & Abd El-Latif, A. A. (2022). A Chaotic Quadratic Oscillator with Only Squared Terms: Multistability, Impulsive Control, and Circuit Design. Symmetry, 14(2), 259. https://doi.org/10.3390/sym14020259







