Similarity Measures Based on T-Spherical Fuzzy Information with Applications to Pattern Recognition and Decision Making
Abstract
:1. Introduction
- To view/observe the limitations of the previous SMs because of their applicability.
- To propose a new SM with flexibility in the environment of TSFSs.
- To check the validity of the proposed SM using some results.
- To apply the proposed SM in pattern recognition and decision making.
- To compare the proposed work with previous works by a comparative analysis where the efficacy of the suggested SM is discussed.
2. Preliminaries
- iff
- iff and
3. A New Similarity Measure between T-Spherical Fuzzy Sets
4. Consequences of the Proposed Work
- If we replace in the proposed SM, then SM for SFSs is obtained and given as:
- If we replace in the proposed SM, then the SM for PFSs is obtained and given as:
- If we neglect the DA in the proposed SM, then the SM for q-ROFSs is obtained and given as:
- If we replace and neglect the DA in the proposed SM, then the SM for PyFSs is obtained and given as:
- If we replace and neglect the DA in the proposed SM, then the SM for IFSs is obtained and given as:
5. Applications and Algorithm
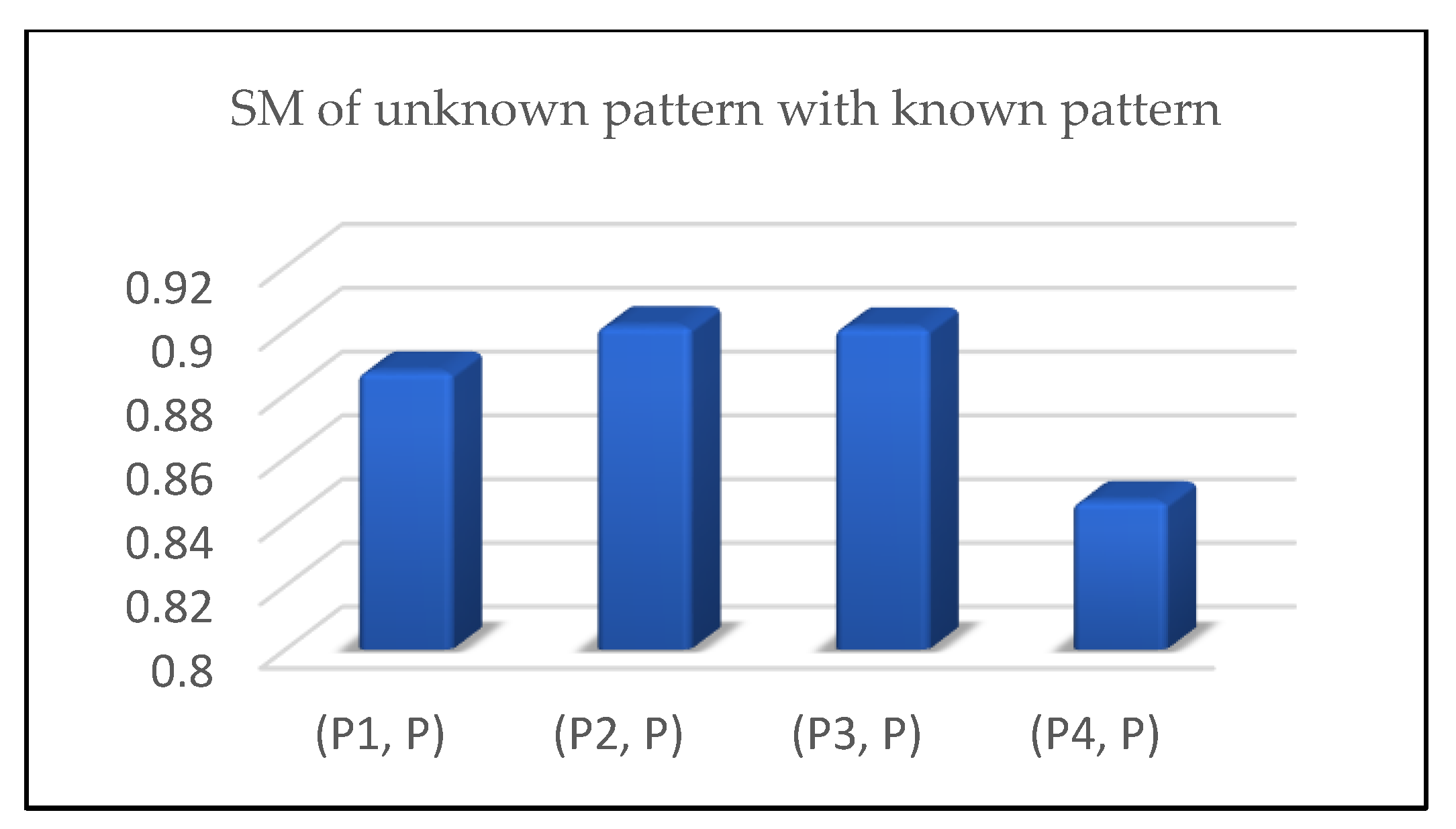
5.1. Algorithm for Pattern Recognition
5.2. Comparative Study
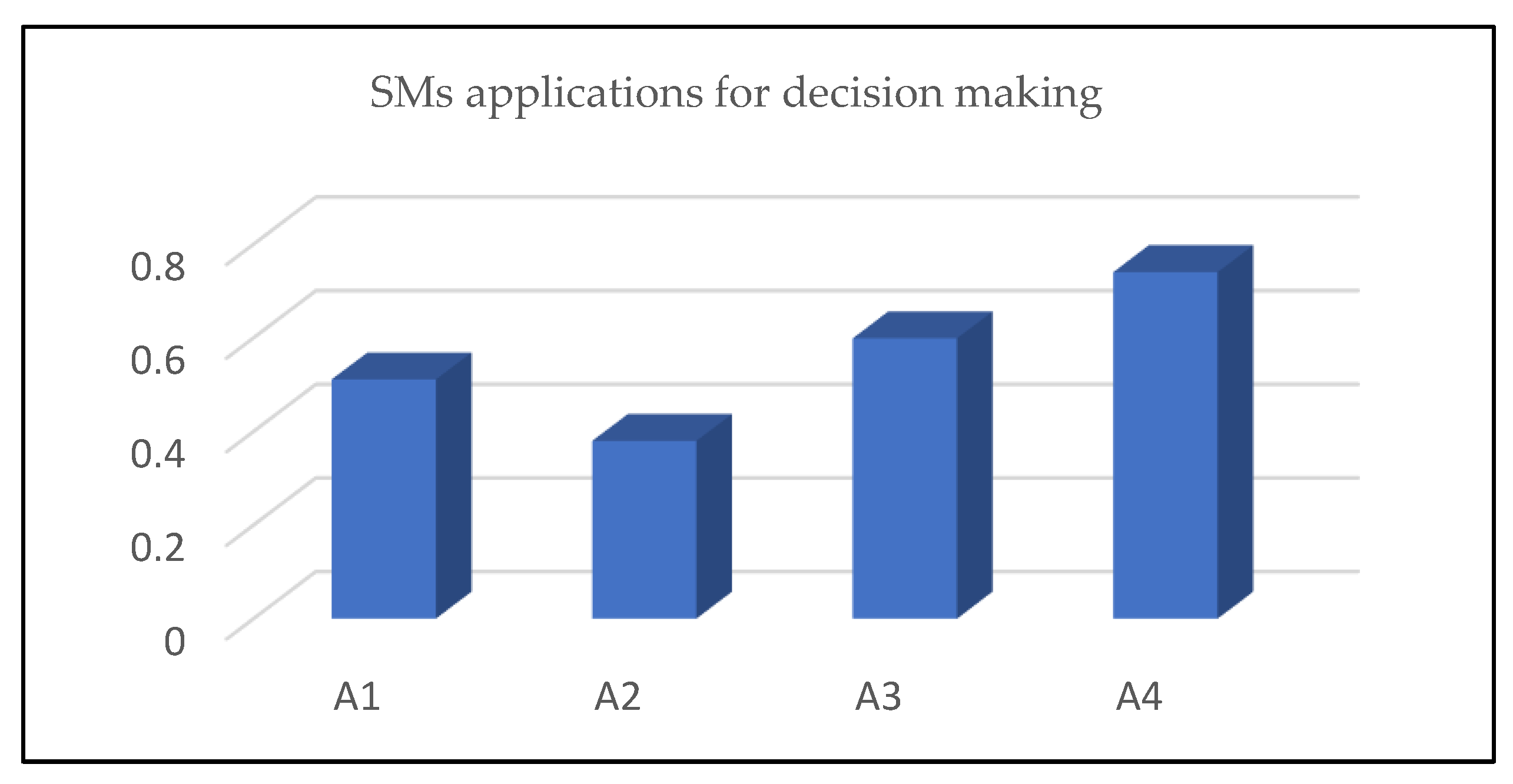
5.3. Applications for Decision Making
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Atanassov, K.T. Intuitionistic fuzzy set. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean fuzzy subsets. In Proceedings of the 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Edmonton, AB, Canada, 24–28 June 2013; pp. 57–61. [Google Scholar]
- Yager, R.R. Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 2016, 25, 1222–1230. [Google Scholar] [CrossRef]
- Cuong, B.C.; Kreinovich, V. Picture fuzzy sets-a new concept for computational intelligence problems. In Proceedings of the 2013 Third World Congress on Information and Communication Technologies (WICT 2013), Hanoi, Vietnam, 15–18 December 2013; pp. 1–6. [Google Scholar]
- Ullah, K. Picture fuzzy maclaurin symmetric mean operators and their applications in solving multiattribute decision-making problems. Math. Probl. Eng. 2021, 2021, e1098631. [Google Scholar] [CrossRef]
- Liu, P.; Munir, M.; Mahmood, T.; Ullah, K. Some similarity measures for interval-valued picture fuzzy sets and their applications in decision making. Information 2019, 10, 369. [Google Scholar] [CrossRef] [Green Version]
- Mahmood, T.; Ullah, K.; Khan, Q.; Jan, N. An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput. Appl. 2019, 31, 7041–7053. [Google Scholar] [CrossRef]
- Akram, M.; Ullah, K.; Pamucar, D. Performance evaluation of solar energy cells using the interval-valued T-spherical fuzzy Bonferroni mean operators. Energies 2022, 15, 292. [Google Scholar] [CrossRef]
- Ullah, K.; Mahmood, T.; Garg, H. Evaluation of the performance of search and rescue robots using T-spherical fuzzy Hamacher aggregation operators. Int. J. Fuzzy Syst. 2020, 22, 570–582. [Google Scholar] [CrossRef]
- Ali, Z.; Mahmood, T.; Yang, M.S. Complex T-spherical fuzzy aggregation operators with application to multi-attribute decision making. Symmetry 2020, 12, 1311. [Google Scholar] [CrossRef]
- Chen, S.-M.; Yeh, M.-S.; Hsiao, P.-Y. A comparison of similarity measures of fuzzy values. Fuzzy Sets Syst. 1995, 72, 79–89. [Google Scholar] [CrossRef]
- Yang, M.S.; Hung, W.L.; Chang-Chien, S.J. On a similarity measure between LR-type fuzzy numbers and its application to database acquisition. Int. J. Intell. Syst. 2005, 20, 1001–1016. [Google Scholar] [CrossRef]
- Dengfeng, L.; Chuntian, C. New Similarity measures of intuitionistic fuzzy sets and application to pattern recognitions. Pattern Recognit. Lett. 2002, 23, 221–225. [Google Scholar] [CrossRef]
- Liang, Z.; Shi, P. Similarity measures on intuitionistic fuzzy sets. Pattern Recognit. Lett. 2003, 24, 2687–2693. [Google Scholar] [CrossRef]
- Li, Y.; Olson, D.L.; Qin, Z. Similarity measures between intuitionistic fuzzy (vague) sets: A comparative analysis. Pattern Recognit. Lett. 2007, 28, 278–285. [Google Scholar] [CrossRef]
- Hwang, C.-M.; Yang, M.-S.; Hung, W.-L. New similarity measures of intuitionistic fuzzy sets based on the Jaccard index with its application to clustering. Int. J. Intell. Syst. 2018, 33, 1672–1688. [Google Scholar] [CrossRef]
- Wei, G.; Wei, Y. Similarity measures of pythagorean fuzzy sets based on the cosine function and their applications. Int. J. Intell. Syst. 2018, 33, 634–652. [Google Scholar] [CrossRef]
- Zeng, W.; Li, D.; Yin, Q. Distance and similarity measures of pythagorean fuzzy sets and their applications to multiple criteria group decision making. Int. J. Intell. Syst. 2018, 33, 2236–2254. [Google Scholar] [CrossRef]
- Peng, X.; Garg, H. Multiparametric similarity measures on pythagorean fuzzy sets with applications to pattern recognition. Appl. Intell. 2019, 49, 4058–4096. [Google Scholar] [CrossRef]
- Hussian, Z.; Yang, M.-S. Distance and similaritymeasures of pythagorean fuzzy sets based on the Hausdorff metric with application to fuzzy TOPSIS. Int. J. Intell. Syst. 2019, 34, 2633–2654. [Google Scholar] [CrossRef]
- Wang, P.; Wang, J.; Wei, G.; Wei, C. Similarity measures of q-rung orthopair fuzzy sets based on cosine function and their applications. Mathematics 2019, 7, 340. [Google Scholar] [CrossRef] [Green Version]
- Wei, G. Some similarity measures for picture fuzzy sets and their applications. Iran. J. Fuzzy Syst. 2018, 15, 77–89. [Google Scholar]
- Mahmood, T.; Ilyas, M.; Ali, Z.; Gumaei, A. Spherical fuzzy sets-based cosine similarity and information measures for pattern recognition and medical diagnosis. IEEE Access 2021, 9, 25835–25842. [Google Scholar] [CrossRef]
- Rafiq, M.; Ashraf, S.; Abdullah, S.; Mahmood, T.; Muhammad, S. The cosine similarity measures of spherical fuzzy sets and their applications in decision making. J. Intell. Fuzzy Syst. 2019, 36, 6059–6073. [Google Scholar] [CrossRef]
- Ullah, K.; Mahmood, T.; Jan, N. Similarity measures for T-spherical fuzzy sets with applications in pattern recognition. Symmetry 2018, 10, 193. [Google Scholar] [CrossRef] [Green Version]
- Ye, J. Similarity measures based on the generalized distance of neutrosophic z-number sets and their multi-attribute decision making method. Soft Comput. 2021, 25, 13975–13985. [Google Scholar] [CrossRef]
- Mahmood, T.; Ur Rehman, U.; Ali, Z.; Mahmood, T. Hybrid vector similarity measures based on complex hesitant fuzzy sets and their applications to pattern recognition and medical diagnosis. J. Intell. Fuzzy Syst. 2021, 40, 625–646. [Google Scholar] [CrossRef]
- Mahmood, T.; Ali, W.; Ali, Z.; Chinram, R. Power aggregation operators and similarity measures based on improved intuitionistic hesitant fuzzy sets and their applications to multiple attribute decision making. Comput. Modeling Eng. Sci. 2021, 126, 1165–1187. [Google Scholar] [CrossRef]
- Chinram, R.; Mahmood, T.; Ur Rehman, U.; Ali, Z.; Iampan, A. Some novel cosine similarity measures based on complex hesitant fuzzy sets and their applications. J. Math. 2021, 2021, 6690728. [Google Scholar] [CrossRef]
- Mahmood, T.; Ur Rehman, U.; Ali, Z.; Chinram, R. Jaccard and dice similarity measures based on novel complex dual hesitant fuzzy sets and their applications. Math. Probl. Eng. 2020, 2020, 5920432. [Google Scholar] [CrossRef]
- Luo, M.; Zhang, Y. A New similarity measure between picture fuzzy sets and its application. Eng. Appl. Artif. Intell. 2020, 96, 103956. [Google Scholar] [CrossRef]
- Wu, M.-Q.; Chen, T.-Y.; Fan, J.-P. Similarity measures of T-spherical fuzzy sets based on the cosine function and their applications in pattern recognition. IEEE Access 2020, 8, 98181–98192. [Google Scholar] [CrossRef]
- Ullah, K.; Garg, H.; Mahmood, T.; Jan, N.; Ali, Z. Correlation coefficients for T-spherical fuzzy sets and their applications in clustering and multi-attribute decision making. Soft Comput. 2020, 24, 1647–1659. [Google Scholar] [CrossRef]
| 0.81 | 0.3 | 0.37 | 0.43 | 0.43 | 0.55 | 0.57 | 0.51 | 0.39 | 0.34 | 0.56 | 0.78 | ||||
| 0.59 | 0.66 | 0.66 | 0.91 | 0.34 | 0.68 | 0.56 | 0.76 | 0.31 | 0.47 | 0.38 | 0.84 | ||||
| 0.42 | 0.56 | 0.71 | 0.81 | 0.41 | 0.35 | 0.27 | 0.59 | 0.72 | 0.55 | 0.44 | 0.65 | ||||
| 0.59 | 0.45 | 0.9 | 0.44 | 0.55 | 0.77 | 0.46 | 0.46 | 0.45 | 0.76 | 0.46 | 0.85 | ||||
| 0.16 | 0.33 | 0.42 | 0.55 | 0.44 | 0.77 | 0.57 | 0.66 | 0.91 | 0.13 | 0.35 | 0.57 | ||||
| 0.68 | 0.46 | 0.88 | 0.47 | 0.66 | 0.75 | 0.41 | 0.73 | 0.41 | 0.24 | 0.54 | 0.45 | ||||
| 0.49 | 0.54 | 0.39 | 0.58 | 0.34 | 0.23 | 0.21 | 0.43 | 0.13 | 0.82 | 0.46 | 0.69 | ||||
| SM | ||||
|---|---|---|---|---|
| Values | 0.8872037 | 0.9014245 | 0.9010272 | 0.8464994 |
| SM | Environment | Results |
|---|---|---|
| The proposed SM for TSFSs | TSFSs | |
| The SM for TSFSs by Ullah et al. [25] | TSFSs | |
| The SM for TSFSs by Wu et al. [32] | TSFSs |
| 0.1 | 0.7 | 0.4 | 0.5 | 0.8 | 0.9 | 0.8 | 0.8 | 0.8 | 0.6 | 0.7 | 0.8 | 0.3 | 0.5 | 0.7 | |
| 0.2 | 0.7 | 0.6 | 0.6 | 0.7 | 0.8 | 0.3 | 0.7 | 0.7 | 0.1 | 0.7 | 0.9 | 0.4 | 0.6 | 0.8 | |
| 0.5 | 0.6 | 0.6 | 0.5 | 0.6 | 0.7 | 0.5 | 0.7 | 0.1 | 0.9 | 0.6 | 0.2 | 0.5 | 0.6 | 0.9 | |
| 0.5 | 0.6 | 0.8 | 0.8 | 0.7 | 0.4 | 0.8 | 0.7 | 0.3 | 0.6 | 0.6 | 0.1 | 0.8 | 0.4 | 0.4 | |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | |
| SM | ||||
|---|---|---|---|---|
| Values | 0.5110507 | 0.3707117 | 0.5988922 | 0.7403513 |
| SM | Environment | Results |
|---|---|---|
| The proposed SM for TSFSs | TSFSs | |
| The SM for TSFSs by Ullah et al. [29] | TSFSs |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abid, M.N.; Yang, M.-S.; Karamti, H.; Ullah, K.; Pamucar, D. Similarity Measures Based on T-Spherical Fuzzy Information with Applications to Pattern Recognition and Decision Making. Symmetry 2022, 14, 410. https://doi.org/10.3390/sym14020410
Abid MN, Yang M-S, Karamti H, Ullah K, Pamucar D. Similarity Measures Based on T-Spherical Fuzzy Information with Applications to Pattern Recognition and Decision Making. Symmetry. 2022; 14(2):410. https://doi.org/10.3390/sym14020410
Chicago/Turabian StyleAbid, Muhammad Nabeel, Miin-Shen Yang, Hanen Karamti, Kifayat Ullah, and Dragan Pamucar. 2022. "Similarity Measures Based on T-Spherical Fuzzy Information with Applications to Pattern Recognition and Decision Making" Symmetry 14, no. 2: 410. https://doi.org/10.3390/sym14020410
APA StyleAbid, M. N., Yang, M.-S., Karamti, H., Ullah, K., & Pamucar, D. (2022). Similarity Measures Based on T-Spherical Fuzzy Information with Applications to Pattern Recognition and Decision Making. Symmetry, 14(2), 410. https://doi.org/10.3390/sym14020410









