Event-Triggered, Adaptive, Exponentially Asymptotic Tracking Control of Stochastic Nonlinear Systems
Abstract
:1. Introduction
- (1)
- An adaptive neural tracking control scheme for non-strict feedback stochastic nonlinear systems based on the event-triggered mechanism is presented. Compared with the time-triggered mechanism generally used in [26,27,28,29,30,31,36,37,38,39,40,42], this paper employs an event-triggered mechanism that reduces the frequency of control signal transmission in the system to reduce the communication burden.
- (2)
- (3)
2. Problem Statement and Some Preliminaries
3. Controller Design and Stability Analysis
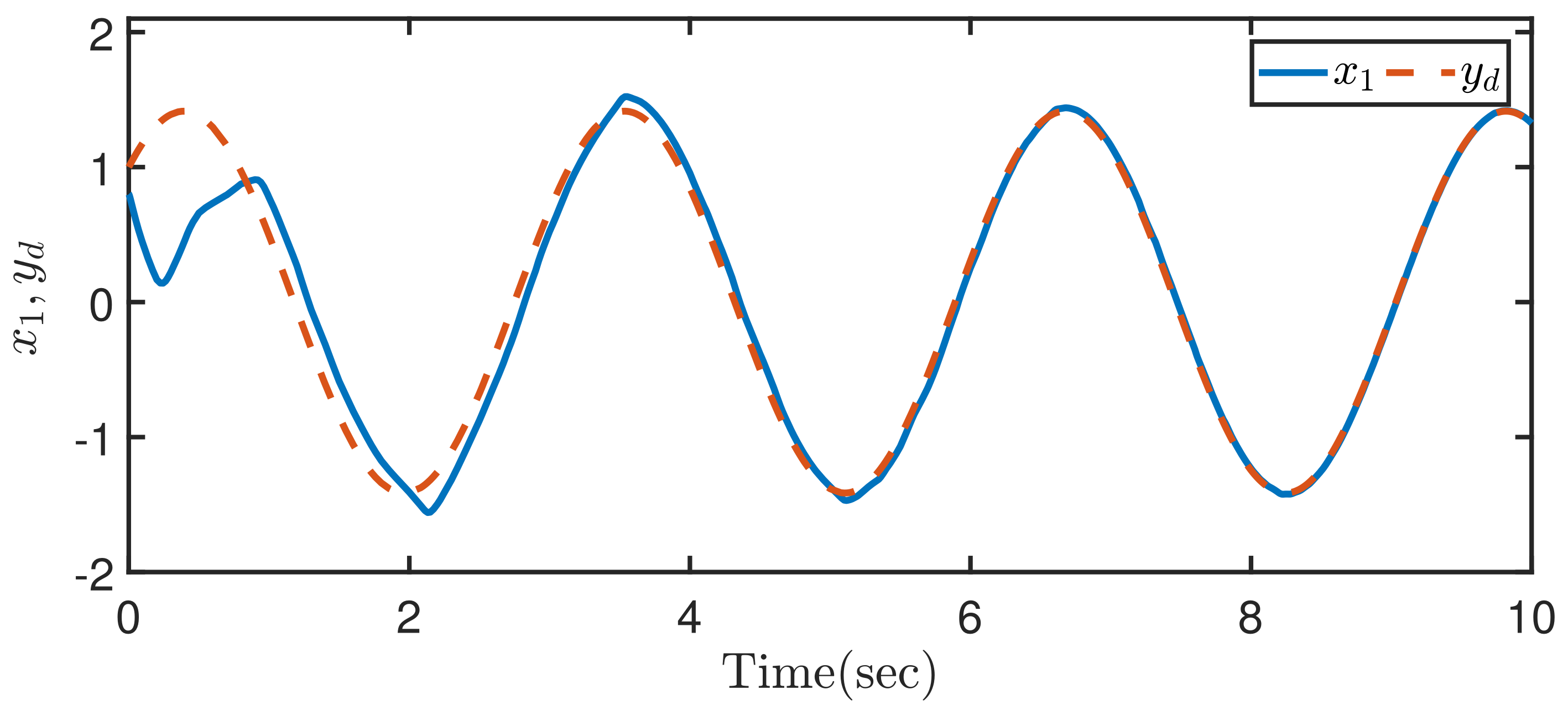
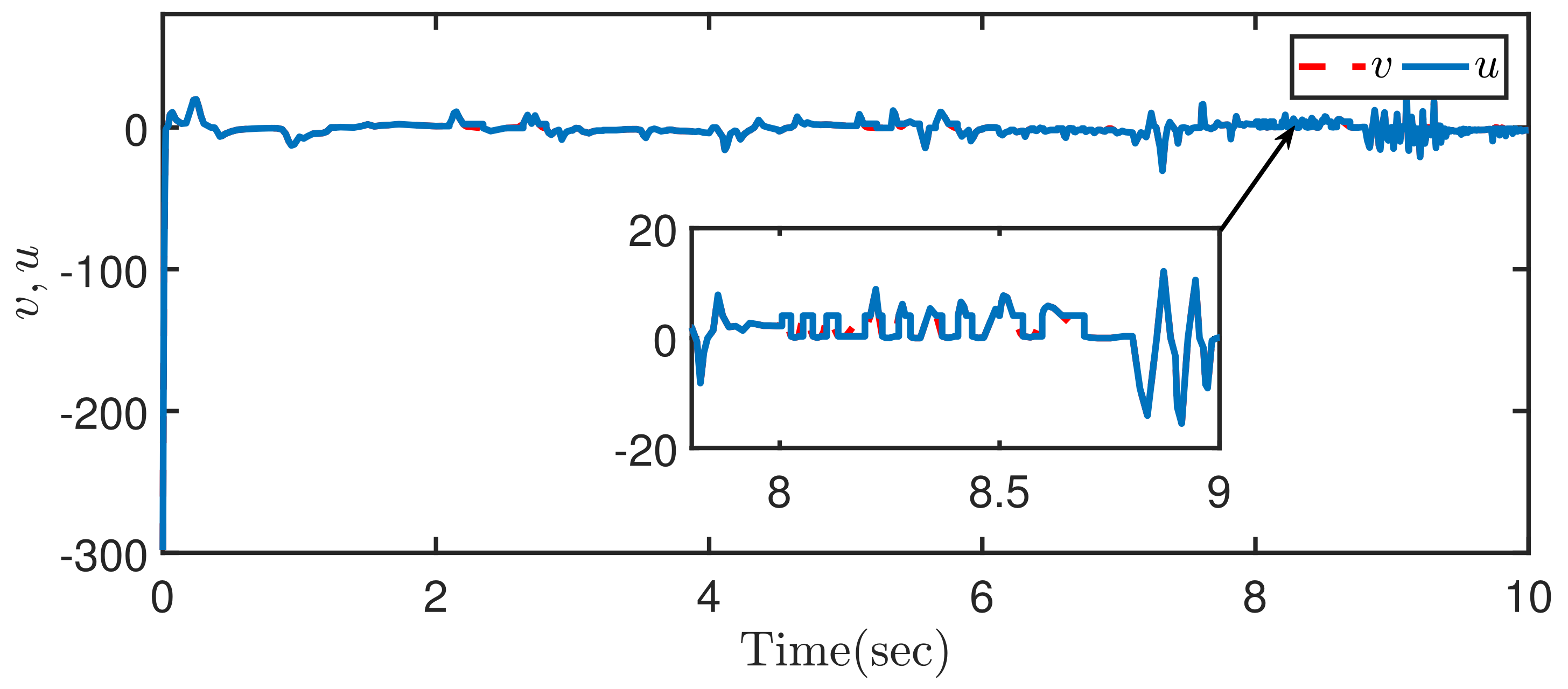
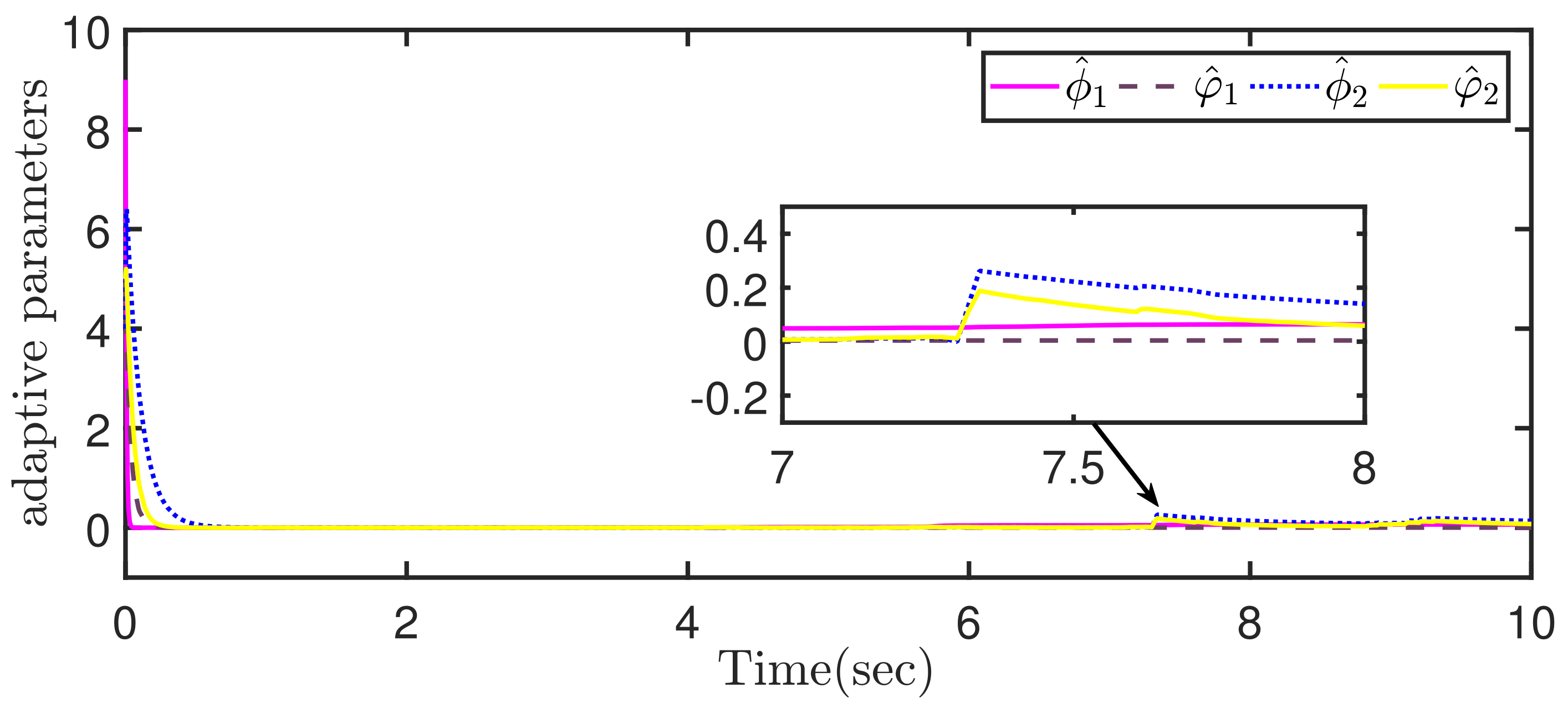
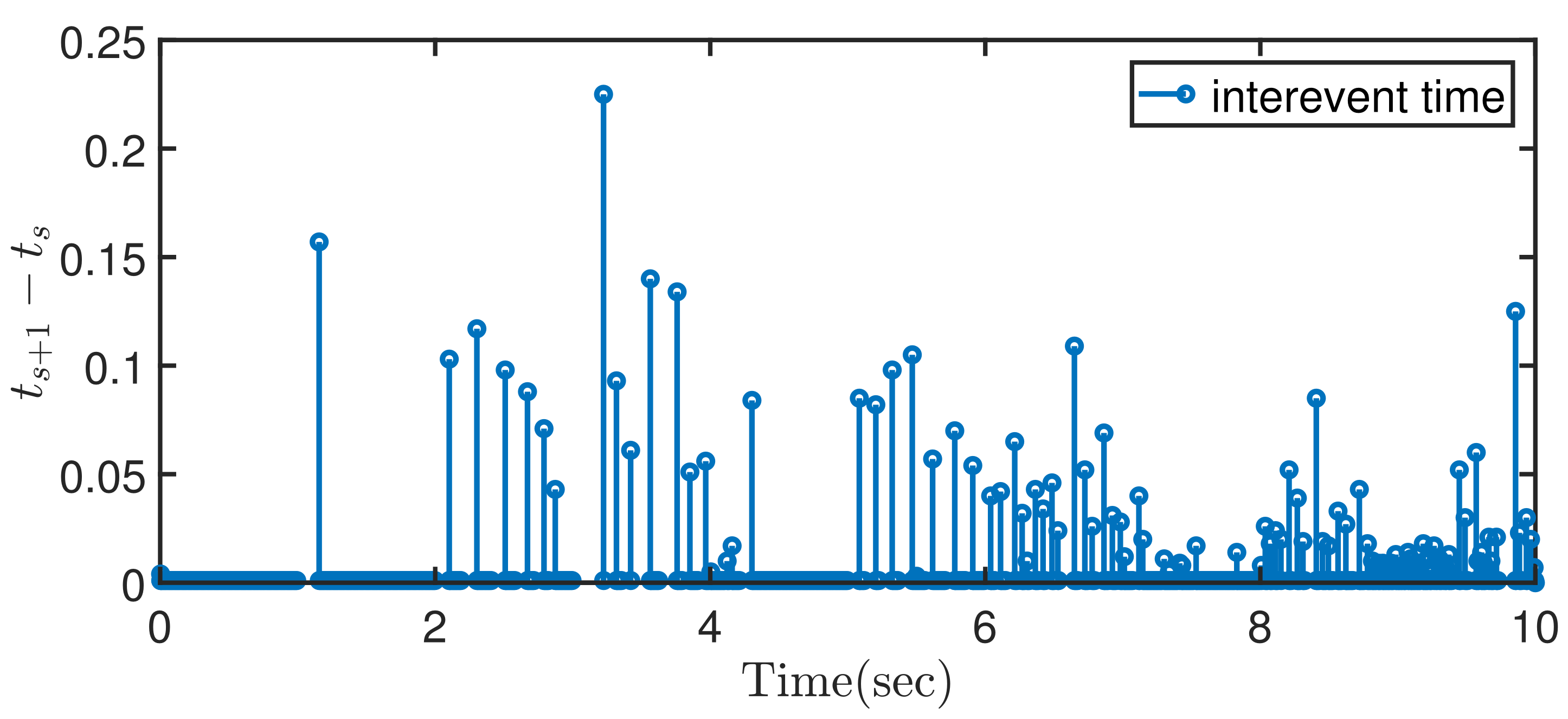
4. Simulation Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fang, L.; Ma, L.; Ding, S.; Zhao, D. Finite-time Stabilization for a Slass of High-Order Stochastic Nonlinear Systems with an Output Constraint. Appl. Math. Comput. 2019, 358, 63–79. [Google Scholar] [CrossRef]
- Liu, Y.; Lu, S.; Tong, S.; Chen, X.; Chen, C.; Li, D. Adaptive Control-Based Barrier Lyapunov Functions for a Class of Stochastic Nonlinear Systems with Full State Constraints. Automatica 2018, 87, 83–93. [Google Scholar] [CrossRef]
- Min, H.; Xu, S.; Zhang, B.; Ma, Q. Output-Feedback Control for Stochastic Nonlinear Systems Subject to Input Saturation and Time-Varying Delay. IEEE Trans. Autom. Control 2019, 64, 359–364. [Google Scholar] [CrossRef]
- Sui, S.; Chen, C.; Tong, S. Fuzzy Adaptive Finite-Time Control Design for Nontriangular Stochastic Nonlinear Systems. IEEE Trans. Fuzzy Syst. 2019, 27, 172–184. [Google Scholar] [CrossRef]
- Wang, F.; Chen, B.; Sun, Y.; Lin, C. Finite Time Control of Switched Stochastic Nonlinear Systems. Fuzzy Sets Syst. 2019, 365, 140–152. [Google Scholar] [CrossRef]
- Niu, B.; Wang, D.; Alotaibi, N.; Alsaadi, F. Adaptive Neural State-Feedback Tracking Control of Stochastic Nonlinear Switched Systems: An Average Dwell-Time Method. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 1076–1087. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Chen, B.; Sun, Y.; Gao, Y.; Lin, C. Finite-Time Fuzzy Control of Stochastic Nonlinear Systems. IEEE Trans. Cybern. 2020, 50, 2617–2626. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, F.; Zhang, Y.; Chen, C. Fuzzy Adaptive Quantized Control for a Class of Stochastic Nonlinear Uncertain Systems. IEEE Trans. Cybern. 2016, 46, 524–534. [Google Scholar] [CrossRef]
- Yu, Z.; Yan, H.; Li, S.; Dong, Y. Approximation-Based Adaptive Tracking Control for Switched Stochastic Strict-Feedback Nonlinear Time-Delay Systems With Sector-Bounded Quantization Input. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 2145–2157. [Google Scholar] [CrossRef]
- Niu, B.; Li, H.; Zhang, Z.; Li, J.; Hayat, T.; Alsaadi, F. Adaptive Neural-Network-Based Dynamic Surface Control for Stochastic Interconnected Nonlinear Nonstrict-Feedback Systems With Dead Zone. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1386–1398. [Google Scholar] [CrossRef]
- Ma, H.; Zhou, Q.; Bai, L.; Liang, H. Observer-Based Adaptive Fuzzy Fault-Tolerant Control for Stochastic Nonstrict-Feedback Nonlinear Systems With Input Quantization. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 287–298. [Google Scholar] [CrossRef]
- Sun, Y.; Mao, B.; Zhou, S.; Liu, H. Finite-Time Adaptive Control for Non-Strict Feedback Stochastic Nonlinear Systems. IEEE Access 2019, 7, 179758–179764. [Google Scholar] [CrossRef]
- Li, H.; Bai, L.; Wang, L.; Zhou, Q.; Wang, H. Adaptive Neural Control of Uncertain Nonstrict-Feedback Stochastic Nonlinear Systems with Output Constraint and Unknown Dead Zone. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2048–2059. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, W.; Zhang, H. Dynamic Event-Based Control of Nonlinear Stochastic Systems. IEEE Trans. Autom. Control 2017, 62, 6544–6551. [Google Scholar] [CrossRef]
- Ning, Z.; Yu, J.; Pan, Y.; Li, H. Adaptive Event-Triggered Fault Detection for Fuzzy Stochastic Systems with Missing Measurements. IEEE Trans. Fuzzy Syst. 2018, 26, 2201–2212. [Google Scholar] [CrossRef]
- Zhu, Q. Stabilization of Stochastic Nonlinear Delay Systems With Exogenous Disturbances and the Event-Triggered Feedback Control. IEEE Trans. Autom. Control 2019, 64, 3764–3771. [Google Scholar] [CrossRef]
- Hu, Z.; Shi, P.; Zhang, J.; Deng, F. Control of Discrete-Time Stochastic Systems With Packet Loss by Event-Triggered Approach. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 755–764. [Google Scholar] [CrossRef]
- Luo, S.; Deng, F. On Event-Triggered Control of Nonlinear Stochastic Systems. IEEE Trans. Autom. Control 2020, 65, 369–375. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Z.; Zhang, Y.; Chen, C. Neural Adaptive Event-Triggered Control for Nonlinear Uncertain Stochastic Systems With Unknown Hysteresis. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3300–3312. [Google Scholar] [CrossRef]
- Zou, W.; Ahn, C.; Xiang, Z. Event-Triggered Consensus Tracking Control of Stochastic Nonlinear Multiagent Systems. IEEE Syst. J. 2019, 13, 4051–4059. [Google Scholar] [CrossRef]
- Zou, W.; Shi, P.; Xiang, Z.; Shi, Y. Consensus Tracking Control of Switched Stochastic Nonlinear Multiagent Systems via Event-Triggered Strategy. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 1036–1045. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Li, H.; Liang, H.; Dong, G. Adaptive Fuzzy Event-Triggered Control for Stochastic Nonlinear Systems with Full State Constraints and Actuator Faults. IEEE Trans. Fuzzy Syst. 2019, 27, 2242–2254. [Google Scholar] [CrossRef]
- Li, B.; Xia, J.; Zhang, H.; Shen, H.; Wang, Z. Event-Triggered Adaptive Fuzzy Tracking Control for Stochastic Nonlinear Systems. J. Frankl. Inst. 2020, 357, 9505–9522. [Google Scholar] [CrossRef]
- Fu, Y.; Li, J.; Wu, S.; Li, X. Dynamic Event-Triggered Adaptive Tracking Control for a Class of Unknown Stochastic Nonlinear Strict-Feedback Systems. Symmetry 2021, 13, 1648. [Google Scholar] [CrossRef]
- Wang, T.; Ma, M.; Qiu, J.; Gao, H. Event-Triggered Adaptive Fuzzy Tracking Control for Pure-Feedback Stochastic Nonlinear Systems With Multiple Constraints. IEEE Trans. Fuzzy Syst. 2021, 29, 1496–1506. [Google Scholar] [CrossRef]
- Hu, J.; Wang, Z.; Gao, H. Joint State and Fault Estimation for Time-Varying Nonlinear Systems with Randomly Occurring Faults and Sensor Saturations. Automatica 2018, 97, 150–160. [Google Scholar] [CrossRef]
- Han, J.; Zhang, H.; Wang, Y.; Zhang, K. Fault Estimation and Fault-Tolerant Control for Switched Fuzzy Stochastic Systems. IEEE Trans. Fuzzy Syst. 2018, 26, 2993–3003. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, Y.; Ren, M.; Zhang, J.; Yan, G. Generalized Correntropy Filter-Based Fault Diagnosis and Tolerant Control for Non–Gaussian Stochastic Systems Subject to Sensor Faults. IEEE Access 2018, 6, 12598–12607. [Google Scholar] [CrossRef]
- Du, Z.; Pan, Y.; Liang, H.; Li, H. Cooperative Control for a Class of Second-Order Stochastic Multi-Agent Systems with Sensor Faults. In Proceedings of the 2020 35th Youth Academic Annual Conference of Chinese Association of Automation (YAC), Zhanjiang, China, 16–18 October 2020. [Google Scholar] [CrossRef]
- Aslam, M.S.; Qaisar, I.; Majid, A.; Ramaraj, P. Design of Sliding Mode Controller for Sensor/Actuator Fault with Unknown Input Observer for Satellite Control System. Soft Comput. 2021, 25, 14993–15003. [Google Scholar] [CrossRef]
- Aslam, M.S. L2–L∞ Control for Delayed Singular Markov Switch System with Nonlinear Actuator Faults. Int. J. Fuzzy Syst. 2021, 23, 2297–2308. [Google Scholar] [CrossRef]
- Aslam, M.S.; L, Q.; Hou, J. Fault Detection for Asynchronous T–S Fuzzy Networked Markov Jump Systems with New Event-Triggered Scheme. IET Control. Theory Appl. 2021, 15, 1461–1473. [Google Scholar] [CrossRef]
- Ma, L.; Wang, Z.; Lam, H. Event-Triggered Mean-Square Consensus Control for Time-Varying Stochastic Multi-Agent System With Sensor Saturations. IEEE Trans. Autom. Control 2017, 62, 3524–3531. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Wang, J.; Chen, C.; Zhang, Y. Event Trigger Fuzzy Adaptive Compensation Control of Uncertain Stochastic Nonlinear Systems With Actuator Failures. IEEE Trans. Fuzzy Syst. 2018, 26, 3770–3781. [Google Scholar] [CrossRef]
- Li, F.; Liu, Y. Event-Triggered Stabilization for Continuous-Time Stochastic Systems. IEEE Trans. Autom. Control 2020, 65, 4031–4046. [Google Scholar] [CrossRef]
- Jin, X.; Li, Y. Adaptive Fuzzy Control of Uncertain Stochastic Nonlinear Systems with All State Constraints. Inf. Sci. 2021, 574, 625–639. [Google Scholar] [CrossRef]
- Liu, L.; Yin, S.; Zhang, L.; Yin, X.; Yan, H. Improved Results on Asymptotic Stabilization for Stochastic Nonlinear Time-Delay Systems with Application to a Chemical Reactor System. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 195–204. [Google Scholar] [CrossRef]
- Chen, C.; Liu, Z.; Xie, K.; Zhang, Y.; Chen, C. Asymptotic Fuzzy Neural Network Control for Pure-Feedback Stochastic Systems Based on a Semi-Nussbaum Function Technique. IEEE Trans. Cybern. 2017, 47, 2448–2459. [Google Scholar] [CrossRef]
- Gnaneswaran, N.; Chinnasamy, K.; Ramasamy, S.; Zhu, Q. Robust Exponential Stability Analysis for Stochastic Systems with Actuator Faults Using Improved Weighted Relaxed Integral Inequality. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3346–3357. [Google Scholar] [CrossRef]
- Liu, L.; Deng, F. Mean-Square Exponential Stability for Stochastic Control Systems with Discrete-Time State Feedbacks and Their Numerical Schemes in Simulation. IEEE Trans. Autom. Control 2020, 651, 5384–5391. [Google Scholar] [CrossRef]
- Xie, W.; Zhu, Q. Self-Triggered State-Feedback Control for Stochastic Nonlinear Systems With Markovian Switching. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 3200–3209. [Google Scholar] [CrossRef]
- Liang, Y.; Li, Y.; Che, W. Exponentially Asymptotic Adaptive Tracking Control of Nonstrict Feedback Nonlinear Systems. Int. J. Syst. Sci. 2022, 53, 337–350. [Google Scholar] [CrossRef]
- Wang, C.; Lin, Y. Decentralized Adaptive Tracking Control for a Class of Interconnected Nonlinear Time-Varying Systems. Automatica 2015, 54, 16–24. [Google Scholar] [CrossRef]

| Control Method | Trigger Num | IAE | ITAE |
|---|---|---|---|
| TTC method | 10,000 | 1.9659 | 3.5466 |
| ETC method | 6087 | 1.9468 | 3.4717 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, F.; Cao, D.; Wu, J.; Li, J. Event-Triggered, Adaptive, Exponentially Asymptotic Tracking Control of Stochastic Nonlinear Systems. Symmetry 2022, 14, 451. https://doi.org/10.3390/sym14030451
He F, Cao D, Wu J, Li J. Event-Triggered, Adaptive, Exponentially Asymptotic Tracking Control of Stochastic Nonlinear Systems. Symmetry. 2022; 14(3):451. https://doi.org/10.3390/sym14030451
Chicago/Turabian StyleHe, Furong, Dewen Cao, Jian Wu, and Jing Li. 2022. "Event-Triggered, Adaptive, Exponentially Asymptotic Tracking Control of Stochastic Nonlinear Systems" Symmetry 14, no. 3: 451. https://doi.org/10.3390/sym14030451






