Analytical and Data-Driven Wave Approximations of an Extended Schrödinger Equation

Abstract

Using both analytical and numerical techniques, we discuss wave solutions within the framework of an extended nonlinear Schrödinger equation with constant coefficients equipped with spatiotemporal dispersion, self-steepening effects, and a Raman scattering term. We present the exact traveling wave solution of the system in terms of Jacobi elliptic functions and mention some symmetry results as they relate to the resulting ordinary differential equation. A constructed bright soliton solution serves as the base to compare a numerical solution of the system using spectral Fourier methods with a precise statistical low-rank approximation using a data-driven approach aided by the Koopman operator theory. We found that the spatiotemporal feature added to the model serves as a regularizing tool that enables a precise reconstruction of the original solution.

1. Introduction

The propagation of waves in different media has been the research subject of many scientists in different branches of the natural sciences, engineering, and beyond. Several systems have been proposed to describe the behavior of such waves, and many of them have been based on the pivotal, and 1933 Nobel Prize winning, work of Erwin Schrödinger during 1925–1926 [1]. His landmark study of wave matters later proved to be fundamental for different areas of physics and engineering, and, as a result, various extensions of the original Schrödinger equation have been proposed to study different phenomena (see, for example, [2,3,4,5,6,7]). Analytic results involving extensions of the Schrödinger equation are abundant, with many of them exploring soliton-related solutions. For example, Gomorov and Malomed studied in [4] soliton dynamics considering a nonlinear Schrödinger-type equation (NLSE) from a system describing the interaction between high and low frequency waves. In [5], the same authors explored dynamics of solitons in a different extension of the NLSE to study surface waves. Similarly, Bandelow and Ahkmediev obtained rogue waves solutions [3] of an integrable extension of the NLSE. More recently, Ali et al. considered in [2] another extension of the NLSE exploring solitons and resulting chaotic behaviors. Motivated by recent advances in Koopman theory for partial differential equations and by recent results on wave propagation within hyperbolic metamaterials, we consider a dimensionless model, which is similar to Equation (2) in reference [2], given by the following extended nonlinear Schrödinger equation (eNLSE):

$$i{\psi }_t-a{\psi }_{xx}-ib{\psi }_{xxx}+c{\psi }_{xt}+d{\left|\psi \right|}^2\psi +ie{\left({\left|\psi \right|}^2\psi \right)}_x-if\psi {\left({\left|\psi \right|}^2\right)}_x=0$$

(1)

with $i=\sqrt{-1}.$ The first term in the system (1) describes the time evolution of the complex wave function $\psi (x,t)$, the parameters a and b describe the second- and third-order dispersion, c captures the spatiotemporal dispersion features, d deals with the cubic nonlinearity (also known as the Kerr law), the parameter e introduces the self-steepening effect, and the last term f describes the Raman scattering effect. It is worth mentioning that symmetries for Schrödinger-type equations have been studied by different researchers  [8,9,10,11,12,13,14] highlighting their importance for constructing explicit traveling wave and soliton solutions. Some of the approaches taken on this work are adopted from results available in the literature regarding symmetries of PDEs.

The system (1) is a natural extension of the model derived in [15] by adding spatiotemporal features of a pulse evolving within hyperbolic metamaterials. Thus, we explore wave solutions of the system (1) motivated by recent results in hyperbolic metamaterials. Both numerical and analytical solutions of the systems are presented and compared with the aid of matrix factorization techniques and the theory of data reduction from statistics.

The use of statistical theory to explore the dynamics of nonlinear behavior in deterministic systems, including Schrödinger’s wave equation, has been an essential tool in looking at the same problem but from a completely different point of view. Results during the last few decades have allowed researchers from many institutions to understand and interpret, to a great extent, the mechanisms of nonlinear features embedded within nonlinear systems. Such systems are usually highly dimensional, and few of them can be described analytically. Thus, in many cases, researchers must rely on accessible big data sets, and such a dependency creates many challenges to advancement in the sciences.

Fortunately, different solution methods have been developed to approximate, with high precision, the dynamics governing such complex systems. Transforming a highly multidimensional nonlinear system to a quasilinear reduced one containing the key features of the original one is an example of such an approach and one of our goals for the numerical results section. Different techniques have been proposed to reduce the dimension of model data. Most utilized among these techniques are singular value decomposition (SVD), principal component analysis (PCA), proper orthogonal decomposition (POD), dynamic mode decomposition (DMD), and their corresponding extensions. The idea to decompose and reduce a system into its most relevant structure may have its roots in a pair of papers [16] by B.O. Koopman and [17] by Koopman and J.V. Neumann; in these papers, the authors depicted the possibility of the relation between dynamical properties of a physical system (focusing on classical mechanical systems) with the structure of the corresponding spectrum. During the subsequent decades, many contributions led to the Koopman operator theory, which is basically an operator theoretic approach to analyze dynamical systems. Connected to the underlying nonlinear dynamics through Koopman operator theory is the DMD approach [18,19,20,21,22,23,24].

Although the above reduction methodologies have been focused purely on data, some work has been done also to study the dynamics of nonlinear systems described by equations aiming to handle them in the near future without analytic calculations [24,25,26,27,28,29,30]. The nonlinear Schrödinger equation [25,28,31,32] has been a source for these types of studies for many reasons, one of them been the feasibility of applying it in different areas of research, for example, in quantum computing.

In this work, we construct both a traveling wave solution and a bright soliton solution and compare the latter with its low-rank statistical approximation generated through the Koopman operator approach, which relies on SVD and DMD and generally can be thought of as a data-driven technique to obtain a linear reduced order model for high-dimensional complex systems. The rest of the manuscript is distributed as follows. In Section 2, we construct an analytic expression first for the traveling wave solution and then for a bright soliton solution. In Section 3, we present and compare the numerical approximations resulting from spectral Fourier methods and the Koopman operator based on the soliton solution. Then, we conclude our work with key final remarks.

2. Analytical Results

For the analytical considerations, we first present a traveling wave solution and then a bright soliton solution. The latter will be the starting point for our numerical results.

2.1. Traveling Waves

In this section, we aim to construct the exact traveling wave solution for the eNLSE (1). Assume the system under consideration supports traveling wave solutions of the form

$$\psi (x,t)=\varphi \left(\xi \right)e^{i(-\kappa x+\omega t+\theta )},\xi =x-\nu t$$

(2)

where $\nu$ is the propagation speed of a wave, $\kappa$ is the wave number, and $\omega$ is the wave frequency. The parameter $\theta$ is just a phase constant. The substitution of (2) into (1) leads to

$$(a+c\nu +3b\kappa ){\varphi }^{″}-[(a+b\kappa ){\kappa }^2-(1-c\kappa )\omega ]\varphi -(d+e\kappa ){\varphi }^3=0$$

(3)

for the real part, and

$$b{\varphi }^{\prime \prime \prime }+[(1-c\kappa )\nu -2a\kappa -3b{\kappa }^2-c\omega ]{\varphi }^{\prime }+(2f-3e){\varphi }^2{\varphi }^{\prime }=0$$

(4)

for the imaginary portion. Integrating the last Equation (4) yields

$${\varphi }^{″}+\frac{1}{b}[(1-c\kappa )\nu -2a\kappa -3b{\kappa }^2-c\omega ]\varphi +\frac{1}{3b}(2f-3e){\varphi }^3=0$$

(5)

after dividing by b and neglecting the constant of integration. Notice the indisputable resemblance of (5) with the unforced Duffing oscillator. Its symmetries and isotypic components in the space corresponding to the actions of its symmetric group were discussed in [33]. Indeed, one can check also that the system (5) is $Z_2-$ equivariant (see also [33] for more details).

Since $\varphi$ must satisfy both (3) and (5), by equating the corresponding coefficients, one gets the main parameters that describe the waveform, e.g., the wave speed, which is given by

$$\nu =\frac{b\Gamma -e(a+2b)}{ce},$$

(6)

the wave number as

$$\kappa =\frac{3e-\Gamma }{3e},$$

(7)

and the frequency takes the form

$$\omega =\frac{3ae[c\Gamma (\Gamma -3e)-9e^2]-b(\Gamma -2e)[c\Gamma (\Gamma -6e)-27e^2]}{9c{e}^2(c\Gamma +3e)}$$

(8)

where ${\displaystyle \Gamma =3d+2f.}$ Equation (5) is a Painleve type-II equation, and, as stated earlier, its likeness with the unforced–undamped Duffing oscillator nonlinear system is evident; thus, a solution in terms of elliptic functions shall fall out. Following the work of Beléndez et al. in [34], the corresponding solution in terms of Jacobi elliptic functions is given by

$$\varphi \left(\xi \right)=\alpha \mathrm{cn}\left(\sqrt{\beta +\gamma {\alpha }^2}\xi ,\frac{\gamma {\alpha }^2}{2(\beta +\gamma {\alpha }^2)}\right)$$

(9)

where

$$\beta =\frac{1}{b}[(1-c\kappa )\nu -2a\kappa -3b{\kappa }^2-c\omega ]$$

(10)

and

$$\gamma =\frac{1}{3b}(2f-3e)>0$$

(11)

in view of the key parameters (6)–(8) and along with onset conditions $\varphi \left(0\right)=\alpha >0$ and ${\varphi }^{\prime }\left(0\right)=0.$ The exact periodic traveling wave solution for the system describing wave propagation in hyperbolic nonlinear materials is given by

$$\psi (x,t)=\alpha \mathrm{cn}\left(\sqrt{\beta +\gamma {\alpha }^2}(x-\nu t),\frac{\gamma {\alpha }^2}{2(\beta +\gamma {\alpha }^2)}\right)e^{i(-\kappa x+\omega t+\theta )}$$

(12)

where the speed, wave number, and frequency are given by (6), (7), and (8), respectively.

A conventional approach can be applied to the eNLSE system in order to establish traveling waves in terms of hyperbolic functions as well. To construct a traveling wave solution to the system (1) in terms of hyperbolic functions, we first retrieve its corresponding speed from the imaginary part (4), which is given by

$$\nu =\frac{c\omega +2a\kappa }{1-c\kappa }$$

(13)

whenever the constraints

$$b=0\mathrm{and}2f=3e$$

(14)

are satisfied. Notice that (13) differs from the speed of the elliptic solution (6) where the parameter b was preserved. Now, in view of such constraints, Equation (3) reduces into

$$(a+c\nu ){\varphi }^{″}-[a{\kappa }^2-(1-c\kappa )\omega ]\varphi -(d+e\kappa ){\varphi }^3=0.$$

(15)

By multiplying (15) by ${\varphi }^{\prime }$ and integrating once with zero initial conditions, we have

$$2(a+c\nu ){\left[{\varphi }^{\prime }\right]}^2-2[a{\kappa }^2-(1-c\kappa )\omega ]{\varphi }^2-(d+e\kappa ){\varphi }^4=0$$

(16)

which can be rewritten as

$$\sqrt{2(a+c\nu )}{\varphi }^{\prime }=\sqrt{{\varphi }^2+\frac{(d+e\kappa )}{2[a{\kappa }^2-(1-c\kappa )\omega ]}{\varphi }^4}.$$

(17)

Using integration by parts and a suitable substitution leads to

$$\int \frac{du}{\sqrt{u^2+u^4}}=\sqrt{\frac{a{\kappa }^2-(1-c\kappa )\omega }{a+c\nu }}(x-\nu t)$$

(18)

whose solution can be written in terms of hyperbolic secant if

$$(d+e\kappa )\times [a{\kappa }^2-(1-c\kappa )\omega ]<0$$

(19)

or in terms of hyperbolic sine if the direction of the last inequality is reversed.

2.2. Bright Soliton

Since we are interested in a soliton solution where $\psi (x,t)\to 0$ as $t\to \pm \infty$, we assume that the eNLSE (1) supports a solution of the form

$$\psi (x,t)=P(x,t)e^{i(-\kappa x+\omega t+\theta )}$$

(20)

where $P(x,t)$ represents the general amplitude, and, in the phase factor, $\omega ,\kappa$, and $\theta$ describe the frequency of the soliton, the wave number, and a phase constant, respectively. Thus, inserting the solution form (20) into the system (1) and decomposing into real and imaginary parts lead to the speed as in the case for the hyperbolic traveling wave (13),

$$v=\frac{c\omega +2a\kappa }{1-c\kappa }$$

(21)

from the imaginary part provided (14) and the identity

$$(b\kappa \omega -\omega -a{\kappa }^2)P+(d+e\kappa )P^3+c{P}_{xt}-a{P}_{xx}=0$$

(22)

from the real portion. For the case of bright soliton, the still unknown $P=P(x,t)$ can be written as

$$P=A{sech}^j\left[\tau \right],\tau =B(x-vt)$$

(23)

where A and B represent the amplitude constant and inverse width correspondingly. The real parameter j will be determined by exploring the balance between nonlinearity and dispersion. One can check that (23) reduces the identity (22) to

$$\begin{array}{ccc}& & [(c\kappa +a{\kappa }^2+b{\kappa }^3-\omega )-p^2(a+cv)B^2]A{sech}^j\left[\tau \right]+(d+e\kappa )A^3{sech}^{3j}\left[\tau \right]\phantom{3333333}\hfill \\ & & +j(1+j)(a+cv)A{B}^2{sech}^{j+2}\left[\tau \right]=0\hfill \end{array}$$

(24)

where the interplay between nonlinearity and dispersion leads to $j=1$. The resulting value of j reduces (24) to the following two identities:

$$A=B\sqrt{\frac{2[\kappa c^2(c+b{\kappa }^2)+a(1+c\kappa +c^2{\kappa }^2)]}{(d+e\kappa )(1-c\kappa -3c^2{B}^2)}},$$

(25)

and

$$\omega =\frac{\kappa (1-c\kappa )(c+b{\kappa }^2)+a[{\kappa }^2-c{\kappa }^3+3(1+c\kappa )B^2]}{1-c\kappa -3c^2{B}^2}$$

(26)

where the speed was retrieved in (21) as long as

$$c\kappa \ne 1$$

(27)

and

$$[\kappa c^2(c+b{\kappa }^2)+a(1+c\kappa +c^2{\kappa }^2)]\times (d+e\kappa )(1-c\kappa -3c^2{B}^2)>0$$

(28)

are satisfied. Consequently, the bright soliton solution of the system (1) has the form

$$\psi (x,t)=Asech\left[B(x-vt)\right]e^{i(-\kappa x+\omega t+\theta )}.$$

(29)

where the amplitude (25) and the frequency (26) were described in terms of the soliton width, and the speed was described in (21). This solution will exist as long as the conditions given in (14), (27), and (28) are satisfied. The profile of the bright soliton (29) will be essential for the numerical solutions of the system, which we present in the next section.

3. Numerical Approximations

In this section, we discuss the numerical solution of the eNLSE (1) using two different approaches. First, we construct a numerical solution (the data) using standard spectral Fourier methods. Then, we apply the dynamic mode decomposition algorithm and Koopman operator approaches to build a statistical low-rank approximation of the wave dynamics embedded in the system with the least possible data.

3.1. Spectral Fourier Methods

While many numerical methods to solve partial differential equations exist, most prominent during the last decades are finite difference methods, finite element methods, gradient discretization methods, and spectral methods. The first three methods are based on local representation of functions while the last makes use of global representation and, thus, usually yields higher order accuracy. The spectral approximation methods to solve PDEs are both efficient and highly accurate and, in our case, based on the Fourier transform to accommodate the highly periodic behavior of the wave dynamics embedded within the examined system. We denote the Fourier transform (FT) of $\psi (x,t)$ by:

$$\mathcal{F}\left[\psi (x,t)\right]=\underset{-\infty }{\overset{\infty }{\int }}{e}^{-ikx}\psi (x,t)dx=\widehat{\psi }(k,t).$$

For simplicity, we use $\widehat{\psi }$ instead of $\widehat{\psi }(k,t).$ One can notice that the transform leads to a result in terms of the wave number k from the original state space x, and such a result is a vector of Fourier coefficients. A straightforward calculation of the FT of the eNLSE (1) yields

$$\widehat{{\psi }_t}=i\frac{(a-bk)k^2}{1+ck}\widehat{\psi }+i\frac{d}{1+ck}\widehat{{\psi \left|\psi \right|}^2}-\frac{e}{1+ck}\widehat{{\left({\psi \left|\psi \right|}^2\right)}_k}+\frac{f}{1+ck}\widehat{\psi {\left({\left|\psi \right|}^2\right)}_k}$$

(30)

for each k. Thus, the FT provides a representation of the time series dynamics in the Fourier space, allowing us to solve the transformation with known iterative schemes or available built-in functions in the computing environment of preference.

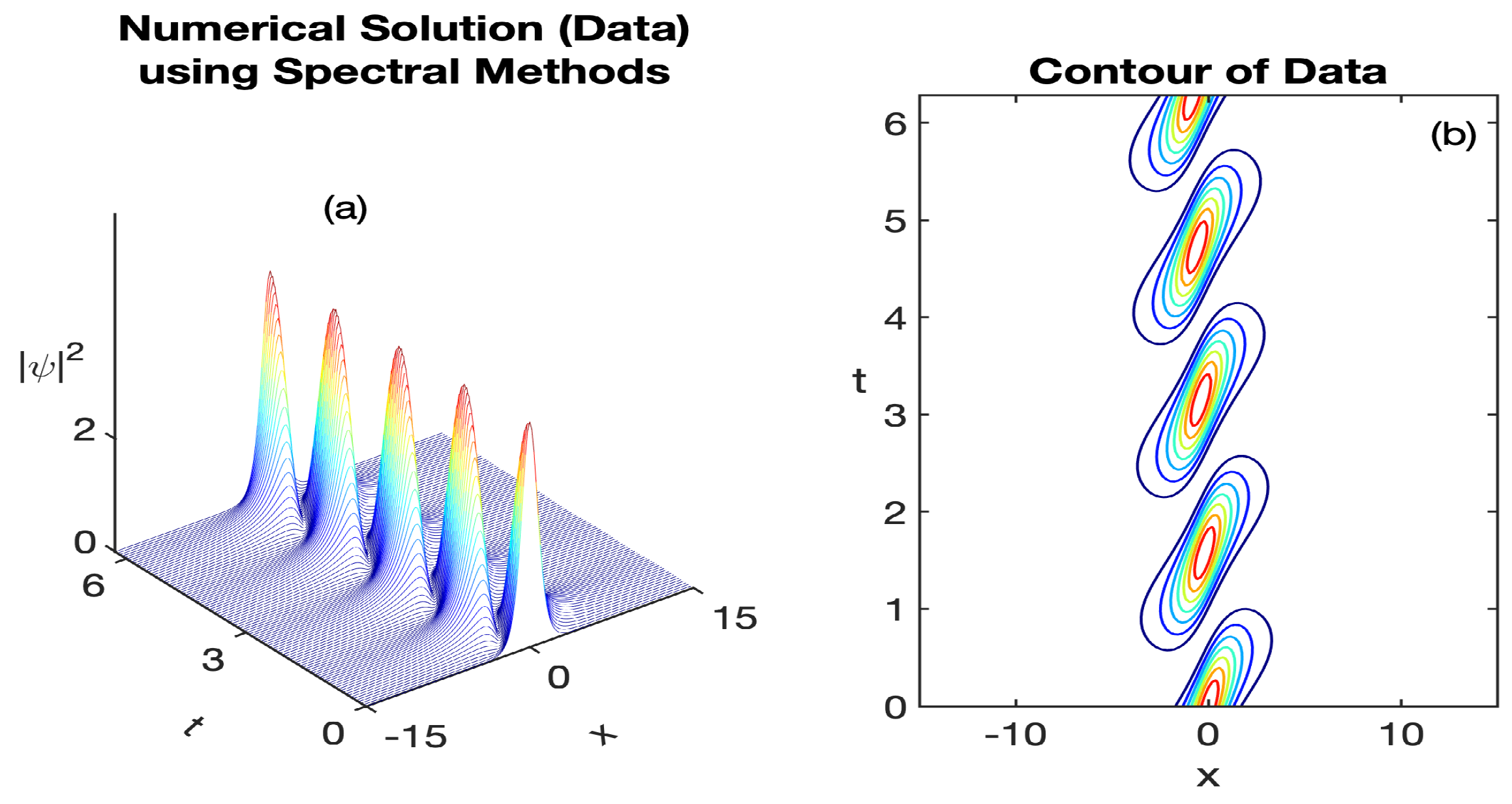
A finite but sufficiently representative space domain, e.g., $x\in [-50,50],$ is selected so that, at the boundaries, the function is well approximated by zero. This resembles the fact that $\psi (x,t)\to 0$ as $t\to \pm \infty .$ The time domain is $t\in [0,2\pi ]$ while the frequency domain will be properly constructed. The initial condition to be considered is $\psi (x,0)=2sech\left(x\right)$ in view of the bright soliton amplitude (23). In Figure 1, the time evolution of the solution profile using spectral methods is provided for $x\in [-15,15]$ to depict a better view, $\left(a\right)$ in terms of its intensity, and $\left(b\right)$ in terms of its corresponding contour. As expected, the wave approximation reveals the periodic behavior typical of many Schrödinger-type equations. We will consider this solution as our original data and will compare with its statistical low-rank counterpart approximation on the next subsections.

3.2. Dynamic Mode Decomposition

Arising from the fluid dynamics community, the Dynamic Mode Decomposition (DMD) is a purely data-driven technique aimed to extract spatio-temporal, coherent structures, or patterns that dominate the observed measurement data, from the system under consideration. The key ingredient of the DMD recipe is the Singular Value Decomposition (SVD), a numerically stable matrix factorization technique used to obtain an optimal low-rank approximation of highly dimensional systems and to calculate pseudo-inverses of non-square arrays that allows for determining the least squares and minimum solutions of a linear matrix system of the form $\mathbf{A}x=b$. Thus, for every complex-valued matrix $\mathbf{X}\in {\mathbf{C}}^{n\times m}$, its exact SVD approximation is ${\displaystyle \mathbf{X}=UD{V}^{★}}$ where both $U\in {\mathbf{C}}^{n\times n}$ and $V\in {\mathbf{C}}^{m\times m}$ are unitary matrices, while $D$ is a matrix containing the singular values of $X{X}^{†}$ such that those values are ordered from the largest to the smallest [35,36]. Here, $V^{★}$ represents the conjugate transpose of matrix V, and $X^{†}$ denotes the More–Penrose pseudoinverse of matrix $X.$ The aim of this process is to retrieve the eigen-decomposition of matrix $A=X{X}^{\prime }$, which contains the dominant coherent patterns of the system under study, without having to compute A. In several situations, the smallest singular value is zero (e.g., when X is not full row-rank); thus, the rank of the matrix $D$ may serve as a point of reference to truncate the SVD while still preserving the key features of the dominant patterns. For a truncation value $r\le rank\left(D\right),$ the truncated SVD to approximate X is now ${\displaystyle X\approx U_r{D}_r{V}_r^{★}}$ where the value of r is selected according to the situation at hand. The amount of toleration in the selection of r is usually tied to the specifics of the given nonlinear system. Therefore, the role of the SVD in the DMD scheme will be to facilitate a lower rank approximation of the original system while keeping its dominant patterns.

Having established the idea behind the SVD method, we proceed to discuss the DMD scheme following the reasoning of Kutz et al. [35], which first requires a data set of the form:

$$X=\left[\begin{array}{cccc}|& |& & |\\ x_1& x_2& \cdots & x_m\\ |& |& & |\end{array}\right]$$

(31)

where usually it is expected the number of rows to be considerably larger than the number of columns. In this work, we arrange the columns into the desired matrix X as presented above in (31). Once we have constructed our data matrix, the DMD algorithm can be implemented as follows:

• Create two matrices from data set given in (31):

  $$X_{1,\dots ,m-1}=\left[\begin{array}{cccc}|& |& & |\\ x_1& x_2& \cdots & x_{m-1}\\ |& |& & |\end{array}\right]\mathrm{and}{X}_{2,\dots ,m}^{{}^{\prime }}=\left[\begin{array}{cccc}|& |& & |\\ x_2& x_3& \cdots & x_m\\ |& |& & |\end{array}\right]$$
• Compute the full rank SVD of $X_{1,\dots ,m-1}:[U,D,V^{\prime }]=\mathrm{svd}(X_{1,\dots ,m-1},0)$
• Based on the selected rank $-r$, construct the reduced matrices $U_r$, $D_r$, and $V_r^{{}^{\prime }}$
• Construct the dynamic operator $\tilde{A}:\tilde{A}=U_r^{*}{X}^{{}^{\prime }}{V}_r^{{}^{\prime }}{D}_r^{-1}$
• Compute eigenvalues and eigenvectors of $\tilde{A}:[W,L]=\mathrm{eig}\left(\tilde{A}\right)$
• Construct the modes (eigenvectors) of the original matrix ${\displaystyle A:\Phi =X^{\prime }V{D}^{-1}W}$
• Construct time series approximation of the original dynamical system:
  ${\displaystyle x\left(t\right)=\sum _{j=1}^n{b}_j{\Phi }_j{e}^{{\lambda }_{j}t}}$ where ${\lambda }_j$ are the eigenvalues of L and $b_j$ are the initial conditions.

The DMD scheme will be an essential tool to construct the Koopman approximation of the wave dynamics embedded in the eNLSE (1) in the following subsection.

3.3. Koopman Approximation

Another approach for analyzing nonlinear systems is based on the Koopman operator $\mathcal{K},$ which relies on the DMD algorithm for its corresponding computations. This approach has recently been adopted by several research groups by including Kernel observables [37,38,39,40,41,42,43,44,45]. The initial success of the DMD in fluid mechanics has led to a large number of similar algorithms being proposed for the computation of the Koopman spectral properties, which seek to approximate $\mathcal{K}$ with a best fit linear model [27,29]. Arbabi and Mezić proved that applying DMD to data arranged in a Hankel-type matrix produces the true Koopman eigenfunctions and eigenvalues [27]. Kutz showed that an observable based on the nonlinearity present in the NLSE gives an approximation whose error is orders of magnitude smaller than the standard DMD. Indeed, for certain systems, the right choice of observable function can linearize the nonlinear manifold on which the system evolves. Typically, analytical expressions for such systems are unavailable, and, as a result, a data-driven approach could be advantageous.

The Koopman operator aims to linearize the manifold in which the nonlinear state dynamics $x=f(x,t)$ are embedded by projecting into a lower dimensional, weakly nonlinear subspace. Consider a continuous-time dynamical system ${\displaystyle \frac{dx}{dt}=f\left(x\right),}$ where x is the state on a smooth n-dimensional manifold M and f is a nonlinear vector-valued function of the same dimension as x. The Koopman operator $\mathcal{K}$ acts on the space of all scalar observable functions ${\displaystyle g:M\to C^k}$ such that $\left(\mathcal{K}g\right)\left(x\right)=g\left(f\right(x\left)\right).$

The typical approach to analyzing nonlinear systems is to linearize the dynamics (which we may not know) in the neighborhood of the critical points, however, the Koopman operator attempts to linearize the state space M itself, providing a global linear representation of the dynamics that is valid far from fixed points and periodic orbits [29]. The operator $\mathcal{K}$ acts on a complete linear vector space, so $\mathcal{K}$ admits an eigen-expansion which completely characterizes the dynamics of the system [26]. The eigenpairs of $\mathcal{K}$ are used to construct the Koopman modes, which are of particular interest since projection of the observable functions allow the system dynamics to be advanced essentially by scalar multiplication. In the case of the system (1), the chosen observables are strictly based on the cubic nonlinear term.

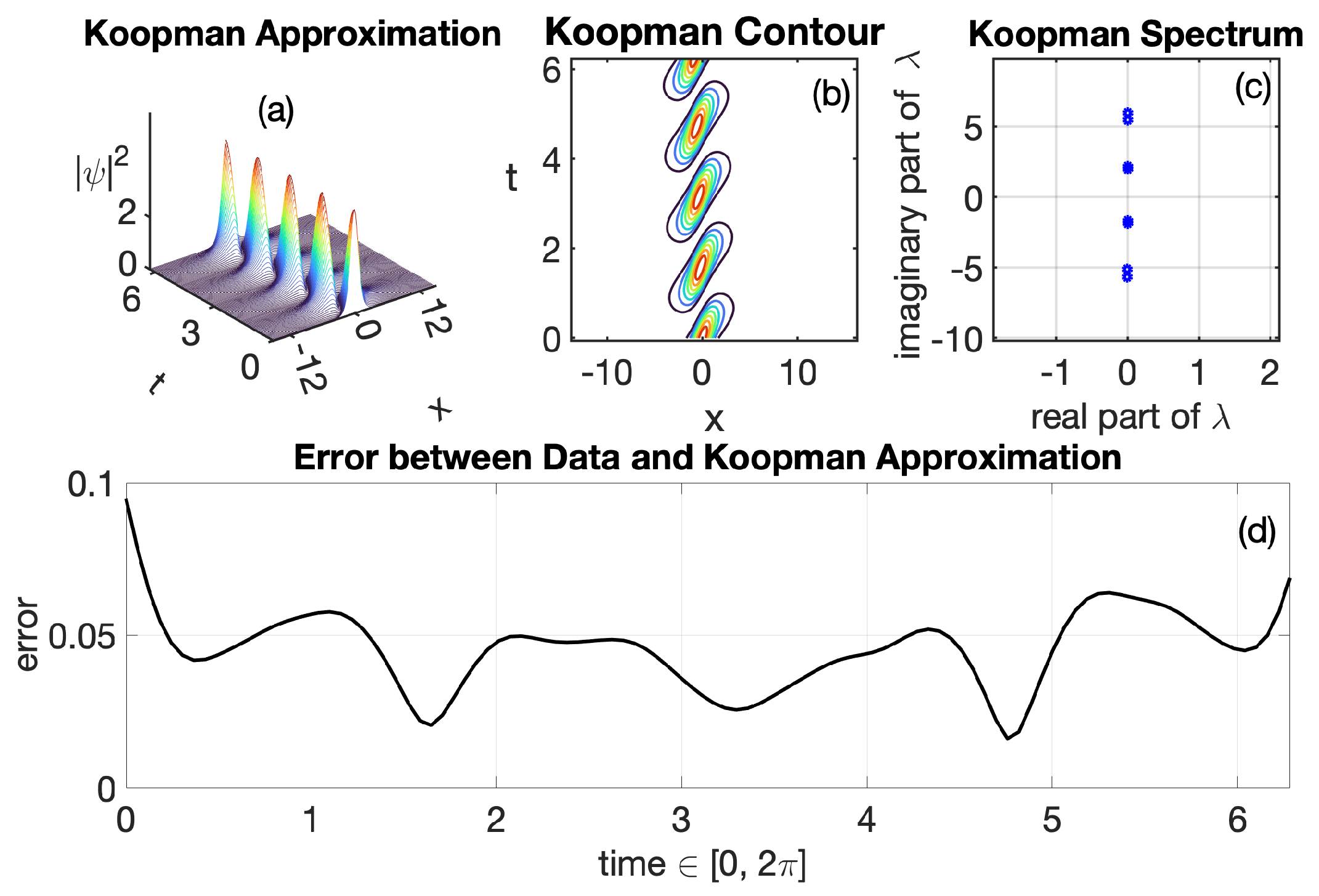
The accuracy of the Koopman reconstruction relies mostly on the selection of the observable function. The Figure 2 depicts the reconstructed dynamics of the eNLSE using Koopman theory after considering for the observable function only the cubic nonlinear part ${\displaystyle g\left(x\right)=\left[\begin{array}{c}x\\ {\left|x\right|}^{2}x\end{array}\right].}$ In our work, the spatio-temporal term play a key role in obtaining the desired approximation. By comparing (a) in Figure 1 and Figure 2, one can appreciate the precise approximation of the Koopman results with the wave dynamics of the eNLSE. The spectra in Figure 2c is approximately purely imaginary, as desired, highlighting the higher precision of the reconstruction. Truncating at $r=8$, and using the observable base on the cubic nonlinearity lead to a good approximation of the dynamics of the eNLSE.

4. Conclusions

The understanding of wave propagation in Schrödinger-type systems is still important due to the possible wide range of applications, from communication systems to the emerging field of quantum computing. The study of the dynamics embedded in a nonlinear system using the methods discussed on this work has been of great interest during the last years due to its possible positive impact in the understanding of the hidden dynamics in data sets. The idea of using only a portion of the data to construct a precise generalization is definitely, in terms of numerical calculations, a cost-effective process. Dimension reduction techniques to approximate the desired outputs in the most possible precise way are desired essential elements in data science. In this work, we explored analytical and numerical wave solutions of a highly nonlinear extension of the original Schrödinger equation motivated by recent results in the field of material sciences. We found that the spatio-temporal dispersion term served as a key regularization tool on the numerical algorithm for the Koopman reconstruction of the profile created with Spectral Methods on Figure 1. The almost purely imaginary resulting Koopman spectrum corroborates the precision of the reconstruction. The dynamic decomposition algorithm is a landmark in the study of the hidden dynamics embedded in data, and recent progress indicates it works. However, much work is still needed to determine a process to construct the exact observables for each case in the Koopman approach. We hope that the results presented in this work will contribute to the advancement of understanding the dynamics within systems described by data. The ability of the spatio-temporal dispersion in balancing the dynamics of highly nonlinear Schrödinger-type equations is essential to reach the desired accuracy approximation of embedded dynamics [46]. Further work on this subject is still necessary to develop a framework to decide a precise observable function $g\left(x\right),$ to better understand the influence the spatio-temporal term and to identify possible corresponding advantages.