Symmetries in Dynamic Models of Biological Systems: Mathematical Foundations and Implications
Abstract
:1. Introduction
2. Mathematical Concepts and Analysis Tools
2.1. Lie Symmetries: Definitions
2.2. Finding Lie Symmetries
2.3. Structural Identifiability and Observability
3. Connections: Symmetries and Other Properties
3.1. Symmetries and SIO
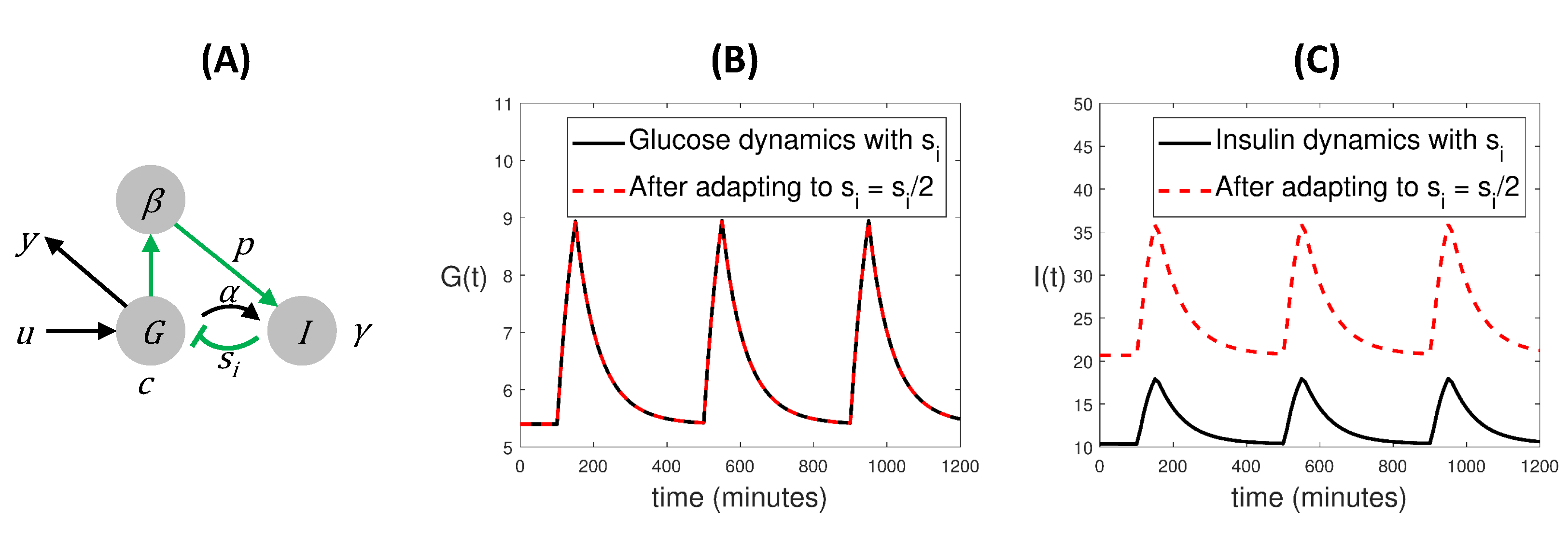
3.2. Symmetries and Biological Robustness
4. Discussion and Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DC | Dynamical compensation |
| FCD | Fold-Change Detection |
| IFFL | Incoherent Feed-Forward Loop |
| IVP | Initial value problem |
| ODE | Ordinary differential equation |
| PDE | Partial differential equation |
| SIM | Scaling Invariance Method |
| SIO | Structural Identifiability and Observability |
| SLI | Structurally locally identifiable |
| SU | Structurally unidentifiable |
References
- Graham, J.H.; Raz, S.; Hel-Or, H.; Nevo, E. Fluctuating asymmetry: Methods, theory, and applications. Symmetry 2010, 2, 466–540. [Google Scholar] [CrossRef] [Green Version]
- DiStefano, J., III. Dynamic Systems Biology Modeling and Simulation; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Oliveri, F. Lie symmetries of differential equations: Classical results and recent contributions. Symmetry 2010, 2, 658–706. [Google Scholar] [CrossRef] [Green Version]
- Bluman, G.; Anco, S. Symmetry and integration methods for differential equations. In Applied Mathematical Sciences; Springer: New York, NY, USA, 2008; Volume 154. [Google Scholar]
- Arrigo, D.J. Symmetry Analysis of Differential Equations: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Merkt, B.; Timmer, J.; Kaschek, D. Higher-order Lie symmetries in identifiability and predictability analysis of dynamic models. Phys. Rev. E 2015, 92, 012920. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shi, X.; Chatzis, M. Lie Symmetries, Observability and Model Transformation of Nonlinear Systems with Unknown Inputs. In Proceedings of the XI International Conference on Structural Dynamics, EURODYN 2020, Athens, Greece, 23–26 November 2020. [Google Scholar]
- Shi, X.; Chatzis, M. Computational Framework of Lie Symmetries of Nonlinear Systems with Unmeasured Inputs. In Proceedings of the 10th International Conference on Structural Health Monitoring of Intelligent Infrastructure, SHMII 10, International Society for Structural Health Monitoring of Intelligent Infrastructure, Porto, Portugal, 30 June–2 July 2021. [Google Scholar]
- Massonis, G.; Villaverde, A.F. Finding and breaking Lie symmetries: Implications for structural identifiability and observability in biological modelling. Symmetry 2020, 12, 469. [Google Scholar] [CrossRef] [Green Version]
- Russo, G.; Slotine, J.J.E. Symmetries, stability, and control in nonlinear systems and networks. Phys. Rev. E 2011, 84, 041929. [Google Scholar] [CrossRef] [Green Version]
- Wieland, F.G.; Hauber, A.L.; Rosenblatt, M.; Tonsing, C.; Timmer, J. On structural and practical identifiability. Curr. Opin. Syst. Biol. 2021, 25, 60–69. [Google Scholar] [CrossRef]
- Villaverde, A.F. Observability and Structural Identifiability of Nonlinear Biological Systems. Complexity 2019, 2019, 8497093. [Google Scholar] [CrossRef] [Green Version]
- Sedoglavic, A. A probabilistic algorithm to test local algebraic observability in polynomial time. J. Symb. Comput. 2002, 33, 735–755. [Google Scholar] [CrossRef] [Green Version]
- Vajda, S.; Godfrey, K.R.; Rabitz, H. Similarity transformation approach to identifiability analysis of nonlinear compartmental models. Math. Biosci. 1989, 93, 217–248. [Google Scholar] [CrossRef]
- Evans, N.D.; Chapman, M.J.; Chappell, M.J.; Godfrey, K.R. Identifiability of uncontrolled nonlinear rational systems. Automatica 2002, 38, 1799–1805. [Google Scholar] [CrossRef]
- Yates, J.W.; Evans, N.D.; Chappell, M.J. Structural identifiability analysis via symmetries of differential equations. Automatica 2009, 45, 2585–2591. [Google Scholar] [CrossRef] [Green Version]
- Meshkat, N.; Sullivant, S. Identifiable reparametrizations of linear compartment models. J. Symb. Comput. 2014, 63, 46–67. [Google Scholar] [CrossRef] [Green Version]
- Anguelova, M.; Karlsson, J.; Jirstrand, M. Minimal output sets for identifiability. Math. Biosci. 2012, 239, 139–153. [Google Scholar] [CrossRef] [PubMed]
- Sedoglavic, A. Reduction of algebraic parametric systems by rectification of their affine expanded lie symmetries. In Proceedings of the International Conference on Algebraic Biology, Castle of Hagenberg, Hagenberg, Austria, 2–4 July 2007; pp. 277–291. [Google Scholar]
- Lemaire, F.; Ürgüplü, A. A method for semi-rectifying algebraic and differential systems using scaling type Lie point symmetries with linear algebra. In Proceedings of the 2010 International Symposium on Symbolic and Algebraic Computation, Munich, Germany, 25–28 July 2010; pp. 85–92. [Google Scholar]
- Ürgüplü, A. Contributions to Symbolic Effective Qualitative Analysis of Dynamical Systems; Application to Biochemical Reaction Networks. Ph.D. Thesis, Université de Lille 1, Lille, France, February 2010. [Google Scholar]
- Villaverde, A.F.; Tsiantis, N.; Banga, J.R. Full observability and estimation of unknown inputs, states, and parameters of nonlinear biological models. J. R. Soc. Interface 2019, 16, 20190043. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Massonis, G.; Banga, J.R.; Villaverde, A.F. AutoRepar: A method to obtain identifiable and observable reparameterizations of dynamic models with mechanistic insights. Internat. J. Robust Nonlinear Control, 2021; in press. [Google Scholar] [CrossRef]
- Castro, M.; de Boer, R.J. Testing structural identifiability by a simple scaling method. PLoS Comput. Biol. 2020, 16, e1008248. [Google Scholar] [CrossRef]
- Villaverde, A.F.; Massonis, G. On testing structural identifiability by a simple scaling method: Relying on scaling symmetries can be misleading. PLoS Comput. Biol. 2021, 17, e1009032. [Google Scholar] [CrossRef]
- Lemaire, F.; Ürgüplü, A. Mabsys: Modeling and analysis of biological systems. In Algebraic and Numeric Biology; Springer: Hagenberg, Austria, 2012; pp. 57–75. [Google Scholar]
- Ingalls, B. Sensitivity analysis: From model parameters to system behaviour. Essays Biochem. 2008, 45, 177–194. [Google Scholar]
- Adler, M.; Alon, U. Fold-change detection in biological systems. Curr. Opin. Syst. Biol. 2018, 8, 81–89. [Google Scholar] [CrossRef]
- Shoval, O.; Goentoro, L.; Hart, Y.; Mayo, A.; Sontag, E.; Alon, U. Fold-change detection and scalar symmetry of sensory input fields. Proc. Natl. Acad. Sci. USA 2010, 107, 15995–16000. [Google Scholar] [CrossRef] [Green Version]
- Shoval, O.; Alon, U.; Sontag, E. Symmetry invariance for adapting biological systems. SIAM J. Appl. Dyn. Syst. 2011, 10, 857–886. [Google Scholar] [CrossRef] [Green Version]
- Karin, O.; Swisa, A.; Glaser, B.; Dor, Y.; Alon, U. Dynamical compensation in physiological circuits. Mol. Syst. Biol. 2016, 12, 886. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sontag, E.D. Dynamic compensation, parameter identifiability, and equivariances. PLoS Comput. Biol. 2017, 13, e1005447. [Google Scholar] [CrossRef]
- Karin, O.; Alon, U.; Sontag, E. A note on dynamical compensation and its relation to parameter identifiability. bioRxiv 2017, 123489. [Google Scholar] [CrossRef] [Green Version]
- Villaverde, A.F.; Banga, J.R. Dynamical compensation and structural identifiability of biological models: Analysis, implications, and reconciliation. PLoS Comput. Biol. 2017, 13, e1005878. [Google Scholar] [CrossRef] [PubMed]

| Name | Language | Reference | Types of Detected Symmetries |
|---|---|---|---|
| MABSys | Maple | [26] | scaling |
| MinimalOutputSets | Mathematica | [18] | translation, scaling, affine |
| symmetryDetection | Python | [6] | up to higher order |
| AutoRepar | Matlab | [23] | up to higher order |
| SIM | – | [24] | scaling |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villaverde, A.F. Symmetries in Dynamic Models of Biological Systems: Mathematical Foundations and Implications. Symmetry 2022, 14, 467. https://doi.org/10.3390/sym14030467
Villaverde AF. Symmetries in Dynamic Models of Biological Systems: Mathematical Foundations and Implications. Symmetry. 2022; 14(3):467. https://doi.org/10.3390/sym14030467
Chicago/Turabian StyleVillaverde, Alejandro F. 2022. "Symmetries in Dynamic Models of Biological Systems: Mathematical Foundations and Implications" Symmetry 14, no. 3: 467. https://doi.org/10.3390/sym14030467
APA StyleVillaverde, A. F. (2022). Symmetries in Dynamic Models of Biological Systems: Mathematical Foundations and Implications. Symmetry, 14(3), 467. https://doi.org/10.3390/sym14030467






