Fast Treetops Counting Using Mathematical Image Symmetry, Segmentation, and Fast k-Means Classification Algorithms

Abstract

Forests are important because they contribute to biodiversity, regulation of carbon dioxide, protection of hydrographic basins, wood production. This article presents a methodology for fast and effective counting of treetops using the mathematical symmetry of the grayscale image. For the treetop counting, the unsupervised k-means classification Algorithm was used with two groups or centroids: treetop and not-treetop. By using these groups and the mathematical symmetry of the image, a fast k-means classification Algorithm is generated. To solve the problem of treetop overlapping and perform a more accurate counting, the watershed Algorithm was used. This methodology has a mean treetop count accuracy of 98.3% with a confidence level of 99% in the interval (97.31, 99.7). Aerial images of the coniferous forest of Alcudia, Mallorca, Spain were used. Forests attenuate climatic changes originated by global warming. Drastic climatic changes cause catastrophes to humanity. This research would help the automatic, massive and recurring counting of treetops with the aim of obtaining forest inventories in order to take care of forests.

1. Introduction

The objective of this research is to present a methodology for fast and effective counting of treetops. Counting treetops using fast Algorithms saves a lot of time, work and is very useful in forest inventories; they give us precise information on the mapping or location of trees and timber resources [1]. Forests mitigate climate change caused by global warming. Drastic climate changes can cause catastrophes for humanity and the planet’s ecosystem in general [2,3]. Therefore, it is necessary to protect and take care of the forests. For better taking care of forests, it is necessary to have forests inventories [4,5,6].

Currently, the automatic counting of treetops is carried out by using satellite images [7,8,9], aerial images [5] or lidar data [10,11,12]. This work was carried out by using aerial images [13,14,15,16,17,18,19] because of their low cost [15].

Aerial digital images are decomposed into three RGB planes (red, green, blue), each plane is a grayscale image [20]. A grayscale image is defined as a function $f:\mathbb{N}x\mathbb{N}\to \left[0, 255\right]$ (where $\mathbb{N}$ is the set of natural numbers). One of the main problems in image analysis is the automatic recognition of objects within an image. In order to achieve this automatic recognition, several processes are generally carried out on the image, such as: preprocessing (to eliminate noise or unwanted information), classification and segmentation [21,22,23].

This paper presents a methodology for fast treetop counting by using the mathematical symmetry of the image. The mathematical symmetry of an object is a set of permutations in such a way that when applied to the object it remains invariant [24,25]. Mathematical symmetry is used to optimize the calculation processes, an example of this is the fast Fourier transform [26].

In this research, the existing mathematical symmetry in the digital image and machine learning Algorithms were integrated to perform the automatic treetop counting. Machine learning is a set of Algorithms or methods that extract patterns from data in order to optimally solve problems. Another goal of machine learning technology is for machines to make sense of data in the same way that humans do. Machine learning can be supervised and unsupervised [27]. Machine learning is very fast and even faster when implemented using parallel programming and can be used in real-time prediction [28,29,30], and it is also scalable with large data sets [31,32,33,34]. In this research, it is proposed to use an unsupervised k-means Algorithm with only two centroids and the watersheds Algorithm to solve the treetops overlap problem. The input to the proposed counting system is an image containing a number of treetops and the output is the approximate number of treetops.

In general, some of the problems in counting treetops to obtain forest inventories are the following: if the counting is carried out walking into the forests, it is tiring, dangerous and very expensive. Another problem is: the visual and manual treetop counting based on aerial or satellite images is also tiring, time-consuming and often incorrect. On the other hand, a problem in automatic treetop counting systems is the overlapping of the treetops, which decreases the counting accuracy. All the above problems arise again when the treetop counting must be carried out massively and recurrently to create or update forest inventories.

Automatic treetop counting systems are needed because forests play a fundamental role in hydrological and carbon cycles. Forests are a main indicator of the state of an ecosystem and provide us with information to understand climate change [35]. Given the global climate changes partially originated by reduction of forests, it is necessary to investigate the effects of damages caused on the different ecosystems [36,37]. For this, we must rely on precise indicators of forests and environmental conditions [38]. Forests mitigate climate change; but on the other hand, climate change affects forests such as increasing severity of insect pests, forest decline and alteration of phenological parameters in crops. Automatic treetop counting systems can provide us with accurate indicators about forests. These systems can be used intensively to cope with massive and recurring counting of treetops needs.

The objective of this proposal is to present a methodology for fast and effective treetop counting. In this methodology, a fast-unsupervised k-means Algorithm is proposed to classify the pixels of the image into treetop and not treetop. To create the fast k-means Algorithm, the mathematical symmetry of the image and the characteristics of the images to be processed were used. Then, the watersheds Algorithm was applied to the image to eliminate the treetops overlapping. The images are aerial images of the coniferous forest located in the region of Alcudia, Mallorca, Spain.

In this proposed methodology, the following results were obtained:

• The mathematical symmetry in grayscale images, the proposal to use only two centroids in the k-means Algorithm and the analysis of the images to be processed allowed us to reduce the computational complexity of the k-means Algorithm.
• The low computational complexity of the k-means Algorithm proposed in this work provides a time advantage over the standard k-means Algorithm. The values of the centroids found by both k-means Algorithms (standard and proposed) are approximately equal.
• The application of the k-means and watersheds Algorithms allowed us to improve treetop counting.
• This methodology has a mean treetop counting accuracy of 98.3% with a confidence level of 99% in the interval (97.31, 99.7).
• This methodology has a mean F1-score of 98%, a mean recall of 97.67% and a mean AUC of 0.98.
• Having mentioned the two previous points, this methodology sound and reliable for the automatic counting of treetops.

In order to measure the effectiveness of the automatic treetop counting system, manual treetop counts based on images were compared with the counts made by the system. Furthermore, the trees were also physically counted in order to know the real number of trees.

The remaining sections are organized as follows: Section 2 describes the mathematical symmetry of the images, the related works, and presents the proposed methodology. Section 3 provides development details of the proposed methodology, here also three k-means classification Algorithms are proposed and compared. Section 4 presents the results of the proposal, comparing computation times and accuracy of the centroids with respect to the standard k-means Algorithm and evaluating the results of the treetop counts. Then the main conclusions are included followed by a list of references.

2. Description of the Methodology and Related Works

One of the main problems in treetop counting using satellite or aerial images is the treetops overlapping and the counting time. This work was realized by using aerial images. These images are decomposed into three RGB planes (red, green, blue); each plane is a grayscale image [20]. The methodology proposed in this work, for fast treetop counting, consists of the application of an optimized k-means Algorithm. To apply the k-means Algorithm we use the mathematical symmetry of the image and classify the pixels that belong to treetop and not treetop, that is, only two centroids $c_1$ and $c_2$ were searched for, then a watershed Algorithm with 8 connected pixels was applied. The watersheds Algorithm separates overlapping treetops.

The mathematical symmetry of an object is a set of permutations in such a way that when applied to the object it remains invariant [24]. In a grayscale image $f:\mathbb{N}x\mathbb{N}\to [0, 255$ (where $\mathbb{N}$ is the set of natural numbers) mathematical symmetry can be observed in pixels that have equal gray values. These pixel values can be swapped in position without the image changing its appearance. The pixels with the same gray levels can be grouped to reduce the number of calculations when applying some Transform on the image [25].

The total gray levels in a digital image go from 0 to 255. In most digital images $f$ of size $Q$, it holds that $PxQ>256$. Therefore, by the Dirichlet principle [39] there will always be pixels with repeated gray level values. In this way, it is ensured that in a grayscale image there is mathematical symmetry [40,41,42,43].

In order to use the mathematical symmetry in some mathematical calculation or computational process of an image, it is necessary to calculate the maximum mathematical symmetry group of the image [41]. Mathematically, images can be 2-dimensional, 3-dimensional, or n-dimensional. In general, an n-dimensional image with m colors can be represented as a set of tuples A.

$$A=\left\{\left(x_1,x_2,\dots ,x_n; c_1,c_2,\dots ,c_m\right)\right\}$$

(1)

where $x_1,x_2,x_3,\dots ,x_n$ are the pixels coordinates of an n-dimensional image and $c_1,c_2,c_3,\dots ,c_m$ are the components of the color vector of each pixel. The elements of the set A are the tuples that represent all the pixels of the image. The place of the tuple in the set A represents the place of the corresponding pixel in the image.

Since we work with gray levels images, we would have a single component in the color vector. Therefore, without losing generality, we have the following:

$$A=\left\{\left(x_1,x_2,\dots ,x_n; c\right)\right\}$$

(2)

Suppose that $N_1,N_2,\dots ,N_n$ is the size of each dimension; then:

$$\begin{array}{c}{x}_1=1,\dots ,N_1\\ x_2=1,\dots ,N_2\\ \dots \\ x_n=1,\dots ,N_n\\ c=0,1,2\dots ,M-1\end{array}$$

(3)

Therefore, the set A can be partitioned according to color, as follows:

$$A=A_0\oplus A_1\oplus A_2\oplus \dots \oplus A_{M-1}$$

(4)

where

$$A_i=\left\{\left(x_1^i,x_2^i,\dots ,x_n^i;i\right)\right\},i=0,1,\dots ,M-1$$

(5)

And ⊕ is the group direct addition operator. Then factoring out the color $A_i$ can be represented as follows:

$$A_i=i\ast \left\{\left(x_1^i,x_2^i,\dots ,x_n^i;i\right)\right\}=i\ast B_i$$

(6)

where * is the multiplication operation of real numbers.

$$B_i=\left\{\left(x_1^i,x_2^i,\dots ,x_n^i;1\right)\right\},\hspace{1em}\hspace{1em}\mathrm{for} i=0,1,\dots ,M-1$$

(7)

Therefore, in (6) the factor $i$ multiplies only the last element of the tuple, which is the color. The sets $B_i$ ($i=0,1,2,\dots ,M-1$)) can be considered as a basis that represent the image as follows:

$$A=B_0\oplus {\displaystyle \sum }_{i=1}^{M-1}i\ast B_i$$

(8)

$B_0$ is the set of pixels in the image with a gray level of zero. Equation (8) allows defining a maximum symmetry group (G) of the image:

$$G=S^0\left(card\left(A_0\right)\right)\times S^1\left(card\left(A_1\right)\right)\times \dots \times S^{M-1}\left(card\left(A_{M-1}\right)\right)$$

(9)

where $card\left(A_i\right)$ is the total number of elements in $A_i$. $S^i\left(card\left(A_i\right)\right)=S^i$ is a symmetry group (permutation group) defined over $A_i$ or $B_i$ ($i=0,1,2,\dots , M-1$).

It is evident that applying the group $S^i$ to the sets $A_i$ or $B_i$ (considered as a set of pixels) modifies the position of each pixel but does not alter the corresponding images that are related to the set of tuples $A_i$ or $B_i$. Applying group G to the image does not produce any change in it. Therefore

$$G\left(A\right)=S^0\left(B_0\right)+{\displaystyle \sum }_{i=1}^{M-1}i\ast S^i\left(B_i\right)=B_0+{\displaystyle \sum }_{i=1}^{M-1}i\ast B_i=A$$

(10)

According to (8), the image can be declared as the sum of partial images $B_i$ ($i=0,1,2,\dots ,M-1$).

These properties of the mathematical symmetry of the grayscale image are used in the k-means Algorithm to find the centroids. In each iteration of the k-means Algorithm, to search for two centroids, a complete traversal of the image has to be performed. In the proposed Algorithm, which uses the mathematical symmetry of the image and two centroids, in each iteration the proposed k-means Algorithm (below in Section 3) only performs an addition and a division to determine to which class a gray level belongs (lines 4–14 of Algorithm 1, lines 11–20 of Algorithm 2 and line 14 of Algorithm 3).

2.1. Related Work

K-means Algorithm has been used in the treetop detection and counting. It also has been optimized in different ways. Some examples of related work are the following: In [44] an optimized k-means Algorithm searches for the invariant centroids in each iteration avoiding thus redundant calculations, but they do not use mathematical symmetry in the elements to be classified. The use of the existing mathematical symmetry in the objects manipulated in the processes allows us to obtain fast Algorithms.

In [45] they use the mathematical symmetry of the image, but they do not optimize the search for the centroids as in [44,46]. In [47] k-means and particle swarm are related to search for centroids. In [48] he obtains the centroids optimally for 2 classes but does not use the mathematical symmetry of the image. In [49] a methodology is proposed to choose the initial centroids and solve the problem of the k-means Algorithm when it is trapped in a local minimum, however, our Algorithm does not have this problem even though the two initial centroids are equal.

In [50], first, the treetops are obtained through a filter, then the watersheds are applied, finally, the k-means Algorithm is applied to segment the treetops from coarse to fine. The number of trees is the number of centroids in the k-means Algorithm. In our proposal, the number of centroids is not the number of cups. Furthermore, the computational complexity of our Algorithm is independent of the number of treetops found in the image and is also independent of the size of the image.

In [51] the detection of treetops is carried out with the inverse methodology that in [50], that is, they apply the k-means Algorithm to obtain the center of each crown and subsequently optimize the Algorithm of watersheds with the mean and variance. In [51] they use LiDAR data and the k-means Algorithm, but they do not optimize it, in our proposal we use aerial images and optimize the k-means Algorithm.

In [52,53] point out that, the k-means Algorithm in conjunction with Deep Learning methods are some of the best tree counting and classification Algorithms. In [54] the 3D methods to identify trees in a forest are presented, some of the methods mentioned in [54] use 2D image processing Algorithms in a dots cloud. These 3D methods also use the k-means Algorithm to classify treetops, but these methods do not use mathematical symmetry.

2.2. Proposed Methodology

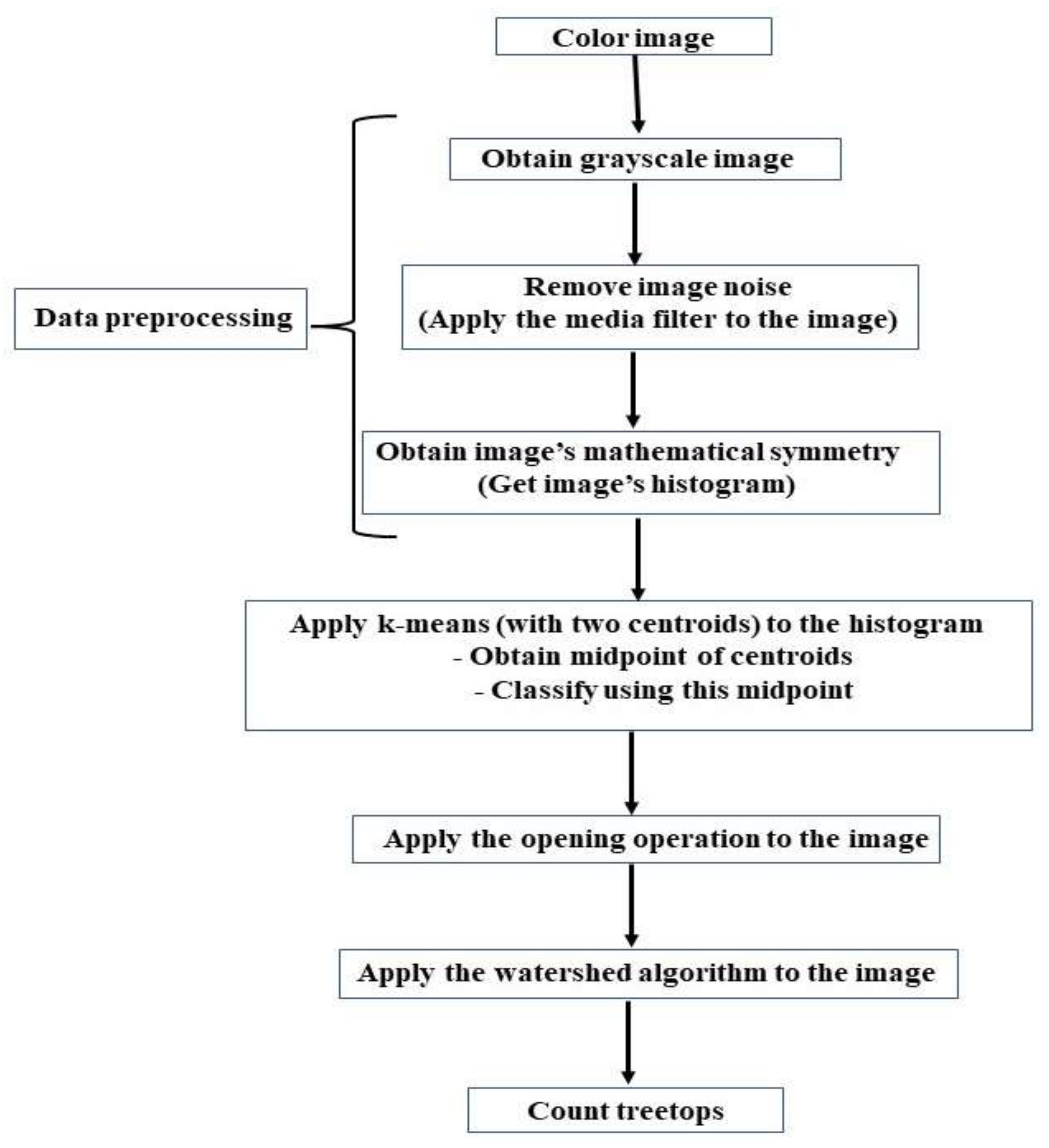
This Section presents the flowchart and the steps of the proposed methodology to classify treetops, based on mathematical symmetry of images and the proposal to use only two centroids. These considerations allowed us to obtain a fast k-means classification Algorithm.

The images are aerial images of the coniferous forest located in the region of Alcudia, Mallorca, Spain.

The methodology used for counting treetops is the following:

• Image preprocessing.

  (a)

  Obtaining the grayscale image.

  (b)

  Apply the medium filter to the grayscale image.

• Classification using the fast k-means Algorithm.

  (a)

  Apply the fast k-means Algorithm using the mathematical symmetry of the image and the classification conditions of treetop and no treetop.

  (b)

  Apply the opening operation.

• Image segmentation applying watersheds.

  (a)

  Segment the image using watershed by flooding.

  (b)

  At the same time that the image is segmented, count the treetops.

Figure 1 shows the blocks diagram of the proposed methodology, this diagram also indicates the preprocessing steps performed on the digital image containing the treetops.

A color image has 3 RGB planes (red, green, blue). Vegetation reflects the wavelengths corresponding to the color green. Therefore, the green plane was taken to process the image. Several tests were carried out and it was found that the green plane shows greater uniformity of gray levels and higher values of gray levels in the regions where the treetops are found [55]. This decreases over-segmentation by applying the watershed Algorithm, obtaining greater accuracy in treetop counting. When using the red and green planes, there is less accuracy in the counting.

The green plane is a grayscale image. To eliminate the noise in this image, the means filter [40] was applied. By doing thus, the k-means Algorithm [44] was more effective. The input to the k-means Algorithm is a gray level image and the output is a segmented binary image.

Pixel classification based on gray level was performed by using the optimized unsupervised k-means Algorithm [45]. This optimization is achieved by the mathematical symmetry found in all gray level images [40,41,42]. The groups used to classify the objects within the image are: treetop and non-treetop. Once the image has been classified, a segmented binarized image is obtained. The bushes are smaller than the treetops. In order to eliminate the bushes, an opening operation is applied to the segmented binary image. The opening operation was applied with a 3 × 3 structural element, with all its elements having a value of one.

The coordinates of the black pixels of the classified image were used to form a new image. In the new image at these coordinates the gray levels of the original image were assigned. In this new image, all pixels were assigned a value of 255 (white) except the coordinates of the classified image.

The watershed Algorithm was applied to this last grayscale image to segment and count the treetops. Watersheds were used to solve the treetops overlapping problem and make the treetop counting more accurate.

3. Development

In this section, three k-means Algorithms are presented, and they use only two centroids. The first k-means Algorithm (standard k-means) does not use the mathematical symmetry of the image, the second k-means Algorithm makes use of the mathematical symmetry of the image, the third k-means Algorithm uses the mathematical symmetry of the image and takes advantage of the fact that only two centroids are calculated.

In this study, it was found that one of the properties of the k-means classification Algorithm using only two centroids is that: given two images A, B of the same size (n × m). If image A contains p treetops and image B contains q treetops such that p >> q, the k-means Algorithm uses the same computation time on each of the images to perform the treetop classification. Therefore, the computational complexity does not depend on the number of treetops to be counted, but on the size of the image.

Mathematical symmetry is used to eliminate redundant calculations and optimize processes [41,42]. By eliminating redundant calculations, processes are performed in less computing time. In this work, the centroids sought $c_1$ (it is a treetop) and $c_2$ (it is not a treetop) are gray levels. If $f_{nxm}$ is a grayscale image, then to obtain $c_1$, $p\times \left(n\times m\right)$ subtractions would have to be performed (where $\times$ is the multiplication operation and p is the total number of iterations carried out by the Algorithm until the centroids are found). If the value of $n$ and $m$ are of the order of megabytes, then the computation time is very long. Using the mathematical symmetry of the image, the k-means Algorithm performs very few operations in each iteration (see

Table 1. Computational complexity.

Operations	Algorithm 1	Algorithm 2	Algorithm 3
Sums	$\left(4\times N\times n\times m\right)+(2\times n\times m)$	$\left(3\times n\times m\right)+\left(4\times 255\times N\right)$	$(3\times n\times m)$
Comparisons	$\left(N\times n\times m\right)+(n\times m)$	$\left(n\times m\right)+\left(255\times N\right)$	$n\times m$
Assignments	$\left(4\times N\times n\times m\right)+(3\times n\times m)$	$\left(4\times n\times m\right)+\left(4\times 255\times N\right)$	$(4\times n\times m)$

), regardless of whether n and m have values of the order of megas or teras. Then we have that $n\times m\gg 255$ and therefore the computation time is much less when using the mathematical symmetry of the grayscale image.

Then the advantages of Algorithm 2 and 3 with respect to Algorithm 1 (standard k-means) is that they use the mathematical symmetry of the grayscale image and therefore the computational complexity is reduced and the computational time in the process of classification. On the other hand, the advantage of Algorithm 3 with respect to Algorithm 2 is that Algorithm 3 takes advantage of the reduced number of centroids and the mathematical symmetry of the image to reduce a little more complexity and computation time. The k-means Algorithms applied to the grayscale image are shown below. The internet link of the document that contains the functions in Matlab that implement these Algorithms are in Appendix A.

Algorithm 1 (Standard Algorithm)
	Inputs: grayscale image bnxm, N (total number of iterations)
	Output: dnxm segmented binary image
	[n, m] = size(b), n and m are respectively the total rows and columns of b
1	Randomly obtain two different centroids c1 and c2 (c1 and c2 are gray levels of the image)
2	$\epsilon ={10}^{-6}$
3	for k = 1 to N
4	s1 = 0
5	n1 = 0
6	s2 = 0
7	n2 = 0
8	for i = 1 to n
9	for j = 0 to m
10	p = abs(b(i,j)-c1)
11	q = abs(b(i,j)-c2)
12	if(p < q)
13	s1 = s1 + b(i,j)
14	n1 = n1 + 1
15	else
16	s2 = s2 + b(i,j)
17	n2 = n2 + 1
18	end
19	end
20	$cu1=s1/n1$
21	$cu2=s2/n2$
22	if(abs(c1-cu1) ≤$\epsilon$ and abs(c2-cu2) ≤$\epsilon$)
23	break
24	end
25	$c1=cu1$
26	$c2=cu2$
27	end
28	for u = 1 to n
29	for v = 1 to m
30	p = (c1-b(u,v))
31	q = (c2-b(u,v))
32	if(p ≤ q)
33	d(u,v) = 0
34	else
35	d(u,v) = 255
36	end
37	end
38	end

Algorithm 2 (Using Mathematical Symmetry)
	Inputs: grayscale image b, N(total number of iterations)
	Output: segmented binary image
	[n, m] = size(b), n and m are respectively the total rows and columns of b
1	Obtain histogram of image h; h is an array of 256 locations.
2	Randomly obtain two different centroids c1 and c2 (c1 and c2 are gray levels of the image)
3	$\epsilon ={10}^{-6}$
4	tg = 0
5	for i = 1:256
6	tg = tg + (i-1)*h(i)
7	end
8	$t=n\ast m$
9	for k = 1 to N
10	%Find all gray levels closest to c1
11	s1 = 0
12	n1 = 0
13	for i = 0 to 255
14	p = abs(i-c1)
15	q = abs(i-c2)
16	if(p<q)
17	s1 = s1 + i*h(i+1)
18	n1 = n1 + h(i+1)
19	end
20	end
21	$cu1=s1/n1$
22	$cu2=\left(tg-s1\right)/\left(t-n1\right)$
23	if(abs(c1-cu1) ≤$\epsilon$ and abs(c2-cu2) ≤$\epsilon$)
24	break
25	end
26	$c1=cu1$
27	$c2=cu2$
28	end
29	d = zeros(n,m)   % create an array filled with zeroes
30	for i = 1 to n
31	for j = 1 to m
32	p = abs(b(i,j)-c1)
33	q = abs(b(i,j)-c2)
34	if(p ≤ q)
35	d(i,j) = 0
36	else
37	d(i,j) = 255
38	end
39	end
40	end

Algorithm 3 (Proposed Algorithm)
	Inputs: grayscale image bnxm, total N of iterations
	Output: dnxm segmented binary image
	[n, m] = size(b), n and m are respectively the total number of rows and columns of b
1	Obtain histogram (h) of the image; h is an array of 256 locations.
2	Randomly obtain two different centroids c1 and c2 (c1 and c2 are gray levels of the image)
3	$\epsilon ={10}^{-6}$
4	$ah\left(1\right)=h\left(1\right)$
5	for k = 2 to 256
6	$ah\left(k\right)=ah\left(k-1\right)+h\left(k\right)$
7	end
8	$as\left(1\right)=0$
9	for k = 2 to 256
10	$as\left(k\right)=as\left(k-1\right)+\left(k-1\right)\ast h\left(k\right)$
11	end
12	for i = 1 to N
13	% find all gray levels closest to c1
14	w = floor((c1 + c2)/2)
15	$cu1=as\left(w\right)/ah\left(w\right)$
16	$cu2=\left(as\left(256\right)-as\left(w\right)\right)/\left(ah\left(256\right)-ah\left(w\right)\right)$
17	if(abs(c1-cu1) ≤$\epsilon$ and abs(c2-cu2) ≤$\epsilon$ )
18	break
19	end
20	$c1=cu1$
21	$c2=cu2$
22	end
23	d = zeros(n,m)
24	for i = 1 to n
25	for j = 1 to m
26	p = abs(c1-b(i,j))
27	q = abs(c2-b(i,j))
28	if(p < q)
29	d(i,j) = 0
30	else
31	d(i,j) = 255
32	end
33	end
34	end

Algorithm 1 can be improved by using the mathematical symmetry found in all grayscale images. This mathematical symmetry is implemented using the histogram of the image.

Algorithm 2 can be improved by using the mathematical symmetry found in all grayscale images and the following properties:

(a)

We want to classify only two groups: treetop and no-treetop. Let c₁ and c₂ be the centroids of each group. c₁ and c₂ are integer values of gray levels, that is, c₁,c₂ ∈ [0.255].

(b)

The gray values of the pixels that form the treetops are always lower than the values of the pixels of other objects (roads, sand). The objects have a different color than the background [56].

(c)

Without losing generality let c₁ < c₂. Let p = (c₁ + c₂)/2. Then all pixels with gray levels g such that g ≤ p will belong to the first group whose centroid is c₁, the rest of the pixels in the image will belong to the second group whose centroid is c₂. That is, any point less than or equal to p is closer to c₁ than to c₂.

(d)

In all grayscale images, there is always mathematical symmetry [39,40,41].

Table 1 shows the total number of operations performed by Algorithm 1, Algorithm 2 and Algorithm 3. The number of multiplications and divisions is neglected since for our study N is a small number (N ≈ 11). The number of sums, comparisons and assignments that are a function of N is also neglected (except for Algorithm 2 and Algorithm 3, since the difference in computational complexity between them is not very large). However, the sums, comparisons and assignments that are a function of n and m are counted, since $n\times m$ is of the order of megabytes.

Once the image was classified, the next step was to apply the open operation to the binary image to remove the bushes. Then, the problem of the overlap between the treetops was solved and counted more accurately. To do this, immersion watersheds with 8-connected neighbors were used [54].

The immersion watershed was implemented by image labeling [20,57,58] and using 8-connected neighbors. Each basin found was counted and in this way, the Algorithm for segmentation and counting of treetops was optimized. That is, at the same time that the image was segmented, the tops of the trees were counted. In order to eliminate bushes, the images were analyzed, and it was determined that a treetop must have a minimum of 70 pixels, that is, only the basins that had more than 70 pixels were counted.

4. Outcomes

This section presents the outcomes of the treetop counts carried out in the RGB planes of the image. That is the results of the proposed methodology, as well as the times of each k-means Algorithm (Algorithm 1, Algorithm 2 and Algorithm 3). The comparison of the centroids found by each k-means Algorithm is shown. Finally, the counting effectiveness for different images is presented. For a fair comparison among the three Algorithms, the centroids in each of them c₁ and c₂ are initialized with the values of 92 and 163 respectively.

Several tests were also carried out to choose the image plane to work with according to [55], and based on the results obtained, the green plane was chosen. Figure 2 shows the counts made in the different image planes (RGB). In this figure, it can be seen that by using the green plane we obtain greater precision in the treetop counting. In Figure 2b (green plane) 86 of 87 treetops were counted, in Figure 2c (blue plane) 104 of 87 treetops were counted, in Figure 2d (red plane) 100 of 87 treetops were counted.

Figure 3 shows the results of the proposed methodology. Figure 3a shows the original image. Figure 3b shows the image in gray scale, it is the green plane of image 3a. The proposed k-means Algorithm was applied to image 3b and the result is shown in Figure 3c. Figure 3d shows the result of applying the opening operation to the image shown in Figure 3c. Figure 3e shows the image shown in 3d with the gray levels of image 3b except for the white pixels. The watersheds Algorithm was applied to the image shown in Figure 3e to be able to count and separate the overlapping treetops, the result is shown in Figure 3f.

The execution times (in seconds) of each of the k-means Algorithms are presented in

Table 2. Times table.

	Image 1		Image 2
Algorithm	Image size in pixels	Time	Image size in pixels	Time
Algorithm 1 (K-means)	1000 × 1000 = 1,000,000 pixels	0.6450 s	12,000 × 12,000 = 144,000,000	198.002 s
Algorithm 2	1000 × 1000 = 1,000,000 pixels	0.4425 s	12,000 × 12,000 = 144,000,000	124.87 s
Algorithm 2 (proposed K-means)	1000 × 1000 = 1,000,000 pixels	0.3312 s	12,000 × 12,000 = 144,000,000	105.05 s

. Image 2 mentioned in Table 2 is a 12 × 12 image of the image shown in Figure 2a. Image 2 size is 12,000 × 12,000 pixels. Image 2 was used to more clearly see the execution time difference between Algorithm 1, Algorithm 2 and Algorithm 3.

Table 3. Centroids calculated by each Algorithm for different images.

	Algorithm 1		Algorithm 2		Algorithm 3 (Proposed k-Means)
Centroids	c1	c2	c1	c2	c1	c2
Figure 3a	60.8322	147.9142	60.8322	147.9142	61.8322	148.9142
Figure 3c	63.1681	147.0440	63.1681	147.0440	64.1681	148.0440
Figure 3e	62.7159	150.2445	62.7159	150.2445	63.7159	151.2445

shows the centroids calculated by each of the k-means Algorithms. In Algorithm 3 the centroids vary with respect to Algorithm 1 and Algorithm 2 by one grayscale unit value. Therefore, there is a relative error of 1.5% with respect to Algorithm 1 and 2. However, the proposed Algorithm 3 is approximately 1.8 times faster than Algorithm 1 (see Table 2).

The proposed methodology was applied to different images. Figure 4 shows the treetop counting in three different images. In Figure 4a the original image is shown in Figure 4b the resulting count is shown, the same was done for Figure 4c–f.

Table 4. Counting effectiveness.

Image	Counting Effectiveness
3a	98.8%
3c	96.9%
3e	99.1%

shows the counting effectiveness for each image in Figure 4. In order to measure the effectiveness of the treetop counting system, the counts made manually in treetops images were compared with the counts made by the system. This methodology has a mean treetop counting accuracy of 98.3% with a confidence level of 99% in the interval (97.31, 99.7).

To evaluate this methodology, several metrics were calculated. This treetop counting methodology has an average F1-score of 98% and an average recall of 97.67%. The ROC curve was constructed [59,60], which is shown in Figure 5 with a mean AUC of 0.98. With the values of the previous metrics, it is concluded that the proposed methodology is sound and reliable for treetop counting.

Thus far, the outcomes of our methodology have been shown when applied to aerial images, however, this methodology can also be used with LiDAR data. To do so, 2D images must be obtained from the LiDAR data using interpolation techniques, as is done in [61]. On the other hand, this methodology can be applied to the analysis, classification and segmentation of Synthetic Aperture Radar (SAR) images [62,63]. In addition, this methodology can be applied to holographic particles counting [64].

5. Conclusions

In this new treetop counting methodology, the k-means Algorithm uses only two centroids. Using only two centroids allowed us to optimize the k-means Algorithm. In addition, the mathematical symmetry in the grayscale images and the analysis of the images to be processed allowed us to reduce the computational complexity of the k-means Algorithm. One of the main findings is that the time that the k-means Algorithm uses to classify the treetops is independent of the number of treetops found in the image but is dependent on the size of the image. However, using the mathematical symmetry of the image, the k-means Algorithm in each iteration performs only 255 × 4 subtraction operations and one multiplication operation regardless of the size of the image. On the other hand, the k-means Algorithm that uses mathematical symmetry and takes advantage of the fact that only two centroids will be obtained only uses a division and an addition to determine to which class a gray level belongs. Preprocessing before applying the k-means Algorithm is very important as it helps us to obtain better classification results. Additionally, after applying the k-means Algorithm to the image, the size of the structural element in the opening operations allowed us to remove the small bushes. The application of the k-means and watersheds Algorithms allowed us a better count of the tree crowns. In this methodology, an average accuracy of 98.3% tree crown count was obtained with a confidence level of 99% in the interval (97.31, 99.7). This methodology has a mean F1-score of 98%, a mean recall of 97.67, and a mean AUC of 0.98. Therefore, the proposed methodology is reliable. This methodology could also be applied to: LiDAR data, Synthetic Aperture Radar (SAR) images or holographic particle counting. However, this methodology does not allow us to detect the classes of trees. In future works, the proposed methodology for denser forests will be improved. On the other hand, in this methodology, one of the processes that uses more computing time is the media filter, in future works it will also be optimized.