LPI Radar Signal Recognition Based on Dual-Channel CNN and Feature Fusion
Abstract
:1. Introduction
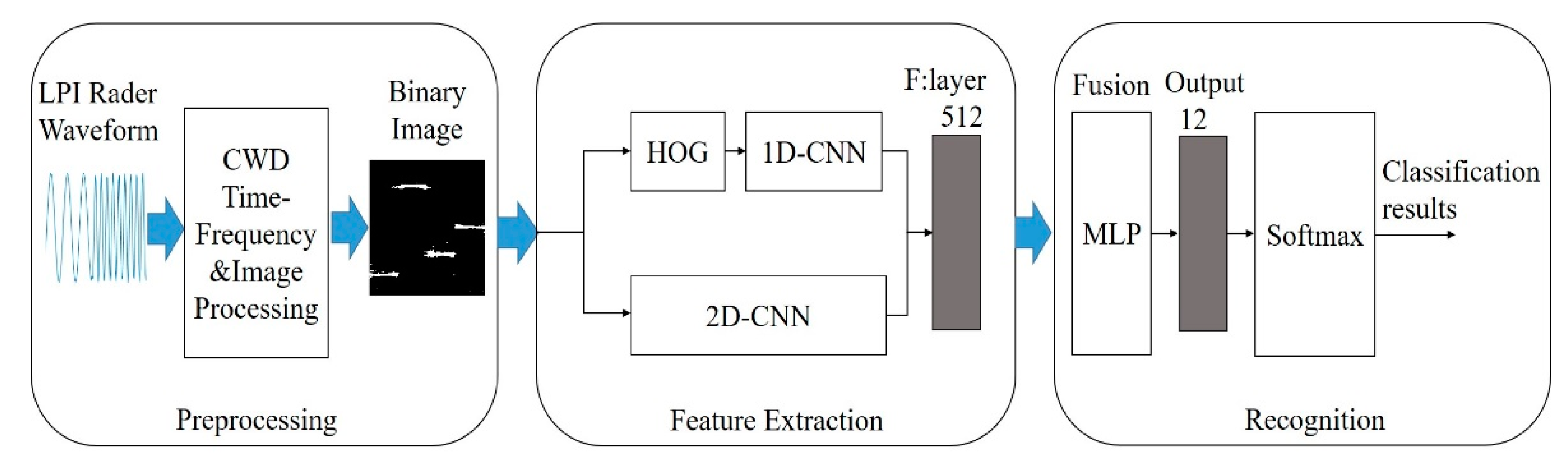
2. Overview of the Proposed Approach
3. Signal Preprocessing
3.1. CWD Transformation
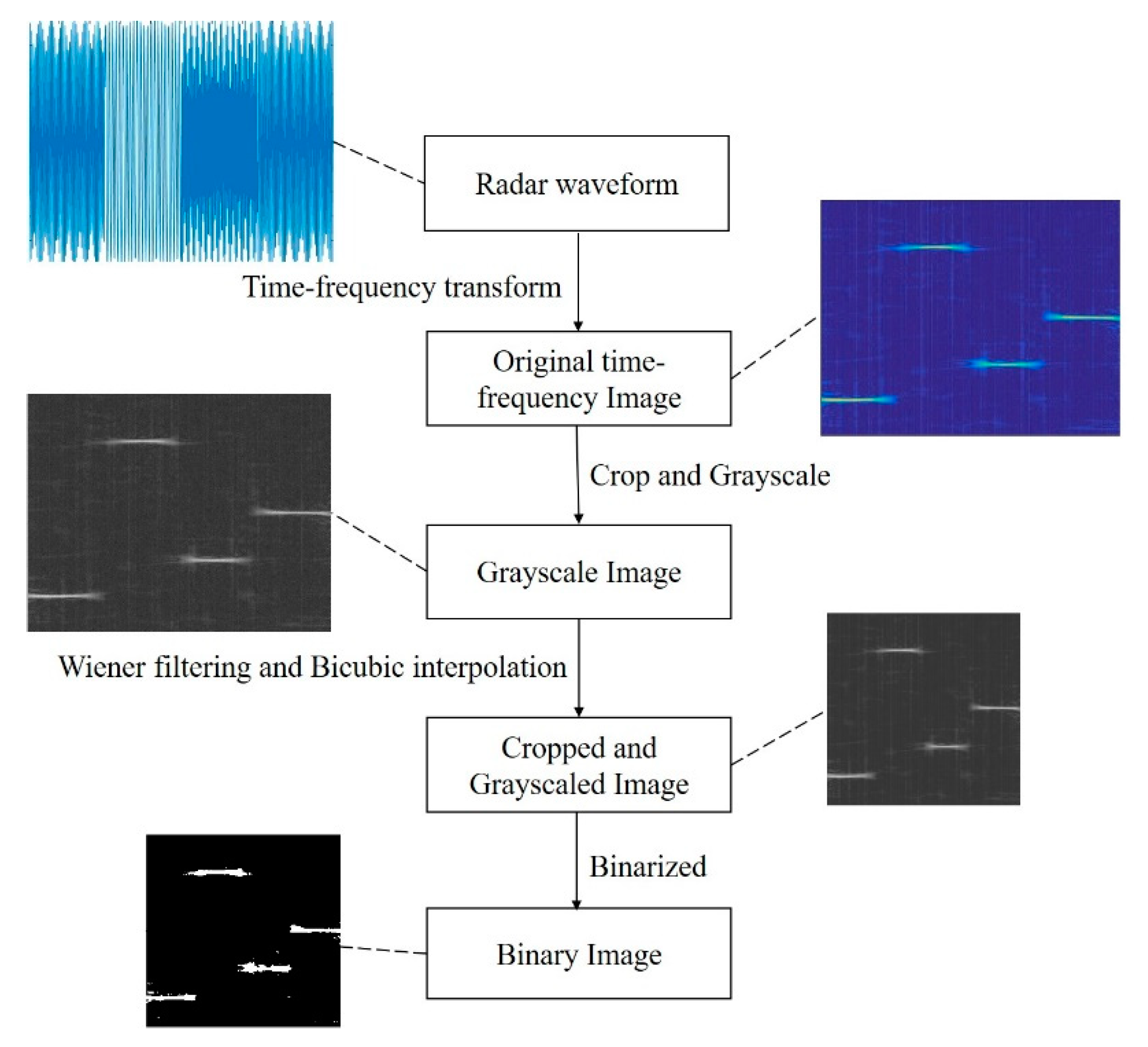
3.2. Time-Frequency Image Preprocessing
4. Feature Extraction and Dual-Channel CNN Model Design
4.1. Feature Extraction
4.2. Dual-Channel Convolutional Neural Network Model
4.2.1. One-Dimensional Convolution Channel
- Gradient calculation
- 2.
- Gradient Direction Histogram Construction
4.2.2. Two-Dimensional Convolution Channel
5. Feature Fusion and Recognition via MLP
6. Experimental Results and Analysis
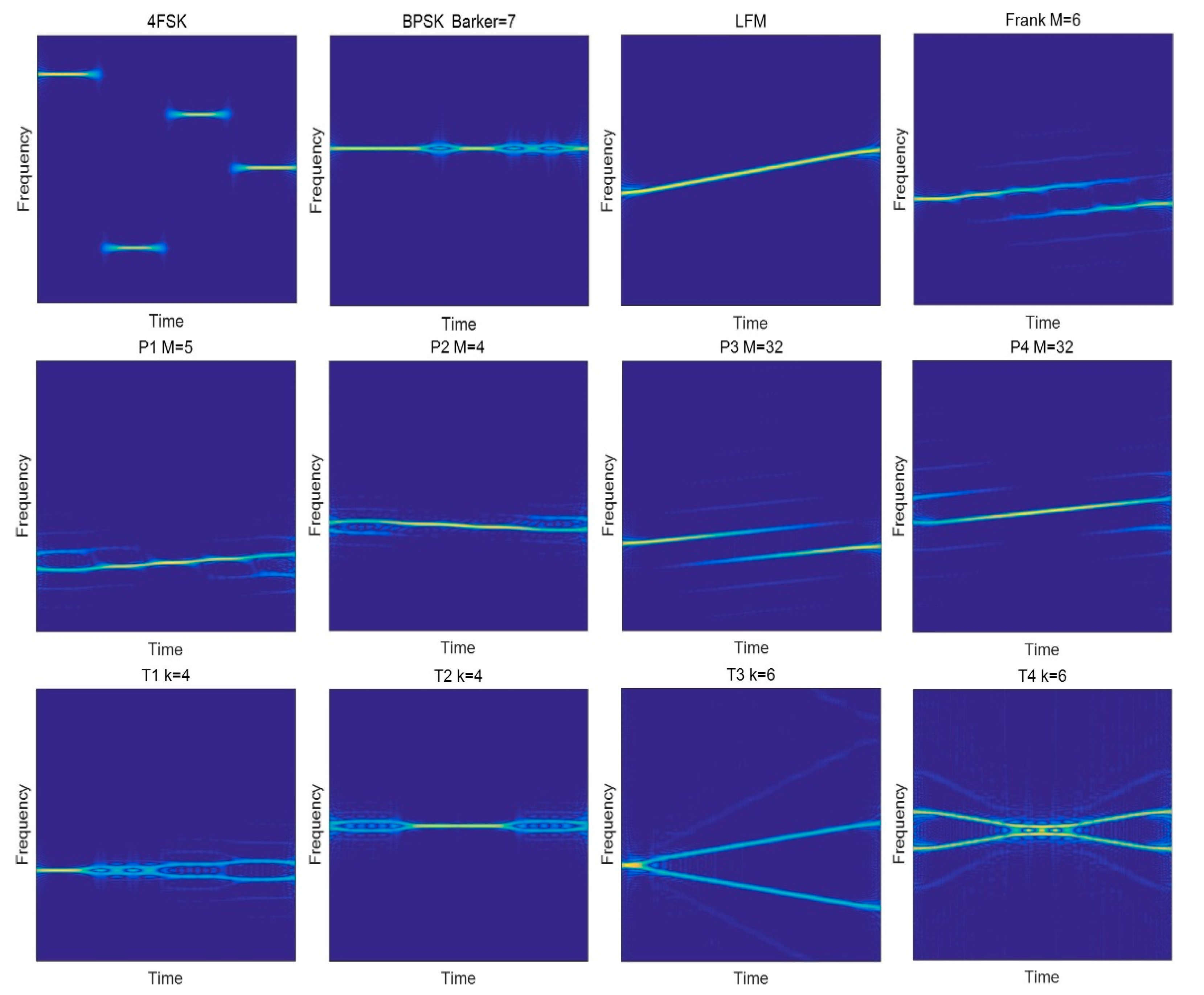
6.1. Signal Generation
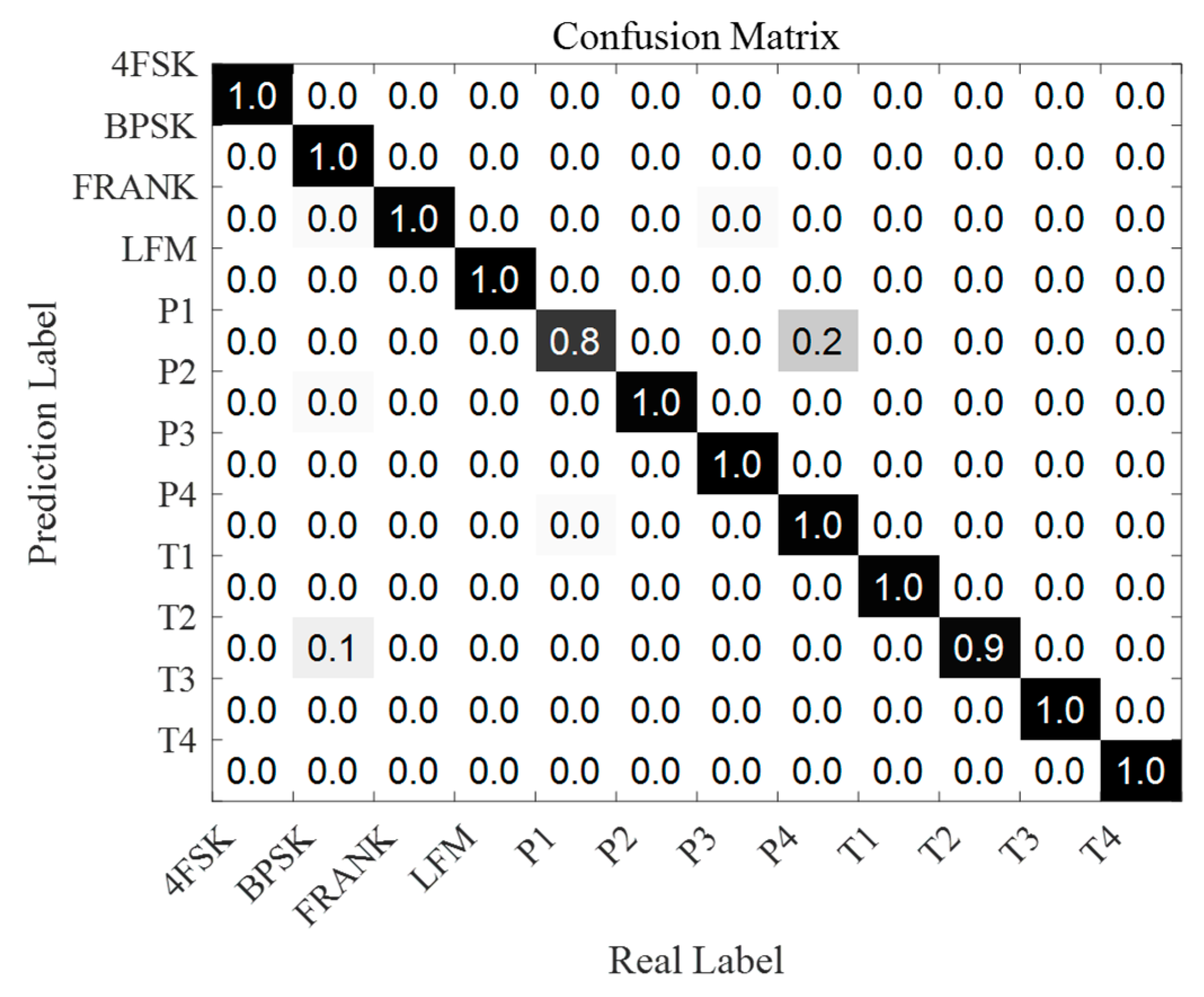
6.2. Recognition Accuracy Analysis
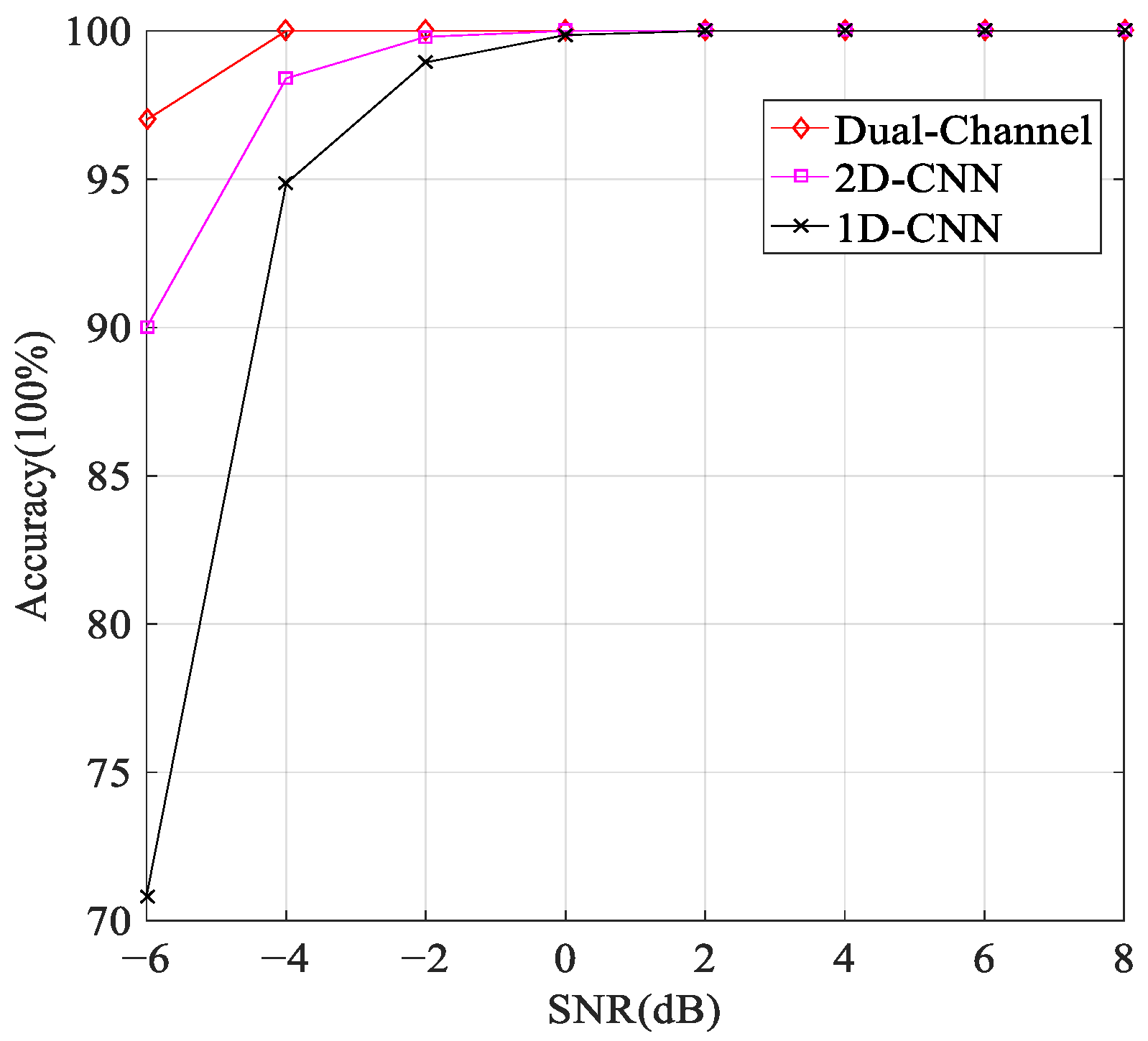
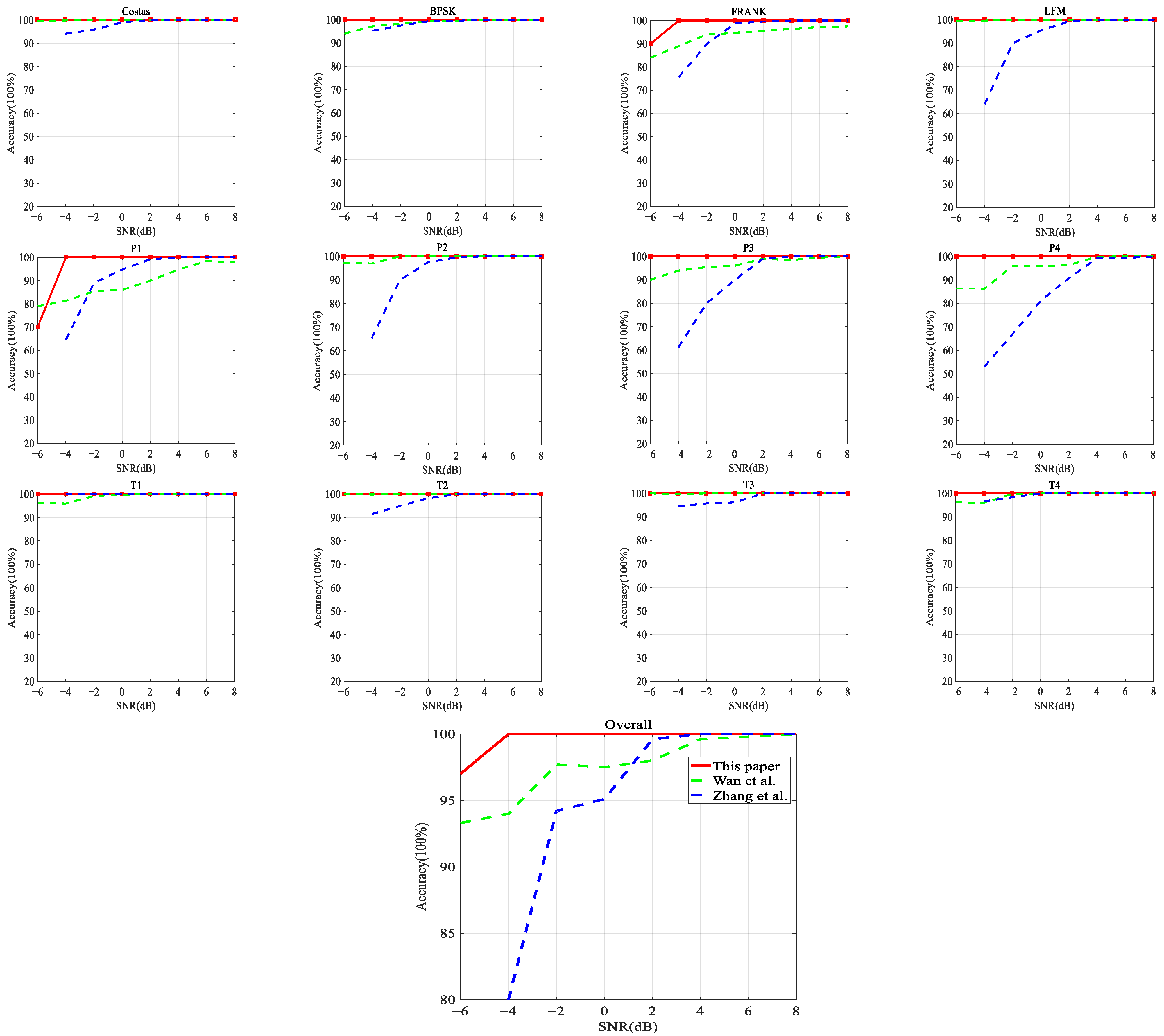
6.3. Algorithmic Comparison Experiment
6.4. Robustness Experiment
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tao, W.A.N.; Kaili, J.; Jingyi, L.; Yanli, T.A.N.G.; Bin, T.A.N.G. Detection and recognition of LPI radar signals using visibility graphs. J. Syst. Eng. Electron. 2020, 31, 1186–1192. [Google Scholar] [CrossRef]
- Shi, C.; Qiu, W.; Wang, F.; Salous, S.; Zhou, J. Cooperative LPI Performance Optimization for Multistatic Radar System: A Stackelberg Game. In Proceedings of the International Applied Computational Electromagnetics Society Symposium—China (ACES), Nanjing, China, 8–11 August 2019; pp. 1–2. [Google Scholar]
- Nandi, A.K.; Azzouz, E.E. Automatic analogue modulation recognition. Signal Processing 1995, 46, 211–222. [Google Scholar] [CrossRef]
- Dudczyk, J.; Kawalec, A. Specific emitter identification based on graphical representation of the distribution of radar signal parameters. Bull. Pol. Acad. Sci. Tech. Sci. 2015, 63, 391–396. [Google Scholar] [CrossRef]
- Gupta, D.; Raj, A.A.B.; Kulkarni, A. Multi-Bit Digital Receiver Design for Radar Signature Estimation. In Proceedings of the 3rd IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), Bangalore, India, 18–19 May 2018; pp. 1072–1075. [Google Scholar]
- Huang, G.; Ning, F.; Liyan, Q. Sparsity-based radar signal sorting method in electronic support measures system. In Proceedings of the 12th IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Qingdao, China, 16–18 July 2015; pp. 1298–1302. [Google Scholar]
- Kishore, T.R.; Rao, K.D. Automatic intrapulse modulation classification of advanced LPI radar waveforms. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 901–914. [Google Scholar] [CrossRef]
- Iglesias, V.; Grajal, J.; Royer, P.; Sanchez, M.A.; Lopez-Vallejo, M.; Yeste-Ojeda, O.A. Real-time low-complexity automatic modulation classifier for pulsed radar signals. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 108–126. [Google Scholar] [CrossRef]
- Schleher, D.C. LPI radar: Fact or fiction. IEEE Aerosp. Electron. Syst. Mag. 2006, 21, 3–6. [Google Scholar] [CrossRef]
- Mingqiu, R.; Jinyan, C.; Yuanqing, Z.; Jun, H. Radar signal feature extraction based on wavelet ridge and high order spectral analysis. In Proceedings of the IET International Radar Conference 2009, Guilin, China, 20–22 April 2009; pp. 1–5. [Google Scholar]
- Wang, C.; Gao, H.; Zhang, X. Radar signal classification based on auto-correlation function and directed graphical model. In Proceedings of the IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Hong Kong, 5–8 August 2016; pp. 1–4. [Google Scholar]
- Cohen, L. Time-frequency distributions-a review. Proc. IEEE 1989, 77, 941–981. [Google Scholar] [CrossRef] [Green Version]
- López-Risueño, G.; Grajal, J.; Sanz-Osorio, A. Digital channelized receiver based on time-frequency analysis for signal interception. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 879–898. [Google Scholar] [CrossRef]
- Zilberman, E.R.; Pace, P.E. Autonomous time-frequency morphological feature extraction algorithm for LPI radar modulation classification. In Proceedings of the International Conference on Image Processing, Atlanta, GA, USA, 8–11 October 2006; pp. 2321–2324. [Google Scholar]
- Zhang, M.; Liu, L.; Diao, M. LPI radar waveform recognition based on time-frequency distribution. Sensors 2016, 16, 1682. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Diao, M.; Gao, L.; Liu, L. Neural networks for radar waveform recognition. Symmetry 2017, 9, 75. [Google Scholar] [CrossRef] [Green Version]
- Wan, J.; Yu, X.; Guo, Q. LPI radar waveform recognition based on CNN and TPOT. Symmetry 2019, 11, 725. [Google Scholar] [CrossRef] [Green Version]
- Guo, Q.; Yu, X.; Ruan, G. LPI radar waveform recognition based on deep convolutional neural network transfer learning. Symmetry 2019, 11, 540. [Google Scholar] [CrossRef] [Green Version]
- Qu, Z.; Mao, X.; Deng, Z. Radar signal intra-pulse modulation recognition based on convolutional neural network. IEEE Access 2018, 6, 43874–43884. [Google Scholar] [CrossRef]
- Wang, H.; Diao, M.; Gao, L. Low probability of intercept radar waveform recognition based on dictionary leaming. In Proceedings of the 10th International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 18–20 October 2018; pp. 1–6. [Google Scholar]
- Zhang, S.; Wang, X. Human detection and object tracking based on Histograms of Oriented Gradients. In Proceedings of the Ninth International Conference on Natural Computation (ICNC), Shenyang, China, 23–25 July 2013; pp. 1–6. [Google Scholar]
- Korkmaz, S.A.; Akçiçek, A.; Bínol, H.; Korkmaz, M.F. Recognition of the stomach cancer images with probabilistic HOG feature vector histograms by using HOG features. In Proceedings of the IEEE 15th International Symposium on Intelligent Systems and Informatics (SISY), Subotica, Serbia, 14–16 September 2017; pp. 339–342. [Google Scholar]
- Rao, Q.; Yu, B.; He, K.; Feng, B. Regularization and Iterative Initialization of softmax for Fast Training of Convolutional Neural Networks. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar]
- Huynh-The, T.; Doan, V.S.; Hua, C.H.; Pham, Q.V.; Nguyen, T.V.; Kim, D.S. Accurate LPI Radar Waveform Recognition with CWD-TFA for Deep Convolutional Network. IEEE Wirel. Commun. Lett. 2021, 10, 1638–1642. [Google Scholar] [CrossRef]
- Ben Atitallah, S.; Driss, M.; Boulila, W.; Koubaa, A.; Ben Ghézala, H. Fusion of convolutional neural networks based on Dempster—Shafer theory for automatic pneumonia detection from chest X-ray images. Int. J. Imaging Syst. Technol. 2022, 32, 658–672. [Google Scholar] [CrossRef]


| Item | Model/Version |
|---|---|
| CPU | Intel(R) Core(TM) i7-10875H |
| GPU | NVIDIA GeForce RTX 2060 |
| RAM | 16 GB |
| SOFTWARE | R2016b/Python 3.7 |
| Radar Waveform | Simulation Parameter | Ranges |
|---|---|---|
| Sampling frequency | 1 ( = 200 MHz) | |
| LFM | Initial frequency Bandwidth | |
| BPSK | Barker codes Carrier frequency | |
| 4FSK | Fundamental frequency | |
| Frank and P1 | Carrier frequency Samples of frequency stem M | |
| P2 | Carrier frequency Samples of frequency stem M | |
| P3 and P4 | Carrier frequency | |
| T1-T4 | Number of segments k |
| Saved Model/dB | Test Data/dB | Recognition Accuracy |
|---|---|---|
| −6 | 0 | 95% |
| −4 | 2 | 92.6% |
| −2 | 2 | 93% |
| 2 | −2 | 96.62% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quan, D.; Tang, Z.; Wang, X.; Zhai, W.; Qu, C. LPI Radar Signal Recognition Based on Dual-Channel CNN and Feature Fusion. Symmetry 2022, 14, 570. https://doi.org/10.3390/sym14030570
Quan D, Tang Z, Wang X, Zhai W, Qu C. LPI Radar Signal Recognition Based on Dual-Channel CNN and Feature Fusion. Symmetry. 2022; 14(3):570. https://doi.org/10.3390/sym14030570
Chicago/Turabian StyleQuan, Daying, Zeyu Tang, Xiaofeng Wang, Wenchao Zhai, and Chongxiao Qu. 2022. "LPI Radar Signal Recognition Based on Dual-Channel CNN and Feature Fusion" Symmetry 14, no. 3: 570. https://doi.org/10.3390/sym14030570
APA StyleQuan, D., Tang, Z., Wang, X., Zhai, W., & Qu, C. (2022). LPI Radar Signal Recognition Based on Dual-Channel CNN and Feature Fusion. Symmetry, 14(3), 570. https://doi.org/10.3390/sym14030570







