Runtime Software Architecture-Based Reliability Prediction for Self-Adaptive Systems
Abstract
:1. Introduction
- We propose a method for constructing the software runtime architecture model, which includes a runtime architecture structural model and a behavioral model. The architecture structural model contains data about the topology of the system, and the behavioral model can be obtained by monitoring the target system to get the observations for updating the behavioral model at runtime according to the adaptation strategy.
- We present a technique to construct a reliability prediction-oriented analysis model. The reliability of components and the transition probability between components are added to obtain the prediction-oriented runtime reliability expansion model, then through model conversion, the prediction-oriented runtime reliability expansion model is converted into a Markov analysis model.
- We provide a method to obtain the reliability prediction result at runtime through the Markov analysis model.
- We conduct an experimental study based on rainbow-znn software to show the effectiveness of the proposed approach.
2. Related Work
- A reliability prediction method based on RSA instead of DSA.
- An approach that leverages the Rainbow framework for the construction of an RSA structural model, then the construction of the RSA behavioral model.
- A way to analyze the impact of changes caused by adaptive strategies on the overall software reliability.
3. Method Development
3.1. The Principle of the Method
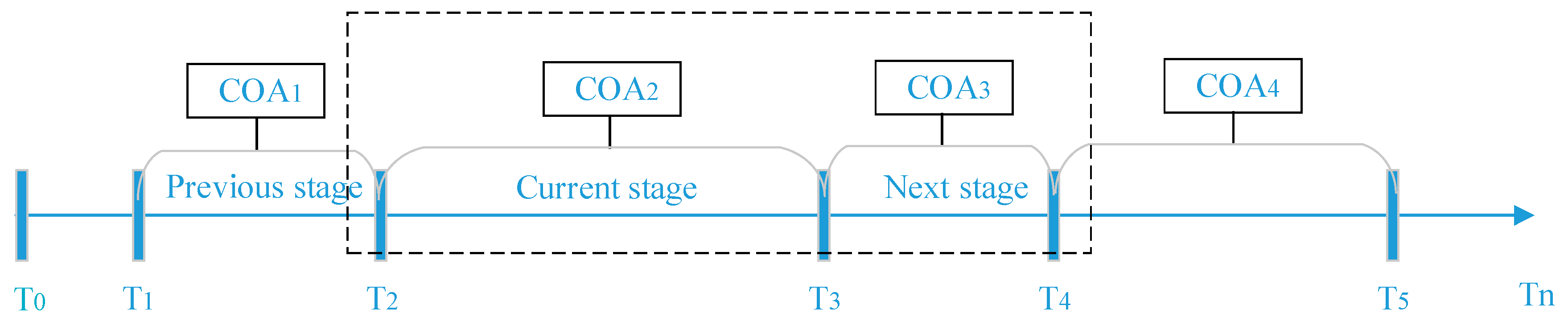
3.1.1. Time
3.1.2. Mechanism
3.1.3. Process
3.2. Key Steps
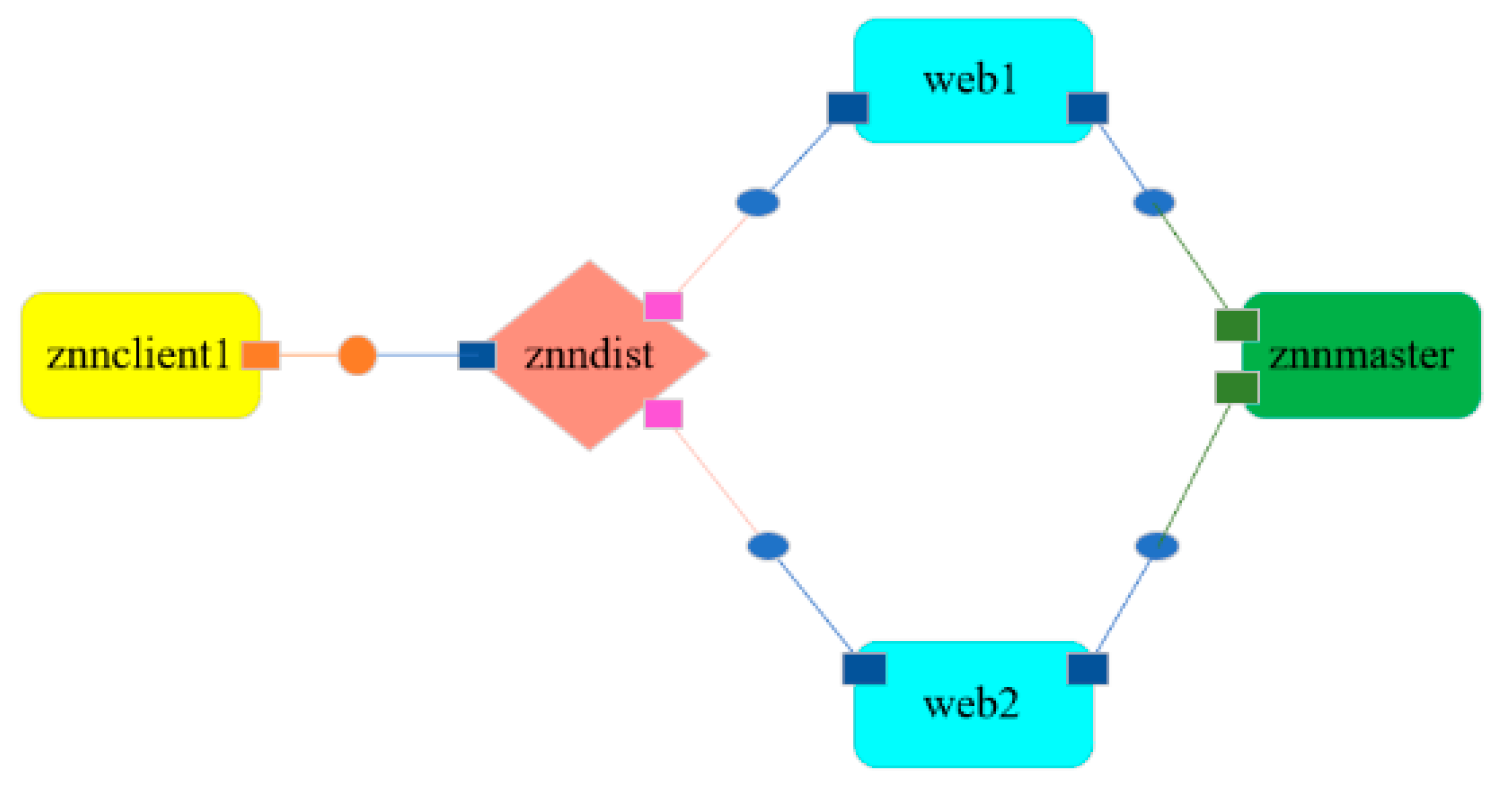
3.2.1. Step 1: Construct RSA Structural Model (RSASM)
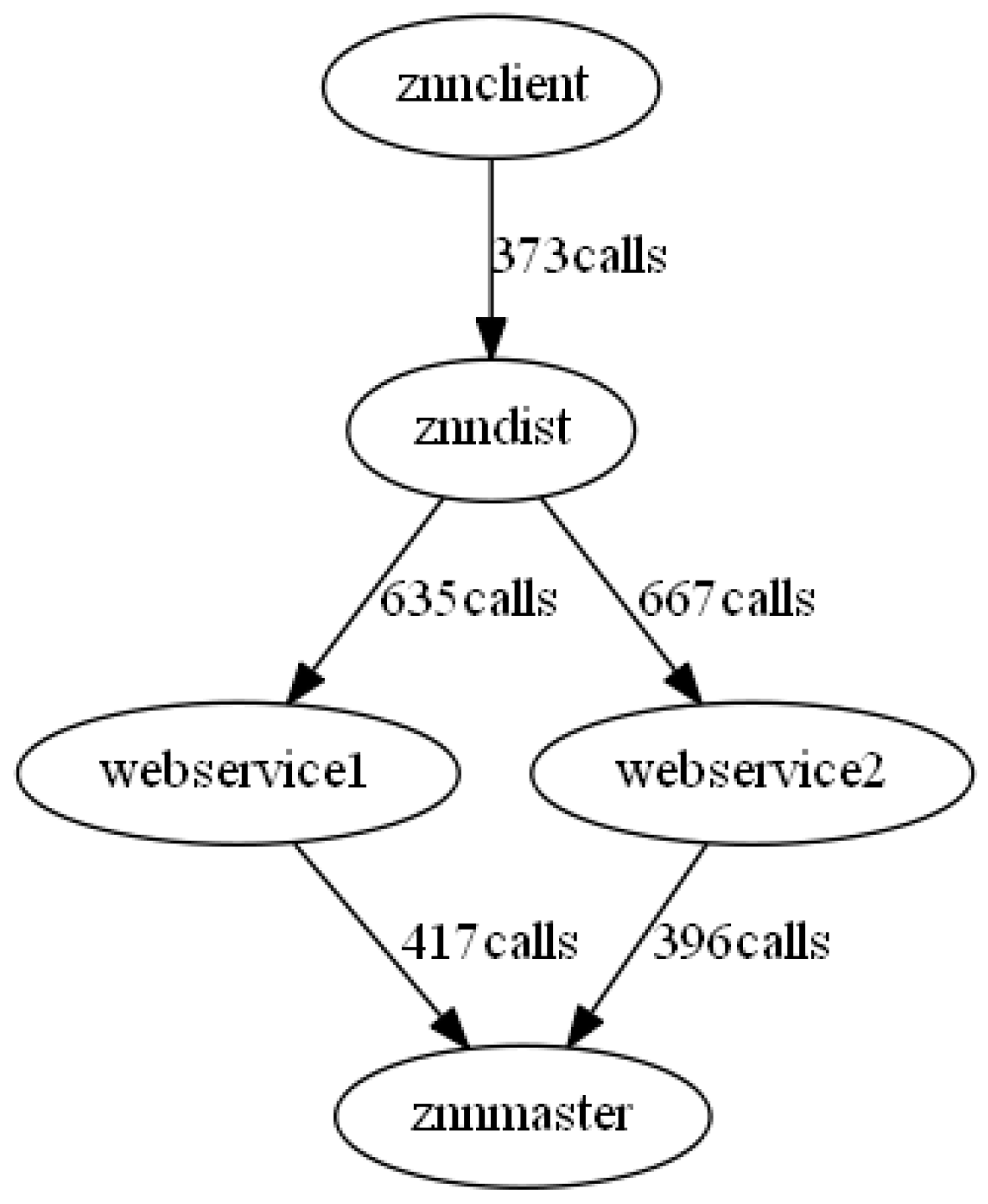
3.2.2. Step 2: Construct RSA Behavioral Model (RSABM)
- According to the RSASM, determine the objects to be monitored.
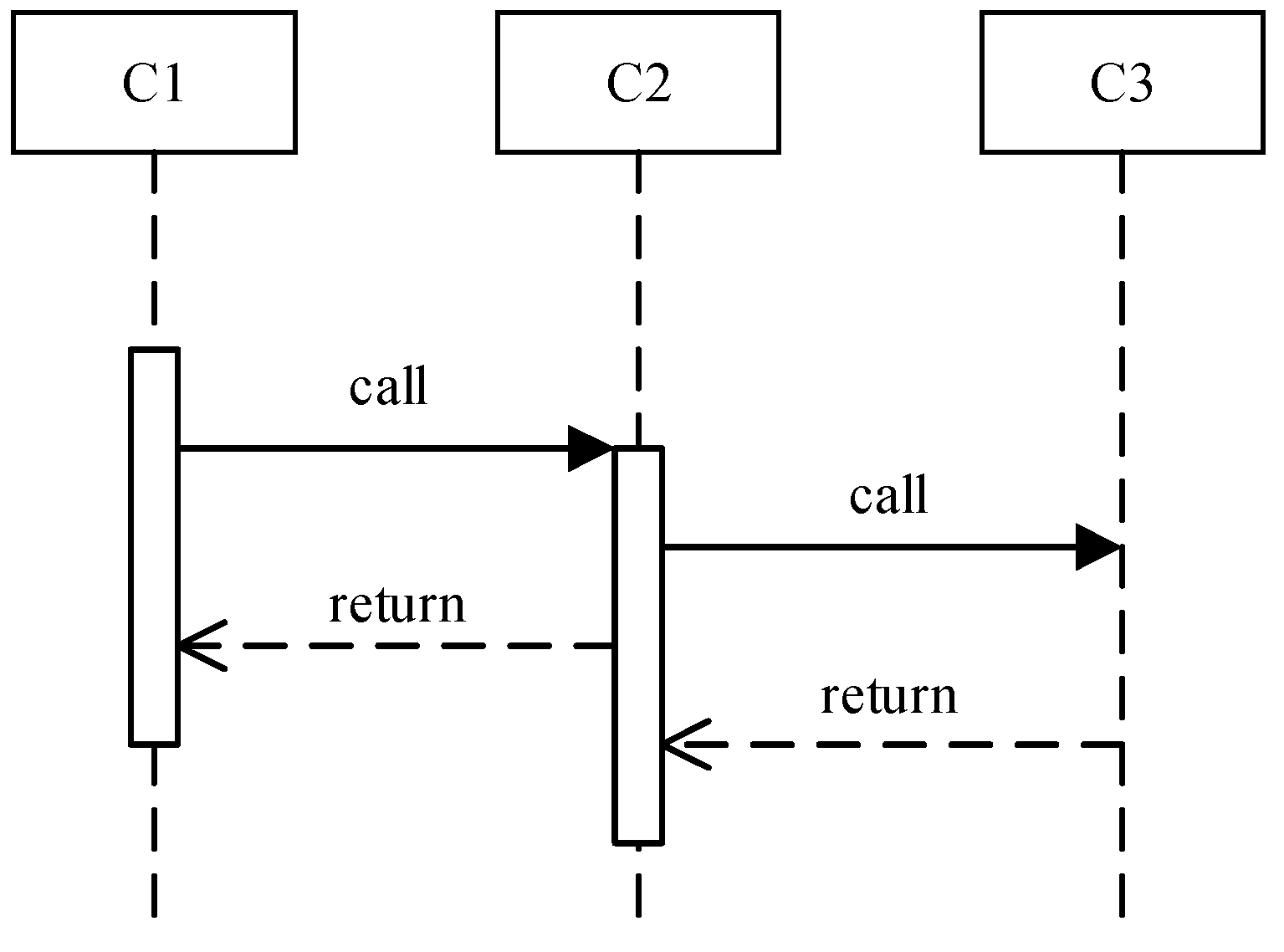
- Declare the proxy bean while monitoring; this corresponds to the application bean and has the same remote interface as the application bean.
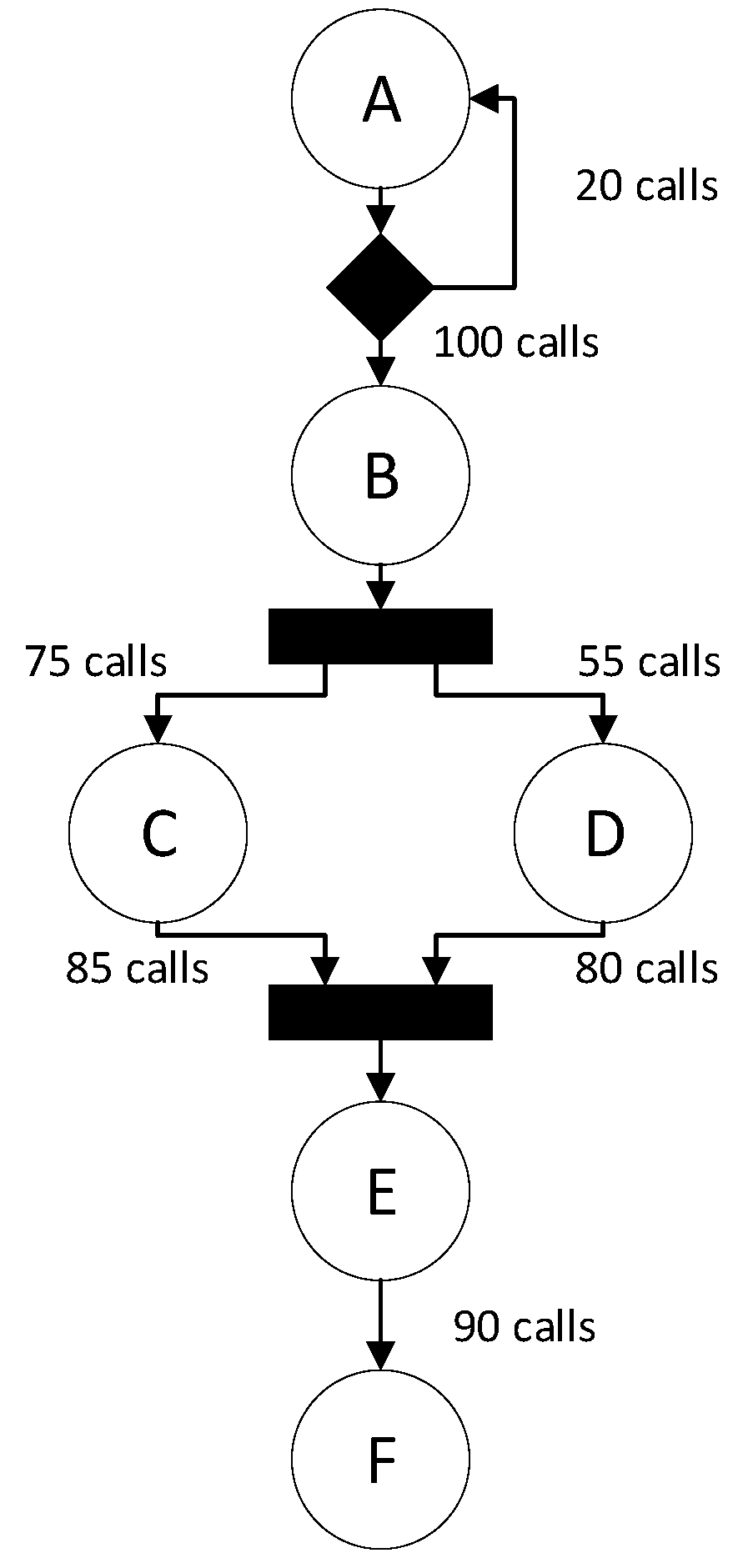
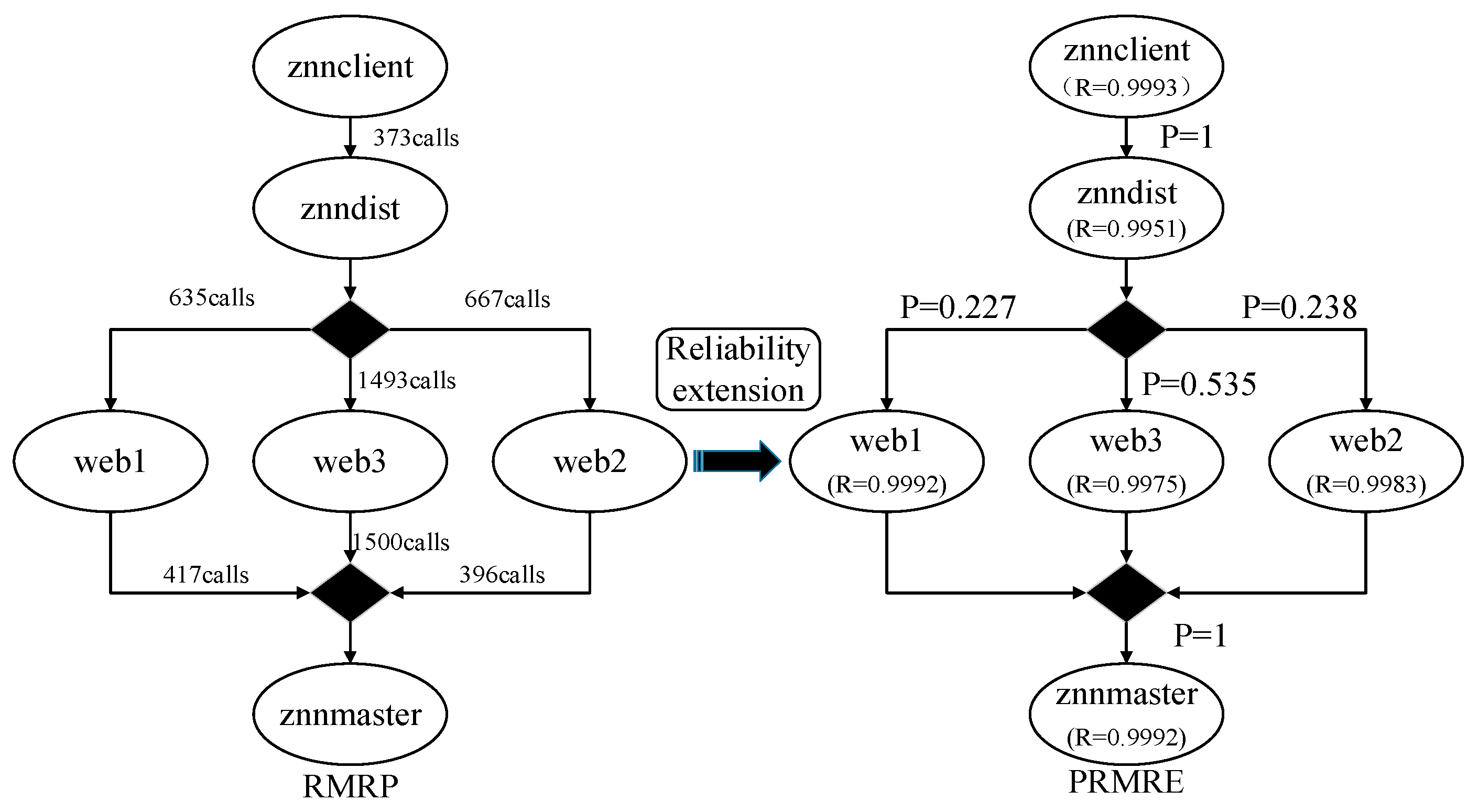
- Declare the monitor bean, which completes the extraction of dynamic component call information, which, in turn, includes the call relationship, the number of calls between components and the call timing.
- Declare the interface between the proxy bean and the monitor bean which have been established in 2 and 3.
- Construct the RSABM basing it on the model construction algorithm, which is shown in Algorithm 1.
| Algorithm 1 Pseudo-code for the RSA behavioral model construction algorithm. |
| Input: The invocation sequence of components, list. The format of each line is: Caller:Callee The original invocation timestamp list, timeList. The format of each line is: ComponentName:IN/OUT: TimeStamp Output: The adjacent matrix of component invocation, invMat 1 Initiate empty stack stackInv and stackTmp; 2 preComp←column 1 of the first element in list; 3 for each line in list do 4 compName←column 1 of line; 5 notation←colunm 2 of line; 6 if notation = ’IN’ then 7 Push compName in stackInv; 8 if Rows of invMat contains compName then 9 Increase the value at row preComp, column compName by 1; 10 end 11 else 12 Add a row and a column in invMat with compName as the name; 13 Set the value at row preComp, column compName as 0; 14 end 15 preComp←compName; 16 end 17 if notation = ’OUT’ then 18 topElement←Pop out the element on top of stackInv; 19 if topElement = compName then 20 Pop out each element in stackTmp and push it into stackInv; 21 end 22 else 23 Set the value at row preComp, column compName as negative; 24 Set the value at row preComp, column topElement as negative; 25 Push topElement in stackTmp; 26 Return to 18 27 end 28 preComp←the element left on top of stackInv 29 end 30 end |
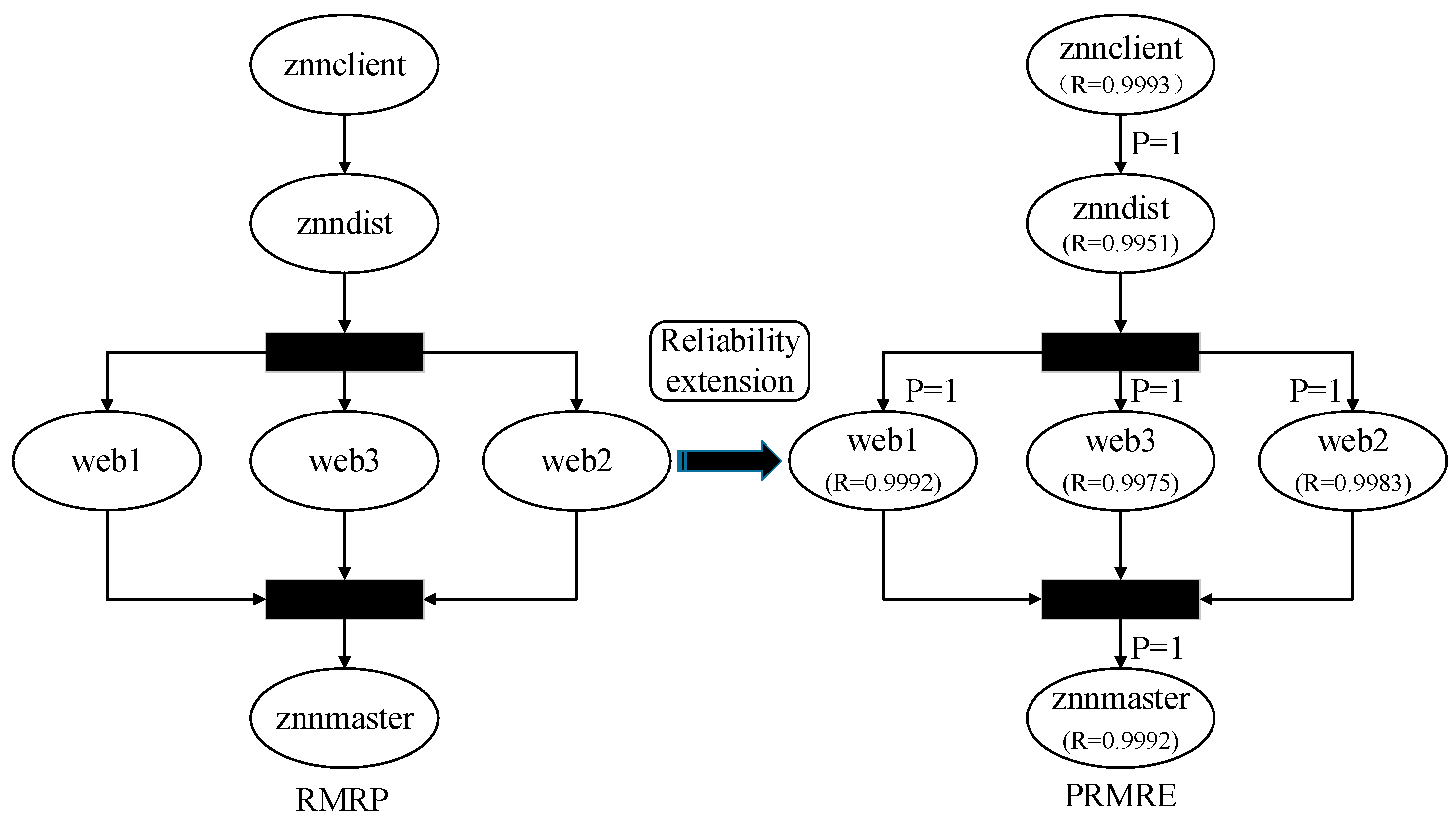
3.2.3. Step 3: Construct a Reliability Prediction-Oriented Runtime Model (RMRP)
- Structure information, i.e., what components are composed of the software.
- Relationship of caller and callee between components.
- The number of calls and transition modes between components. The determination of the transition probability between components is affected by the number of calls and the transfer mode between components, therefore, the number of calls and the transfer mode should also be given in RMRP.
- Construct the RSABM running in the current adaptation phase
- 2.
- Determine the adaptive strategies
- 3.
- Acquire the RMRP on the basis of the RSABM and adaptive strategies
- Perform adding component operation with the conditional transfer mode
- 2.
- Perform component replacement operation with the conditional transfer mode
- 3.
- Perform deleting component operation with the conditional transfer mode
- 4.
- Perform changing the message calling mode operation with the conditional transfer mode
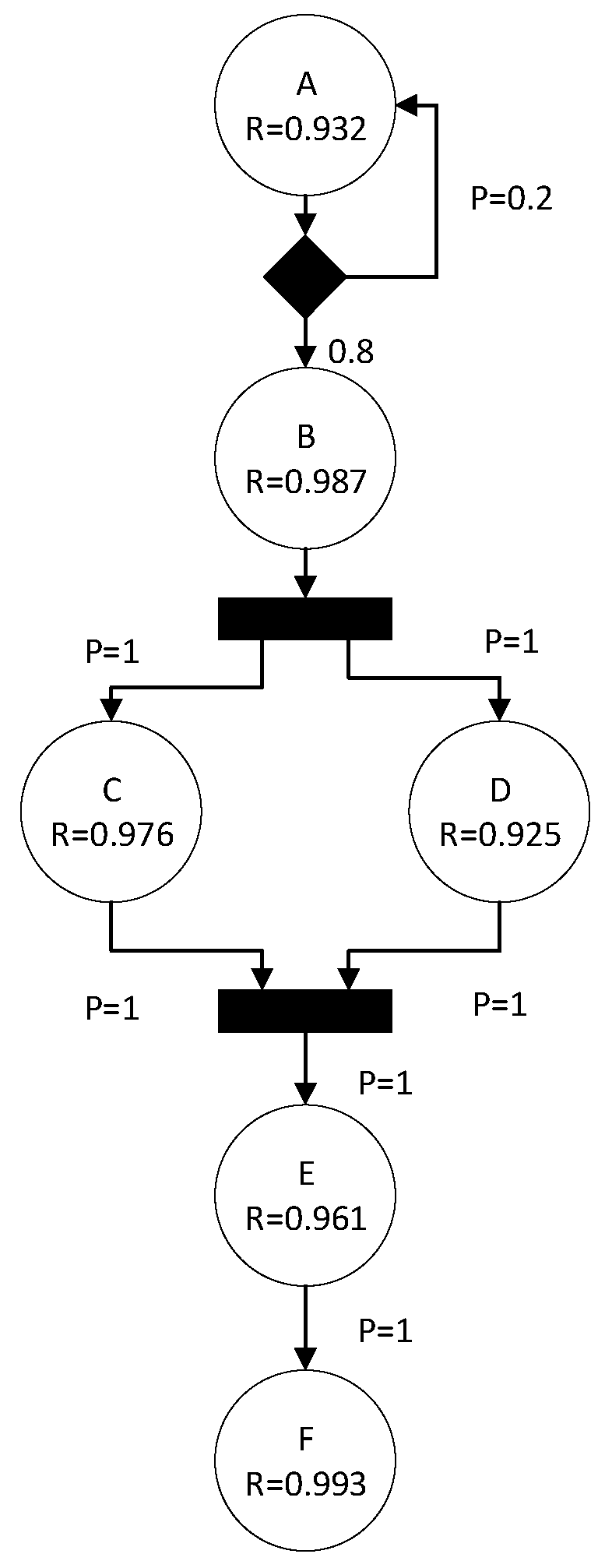
3.2.4. Step 4: Extend Reliability Information to RMRP
- Transition probability between components under the sequential transition mode
- 2.
- Transition probability between components under the concurrent transition mode
- 3.
- Transition probability between components under the conditional transition mode
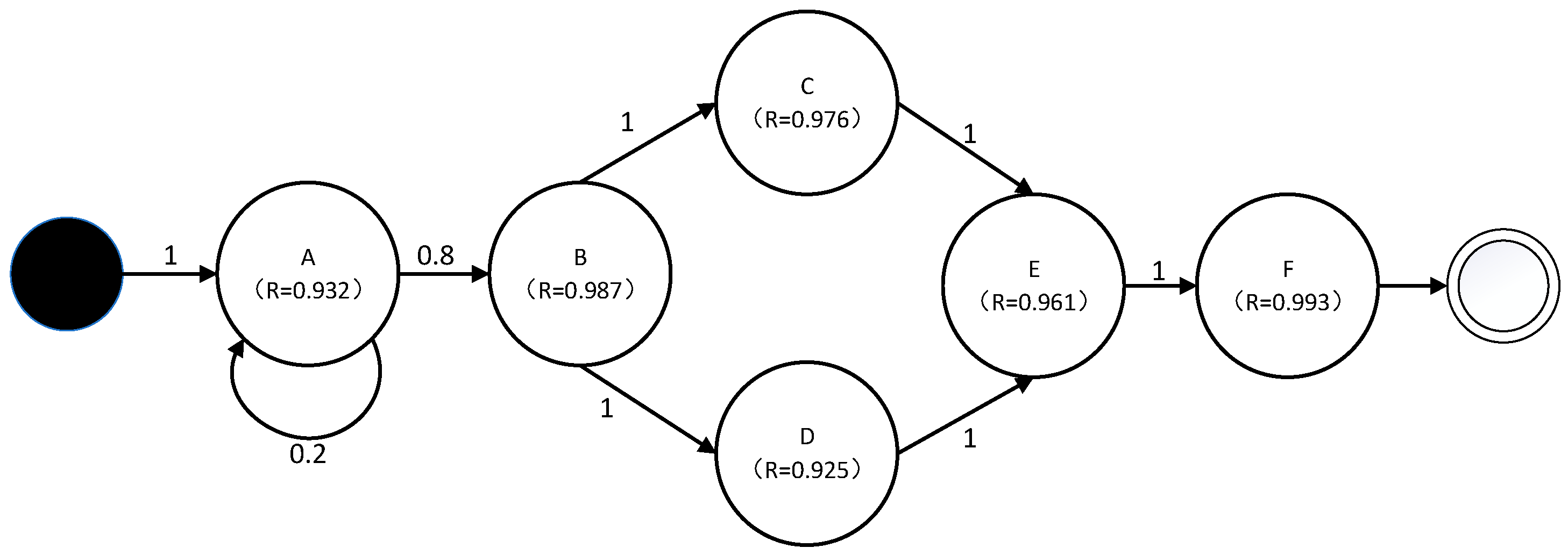
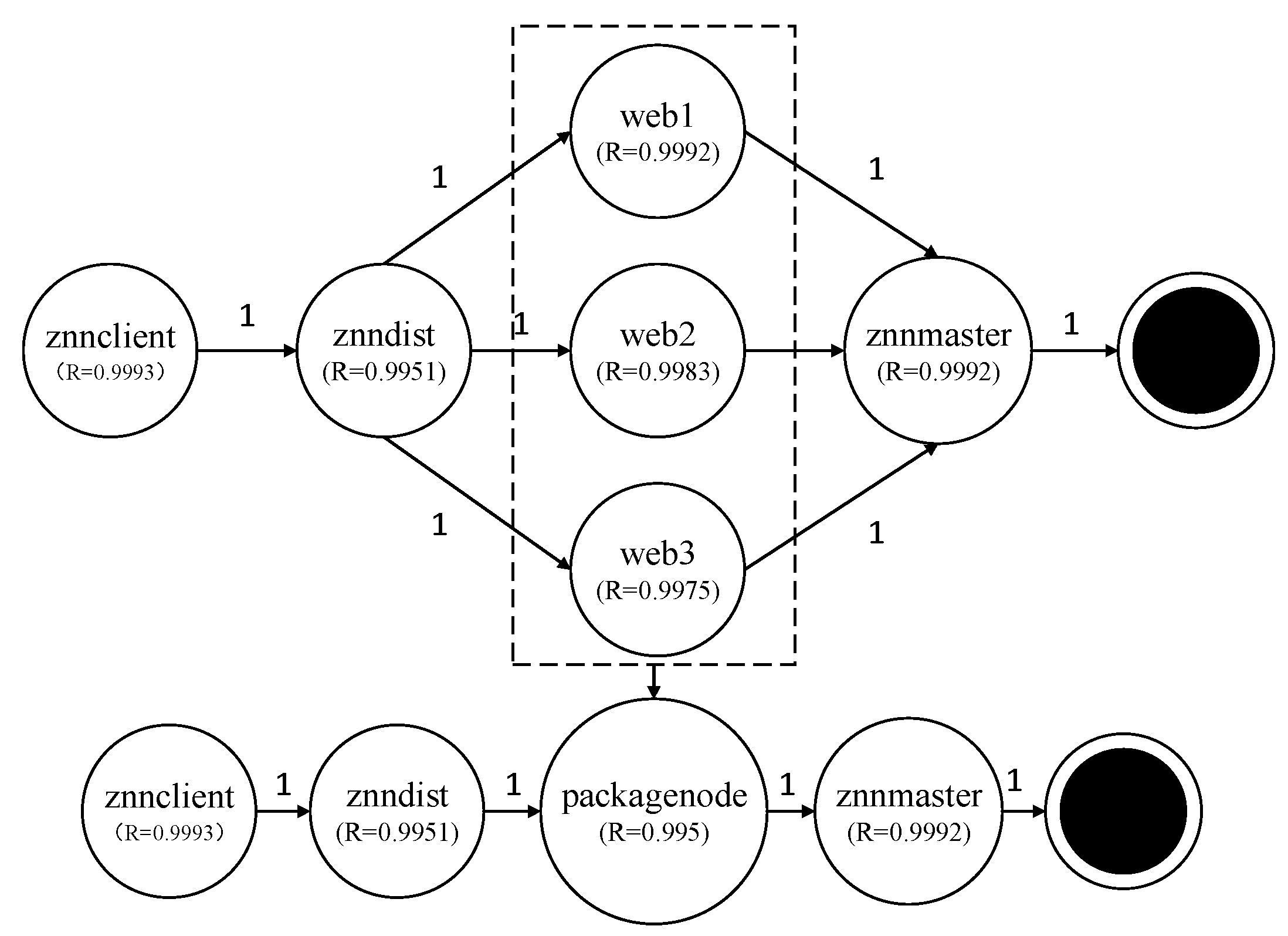
3.2.5. Step 5: Convert PRMRE to a Markov Analysis Model
3.2.6. Step 6: Obtain Reliability Prediction
4. Case Study
4.1. Experimental Setup
- The web services 1 to 4 are the four content servers running Apache-2.2.16 respectively.
- Znnmaster service (rainbow-znn server) is deployed in Node 3, a separate machine, running Hyperic-sigar, COMPAS J2EE and mysql-5.5.25.
- Znndist is the proxy machine realizing the load balancing service running distributor-0.7 provided by install-lb.sh in the Znn.com installation package.
- Znnclient is deployed in Node 1 running Jmeter-2.5.1 to simulate user access to the Znn.com.
4.2. Experiment Procedure
- Step 1:
- Start the Znn.com through the Rainbow and znnmaster console.
- Step 2:
- Activate web service 1 when the system starts running and let other services be in waiting state.
- Step 3:
- Start Jmeter to simulate the user access of the client and write a script for simulating the service request sent by the Znn.com client.
- Step 4:
- Collect the environmental data of Node 3 through the aid of Hyperic-sigar after the system is instantiated.
- Step 5:
- Enter the ‘show-znn.sh-configuration’ command on the console to record the start and end time of each adaptation stage, and the times that the Znn.com has performed adaptation, at which adaptation phase the system enters, while the environmental information of Node 3 is continuously calculated.
- Step 6:
- When the Znn.com enters the fourth adaptation stage, the environmental data collected in the first three adaptation stages should be used to perform the behavior trend analysis of the CPU usage.
- Step 7:
- When the Znn.com enters the fifth adaptation stage, the reliability prediction will be started and the CPU usage behavior trend analysis model obtained in the fourth adaptation stage will be used to analyze the behavior trend of CPU usage during the fifth adaptation stage.
- Step 8:
- We make a copy of the software architecture for each eligible strategy and apply its changes. As previously discussed, at this moment there are three eligible strategies.
- Step 9:
- Generate RMRP for each eligible strategy alternative.
- Step 10:
- Generate PRMRE for each strategy alternative.
- Step 11:
- Generate DTMC for each strategy alternative and calculate the reliability prediction results.
- Step 12:
- Determine the best strategy according to the reliability prediction results.
4.3. Experimental Results
4.3.1. RSABM of the Znn.com
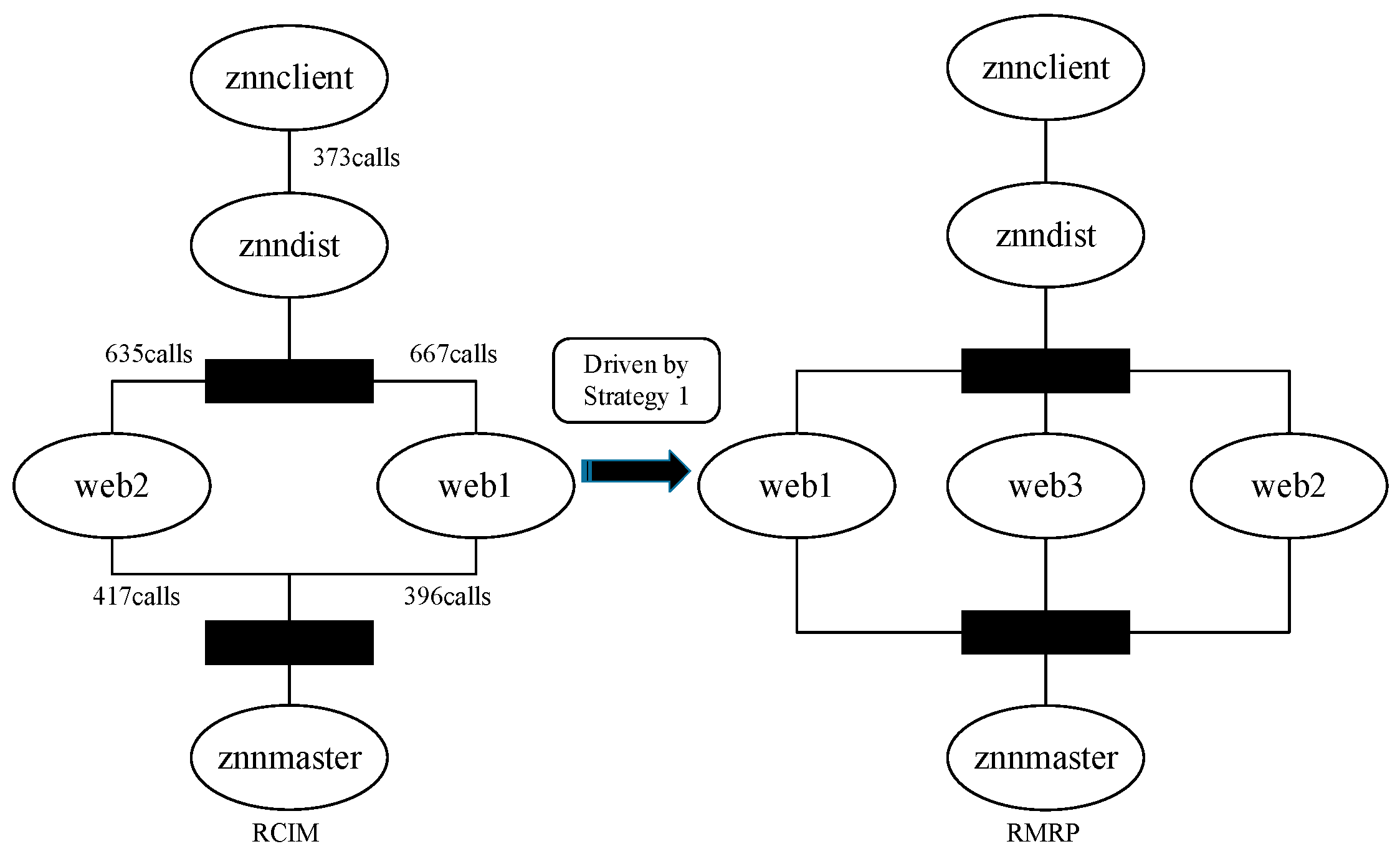
4.3.2. RMRP of the Znn.com
- Strategy 1:
- When the CPU usage rate reaches 80%, an additional server will be added and the schedule mode of the load balancing server will be set to random (supporting concurrency).
- Strategy 2:
- When the CPU usage rate reaches 80%, switch the news-providing mode from the multimedia mode to the text mode, and set the schedule mode of the load balancing server to the polling mode.
- Strategy 3:
- When the CPU usage rate reaches 80%, add an additional server and set the schedule mode of the load balancing server to the polling mode.
- RMRP driven by Strategy 1
- 2.
- RMRP driven by Strategy 2
- 3.
- RMRP driven by Strategy 3
4.3.3. PRMRE of the Znn.com
- Reliability extension on RMRP driven by Strategy 1
- 2.
- Reliability extension on RMRP driven by Strategy 2
- 3.
- Reliability extension on RMRP driven by Strategy 3
4.3.4. Analyze the Runtime Reliability Prediction Results Based on Markov Model
5. Conclusions and Future Work
- Assess the impact of adaptive strategies. This approach presents a method to predict the reliability impact of each adaptive strategy at runtime. We applied the changes imposed by each strategy at the architecture level and predicted the reliability outcome of such changes to support the planning of the self-adaptive system.
- Formal description of the translation from architectural model to DTMC. This method proposed a formal description to a stochastic model. The goal was to support a universal interpretation for the translation.
- Experiment on rainbow-znn software to validate the feasibility of this method.
- The content of the experiment is not sufficient in that the work lacks performance verification and efficiency analysis.
- No sensitivity analysis has been performed on factors which may have an impact on the software reliability prediction results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, B.; de Lemos, R.; Giese, H.; Inverardi, P.; Magee, J.; Andersson, J.; Becker, B.; Bencomo, N.; Brun, Y.; Cukic, B.; et al. Software engineering for self-adaptive systems: A research roadmap. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5525, pp. 1–26. [Google Scholar] [CrossRef] [Green Version]
- Kluge, T. A Role-Based Architecture for Self-Adaptive Cyber-Physical Systems. In Proceedings of the IEEE/ACM 15th International Symposium on Software Engineering for Adaptive and Self-Managing Systems (SEAMS ’20), Seoul, Korea, 7–8 October 2020; ACM: New York, NY, USA, 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Heinrich, R. Architectural run-time models for performance and privacy analysis in dynamic cloud applications. ACM Sigmetrics Perform. Eval. Rev. 2016, 43, 13–22. [Google Scholar] [CrossRef]
- Filieri, A.; Ghezzi, C.; Leva, A.; Maggio, M. Self-adaptive software meets control theory: A preliminary approach supporting reliability requirements. In Proceedings of the IEEE/ACM International Conference on Automated Software Engineering, ACM, Lawrence, KS, USA, 6–10 November 2011; IEEE Computer Society: Los Alamitos, CA, USA; pp. 283–292. [Google Scholar] [CrossRef] [Green Version]
- Angelopoulos, K.; Papadopoulos, A.V.; Souza, V.E.; Mylopoulos, J. Engineering Self-Adaptive Software Systems. ACM Trans. Auton. Adapt. Syst. (TAAS) 2018, 13, 1–27. [Google Scholar] [CrossRef]
- Filieri, A.; Maggio, M.; Angelopoulos, K.; D’ippolito, N.; Gerostathopoulos, I.; Hempel, A.B.; Hoffmann, H.; Jamshidi, P.; Kalyvianaki, E.; Klein, C.; et al. Control Strategies for Self-Adaptive Software Systems. ACM Trans. Auton. Adapt. Syst. 2017, 11, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Kramer, J.; Magee, J. Self-Managed Systems: An Architectural Challenge. In Proceedings of the Future of Software Engineering (FOSE ’07), Minneapolis, MN, USA, 23–25 May 2007. [Google Scholar]
- Chen, B.; Peng, X.; Liu, Y.; Song, S.; Zheng, J.; Zhao, W. Architecture-based behavioral adaptation with generated alternatives and relaxed constraints. IEEE Trans. Serv. Comput. 2019, 12, 73–87. [Google Scholar] [CrossRef]
- Wang, W.-L.; Pan, D.; Chen, M.-H. Architecture-based software reliability modeling. J. Syst. Softw. 2006, 79, 132–146. [Google Scholar] [CrossRef]
- Bass, L.; Clements, P.; Kazman, R. Software Architecture in Practice; Addison-Wesley Longman, Inc.: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Medvidovic, N.; Oreizy, P.; Taylor, R.N. Reuse of off-the-shelf components in C2 style architectures. Proceedings of 19th International Conference on Software Engineering, Boston, MA, USA, 17–23 May 1997; pp. 692–700. [Google Scholar]
- Oreizy, P.; Medvidovic, N.; Taylor, R.N. Architecture-based runtime software evolution. In Proceedings of the 20th International Conference on Software Engineering, Kyoto, Japan, 19–25 April 1998; IEEE Computer Society: Los Alamitos, CA, USA, 1998; pp. 177–186. [Google Scholar]
- Blair, G.; Bencomo, N.; France, B. Models@ run.time. Computer 2009, 42, 22–27. [Google Scholar] [CrossRef]
- Heinrich, R.; Jung, R.; Schmieders, E.; Metzger, A.; Hasselbring, W.; Reussner, R.; Pohl, K. Architectural run-time models for operator-in-the-loop adaptation of cloud applications. In Proceedings of the IEEE 9th Symposium on the Maintenance and Evolution of Service-Oriented Systems and Cloud-Based Environments, Bremen, Germany, 2 October 2015. [Google Scholar]
- Huang, G.; Wang, Q.X.; Mei, H.; Yang, F.Q. Research on architecture-based reflective middleware. Ruan Jian Xue Bao/J. Softw. 2003, 14, 1819–1826. (In Chinese) [Google Scholar]
- De Lemos, R.; Giese, H.; Müller, H.A.; Shaw, M.; Andersson, J.; Litoiu, M.; Schmerl, B.; Tamura, G.; Villegas, N.M.; Vogel, T.; et al. Software Engineering for Self-Adaptive Systems: A Second Research Roadmap; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–32. [Google Scholar]
- Szvetits, M.; Zdun, U. Systematic literature review of the objectives, techniques, kinds, and architectures of models at runtime. Softw. Syst. Model. 2016, 15, 31–69. [Google Scholar] [CrossRef]
- Lehmann, G.; Blumendorf, M.; Trollmann, F.; Albayrak, S. Meta-modeling runtime models. In Proceedings of the 2010 International Conference on Models in Software Engineering, Oslo, Norway, 3 October 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 209–223. [Google Scholar]
- Bencomo, N.; France, R.; Cheng, B.; Aßmann, U. Models@run.time: Foundations, Applications, and Roadmaps. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8378, pp. 1–318. [Google Scholar]
- Song, H.; Huang, G.; Wu, Y.; Chauvel, F.; Sun, Y.; Shao, W.; Mei, H. Modeling and maintaining runtime software architectures. Ruan Jian Xue Bao/J. Softw. 2013, 24, 1731–1745. (In Chinese) [Google Scholar] [CrossRef]
- Garlan, D.; Cheng, S.W.; Huang, A.C.; Schmerl, B.; Steenkiste, P. Rainbow: Architecture-based self-adaptation with reusable infrastructure. Computer 2004, 37, 46–54. [Google Scholar] [CrossRef]
- Floch, J.; Hallsteinsen, S.; Stav, E.; Eliassen, F.; Lund, K.; Gjorven, E. Using Architecture Models for Runtime Adaptability. IEEE Softw. 2006, 23, 62–70. [Google Scholar] [CrossRef]
- Hong, M.; Gang, H. PKUAS: An architecture-based reflective component operating platform. In Proceedings of the IEEE International Workshop on Distributed Computing Systems, Suzhou, China, 26–28 May 2004; IEEE Computer Society: Los Alamitos, CA, USA, 2004. [Google Scholar]
- Morin, B.; Barais, O.; Nain, G.; Jezequel, J.-M. Taming dynamically adaptive systems using models and aspects. In Proceedings of the 2009 IEEE 31st International Conference on Software Engineering, Vancouver, BC, Canada, 16–24 May 2009; pp. 122–132. [Google Scholar]
- Elkhodary, A.; Esfahani, N.; Malek, S. FUSION: A framework for engineering self-tuning self-adaptive software systems. In Proceedings of the Eighteenth ACM SIGSOFT International Symposium on Foundations of Software Engineering, Santa Fe, NM, USA, 7–11 November 2010; pp. 7–16. [Google Scholar]
- D’Ippolito, N.; Braberman, V.; Kramer, J.; Magee, J.; Sykes, D.; Uchitel, S. Hope for the best, prepare for the worst: Multi-tier control for adaptive systems. In Proceedings of the 36th International Conference on Software Engineering, Hyderabad, India, 31 May–7 June 2014; pp. 688–699. [Google Scholar]
- Chen, B.; Peng, X.; Yu, Y.; Nuseibeh, B.; Zhao, W. Self-adaptation through incremental generative model transformations at runtime. In Proceedings of the 36th International Conference on Software Engineering, Hyderabad, India, 31 May–7 June 2014; pp. 676–687. [Google Scholar]
- Zhu, Y.; Huang, G.; Mei, H. Quality Attribute Scenario Based Architectural Modeling for Self-Adaptation Supported by Architecture-based Reflective Middleware. In Proceedings of the 11th Asia-Pacific Software Engineering Conference, Busan, Korea, 30 November–3 December 2004. [Google Scholar]
- Calinescu, R.; Ghezzi, C.; Kwiatkowska, M.; Mirandola, R. Self-Adaptive Software Needs Quantitative Verification at Runtime. Commun. ACM 2012, 55, 69–77. [Google Scholar] [CrossRef]
- Calinescu, R.; Weyns, D.; Gerasimou, S.; Iftikhar, M.U.; Habli, I.; Kelly, T. Engineering Trustworthy Self-Adaptive Software with Dynamic Assurance Cases. IEEE Trans. Softw. Eng. 2017, 44, 1039–1069. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Zhang, J. Combinatorial Testing: Principles and Methods. J. Softw. 2009, 20, 1393–1405. (In Chinese) [Google Scholar]
- Loukil, S.; Kallel, S.; Jmaiel, M. An approach based on runtime models for developing dynamically adaptive systems. Future Gener. Comput. Syst. 2016, 68, 365–375. [Google Scholar] [CrossRef]
- Chen, L. Design and Implementation of Strategy-Driven Adaptive Software Simulation Platform; Peking University: Beijing, China, 2014. (In Chinese) [Google Scholar]
- Perez-Palacin, D.; Mirandola, R.; Merseguer, J. QoS and energy management with Petrinets: A self-adaptive framework. J. Syst. Softw. 2012, 85, 2796–2811. [Google Scholar] [CrossRef] [Green Version]
- Franks, G.; Al-Omari, T.; Woodside, M.; Das, O.; Derisavi, S. Enhanced modeling and solution of layered queueing networks. IEEE Trans. Softw. Eng. 2009, 35, 148–161. [Google Scholar] [CrossRef]
- Sato, N.; Trivedi, K.S. Stochastic modeling of composite web services for closed-form analysis of their performance and reliability bottlenecks. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4749, pp. 107–118. [Google Scholar]
- Hessel, A.; Larsen, K.G.; Mikucionis, M.; Nielsen, B.; Pettersson, P.; Skou, A. Testing real-time systems using UPPAAL. In Formal Methods and Testing: An Outcome of the FORTEST Network; Hierons, R.M., Bowen, J.P., Harman, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 77–117. [Google Scholar] [CrossRef]
- Kwiatkowska, M.; Norman, G.; Parker, D. PRISM 4.0: Verification of probabilistic real-time systems. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6806, pp. 585–591. [Google Scholar]
- Behrmann, G.; David, A.; Larsen, K.G.; Hakansson, J.; Petterson, P.; Yi, W.; Hendriks, M. UPPAAL 4.0. In Proceedings of the 3rd International Conference on Quantitative Evaluation Systems, Riverside, CA, USA, 11–14 September 2006; pp. 125–126. [Google Scholar] [CrossRef]
- Filieri, A.; Ghezzi, C.; Tamburrelli, G. A formal approach to adaptive software: Continuous assurance of non-functional requirements. Formal Aspects Comput. 2012, 24, 163–186. [Google Scholar] [CrossRef] [Green Version]
- Filieri, A.; Tamburrelli, G.; Ghezzi, C. Supporting Self-Adaptation via Quantitative Verification and Sensitivity Analysis at Run Time. IEEE Trans. Softw. Eng. 2016, 42, 75–99. [Google Scholar] [CrossRef]
- Calinescu, R.; Kwiatkowska, M. Using quantitative analysis to implement autonomic it systems. In Proceedings of the 2009 IEEE 31st International Conference on Software Engineering, Vancouver, BC, Canada, 16–24 May 2009; pp. 100–110. [Google Scholar]
- Calinescu, R.; Grunske, L.; Kwiatkowska, M.; Mirandola, R.; Tamburrelli, G. Dynamic QoS management and optimization in service-based systems. IEEE Trans. Softw. Eng. 2011, 37, 387–409. [Google Scholar] [CrossRef]
- Ghezzi, C.; Pinto, L.S.; Spoletini, P.; Tamburrelli, G. Managing non-functional uncertainty via model-driven adaptivity. In Proceedings of the 2013 35th International Conference on Software Engineering (ICSE), San Francisco, CA, USA, 18–26 May 2013; pp. 33–42. [Google Scholar]
- Moreno, G.A.; Càmara, J.; Garlan, D.; Schmerl, B. Proactive self-adaptation under uncertainty: A probabilistic model checking approach. In Proceedings of the 2015 10th Joint Meeting on Foundations of Software Engineering, El Paso, TX, USA, 30 August 2015; pp. 1–12. [Google Scholar]
- Cheng, S.W. Rainbow: Cost-Effective Software Architecture-Based Self-Adaptation; Carnegie Mellon University: Schenley Park Pittsburgh, PA, USA, 2016. [Google Scholar]
- Cheung, R.C. A User-Oriented Software Reliability Model. IEEE Trans. Softw. Eng. 1980, SE-6, 118–125. [Google Scholar] [CrossRef]












| Transition Mode | Graphical Description |
|---|---|
| Sequential transition | 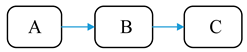 |
| Conditional transition | 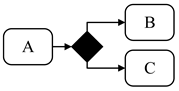 |
| Concurrent transition | 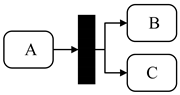 |
| Znnclient | Znndist | Packagenode | Znnmaster | End | Fail | |
|---|---|---|---|---|---|---|
| znnclient | 0 | 0.9993 | 0 | 0 | 0 | 0.0007 |
| znndist | 0 | 0 | 0.9951 | 0 | 0 | 0.0049 |
| packagenode | 0 | 0 | 0 | 0.995 | 0 | 0.005 |
| znndb | 0 | 0 | 0 | 0 | 0.9992 | 0.0008 |
| end | 0 | 0 | 0 | 0 | 1 | 0 |
| fail | 0 | 0 | 0 | 0 | 0 | 1 |
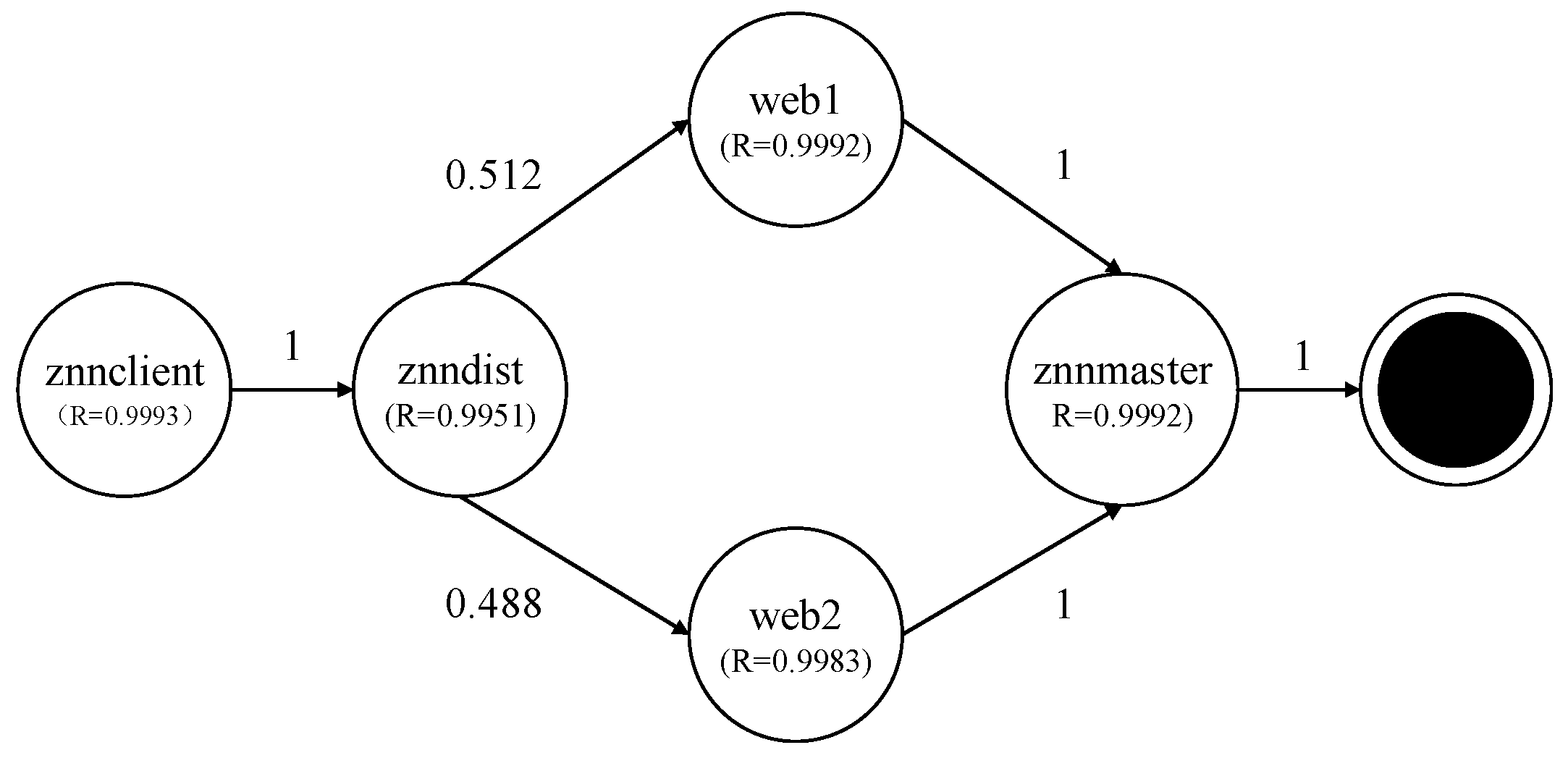
| Znnclient | Znndist | Web1 | Web2 | Znnmaster | End | Fail | |
|---|---|---|---|---|---|---|---|
| znnclient | 0 | 0.9993 | 0 | 0 | 0 | 0 | 0.0007 |
| znndist | 0 | 0 | 0.5095 | 0.4856 | 0 | 0 | 0.0049 |
| web1 | 0 | 0 | 0 | 0 | 0.9992 | 0 | 0.0008 |
| web2 | 0 | 0 | 0 | 0 | 0.9983 | 0 | 0.0017 |
| znndb | 0 | 0 | 0 | 0 | 0 | 0.9992 | 0.0008 |
| end | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| fail | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Znnclient | Znndist | Web1 | Web2 | Web3 | Znnmaster | End | Fail | |
|---|---|---|---|---|---|---|---|---|
| znnclient | 0 | 0.9993 | 0 | 0 | 0 | 0 | 0 | 0.0007 |
| znndist | 0 | 0 | 0.2259 | 0.2368 | 0.5324 | 0 | 0 | 0.0049 |
| web1 | 0 | 0 | 0 | 0 | 0 | 0.9992 | 0 | 0.0008 |
| web2 | 0 | 0 | 0 | 0 | 0 | 0.9983 | 0 | 0.0017 |
| web3 | 0 | 0 | 0 | 0 | 0 | 0.9975 | 0 | 0.0025 |
| znndb | 0 | 0 | 0 | 0 | 0 | 0 | 0.9992 | 0.0008 |
| end | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| fail | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Lu, M.; Gu, T.; Wu, Y. Runtime Software Architecture-Based Reliability Prediction for Self-Adaptive Systems. Symmetry 2022, 14, 589. https://doi.org/10.3390/sym14030589
Li Q, Lu M, Gu T, Wu Y. Runtime Software Architecture-Based Reliability Prediction for Self-Adaptive Systems. Symmetry. 2022; 14(3):589. https://doi.org/10.3390/sym14030589
Chicago/Turabian StyleLi, Qiuying, Minyan Lu, Tingyang Gu, and Yumei Wu. 2022. "Runtime Software Architecture-Based Reliability Prediction for Self-Adaptive Systems" Symmetry 14, no. 3: 589. https://doi.org/10.3390/sym14030589
APA StyleLi, Q., Lu, M., Gu, T., & Wu, Y. (2022). Runtime Software Architecture-Based Reliability Prediction for Self-Adaptive Systems. Symmetry, 14(3), 589. https://doi.org/10.3390/sym14030589






