Coupled Fixed Points for Hardy–Rogers Type of Maps and Their Applications in the Investigations of Market Equilibrium in Duopoly Markets for Non-Differentiable, Nonlinear Response Functions
Abstract
:1. Introduction
2. Materials and Methods
- 1.
- there is a unique fixed point of T and, moreover, for any initial guess , the iterated sequence for converges to the fixed point ξ;
- 2.
- there holds a priori error estimates ;
- 3.
- there holds a posteriori error estimate ;
- 4.
- the rate of convergence is ;
3. Main Result
- 1.
- there is a unique coupled fixed point of and, moreover, for any initial guess the iterated sequences and for converge to the coupled fixed point ;
- 2.
- there holds a priori error estimate;
- 3.
- there holds a posteriori error estimate;
- 4.
- the rate of convergence is
4. Applications of of the Main Result
4.1. Generalization of Some Known Results about Coupled Fixed Points and Corollaries
4.2. Application in the Investigation of Market Equilibrium in Duopoly Markets
4.2.1. The Basic Model
4.2.2. Connection between the Second-Order Conditions and the Contraction-Type Conditions
- 1.
- The two player are producing homogeneous goods that are perfect substitutes.
- 2.
- The first player can produce quantities from the set , and the second one can produce quantities from the set , where and are closed, nonempty subsets of a complete metric space .
- 3.
- Let there be a closed subset and maps , , so that:for every , are the response functions for Players One and Two, respectively.
- 4.
- Let , so that the inequality:holds for all .
4.2.3. Comments on the Coefficients , , , and
4.2.4. Some Applications on Newly Investigated Oligopoly Models
4.2.5. A Generalized Response Function
- 1.
- The two players are producing homogeneous goods that are perfect substitutes.
- 2.
- The player i, can produce quantities from the set , its set of the realized, on-the-market production as , and the set of its surplus production is , where and are closed, nonempty subsets of a complete metric space .
- 3.
- Let there be a closed subset and maps and , such that for every is the generalized response function of the player and the market for Players One and Two, respectively.
- 4.
- Let , so that the inequality:holds for all .
4.2.6. Applications of Theorem 2 for Optimization of Non-Differentiable Payoff Functions and Examples
- 1.
- The two players are producing homogeneous goods that are perfect substitutes.
- 2.
- The first player can produce quantities from the set , and the second one can produce quantities from the set , where and are closed, nonempty subsets of a complete metric space .
- 3.
- Let there be a closed subset and maps , so that:for every are the response functions for Players One and Two, respectively.
- 4.
- Let , so that the inequality:holds for all .
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, D.; Lakshmikantham, V. Coupled fixed points of nonlinear operators with application. Nonlinear Anal. 1987, 11, 623–632. [Google Scholar] [CrossRef]
- Radenović, S. Coupled fixed point theorems for monotone mappings in partially ordered metric spaces. Kragujev. J. Math. 2014, 38, 249–257. [Google Scholar] [CrossRef]
- Dorić, D.; Kadelburg, Z.; Radenović, S. Coupled fixed point results for mappings without mixed monotone property. Appl. Math. Lett. 2012, 25, 1803–1808. [Google Scholar] [CrossRef] [Green Version]
- Tian, J.; Hu, X.; O’regan, D. On ψ–contractions and common fixed point results in probabilistic metric spaces. Fixed Point Theory 2020, 21, 319–338. [Google Scholar] [CrossRef]
- Sharma, Y.; Jain, S. Coupled Fixed Point Theorems in Modular Metric Spaces Endowed with a Graph. Kyungpook Math. J. 2021, 61, 441–453. [Google Scholar] [CrossRef]
- Boudaoui, A.; Mebarki, K.; Shatanawi, W.; Abodayeh, K. Solution of some impulsive differential equations via coupled fixed point. Symmetry 2021, 13, 501. [Google Scholar] [CrossRef]
- Waheed, M.; Rehman, S.; Jan, N.; Gumaei, A.; Al-Rakhami, M. Some New Coupled Fixed-Point Findings Depending on Another Function in Fuzzy Cone Metric Spaces with Application. Math. Probl. Eng. 2021, 2021, 4144966. [Google Scholar] [CrossRef]
- Karusala, K.; Namana, S.; Mishra, L. Coupled fixed points theorems for generalized weak contractions in ordered b-metric spaces. Asian-Eur. J. Math. 2021, 2021, 2250050. [Google Scholar] [CrossRef]
- Ghasab, E.; Majani, H. Function weighted g–metric spaces and hausdorff Δ–distances; an application to fixed point theory. Int. J. Nonlinear Anal. Appl. 2021, 12, 1441–1452. [Google Scholar] [CrossRef]
- Sintunavarat, W.; Kumam, P. Coupled best proximity point theorem in metric Spaces. Fixed Point Theory Appl. 2012, 2012, 93. [Google Scholar] [CrossRef] [Green Version]
- Konar, P.; Chandok, S.; Dutta, S.; De la Sen, M. Coupled optimal results with an application to nonlinear integral equations. Axioms 2021, 10, 73. [Google Scholar] [CrossRef]
- Khazou, M.; Taoudi, M. Existence and uniqueness of fixed points for monotone operators in partially ordered Banach spaces and applications. J. Fixed Point Theory Appl. 2021, 23, 12. [Google Scholar] [CrossRef]
- Fazli, H.; Nieto, J. Fractional Langevin equation with anti-periodic boundary conditions. Chaos Solitons Fractals 2018, 114, 332–337. [Google Scholar] [CrossRef]
- Nashine, H.; Ibrahim, R. Monotone solutions of iterative fractional equations found by modified Darbo-type fixed-point theorems. J. Fixed Point Theory Appl. 2017, 19, 3217–3229. [Google Scholar] [CrossRef]
- Ramadan, M.; El-Shazly, N. On the Maximal Positive Definite Solution of the Nonlinear Matrix Equation (Formula presented). Appl. Math. Inf. Sci. 2020, 14, 349–354. [Google Scholar] [CrossRef]
- Dzhabarova, Y.; Kabaivanov, S.; Ruseva, M.; Zlatanov, B. Existence, Uniqueness and Stability of Market Equilibrium in Oligopoly Markets. Adm. Sci. 2020, 10, 70. [Google Scholar] [CrossRef]
- Kabaivanov, S.; Zlatanov, B. A variational principle, coupled fixed points and market equilibrium. Nonlinear Anal. Model. Control. 2021, 26, 169–185. [Google Scholar] [CrossRef]
- Gecheva, G.; Hristov, M.; Nedelcheva, D.; Ruseva, M.; Zlatanov, B. Applications of coupled fixed points for multivalued maps in the equilibrium in duopoly markets and in aquatic ecosystems. Axioms 2021, 10, 44. [Google Scholar] [CrossRef]
- Choudhury, B.; Metiya, N.; Kundu, S. Existence, uniqueness and well-posedness results for relation theoretic coupled fixed points problem using C–class function with some consequences and an application. J. Anal. 2021, 29, 227–245. [Google Scholar] [CrossRef]
- Petruşel, A. Fixed points vs. coupled fixed points. J. Fixed Point Theory Appl. 2018, 20, 150. [Google Scholar] [CrossRef]
- Cournot, A.A. Researches into the Mathematical Principles of the Theory of Wealth; Macmillan: New York, NY, USA, 1897. [Google Scholar]
- Udhayanan, P.; Mishra, S.; Rao, S. Firm dynamics and employee performance management in duopoly markets. Phys. A Stat. Mech. Appl. 2021, 583, 126298. [Google Scholar] [CrossRef]
- Gutiérrez, O. Planned Obsolescence with Network Effects. Rev. Netw. Econ. 2021, 19, 221–247. [Google Scholar] [CrossRef]
- Okuguchi, K.; Szidarovszky, F. The Theory of Oligopoly with Multi–Product Firms; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Bischi, G.; Chiarella, C.; Kopel, M.; Szidarovszky, F. Nonlinear Oligopolies Stability and Bifurcations; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Matsumoto, A.; Szidarovszky, F. Dynamic Oligopolies with Time Delays; Springer Nature Singapore Pte Ltd.: Singapore, 2018. [Google Scholar]
- Reich, S. Kannan’s fixed point theorem. Bull. Univ. Mat. Ital. 1971, 4, 1–11. [Google Scholar]
- Hardy, G.; Rogers, T. A generalization of a fixed point theorem of Reich. Canad. Math. Bull. 1973, 16, 201–206. [Google Scholar] [CrossRef]
- Kannan, R. Some results on fixed points. Bull. Calcutta Math. Soc. 1968, 10, 71–76. [Google Scholar]
- Chatterjea, S. Fixed-point theorems. Bull. Calcutta Math. Soc. 1972, 25, 727–730. [Google Scholar] [CrossRef]
- Friedman, J.W. Oligopoly Theory; Cambradge University Press: Cambridge, UK, 1983; Online publication date: September 2009. [Google Scholar] [CrossRef]
- Andaluz, J.; Elsadany, A.A.; Jarne, G. Dynamic Cournot oligopoly game based on general isoelastic demand. Nonlinear Dyn. 2020, 99, 1053–1063. [Google Scholar] [CrossRef]
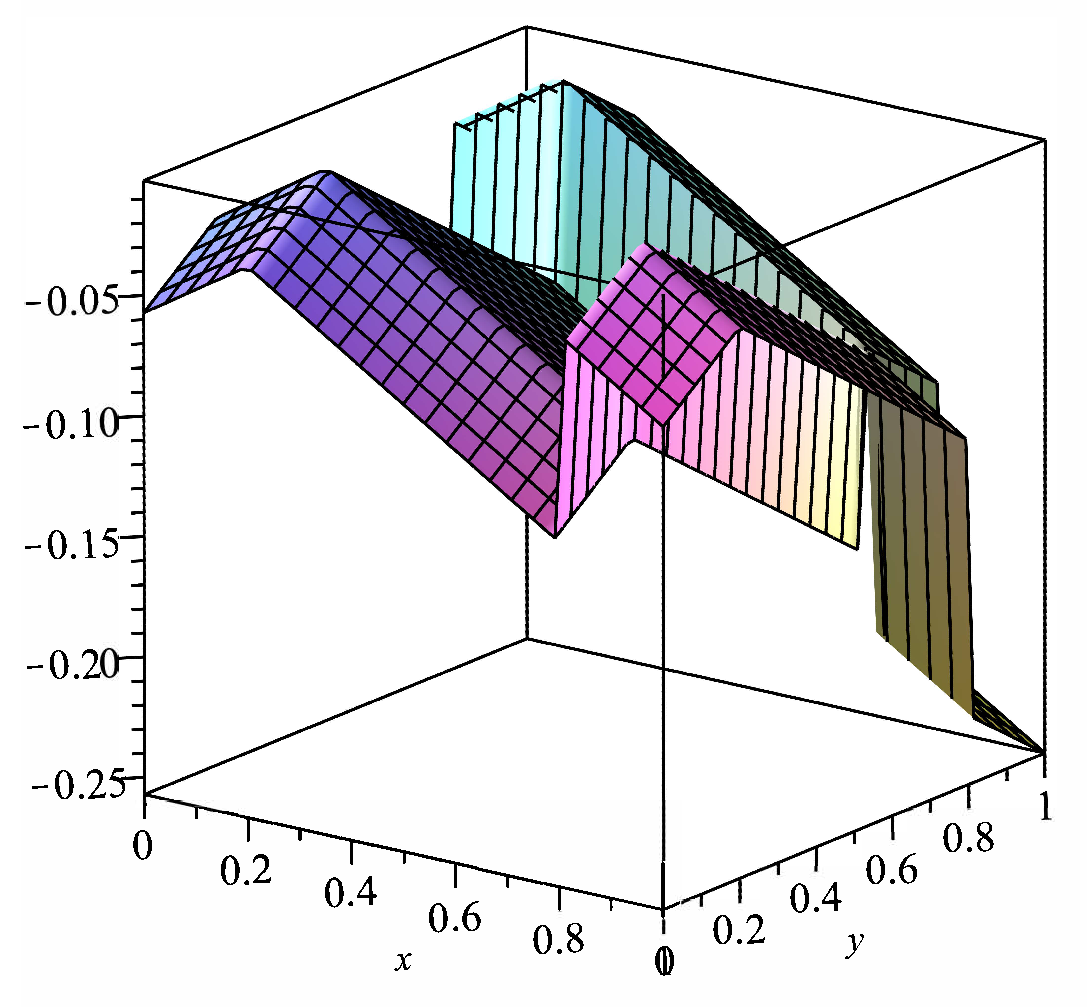
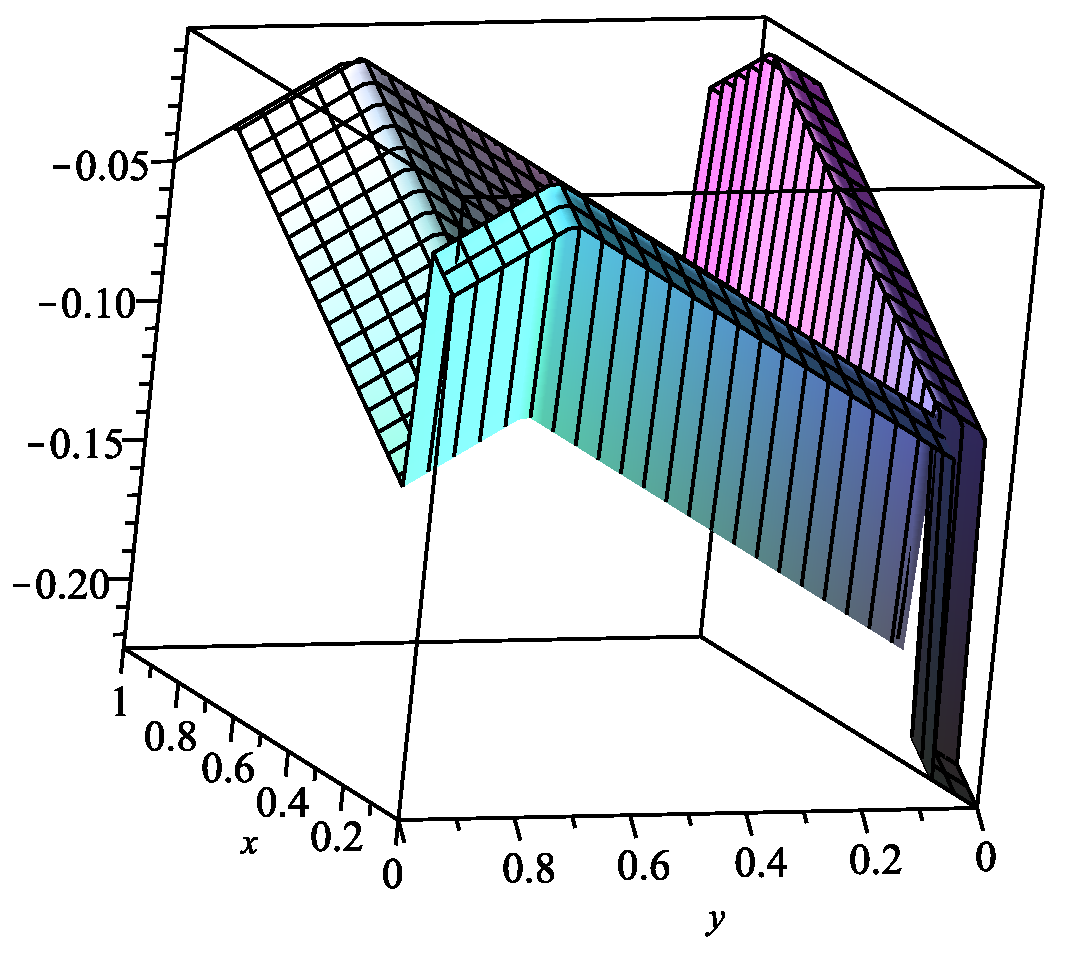
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 20 | 29 | 24 | 17 | 60 | 0 | 100 | |
| 31 | 18 | 35 | 6 | 71 | 0 | 100 |
| n | 0 | 1 | 2 | ⋯ | 2k | 2k + 1 |
|---|---|---|---|---|---|---|
| 20 | 30 | 20 | ⋯ | 20 | 30 | |
| 30 | 20 | 30 | ⋯ | 30 | 20 |
| n | 0 | 1 | 2 | 3 | 4 | 5 | 10 | 21 | 50 | 51 | 120 | 121 | 599 | 600 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 37 | 12 | 35 | 13 | 33.7 | 16.8 | 30.8 | 21.1 | 26.9 | 22.64 | 25.43 | 24.07 | 24.05 | |
| 30 | 18 | 33 | 20 | 31 | 21.4 | 28.6 | 24.1 | 25.8 | 26.4 | 26.03 | 26.34 | 26.19 | 26.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kabaivanov, S.; Zhelinski, V.; Zlatanov, B. Coupled Fixed Points for Hardy–Rogers Type of Maps and Their Applications in the Investigations of Market Equilibrium in Duopoly Markets for Non-Differentiable, Nonlinear Response Functions. Symmetry 2022, 14, 605. https://doi.org/10.3390/sym14030605
Kabaivanov S, Zhelinski V, Zlatanov B. Coupled Fixed Points for Hardy–Rogers Type of Maps and Their Applications in the Investigations of Market Equilibrium in Duopoly Markets for Non-Differentiable, Nonlinear Response Functions. Symmetry. 2022; 14(3):605. https://doi.org/10.3390/sym14030605
Chicago/Turabian StyleKabaivanov, Stanimir, Vasil Zhelinski, and Boyan Zlatanov. 2022. "Coupled Fixed Points for Hardy–Rogers Type of Maps and Their Applications in the Investigations of Market Equilibrium in Duopoly Markets for Non-Differentiable, Nonlinear Response Functions" Symmetry 14, no. 3: 605. https://doi.org/10.3390/sym14030605
APA StyleKabaivanov, S., Zhelinski, V., & Zlatanov, B. (2022). Coupled Fixed Points for Hardy–Rogers Type of Maps and Their Applications in the Investigations of Market Equilibrium in Duopoly Markets for Non-Differentiable, Nonlinear Response Functions. Symmetry, 14(3), 605. https://doi.org/10.3390/sym14030605






