Uncovering Disturbance Observer and Ultra-Local Plant Models in Series PI Controllers

Abstract

The paper settles two major liabilities and asymmetries of the theory of automatic control to the design of simple system controllers. It shows the most frequently used series proportional integral (PI) controllers as disturbance reconstruction and compensation-based structures and solves their designs using two types of linear system models. Beginning with the example of a simple integrator controlled by a P controller, it shows that constant input disturbances can be reconstructed by evaluating steady state values of the controller output. Thereby, the nearly steady state controller output can be simply achieved by using a low-pass filter with a time constant significantly longer than the time constant of stabilized processes. This disturbance observer (DOB) functionality can be demonstrated as being kept by series PI controllers designed by the pole assignment method. The DOB design can also be extended to first-order systems with internal feedback. However, there, the reconstructed disturbances depend both on the controller and the plant output steady state values. Because this feature is missing in industrial PI controllers, it indicates their connections with simpler, ultra-local (integral) linear system models. The interpretation of PI controllers as DOB-based structures allows a systematic consistent classification of all existing disturbance compensation structures and simplifies their comparisons with other modern and postmodern DOB-based alternatives. Given the breadth of use, improved understanding of PI control functionality also represents an important step to their optimal implementation and to research of innovative modifications, as illustrated by facilitating the flexible use of the new functional capabilities offered by embedded controls. By enhancing “the birth” of new solutions, it is then possible to better satisfy the permanently growing requirements of practice.

1. Introduction

Automatic control can be found everywhere around us, but there are many reasons to believe that it remains in a position of hidden technology. For example, a brief look at the definitions on the web shows that automatic control deals with the application of control theory to the regulation of processes without direct human intervention. Then, in addition to introducing several useful items in automatic control terminology (such as the concept of disturbances or negative feedback), the first of the web-provided definitions made such misleading claims as “designing a system with features of automatic control generally requires the feeding of electrical or mechanical energy to enhance the dynamic features of an otherwise sluggish or variant, even errant system”. This is misleading in the sense that the substitution of human intervention for the regulation of processes is far from being linked only to electrical or mechanical energy. For many decades, automatic control was important in many other areas, such as chemistry, biology, medicine, etc. However, there was no mention that one of the main goals of automatic control was to achieve and maintain system stability. The concept of stability means the ability to remain functioning in the vicinity of a required state (working point) even under the influence of external disturbances. In the case of automatic control of a simple dynamic system, framed frequently as a proportional integral derivative (PID) control, it is mainly a matter of system stabilization augmented by reconstruction and compensation of acting disturbances.

The article begins with providing a brief examination of developments in the design of PID control and discusses its importance in a broader social context. It shows that, despite the apparent simplicity and apparent exhaustion of related research topics, there are a number of new stimuli that can only be successfully resolved by overcoming the stereotypes of previous developments. New solutions do not only have to come thanks to sophisticated breathtaking mathematical constructions, but can also be obtained by a new combination and interpretation of simple well-known approaches and facts. Incentives for such development include the development of the technological basis of automatic control (progress in embedded control, materials, sensors, actuators, communications, etc.) as well as new requirements, mainly from unstable and strongly nonlinear systems with delays encountered in automotive mechatronics, robotics, electromobility, chemistry, and biology (e.g., in connection with epidemics).

Although in the past, various mechanical devices have played an important role, real use of automatic control has long outgrown these limitations. Episodic applications of automatic control can be traced back to ancient Greece [1]. However, the increase in its importance came much later. The advent of the industrial revolution has already indicated something. Automatic control was used to be associated with Watt’s steam engine, in which the centrifugal speed controller, created by borrowing an older solution used to regulate wind and water mills, played an important role. Its task was to ensure a constant speed of rotation even with a variable load or operating parameters of the boiler. The controller existed in numerous modifications and already here it would be possible to find some features of PID control. Properties of the obtained regulation, especially its stability, were dealt with by a number of important researchers of the 19th century, such as W. Siemens (1823–1883), J. C. Maxwell (1831–1879), or E. J. Routh (1831–1907). However, the centrifugal speed governor was still a device that was an integral part of the steam engine, not a universal device also applicable to control numerous other processes. It was similar with the controllers used to control steam turbines, made famous by the founder of automation in German-speaking countries, A.B. Stodola (1859–1942). With A. Hurwitz (1859–1919), they also contribute to the stability analysis.

1.1. A Brief Look at the Beginnings of the PID Control and the Need for Abstraction

Controllers representing a self-traded industrial commodity that could be used to control multiple processes began to be used more widely in the early 20th century. Around 1910, they were limited mainly to simple on–off (relay) control, whether they were implemented as electromagnetic relays or on the basis of pneumatic a flapper–nozzle (sometimes called as baffle–nozzle system, Figure 1a) and/or membrane amplifier. However, on–off controls, in which steady states of the plant output were maintained in the form of steady state oscillations, did not always meet practical requirements and the following decades brought a rapid development of knowledge related to amplifiers for automatic control (see e.g., [2,3,4]). Moreover, it was no longer just about machine control, but also about other areas with an important role for dynamic systems; for example, transatlantic communications, the political economy, the fight against the tuberculosis pandemic (by milk pasteurization), etc.

Today, there are still several reasons to look for the simplest controllers. One reason is to ensure that the content of introductory courses in the field of automatic control meets the requirements of practice, taking into account the dynamics of their development and delays in the educational process itself. In connection with the survey of these needs, several articles were published in recent years (see, for example [5,6,7,8]). However, the dynamics of research in the field must also be paid attention to. Because the range of basic knowledge needed to understand automatic control is constantly growing, and the scope for covering it in university education is declining, basic ideas and principles must inevitably be abstracted, as an appropriate abstraction represents the only effective tool for compressing the ever-growing scope of the knowledge, and keeping it sizable to the scope of the curriculum, often a single course in the field of automatic control. The problem is that many of the findings from the early period have remained secret in the competitive struggle of companies, and today, when needing to adapt older solutions to new technological requirements, we are often approaching their interpretations in roles similar to archaeologists, who are only left with the material remnants of existing cultures.

Changes in core technologies bring, from time-to-time, the need to re-evaluate existing solutions and adapt them to new conditions [9]. Today, such a wave is coming again, caused by the widespread need to digitize and automate processes as part of the Industry 4.0 campaign, or the building of the Internet of Things (IoT). The stimuli of the current wave of innovations also include the development of the technological basis of automatic control (progress in embedded control, materials, sensors, communications, etc.), and new requirements, mainly from the control of unstable and strongly nonlinear systems with delays, encountered in automotive mechatronics, robotics, electromobility, transport (driving autonomous vehicles, and entire platoon), and many other applications, or in connection with epidemics, such as COVID-19. While the design of process control has been tied to a “not very diverse” traditional hardware of existing facilities and has mainly focused on controlling stable systems, in the new applications field, where the development of the technological base is much faster, unstable processes are common. As was the case with the birth of mechatronics around 1990, in these new areas, the simplest possible control algorithms are required, which can also be implemented in low-cost platforms, while at the same time achieve the required performance, robustness, and accuracy of control. Their basic common feature is the systemic flexible approach, which, when applied consistently, often leads to surprising findings. On a daily basis, in the context of the fight against the COVID-19 pandemic, we can see that many people have difficulty understanding the specifics of unstable dynamic processes with large time delays. A reassessment of older solutions may show that not all of the results of previous historical developments have been understood correctly in the past, but also that the essence of some already discovered solutions has been forgotten.

1.2. Signals, Systems, and Feedback

At the beginning of the development of PID control, achieving smoother control signals of the pneumatic controllers (i.e., by increasing their proportional bands) was made possible by introducing negative feedback from the controller output (approximately 1928, Figure 1b). The resulting signal amplifier permitted the adjustment of the controller gain over a wide range and was denoted as a proportional (P) controller.

Analogous development of electronic amplifiers was not so simple—the electromagnetic relay has been replaced by a completely new element—a vacuum tube. It represented a serious obstacle to the further development, known well from the history of transatlantic telephony. The electronic amplifiers used around 1920 introduced strong signal distortions, which significantly limited their repeated applications. In 1927, H. S. Black (1898–1983) showed that the distortion of a high-gain amplifier could reasonably be reduced by feeding back part of the output signal. Subsequently, his Bell Lab colleague, H. Nyquist (1889–1976), published in “Regeneration Theory” (1932), foundations of the so-called Nyquist analysis in the frequency domain, providing a practical guide for designing negative feedback-based amplifier systems using experimental data of the measured frequency response.

Contemporaneously, the pneumatic negative feedback amplifier was developed by C.E. Mason [10] of the Foxboro Company. The flapper–nozzle amplifier (as in Figure 1a) is based on the pressure drop along the pneumatic resistance created by the narrowing of the orifice in the supply pipe when the air flow changes. By means of the negative feedback generated by the insertion of the bellows with the elasticity constant $K_b$, which expanded or contracted when the pressure $P_o$ changed (thus reducing the impact of opening the nozzle X by the oppositely oriented movement of the baffle), the dependence of $P_o$ on the input control error e was linearized. In 1931, the Foxboro Company began selling pneumatic controllers that incorporated both adjustable linear amplifications (based on such a negative feedback principle) and integral action (called as automatic reset, Figure 2). The rate of this “positive” feedback (acting against the bellows used to linearize the flapper–nozzle amplifier) depended on the volume of the upper bellows and the magnitude of the pneumatic resistance $R_i$. This caused an automatic reset with a delay specified by a time constant $T_i$.

Even before the beginning of the Second World War, this controller was extended by a derivative action (denoted originally as “pre-act”) achieved by including an additional pneumatic resistor $R_d$ (with a similar role as $R_i$ in the integral action) at the input of the lower bellows. Due to this, the negative feedback was accomplished by a delay. The modular set of proportional integral derivative (PID) controllers created in this way had a revolutionary impact on a number of industries; for example, more PID controllers were used to develop the atomic bomb than was ever produced.

The instructions for the use of new types of controllers provided by the manufacturers were supplemented by a more research-tuned publication by Ziegler and Nichols [11], which is the most cited, but still not always sufficiently understood work in the field of automatic control design [12]. Cheap, reliable, and robust pneumatic controllers were supplemented in the 1950s by a new generation of controllers based on transistor amplifiers, which soon complemented controllers based on operational amplifiers, copying a proven high-gain amplifier scheme supplemented by delayed negative and positive feedback to set the required gain and derivative, or integral action.

Based on these facts, it might seem that the story of PID controllers was an example of a perfectly managed scenario. Paradoxically, first, problems arose where simplifications and progress were expected—in the design of the digital controllers. These problems are best known as unwanted integration, leading to output overshooting or even instability—abbreviated as integrator windup. Windup also relates to the insufficient distinction between series and parallel PID controllers and to their roles in disturbance reconstruction and compensation. The relationship to other alternative methods used for disturbance reconstruction and compensation have also been insufficiently declared.

Over time, the range of open problems has grown, and even today, the design of PID controllers is a part of living scientific research [13,14,15,16,17,18,19,20]. The research focuses on the impacts of transport and communication delays, nonlinearities, intelligent approaches (as fuzzy control), on–off actuators and pulse-width-modulated (PWM) control, compensation of periodic and composite disturbances, etc.

1.3. Intelligent, Model-Based, or Fractional-Order PID Control?

The majority of early controllers were constructed on what could be denoted as “intelligent control”; that is, heuristic control based on the observation of the human operator [3]. The inventors had an intuitive understanding of adequate control achieved by observation of the actions of human operators involved in control activities. Such an approach is still popular and has resulted in the so-called “fuzzy” PID control [17,21]. Paradoxically, despite the extraordinary success of the feedback structures of series PI and PID controllers and the detailed mappings of their historical development [2,3], little is known about the impulses leading their inventors to design these structures. In one of the best-known textbooks on PID control [22], one can read about the automatic resetting of the output of a simple P controller, which aimed to eliminate the permanent control error in the event of constant disturbances, as a result of which, the “automatic reset” (today denoted as integral action) controller was created. However, one will not learn about the arguments that gave birth to this solution.

Of course, from the beginning, an analytical approach to the problem emerged, from which a model-based approach later evolved. By observing a helmsman steering activity, in 1922, N. Minorsky (1885–1970) [23] presented a ship control analysis formulated as a three-term or proportional integral derivative (PID) control. The approach of Minorsky strongly influenced further developments based on a three-term control.

Without clearly defining the role of disturbance reconstruction and compensation in PID control, this problem was later analyzed in great detail in state-space control (SSC) methods of the “modern control” theory [24,25,26,27] and in numerous “post-modern” approaches: in internal model control (IMC) [28], disturbance observer based control (DOBC) [29,30,31,32,33], active disturbance rejection control (ADRC) [34], model-free control (MFC) [35], or fractional-order PID (FO-PID) control [36]. At the time of formulating these approaches, their authors emphasized the differences between these approaches and PID control. However, in order to further develop automatic control methods, including streamlining their teaching, it is equally important to analyze their context and define areas for their effective use. In order to clarify the structures of PI and PID controllers in the same way, it needs to be explained more precisely, when the same interpretation of reconstruction and disturbance compensation is possible [33].

The aims of this paper was to introduce PI control as a stabilizing P control extended by a disturbance observer based disturbance reconstruction and compensation. Another important factor involves how to adjust the individual structures in the case of control systems approximated by the first-order models, which represent a big part of all real control loops and can be used to approximate more complex inertial plants [37]. Another extremely important aspect is to stress the roles and impacts of control signal constraints and the roles of two possible linear models of the plants to be controlled.

The rest of the paper is structured as follows. Section 2 shows the series PI control as a modified P control augmented by disturbance feedforward based on an integral plant model, with input disturbance estimate given by the steady state control signal value. Section 3 compares, in several examples, the optimal settings of controllers without and with the I-action method of multiple dominant real poles and shows that the integral component is always significantly slower than the time constant of the dominant dynamics. Section 4 deals with a state-space approach to reconstruction and compensation of input disturbances based on the extended state observer concept. The results achieved are discussed in Section 5, followed by comments related to future research (Section 6) and a summarization in the conclusions.

2. From P Controller with Manual Offset to Automatic Reset Control

In the search for interpretations of the pioneering designs of pneumatic PI controllers (from the beginning of the last century), we can help, today, with a large amount of research devoted to the control of simple systems.

We know that, for example, in effort to stabilize all of the stable, integral, and unstable first-order systems, a proportional (P) controller should be used.

Then, in order to track precisely the required setpoint value w [8], for time-invariant first-order plants (1) with $a\ne 0$ it is necessary to add the static feedforward control $u_w$ (Figure 3) with the gain $a/K_s$ based on estimates of the parameters $\overline{a}$ and ${\overline{K}}_s$. The presence of saturation nonlinearity $u_r=sat\left(u\right)$ causes the controller to reduce the high control error caused for admissible initial states and by admissible input variables by the limit control values [38]. In the proportional zone of control (when $u_r=u$) and with piece-wise constant inputs (reference setpoint variable $w=const$ and input disturbance $d_i=const$) it can be shown that for the plant differential equation

$$\dot{y}=K_s[u_r+d_i]-ay$$

(1)

and the tracking error defined as

$$e=w-y$$

(2)

it fulfills requirement of an exponential decrease specified by an exponent $\lambda$ according to

$$\dot{e}=\lambda e;\lambda <0,$$

(3)

if the control signal u is calculated by means of a P controller

$$\begin{array}{c}u=K_p(w-y)+aw/K_s-d_i\hfill \\ K_p=-\left(\lambda +a\right)/K_s=(1/T_p-a)/K_s\hfill \end{array}$$

(4)

Thereby, $\lambda$ denotes the closed loop pole and $T_p=-1/\lambda$ the closed loop time constant. With respect to (4), the stability condition $\lambda <0$ may also be expressed as

$$K_s{K}_p+a>0$$

(5)

The achieved input–output behavior is specified by the transfer functions

$$F_{wy}\left(s\right)={\displaystyle \frac{Y\left(s\right)}{W\left(s\right)}}={\displaystyle \frac{1}{T_{p}s+1}};F_{iy}\left(s\right)={\displaystyle \frac{Y\left(s\right)}{D_i\left(s\right)}}={\displaystyle \frac{K_s}{T_{p}s+1}}$$

(6)

In the time domain the setpoint-to-output transfer function $F_{wy}\left(s\right)$ corresponds to unit setpoint step responses

$$h_p\left(t\right)=1-e^{-t/T_p}$$

(7)

Using the time constant $T_p$, we can easily express the length of transients of control processes. For its evaluation, we often use the term “settling time”.

Definition 1

(Settling time). Settling time $T_{st}$ is often used to quantify the duration of exponential transients, which is defined by the decrease of the tracking error expressed in the unit step response (7) by the term $e^{-t/T_p}$ below a certain percentage of the maximum value:

• When considering settling time $T_{st}=3T_p$, the error of approaching the plant output to the steady state setpoint value is less than 5%.
• When considering $T_{st}=4T_p$, it is only 1.8%.
• With $T_{st}=5T_c$, the tracking error is below 0.7% of the initial value for $t\ge T_{st}$.

Remark 1

(Distinguishing model and plant parameters.). It should be noted that plant parameters a and $K_s$ in (1) are an “abstraction” and we never know them exactly. When it is necessary to stress that the parameters to be used in the control algorithm (4), which are based on some plant identification and can be different from the not known a and $K_s$, symbols $\overline{a}$ and ${\overline{K}}_s$ will be used.

Remark 2

(Use of stabilizing controller.). The stabilizing controller is used, not only to stabilize the state of unstable systems, but also to reduce fluctuations in the properties of transients when controlling possibly stable, and time-variable systems with uncertainties and operating disturbances, or to accelerate transients.

Remark 3

(Equivalent total input disturbance.). We note that the parameter uncertainties, together with unmodeled dynamics, are combined with various external disturbances (forces) that enter into the plant at various points, to form the “equivalent total input disturbance”. The concept of “total disturbance” was first coined by Han [39] and explained by Gao [34] so that any output changes not caused by the control input are traced back to an equivalent input disturbance, to be reconstructed and compensated by the controller. The term “total” indicates that ${\overline{d}}_i$ in Figure 3 includes, in totality, both internal disturbances (unknown and uncertain dynamics of the plant manifested by $\overline{a}\ne a$, or ${\overline{K}}_s\ne K_s$) and external disturbances represented by $d_i$. For example, if we simplify the controller design by considering $\overline{a}=0$, which corresponds to integral plant model, the equivalent “total” input disturbance of such an integrator changes to ${\overline{d}}_i=d_i-aw/K_s$ for $y=w$.

Because the approximation of the parameter a plays an important role in the design of the control structures considered in the article, for better orientation, we will highlight it in red.

Disturbance Reconstruction and Compensation—Integral Plants

Any input disturbance $d_i$ with the estimated value ${\overline{d}}_i$ had to be compensated by the opposite offset signal $u_{off}=-{\overline{d}}_i$ at the controller output; without an appropriate disturbance compensation, a steady state control error occurs.

For the sake of simplicity, we will first focus on the control of integral plants with $\overline{a}=a=0,u_w=0$. Furthermore, if we are able to find a stable $K_p$ (4) without knowing the parameter a, by assuming $\overline{a}=0$ we can also avoid to use the static feedforward $u_w$. To keep the loop properties, such an approach formally leads to shifting the omitted controller term $u_w$ into the “equivalent total input disturbance”

$$d_e=d_i-u_w.$$

(8)

In the time of the early pneumatic P controllers developed after 1914 [2,3], a manually controlled offset $u_{off}$ (added to the P controller output) was used to compensate for constant disturbances, manifested without a compensation by a permanent control error. The operator had to monitor the process, which led to increased costs. Or, in case of an irresponsible approach of the operator, it led to a reduced control performance, which also provided an incentive to replace the operator with an automatic device.

According to Figure 3, considered with $a=0$, to keep a steady state of the integral systems, a zero summary plant (integrator) input value

$$u_{r0}+d_i=0$$

(9)

must be achieved. Thus, assuming the output of the controller from the interval of admissible (unconstrained) values, when $u_{r0}=u_0$, the estimate of the input disturbance can be calculated from the steady state loop parameters according to

$${\widehat{d}}_i=-u_0$$

(10)

Next, for a constant acting disturbance value $d_i=const$, the compensating offset

$$u_{off}=-{\widehat{d}}_i=u_0$$

(11)

must be applied.

Definition 2

(Steady state-based disturbance observer (DOB) for integral plants). For integral plants with $\overline{a}=0$, the input disturbance estimate ${\widehat{d}}_i$ can be achieved by measuring the steady state values of the non-saturated controller output $u_0=u_{r0}$ (11) for some $t\ge T_{st}$.

Then, by applying the control algorithm according to Figure 3 with the value $u_{off}=u_0$, determined according to Definition 2 (and depending on the settling time definition), we would get transient responses with a (near) zero permanent tracking error in the next course of the control.

The reconstruction of disturbances by evaluating steady state control signal values was first mentioned in [40]. The above analysis shows that the operator of a process stabilized by a P controller should:

• Wait firstly for a steady state (it means, for some chosen $T_{st}$, up to $t\ge T_{st}$);
• Look at the steady state value of the control action $u_0$; and
• Reset the offset of the controller to that value $u_{off}=u_0$.

Definition 3

(Steady state-based DOB for static plants with $\overline{a}\ne 0$). As it directly follows from (1) with $dy/dt=0$, for static plants with a feedback estimate $\overline{a}\ne 0$, an estimate of a constant input disturbance around an output $y_0$ is

$${\widehat{d}}_i=-u_0+\overline{a}{y}_0/{\overline{K}}_s$$

(12)

An exact calculation of input disturbance requires to measure both the steady state values of the (non-saturated) controller output $u_0$ (11) and of the plant output $y_0$. We will show that such a DOB cannot directly correspond to series PI or PID control.

Remark 4

(Automatic reset for first-order plants.). When implementing “automatic reset” of the disturbance compensation based on the input disturbance estimate (12), according to the scheme in Figure 3, the corresponding offset can be described as

$$u_{off}=-{\widehat{d}}_i=u_0-\overline{a}{y}_0/{\overline{K}}_s$$

(13)

By moving static feedforward control $\overline{a}w/{\overline{K}}_s$ from the P controller (4) into the offset, the controller will be simplified into a pure P controller, similar to the case with $\overline{a}=0$. The newly established “lumped offset” can then be described as

$$u_{loff}=-{\widehat{d}}_i+\overline{a}w/{\overline{K}}_s=u_0+\overline{a}(w-y_0)/{\overline{K}}_s$$

(14)

Theorem 1

(Relationship of automatic reset structures for $\overline{a}=0$ and $\overline{a}\ne 0$). In a sufficiently narrow vicinity of the desired state (with the initial output value $y_0\to w$) and with a sufficiently small value $T_p\to 0$, the transients corresponding to $\overline{a}=0$ and $\overline{a}\ne 0$ are indistinguishable with limited measurement accuracy.

Proof. 

It can be seen that for $y_0\to w$, the resulting DOB accomplishing (12) is approaching in its functionality the “automatic reset” derived for $\overline{a}=0$ (10), when it holds

$$u_{loff}\approx u_0$$

(15)

Since for sufficiently short $T_p$ also $K_p$ (4) corresponding to $\overline{a}\ne 0$ converges to $K_p$ derived for $\overline{a}=0$, it can be expected that the automatic reset designed for $\overline{a}=0$ will provide a satisfactory transient dynamics also for $\overline{a}\ne 0$. □

Theorem 1 suggests the possibility that the P controller with a disturbance feedforward using a DOB derived both with respect to $\overline{a}\ne 0$ and $\overline{a}=0$ can be used for reconstruction and compensation of disturbances in loops with linear first-order systems. If we were to appropriately limit the properties of the considered feedback, it could be extended to the control of nonlinear systems.

3. P Controllers Extended by “Automatic Reset”

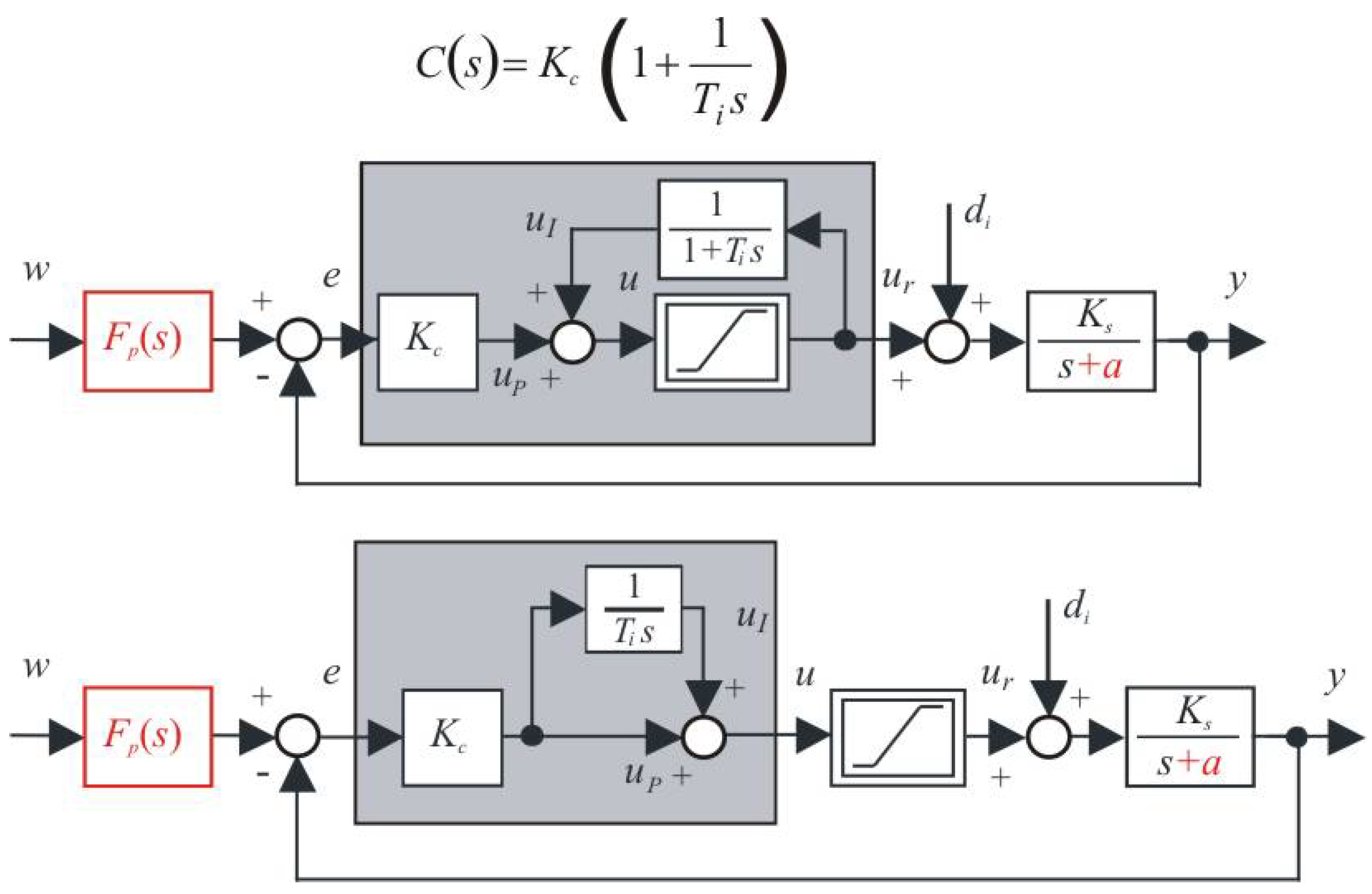
Today, due to the large time lag, we are not able to accurately reconstruct all of the motives that, at the time of birth, influenced the assertion of today’s known form of “automatic reset”, or the “series” PI controller, according to Figure 2. The inventors themselves were not interested in publishing the key moments of their solution, and other researchers did not have to do so concisely enough. Of course, today we would be able to algorithmize the whole process of disturbance reconstruction and compensation based on evaluation of steady states by using appropriate digital controllers. However, those in the early period of automatic control did not yet exist.

We will further show that the “automatic reset” design can be explained by replacing the steady state values of the controller output in $u_{off}=u_0$ (10) with the value of the controller output u delayed with a sufficiently large time constant $T_i>>T_p$ (see Figure 4 above). In Laplace transform, it is possible to write

$${\widehat{D}}_i\left(s\right)=-{\displaystyle \frac{1}{1+T_{i}s}}U\left(s\right);U_I\left(s\right)=-{\widehat{D}}_i\left(s\right).$$

(16)

The introduced low-pass filter can also contribute to noise filtering that, due to the positive controller feedback, becomes more critical.

Furthermore, we will also show that a seemingly more perfect reconstruction of disturbances can be based on the relation ${\widehat{d}}_i=(\overline{a}{y}_0-u_0)/{\overline{K}}_s$ (12), in which we will replace the steady values of the outputs of the controller and the system according to

$${\widehat{D}}_i\left(s\right)={\displaystyle \frac{1}{1+T_{i}s}}\left({\displaystyle \frac{\overline{a}Y\left(s\right)}{{\overline{K}}_s}}-U\left(s\right)\right).$$

(17)

However, in terms of input–output dynamics, it does not bring any significant changes. The only difference will be that we get a reconstruction of the net input disturbance ${\widehat{d}}_i$, instead of the equivalent total disturbance (8) obtained using the series PI controller.

In terms of the design of the overall control structure with the disturbance reconstruction and compensation and its optimal setting, based on $\overline{a}=0$, or $\overline{a}\ne 0$, two levels need to be distinguished: the first is the DOB and controller structure specification and the second is its optimal tuning. If we limit ourselves to two options at each level (indicated by indices 0 and 1), a total of four emerging situations will need to be addressed.

3.1. Traditional “Automatic Reset” Controller

In transition from the P controller with disturbance feedforward in Figure 3 to the “automatic reset” (i.e., PI) controller (patented around 1930 [3]), we will use the symbol $K_c$ to distinguish the generally different value of the proportional gain $K_p$ from the first case.

Definition 4

(Proportional integral (PI) controller). Controller (18) established as an extension of the P controller (4) (designed with $\overline{a}=0$) by a disturbance feedforward based on the disturbance reconstruction from steady state controller output values according to (16) (derived again on an assumption $\overline{a}=0$), will be denoted as (series) PI controller.

Similar to Figure 3, the fact that the pressure at the controller output could not exceed the value of the source pressure and could not even fall below zero, we took it into account by including the saturation block in the diagrams in Figure 4. The saturation block has played a very important role in the development of the PID control. However, when characterizing the basic properties of the obtained controller tuning in the proportional band of control, we first neglected the nonlinear aspects related to the control signal limitation by assuming $u_r\left(t\right)=u\left(t\right)$. Such linear dynamics of the controller itself can then be expressed by the transfer function

$$C\left(s\right)={\displaystyle \frac{U\left(s\right)}{E\left(s\right)}}={\displaystyle \frac{K_c}{1-{\displaystyle \frac{1}{1+T_{i}s}}}}=K_c{\displaystyle \frac{1+T_{i}s}{T_{i}s}}=K_c\left(1+{\displaystyle \frac{1}{T_{i}s}}\right)=K_c+\frac{K_i}{s}.$$

(18)

It has a P action with the gain $K_c$ and an I action with the gain $K_i=K_c/T_i$.

3.2. 2DoF PI Controller Tuning for Integral Plants (PI00)

In the simplest case, we use the DOB design from the integral model of the system with $\overline{a}=0$ and use the same plant model to describe the overall control loop. The loops from Figure 4 corresponding to $\overline{a}=0$ and no pre-filter ($F_p\left(s\right)=1)$ can be described by the transfer functions

$$\begin{array}{c}{F}_{wy}\left(s\right)={\displaystyle \frac{Y\left(s\right)}{W\left(s\right)}}={\displaystyle \frac{K_c{K}_s(1+T_{i}s)}{T_i{s}^2+K_c{K}_s(1+T_{i}s)}};F_{iy}\left(s\right)={\displaystyle \frac{Y\left(s\right)}{D_i\left(s\right)}}={\displaystyle \frac{s{K}_s{T}_i}{T_i{s}^2+K_c{K}_s(1+T_{i}s)}}.\hfill \end{array}$$

(19)

It has the closed loop poles

$${\lambda }_{1,2}={\displaystyle \frac{-K_c{K}_s{T}_i\pm \sqrt{{\left(K_c{K}_s{T}_i\right)}^2-4K_c{K}_s{T}_i}}{2T_i}}.$$

(20)

The fastest possible non-oscillatory transients correspond to ${\left(K_c{K}_s{T}_i\right)}^2-4K_c{K}_s{T}_i=0$, i.e., to

$${\lambda }_{1,2}=-2/T_i\mathrm{for}{K}_c{K}_s{T}_i=4$$

(21)

It means that one has to deal with the second-order order setpoint step responses with the closed loop time constant

$$\begin{array}{c}{T}_c=-1/{\lambda }_{1,2}=2/\left(K_c{K}_s\right)\Rightarrow K_c=2/\left(K_s{T}_c\right)\hfill \\ T_i=4/\left(K_c{K}_s\right)=2T_c\hfill \end{array}$$

(22)

Furthermore, to eliminate overshooting of the setpoint step responses resulting from zero in the numerator of $F_{wy}\left(s\right)$ (19), it is necessary to use a two-degrees-of-freedom (2DoF) PI controller with a pre-filter

$$\begin{array}{c}{F}_p\left(s\right)={\displaystyle \frac{bs+1}{T_{i}s+1}}\hfill \end{array}$$

(23)

Thereby, the weighting coefficient

$$b=-1/{\lambda }_{1,2}=T_c$$

(24)

gives the possibility to cancel one of the closed loop poles ${\lambda }_{1,2}$ of $F_{wy}\left(s\right)$ (19). Then, for (21)–(24)

$$\begin{array}{c}{F}_{wy}\left(s\right)={\displaystyle \frac{1}{T_{c}s+1}};F_{iy}\left(s\right)={\displaystyle \frac{s{K}_s{T}_c^2}{{(T_{c}s+1)}^2}}\hfill \end{array}$$

(25)

Remark 5

(Gains of P and 2DOF PI controllers). First, it should be noted that, at the same values of the time constants of the setpoint step responses $T_c=T_p$ in (4), (6), (22) and (25), the gain of the P action of the PI controller increases to

$$K_c=2K_p$$

(26)

which will be reflected in a higher level of noise signals.

Therefore, if we do not want to increase the oscillatory character of the processes, or noise amplification, we will often be faced with the question of whether it is better not to tolerate a possible permanent control error, or to introduce an automatic reset in another way, without using positive controller feedback leading to increased controller gains and slowed-down responses.

Remark 6

(Choice of $T_i$ for 2DOF PI controllers.). In the comparison based on the same proportional gains $K_c=K_p$ in (4), (6), (22) and (25), we see that $T_c=2T_p$ and, thus, the integration time constant $T_i=2T_c$, results in

$$T_i=4T_p$$

(27)

At the time moment $T_i$ (27), the (exponential) transients of the primary circuit with P controller can already be considered with a relatively high accuracy as finished. At the same time, $T_i$ is sufficiently long to filter out the control signal changes needed to stabilize the plant output at the required setpoint value. Thus, if we want to briefly and concisely characterize the DOB used for disturbance reconstruction, we call it DOB with disturbance reconstruction from the steady state values of the controller output.

3.3. 2DoF PI Controller Tuning for Plants with Internal Feedback (PI01)

Although the 2DoF PI controller (18) results from the choice of the DOB integral model with $\overline{a}=0$, the overall loop dynamics can also be specified for the plant with $a\ne 0$. Without a pre-filter ($F_p\left(s\right)=1)$ one gets from Figure 4

$$\begin{array}{c}{F}_{wy}\left(s\right)={\displaystyle \frac{K_c{K}_s(1+T_{i}s)}{T_i{s}^2+T_{i}s(K_c{K}_s+a)+K_c{K}_s}};F_{iy}\left(s\right)={\displaystyle \frac{s{K}_s{T}_i}{T_i{s}^2+T_{i}s(K_c{K}_s+a)+K_c{K}_s}}\hfill \end{array}$$

(28)

The corresponding closed loop poles are

$${\lambda }_{1,2}={\displaystyle \frac{-K_c{K}_s{T}_i-a{T}_i\pm \sqrt{{(K_c{K}_s+a)}^2{T}_i^2-4K_c{K}_s{T}_i}}{2T_i}}$$

(29)

The fastest possible non-oscillatory transients correspond to the double real dominant pole, when ${(K_c{K}_s+a)}^2{T}_i^2-4K_c{K}_s{T}_i=0$. Then

$${\lambda }_{1,2}=-\frac{K_c{K}_s+a}{2}\mathrm{for}{T}_i=\frac{4K_c{K}_s}{{(K_c{K}_s+a)}^2}$$

(30)

When replacing ${\lambda }_{1,2}$ (29) by the corresponding closed loop time constant $T_c$, we get the controller tuning

$$\begin{array}{c}{T}_c=-1/{\lambda }_{1,2}=2/(K_c{K}_s+a)\Rightarrow K_c=(2/T_c-a)/K_s\hfill \\ T_i=T_c(2-a{T}_c)\hfill \end{array}$$

(31)

Obviously, these tuning formulas correspond to (22) just for $a=0$. To eliminate overshooting of the setpoint step responses resulting from zero of $F_{wy}\left(s\right)$ (19), it is necessary to use a two-degree-of-freedom (2DoF) PI controller with a pre-filter (23). The weighting coefficient b can again be derived to cancel one of the closed loop poles ${\lambda }_{1,2}=-1/T_c$ (30) as

$$b=T_c$$

(32)

Formally it is again a pre-filter (23) with setting (24), but the values of b, $T_i$ and $T_c$ are bound by different relationships (31).

Remark 7

(Use of 2DOF PI controller for systems with internal feedback ). When using the controller (18) derived for $\overline{a}=0$ to control systems with $a\ne 0$, to get the fastest not oscillatory transients, its parameters have to be specified according to (31).

3.4. 2DoF Augmented PI (API) Controller for Plants with Internal Feedback (PI11)

The input disturbances can also be reconstructed from steady states of systems with internal feedback $a\ne 0$. When substituting disturbance estimate (17) into the P controller with disturbance feedforward Equation (4) written for the nominal values $\overline{a}=a$ and ${\overline{K}}_s=K_s$, in Laplace transform (see Figure 5) we get

$$U\left(s\right)=K_p(W\left(s\right)-Y\left(s\right))+\frac{aW\left(s\right)}{K_s}-{\displaystyle \frac{1}{1+T_{i}s}}{\displaystyle \frac{aY\left(s\right)-U\left(s\right)}{K_s}}$$

(33)

A manipulation then yields

$$\frac{T_{i}s}{1+T_{i}s}U\left(s\right)=K_p(W\left(s\right)-Y\left(s\right))+\frac{a\left(W\right(s)-Y(s\left)\right)}{K_s}+{\displaystyle \frac{T_{i}s}{1+T_{i}s}}{\displaystyle \frac{aY\left(s\right)}{K_s}}$$

(34)

and

$$U\left(s\right)=K_c{\displaystyle \frac{1+T_{i}s}{T_{i}s}}\left(W\left(s\right)-Y\left(s\right)\right)+{\displaystyle \frac{aY\left(s\right)}{K_s}};K_c=K_P+\frac{a}{K_s}$$

(35)

Definition 5

(Augmented PI controller (API)). Controller (35) represents and augmented version of the traditional (series) PI controller obtained by extending the P controller (4) for $a\ne 0$ by the feedforward disturbance based on the relation (18) (as in Figure 5).

The essence of the API controller’s benefit is that, by local positive feedback $aY\left(s\right)/K_s$ around the system $K_s/(s+a)$, it nominally transforms this system into an integrator $K_s/s$, to which the design from Section 3.2 can be simply applied, including the pre-filter design to remove unwanted overshooting. With the tuning (22) and pre-filter (23) and (24), this controller yields the closed loop transfer functions identical with (19).

Remark 8

(Equivalence of traditional and modified 2DoF PI controllers.). In terms of using two types of process models with $\overline{a}=0$ and $\overline{a}=a\ne 0$, two different decision levels need to be considered. At the first level, by specifying $\overline{a}=0$, the traditional 2DOF PI controller (18), or by specifying $\overline{a}=a\ne 0$, the modified 2DOF PI controller (35), augmented by an additional feedback from the plant output, can be proposed. After choosing one of these solutions at the first level, even at the second level, when specifying the plant model parameters to set the overall loop dynamics, we can reconsider both previous options. All of these combinations can be denoted by acronyms PI00, PI01, P10, and PI11. Due to the choice $\overline{a}=0$ in the second step, the second term of controller (35) drops out, and so on PI10 (considering in the first step $\overline{a}=a\ne 0$) becomes identical with PI00.

However, in terms of a setting with the double real pole of the closed loop dynamics, both these controllers become fully equivalent and the differences will be reflected only in the different settings of individual parameters (22), or (31). In tuning the pre-filter (23), in both situations, the value (24) has to be used.

However, for $a\ne 0$ and $w\ne 0$, the “net” external disturbance will be reconstructed just according to (17) by the modified controller. The series 2DOF PI controller with the disturbance reconstruction according to (16) yields the reconstruction of the equivalent total disturbance, including the internal plant feedback contribution (8).

Remark 9

(Compactness of series controllers). The acting input disturbance can also be reconstructed from the “steady state” output of the parallel PI controllers, but an additional filter with a time constant selected for simplicity as $T_i$ must be used. Furthermore, the reconstructed disturbance will not be used by the controller—its calculation represents an additional effort. From this point of view, the series controller is a more compact solution, which also has other advantages in terms of control action limitations (anti-windup). The attempts to extend the PI controller with an additional disturbance observer [41,42,43] may lead to unexpected problems and require special attention.

3.5. Example 1: Integral Model-Based First-Order Plant Control with a Strict Evaluation of Steady States

Although the idea of reconstruction of the input disturbance by evaluating the steady value of the control signal of the system approximated by the first-order integral model is very simple, its implementation in the MATLAB/Simulink environment is not. While a human operator decides on the steady state by seeing a sufficiently “frozen” systems behavior, to evaluate the same from the values of the system variables requires some additional Simulink blocks (Figure 6).

In the simplest case, reaching the steady state is tested by monitoring the absolute value of the output difference

$$|\Delta y|=|y\left(t\right)-y(t-T_{dy})|\le {ϵ}_2$$

(36)

at the output of Switch2. If this difference falls below the selected threshold value ${ϵ}_2=0.001$, the new offset value is set, based on the output of the first-order filter with a time constant $T_f$, with the current value of the control $u\left(t\right)$ at its input. The delay value in (36) was intuitively chosen as $T_{dy}=T_p/10$. During transient responses, when (36) does not hold, the output of Switch 2 remains at the position, guaranteeing a hold of the previous offset value.

Figure 6. Simulink schemes of the P controller derived according to (4) with $\overline{a}=0$, extended by disturbance reconstruction according to ${\overline{D}}_i\left(s\right)=U_r\left(s\right)/(1+T_{f}s)$ from steady state controller output values, with steady states tested by evaluating the absolute value of the output difference (36).

Figure 6. Simulink schemes of the P controller derived according to (4) with $\overline{a}=0$, extended by disturbance reconstruction according to ${\overline{D}}_i\left(s\right)=U_r\left(s\right)/(1+T_{f}s)$ from steady state controller output values, with steady states tested by evaluating the absolute value of the output difference (36).

If the absolute value of the output changes remain above the threshold value, the offset remains at the initial value. Therefore, given the existing measurement noise, it is not possible to choose a threshold value ${ϵ}_2$ that is too small. Moreover, the filter time constant $T_f$, used to eliminate measurement noise, cannot be chosen too small.

Switch1 is used to set the initial value of the offset to 0 and to exclude its readjustment as soon as the simulation is started. A delay in its output is necessary to eliminate the algebraic loop. In our case, it was equal to the numerical integration step $T_s=0.005$.

In all responses, a constant input disturbance value $d_i=1$ was applied. Thus, when using the P controller, the output first stabilized at the steady state value $y>w$ (Figure 7 left). After evaluating the fulfillment of the steady state condition, the first offset correction takes place. With regard to the non-zero threshold and the used filter, small changes of the offset will occur in the further course of transients even at the value $a=0$. At the next change of the setpoint value w, for $a=0$, the value of the lumped disturbance is already known, the transient is almost ideal (without more significant offset corrections).

With non-zero values $a\ne 0$, the changing contribution of the internal plant feedback to the lumped disturbance is reflected by the changing offset values. As the value of $T_f$ increases from $T_f=0.02T_p$ to $T_f=2T_p$ (blue curves in Figure 7 left), the iterations of the offset during the transients increase even at $a=0$.

By omitting the evaluation of steady state conditions and continuously updating the offset through the filter with the time constant $T_f=T_i$, we would get a 1DOF PI controller. The responses in Figure 7 show that at a small value of $T_f=T_i$, the circuit oscillates in the form of weakly damped oscillations. With a higher value of $T_f=T_i$, the input and output responses of the system are already smooth, but with overshooting, or undershooting of the output variable in particular steps.

4. Controller with Input Disturbance Reconstruction by ESO

The specifics of DOB contained in series PI controllers can be most clearly explained by comparing with the solution of the task of disturbance reconstruction and compensation developed within the state-space approach of modern theory of automatic control [25,26,44]. There, piece-wise constant disturbances $d_i$ (including possible model uncertainties) can be modelled by a sequence of Dirac pulses $\delta$ at a non-measurable integrator input [8], which yields an extended state-space plant model with two-inputs u and $\delta$

$$\begin{array}{c}\dot{\mathbf{x}}=\left[\begin{array}{cc}-a& K_s\\ 0& 0\end{array}\right]\mathbf{x}+\left[\begin{array}{c}{K}_s\\ 0\end{array}\right]u+\left[\begin{array}{c}0\\ 1\end{array}\right]\delta ;\mathbf{x}=\left[\begin{array}{c}y\\ {\overline{d}}_i\end{array}\right]\hfill \\ y=\left[\begin{array}{c}10\end{array}\right]\mathbf{x}\hfill \end{array}$$

(37)

and with the extended state vector $\mathbf{x}$ consisting of the plant output y and of the external disturbance $d_i$. For its reconstruction, an extended state observer (ESO) will be used, based on an “identical” plant model

$$\begin{array}{c}\dot{\widehat{\mathbf{x}}}=\left[\begin{array}{cc}-\overline{a}& {\overline{K}}_s\\ 0& 0\end{array}\right]\widehat{\mathbf{x}}+\left[\begin{array}{c}{\overline{K}}_s\\ 0\end{array}\right]u+\left[\begin{array}{c}{p}_1\\ p_2\end{array}\right](y-\widehat{y})\hfill \\ \widehat{\mathbf{x}}=\left[\begin{array}{c}\widehat{x}\\ {\widehat{d}}_i\end{array}\right];\widehat{y}=\left[\begin{array}{c}10\end{array}\right]\widehat{\mathbf{x}}\hfill \end{array}$$

(38)

In order to guarantee stable tracking of $\mathbf{x}$ by $\widehat{\mathbf{x}}$ and of y by $\widehat{y}$, it has to be augmented by correction of the particular state variables proportional to the difference of the plant and model outputs y - $\widehat{y}$ multiplied by parameters $p_1$ and $p_2$. Since the ESO inputs are given by the plant output y and input u, whereas the unknown input $\delta$ producing disturbances $d_i$ is omitted, after some modification, in the nominal case with $\overline{a}=a$ and ${\overline{K}}_s=K_s$, we get its description as

$$\begin{array}{c}\dot{\widehat{\mathbf{x}}}=\left[\begin{array}{cc}-p_1-a& K_s\\ -p_2& 0\end{array}\right]\widehat{\mathbf{x}}+\left[\begin{array}{c}{K}_s\\ 0\end{array}\right]u+\left[\begin{array}{c}{p}_1\\ p_2\end{array}\right]y\hfill \\ \widehat{\mathbf{x}}=\left[\begin{array}{c}\widehat{x}\\ {\widehat{d}}_i\end{array}\right];\widehat{y}=\left[\begin{array}{c}10\end{array}\right]\widehat{\mathbf{x}}\hfill \end{array}$$

(39)

To minimize the number of unknown tuning coefficients, ESO state matrix

$$\begin{array}{c}{\mathbf{A}}_s=s\mathbf{I}-\mathbf{A}=\left[\begin{array}{cc}s+p_1+a& -K_s\\ p_2& s\end{array}\right];\hfill \end{array}$$

(40)

with the characteristic polynomial

$$A_s\left(s\right)=s^2+\left(p_1+a\right)s+p_2{K}_s={(s-\lambda )}^2=s^2-2\lambda s+{\lambda }^2$$

(41)

will be specified by choosing a double pole $\lambda <0$, or the corresponding time constant $T_o=-1/\lambda$, which yields

$$p_1=-2\lambda -a=2/T_o-a;p_2={\lambda }^2/K_s=1/\left(T_o^2{K}_s\right)$$

(42)

With $\overline{a}=0$, such ESO is frequently used in (linear) active disturbance rejection control (L)ADRC [34,45]. Possible simulation scheme of the P controller (4) augmented by disturbance feedforward based on ESO (39), applicable to any parameters $\overline{a}$ and ${\overline{K}}_s$ is in Figure 8.

Example 2: Comparison of PI, API, and ESO-Based Controllers Using Both Types of Linear First-Order Models

The second example focuses on comparing P control extended by disturbance feedforward using either disturbance reconstruction from steady states by means of (17), or by ESO (39). Both of these possibilities verify for $\overline{a}=a$ and $\overline{a}=0$ the set of parameters

$$a=\{0.7,0,-0.7\};K_s={\overline{K}}_s=1.$$

(43)

Exaples of transient responses achieved with ESO-based PI from Figure 8 and by modifying the P controller with a disturbance feedforward using disturbance reconstruction from steady state control signal values (approximated by the output of a low-pass filter with the time constant $T_i$, and by a pre-filter to the 2DoF PI, or the 2DoF API controller, see Figure 5) for the nominal ($\overline{a}=a$) and simplified ($\overline{a}=0$) tuning, are in Figure 9. In this case, the input disturbance changed step-wise from $d_i=0$ to $d_i=1$ at $t=4$.

Note that both PI and API evaluate non-zero disturbance values already at the initial intervals $t<4$, when $d_i=0$. In the case of waveforms corresponding to the simplified setting $\overline{a}=0$, i.e., 2DoF PI and ESO-based controller denoted usually as ADRC, for $a\ne 0$, the steady state values of the reconstructed disturbance differ from the actual external value $d_i$.

5. Discussion

Thus far, we have shown that series PI and API controllers can be interpreted as stabilizing P controllers with a disturbance feedforward based on a DOB reconstructing input disturbance related to the first-order plant models from steady state outputs of the controller and plant.

The strict evaluation of steady state conditions, bringing some elements of discrete event dynamical systems, can be avoided by filtering the controller and plant outputs with first-order filters, having a time constant $T_i$ substantially longer than the time constants $T_p$ of the transients stabilized by the P controller without disturbance reconstruction.

Thereby, the most interesting point is that this DOB-based interpretation of series PI controllers was industrially exploited just for the controller structure based on ultra-local (linear integral) process models with $\overline{a}=0$.

By using local (static) linear models of the controlled process with $\overline{a}\ne 0$, more general types of DOB can be derived, leading to API controllers in Figure 5.

In terms of the setpoint-to-output transfer functions corresponding to the double real closed loop poles, both PI (with $\overline{a}=0$) and API (with $\overline{a}\ne 0$) lead to fully equivalent results (see Figure 9). Just the reconstructed disturbances will be different.

The specifics of DOB contained in series PI and API controllers can be most clearly explained by comparing with the solutions using the disturbance reconstruction and compensation developed within the state-space approach of modern theory of automatic control [26,44]. Of course, the DOB used in PI and API controllers (see Figure 5) is much simpler than ESO in Figure 8. However, the separability of setpoint tracking and disturbance reconstruction in the state-space approach brings several advantages that should be noted when comparing both disturbance reconstruction and compensation approaches. In addition, ESO-based disturbance reconstruction and compensation can be extended to a much wider range of signals than just step disturbances, such as frequently considered periodic disturbances [19].

When interpreting responses in Figure 8, we can start with saying:

In ESO, the reconstruction time constant $T_o$ can be selected independently of the time constant $T_p$ for control. If we neglect the effect of noise, $T_o$ is not limited from below as the integration time constant $T_i$. By choosing the API controller gain $K_c=(2/T_p-\overline{a})/{\overline{K}}_s$, we do not directly affect the disturbance reconstruction speed (which depends dominantly on $T_i$). $T_i$ cannot be chosen shorter than the time constant of the stabilized transients $T_p$, so that the reconstruction is not significantly affected by the initial control interventions needed for output stabilization in the vicinity of the required reference setpoint value. Thus, even with a nominal tuning, PI and API show “phantom” disturbances even when no external disturbances are present. The nominally set circuit with ESO does not show such an imperfection.

The required value of the proportional gain $K_P=(1/T_p-\overline{a})/{\overline{K}}_s$ does not depend on whether we compensate the disturbances reconstructed by ESO or not. However, when extending $K_P$ of the P controller to $K_c$ in PI and API controls for disturbance reconstruction and compensation (see Remark 5), for the same dynamics of setpoint responses, the proportional gain $K_p$ has to be increased to $K_c=(2/T_p-\overline{a})/{\overline{K}}_s$.

If the most accurate perception of external or equivalent disturbances is important, the ESO is definitely better from this point of view. In addition, the ESO methodology also allows the reconstruction and compensation of time-varying disturbance signals (e.g., periodic and composite signals) [25,30,46].

No pre-filter is required for $d_i$ reconstruction with ESO. When using PI or API, omitting $F_p\left(s\right)$ leads to overshooting during setpoint tracking.

However, common features should also be mentioned. With the use of significantly simpler API and ESO based on integral models with $\overline{a}=0$ (i.e., PI and ADRC), simplifications of the controller structure and its setting can be achieved in both approaches. From the reconstruction of the disturbances, we then receive the equivalent total input disturbance, which also includes contributions from the neglected internal feedback of the controlled system (as in Figure 9 right).

Although it might seem that the accuracy of the parameter a identification influences very little the input and output responses of the system, it should be noted that such a conclusion applies only to systems without further time delays, when the correction possibilities of the feedback used are practically unlimited. However, the presence of additional time delays limits the speed of correction processes, leading to an increase in the importance of accurate identification of a, which applies not only to PI and API, but also to ESO-based solutions used in active disturbance rejection control (ADRC).

It should also be noted that ESO provides a reconstruction of the system output $\widehat{y}$, which can be used to control systems with a higher output measurement noise level. The use of DOB with the inverse system model gives similar results as ESO. However, it also makes it possible to simplify DOB against ESO by choosing low-pass filters of lower order [8].

5.1. Parallel versus Series PI Control

In order to compare the basic approaches to the control of simple systems with compensation of disturbances, in [8], we discussed several key ideas that could be extracted from a mass of details known about the most frequently used controllers with the I-action. Of course, with regard to the limitations of the conference paper, we did not get to answer all the basic questions. One of them gives special attention to the interpretation of parallel PI controllers.

It is clear that the integral (I) action $u_I\left(t\right)$ acts against the possible input disturbance (see Figure 4) and, thus, actually compensates for its effect. However, to what degree is such an I-action actually suitable for reconstruction of input disturbances? In other words, to what extent is it enough to simplify a PID controller design by setting the gains of the P, I, and D actions (satisfying to Minorsky’s three-term controller) and to what extent are its properties determined by the overall controller structure (as in the case of the series PI controller), which can be more complex then the parallel PI or PID controller?

After all, already in a very simplified situation with $d_i=1$; $K_s=1$; $a=0$; $w\left(t\right)=1$ and with an initial output $y\left(0\right)=0,e\left(0\right)=1$ and an initial value $u_I\left(0\right)=0$, we can point out the problems. Due to Figure 4, the parallel I action

$$\frac{d{u}_I}{dt}=\frac{K_c}{T_i}e\left(t\right),$$

(44)

with $u_I\left(t\right)$ corresponding to an integral of the control error $e\left(t\right)$ multiplied by a positive gain, it will not decrease from $u\left(0\right)=0$ to $u=-1$ (i.e., to the value compensating the disturbance), until the output $y\left(t\right)$ exceeds the reference setpoint value w. Just then $e\left(t\right)$ changes its sign, $u_I\left(t\right)$ can start to decrease. Despite the fact that for a compensation of $d_i$ it should decrease from $t=0$. The meaningless initial $u_I\left(t\right)$ increase and the resulting output overshooting can be avoided by using a pre-filter. However, this still does not clarify the role of I-action in terms of disturbance reconstruction, because it does not explain, why it starts to fall below zero, independently from the required final value ${\widehat{d}}_i=1$ (Figure 9 right). In this aspect, the parallel PI controller differs significantly from all other DOB-based methods, allowing a more transparent and efficient reconstruction and compensation of $d_i$.

Improper control error integration is further prolonged by limiting the control signal, when a longer time is required to reach the setpoint value and to change the sign of $e\left(t\right)$. At this point, it should be noted that, when using a 1DOF PI controller, the essence of the windup problem is the opposite increase in $u_I\left(t\right)$, as needed to compensate for the disturbance, which even occurs without the limitations of the control action.

5.2. Windup Problems

Today, we do not know if the inventors of series PI and PID controllers really understood their role in terms of reconstruction and compensation of disturbances, or fully relied on intuition. We can only summarize that the series PI and PID controllers, which were among the first separately tradable industrial controllers for simple plants, represented a modular compact solution that used disturbance reconstruction based on a steady state control signal value. Thanks to this physically and functionally clear interpretation, they did not find the problems with the limitations of the control action. However, when, after the discovery of digital computers, they began to be replaced by parallel discrete-time controllers, implementing integration by summation, the problem of redundant (unwanted) integration emerged, which led to transients with overshooting, or even instability. It is true that digital controllers provide a number of simple options to prevent unwanted integration, and various anti-windup methods have been developed, applicable to continuous-time controllers [47,48,49,50,51]. However, in terms of the understanding, use, and teaching of automatic control, it is always best to avoid unwanted phenomena.

5.3. Example 3: Hybrid and Discrete-Time PI Controllers

The advantages of revealing the functionality of series PI controllers are particularly shown in the design of hybrid and dual-rate controllers containing discrete-time blocks operating with a relatively large sampling period $T_{samp}$ and continuous-, or quasi-continuous-time blocks, operating with a relatively short sampling period, or simulated with a short simulation step $T_s$.

A discrete-time reconstruction of the input disturbance and its compensation by means of positive feedback from the controller output mitigates the adverse effects of continuous positive feedback (requiring an increase in the stabilization gain $K_c$, see Remark 5) by less frequent re-calculation of offset values repeated with the sampling period $T_{samp}$. Between the sampling moments, the controller dynamics is limited to the stabilizing P control, whereas the offset signal is constant. Hence, the P controller gain can ideally remain at the lower value $K_p$ (4) (calculated without the continuous positive feedback). This is especially important when controlling systems with higher levels of measurement noise.

Described in the z-transform by means of the relations

$${\widehat{D}}_i\left(z\right)=-{\displaystyle \frac{1-D_f}{z-D_f}}U\left(z\right);U_I\left(z\right)=-{\widehat{D}}_i\left(z\right);D_f=e^{-T_{samp}/T_i},$$

(45)

this solution (corresponding to (16)) allows for a sufficiently large sampling period $T_{samp}$ to stay with the proportional gain taken from (4), without needing to consider a feedforward setpoint, when

$$u=K_p(w-y);K_p=(1/T_p-\overline{a})/K_s$$

(46)

Thus, it also avoids the need to increase the stabilizing gain to $K_c=(2/T_c-\overline{a})/K_s$ corresponding to continuous PI controller (31), when requiring to get equally fast responses with $T_c=T_p$.

For the sake of simplicity, so that we do not further increase the number of parameters, let us choose $T_{samp}=T_p$ and first examine for $\overline{a}=a=0$ the influence of the $T_i$ choice on the shapes of transients, realizing in discrete-time only the disturbance reconstruction and compensation. We will carry out the transient responses similarly as in Example 2, under the permanent action of the input disturbance $d_i=1$. The continuously working P controller with a pre-filter (23) tuned for $b=T_p=0.15$ will be simulated with the simulation step $T_s=0.001$. To show impact of control constraints, the proportional band of control will be narrowed to $u\in [-2,0.5]$. Figure 10 demonstrates that in specifying an appropriate value of $T_i$ one can rely on the settling time definition (see Definition 1 and (27)). Obviously, to get nearly-monotonic setpoint step responses, it is enough to work with a simple tuning $T_i=4T_p$.

Figure 11 shows that this setting $T_i=4T_p$ (27) can be successfully used together with the P controller (46) to control both the stable and the unstable systems. Smoothing of the control signal can be achieved by including a zero-order holder in the proportional channel. Obviously, this simple solution causes no windup and is particularly suitable for implementation using an embedded control. Since the disturbance reconstruction runs with a relatively long $T_i$, application of a longer sampling period $T_{samp}=T_p$ does not cause a visible slow-down of the disturbance reconstruction process.

Because the simple P controller (46) does not include a feedforward setpoint and the feedback from the system output derived for the API (35) is used, the total equivalent disturbance (8) is reconstructed. However, an alternative solution could similarly be designed based on a discrete-time alternative to (17).

6. Possible Future Works

The integrator plus dead-time (IPDT) and the first-order time-delay (FOTD) models are the most often used in practice; this is known from the experiences dealing with practical applications (see, e.g., [12]) and from the literature [37,52] dealing with the design of PI and PID controllers.

Although the extension of the main conclusions of this article regarding P, PI, or DOB-PI controllers applied to IPDT models can already be deduced from previous publications [53,54], the new interpretation of PI, PID, and proportional integral derivative accelerative (PIDA) controllers and their optimal analytical design for FOTD models we have discussed in [55]. In addition, we have also discussed the design of PD and PID controllers based on double-integrator plus dead-time (DIPDT) models, offering numerous interesting applications in motion control and mechatronics in [56,57]. It was the experimental results of controlling the unstable magnetic levitation system [58] that were the immediate impetus for a more detailed analysis of PD and PID controllers as stabilizing and disturbance–counteracting solutions. The achieved results should be analyzed in a broader context, as in [13,14,15,16,17,18,19,20]. Nevertheless, the preliminary analysis of a much wider sample of analytical and numerical settings of PI, PID, and PIDA controllers based on IPDT, FOTD, and DIPDT models, allows us to declare that the proposed interpretation of the DOB functionality included in these controllers helps significantly in understanding principles of their optimal tuning. Thus, it can be used for further modifications and optimization of their operations, taking into account various other limitations of the controller design and establishing a unique research and educational framework to cover symmetrically all the existing traditional, modern and postmodern controllers.

7. Conclusions

The paper shows that the series PI controllers, which represent a frequently used item of three-term PID controllers, can be interpreted as P controllers with disturbance feedforward using DOB-based reconstruction of input disturbances. The essence of the included DOB activity is the evaluation of the steady value of the controller output, which, in the case of integral systems, is equal to the negatively taken value of the input disturbance. It means it is related to ultra-local (integral) linear plant models. Asymmetry of this approach can be eliminated through careful work with two types of linear models, where the article also reveals a hitherto unnoticed alternative to series PI controllers, tentatively called augmented PI controllers (APIs). Their design is also based on a P controller with disturbance feedforward and a steady state-based DOB consisting of a low-pass filter with a long time constant $T_i$. However, in addition to the output of the controller, the output of the system also enters the DOB.

In series PI and API controllers, the DOB is explicitly included as a part of the positive feedback from the controller output through a low-pass filter with a time constant $T_i$. In both cases, $T_i$ should be substantially longer than the time constant $T_p$ of the stabilized transients. This basic requirement for $T_i$ also explains the impossibility to speed up the reconstruction of the disturbances and thus the speed of their compensation when using PI and API controllers. Due to the nature of the disturbance reconstruction from the steady values of the controller output, it is therefore impossible to speed up the reconstruction processes by reducing $T_i$, which must remain significantly longer than the time constant of transients with stabilizing P controller.

Understanding the nature of DOBs contained in PI controllers reveals why even with the use of state-of-the-art artificial intelligence optimization methods and their dynamic properties cannot be further enhanced by accelerating transients. However, it is possible to decrease the PI gains to the level of the stabilizing P controller by a discrete-time controller implementation.

As a novel contribution of the paper, it is possible to denote the interpretation of a century-old series PI control (originally automatic reset), but also the brief analysis of its basic features explained in terms of loop stabilization and disturbance compensation by counteracting signals achieved by a very simple DOB. Advantages of the new look at the series PI control have been briefly demonstrated by an example of a possible discrete time controller design capable of keeping the dynamics of the continuous-time PI controller with decreased controller gains. This controller does not explore all aspects of the discrete-time controller design and can be continued by numerous other solutions. The proposed controller interpretation will also be expected to facilitate the unified, symmetrical, and consistent classification, and more specified use of all possible disturbance compensation solutions. At the same time, it brings new impetus to deeper and symmetrical research regarding the use of two types of linear models.