Stability Switching Curves and Hopf Bifurcation of a Fractional Predator–Prey System with Two Nonidentical Delays
Abstract
:1. Introduction
2. Stability Analysis
2.1. Local Stability Analysis of the Positive Equilibrium
- (i)
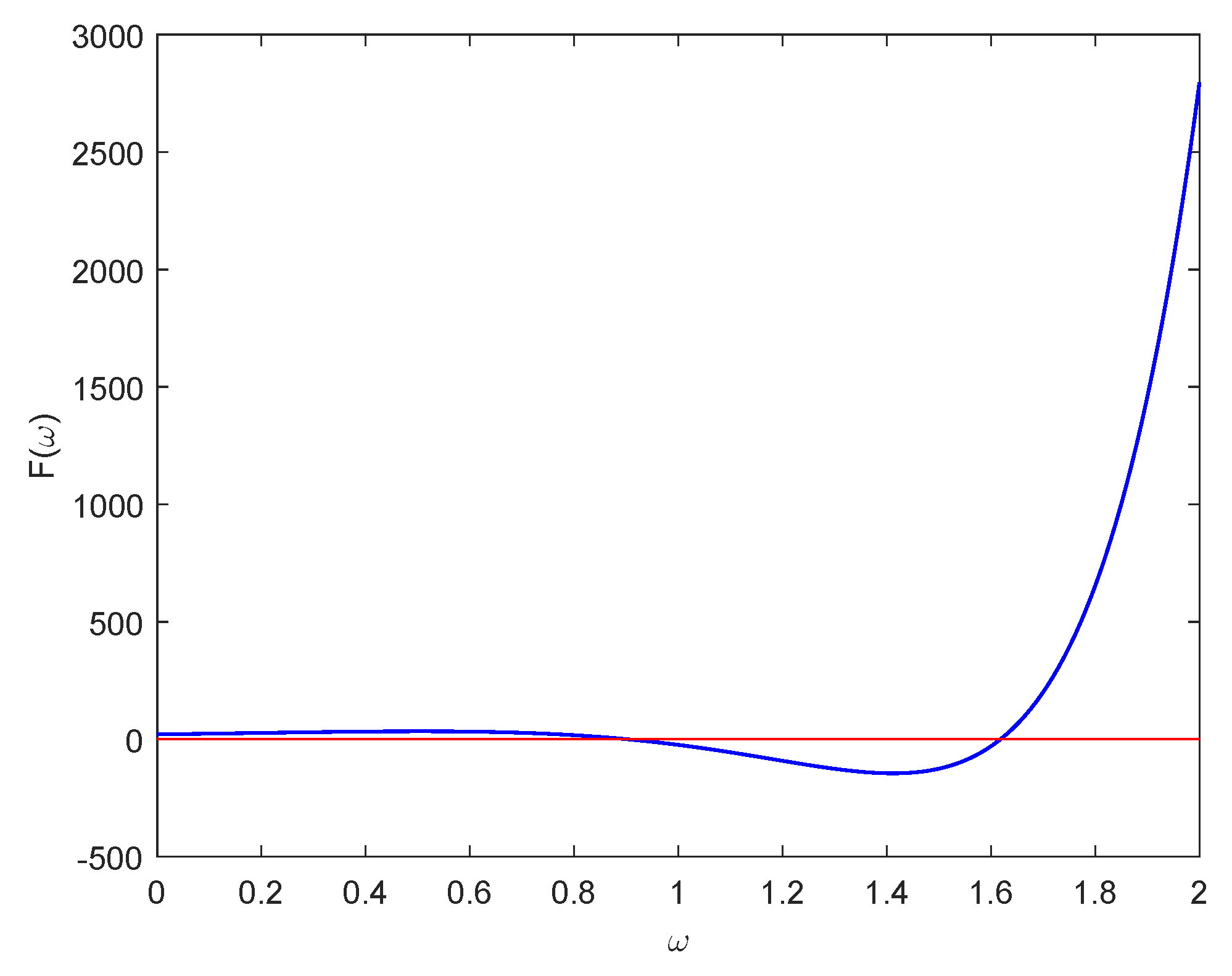
- Finite number of characteristic roots on under the condition:
- (ii)
- Zero frequency: = 0 is not a characteristic root for any and , i.e.,
- (iii)
- The polynomials , and have no common zeros, i.e., , , and are coprime polynomials;
- (iv)
- satisfy:
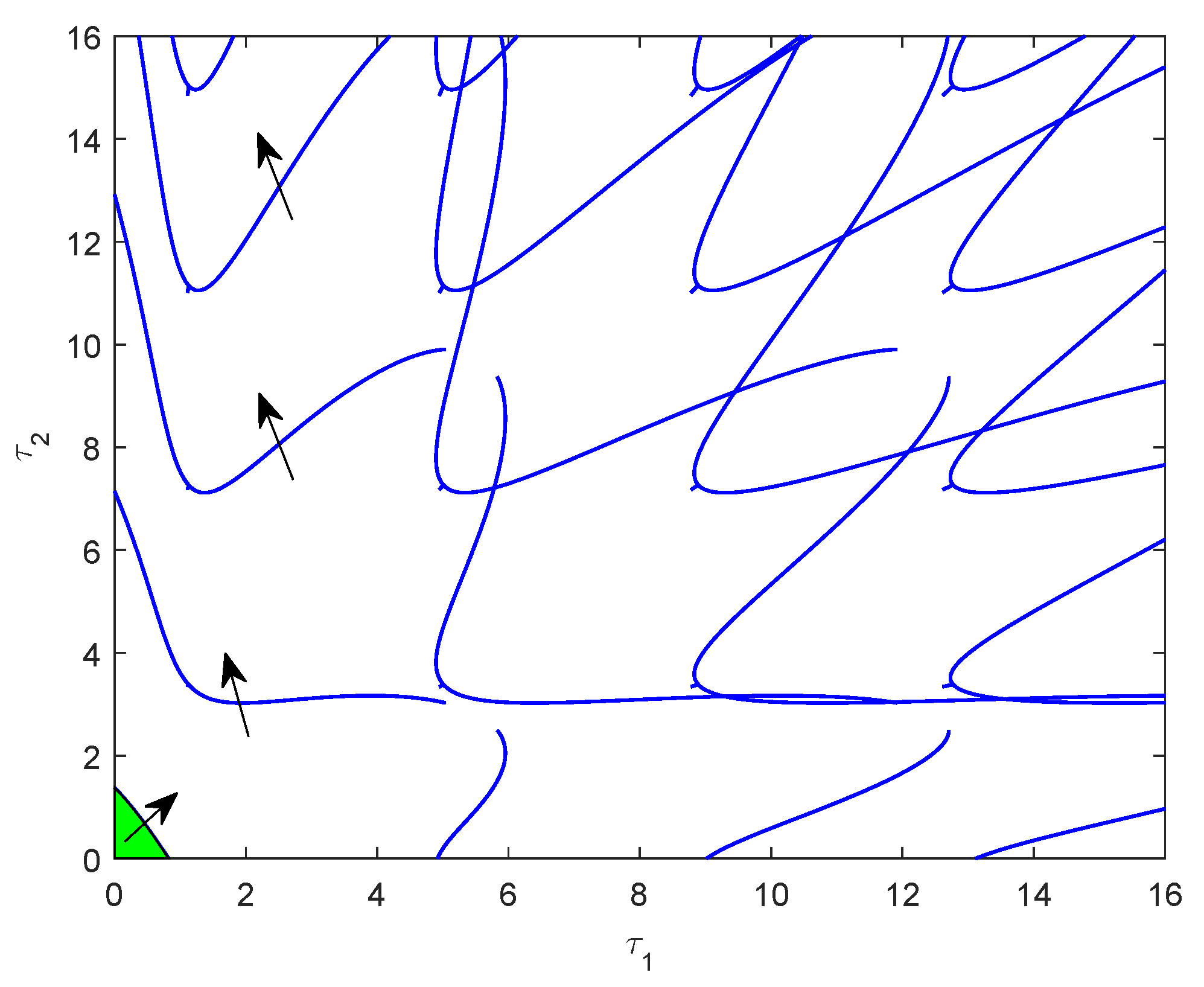
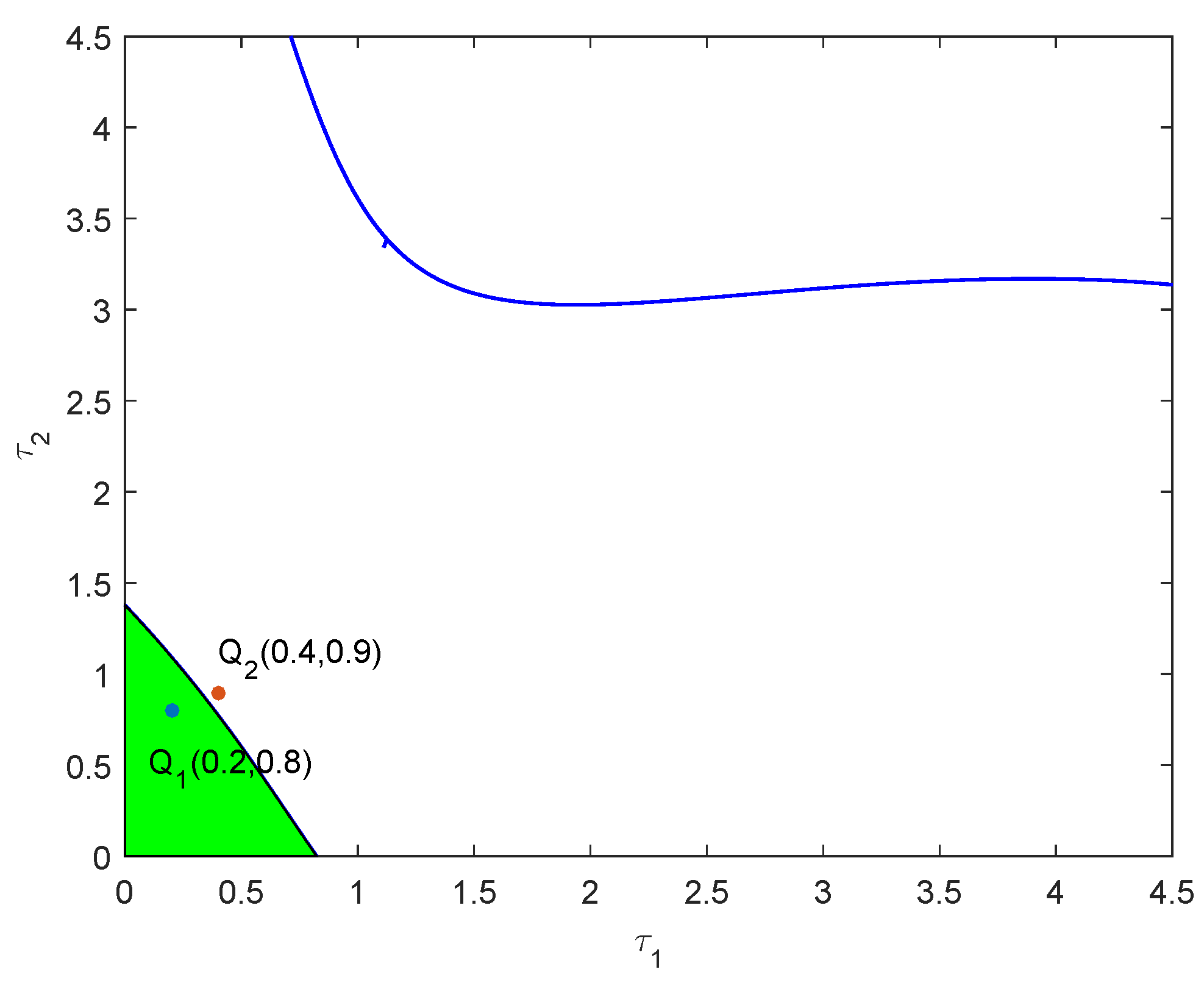
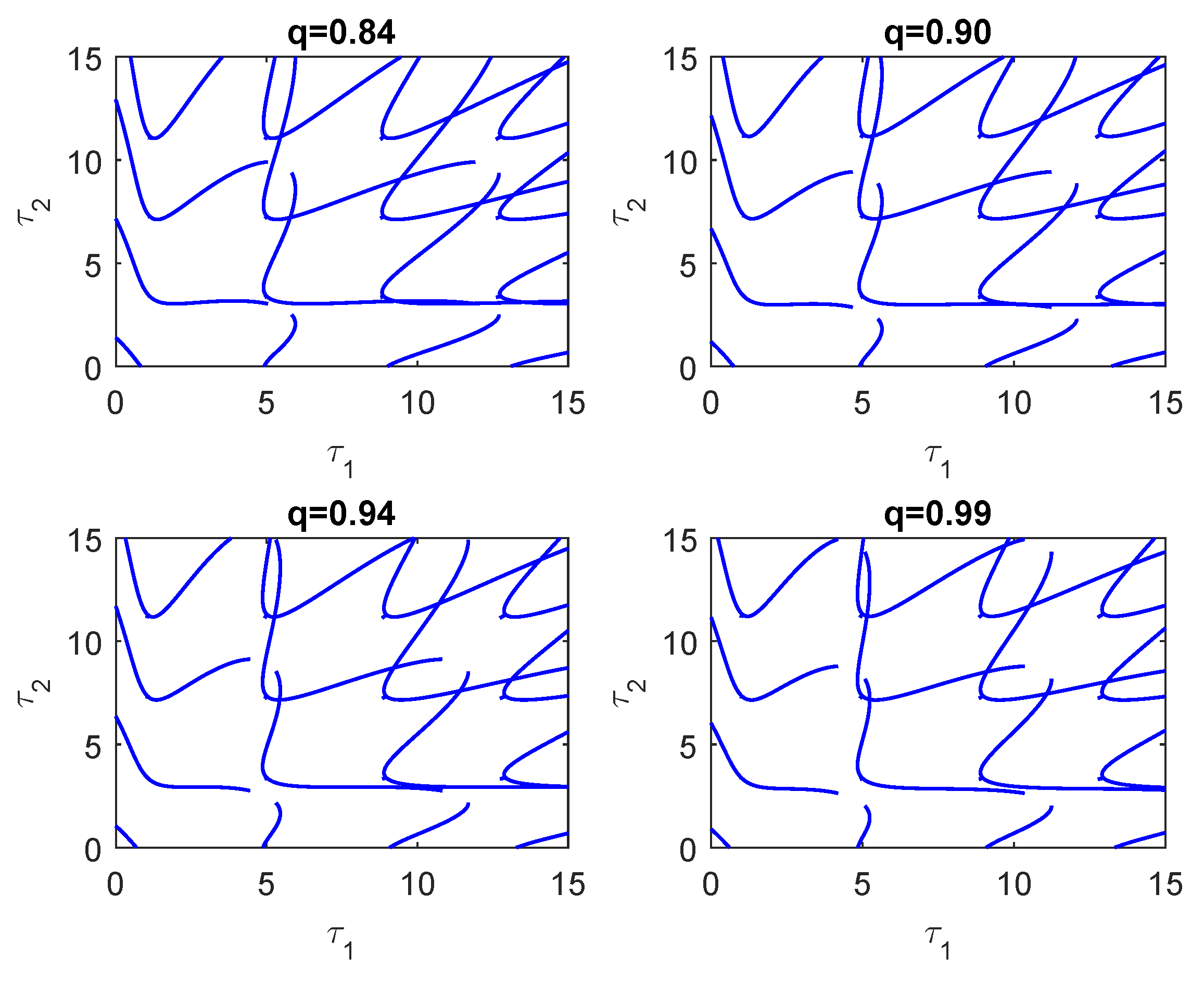
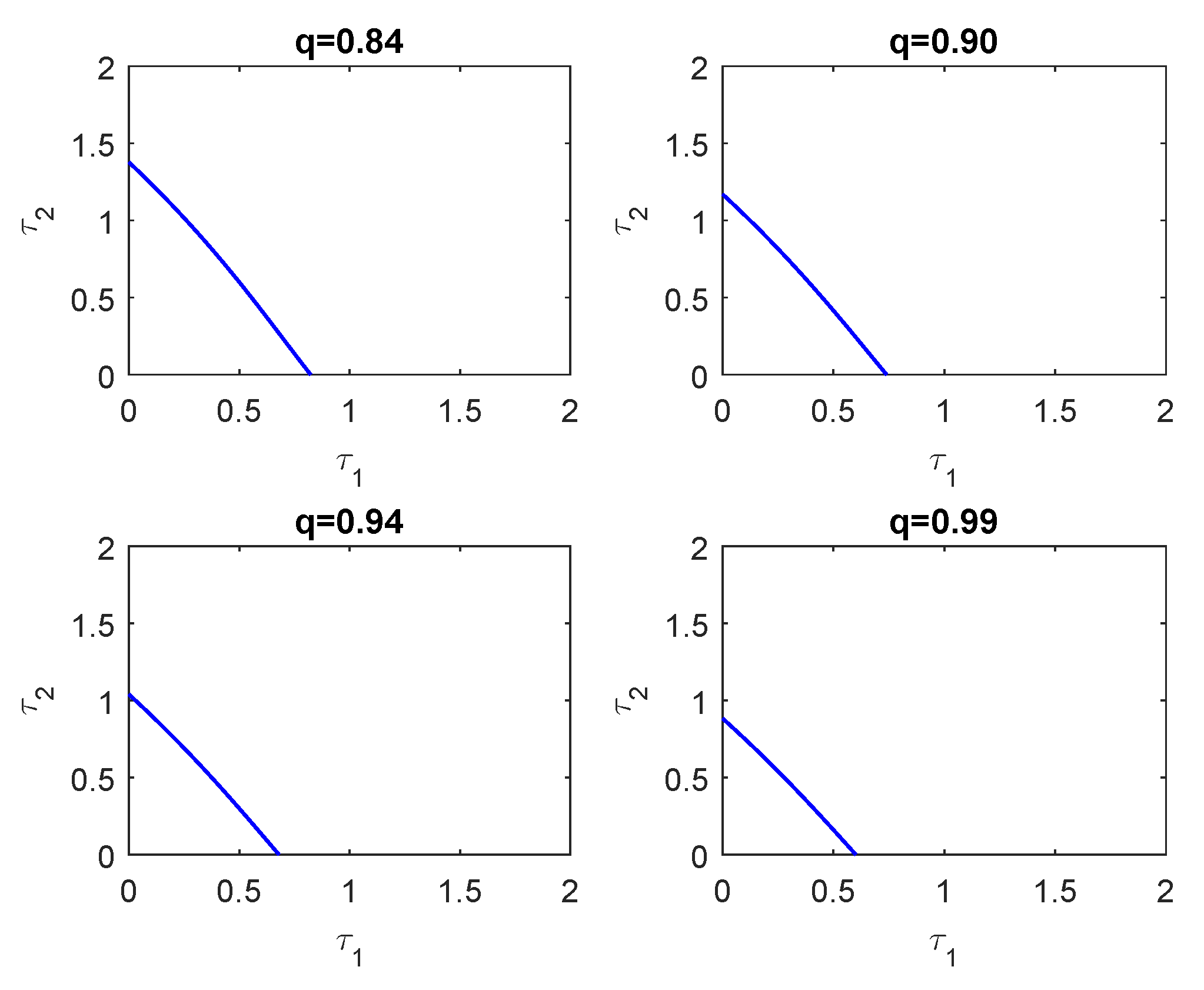
2.2. Stability Switching Curves
2.3. Crossing Directions
3. Hopf Bifurcation
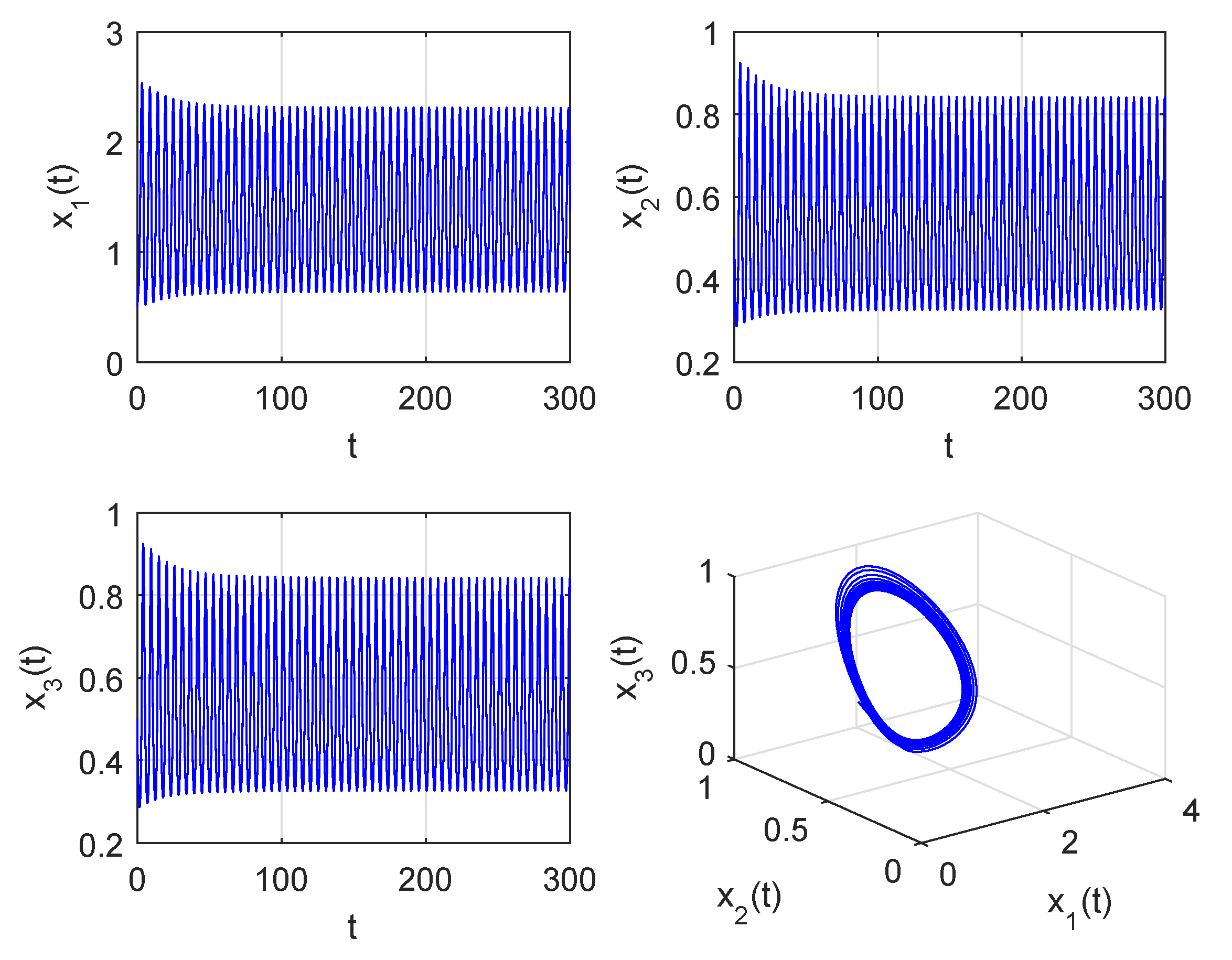
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Javidi, M.; Nyamoradi, N. Dynamic analysis of a fractional order prey-predator interaction with harvesting. Appl. Math. Model. 2013, 37, 8946–8956. [Google Scholar] [CrossRef]
- Li, W.; Ji, J.; Huang, L.; Guo, Z. Global dynamics of a controlled discontinuous diffusive SIR epidemic system. Appl. Math. Lett. 2021, 121, 107420. [Google Scholar] [CrossRef]
- Li, W.; Ji, J.; Huang, L. Dynamics of a controlled discontinuous computer worm system. Proc. Am. Math. Soc. 2020, 148, 4389–4403. [Google Scholar] [CrossRef]
- Perumal, R.; Munigounder, S.; Mohd, M.H. Stability analysis of the fractional order prey-predator model with infection. Int. J. Simul. Model. 2020, 2020, 1–17. [Google Scholar]
- Dubey, B.; Kumar, A. Dynamics of prey-predator model with stage structure in prey including maturation and gestation delays. Nonlinear Dyn. 2019, 96, 2653–2679. [Google Scholar] [CrossRef]
- Hu, G.P.; Li, W.T.; Yan, X.P. Hopf bifurcations in a predator–prey system with multiple delays. Chaos Solitons Fractals. 2009, 42, 1273–1285. [Google Scholar] [CrossRef]
- Deng, W. Short memory principle and a predictor-corrector approach for fractional differential equations. J. Comput. Appl. Math. 2007, 206, 174–188. [Google Scholar] [CrossRef] [Green Version]
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982. [Google Scholar]
- Rihan, F.A. Numerical Modeling of fractional-order biological systems. Abstr. Appl. Anal. 2013, 2013, 816803. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Liu, H.; Shi, X. Bifurcations in a fractional-order neural network with multiple leakage delays. Neural Netw. 2020, 131, 115–126. [Google Scholar] [CrossRef]
- You, X.; Song, Q.; Zhao, Z. Existence and finite-time stability of discrete fractional-order complex-valued neural networks with time delays. Neural Netw. 2020, 123, 248–260. [Google Scholar] [CrossRef]
- Diethelm, K. A fractional calculus based model for the simulation of an outbreak of dengue fever. Nonlinear Dyn. 2013, 71, 613–619. [Google Scholar] [CrossRef]
- Dhar, B.; Gupta, P.K.; Sajid, M. Solution of a dynamical memory effect COVID-19 infection system with leaky vaccination efficacy by non-singular kernel fractional derivatives. Math. Biosci. Eng. 2022, 19, 4341–4367. [Google Scholar] [CrossRef]
- N’Doye, I.; Voos, H. Chaos in a fractional-order cancer system. In Proceedings of the 2014 European Control Conference (ECC), Strasbourg, France, 24–27 June 2014; pp. 171–176. [Google Scholar]
- Zhao, H.; Lin, Y.; Dai, Y. Bifurcation analysis and control of chaos for a hybrid ratio-dependent three species food chain. Appl. Math. Comput. 2011, 218, 1533–1546. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Atangana, A. Spatiotemporal dynamics of fractional predator–prey system with stage structure for the predator. Int. J. Appl. Comput. Math. 2017, 3, 903–924. [Google Scholar] [CrossRef]
- Tian, J.; Yu, Y.; Wang, H. Stability and bifurcation of two kinds of three-dimensional fractional Lotka–Volterra systems. Math. Probl. Eng. 2014, 2014, 695871. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Wang, Z.; Meng, B. Dynamical analysis for a fractional-order prey-predator model with Holling III type functional response and discontinuous harvest. Appl. Math. Lett. 2020, 106, 106342. [Google Scholar] [CrossRef]
- Huang, C.; Cao, J. Impact of leakage delay on bifurcation in high-order fractional BAM neural networks. Neural Netw. 2018, 98, 223–235. [Google Scholar] [CrossRef]
- Rihan, F.A.; Lakshmanan, S.; Hashish, A.H. Fractional-order delayed predator–prey systems with Holling type-II functional response. Nonlinear Dyn. 2015, 80, 777–789. [Google Scholar] [CrossRef]
- Huang, C.; Li, H.; Cao, J. A novel strategy of bifurcation control for a delayed fractional predator–prey model. Appl. Math. Comput. 2019, 347, 808–838. [Google Scholar] [CrossRef]
- Yuan, J.; Zhao, L.; Huang, C. Stability and bifurcation analysis of a fractional predator–prey model involving two nonidentical delays. Math. Comput. Simul. 2020, 181, 562–580. [Google Scholar] [CrossRef]
- Xu, C.; Aouiti, C.; Liu, Z. A further study on bifurcation for fractional order BAM neural networks with multiple delays. Neurocomputing 2020, 417, 501–515. [Google Scholar] [CrossRef]
- Xu, C.; Liu, Z. Fractional-order bidirectional associate memory (BAM) neural networks with multiple delays: The case of Hopf bifurcation. Math. Comput. Simul. 2021, 182, 471–494. [Google Scholar] [CrossRef]
- Xu, C.; Liao, M.; Li, P. Influence of multiple time delays on bifurcation of fractional-order neural networks. Appl. Math. Comput. 2019, 361, 565–582. [Google Scholar] [CrossRef]
- Zeeman, M.L.; van den Driessche, P. Three-Dimensional Competitive Lotka–Volterra Systems with no Periodic Orbits. Siam J. Appl. Math. 1998, 58, 227–234. [Google Scholar] [CrossRef]
- Gu, K.; Niculescu, S.I. On stability crossing curves for general systems with two delays. J. Math. Anal. Appl. 2005, 311, 231–253. [Google Scholar] [CrossRef] [Green Version]
- Lin, X.; Wang, H. Stability analysis of delay differential equations with two discrete delays. Can. Appl. Math. Q. 2012, 20, 519–533. [Google Scholar]
- Matsumoto, A.; Szidarovszky, F. Stability switching curves in a Lotka—Volterra competition system with two delays. Math. Comput. Simul. 2020, 178, 422–438. [Google Scholar] [CrossRef]
- Hale, J.K.; Huang, W.Z. Global geometry of the stable regions for two delay differential equations. J. Math. Anal. Appl. 1993, 178, 344–362. [Google Scholar] [CrossRef] [Green Version]
- An, Q.; Beretta, E.; Kuang, Y. Geometric stability switch criteria in delay differential equations with two delays and delay dependent parameters. J. Differ. Equ. 2019, 266, 7073–7100. [Google Scholar] [CrossRef]
- Li, H.; Huang, C.; Li, T. Dynamic complexity of a fractional-order predator–prey system with double delays. Physica A 2019, 526, 120852. [Google Scholar] [CrossRef]
- Zhao, L.; Huang, C.; Cao, J. Dynamics of fractional-order predator–prey model incorporating two delays. Fractals 2021, 29, 2150014. [Google Scholar] [CrossRef]
- Deng, W.; Li, C.; Lü, J. Stability analysis of linear fractional differential system with multiple time delays. Nonlinear Dyn. 2007, 48, 409–416. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Zhu, Y.; Dai, Y.; Lin, Y. Stability Switching Curves and Hopf Bifurcation of a Fractional Predator–Prey System with Two Nonidentical Delays. Symmetry 2022, 14, 643. https://doi.org/10.3390/sym14040643
Li S, Zhu Y, Dai Y, Lin Y. Stability Switching Curves and Hopf Bifurcation of a Fractional Predator–Prey System with Two Nonidentical Delays. Symmetry. 2022; 14(4):643. https://doi.org/10.3390/sym14040643
Chicago/Turabian StyleLi, Shuangfei, Yingxian Zhu, Yunxian Dai, and Yiping Lin. 2022. "Stability Switching Curves and Hopf Bifurcation of a Fractional Predator–Prey System with Two Nonidentical Delays" Symmetry 14, no. 4: 643. https://doi.org/10.3390/sym14040643
APA StyleLi, S., Zhu, Y., Dai, Y., & Lin, Y. (2022). Stability Switching Curves and Hopf Bifurcation of a Fractional Predator–Prey System with Two Nonidentical Delays. Symmetry, 14(4), 643. https://doi.org/10.3390/sym14040643





