Shaking Table Tests and Simulations of Grouting Sleeve Connecting Prefabricated Bridge Piers
Abstract
:1. Introduction
2. Shaking Table Test
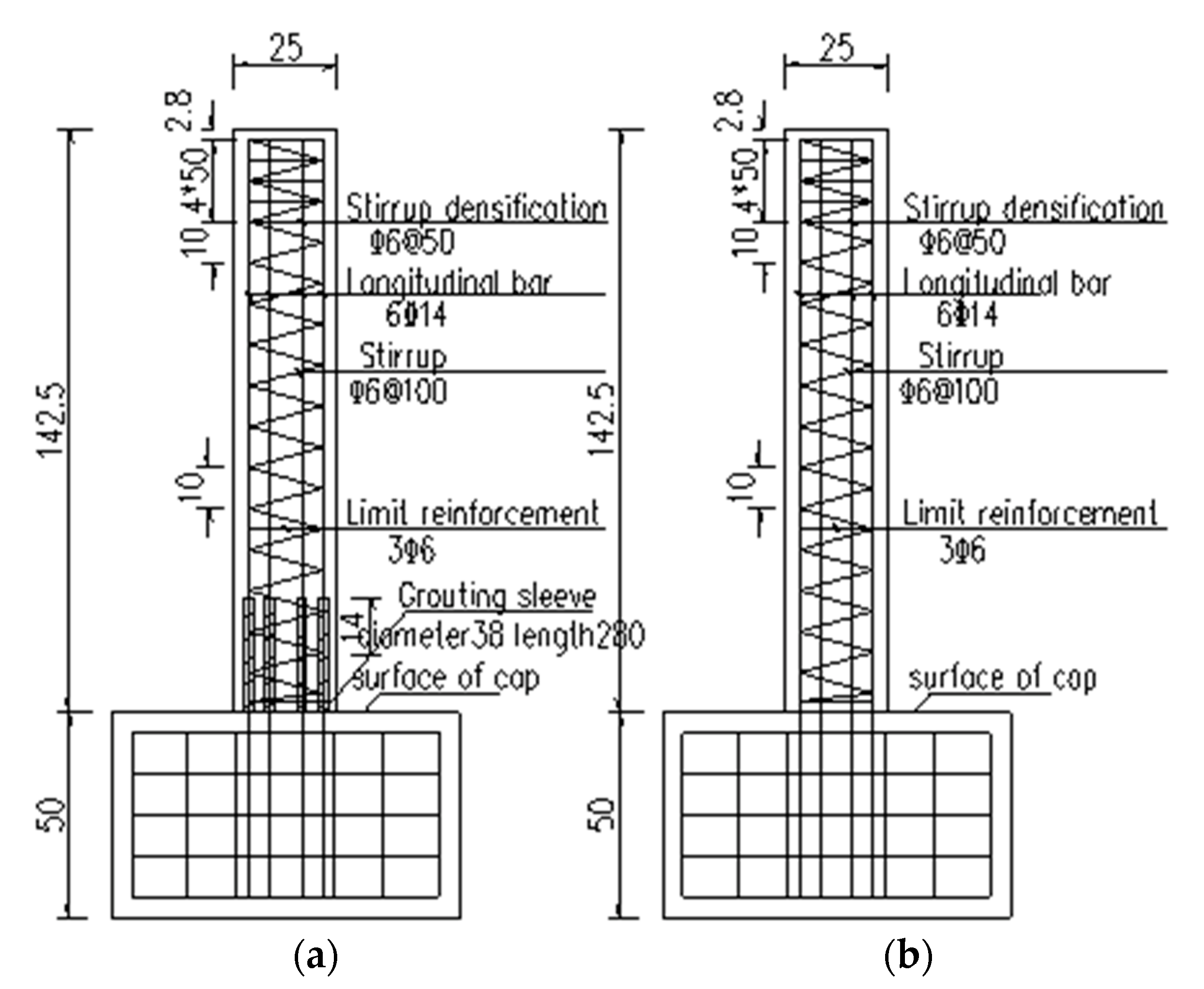
2.1. Specimen Design and Fabrication
2.2. Test Scheme Design
2.3. Test Conditions
3. Analysis of the Test Results
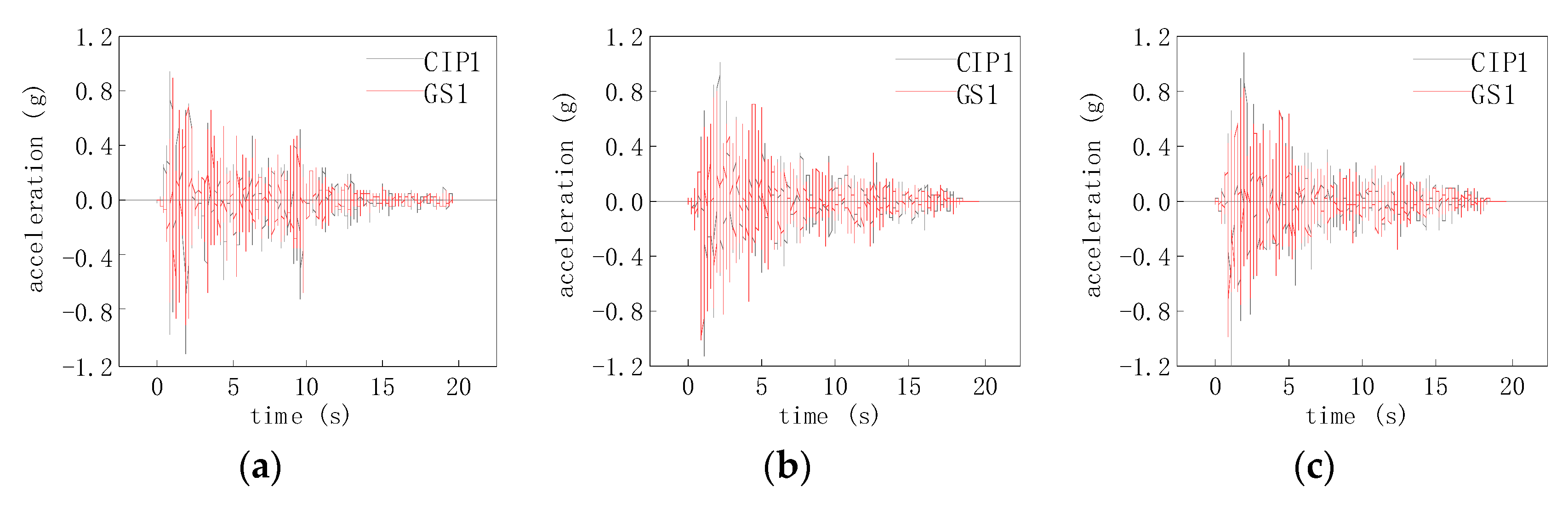
3.1. Dynamic Characteristics of Specimens
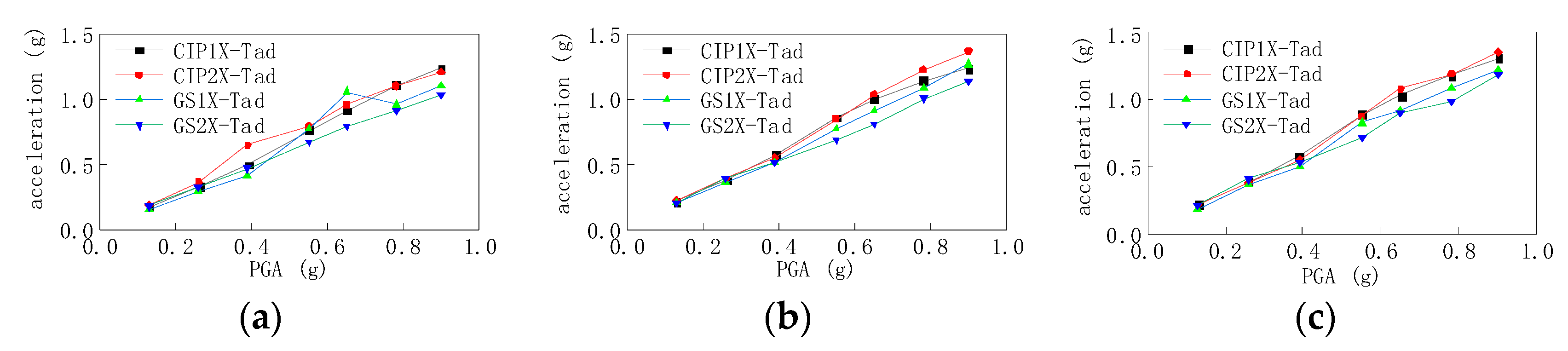
3.2. Acceleration Response of the Specimen Pier Top
3.3. Displacement Analysis
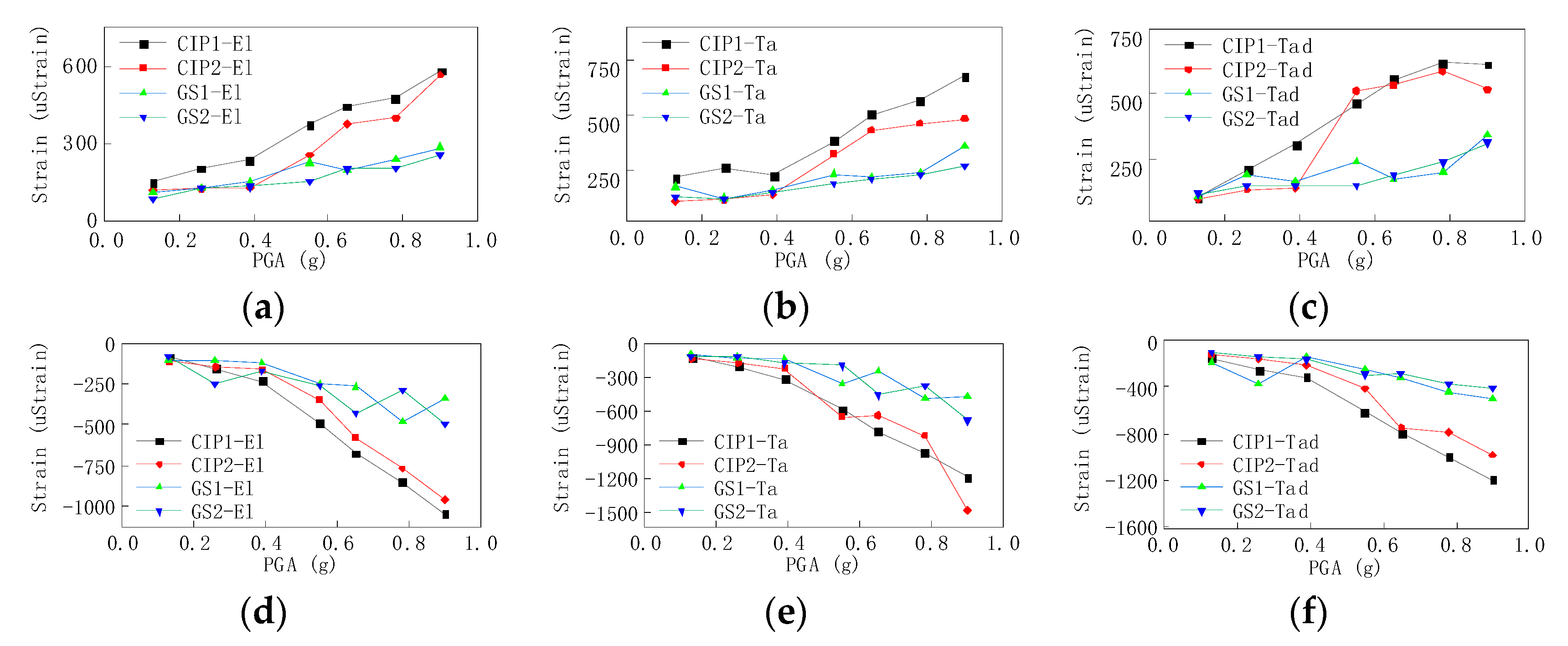
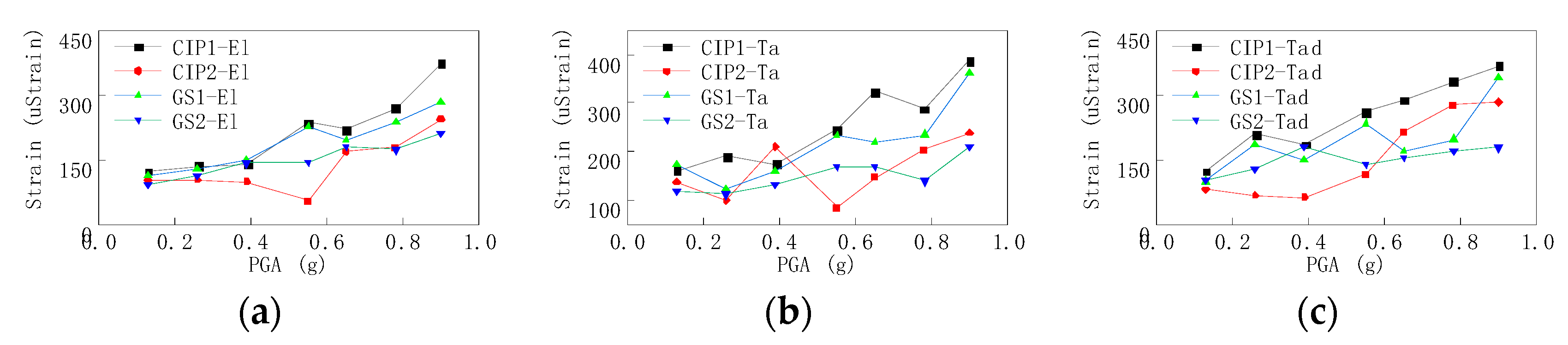
3.4. Strain Analysis
4. Comparison between the Finite Element Simulations and Test Results
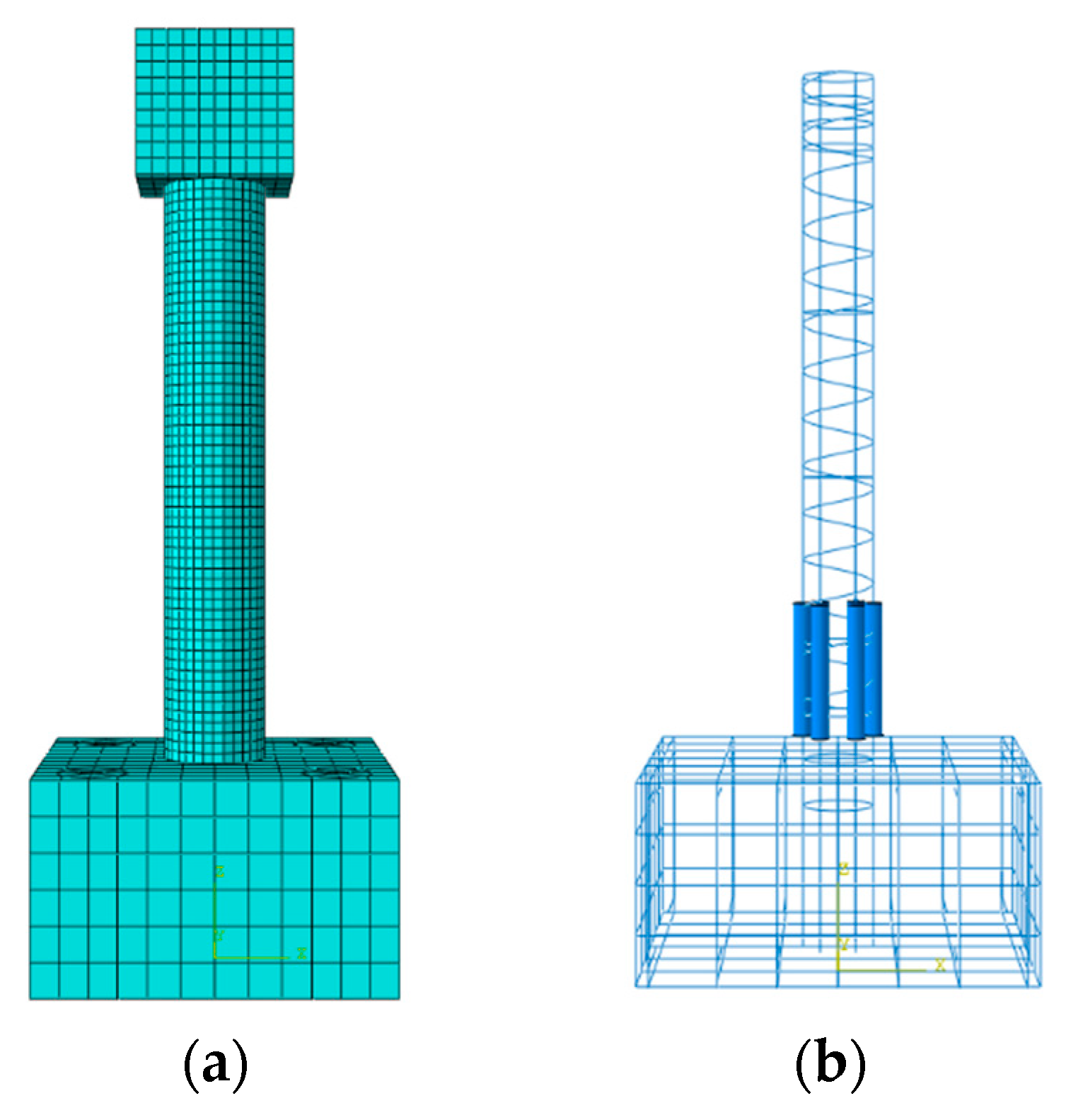
4.1. Finite Element Modeling Process
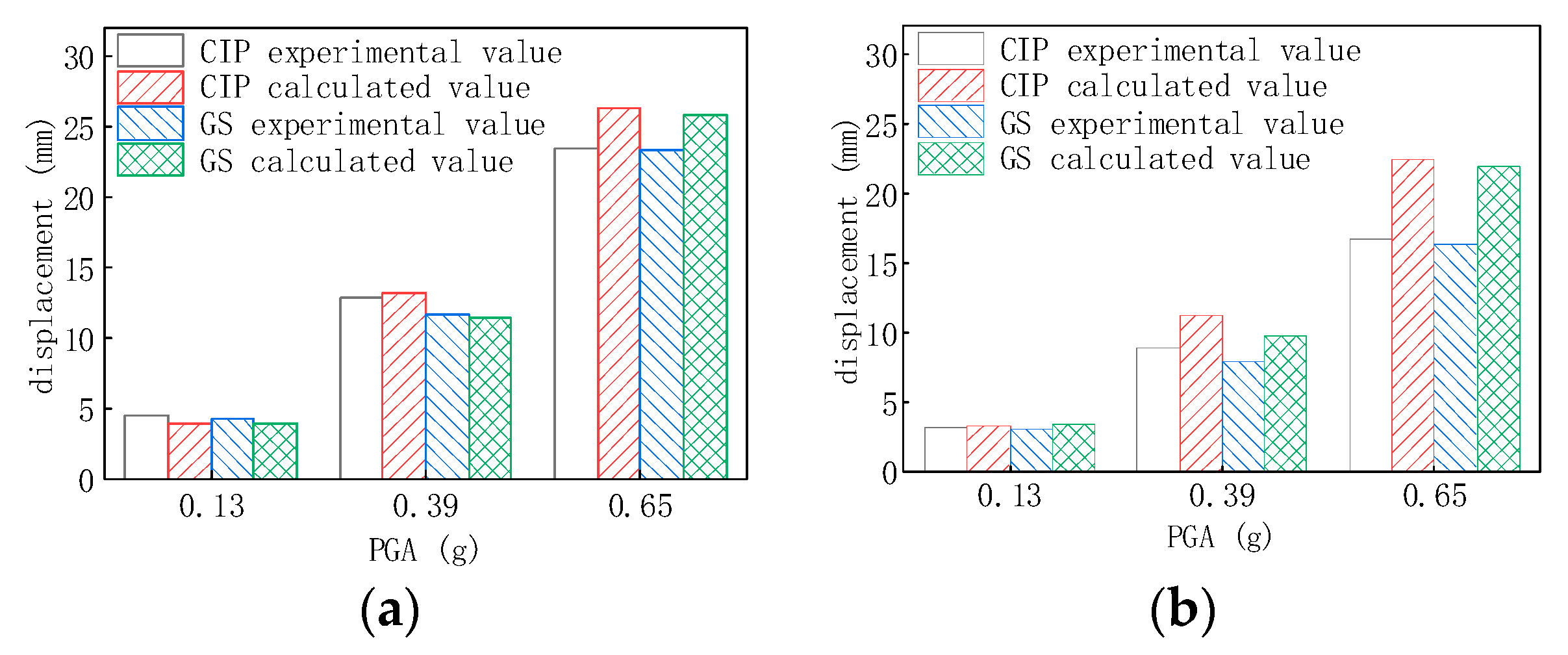
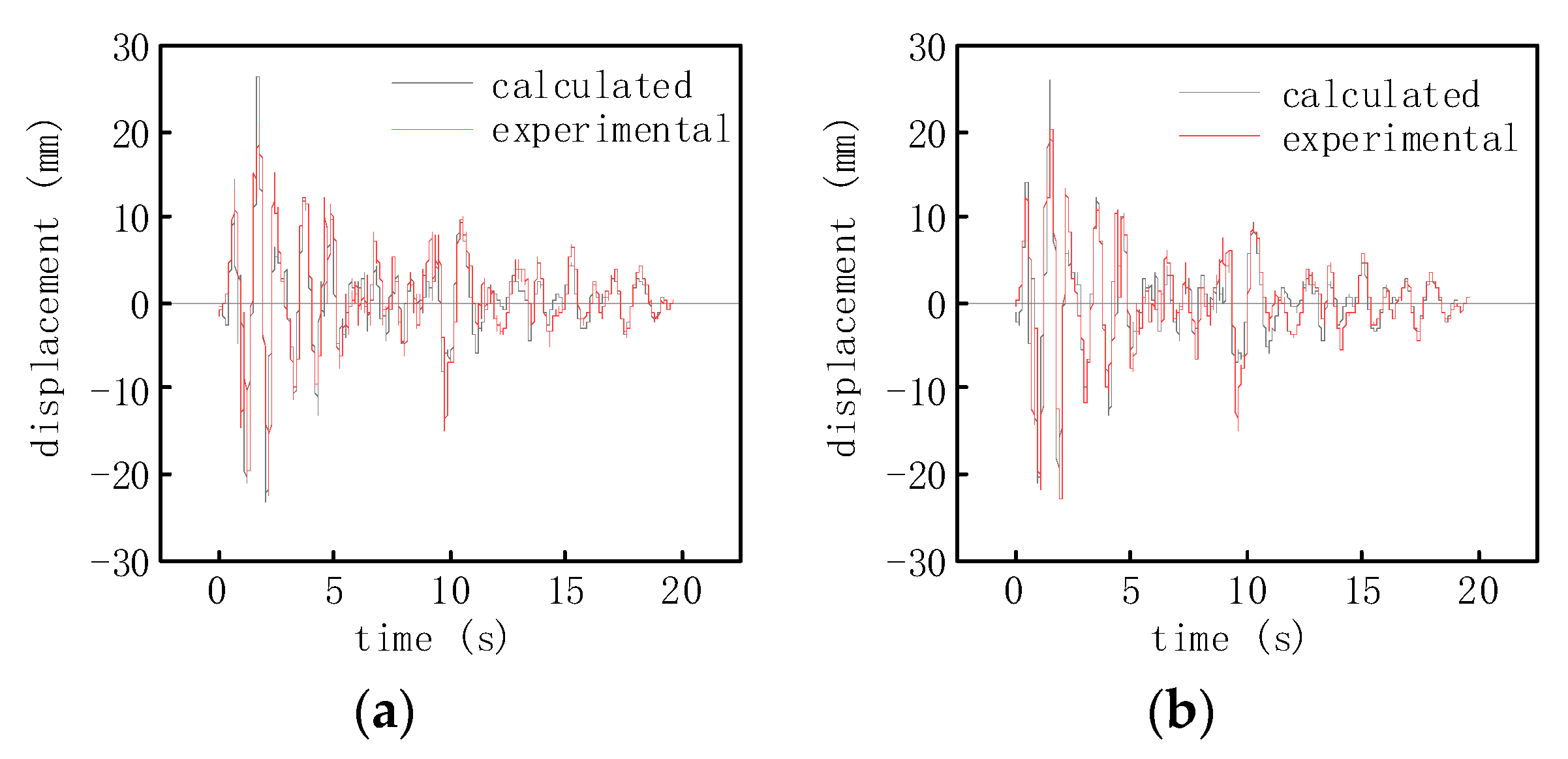
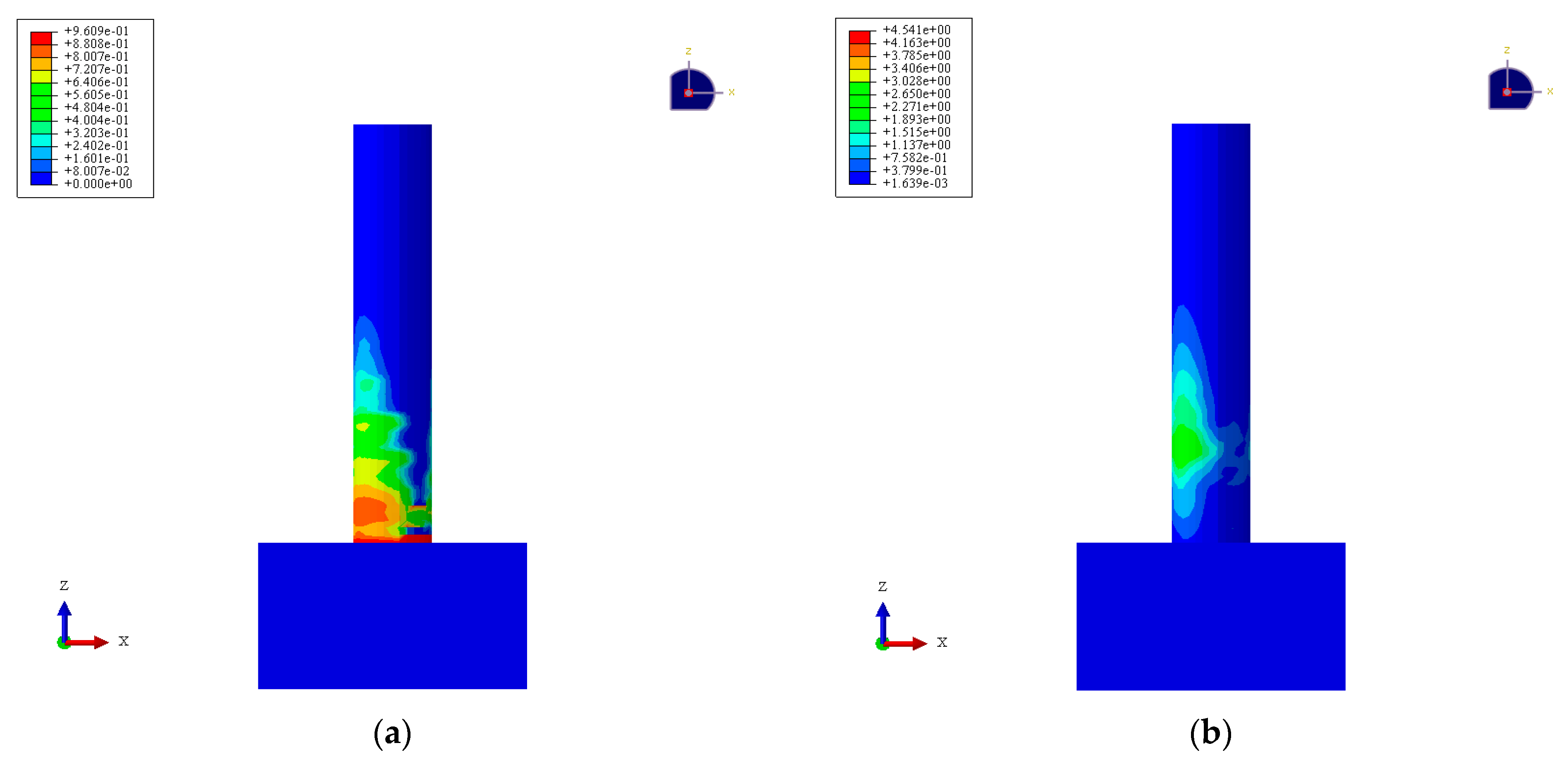
4.2. Comparison of Finite Element Numerical Results
4.3. Comparisons of the Pier Body Failure State
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Wu, J. Earthquake disaster investigation and risk assessment. City Dis. Reduct. 2021, 2, 10–13. [Google Scholar]
- Li, J.Z.; Guan, Z.G. Research Progress on Bridge Seismic Design: Target from Seismic Alleviation to Post earthquake Structural Resilience. China J. Highw. Transp. 2017, 30, 1–9, 59. [Google Scholar]
- Xiang, Y.; Zhu, S.; Zhao, Y. Research and development on accelerated bridge construction technology. China J. Highw. Transp. 2018, 31, 1–27. [Google Scholar]
- Han, Q.; Li, X.; Xu, K.; Lu, Y.; Wang, Z. Shear strength and cracking mechanism of precast bridge columns with grouted sleeve connections. Eng. Struct. 2021, 230, 111616. [Google Scholar] [CrossRef]
- Liu, Y. Study on the Joint Mechanical Behavior of Precast Bridge Piers with Grouted Sleeve Connection. Master’s Thesis, South China University of Technology, Guangzhou, China, 2020. [Google Scholar]
- Liu, Y.; Li, X.; Zheng, X. Experimental study on seismic response of precast bridge piers with double-grouted sleeve connections. Eng. Struct. 2020, 221, 111023. [Google Scholar] [CrossRef]
- Xin, G.; Xu, W.; Wang, J. Seismic performance of fabricated concrete piers with grouted sleeve joints and bearing-capacity estimation method. Structures 2021, 33, 169–186. [Google Scholar] [CrossRef]
- Wang, R.; Ma, B.; Chen, X. Seismic performance of pre-fabricated segmental bridge piers with grouted splice sleeve connections. Eng. Struct. 2021, 229, 111668. [Google Scholar] [CrossRef]
- Ameli, M.J.; Pantelides, C.P. Seismic Analysis of Precast Concrete Bridge Columns Connected with Grouted Splice Sleeve Connectors. J. Struct. Eng. 2016, 143, 04016176.1–04016176.13. [Google Scholar] [CrossRef]
- Wei, Y.; Guo, A.; Wei, Y. Shaking table tests of coastal bridge piers with different levels of corrosion damage caused by chloride penetration. Constr. Build. Mater. 2018, 173, 160–171. [Google Scholar]
- Yun, G.; Liu, C. Shaking table tests on a deep-water high-pier whole bridge under joint earthquake, wave and current action. Appl. Ocean. Res. 2020, 103, 102329. [Google Scholar] [CrossRef]
- Li, Z.; Kang, S.; You, C. Seismic Mitigation of Curved Continuous Girder Bridge Considering Collision Effect. Symmetry 2022, 14, 129. [Google Scholar] [CrossRef]
- Xia, X.; Zhang, X.; Wang, J. Shaking table test of a novel railway bridge pier with replaceable components. Eng. Struct. 2021, 232, 111808. [Google Scholar] [CrossRef]
- Deng, B.; Jia, Y.; Liang, D. Study on the Seismic Performance of Prefabricated Single-Segment Steel Jacket Bridge Piers. Symmetry 2021, 13, 2312. [Google Scholar] [CrossRef]
- Zhang, M. Study on similitude laws for shaking table tests. Earthq. Eng. Eng. Dyn. 1997, 2, 52–58. [Google Scholar]







| Physical Quantity | Similarity Relation | Similitude Ratio |
|---|---|---|
| length | 1/4 | |
| area | 1/16 | |
| displacement | 1/4 | |
| elastic modulus | 0.689 | |
| equivalent density | 1.409 | |
| time | 0.358 | |
| speed | 0.699 | |
| acceleration | 1.957 |
| Platform Size | Maximum Load | Maximum Overturning Moment | Maximum Acceleration at Full Load | Maximum Speed | Maximum Displacement | Frequency Range |
|---|---|---|---|---|---|---|
| 5 m × 5 m | 30 t | 75 t-m | 1 g | 60 cm/s | ±8 cm | 0.5–40 Hz |
| Condition | Loading Mode | PGA | Condition | Loading Mode | PGA |
|---|---|---|---|---|---|
| 1 | El Centro | 0.137 g | 5 | El Centro | 0.650 g |
| Taft 111 | Taft 111 | ||||
| taft111/taft21 | taft111/taft21 | ||||
| 2 | El Centro | 0.274 g | 6 | El Centro | 0.783 g |
| Taft 111 | Taft 111 | ||||
| taft111/taft21 | taft111/taft21 | ||||
| 3 | El Centro | 0.391 g | 7 | El Centro | 0.900 g |
| Taft 111 | Taft 111 | ||||
| taft111/taft21 | taft111/taft21 | ||||
| 4 | El Centro | 0.550 g | |||
| Taft 111 | |||||
| taft111/taft21 |
| Loading Conditions | Test Observations |
|---|---|
| 0.137 g | The specimens vibrated slightly, and no visible cracks were observed. |
| 0.274 g | The vibration of the specimens was obvious and slight cracks began to appear. Short cracks were observed within a range of 25 cm at the bottom of the CIP specimens, while cracks appeared within a range of 35–60 cm from the bottom of the prefabricated specimens. The majority of the cracks were horizontal. |
| 0.391 g | The vibration of the specimens intensified, and the cracks increased. The original cracks began to develop and became longer. The crack widths barely changed. |
| 0.55 g | The vibration of the specimens was markedly enhanced, and the cracks continued to increase. The original cracks began to develop and became longer. |
| 0.65 g | The original cracks began to widen and continued to extend. |
| 0.783 g | The specimens swung obviously and there was a sound of collision between the pile cap and the table surface in test. The newly added cracks of the CIP specimen were reduced, and the cracks gradually formed a circular connection. The cracks of the prefabricated specimens no longer increased, and the original cracks continued to extend laterally. |
| 0.9 g | The vibration of the specimens became severe, and circular through-cracks were observed. For the CIP specimens, new cracks no longer appeared, and the original cracks continued to widen and extend laterally. The original cracks of the prefabricated specimens widened and extended gradually to form horizontal penetrating cracks, while for the CIP specimens, the cracks continued upward. |
| PGA/g | CIP1 | CIP2 | GS1 | GS2 |
|---|---|---|---|---|
| initial | 9.60 | 9.76 | 9.91 | 10.90 |
| 0.137 | 9.03 | 9.19 | 9.29 | 10.48 |
| 0.274 | 8.44 | 8.51 | 8.87 | 9.93 |
| 0.391 | 8.82 | 8.13 | 9.08 | 10.10 |
| 0.550 | 8.18 | 8.17 | 8.18 | 9.98 |
| 0.650 | 7.47 | 7.34 | 8.50 | 9.73 |
| 0.783 | 7.27 | 7.47 | 8.05 | 10.10 |
| 0.900 | 6.89 | 6.88 | 8.03 | 9.27 |
| change rate | 28.15% | 29.51% | 18.97% | 15.88% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Jia, Y.; Liang, D. Shaking Table Tests and Simulations of Grouting Sleeve Connecting Prefabricated Bridge Piers. Symmetry 2022, 14, 652. https://doi.org/10.3390/sym14040652
Yang M, Jia Y, Liang D. Shaking Table Tests and Simulations of Grouting Sleeve Connecting Prefabricated Bridge Piers. Symmetry. 2022; 14(4):652. https://doi.org/10.3390/sym14040652
Chicago/Turabian StyleYang, Meng, Yanmin Jia, and Dongwei Liang. 2022. "Shaking Table Tests and Simulations of Grouting Sleeve Connecting Prefabricated Bridge Piers" Symmetry 14, no. 4: 652. https://doi.org/10.3390/sym14040652
APA StyleYang, M., Jia, Y., & Liang, D. (2022). Shaking Table Tests and Simulations of Grouting Sleeve Connecting Prefabricated Bridge Piers. Symmetry, 14(4), 652. https://doi.org/10.3390/sym14040652





