Tunable Geometries in Sparse Clifford Circuits
Abstract
:1. Introduction
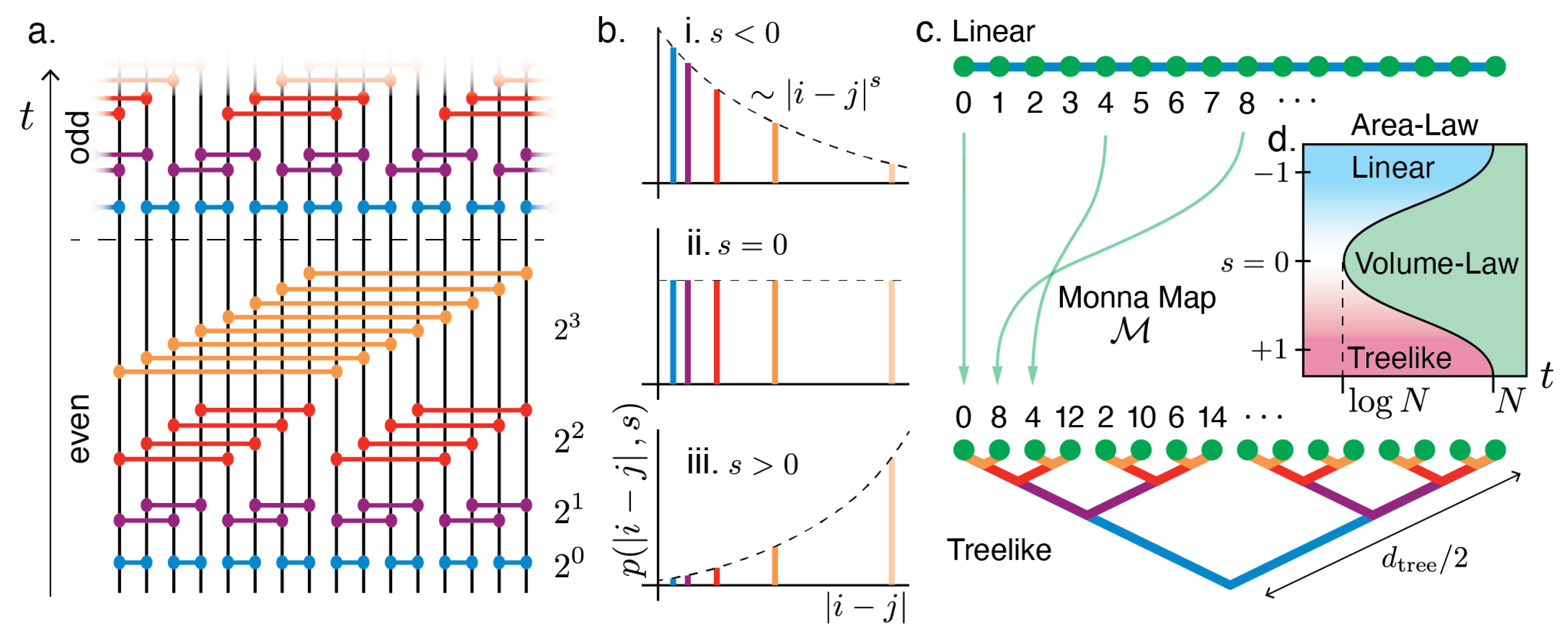
2. Sparse Clifford Circuits
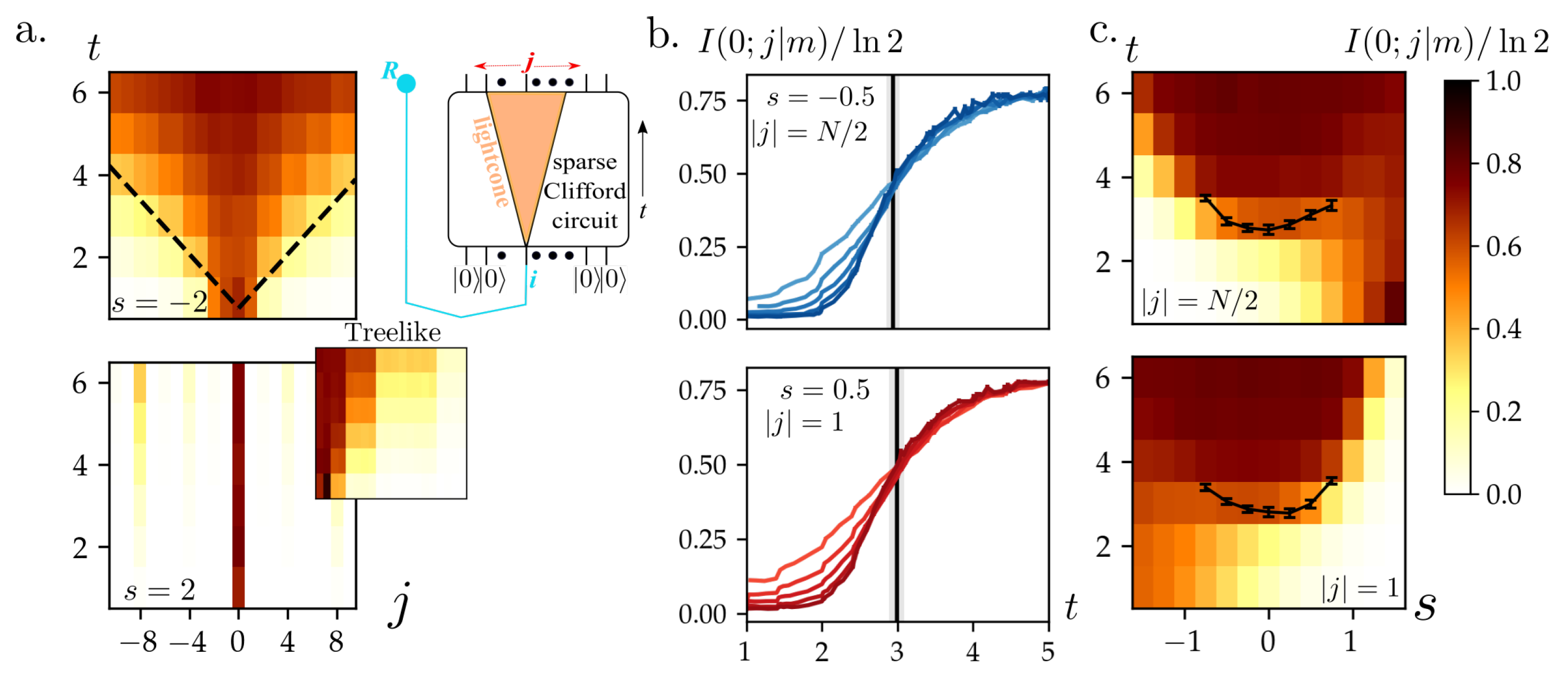
3. Probing Emergent Geometry with Entanglement Entropy
4. Scrambling and Negativity of Tripartite Mutual Information
5. Characterizing the Many-Body Lightcone via Teleportation
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Stabilizer Formalism and Clifford Circuits
Appendix A.1. Classical Simulation of Clifford Circuits
Appendix A.2. Reduced Density Matrices and Entanglement Entropy
Appendix B. Normalization Factor Js of the Sparse Probability Distribution
Appendix C. p-Adic Numbers and the Monna Map
Monna Map
Appendix D. Curve Fits for the Timescale tvol.

Appendix E. Time Dependence of Tripartite Mutual Information

Appendix F. The Limiting Behavior of at s = 0 for Large System Sizes


Appendix G. Tripartite Mutual Information at the Scrambling Limit
Appendix H. Time Dependence of Teleportation Fidelities
Appendix H.1. Teleportation Fidelity for Fixed s and Varying Sites B

Appendix H.2. Teleportation Fidelity for Fixed Sites and Varying s

Appendix I. Finite Size Scaling for Finding tc of Teleportation Fidelity

References
- Gioev, D.; Klich, I. Entanglement Entropy of Fermions in Any Dimension and the Widom Conjecture. Phys. Rev. Lett. 2006, 96, 100503. [Google Scholar] [CrossRef] [Green Version]
- Wolf, M.M. Violation of the Entropic Area Law for Fermions. Phys. Rev. Lett. 2006, 96, 010404. [Google Scholar] [CrossRef] [Green Version]
- Hastings, M.B.; Koma, T. Spectral Gap and Exponential Decay of Correlations. Commun. Math. Phys. 2006, 265, 781–804. [Google Scholar] [CrossRef] [Green Version]
- Vidal, G. Entanglement Renormalization. Phys. Rev. Lett. 2007, 99, 220405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hastings, M.B. An area law for one-dimensional quantum systems. J. Stat. Mech. Theory Exp. 2007, 2007, P08024. [Google Scholar] [CrossRef]
- Eisert, J.; Cramer, M.; Plenio, M.B. Colloquium: Area laws for the entanglement entropy. Rev. Mod. Phys. 2010, 82, 277–306. [Google Scholar] [CrossRef] [Green Version]
- Bianchi, E.; Hackl, L.; Kieburg, M.; Rigol, M.; Vidmar, L. Volume-Law Entanglement Entropy of Typical Pure Quantum States. arXiv 2021, arXiv:2112.06959. [Google Scholar]
- Nahum, A.; Ruhman, J.; Vijay, S.; Haah, J. Quantum Entanglement Growth under Random Unitary Dynamics. Phys. Rev. X 2017, 7, 031016. [Google Scholar] [CrossRef] [Green Version]
- Nahum, A.; Vijay, S.; Haah, J. Operator Spreading in Random Unitary Circuits. Phys. Rev. X 2018, 8, 021014. [Google Scholar] [CrossRef] [Green Version]
- Skinner, B.; Ruhman, J.; Nahum, A. Measurement-Induced Phase Transitions in the Dynamics of Entanglement. Phys. Rev. X 2019, 9, 31009. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Fisher, M.P. Statistical mechanics of quantum error correcting codes. Phys. Rev. B 2021, 103, 104306. [Google Scholar] [CrossRef]
- Maldacena, J. The large-N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1999, 38, 1113–1133. [Google Scholar] [CrossRef] [Green Version]
- Gubser, S.S.; Klebanov, I.R.; Polyakov, A.M. Gauge theory correlators from non-critical string theory. Phys. Lett. B 1998, 428, 105–114. [Google Scholar] [CrossRef] [Green Version]
- Witten, E. Anti de Sitter space and holography. arXiv 1998, arXiv:hep-th/9802150. [Google Scholar] [CrossRef]
- Hartnoll, S.A. Lectures on holographic methods for condensed matter physics. Class. Quantum Gravity 2009, 26, 224002. [Google Scholar] [CrossRef] [Green Version]
- Swingle, B. Entanglement renormalization and holography. Phys. Rev. D 2012, 86, 065007. [Google Scholar] [CrossRef]
- Gubser, S.S.; Knaute, J.; Parikh, S.; Samberg, A.; Witaszczyk, P. p-Adic AdS/CFT. Commun. Math. Phys. 2017, 352, 1019–1059. [Google Scholar] [CrossRef] [Green Version]
- Heydeman, M.; Marcolli, M.; Saberi, I.; Stoica, B. Tensor networks, p-adic fields, and algebraic curves: Arithmetic and the AdS3/CFT2 correspondence. arXiv 2017, arXiv:hep-th/1605.07639. [Google Scholar]
- Ryu, S.; Takayanagi, T. Holographic Derivation of Entanglement Entropy from the anti–de Sitter Space/Conformal Field Theory Correspondence. Phys. Rev. Lett. 2006, 96, 181602. [Google Scholar] [CrossRef] [Green Version]
- Ryu, S.; Takayanagi, T. Aspects of holographic entanglement entropy. J. High Energy Phys. 2006, 2006, 045. [Google Scholar] [CrossRef] [Green Version]
- Hubeny, V.E.; Rangamani, M.; Takayanagi, T. A covariant holographic entanglement entropy proposal. J. High Energy Phys. 2007, 2007, 62. [Google Scholar] [CrossRef]
- Islam, R.; Ma, R.; Preiss, P.M.; Eric Tai, M.; Lukin, A.; Rispoli, M.; Greiner, M. Measuring entanglement entropy in a quantum many-body system. Nature 2015, 528, 77–83. [Google Scholar] [CrossRef] [PubMed]
- Hucul, D.; Inlek, I.V.; Vittorini, G.; Crocker, C.; Debnath, S.; Clark, S.M.; Monroe, C. Modular entanglement of atomic qubits using photons and phonons. Nat. Phys. 2015, 11, 37–42. [Google Scholar] [CrossRef] [Green Version]
- Kaufman, A.M.; Tai, M.E.; Lukin, A.; Rispoli, M.; Schittko, R.; Preiss, P.M.; Greiner, M. Quantum thermalization through entanglement in an isolated many-body system. Science 2016, 353, 794–800. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hosten, O.; Engelsen, N.J.; Krishnakumar, R.; Kasevich, M.A. Measurement noise 100 times lower than the quantum-projection limit using entangled atoms. Nature 2016, 529, 505–508. [Google Scholar] [CrossRef] [PubMed]
- Lukin, A.; Rispoli, M.; Schittko, R.; Tai, M.E.; Kaufman, A.M.; Choi, S.; Khemani, V.; Léonard, J.; Greiner, M. Probing entanglement in a many-body–localized system. Science 2019, 364, 256–260. [Google Scholar] [CrossRef]
- Brydges, T.; Elben, A.; Jurcevic, P.; Vermersch, B.; Maier, C.; Lanyon, B.P.; Zoller, P.; Blatt, R.; Roos, C.F. Probing Renyi entanglement entropy via randomized measurements. Science 2019, 364, 260–263. [Google Scholar] [CrossRef] [Green Version]
- Periwal, A.; Cooper, E.S.; Kunkel, P.; Wienand, J.F.; Davis, E.J.; Schleier-Smith, M. Programmable interactions and emergent geometry in an array of atom clouds. Nature 2021, 600, 630–635. [Google Scholar] [CrossRef]
- Bentsen, G.; Hashizume, T.; Buyskikh, A.S.; Davis, E.J.; Daley, A.J.; Gubser, S.S.; Schleier-Smith, M. Treelike Interactions and Fast Scrambling with Cold Atoms. Phys. Rev. Lett. 2019, 123, 130601. [Google Scholar] [CrossRef] [Green Version]
- Gubser, S.S.; Jepsen, C.; Ji, Z.; Trundy, B. Continuum limits of sparse coupling patterns. Phys. Rev. D 2018, 98, 045009. [Google Scholar] [CrossRef] [Green Version]
- Gubser, S.S.; Jepsen, C.; Ji, Z.; Trundy, B. Mixed field theory. J. High Energ. Phys. 2019, 2019, 136. [Google Scholar] [CrossRef] [Green Version]
- Hashizume, T.; Bentsen, G.S.; Weber, S.; Daley, A.J. Deterministic Fast Scrambling with Neutral Atom Arrays. Phys. Rev. Lett. 2021, 126, 200603. [Google Scholar] [CrossRef] [PubMed]
- Lieb, E.H.; Robinson, D.W. The finite group velocity of quantum spin systems. Commun. Math. Phys. 1972, 28, 251–257. [Google Scholar] [CrossRef]
- Hastings, M.B. Locality in quantum systems. Quantum Theory Small Large Scales 2010, 95, 171–212. [Google Scholar]
- Roberts, D.A.; Swingle, B. Lieb–Robinson Bound and the Butterfly Effect in Quantum Field Theories. Phys. Rev. Lett. 2016, 117, 091602. [Google Scholar] [CrossRef] [Green Version]
- Else, D.V.; Machado, F.; Nayak, C.; Yao, N.Y. Improved Lieb–Robinson bound for many-body Hamiltonians with power-law interactions. Phys. Rev. A 2020, 101, 022333. [Google Scholar] [CrossRef] [Green Version]
- Bentsen, G.; Gu, Y.; Lucas, A. Fast scrambling on sparse graphs. Proc. Natl. Acad. Sci. USA 2019, 116, 6689–6694. [Google Scholar] [CrossRef] [Green Version]
- Tran, M.C.; Guo, A.Y.; Baldwin, C.L.; Ehrenberg, A.; Gorshkov, A.V.; Lucas, A. Lieb-Robinson Light Cone for Power-Law Interactions. Phys. Rev. Lett. 2021, 127, 160401. [Google Scholar] [CrossRef]
- Page, D.N. Average entropy of a subsystem. Phys. Rev. Lett. 1993, 71, 1291–1294. [Google Scholar] [CrossRef] [Green Version]
- Sekino, Y.; Susskind, L. Fast scramblers. J. High Energy Phys. 2008, 2008, 065. [Google Scholar] [CrossRef] [Green Version]
- Rammal, R.; Toulouse, G.; Virasoro, M.A. Ultrametricity for Physicists. Rev. Mod. Phys. 1986, 58, 765–788. [Google Scholar] [CrossRef]
- Gottesman, D. The Heisenberg representation of quantum computers. arXiv 1998, arXiv:quant-ph/9807006. [Google Scholar]
- Aaronson, S.; Gottesman, D. Improved simulation of stabilizer circuits. Phys. Rev. A 2004, 70, 052328. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Chen, X.; Fisher, M.P.A. Measurement-Driven Entanglement Transition in Hybrid Quantum Circuits. Phys. Rev. B 2019, 100, 134306. [Google Scholar] [CrossRef] [Green Version]
- Cleve, R.; Leung, D.; Liu, L.; Wang, C. Near-Linear Constructions of Exact Unitary 2-Designs. Quantum Inf. Comput. 2016, 16, 721–756. [Google Scholar] [CrossRef]
- Hashizume, T.; Bentsen, G.; Daley, A.J. Measurement-induced phase transitions in sparse nonlocal scramblers. arXiv 2021, arXiv:2109.10944. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics; University of California Press: Berkeley, CA, USA, 1961; Volume 4, pp. 547–562. [Google Scholar]
- Huang, A.; Stoica, B.; Yau, S.T. General relativity from p-adic strings. arXiv 2021, arXiv:1901.02013. [Google Scholar]
- Stoica, B. Building Archimedean Space. arXiv 2021, arXiv:1809.01165. [Google Scholar]
- Gubser, S.S.; Heydeman, M.; Jepsen, C.; Marcolli, M.; Parikh, S.; Saberi, I.; Stoica, B.; Trundy, B. Edge length dynamics on graphs with applications to p-adic AdS/CFT. J. High Energ. Phys. 2017, 2017, 157. [Google Scholar] [CrossRef]
- Bentsen, G.S.; Hashizume, T.; Davis, E.J.; Buyskikh, A.S.; Schleier-Smith, M.H.; Daley, A.J. Tunable geometries from a sparse quantum spin network. In Proceedings of the Optical, Opto-Atomic, and Entanglement-Enhanced Precision Metrology II; International Society for Optics and Photonics: Bellingham, WA, USA, 2020; Volume 11296, p. 112963W. [Google Scholar]
- Lashkari, N.; Stanford, D.; Hastings, M.; Osborne, T.; Hayden, P. Towards the fast scrambling conjecture. J. High Energ. Phys. 2013, 2013, 22. [Google Scholar] [CrossRef] [Green Version]
- Yao, N.Y.; Grusdt, F.; Swingle, B.; Lukin, M.D.; Stamper-Kurn, D.M.; Moore, J.E.; Demler, E.A. Interferometric approach to probing fast scrambling. arXiv 2016, arXiv:1607.01801. [Google Scholar]
- Marino, J.; Rey, A. Cavity-QED simulator of slow and fast scrambling. Phys. Rev. A 2019, 99, 051803(R). [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Choudhury, S.; Liu, W.V. Fast scrambling without appealing to holographic duality. Phys. Rev. Res. 2020, 2, 043399. [Google Scholar] [CrossRef]
- Belyansky, R.; Bienias, P.; Kharkov, Y.A.; Gorshkov, A.V.; Swingle, B. Minimal Model for Fast Scrambling. Phys. Rev. Lett. 2020, 125, 130601. [Google Scholar] [CrossRef] [PubMed]
- Hayden, P.; Headrick, M.; Maloney, A. Holographic Mutual Information Is Monogamous. Phys. Rev. D 2013, 87, 046003. [Google Scholar] [CrossRef] [Green Version]
- Hosur, P.; Qi, X.L.; Roberts, D.A.; Yoshida, B. Chaos in quantum channels. J. High Energy Phys. 2016, 2016, 4. [Google Scholar] [CrossRef] [Green Version]
- Gullans, M.J.; Huse, D.A. Dynamical Purification Phase Transition Induced by Quantum Measurements. Phys. Rev. X 2020, 10, 041020. [Google Scholar] [CrossRef]
- Bao, Y.; Block, M.; Altman, E. Finite time teleportation phase transition in random quantum circuits. arXiv 2021, arXiv:2110.06963. [Google Scholar]
- Hayden, P.; Preskill, J. Black holes as mirrors: Quantum information in random subsystems. J. High Energy Phys. 2007, 2007, 120. [Google Scholar] [CrossRef] [Green Version]
- Yoshida, B.; Kitaev, A. Efficient decoding for the Hayden-Preskill protocol. arXiv 2017, arXiv:1710.03363. [Google Scholar]
- Yoshida, B.; Yao, N.Y. Disentangling Scrambling and Decoherence via Quantum Teleportation. Phys. Rev. X 2019, 9, 011006. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.; Jian, S.K.; Liu, C.; Chen, X. Emergent Replica Conformal Symmetry in Non-Hermitian SYK _2 Chains. Quantum 2021, 5, 579. [Google Scholar] [CrossRef]
- Bentsen, G.S.; Sahu, S.; Swingle, B. Measurement-induced purification in large-N hybrid Brownian circuits. Phys. Rev. B 2021, 104, 094304. [Google Scholar] [CrossRef]
- Selinger, P. Generators and relations for n-qubit Clifford operators. Log. Meth. Comput. Sci. 2015, 11, 80–94. [Google Scholar] [CrossRef] [Green Version]
- Nahum, A.; Roy, S.; Skinner, B.; Ruhman, J. Measurement and Entanglement Phase Transitions in All-To-All Quantum Circuits, on Quantum Trees, and in Landau-Ginsburg Theory. PRX Quantum 2021, 2, 010352. [Google Scholar] [CrossRef]
- Gouvêa, F.Q. p-Adic Numbers, 3rd ed.; Springer: Cham, Switzerland, 1997. [Google Scholar]
- Dyson, F.J. Existence of a Phase-Transition in a One-Dimensional Ising Ferromagnet. Commun. Math. Phys. 1969, 12, 91–107. [Google Scholar] [CrossRef]
- Bleher, P.; Sinai, J. Investigation of the critical point in models of the type of Dyson’s hierarchical models. Commun. Math. Phys. 1973, 33, 23–42. [Google Scholar] [CrossRef]
- Lerner, E.; Missarov, M. Scalar models of p-adic quantum field theory and hierarchical models. Theor. Math. Phys. 1989, 78, 177–184. [Google Scholar] [CrossRef]
- Monna, A. Sur une transformation simple des nombres P-adiques en nombres reels. Indag. Math. (Proc.) 1952, 55, 1–9. [Google Scholar] [CrossRef]
- Kolchin, V. Random Graphs; Encyclopedia of Mathematics and its Applications; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hashizume, T.; Kuriyattil, S.; Daley, A.J.; Bentsen, G. Tunable Geometries in Sparse Clifford Circuits. Symmetry 2022, 14, 666. https://doi.org/10.3390/sym14040666
Hashizume T, Kuriyattil S, Daley AJ, Bentsen G. Tunable Geometries in Sparse Clifford Circuits. Symmetry. 2022; 14(4):666. https://doi.org/10.3390/sym14040666
Chicago/Turabian StyleHashizume, Tomohiro, Sridevi Kuriyattil, Andrew J. Daley, and Gregory Bentsen. 2022. "Tunable Geometries in Sparse Clifford Circuits" Symmetry 14, no. 4: 666. https://doi.org/10.3390/sym14040666
APA StyleHashizume, T., Kuriyattil, S., Daley, A. J., & Bentsen, G. (2022). Tunable Geometries in Sparse Clifford Circuits. Symmetry, 14(4), 666. https://doi.org/10.3390/sym14040666





