1. Introduction
The piles are a type of the direct foundation. Plates resting on piles as building elements find wide application, especially in constructions settled on wetlands and permafrost. It is common to build plates on piles as drilling platforms on seas as well as viewing terraces on seashores and lakes or on marshes close to the shores.
Rotationally symmetric circular plates, subjected to axisymmetric loading, are such a type of plates for which it is possible to find exact analytical solutions [
1]. For rectangular plates, the more for otherwise shaped plates, it will be only approximate solutions (often in a form of infinite trigonometric series, usually numerical). Theory of plates, cooperating with a subsoil or without such cooperation, has been already well developed and a lot of problems has been well examined. The classical items concerning statics of plates are the books by Timoshenko [
2] and Kączkowski [
3], both of them republished several times, and of newer items it is worth to name a book by Blaauwendraad [
4], comprising also a FEM analysis with reference to plates. Since then, many authors have dealt with circular plates on an elastic subsoil, both in terms of statics and dynamics as well as stability.
In recent years, an interest in elements with variable features has increased. Such elements give greater possibilities of shaping of a behavior of a construction and optimization of execution costs, e.g., by reduction of an element thickness in a place where it is subjected to a lower load. Due to that, methods should be developed which allow more effective calculation of such elements. The circular plates with variable features were also the subject of interest of many authors, wherein it is worth to cite the publications by Reddy [
5,
6], which treat of plates with functional gradation of features in the radial direction.
Another problem is a modelling of the cooperation of plates with piles and piles with a subsoil. Publications concerning this topic, however, do not refer to a behavior of plates settled on piles and elevated over a subsoil, i.e., not cooperating with a subsoil. All works found in the literature by the authors of this study concern the design of piles as well as behavior of plates on a subsoil reinforced by the piles. However, the plates described above, i.e., for example drilling or viewing platforms over the water and laid on piles put on a seabed, require calculations without consideration of the cooperation with subsoil (because there is no any), but with consideration of a point support in selected places. The authors were not able to find such publications.
Due to that, the task of this study is to calculate a deflection and internal forces (i.e., radial and tangential moments as well as radial shear forces) of a radially symmetric circular plate, supported in points (on piles) distributed on a circle (or circles) having a certain radius, in particular on a circumference. The term “radially symmetric” means that:
the load and stiffness of the plate are axisymmetric, i.e., they are variable in the radial direction and constant in the tangent direction,
the supports (piles) are evenly distributed, i.e., if straight sections are dragged from the center of the plate to each support, then between two such sections always exists a constant angle, even if the supports are distributed on the circles with different radii.
The main topic of the study are the plates with discontinuous (piecewise constant) stiffness, however the plates with functionally varying stiffness have been also examined as a comparison. The stiffness variability has been introduced through the thickness variability—the material itself is homogeneous. For the case of plates with discontinuous stiffness, the plate was approximated by homogeneous rings with different stiffnesses. Such approach was applied for example by Utku et al. [
7]. It has been assumed as well, that one ring in such plate is wholly loaded or wholly unloaded on its surface—there is no situation where it is loaded only on a part of its surface. All plates have been calculated with use of the Kirchhoff’s theory of thin plates.
2. Materials and Methods
The plate presented in the Introduction can be calculated in two ways:
using formulas for a plate on an elastic subsoil, wherein for the rings different than the external one, assuming a zero stiffness of subsoil and for the external ring a stiffness described by the “Dirac comb” (
Figure 1a),
treating the plate as supported around the middle on a small, defined radius (“supported” means clamped if there is no opening in the middle of the original plate or hinged if there is) and loaded by concentrated forces, in fact, being reactions to an external, real load (
Figure 1b).
The first approach is much more difficult as the deflection of a circular plate on a subsoil requires a lot of complicated calculations (the formula contains the Bessel functions and functions related to them). Therefore, the second approach has been chosen.
According [
2,
3], the equation of deflection of a circular plate is following:
and the formulas for internal forces—following:
In the above formulas and further, w denotes deflection, q—surface load, r and —radial and angular coordinates, respectively, and —the plate stiffness: .
A solution to Equation (1) for a general case can be sought if the deflection and load are expanded into a cosine-sine series:
where,
i.e., it is assumed that the expansion occurs only in the tangential direction, wherein δ is the Kronecker symbol: δ
mn = 0 for
m ≠
n and δ
mn = 1 for
m =
n.
If the deflection and load in the Formula (5) is substituted into Equation (1), then the differentiation with respect to
r and φ will remain the cosine and sine without changes (only the expansion coefficient
wm will be differentiated), moreover the differentiation with respect to φ—as it is always twice or fourfold—can change their sign and will cause their multiplication by
m2 or
m4:
Equation (7) will be satisfied if two separate equations are satisfied:
In general case, the complementary functions of these equations are following:
however, for
m = 0 and
m = 1 it is,
In Formulas (9) and (10) A0–D0 and Am–Dm are the integration constants, calculated from boundary and continuity conditions.
Assume a load in a form of several concentrated forces
P, evenly distributed on circles having a certain radius (in particular, on a circumference) and summing in total to the real force in the middle. Such a load can be presented in the form of “Dirac comb” (
Figure 2), i.e., the expression:
where
n—the number of piles and the difference φ
k–φ
k−1 is an integer submultiple of 2π (i.e., all forces are applied to the points laying on the radii situated in the same angular distance from each other),
δ is the Dirac delta.
Formula (6) can be simplified, if special cases of measuring angular coordinates of piles are assumed (
Figure 3).
If the angle φ
1 = 0° is attributed to the pile 1 (
Figure 3a), then for the load presented in
Figure 2 the integrals from Formula (6) are equal to:
Thus,
It is easy to note a following feature: as
m is always an integer number, then,
Therefore, if φ1 = 0, then only w0 and wm for m = in, i ∈ Z, are taken in further calculation (i.e., for m being an integer multiple of the number of piles). It must be noted that w0 is a solution for a plate subjected to a uniform load. Moreover, the more concentrated forces it is applied on a circle (i.e., the more piles support the plate), the more rarely a non-zero term occurs in the series; if there was an infinite number of piles (uniform load, continuous support), then all terms in the series would assume the zero value and only w0 would be taken for calculations.
If the angle equal to the half of the angular distance between the piles is attributed to the pile 1 (
Figure 3b), then
as well, but,
Due to that, if φ1 = α/2, then also only w0 and wm for m = in, i ∈ Z, are taken in further calculation but these terms will have alternately different signs (starting from the positive w0).
If, however, the angle of the first pile is different than 0 or α/2, then and qm(r) assumes other values than in (14) and (15).
The configuration of the plate examined in the paper is presented in
Figure 4. The plate has
j rings, wherein a ring with the number
i (
i = 1, …,
j) is limited by the radii
Ri and
Ri+1 (i.e., there are
j + 1 radii). The radius
R1 is the radius of a post supporting the plate. Each ring has the plate stiffness
and the Poisson number ν
i. The coefficients
A0–
D0 and
Am–
Dm in Formulas (9), (10) are being sought from:
continuity conditions:
where
qm(
Ri+1) are forces defined by Formulas (14), (15) and applied on the radius
Ri+1, in particular equal to 0,
boundary conditions for the clamped internal ring:
boundary conditions for the hinged internal ring:
boundary conditions for the external ring (free edge):
Figure 4.
General configuration of the plate analyzed in the paper.
Figure 4.
General configuration of the plate analyzed in the paper.
The individual quantities in Formulas (16)–(19) are equal to:
radial bending moment (acc. (2)):
radial shear force (acc. (4)):
If some ring of the plate is subjected to a uniform load
q, then its deflection is described by Formula (9) with a particular integral added:
In a similar way, the remaining quantities (slope angle, radial bending moment, radial shear force) require adding appropriate particular integrals:
4. Discussion of Results and Convergence Analysis
As seen in the graphs and maps, the maximum deflection of the plate 2 is lower than of the plate 1, similar relation is between the plates 4 and 3, 6 and 5, 8 and 7—the plates 1, 3, 5, 7 have more freedom in movement on the circumference. For the plates 9 and 10, this effect is glaring in the face. The radial and tangential bending moments for the plates 2, 4, 6, 8 are approximately a mean of the moments for the plates 1, 3, 5, 7, respectively; this effect is very weak for the plates 9 and 10. A sudden fall visible in the graphs of the radial moments in the vicinity of the plate center and an analogical rise in the graphs of the tangential moments (both would be visible in the 3D polar graphs as “funnels” directed upward or downward) are due to the fact that during the calculations the narrow post had to be placed there (cf.
Figure 7) and the more the radius of this post is, the higher the radial and the lower the tangential bending moments are. Of course, there should not be any fall or rise—this is only a calculational side effect. The differences between the plates supported on piles and on a hoop in the graphs increase along with the growth in the distance from the plate center.
The most positive tangential moments for the plates supported on piles are just over the piles—the plate is bent most in the tangential direction exactly over there. The most negative tangential moment is in a midpoint between the piles. The shape of the graph of the tangential moment reflects the dependence of the stiffness on the radial coordinate.
The graphs of radial shear forces require a broader discussion. It results from the graphs for the plates 1, 3, 5, 7 that the force over the pile is equal to 70.56 kN/m, whereas the reaction should be 26.88π = 88.45 kN. It is due to the fact that the piles are modelled as a point, hence the concentrated force is applied in point. As it was mentioned above, only four terms have been taken to the calculations—this is enough for the accuracy of calculations of the deflection and moments, taking more terms does not improve the results significantly. However, it is different for the forces. If a force is applied in a point, hence on a zero area (length), then the value in the graph should go to infinity—it is indeed the case if the number of terms is being increased what results from the formula for expansion of the Dirac delta/comb function in a trigonometric series. In aim to obtain a real value of the reaction in the graph, it should be assumed some dimensions of the pile, and the load—not as a concentrated force but a load distributed on some area what complicates the calculation, not contributing significantly to its results (it should be assumed an additional ring, having width equal to the pile diameter, and another load function, e.g., series of rectangular impulses, instead of the Dirac delta/comb, but it would not affect the graphs of deflection and moments). The value of 70.56 kN/m, visible in the graph, results from the right sides of the last equations of the sets (25) and (26): for m = 0 it is kN/m, for m = 6, 12, 18 it is kN/m, hence for all these m it yields 70.56 kN/m. Thus, the graphs of the shear force are only indicative: they show that the radial shear force in the center of the plates 1 and 2 is equal to 0, the force on the circumference of the plate 2 and between the piles on the plate 1 is equal to kN/m, the shape of the whole graph is consistent with the engineer’s intuition and the superposition gives proper results. The graphs of the shear force must be treated with caution especially in the vicinity of piles.
In an analogical way, for the plate 9 it can be read from the graph of the shear forces (
Figure 19d) that the reaction in the internal piles (the difference between the values from both sides of the coordinate
r = 4.8 m for the orange line) is 75.07 kN/m and the reaction in the external piles (the value for the coordinate
r = 8 m for the blue line) is 25.42 kN/m. In a similar way as for the plates 1, 3, 5, 7, these values are obtained as follows: for
m = 0 and the internal piles (
R =
R4 = 4.8 m) it is
kN/m, for the external piles (
R =
R6 = 8 m) it is 3.63 kN/m; for
m = 6, 12, 18 and the internal piles it is
kN/m for the external piles it is 7.26 kN/m. Hence for all these
m it gives 75.07 kN/m for the internal piles and 25.41 kN/m for the external ones. The real values of reactions are 18.679π = 58.68 kN and 8.201π = 25.76 kN.
Regarding the results of FEM (ROBOT Autodesk), they must be acknowledged as less credible, though they are close to these from MATHEMATICA. It is evident that the radial bending moment has non-zero values on the circumference, hence it does not fulfill the boundary condition. The shear forces have discontinuities on the borders between the rings, hence they do not fulfill the continuity conditions, moreover the values of these forces over the piles depend on the size of the finite element and cannot be referred as reactions. The reactions are not visible in the maps because they are presented in another window in ROBOT. The reactions over the piles for the plate 1 amounted between 83.62 and 84.86 kN, hence almost equal to 26.88π, for the plate 3 it was between 83.66 and 84.84 kN. For the plate 9 it was within the range 55.85–56.11 kN for the internal piles and 28.17–28.60 kN for the external ones, thus the differences in relation to the forces obtained in MATHEMATICA are ca. ±10%.
Regarding the plates 5–8, generally, it has been stated a high concordance of the relations obtained for the plates with continuously and stepwise varying stiffness. The deflection of these plates is a bit smaller than for the corresponding plates 1–4, i.e., a plate with a stiffness varying continuously according to the assumed relations (30) and (31) is a bit stiffer than the related plate with stepwise varying stiffness (in the presented cases—ca. 2%). The conformity of the relations decreases as the order of derivatives in the formulas increases and the radial coordinate decreases. Each differentiation accentuates inaccuracies in calculations, hence the lowest conformity is for the radial shear forces in the vicinity of the radius R0 (even a sudden fall as a calculational side effect can be observed there what was not the case for the other plates).
For the plate 9, in general, it can be noted that the conformity between the results from MATHEMATICA and ROBOT Autodesk is a bit lower than for the other plates.
For the results from the ROBOT Autodesk, a short convergence analysis has been also performed. It consisted in checking, how the mesh size
s affects the results. The analysis was performed for the plate 1 and 9. As mentioned in
Section 3.1, the basic mesh size was equal to 0.5 m and all results in the contour maps of the right sides have been obtained for such size. Apart of this size, the following sizes have been assumed in the analysis:
s = 0.1 m (18,714 nodes),
s = 0.25 m (3525 nodes) and
s = 0.75 m (454 nodes).
Figure 21 shows the maps for the plate 1.
The purpose of these maps is to present similarities and trends in the changes of the quantities being presented. The trends and similarities are best visible in the case of the deflection, radial moment and tangential moment. The shear forces—according to the prior conclusions—are the least credible: the extreme points change their position depending on the mesh size, the values are excessively high; if the size decreases, then the values at the edge of the plate and the differences between the values at the boundaries between the rings increase.
Table 1 presents the values of ordinates of characteristic points of the graphs of the deflection, radial moment and tangential moment for the plates 1 and 9. The shear forces have not been considered due to the abovementioned reasons. These characteristic points, showed in
Figure 22, are: the maximum values of the quantity for the angle φ = 0° (A) and φ = 30° (B) (for each angle, it can be either one point in the plate center or two points at the same radii but opposite with respect to the plate center—as in
Figure 22) as well as the edge values for the angle φ = 0° (C) and φ = 30° (D) (for the moments in the plate 9, the points B correspond to the internal supports).
As seen, the worst results are for the “coarse” mesh (s = 0.75 m), what seems expectable, whereas the results for the remaining mesh sizes are close to each other and similar to those from MATHEMATICA (although, some small deviations can be visible for the finest size—s = 0.1 m). Therefore, taking calculation costs into consideration, it is enough to assume the mesh size 0.5 m (besides, it was assumed as default by ROBOT for the task being presented).
The moment values at the supports seem to be a problem, however—they increase far over the theoretical values (obtained in MATHEMATICA) along with the decrease of the mesh size, though, according to an engineer’s intuition, it should be other way. It is the radial and tangential moment for the plate 1 and 9 in the point C (the support for the angle φ = 0) as well as for the plate 9 in the point B (the support for the φ = 30°). The radial moment in the points C and D should be equal to 0—only the second one approaches this value.
However, after a more exact examination of the graphs for the mesh size s = 0.1 m, it can be noted that already in the second or even the first node from the support in the radial direction, the values stabilize. For example, in the plate 1, the radial moment varies as follows: for r = 8 m (point C, support) it is Mr = 20.15 kNm/m (it should be 0), then for r = 7.9 m Mr = −19.94 kNm/m (change of sign), for r = 7.8 m Mr = −12.26 kNm/m and for r = 7.6 m Mr = −12.15 kNm/m, i.e., almost as much as in MATHEMATICA. The tangential moment in the point C is Mφ = 88.14 kNm/m (ca. 80% more than in MATHEMATICA) but for r = 7.9 m it is already 42.45 kNm/m—almost as much as in MATHEMATICA as well. For the plate 9, the radial moment in the point B (r = 4.8 m) is equal to 23.52 kNm/m, i.e., ca. 50% more than in MATHEMATICA, but in the distance 0.1 m toward the plate center (r = 4.7 m) it is ca. 11.0 kNm/m and toward the circumference (r = 4.9 m) ca. 11.4 kNm/m, i.e., a bit lower than in MATHEMATICA (these two values are approximate as there are no nodes in these points and an interpolation is required). Similar relations can be observed for the remaining supporting points. Hence, as the mesh size decreases, for the edge supports one can note significant oscillations of the values which, however, rapidly fade away with distance from the support; for the internal supports, an excessive point growth is visible, but it no longer encompasses neighboring nodes. All of that shows imperfections of the ROBOT Autodesk and makes a user be cautious in the interpretation of obtained results. These phenomena are quite puzzling and require a more exact knowledge of the ROBOT internal code what, however, may be behind possibilities of an average user due to a producer secrecy.


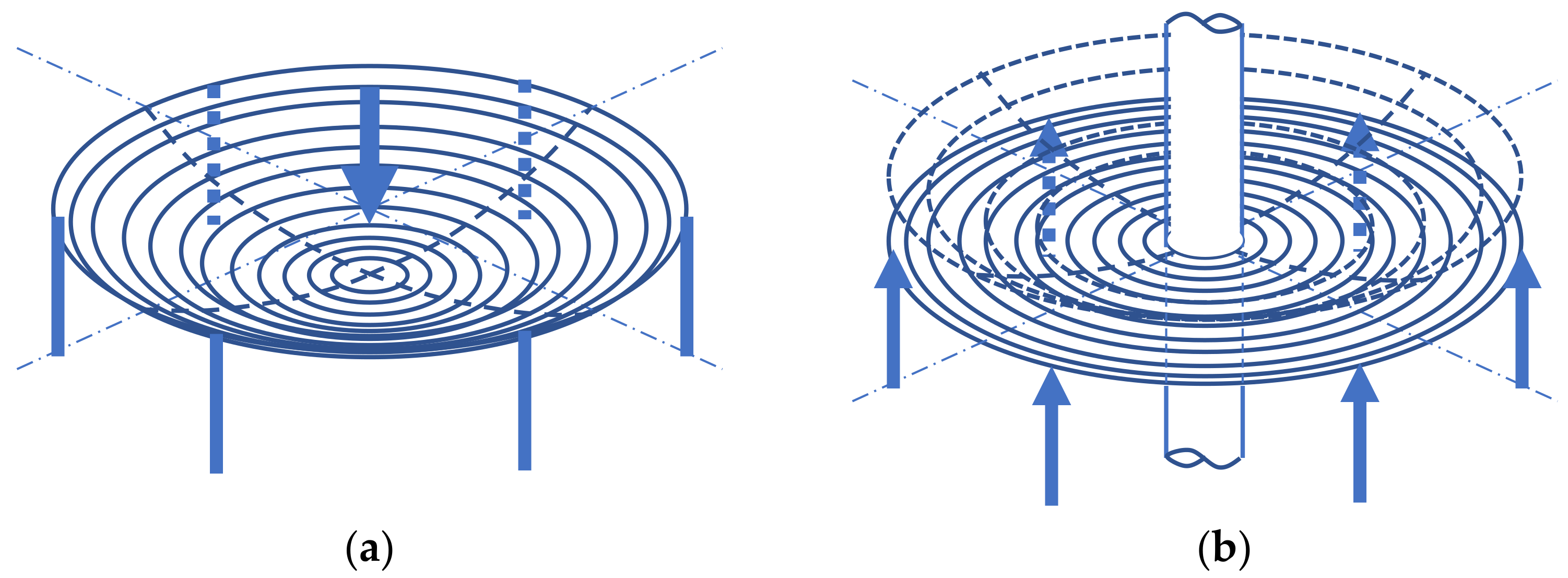





 plate 1, angle φ = 0,
plate 1, angle φ = 0,  plate 1, angle φ = π/6,
plate 1, angle φ = π/6,  plate 2. (a) deflection, (b) radial moment, (c) tangential moment, (d) radial force.
plate 2. (a) deflection, (b) radial moment, (c) tangential moment, (d) radial force.
 plate 1, angle φ = 0,
plate 1, angle φ = 0,  plate 1, angle φ = π/6,
plate 1, angle φ = π/6,  plate 2. (a) deflection, (b) radial moment, (c) tangential moment, (d) radial force.
plate 2. (a) deflection, (b) radial moment, (c) tangential moment, (d) radial force.



 plate 3, angle φ = 0,
plate 3, angle φ = 0,  plate 3, angle φ = π/6,
plate 3, angle φ = π/6,  plate 4. (a) deflection, (b) radial moment, (c) tangential moment, (d) radial force.
plate 4. (a) deflection, (b) radial moment, (c) tangential moment, (d) radial force.
 plate 3, angle φ = 0,
plate 3, angle φ = 0,  plate 3, angle φ = π/6,
plate 3, angle φ = π/6,  plate 4. (a) deflection, (b) radial moment, (c) tangential moment, (d) radial force.
plate 4. (a) deflection, (b) radial moment, (c) tangential moment, (d) radial force.








 plate 9, angle φ = 0,
plate 9, angle φ = 0,  plate 9, angle φ = π/6,
plate 9, angle φ = π/6,  plate 10. (a) deflection, (b) radial moment, (c) tangential moment, (d) radial force.
plate 10. (a) deflection, (b) radial moment, (c) tangential moment, (d) radial force.
 plate 9, angle φ = 0,
plate 9, angle φ = 0,  plate 9, angle φ = π/6,
plate 9, angle φ = π/6,  plate 10. (a) deflection, (b) radial moment, (c) tangential moment, (d) radial force.
plate 10. (a) deflection, (b) radial moment, (c) tangential moment, (d) radial force.












