Remarks on Parameterized Complexity of Variations of the Maximum-Clique Transversal Problem on Graphs

Abstract

With the rapid growth in the penetration rate of mobile devices and the surge in demand for mobile data services, small cells and mobile backhaul networks have become the critical focus of next-generation mobile network development. Backhaul requirements within current wireless networks are almost asymmetrical, with most traffic flowing from the core to the handset, but 5G networks will require more symmetrical backhaul capability. The deployment of small cells and the placement of transceivers for cellular phones are crucial in trading off the symmetric backhaul capability and cost-effectiveness. The deployment of small cells is related to the placement of transceivers for cellular phones. Chang, Kloks, and Lee transformed the placement problem into the maximum-clique transversal problem on graphs. From the theoretical point of view, our paper considers the parameterized complexity of variations of the maximum-clique transversal problem for split graphs, doubly chordal graphs, planar graphs, and graphs of bounded treewidth.

1. Introduction

Fixed/mobile network convergence enhances the competitive advantage of telecommunications operators/companies. With the rapid growth in the penetration rate of mobile devices and the surge in demand for mobile data services, telecommunications operators are stepping up their pace to actively improve their wireless network infrastructure to cope with the advent of the mobile broadband networks era. They have to extend broadband networks to any place through the seamless connection between fixed and mobile networks, which helps accelerate the deployment time, reduces maintenance costs, and further enhances market competitiveness. Under the circumstances, small cells and mobile backhaul networks have become the critical focus of next-generation mobile network development.

The so-called mobile backhaul network transmits the mobile signal traffic between the base station and the mobile terminal device to the wireless node, and then aggregates and transmits it to the telecommunications core network. Backhaul requirements within current wireless networks are almost asymmetrical, with most traffic flowing from the core to the handset, but 5G networks will require more symmetrical backhaul capability. Furthermore, we must backhaul massive broadband traffic from small cells to the control center when small cells grow very large. Hence, the deployment of small cells and the placement of transceivers for cellular phones are crucial in trading off the symmetric backhaul capability and cost-effectiveness. The deployment of small cells is related to the placement of transceivers for cellular phones. Chang, Kloks, and Lee transformed the placement problem into the maximum-clique transversal problem on graphs [1]. One of their main objectives is as follows. Modern cellular telecommunications systems divide the entire service area into a set of small regions, which are called cells. Cells are generally thought of as hexagonal grids. One standard method used to place transceivers for cellular telephones is to place them at the corner points of each hexagonal grid. Since the need for communication proliferates, one transceiver cannot handle all communication requirements in its reach. The most widely used solution is to place another transceiver close to it. The system needs to assign a different frequency to this new transceiver to avoid interference. However, the number of available frequencies is limited. The rapidly increasing demand for communications makes the number of transceivers, placed close to each other, grow very large. It is desirable to replace them with a more efficient big transceiver tower. These towers are pretty large and rise hundreds of feet into the air. They contain very costly hardware to switch between different frequencies between transceivers in some optimal way to allocate and handle them with great care. Nevertheless, since transceiver towers are very costly, their number is expected to be as small as possible. The placement of transceivers for cellular telephones motivated Chang et al. to introduce the maximum-clique transversal problem on graphs [1]. Later, several studies have proposed and worked on variations of the maximum-clique transversal set problem from the theoretical point of view [2,3,4,5,6,7,8,9]. Most of them either develop algorithms to solve the problems and evaluate algorithms’ performance by asymptotic analysis (based on big O notation) to see if the algorithms can solve the problems in polynomial time or prove the NP-completeness of the problems for some graph classes. Their approaches are concerned with two classical computational complexity classes: P and NP.

This paper considers the parameterized complexity of the clique transversal problem (CTP) and variations of the maximum-clique transversal problem (MCTP) on graphs, such as the k-fold maximum-clique transversal problem (k-FMCTP), the $\left\{k\right\}$-maximum-clique transversal problem ($\left\{k\right\}$-MCTP), the signed maximum-clique trasversal problem (SMCTP), and the minus maximum-clique transversal problem (MMCTP).

Parameterized complexity is a new branch of computational complexity theory. Consider an algorithm for a parameterized problem $(I,k)$, where I is the problem instance and k the parameter. The algorithm is uniformly polynomial if it runs in $O\left(f\left(k\right)\right|I{|}^c)$ time, where $\left|I\right|$ is the size of I, $f\left(k\right)$ an arbitrary function, and c a constant independent of k. A parameterized problem is fixed-parameter tractable (FPT) if it admits a uniformly polynomial algorithm [10]. An fpt-reduction is a reduction transforming an instance of some parameterized problem into an equivalent instance of another parameterized problem and can be computed in uniformly polynomial time. A parameterized problem is para-NP-complete if it is NP-complete for fixed values of the parameter(s).

The W-hierarchy is another way to classify parameterized problems into computation complexity classes [10]. A parameterized problem is in the class $W\left[i\right]$ if it is fpt-reducible to the circuit-satisfiability problem that has weft at most i [10]. If a problem $Q\in W\left[i\right]$ and every problem in $W\left[i\right]$ can be fpt-reduced to Q, problem Q is $W\left[i\right]$-complete. Note that $FPT=W\left[0\right]$ and $W\left[i\right]\subseteq W\left[j\right]$ for all $i<j$.

There are very few algorithmic results for the parameterized complexity of the CTP and variations of the MCTP.

Table 1. Previous results and our fixed parameter intractable results.

Parameter: The Solution Size or Weight
Graphs	CTP	$\mathit{k}$-FMCTP	$\left\{\mathit{k}\right\}$-MCTP	SMCTP	MMCTP
Chordal	$W\left[2\right]$-c ${}^{*}$	$W\left[2\right]$-c [1]	$W\left[2\right]$-c [1]	para-NP-c ${}^{*}$	−
		($k=1$)	($k=1$)
Doubly Chordal	−	−	−	para-NP-c ${}^{*}$	−
Split	$W\left[2\right]$-c ${}^{*}$	−	−	−	−
Planar	−	−	−	para-NP-c ${}^{*}$	para-NP-c ${}^{*}$

lists previous results and our fixed parameter intractable results for the considered problems, and uses “$W\left[2\right]$-c” and “para-NP-c” to represent “$W\left[2\right]$-complete” and “para-NP-complete”, respectively.

Table 2. Previous results and our fixed parameter tractable results.

Problem	Bounded Treewdith Graph	Planar Graph
	Parameter: Treewidth t	Parameter: The Solution Size ℓ
CTP	$O(4^t·t·n)$ [6]	*−
MCTP	$O{(2^t·t·n)}^{*}$	$min\{O({\omega }^{\ell }·{\ell }^2+n),O(c^{\sqrt{\ell }}·{\ell }^2+n)\}$ [1]
k-FMCTP	$O{(2^t·t·n)}^{*}$	−
$\left\{k\right\}$-MCTP	$O{({(k+1)}^{t+1}·t·n)}^{*}$	−
SMCTP	$O{(2^t·t·n)}^{*}$	−
MMCTP	$O{(3^t·t·n)}^{*}$	−

lists previous results and our fixed parameter tractable results for the considered problems and uses n and $\omega$ to represent the number of vertices and the maximum size of a clique in a graph. Both tables use starred entries to denote our results. In Table 2, c is a moderate constant. As far as we know, $c=4^{6\sqrt{34}}$ by the paper [11]. The rest of the paper is organized as follows.

• Section 2 reviews the definitions of the considered problems and the most well-known notions from graph theory.
• We prove in Section 3 that the clique transversal problem parameterized by the solution size is $W\left[2\right]$-complete for split graphs, and the following problems are para-NP-complete: the minus maximum-clique transversal problem parameterized by the solution weight for planar graphs, and the signed maximum-clique transversal problem parameterized by the solution weight for doubly chordal graph and planar graphs with clique number three.
• We show the FPT results for graphs of bounded treewidth in Section 4.
  • Section 4.1 shows that the k-fold maximum-clique transversal problem can be solved in $O(2^{tw\left(G\right)}·tw\left(G\right)·|V\left(G\right)|)$ time for any graph G with bounded treewidth $tw\left(G\right)$.
  • Section 4.2 reduces the $\left\{k\right\}$-maximum-clique transversal problem to the k-fold maximum-clique transversal problem and solves the problem in $O(2^{k\left(tw\right(G)+1)}·k^2·(tw\left(G\right)+1)·|V\left(G\right)|)$ time. We develop a dynamic programming algorithm to improve the complexity of the problem to $O({(k+1)}^{tw\left(G\right)+1}·tw\left(G\right)·|V\left(G\right)|)$ time.
  • Section 4.3 deals with the signed and minus maximum-clique transversal problems. We reduce the signed and minus maximum-clique transversal problems to the k-fold maximum-clique transversal problem and solve these problems in $O(2^{tw\left(G\right)}·tw\left(G\right)·|V\left(G\right)|)$ and $O(4^{tw\left(G\right)}·tw\left(G\right)·|V\left(G\right)|)$ time, respectively. The complexity of the minus maximum-clique transversal problem for graphs of bounded treewidth can be improved to $O(3^{tw\left(G\right)}·tw\left(G\right)·|V\left(G\right)|)$ by our dynamic programming technique used for the $\left\{k\right\}$-maximum-clique transversal problem.
• Finally, we conclude the paper and present some future works in Section 5.

2. Definitions and Notations

All graphs in this paper are undirected graphs without self-loops and multiple edges. Let $G=(V,E)$ be a graph with $\left|V\right|=n$ and $\left|E\right|=m$. The vertex set of G is also referred to as $V\left(G\right)$ and its edge set as $E\left(G\right)$. We use $uv$ to denote the edge between the vertices u and v in a graph. If any two distinct vertices in a graph are adjacent, then the graph is a complete graph. We use $G\left[W\right]$ to denote the subgraph of G induced by a subset W of V. The neighborhood of a vertex v in a graph G, denoted by $N_G\left(v\right)$, is the set of all v’s neighbors in G. The closed neighborhood of a vertex v in G, denoted by $N_G\left[v\right]$, is $N_G\left(v\right)\cup \left\{v\right\}$. The degree of a vertex v in G, denoted by $de{g}_G\left(v\right)$, is the number of v’s neighbors in G. A dominating set of G is a set $D\subseteq V$ such that $|D\cap N_G\left[v\right]|\ge 1$ for every $v\in V$. The domination number of G, denoted by $\gamma \left(G\right)$, is the minimum cardinality of a dominating set of G. The domination problem is to find a minimum dominating set of G.

A set $S\subseteq V$ is a clique if $xy\in E$ for any two distinct vertices $x,y\in S$. If $\left|S\right|=k$, then S is a k-clique. If a clique C is not a proper subset of any other clique, then C is a maximal clique. A set $D\subseteq V$ is a clique transversal set of G if $|C\cap D|\ge 1$ for every maximal clique C of G. The clique transversal number of G, denoted by ${\tau }_C\left(G\right)$, is the minimum cardinality of a clique transversal set of G. The clique transversal problem is to find a clique transversal set of G of minimum cardinality.

A maximal clique S is a maximum clique if $\left|S\right|\ge |S^{\prime }|$ for any maximal clique $S^{\prime }$ of G. The clique number of G, denoted by $\omega \left(G\right)$, is the cardinality of a maximum clique of G. We use $Q\left(G\right)$ to denote the set of all maximum cliques of G. A set $D\subseteq V$ is a maximum-clique transversal set of G if $|D\cap Q|\ge 1$ for every $Q\in Q\left(G\right)$. The maximum-clique transversal number of G, denoted by ${\tau }_M\left(G\right)$, is the minimum cardinality of a maximum-clique transversal set of G. The maximum-clique transversal problem is to find a maximum-clique transversal set of G of minimum cardinality.

Assume that $Y\subset \mathbb{R}$ and $f:S\to Y$ is a function. Let $f\left(S^{\prime }\right)={\sum }_{s\in S^{\prime }}f\left(s\right)$ for $S^{\prime }\subseteq S$, and let $f\left(S\right)$ be the weight of f. A maximum-clique transversal set of G can be expressed as a function f whose domain is $V\left(G\right)$ and range is $\{0,1\}$, and $f\left(Q\right)\ge 1$ for $Q\in Q\left(G\right)$. The function f is a maximum-clique transversal function of G and ${\tau }_M\left(G\right)$ is the minimum weight of a maximum-clique transversal function of G. The k-fold maximum-clique, $\left\{k\right\}$-maximum-clique, minus maximum-clique, and signed maximum-clique transversal problems are variations of the maximum-clique transversal set problem. They are defined as follows.

Definition 1

([3]). Suppose that $k\in {\mathbb{Z}}^{+}$ is fixed and G is a graph. A set $D\subseteq V\left(G\right)$ is a k-fold maximum-clique transversal set of G if $|Q\cap D|\ge k$ for $Q\in Q\left(G\right)$. The number ${\tau }_{\times k}\left(G\right)=min\left\{\right|S|\mid S$ is a k-fold maximum-clique transversal set of $G\}$ is the k-fold maximum-clique transversal number of G. The k-fold maximum-clique transversal problem is to find a k-fold maximum-clique transversal set of G of minimum cardinality.

Definition 2

([3]). Suppose that $k\in {\mathbb{Z}}^{+}$ is fixed and G is a graph. A function f is a $\left\{k\right\}$-maximum-clique transversal function of G if the domain and range of f are $V\left(G\right)$ and $\{0,1,2,\dots ,k\}$, respectively, and $f\left(Q\right)\ge k$ for $Q\in Q\left(G\right)$. The number ${\tau }_{\left\{k\right\}}\left(G\right)=min\{f\left(V\left(G\right)\right)\mid f$ is a $\left\{k\right\}$-maximum-clique transversal function of $G\}$ is the $\left\{k\right\}$-maximum-clique transversal number of G. The $\left\{k\right\}$-maximum-clique transversal problem is to find a $\left\{k\right\}$-maximum-clique transversal function of G of minimum weight.

Definition 3

([3]). Suppose that G is a graph. A function f is a signed maximum-clique transversal function of G if the domain and range of f are $V\left(G\right)$ and $\{-1,1\}$, respectively, and $f\left(Q\right)\ge 1$ for $Q\in Q\left(G\right)$. If the domain and range of f are $V\left(G\right)$ and $\{-1,0,1\}$, respectively, and $f\left(Q\right)\ge 1$ for $Q\in Q\left(G\right)$, then f is a minus maximum-clique transversal function of G. The number ${\tau }_M^s\left(G\right)=min\{f\left(V\left(G\right)\right)\mid f$ is a signed maximum-clique transversal function of $G\}$ is the signed maximum-clique transversal number of G. The minus maximum-clique transversal number of G is ${\tau }_M^{-}\left(G\right)=min\{f\left(V\left(G\right)\right)\mid f$ is a minus maximum-clique transversal function of $G\}$. The minus (signed) maximum-clique transversal problem is to find a minus (signed) maximum-clique transversal function of G of minimum weight.

3. The Fixed-Parameter Intractable Results

A chord of a cycle is an edge joining two non-consecutive vertices of the cycle. A graph is chordal if it does not contain a chordless cycle of length greater than three [12]. A graph is split if its vertices can be partitioned into two sets C and S, such that C is a clique and S is an independent set.

Theorem 1.

The clique transversal problem parameterized by the solution size is $W\left[2\right]$-complete for split graphs.

Proof. 

Assume that $G=(V,E)$ is a graph with $V=\{v_i\mid 1\le i\le n\}$. Let $X=\{x_i\mid 1\le i\le n\}$ and let H be a split graph obtained from G by $V\left(H\right)=V\cup X$ and $E\left(H\right)=\{v_i{v}_j\mid 1\le i<j\le n\}\cup \left\{x_{i}v\right|v\in N_G\left[v_i\right],1\le i\le n\}$. In H, the maximal cliques are the sets V and $N_G\left[v_i\right]\cup \left\{x_i\right\}$ for $1\le i\le n$. A minimum dominating set of G is a clique transversal set of H. Clearly, there exists a minimum clique transversal set D of H such that $D\cap X=\varnothing$. Then, a minimum clique transversal set of H is a dominating set of G. We have $\gamma \left(G\right)={\tau }_C\left(H\right)$ following the discussion above. Hence, ${\tau }_C\left(H\right)\le k$ if, and only if, $\gamma \left(G\right)\le k$. The domination problem for a graph G can be reduced to the clique transversal problem for a split graph H. Since the domination problem parameterized by the solution size k is $W\left[2\right]$-complete [10], the clique transversal problem parameterized by the solution size is $W\left[2\right]$-complete for split graphs.  □

Remark 1.

The maximum-clique transversal is a particular case of the k-fold maximum-clique transversal problem with $k=1$. The k-fold maximum-clique, $\left\{k\right\}$-maximum-clique, minus maximum-clique, and signed maximum-clique transversal problems are linear-time solvable for split graphs [3].

Consider the following two decision problems.

• The nonpositive minus maximum-clique transversal problem.
  Instance: A graph G
  Question: Does G have a minus maximum-clique transversal function of weight at most 0?
• The nonpositive signed maximum-clique transversal problem.
  Instance: A graph G
  Question: Does G have a signed maximum-clique transversal function of weight at most 0?

Definition 4.

Let k be a nonnegative integer and let F be a set of k vertices. The $f_k$-transformation of a graph $G=(V,E)$, denoted by $f_k\left(G\right)$, is the graph $H=(V\cup F,E)$.

Theorem 2.

Let $\mathcal{G}$ and $\mathcal{H}$ be graph classes such that $\mathcal{H}=\{f_k\left(G\right)\mid G\in \mathcal{G}\}$. The following statements are true.

(1) 

If the signed (minus) maximum-clique transversal problem is NP-complete for $\mathcal{G}$, the nonpositive signed (minus) maximum-clique transversal problem is NP-complete for $\mathcal{H}$.

(2) 

If the nonpositve signed (minus) maximum-clique transversal problem is NP-complete for graph class $\mathcal{H}$, the signed (minus) maximum-clique transversal problem parameterized by the solution weight is para-NP-complete for $\mathcal{H}$.

Proof. 

(1) Let k be a nonnegative integer and let F be a set of k vertices. Let $G=(V,E)\in \mathcal{G}$ and $H=(V\cup F,E)\in \mathcal{H}$. In H, every vertex $x\in F$ is isolated and not in any maximum clique of H. Then, $f\left(x\right)=-1$ for any signed (minus) maximum-clique transversal function f of H of “minimum weight”. Clearly, ${\tau }_M^s\left(H\right)={\tau }_M^s\left(G\right)-\left|F\right|={\tau }_M^s\left(G\right)-k$. It follows that ${\tau }_M^s\left(H\right)\le 0$ if and only if ${\tau }_M^s\left(G\right)\le k$. Similarly, ${\tau }_M^{-}\left(H\right)={\tau }_M^{-}\left(G\right)-\left|F\right|={\tau }_M^{-}\left(G\right)-k$. Then, ${\tau }_M^{-}\left(H\right)\le 0$ if and only if ${\tau }_M^{-}\left(G\right)\le k$. The statement (1) is therefore true.

(2) The nonpositive signed (minus) maximum-clique transversal problem for $\mathcal{H}$ is a particular case of the signed (minus) maximum-clique transversal problem parameterized by solution weight for $\mathcal{H}$. Hence, the statement (2) is true.  □

Corollary 1.

Let ${\mathcal{G}}_1$ be the graph class of planar graphs and let ${\mathcal{G}}_2$ be the graph class of doubly chordal graphs and planar graphs with the clique number 3. The following statements are true.

(1) 

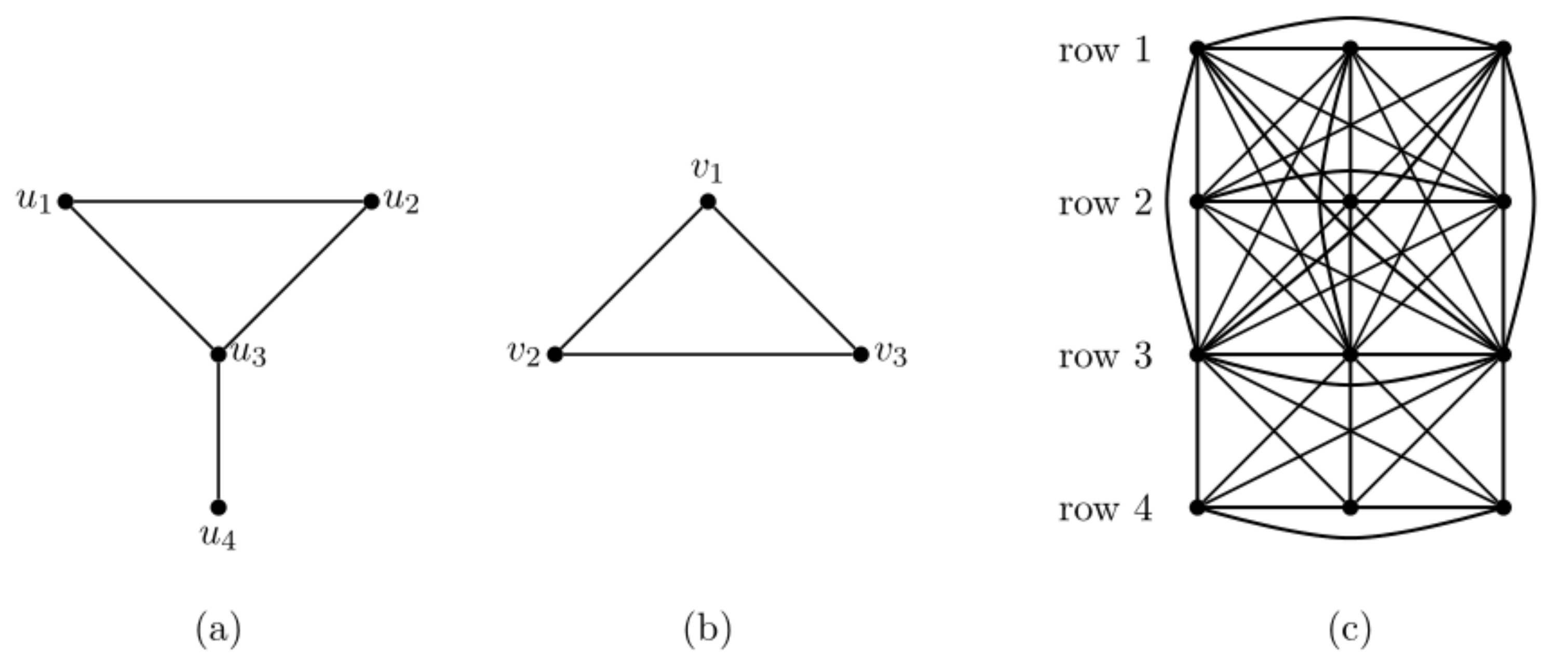
The nonpositive minus maximum-clique transversal problem is NP-complete for ${\mathcal{G}}_1$.

(2) 

The nonpositive signed maximum-clique transversal problem is NP-complete for ${\mathcal{G}}_2$.

Proof. 

(1) Let $G\in {\mathcal{G}}_1$ and $H=f_k\left(G\right)$. Clearly, $H\in {\mathcal{G}}_1$. It is known that the minus maximum-clique transversal problem is NP-complete for ${\mathcal{G}}_1$ [3]. By Theorem 2, the nonpositive minus maximum-clique transversal problem is NP-complete for ${\mathcal{G}}_1$.

(2) Let $G\in {\mathcal{G}}_2$ and $H=f_k\left(G\right)$. Clearly, $H\in {\mathcal{G}}_2$. It is known that the signed maximum-clique transversal problem is NP-complete for ${\mathcal{G}}_2$ [3]. By Theorem 2, the nonpositive signed maximum-clique transversal problem is NP-complete for ${\mathcal{G}}_2$.  □

Corollary 2.

Let ${\mathcal{G}}_1$ be the graph class of planar graphs and let ${\mathcal{G}}_2$ be the graph class of doubly chordal graphs and planar graphs with the clique number 3. The following statements are true.

(1) 

The minus maximum-clique transversal problem parameterized by the solution weight is para-NP-complete for ${\mathcal{G}}_1$.

(2) 

The signed maximum-clique transversal problem parameterized by the solution weight is para-NP-complete for ${\mathcal{G}}_2$.

Proof. 

The corollary holds by Theorem 2 and Corollary 1.  □

4. Fixed-Parameter Tractable Results for Graphs of Bounded Treewidth

Assume that G is a graph with $V\left(G\right)=\{v_1,v_2,\dots ,v_n\}$. Let $N_i\left[v\right]$ denote the closed neighborhood of v in $G\left[\{v_i,v_{i+1},\dots ,v_n\}\right]$. The ordering $(v_1,v_2,\dots ,v_n)$ of V is a perfect elimination ordering of G if for all $i\in \{1,\dots ,n\}$, $N_i\left[v_i\right]$ is a clique. A graph G is chordal if and only if G has a perfect elimination ordering [13].

A chordal graph H with n vertices is a t-tree if and only if either H is a complete graph of t vertices or H has more than t vertices and there exists a perfect elimination ordering $(v_1,v_2,\dots ,v_n)$ such that $N_i\left[v_i\right]$ is a $(t+1)$-clique for $1\le i\le n-t$. For convenience, we define a t-tree to have at least $t+1$ vertices. With this definition, a complete graph of t vertices is a $(t-1)$-tree.

A triangulation of a graph G is a graph H with the same set of vertices such that H is chordal and G is a subgraph of H. We say that G is triangulated into H. Subgraphs of t-trees are called partial t-trees. The treewidth of a graph G is the minimum value t such that G is a partial t-tree. It is clear that a graph of treewidth t is also a partial ℓ-tree for every $\ell \ge t$. The class of partial t-trees is exactly the class of graphs of treewidth at most t. Therefore, $\omega \left(G\right)=t+1$ for any graph G of treewidth t. The treewidth of a graph can be defined by the concept of tree decomposition of a graph.

Definition 5.

A tree decomposition of a graph G is a pair $D=(T,B)$, where T is a tree with $V\left(T\right)=\{1,2,\dots ,\ell \}$ and $B=\{B_i\mid i\in V\left(T\right)\}$ is a collection of subsets of vertices of G such that the following three conditions are satisfied.

1. 

Every vertex $x\in V\left(G\right)$ appears in at least one set $B_i\in B$.

2. 

For every edge $e\in E\left(G\right)$, there is at least one set $B_i\in B$ containing both vertices of e.

3. 

For each vertex $x\in V\left(G\right)$, the set $\{i\mid x\in B_i\}$ forms a subtree of T.

For simplicity, we use T to represent the vertex set of T if T is understood as a tree and we call its vertices nodes. We also refer to all elements of B as bags. Lemma 1 shows an alternative way to formulate the third condition of Definition 5.

Lemma 1.

Let $D=(T,\{B_i\mid i\in T\})$ be a tree decomposition of a graph G. If a vertex x appears in two bags $B_i,B_j\in B$, then it appears in every bag $B_k$ for the node k on the tree path from node i to node j in T.

Definition 6.

The width of a tree decomposition $D=(T,\{B_i\mid i\in T\})$ of a graph G is ${max}_{i\in T}\left\{\right|B_i\left|\right\}-1$. The treewidth of a graph G, denoted by $tw\left(G\right)$, is the minimum width over all tree decompositions of G.

Theorem 3

(See also Lemma 2.1.13 in [14]). If G is a chordal graph with at least $t+1$ vertices and $\omega \left(G\right)\le t+1$, then G can be triangulated into a t-tree.

Theorem 4

([15]). Any partial t-tree with at least $t+1$ vertices can be triangulated into a t-tree with the same number of vertices.

Definition 7.

A tree decomposition is rooted if the tree is equipped with a root node. A nice tree decomposition $D=(T,\{B_i\mid i\in T\})$ is a rooted tree decomposition satisfying the following conditions.

1. 

Every node of T has at most two child nodes.

2. 

If a node i has two child nodes—j and k—then $B_i=B_j=B_k$. The node is called a join node.

3. 

If a node i has only one child node j, then either (1) $B_j\subset B_i$ and $|B_i|=|B_j|+1$, or (2) $B_i\subset B_j$ and $|B_i|=|B_j|-1$. In the case (1), the node is called an introduce node, whereas in the case (2), the node is called a forget node.

Remark 2.

Figure 1 shows a nice tree decomposition $D=(T,\{B_i\mid i\in T\})$ of a graph G, where T has 17 nodes. Node 3 is a join node since it has two child nodes, 4 and 9, and $B_3=B_4=B_9=\{b,c,d\}$. Node 6 is an introduce node since it has only one child node 7, and $B_7\subset B_6$ and $|B_6|=|B_7|+1$. Node 10 is a forget node since it has only one child node 11, and $B_{10}\subset B_{11}$ and $|B_{10}|=|B_{11}|-1$.

Lemma 2

([14]). For any constant t, given a tree decomposition of a graph G of width t and $O\left(\right|V\left(G\right)\left|\right)$ nodes, one can find a nice tree decomposition of G of width t and with at most $4·\left|V\right(G\left)\right|$ nodes in $O\left(\right|V\left(G\right)\left|\right)$ time.

This paper assumes that a nice tree decomposition of a graph G of width $tw\left(G\right)$ and with $O\left(\right|V\left(G\right)\left|\right)$ nodes is part of the input by Lemma 2.

4.1. The k-Fold Maximum-Clique Transversal Problem

This section studies the k-fold maximum-clique transversal problem on graphs of bounded treewidth.

Definition 8.

Let $D=(T,\{B_i\mid i\in T\})$ be a rooted tree decomposition of G. For each node $i\in T$, let $T_i$ be the subtree of T rooted at i and and let $G_i$ be the induced subgraph $G\left[{\cup }_{s\in T_i}{B}_s\right]$. Clearly, $T=T_r$ and $G=G_r$.

Theorem 5

([16]). Assume that $D=(T,B)$ is a tree decomposition of a graph G. For every clique C of G, there exists a bag $B_p\in B$ such that $C\subseteq B_p$.

Lemma 3.

Let $D=(T,B)$ be a tree decomposition of a graph G of width $tw\left(G\right)$. For each maximum clique Q of G, there exists a bag $B_p\in B$ such that $Q=B_p$.

Proof. 

Following Theorem 5, there exists a bag $B_p\in B$ such that $Q\subseteq B_p$ for a maximum clique Q of G. Then, $\left|Q\right|\le |B_p|$. Clearly, $|B_p|\le tw\left(G\right)+1\le \omega \left(G\right)=|Q|$. Hence, $Q=B_p$.  □

Definition 9.

Let G be a graph of bounded treewidth with a nice tree decomposition $(T,\{B_i\mid i\in T\})$ rooted at node r. Let k be a fixed positive integer such that $k\le \omega \left(G\right)$. For each node $i\in T$, let $F_{k,i}\left(X\right)$ be a minimum subset S of $V\left(G_i\right)$ satisfying all the following conditions.

(1) 

$S\cap B_i=X$.

(2) 

$|S\cap Q|\ge k$ for every maximum clique $Q\in Q\left(G_i\right)\cap Q\left(G\right)$.

If $F_{k,i}\left(X\right)$ does not exist, let $F_{k,i}\left(X\right)=\Phi$ with $|\Phi |=\infty$.

Remark 3.

By Definition 9, $T=T_r$, $G=G_r$, and ${\tau }_{\times k}\left(G\right)=min\left\{\right|F_{k,r}\left(X\right)|\mid X\subseteq B_r\}$.

Lemma 4.

Let $D=(T,\{B_i\mid i\in T\})$ be a nice tree decomposition of a graph G of width $tw\left(G\right)$. Suppose that node i is a leaf node of T. Then, all sets $F_{k,i}\left(X\right)$ of $G_i$ can be computed in $O(2^{tw\left(G\right)}·tw\left(G\right))$ time.

Proof. 

Since node i is a leaf node, $G_i=G\left[B_i\right]$ and $Q\left(G_i\right)\cap Q\left(G\right)=Q\left(G\left[B_i\right]\right)$. By the definition of tree decomposition, $|B_i|\le tw\left(G\right)+1$ and $\omega \left(G\right)=tw\left(G\right)+1$. If $B_i$ is not a maximum clique of G, then $F_{k,i}\left(X\right)=\Phi$ for $X\subseteq B_i$. It takes $O\left(tw{\left(G\right)}^2\right)$ time to check if $B_i$ is a maximum clique. We therefore assume that $B_i$ is a maximum clique of G. Note that $F_{k,i}\left(X\right)=X\subseteq B_i$ in this case. There are $O\left(2^{tw\left(G\right)}\right)$ subsets of $B_i$. For each $F_{k,i}\left(X\right)$ of $B_i$, we verify if $F_{k,i}\left(X\right)$ has at least k vertices in $B_i$. The verification process can be done in $O\left(tw\right(G\left)\right)$ time. Following the discussion above, all sets $F_{k,i}\left(X\right)$ of $G_i$ can be computed in $O(2^{tw\left(G\right)}·tw\left(G\right))$ time.  □

Lemma 5.

Let $D=(T,\{B_i\mid i\in T\})$ be a nice tree decomposition of a graph G of width $tw\left(G\right)$. Suppose that node i is a forget node of T. Let j be the child node of i and let $x\in B_j$ be the vertex such that $B_i=B_j\backslash \left\{x\right\}$. Let $X\subseteq B_j$ such that $s_1=\left|F_{k,j}\left(X\right)\right|$ and $s_2=\left|F_{k,j}(X\cup \left\{x\right\})\right|$. Then,

$$F_{k,i}\left(X\right)=\left\{\begin{array}{cc}{F}_{k,j}\left(X\right)\hfill & if{s}_1\le s_2,\hfill \\ \hfill F_{k,j}(X\cup \left\{x\right\})\hfill & \hfill if{s}_2<s_1.\hfill \end{array}\right.$$

Proof. 

Since $B_i=B_j\backslash \left\{x\right\}$, $G_i=G_j$. Then, $X=F_{k,i}\left(X\right)\cap B_i=F_{k,i}\left(X\right)\cap (B_j\backslash \left\{x\right\})$. Therefore, either $F_{k,i}\left(X\right)\cap B_j=X$ or $F_{k,i}\left(X\right)\cap B_j=X\cup \left\{x\right\}$. We have $|F_{k,i}\left(X\right)|=min\{|F_{k,j}\left(X\right)|,|F_{k,j}(X\cup \left\{x\right\}|\}$. Hence, the lemma holds.  □

Lemma 6.

Let $D=(T,\{B_i\mid i\in T\})$ be a nice tree decomposition of a graph G of width $tw\left(G\right)$. Suppose that node i is an introduce node of T. Let j be the child node of i and let x be the vertex such that $B_i=B_j\cup \left\{x\right\}$. For $X\subseteq B_i$,

$$F_{k,i}\left(X\right)=\left\{\begin{array}{cc}{F}_{k,j}\left(X\right)\hfill & if{B}_i\notin Q\left(G\right)andx\notin X,\hfill \\ F_{k,j}(X\backslash \left\{x\right\})\cup \left\{x\right\}\hfill & if{B}_i\notin Q\left(G\right)andx\in X,\hfill \\ F_{k,j}\left(X\right)\hfill & if{B}_i\in Q\left(G\right),x\notin X,and\left|X\right|\ge k,\hfill \\ F_{k,j}(X\backslash \left\{x\right\})\cup \left\{x\right\}\hfill & if{B}_i\in Q\left(G\right),x\in X,and\left|X\right|\ge k,\hfill \\ \Phi \hfill & otherwise.\hfill \end{array}\right.$$

Proof. 

Let d be a proper descendant of the subtree $T_j$. Since $x\notin B_j$, $x\notin V\left(G_j\right)$, by the third condition of Definition 5. Then, $x\notin B_d$. We consider the following two cases.

Case 1: $B_i\notin Q\left(G\right)$. Assume that there exists a set $S\subseteq B_d$ such that $S\cup \left\{x\right\}$ is a maximum clique of G. By Lemmma 3, there exists a bag $B_p$ such that $S\cup \left\{x\right\}=B_p$. Since $B_p$ contains the vertex x, the corresponding node p is not in $T_j$. Then, every tree path from node d to node p contains the nodes i and j. By Lemma 1, $S=B_j=B_i\backslash \left\{x\right\}$. Then, $B_i=S\cup \left\{x\right\}$ is a maximum clique of G, but it contradicts that $B_i\notin Q\left(G\right)$. Therefore, there is no set $S\subseteq B_d$ such that $S\cup \left\{x\right\}\in Q\left(G\right)$. We have $Q\left(G_i\right)\cap Q\left(G\right)=(Q\left(G_j\right)\cap Q\left(G\right))$. Then, $F_{k,i}\left(X\right)=F_{k,j}\left(X\right)$ if $x\notin X$. Otherwise, $F_{k,i}\left(X\right)=F_{k,j}(X\backslash \left\{x\right\})\cup \left\{x\right\}$.

Case 2: $B_i\in Q\left(G\right)$. Assume that there exists a set $S\subseteq B_d$ such that $S\cup \left\{x\right\}\in Q\left(G\right)$. By the arguments similar to those for proving Case 1, $B_i=S\cup \left\{x\right\}$. Therefore, $Q\left(G_i\right)\cap Q\left(G\right)=(Q\left(G_j\right)\cap Q\left(G\right))\cup \left\{B_i\right\}$. Conversely, we assume that there is no set $S\subseteq B_d$ such that $S\cup \left\{x\right\}\in Q\left(G\right)$. Clearly, $Q\left(G_i\right)\cap Q\left(G\right)=(Q\left(G_j\right)\cap Q\left(G\right))\cup \left\{B_i\right\}$. Since $X\subseteq B_i$, $\left|X\right|\ge k$. If $\left|X\right|<k$, then $F_{k,i}\left(X\right)$ does not exist. Therefore, $F_{k,i}\left(X\right)=F_{k,j}\left(X\right)$ if $x\notin X$ and $\left|X\right|\ge k$. If $x\in X$ and $\left|X\right|\ge k$, then $F_{k,i}\left(X\right)=F_{k,j}(X\backslash \left\{x\right\})\cup \left\{x\right\}$.  □

Remark 4.

The method used for proving Lemma 6 is similar to the one adopted in estimating Roman domination [17].

Lemma 7.

Let G be a graph of bounded treewidth with a nice tree decomposition $(T,\{B_i\mid i\in T\})$. Suppose that node i is a join node of T. Let j and ℓ be the child nodes of i. For $X\subseteq B_i$,

$$F_{k,i}\left(X\right)=F_{k,j}\left(X\right)\cup F_{k,\ell }\left(X\right).$$

Proof. 

Since node i is a join node, $B_i=B_j=B_{\ell }$. Then, $Q\left(G_i\right)=Q\left(G_j\right)\cup Q\left(G_{\ell }\right)$. Let $S=F_{k,j}\left(X\right)\cup F_{k,\ell }\left(X\right)$. Clearly, $S\cap B_i=X$ and $|S\cap Q|\ge k$ for $Q\in Q\left(G_i\right)\cap Q\left(G\right)$. We have $|F_{k,i}\left(X\right)|\le |S|=|F_{k,j}\left(X\right)\cup F_{k,\ell }\left(X\right)|$.

Let $S_1=F_{k,i}\left(X\right)\cap V\left(G_j\right)$ and $S_2=F_{k,i}\cap V\left(G_{\ell }\right)$. Since X is a subset of $S_1\cup S_2$, $|F_{k,i}\left(X\right)|=|(S_1\cup X)\cup (S_2\cup X)|$. Let $S_j=S_1\cup X$ and $S_{\ell }=S_2\cup X$. Clearly, $S_j\cap B_j=X$ and $S_{\ell }\cap B_{\ell }=X$. Futhermore, $|S_j\cap Q|\ge k$ for $Q\in Q\left(G_j\right)\cap Q\left(G\right)$ and $|S_{\ell }\cap Q|\ge k$ for $Q\in Q\left(G_{\ell }\right)\cap Q\left(G\right)$. Therefore, $|F_{k,j}\left(X\right)|\le |S_j|$ and $|F_{k,\ell }\left(X\right)|\le |S_{\ell }|$. We have $|F_{k,j}\left(X\right)\cup F_{k,\ell }\left(X\right)|\le |S_j\cup S_{\ell }|=|F_{k,i}\left(X\right)|$. Following the discussion above, $|F_{k,i}\left(X\right)|=|F_{k,j}\left(X\right)\cup F_{k,\ell }\left(X\right)|$ and the lemma holds.  □

Theorem 6.

Let $D=(T,\{B_i\mid i\in T\})$ be a nice tree decomposition of a graph G of width $tw\left(G\right)$ and $O\left(\right|V\left(G\right)\left|\right)$ nodes. The k-fold maximum-clique transversal problem can be solved in $O(2^{tw\left(G\right)}·tw\left(G\right)·|V\left(G\right)\left|\right)$ time.

Proof. 

Assume that T is rooted at r. Then, $T=T_r$, $G=G_r$, and ${\tau }_{\times k}\left(G\right)=min\left\{\right|F_{k,r}\left(X\right)|\mid X\subseteq B_r\}$. Our algorithm works from the leaves in T up to the root, computing the solutions $F_i\left(X\right)$ for each visited node i on the way through the dynamic programming technique. For all $X\in B_i$, the solutions can be computed in $O(2^{tw\left(G\right)}·tw\left(G\right))$ time by Lemmas 4–7. Since T contains $O\left(\right|V\left(G\right)\left|\right)$ nodes, the k-fold maximum-clique transversal problem can be solved in $O(2^{tw\left(G\right)}·tw\left(G\right)·|V\left(G\right)|)$ time.  □

4.2. The $\left\{k\right\}$-Maximum-Clique Transversal Problem

This section studies the $\left\{k\right\}$-maximum-clique transversal problem on graphs of bounded treewidth and solves the problem with reduction and the dynamic programming technique.

4.2.1. Problem Solving by Reduction

The section shows a reduction from the $\left\{k\right\}$-maximum-clique transversal problem to the k-fold maximum-clique transversal problem by the concept of the strong product of two graphs.

Definition 10.

The strong product $G⊠H$ is defined on the vertex set $V\left(G\right)\times V\left(H\right)$, where two vertices $(u_1,v_1)$ and $(u_2,v_2)$ are adjacent if and only if $u_1=u_2$ and $v_1{v}_2\in E\left(H\right)$, or $v_1=v_2$ and $u_1{u}_2\in E\left(G\right)$, or $v_1{v}_2\in E\left(H\right)$ and $u_1{u}_2\in E\left(G\right)$.

Figure 2 shows the strong product of a graph G and a complete graph H. The graph $G⊠H$, as shown in Figure 2c, consists of twelve vertices. From left to right, the vertices in row i are $(u_i,v_1)$, $(u_i,v_2)$, and $(u_i,v_3)$ for $i\in \{1,2,3,4\}$.

Lemma 8.

Let G and H be graphs. Then, $Q(G⊠H)=\{V(G\left[Q_1\right]⊠H\left[Q_2\right])\mid Q_1\in Q\left(G\right),Q_2\in Q\left(H\right)\}$.

Proof. 

Let $Q_1\in Q\left(G\right)$ and $Q_2\in Q\left(H\right)$. The vertex set, $V(G\left[Q_1\right]⊠H\left[Q_2\right])$, is a clique of $G⊠H$. We have $\omega \left(G\right)·\omega \left(H\right)\le \omega (G⊠H)$.

Let $V\left(G\right)=\{u_1,\dots ,u_n\}$ and $V\left(H\right)=\{v_1,\dots ,v_k\}$. Let $Q\in Q(G⊠H)$. For any two distinct vertices $(u_p,v_x),(u_q,v_y)\in Q$, (1) $u_p=u_q$ and $v_x{v}_y\in E\left(H\right)$, or (2) $u_p{u}_q\in E\left(G\right)$ and $v_x=v_y$, or (3) $u_p{u}_q\in E\left(G\right)$ and $v_x{v}_y\in E\left(H\right)$. Therefore, $u_p{u}_q\in E\left(G\right)$ if $u_p\ne u_q$ for any two distinct vertices $(u_p,v_x),(u_q,v_y)\in Q$. Similarly, $v_x{v}_y\in E\left(H\right)$ if $v_x\ne v_y$ for any two distinct vertices $(u_p,v_x),(u_q,v_y)\in Q$, Then, $C_1=\{u_i\mid (u_i,v_j)\in Q,1\le i\le n,1\le j\le k\}$ is a clique of G and $C_2=\{v_j\mid (u_i,v_j)\in Q,1\le i\le n,1\le j\le k\}$ is a clique of H. Let $Q_1\in Q\left(G\right)$ and $Q_2\in Q\left(H\right)$ such that $C_1\subseteq Q_1$ and $C_2\subseteq Q_2$. Hence, $Q\subseteq V(G\left[C_1\right]⊠H\left[C_2\right])\subseteq V(G\left[Q_1\right]⊠H\left[Q_2\right])$. We have $\omega (G⊠H)\le \omega \left(G\right)·\omega \left(H\right)$. Therefore, $\omega (G⊠H)=\omega \left(G\right)·\omega \left(H\right)$ by the discussion above, and the lemma holds.  □

Theorem 7.

Let k be a fixed positive integer and let H be a complete graph with k vertices. For any graph G and $k\ge 1$, ${\tau }_{\left\{k\right\}}\left(G\right)={\tau }_{\times k}(G⊠H)$.

Proof. 

Let $V\left(G\right)=\{u_1,\dots ,u_n\}$ and $V\left(H\right)=\{v_1,\dots ,v_k\}$. By Lemma 8, $Q(G⊠H)=\left\{V\right(G\left[Q\right]⊠H)\mid Q\in Q(G\left)\right\}$. Clearly, $\left|Q\right(G⊠H\left)\right|=\left|Q\right(G\left)\right|$ and $\omega (G⊠H)=k·\omega \left(G\right)$.

Let f a $\left\{k\right\}$-maximum-clique transversal function of G of minimum weight. Let D be a subset of $V(G⊠H)$ defined by

$$D=\bigcup _{i=1}^n\{(u_i,v_j)\mid j=1,2,\dots ,f\left(u_i\right)\}.$$

Since f is a $\left\{k\right\}$-maximum-clique transversal function, $0\le f\left(u_i\right)\le k$ for $1\le i\le n$. Indeed, the set D exists, and $\left|D\right|={\sum }_{i=1}^{n}f\left(u_i\right)={\tau }_{\left\{k\right\}}\left(G\right)$. Let $C=\{u_{b_i}\mid 1\le i\le \omega \left(G\right)\}$ be a maximum clique of G such that $V(G\left[C\right]⊠H)=\{(u_{b_i},v_j)\mid 1\le i\le \omega \left(G\right),1\le j\le k\}$ is a maximum clique of $G⊠H$. Since $f\left(C\right)={\sum }_{i=1}^{\omega \left(G\right)}f\left(u_{b_i}\right)\ge k$,

$$|D\cap V(G\left[C\right]⊠H)|=|\{(u_{b_i},v_j)\mid 1\le i\le \omega \left(G\right),1\le j\le f\left(u_{b_i}\right)\}|=\sum _{i=1}^{\omega \left(G\right)}f\left(u_{b_i}\right)\ge k.$$

The set D is a k-fold maximum-clique transversal set of $G⊠H$. We have ${\tau }_{\times k}(G⊠H)\le {\tau }_{\left\{k\right\}}\left(G\right)$.

In the following, we show that ${\tau }_{\left\{k\right\}}\left(G\right)\le {\tau }_{\times k}(G⊠H)$. Let S be a k-fold maximum-clique transversal set of $G⊠H$ such that $\left|S\right|={\tau }_{\times k}(G⊠H)$.

Let $f:V\left(G\right)\to \{0,1,\dots ,k\}$ be a function of G such that $f\left(u_i\right)=|S\cap \{(u_i,v_j)\mid j=1,\dots ,k\}|$ for $1\le i\le n$. Clearly, $f\left(V\left(G\right)\right)={\tau }_{\times k}(G⊠H)$ and $0\le f\left(u_i\right)\le k$ for $1\le i\le n$. Recall that $Q(G⊠H)=\left\{V\right(G\left[C\right]⊠H)\mid C\in Q(G\left)\right\}$. Let $C=\{u_{b_i}\mid 1\le i\le \omega \left(G\right)\}$ be a maximum clique of G such that $Q=V\left(G\right[C]⊠H)$ is a maximum clique of $G⊠H$. Then, $Q=\{(u_{b_i},v_j)\mid 1\le i\le \omega \left(G\right),1\le j\le k\}$.

Since S is a k-fold maximum-clique transversal set of $G⊠H$, $|S\cap Q|=|S\cap \{(u_{b_i},v_j)\mid 1\le i\le \omega \left(G\right),1\le j\le k\left\}\right|\ge k$. Therefore,

$$f\left(C\right)=\sum _{i=1}^{\omega \left(G\right)}f\left(u_{b_i}\right)=\sum _{i=1}^{\omega \left(G\right)}|S\cap \{(u_{b_i},v_j)\mid 1\le j\le k\}|=|S\cap Q|\ge k.$$

The function f is a $\left\{k\right\}$-maximum-clique transversal function of G. We have ${\tau }_{\left\{k\right\}}\left(G\right)\le f\left(V\left(G\right)\right)={\tau }_{\times k}(G⊠H)$. Hence, ${\tau }_{\left\{k\right\}}\left(G\right)={\tau }_{\times k}(G⊠H)$ by the discussion above.  □

Lemma 9.

Let k be a fixed positive integer and let H be a complete graph with k vertices. Given a nice tree decomposition $D=(T,B=\{B_i\mid i\in T\})$ of a graph G of width $tw\left(G\right)$ and $O\left(\right|V\left(G\right)\left|\right)$ nodes, one can find a nice tree decomposition of $G⊠H$ of width $k\left(tw\right(G)+1)-1$ and with at most $4·\left|V\right(G⊠H\left)\right|$ nodes in $O\left(\right|V(G⊠H)\left|\right)$ time.

Proof. 

Let $V\left(G\right)=\{u_i\mid 1\le i\le n\}$ and $V\left(H\right)=\{v_i\mid 1\le i\le k\}$. Let $B_i^{\prime }=\left\{(u_{\ell },v_j)\right|u_{\ell }\in B_i,1\le j\le k\}$ and $D^{\prime }=(T,B^{\prime }=\{B_i^{\prime }\mid i\in T\})$. We show as follows that $D^{\prime }$ is a tree decomposition of $G⊠H$.

(1)

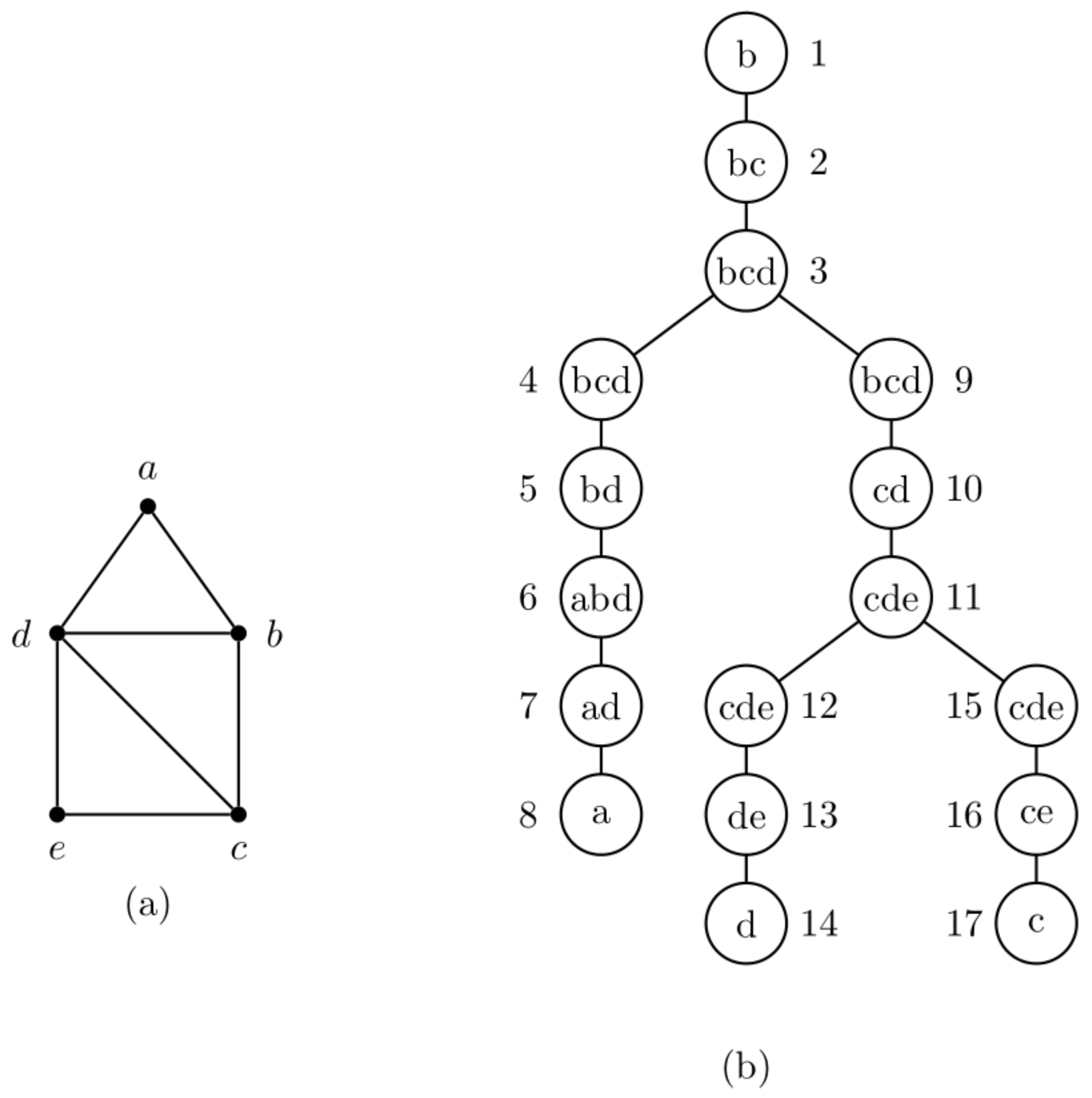
Every vertex $u_{\ell }\in V\left(G\right)$ appears in at least one bag of B. Suppose that $u_{\ell }\in B_i$. The vertices $(u_{\ell },v_1)$, $(u_{\ell },v_2),\dots ,(u_{\ell },v_k)$ all appear in $B_i^{\prime }\in B^{\prime }$. Therefore, every vertex $(u_{\ell },v_j)\in V(G⊠H)$ appears in at least one bag $B_i^{\prime }\in B^{\prime }$.

(2)

For any two adjacent vertices $(u_x,v_p),(u_y,v_q)\in V(G⊠H)$, $u_x=u_y$ and $v_p{v}_q\in E\left(H\right)$, or $u_x{u}_y\in E\left(G\right)$ and $v_p=v_q$, or $u_x{u}_y\in E\left(G\right)$ and $v_p{v}_q\in E\left(H\right)$. Consider $u_x$ and $u_y$. Either $u_x=u_y$ or $u_x{u}_y\in E\left(G\right)$. If $u_x=u_y$, then $u_x$ and $u_y$ are in the same bags. Suppose that $u_x\ne u_y$ and $u_x{u}_y\in E\left(G\right)$. Since there is at least one bag of B containing both vertices of e for every edge $e\in E\left(G\right)$, at least one bag contains the vertices $u_x$ and $u_y$. Let $u_x,u_y\in B_i$. The vertices $(u_x,v_1)$, $(u_x,v_2),\dots ,(u_x,v_k)$ and $(u_y,v_1)$, $(u_y,v_2),\dots ,(u_y,v_k)$ are in $B_i^{\prime }\in B^{\prime }$. The bag $B_i^{\prime }$ contains $(u_x,v_p)$ and $(u_y,v_q)$. Therefore, there is at least one bag of $B^{\prime }$ containing every pair of adjacent vertices of $G⊠H$.

(3)

Suppose that $(u_{\ell },v_j)$ is a vertex of $G⊠H$ and it appears in two bags $B_i^{\prime },B_p^{\prime }\in B^{\prime }$. Let j be a node on the tree path from node i to node p in T. Since $(u_{\ell },v_j)$ appears in $B_i^{\prime }$ and $B_p^{\prime }$, we know that $u_{\ell }\in B_i$ and $u_{\ell }\in B_p$. Then, $u_{\ell }\in B_j$ by Lemma 1. The vertices $(u_{\ell },v_1)$, $(u_{\ell },v_2),\dots ,(u_{\ell },v_k)$ are in $B_j^{\prime }$. Clearly, $(u_{\ell },v_j)\in B_j^{\prime }$. Hence, a vertex $(u_{\ell },v_j)$ appears in every bag $B_j^{\prime }$ for the node j on the tree path from node i to node p in T if it appears in $B_i^{\prime },B_j^{\prime }\in B^{\prime }$.

Following the discussion above, $D^{\prime }=(T,B^{\prime })$ is a tree decomposition of $G⊠H$ of width $k\left(tw\right(G)+1)-1$ and with $O\left(\right|V\left(G\right)\left|\right)$ nodes. By Lemma 2, we can obtain a nice tree decomposition of $G⊠H$ of width $k\left(tw\right(G)+1)-1$ with at most $4·\left|V\right(G⊠H\left)\right|$ nodes in $O\left(\right|V(G⊠H))$ time.  □

Theorem 8.

Let G be a graph of bounded treewidth. Given a nice tree decomposition $D=(T,B=\{B_i\mid i\in T\})$ of G of width $tw\left(G\right)$ and $O\left(\right|V\left(G\right)\left|\right)$ nodes, the $\left\{k\right\}$-maximum-clique transversal problem can be solved in $O(2^{k\left(tw\right(G)+1)}·k^2·(tw\left(G\right)+1)|V\left(G\right)|)$ time.

Proof. 

Let H be a complete graph of k vertices. By Lemma 9, we can obtain a nice tree decomposition of $G⊠H$ of width $k\left(tw\right(G)+1)-1$ with at most $4·\left|V\right(G⊠H)$ nodes in $O\left(\right|V(G⊠H)\left|\right)$ time. Since k is fixed and G is a graph of bounded treewidth, $G⊠H$ is a graph of bounded treewidth $k\left(tw\right(G)+1)-1$. Note that $\left|V\right(G⊠H\left)\right|=k·\left|V\right(G\left)\right|$. By Theorems 6 and 7, the $\left\{k\right\}$-maximum-clique transversal problem can be solved in $O(2^{k\left(tw\right(G)+1)}·k^2·(tw\left(G\right)+1)|V\left(G\right)|)$ time.  □

4.2.2. Problem Solving by Dynamic Programming

This section studies the $\left\{k\right\}$-maximum-clique transversal problem by the dynamic programming technique for graphs of bounded treewidth.

Definition 11.

Assume that G is a graph and k is a positive integer. Let $X=(X_0,X_1,\dots ,X_k)$ be a $(k+1)$-tuple of subsets of $V\left(G\right)$. The weight of the $(k+1)$-tuple X, denoted by $w\left(X\right)$, is ${\sum }_{i=0}^k\left(\right|X_i|·i)$. Let $\ell \in \{0,1,\dots ,k\}$ and let $V^{\prime }\subseteq V\left(G\right)$. Let $Y=(Y_0,Y_1,\dots ,Y_k)$ be another $(k+1)$-tuple of subsets of $V\left(G\right)$. We give the following notations and definitions.

1. 

$X\oplus Y$ denotes the $(k+1)$-tuple $(X_0\cup Y_0,\dots ,X_k\cup Y_k)$.

2. 

$X\oplus V^{\prime }$ denotes the $(k+1)$-tuple $(X_0\cup V^{\prime },\dots ,X_k\cup V^{\prime })$.

3. 

$X{\oplus }_{\ell }{V}^{\prime }$ denotes the $(k+1)$-tuple $(S_0,\dots ,S_k)$ such that $S_{\ell }=X_{\ell }\cup V^{\prime }$ and $S_i=X_i$ for $i\in \{0,1,\dots ,k\}\backslash \{\ell \}$.

4. 

$X\otimes V^{\prime }$ denotes the $(k+1)$-tuple $(X_0\cap V^{\prime },\dots ,X_k\cap V^{\prime })$.

5. 

$X{\ominus }_{\ell }{V}^{\prime }$ denotes the $(k+1)$-tuple $(S_0,\dots ,S_k)$ such that $S_{\ell }=X_{\ell }\backslash V^{\prime }$ and $S_i=X_i$ for $i\in \{0,1,\dots ,k\}\backslash \{\ell \}$.

6. 

A $(k+1)$-tuple $S=(S_0,\dots ,S_k)$ is a $(k+1)$-partition of $V\left(G\right)$ satisfying the following conditions.

(a) 

${\bigcup }_{i=0}^k{S}_i=V\left(G\right)$.

(b) 

$S_i\cap S_j=\varnothing$ for $0\le i<j\le k$.

7. 

A $(k+1)$-assignment of $V\left(G\right)$ is a $(k+1)$-partition $F=(F_0,\dots ,F_k)$ of $V\left(G\right)$ such that $w(F\otimes Q)\ge k$ for every $Q\in Q\left(G\right).$

Remark 5.

For a fixed positive integer k, a $\left\{k\right\}$-maximum clique transversal function of a graph G can be regarded as a $(k+1)$-assignment of $V\left(G\right)$, and vice versa. Then, ${\tau }_{\left\{k\right\}}\left(G\right)=min\{w\left(S\right)\mid S$ is a $(k+1)$-assignment of $V\left(G\right)\}$.

Definition 12.

Let k be a fixed positive integer and let G be a graph of bounded treewidth with a nice tree decomposition $(T,\{B_i\mid i\in T\})$ rooted at node r. For each node $i\in T$, let $X=(X_0,\dots ,X_k)$ be a $(k+1)$-partition of $B_i$ and let $F_i\left(X\right)$ be a $(k+1)$-assignment $S=(S_0,\dots ,S_k)$ of $V\left(G_i\right)$ of minimum weight satisfying all the following conditions.

(1) 

$S\otimes B_i=X$.

(2) 

$w(S\otimes Q)\ge k$ for every $Q\in Q\left(G_i\right)\cap Q\left(G\right)$.

If $F_i\left(X\right)$ does not exist, let $F_i\left(X\right)=\Phi$ with $w(\Phi )=\infty$.

Remark 6.

By Definition 12, $T=T_r$, $G=G_r$, and ${\tau }_{\left\{k\right\}}\left(G\right)=min\{w\left(F_r\left(X\right)\right)\mid X$ is a $(k+1)$-partition of $B_r\}$.

Lemma 10.

Let $D=(T,\{B_i\mid i\in T\})$ be a nice tree decomposition of a graph G of width $tw\left(G\right)$. Suppose that node i is a leaf node of T. For all $(k+1)$-partitions X of $B_i$, $F_i\left(X\right)$ of $G_i$ can be computed in $O({(k+1)}^{tw\left(G\right)+1}·tw\left(G\right))$ time.

Proof. 

Since node i is a leaf node, $G_i=G\left[B_i\right]$ and $Q\left(G_i\right)\cap Q\left(G\right)=Q\left(G\left[B_i\right]\right)$. By the definition of tree decomposition, $|B_i|\le tw\left(G\right)+1$ and $\omega \left(G\right)=tw\left(G\right)+1$. If $B_i$ is not a maximum clique of G, then $F_i\left(X\right)=\Phi$ for every $(k+1)$-partition X of $B_i$. It takes $O(tw{\left(G\right)}^2)$ time to check if $B_i$ is a maximum clique. We therefore assume that $B_i$ is a maximum clique of G. The number of $(k+1)$-assignments of $B_i$ is ${(k+1)}^{tw\left(G\right)+1}$. For each $(k+1)$-assignment $F_i\left(X\right)$ of $B_i$, we verify if $w\left(F_i\left(X\right)\right)\ge k$. The verification process can be done in $O\left(tw\right(G\left)\right)$ time. Following the discussion above, all $(k+1)$-assignments $F_i\left(X\right)$ of $G_i$ can be computed in $O({(k+1)}^{tw\left(G\right)+1}·tw\left(G\right))$ time.  □

Lemma 11.

Let $D=(T,\{B_i\mid i\in T\})$ be a nice tree decomposition of a graph G of width $tw\left(G\right)$. Suppose that node i is a forget node of T. Let j be the child node of i and let $x\in B_j$ such that $B_i=B_j\backslash \left\{x\right\}$. Let X be a $(k+1)$-partition of $B_i$ and $Y=\{\left(X{\oplus }_{\ell }\left\{x\right\}\right)\mid 0\le \ell \le k\}$. Let $Z\in Y$ such that $w\left(F_j\left(Z\right)\right)=min\{w\left(F_j\left(X^{\prime }\right)\right)\mid X^{\prime }\in Y\}$. Then, $F_i\left(X\right)=F_j\left(Z\right)$.

Proof. 

Since $B_i=B_j\setminus \left\{x\right\}$, $G_i=G_j$. The $(k+1)$-assignment $F_i\left(X\right)$ is also a $(k+1)$-assignment of $V\left(G_j\right)$. Let $X^{\prime }=F_i\left(X\right)\otimes B_j$. Then, $X^{\prime }$ is a $(k+1)$-partition of $B_j$. There exists exactly one integer $\ell \in \{0,1,\dots ,k\}$ such that $X^{\prime }=\left(X{\otimes }_{\ell }\left\{x\right\}\right)$. Let $Y=\{\left(X{\oplus }_{\ell }\left\{x\right\}\right)\mid 0\le \ell \le k\}$. Hence, $F_i\left(X\right)=F_j\left(Z\right)$, where $Z\in Y$ and $w\left(F_j\left(Z\right)\right)=min\{w\left(F_j\left(X^{\prime }\right)\right)\mid X^{\prime }\in Y\}$.  □

Lemma 12.

Let $D=(T,\{B_i\mid i\in T\})$ be a nice tree decomposition of a graph G of width $tw\left(G\right)$. Suppose that node i is an introduce node of T. Let j be the child node of i and let x be the vertex such that $B_i=B_j\cup \left\{x\right\}$. Let $\ell \in \{0,1,\dots ,k\}$ and let $X=(X_0,\dots X_k)$ be a $(k+1)$-partition of $B_i$ such that $x\in X_{\ell }$. Then,

$$F_i\left(X\right)=\left\{\begin{array}{cc}{F}_j\left(X{\ominus }_{\ell }\left\{x\right\}\right){\oplus }_{\ell }\left\{x\right\}\hfill & if either B_i\notin Q\left(G\right),or B_i\in Q\left(G\right)and w\left(X\right)\ge k,\hfill \\ \Phi \hfill & otherwise.\hfill \end{array}\right.$$

Proof. 

Let d be a proper descendant of the subtree $T_j$. Since $x\notin B_j$, $x\notin V\left(G_j\right)$, by the third condition of Definition 5. Then, $x\notin B_d$. We consider the following two cases.

Case 1: $B_i\notin Q\left(G\right)$. By the arguments for the discussion of Case 1 in the proof of Lemma 6, $Q\left(G_i\right)\cap Q\left(G\right)=Q\left(G_j\right)\cap Q\left(G\right)$. For any $(k+1)$-partition $X^{\prime }$ of $B_j$, $w(F_j\left(X^{\prime }\right)\otimes Q))\ge k$ for every $Q\in Q\left(G_i\right)\cap Q\left(G\right)$.

Let $\ell \in \{0,1,\dots ,k\}$ and let X be a $(k+1)$-partition of $B_i$ such that $X=X^{\prime }{\oplus }_{\ell }\left\{x\right\}$. Then, $F_j\left(X^{\prime }\right){\oplus }_{\ell }\left\{x\right\}$ is a $(k+1)$-assignment S of $V\left(G_i\right)$ such that $S\otimes B_i=X$. Therefore, $w\left(F_i\left(X\right)\right)\le w\left(F_j\left(X^{\prime }\right){\oplus }_{\ell }\left\{x\right\}\right)$.

Conversely, let $X=(X_0,X_1,\dots ,X_k)$ be a $(k+1)$-partition of $B_i$ such that $x\in X_{\ell }$. Then, $F_i\left(X\right){\ominus }_{\ell }\left\{x\right\}$ is a $(k+1)$-assignment $S^{\prime }$ of $V\left(G_j\right)$ such that $S^{\prime }\otimes B_j=X{\ominus }_{\ell }\left\{x\right\}$. Let $X^{\prime }=X{\ominus }_{\ell }\left\{x\right\}$. Therefore, $w\left(F_i\left(X\right)\right)\ge w\left(F_j\left(X^{\prime }\right){\oplus }_{\ell }\left\{x\right\}\right)$.

Following the discussion above, we know that $F_i\left(X\right)=F_j\left(X{\ominus }_{\ell }\left\{x\right\}\right){\oplus }_{\ell }\left\{x\right\}$.

Case 2: $B_i\in Q\left(G\right)$. By the arguments for the discussion of Case 2 in the proof of Lemma 6, $Q\left(G_i\right)\cap Q\left(G\right)=(Q\left(G_j\right)\cap Q\left(G\right))\cup \left\{B_i\right\}$. Since $B_i\in Q\left(G\right)$ and $F_i\left(X\right)\otimes B_i=X$, we have $w\left(X\right)\ge k$. If $w\left(X\right)<k$, then $F_i\left(X\right)$ does not exist. Following the arguments similar to those for proving Case 1, we know that $w\left(F_i\left(X\right)\right)=w\left(F_j\left(X^{\prime }\right){\oplus }_{\ell }\left\{x\right\}\right)$. Therefore, $F_i\left(X\right)=F_j\left(X{\ominus }_{\ell }\left\{x\right\}\right){\oplus }_{\ell }\left\{x\right\}$.  □

Lemma 13.

Let G be a graph of bounded treewidth with a nice tree decomposition $(T,\{B_i\mid i\in T\})$. Suppose that node i is a join node of T. Let j and ℓ be the child nodes of i. For each $(k+1)$-partition $X=(X_0,X_1,\dots ,X_k)$ of $B_i$,

$$F_i\left(X\right)=F_j\left(X\right)\oplus F_{\ell }\left(X\right).$$

Proof. 

Since node i is a join node, $B_i=B_j=B_{\ell }$. Then, $Q\left(G_i\right)=Q\left(G_j\right)\cup Q\left(G_{\ell }\right)$. Let $S=F_j\left(X\right)\oplus F_{\ell }\left(X\right)$. Clearly, $S\otimes B_i=X$ and $w(S\otimes Q)\ge k$ for $Q\in Q\left(G_i\right)\cap Q\left(G\right)$. We have $w\left(F_i\left(X\right)\right)\le w\left(S\right)=w(F_j\left(X\right)\oplus F_{\ell }\left(X\right))$.

Let $S_1=F_i\left(X\right)\otimes V\left(G_j\right)$ and $S_2=F_i\left(X\right)\otimes V\left(G_{\ell }\right)$. Then, $S_1$ and $S_2$ are $(k+1)$-assignments of $V\left(G_j\right)$ and $V\left(G_j\right)$, respectively. Furthermore, $S_1\otimes B_j=S_2\otimes B_{\ell }=X$. Therefore, $w(F_j\left(X\right)\oplus F_{\ell }\left(X\right))\le w(S_1\oplus S_2)=w\left(F_i\left(X\right)\right)$.

Following the discussion above, $w\left(F_i\left(X\right)\right)=w(F_j\left(X\right)\oplus F_{\ell }\left(X\right))$ and the lemma holds.  □

Theorem 9.

Let $D=(T,\{B_i\mid i\in T\})$ be a nice tree decomposition of a graph G of width $tw\left(G\right)$ and $O\left(\right|V\left(G\right)\left|\right)$ nodes. The $\left\{k\right\}$-maximum-clique transversal problem can be solved in $O({(k+1)}^{tw\left(G\right)+1}·tw\left(G\right)·|V\left(G\right)|)$ time.

Proof. 

Assume that T is rooted at r. Then, $T=T_r$, $G=G_r$, and ${\tau }_{\times k}\left(G\right)=min\{w\left(F_r\left(X\right)\right)\mid X$ is a $(k+1)$-partition of $B_r\}$. Our algorithm works from the leaves in T up to the root, computing the solutions $F_i\left(X\right)$ for each visited node i on the way through the dynamic programming technique. For all $(k+1)$-partitions X of $B_i$, the solutions can be computed in $O({(k+1)}^{tw\left(G\right)+1}·tw\left(G\right))$ time by Lemmas 10–13. Since T contains $O\left(\right|V\left(G\right)\left|\right)$ nodes, the $\left\{k\right\}$-maximum-clique transversal problem can be solved in $O({(k+1)}^{tw\left(G\right)+1}·tw\left(G\right)·|V\left(G\right)|)$ time.  □

4.3. The Signed and Minus Maximum-Clique Transversal Problems

The section deals with the signed and minus maximum-clique transversal problems on graphs of bounded treewidth.

Theorem 10.

Assume that $G=(V,E)$ is a graph and $\omega \left(G\right)$ is fixed. Let $k=\lfloor \omega \left(G\right)/2\rfloor +1$. Then, ${\tau }_M^s\left(G\right)=2{\tau }_{\times k}\left(G\right)-n$.

Proof. 

The theorem holds by Theorem 7 in Lee’s article [3].  □

Theorem 11.

Let $D=(T,\{B_i\mid i\in T\})$ be a nice tree decomposition of a graph G of width $tw\left(G\right)$ and $O\left(\right|V\left(G\right)\left|\right)$ nodes. The signed maximum-clique transversal problem can be solved in $O(2^{tw\left(G\right)}·tw\left(G\right)·|V\left(G\right)|)$ time.

Proof. 

It follows from Theorems 6 and 10.  □

We introduce the 2-clique graph extension and positive maximum-clique transversal functions as follows.

Definition 13.

The 2-clique graph extension H of a graph G is defined as follows.

1. 

$V\left(H\right)=\{v_1,v_2\mid v\in V\left(G\right)\}$.

2. 

$E\left(H\right)=\{v_1{v}_2\mid v\in V\left(G\right)\}\cup \{u_1{v}_1,u_1{v}_2,u_2{v}_1,u_2{v}_2\mid uv\in E\left(G\right)\}$.

Figure 3 shows an example of the 2-clique graph extension H of a graph G.

Definition 14.

Assume that G is a graph. A function $f:V\left(G\right)\to \{0,1,2\}$ is a positive maximum-clique transversal function of G if $f\left(Q\right)\ge \omega \left(G\right)+1$ for $Q\in Q\left(G\right)$. The positive maximum-clique transversal number of G, denoted by ${\tau }_M^{+}\left(G\right)$, is the minimum weight of a positive maximum-clique transversal function of G. The positive maximum-clique transversal problem is to find a positive maximum-clique transversal function of G of minimum weight.

Lemma 14.

For any graph G, ${\tau }_M^{+}\left(G\right)={\tau }_M^{-}\left(G\right)+\left|V\left(G\right)\right|$.

Proof. 

Let f be a minus maximum-clique transversal function of G of minimum weight. We define a function h of G by $h\left(v\right)=f\left(v\right)+1$ for every $v\in V\left(G\right)$. Since $f\left(v\right)\in \{-1,0,1\}$, $h\left(v\right)\in \{0,1,2\}$ for $v\in V\left(G\right)$. Let Q be a maximum clique of G. Then $h\left(Q\right)={\sum }_{v\in Q}(f\left(v\right)+1)=f\left(Q\right)+\left|Q\right|\ge 1+\omega \left(G\right)$. The function h is a positive maximum-clique function of G. We have ${\tau }_M^{+}\left(G\right)\le {\tau }_M^{-}\left(G\right)+\left|V\left(G\right)\right|$.

Conversely, let h be a positive maximum-clique transversal function of G of minimum weight. We define a function f of G by $f\left(v\right)=h\left(v\right)-1$ for every $v\in V\left(G\right)$. Since $h\left(v\right)\in \{0,1,2\}$, $f\left(v\right)\in \{-1,0,1\}$ for every $v\in V\left(G\right)$. Let Q be a maximum clique of G. Then $f\left(Q\right)={\sum }_{v\in Q}(h\left(v\right)-1)=h\left(Q\right)-\left|Q\right|\ge 1$. The function f is a minus maximum-clique function of G. We have ${\tau }_M^{-}\left(G\right)\le {\tau }_M^{+}\left(G\right)-\left|V\left(G\right)\right|$. Following what we have discussed above, we know that ${\tau }_M^{+}\left(G\right)={\tau }_M^{-}\left(G\right)+\left|V\left(G\right)\right|$.  □

Lemma 15.

Assume that G is a graph with fixed clique number $\omega \left(G\right)$. Let H be the 2-clique graph extension of G and $k=\omega \left(G\right)+1$. Then, ${\tau }_M^{+}\left(G\right)={\tau }_{\times k}\left(H\right)$.

Proof. 

Let $Q\left(G\right)=\{C_1,\dots ,C_{\ell }\}$ and let $Q_i=\{v_1,v_2\mid v\in C_i\}$ for $1\le i\le \ell$. By the construction of H, it can be easily verified that $Q\left(H\right)=\{Q_1,\dots ,Q_{\ell }\}$.

Let f be a positive maximum-clique transversal function of G of minimum weight. We define a subset D of $V\left(H\right)$ as follows.

• For any vertex $v\in V\left(G\right)$ with $f\left(v\right)=2$, D includes both of the vertices $v_1$ and $v_2$.
• For any vertex $v\in V\left(G\right)$ with $f\left(v\right)=1$, D contains precisely one of the vertices $v_1$ and $v_2$.
• For any vertex $v\in V\left(G\right)$ with $f\left(v\right)=0$, D comprises none of the vertices $v_1$ and $v_2$.

Let $i\in \{1,\dots ,\ell \}$. Then,

$$|D\cap Q_i|=\sum _{v\in C_i}|D\cap \{v_1,v_2\}|=\sum _{v\in C_i}f\left(v\right)=f\left(C_i\right)\ge \omega \left(G\right)+1\ge k.$$

The set D is a k-fold maximum-clique transversal set of H. Hence, ${\tau }_{\times k}\left(H\right)\le {\tau }_M^{+}\left(G\right)$.

Conversely, let S be a k-fold maximum-clique transversal set of H with ${\tau }_{\times k}\left(H\right)$ vertices. We define a function h of G as follows.

• For any two vertices $v_1,v_2\in V\left(H\right)$, $h\left(v\right)=2$ if S includes both of them.
• For any two vertices $v_1,v_2\in V\left(H\right)$, $h\left(v\right)=1$ if S contains precisely one of them.
• For any two vertices $v_1,v_2\in V\left(H\right)$, $h\left(v\right)=0$ if S comprises none of them.

Let $i\in \{1,\dots ,\ell \}$. Then,

$$h\left(C_i\right)=\sum _{v\in C_i}h\left(v\right)=\sum _{v\in C_i}|S\cap \{v_1,v_2\}|=|S\cap Q_i|\ge k\ge \omega \left(G\right)+1.$$

The function h is a positive maximum-clique transversal function of G. Hence, ${\tau }_M^{+}\left(G\right)\le {\tau }_{\times k}\left(H\right)$. Following the discussion above, we have ${\tau }_M^{+}\left(G\right)={\tau }_{\times k}\left(H\right)$.  □

Theorem 12.

Assume that G is a graph with fixed clique number $\omega \left(G\right)$. Let H be the 2-clique graph extension of G and $k=\omega \left(G\right)+1$. Then, ${\tau }_M^{-}\left(G\right)={\tau }_{\times k}\left(H\right)-\left|V\left(G\right)\right|$.

Proof. 

The theorem follows from Lemmas 14 and 15.  □

Lemma 16.

Let G be a graph of bounded treewidth nd let H be a 2-clique graph extension of G. Given a nice tree decomposition $D=(T,B=\{B_i\mid i\in T\})$ of G of width $tw\left(G\right)$ and $O\left(\right|V\left(G\right)\left|\right)$ nodes, one can find a nice tree decomposition of H of width $2\left(tw\right(G)+1)$ and with at most $4\left|V\right(H\left)\right|$ nodes in $O\left(\right|V\left(H\right)\left|\right)$ time.

Proof. 

Let $B_i^{\prime }=\{v_1,v_2|v\in B_i\}$ for $B_i\in B$ and $D^{\prime }=(T,B^{\prime }=\{B_i^{\prime }\mid i\in T\})$. We show as follows that $D^{\prime }$ is a tree decomposition of H.

(1)

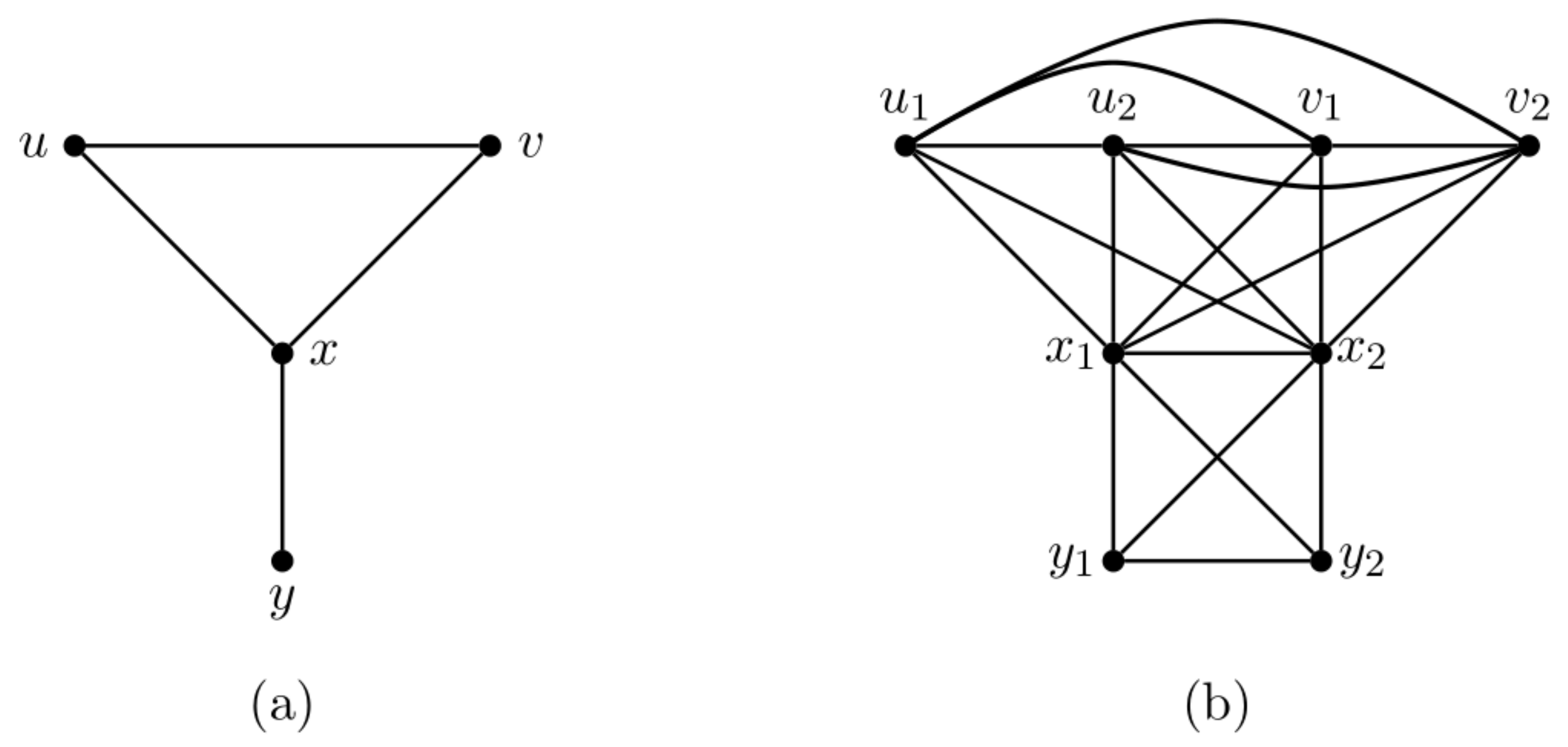
Every vertex $v\in V\left(G\right)$ appears in at least one bag of B. Suppose that $v\in B_i$. Since $V\left(H\right)=\{v_1,v_2\mid v\in V\left(G\right)\}$, $v_1,v_2\in B_i^{\prime }$. Therefore, every vertex of H appears in at least one bag $B_i^{\prime }\in B^{\prime }$.

(2)

For each edge $e=uv\in E\left(G\right)$, there is at least one bag of B containing the vertices u and v. Suppose that $u,v\in B_i$. Since $E\left(H\right)=\{v_1{v}_2\mid v\in V\left(G\right)\}\cup \{u_1{v}_1,u_1{v}_2,u_2{v}_1,u_2{v}_2\mid uv\in E\left(G\right)\}$, $u_1$, $u_2$, $v_1$, and $v_2$, are in the bag $B_i^{\prime }$. Therefore, there is at least one bag of $B^{\prime }$ containing both x and y for all edges $xy\in E\left(H\right)$.

(3)

Let $v\in V\left(G\right)$. Then, $v_1,v_2\in V\left(H\right)$. Clearly, $v_1,v_2\in B_i^{\prime }$ if and only if $v\in B_i$. By Lemma 1, if v appears in two bag $B_p,B_q\in B$, then it appears in every bag $B_j$ for the node j on the tree path from node p to node q in T. Since $V\left(H\right)=\{v_1,v_2\mid v\in V\left(G\right)\}$, $v_1$ and $v_2$ are both in $B_p^{\prime }$ and $B_q^{\prime }$ and they appear in every bag $B_j^{\prime }$ for the node j on the tree path from node p to node q in T.

Following the discussion above, $D^{\prime }=(T,B^{\prime })$ is a tree decomposition of H of width $2\left(tw\right(G)+1)$ and with $O\left(\right|V\left(G\right)\left|\right)$ nodes. By Lemma 2, we can obtain a nice tree decomposition of H of width $2\left(tw\right(G)+1)$ with at most $4\left|V\right(H\left)\right|$ nodes in $O\left(\right|V\left(H\right))$ time.  □

Theorem 13.

Let G be a graph of bounded treewidth. Given a nice tree decomposition $D=(T,B=\{B_i\mid i\in T\})$ of G of width $tw\left(G\right)$ and $O\left(\right|V\left(G\right)\left|\right)$ nodes, the minus maximum-clique transversal problem can be solved in $O(4^{tw\left(G\right)}·tw\left(G\right)·|V\left(G\right)|)$ time.

Proof. 

Let H be the 2-clique graph extension of G. By Lemma 16, we can obtain a nice tree decomposition of H of width $2\left(tw\right(G)+1)-1$ with at most $4\left|V\right(H\left)\right|$ nodes in $O\left(\right|V\left(H\right)\left|\right)$ time. Since G is a graph of bounded treewidth, H is a graph of bounded treewidth $2\left(tw\right(G)+1)-1$. Note that $\left|V\right(H\left)\right|=2·\left|V\right(G\left)\right|$. By Theorems 6 and 7, the minus maximum-clique transversal function problem can be solved in $O(4^{tw\left(G\right)}·tw\left(G\right)·|V\left(G\right)|)$ time.  □

Remark 7.

The complexity of the minus maximum-clique transversal problem for graphs of bounded treewidth can be improved to $O(3^{tw\left(G\right)}·tw\left(G\right)·|V\left(G\right)|)$ by our dynamic programming technique used for the $\left\{k\right\}$-maximum-clique transversal problem. We leave it to interested readers.

5. Conclusions

In this paper, we have shown that the k-fold maximum-clique transversal problem can be solved in $O(2^{tw\left(G\right)}·tw\left(G\right)·|V\left(G\right)|)$ time for any graph G with bounded treewidth $tw\left(G\right)$. The maximum-clique transversal problem is a particular case of the k-fold maximum-clique transversal problem and the $\left\{k\right\}$-maximum-clique transversal problem with $k=1$. Therefore, the problem can be solved in the same running time. Lokshtanov et al. [18] obtained a number of lower bounds on the running time of algorithm solving problems on graphs of bounded treewidth under the strong exponential time hypothesis (SETH) of Impagliazzo and Paturi [19]. Based on SETH, we conjecture that the maximum-clique transversal problem cannot be solved in ${(2-ϵ)}^{tw\left(G\right)}{\left|V\left(G\right)\right|}^{O\left(1\right)}$ time for any $ϵ>0$. Although SETH is still somewhat controversial and not entirely accepted by the computational complexity community, the lower bound still delivers valuable messages. If the lower bound can be obtained under SETH, then the $\left\{k\right\}$-maximum-clique transversal problem cannot be solved in in ${(k+1-ϵ)}^{tw\left(G\right)}{\left|V\left(G\right)\right|}^{O\left(1\right)}$ time for any $ϵ>0$. Our algorithms on graphs of bounded treewidth are probably optimal. Finally, we suggest the following open questions for future work:

(1)

Table 1 and Table 2 show that the respective parameterized complexities of the clique transversal, k-fold maximum-clique transversal, and $\left\{k\right\}$-maximum-clique transversal problems remain unknown for planar graphs. Can we find fixed-parameter tractable algorithms to solve them for planar graphs if the considered problem is parameterized by the solution size or weight? Or is it possible to find improved algorithms for planar graphs of bounded treewidth?

(2)

In Table 2, all the considered problems parameterized by treewidth are fixed-parameter tractable. Can we prove that all the considered problems remain fixed-parameter tractable if given other parameters?

(3)

This paper considers only maximum cliques for simple graphs. In reality, dicliques also appear in more general directed graphs [20]. It is interesting to consider the problems for directed ones.