Shared Quantum Key Distribution Based on Asymmetric Double Quantum Teleportation
Abstract
:1. Introduction
- A notable rate of success for the coincident basis scenario between the sender and the receiver closer to the ideal case in the original BB84 protocol;
- A dramatic reduction of success for an eavesdropper under individual attacks for the undetected scenario during a reconciliation step;
- A practical reduced time of action for an eavesdropper due to the non-local properties of the key assembling and the absence of a physical quantum channel;
- A configurable setup to adjust some quantitative working features in the procedure as the eavesdropper success ratio or the Quantum Bit Error Rate (QBER).
2. Introductory Remarks for Contemporary Post-Quantum Cryptography
3. Double Teleportation as Superposition and Parallel Post-Processing
3.1. Double Teleportation Process as Superposition
3.2. Post-Processing Following to Double Teleportation
3.3. Entanglement and Non-Locality Activation
3.4. Concrete Post-Processing and Information Transference via Post-Measurement
4. Transference of Programmed Quantum States Using Double Teleportation
4.1. Generation of Quantum States as a Collaboration among Three Parties
4.2. General Notation for the Control of Post-Selection Problem
4.3. Control Prescriptions for the Quantum State Transference
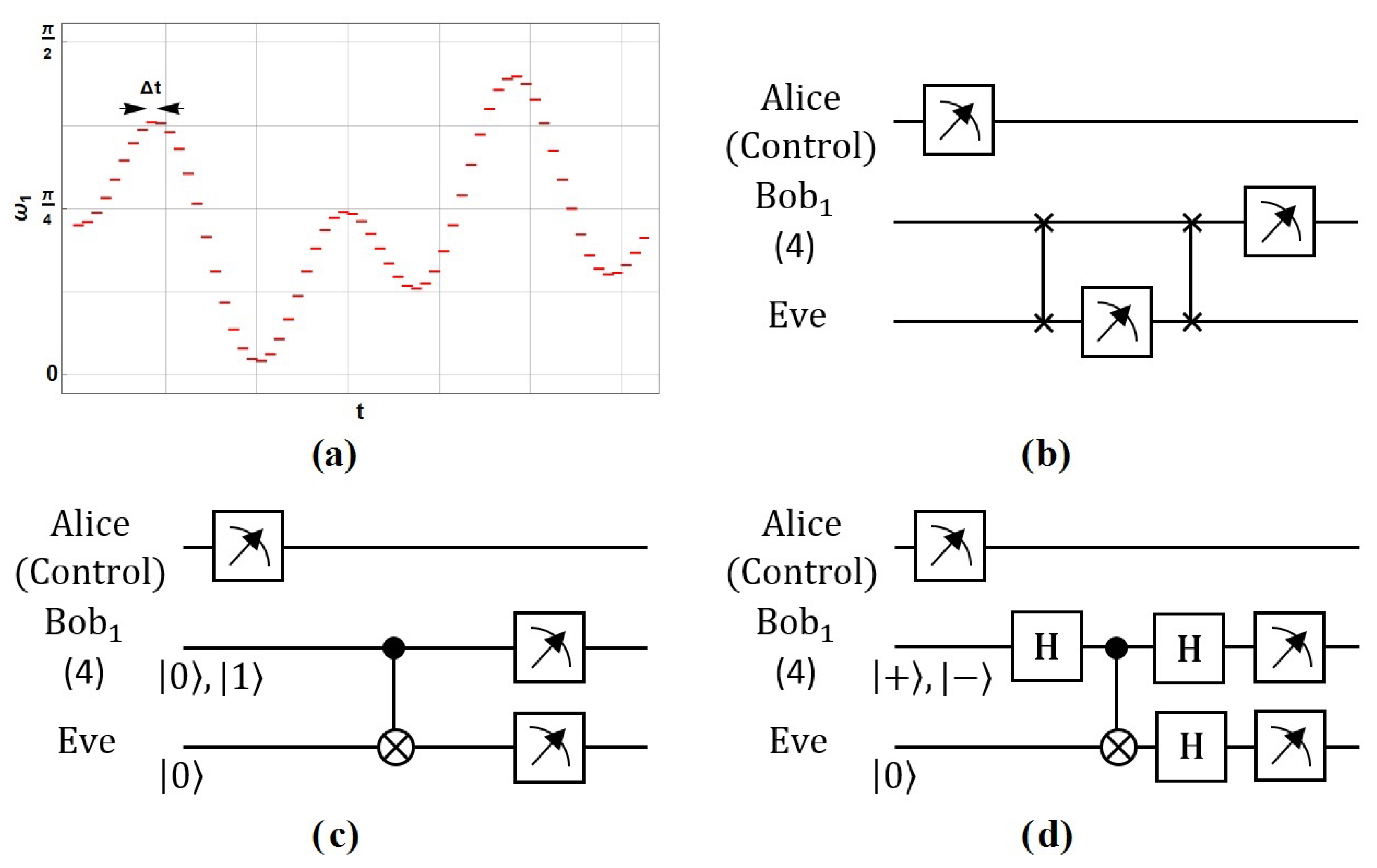
5. A QKD Protocol Based on a Shared Collaboration among Three Parties
5.1. QKD Protocol Description Based on a Shared Generation
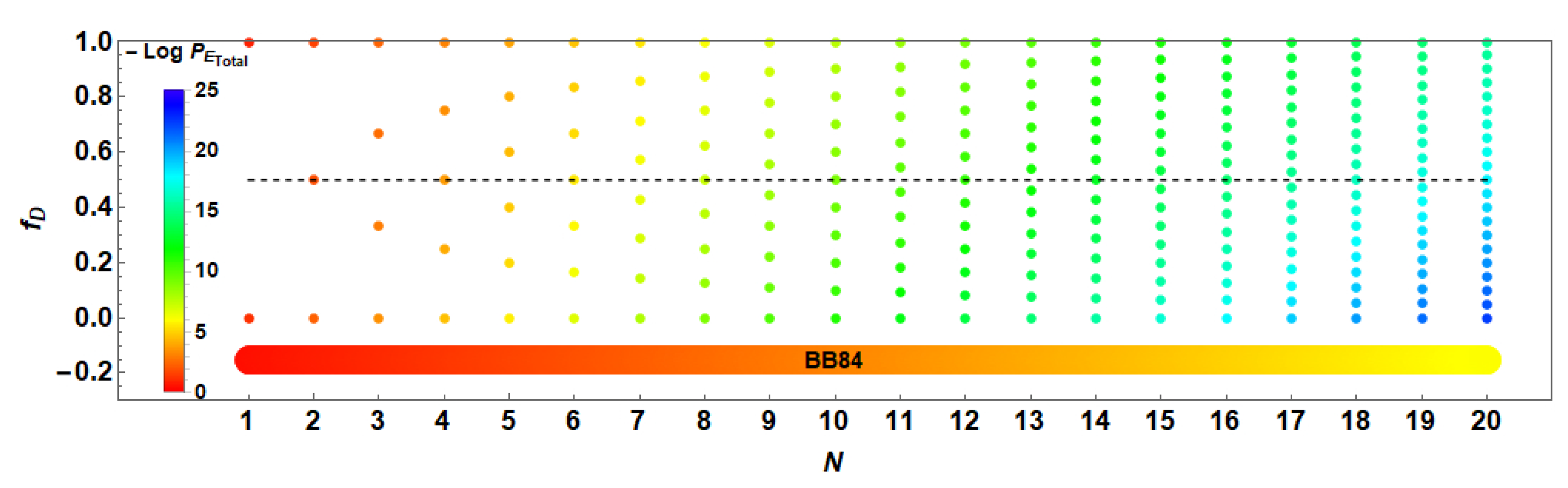
5.2. Action and Impact of a Possible Eavesdropper under an Individual Attack
5.3. Considerations for Complexity and Number of Resources in the Procedure
6. Some Final Considerations about Benchmarking, Decoherence Effects, and Fidelity
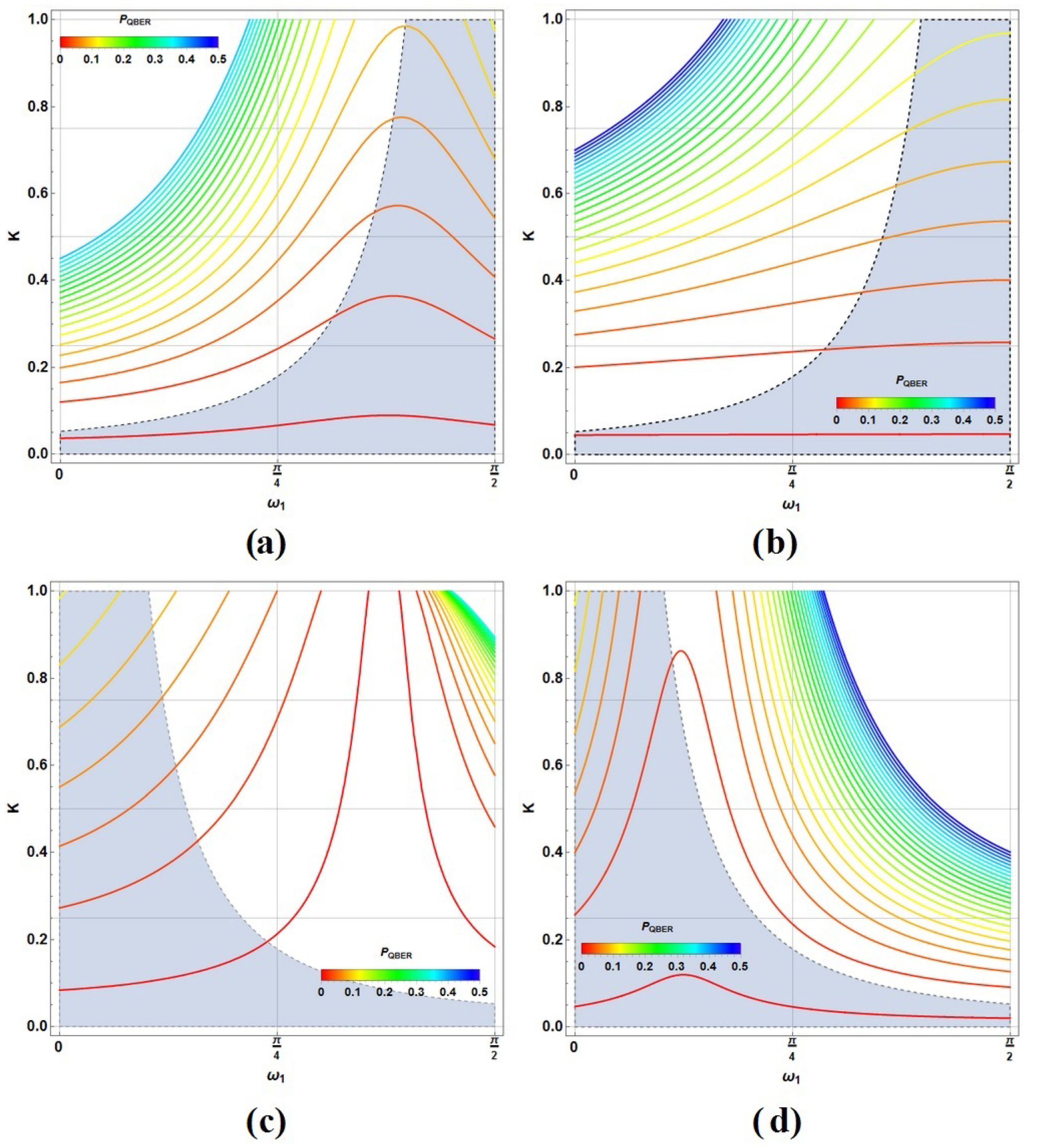
6.1. QBER and a Brief Comparison with Other Similar QKD Protocols
6.2. Fidelity and Possible Decoherence Effects Due to the Environment
6.3. Quantum Processing in QKD Developments and Post-Quantum Cryptography
7. Conclusions
7.1. Summarizing and Featuring the Protocol
7.2. Future and Additional Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Control on Faraway Non-Local Resources
Appendix B. SWAP Operations between Faraway Non-Local Parties
Appendix C. Conditional Probability for Eve Success in the Protocol
Appendix D. Conditional QBER in the Protocol
References
- Hong, K.W.; Foong, O.M.; Low, T.J. Challenges in Quantum Key Distribution: A Review. In ICINS ’16: Proceedings of the 4th International Conference on Information and Network Security; Association for Computing Machinery: New York, NY, USA, 2016; pp. 29–33. [Google Scholar]
- Ghosh, C.; Parag, A.; Datta, S. Different Vulnerabilities And Challenges Of Quantum Key Distribution Protocol: A Review. Int. J. Adv. Res. Comput. Sci. 2017, 8, 307–311. [Google Scholar] [CrossRef]
- Ribeiro, J. Cryptography. In Theoretical Advances in Practical Quantum Cryptography; Delft University of Technology: Delft, The Netherlands, 2020; p. 32. [Google Scholar]
- Makarov, V.; Anisimov, A.; Skaar, J. Effects of detector efficiency mismatch on security of quantum cryptosystems. Phys. Rev. A 2006, 74, 022313. [Google Scholar] [CrossRef] [Green Version]
- Sajeed, S.; Radchenko, I.; Kaiser, S.; Bourgoin, J.P.; Pappa, A.; Monat, L.; Legré, M.; Makarov, V. Attacks exploiting deviation of mean photon number in quantum key distribution and coin tossing. Phys. Rev. A 2015, 91, 032326. [Google Scholar] [CrossRef] [Green Version]
- Sen, D. The Uncertainty relations in quantum mechanics. Curr. Sci. 2014, 107, 203–218. [Google Scholar]
- Miller, D.A.B. Entanglement. In Quantum Mechanics for Scientists and Engineers; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Gyongyosi, L.; Imre, S. Dense Quantum Measurement Theory. Sci. Rep. 2019, 9, 6755. [Google Scholar] [CrossRef] [Green Version]
- Cao, W.-F.; Zhen, Y.-Z.; Zheng, Y.-L.; Chen, Z.-B.; Liu, N.-L.; Chen, K.; Pan, J.-W. Highly Efficient Quantum Key Distribution Immune to All Detector Attacks. arXiv 2014, arXiv:1410.2928. [Google Scholar]
- Singh, H.; Gupta, D.-L.; Singh, A.-K. Quantum Key Distribution Protocols: A Review. IOSR J. Comput. Eng. 2014, 16, 1–9. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum Cryptography: Public Key Distribution and Coin Tossing. In Proceedings of the Computer System and Signal Processing, Bangalore, India, 10–12 December 1984; pp. 175–179. [Google Scholar]
- Bennett, C.H. Quantum cryptography using any two nonorthogonal states. Phys. Rev. Lett. 1992, 68, 3121. [Google Scholar] [CrossRef]
- Scarani, V.; Acin, A.; Ribordy, G.; Gisin, N. Quantum Cryptography Protocols Robust against Photon Number Splitting Attacks for Weak Laser Pulse Implementations. Phys. Rev. Lett. 2004, 92, 057901. [Google Scholar] [CrossRef] [Green Version]
- Ekert, A.-K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661. [Google Scholar] [CrossRef] [Green Version]
- Padmavathi, V.; Vishnu-Vardhan, B.; Krishna, A.-V.-N. Quantum Cryptography and Quantum Key Distribution Protocols: A Survey. In Proceedings of the IEEE 6th International Conference on Advanced Computing, Bhimavaram, India, 27–28 February 2016; pp. 556–562. [Google Scholar]
- Hughes, R.; Nordholt, J. Refining Quantum Cryptography. Science 2011, 333, 1584–1586. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bernstein, D.J.; Lange, T. Post-Quantum Cryptography: Dealing with the Fallout of Physics Success; Cryptology ePrint Archive: Report 2017/314; TU/e: Eindhoven, Denmark, 2017. [Google Scholar]
- Lo, H.K.; Chau, H.F. Unconditional Security of Quantum Key Distribution over Arbitrarily Long Distances. Science 1999, 283, 2050–2056. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bouwmeester, D.; Pan, J.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575–579. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.-H.; Kulik, S.P.; Shih, Y. Quantum Teleportation of a Polarization State with a Complete Bell State Measurement. Phys. Rev. Lett. 2001, 86, 1370. [Google Scholar] [CrossRef] [Green Version]
- Sun, Q.C.; Mao, Y.L.; Chen, S.J.; Zhang, W.; Jiang, Y.F.; Zhang, Y.B.; Zhang, W.J.; Miki, S.; Yamashita, T.; Terai, H.; et al. Quantum teleportation with independent sources and prior entanglement distribution over a network. Nat. Photonics 2016, 10, 671–675. [Google Scholar] [CrossRef]
- Liu, Q. Cryptography in the Age of Quantum Computers 2.0; Princeton University: Princeton, NJ, USA, 2021. [Google Scholar]
- Metcalf, B.J.; Spring, J.B.; Humphreys, P.C.; Thomas-Peter, N.; Barbieri, M.; Kolthammer, W.S.; Jin, X.M.; Langford, N.K.; Kundys, D.; Gates, J.C.; et al. Quantum teleportation on a photonic chip. Nat. Photonics 2014, 8, 770–774. [Google Scholar] [CrossRef] [Green Version]
- Lima, D.; Rigolin, G. Asymptotic security analysis of teleportation-based quantum cryptography. Quantum Inf. Process. 2020, 19, 201. [Google Scholar] [CrossRef]
- de Riedmatten, H.; Marcikic, I.; Tittel, W.; Zbinden, H.; Collins, D.; Gisin, N. Long Distance Quantum Teleportation in a Quantum Relay Configuration. Phys. Rev. Let. 2004, 92, 047904. [Google Scholar] [CrossRef] [Green Version]
- Ursin, R.; Jennewein, T.; Aspelmeyer, M.; Kaltenbaek, R.; Lindenthal, M.; Walther, P.; Zeilinger, A. Quantum teleportation across the Danube. Nature 2004, 430, 849. [Google Scholar] [CrossRef]
- Takesue, H.; Dyer, S.D.; Stevens, M.J.; Verma, V.; Mirin, R.P.; Nam, S.W. Quantum teleportation over 100 km of fiber using highly efficient superconducting nanowire single-photon detectors. Optica 2015, 2, 832–835. [Google Scholar] [CrossRef] [Green Version]
- Cardoso-Isidoro, C.; Delgado, F. Symmetries in Teleportation Assisted by N-Channels under Indefinite Causal Order and Post-Measurement. Symmetry 2020, 12, 1904. [Google Scholar] [CrossRef]
- Cardoso-Isidoro, C.; Delgado, F. Post-selected double teleportation and the modelling of its related non-local properties. J. Phys. Conf. Ser. 2021, 2090, 012033. [Google Scholar]
- Cardoso-Isidoro, C.; Delgado, F. Quantum authentication using double teleportation. J. Phys. Conf. Ser. 2021, in press. [Google Scholar]
- Zhou, N.; Zeng, G.; Xiong, J. Quantum key agreement protocol. Electron. Lett. 2004, 40, 1149. [Google Scholar] [CrossRef]
- Chen, L.; Jordan, S.; Liu, Y.; Moody, D.; Peralta, R.; Perlner, R.; Smith-Tone, D. Report on Post-Quantum Cryptography; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2016. [Google Scholar]
- Bernstein, D. Introduction to post-quantum cryptography. In Post-Quantum Cryptography; Bernstein, D.J., Buchmann, J., Dahmen, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar] [CrossRef] [Green Version]
- Cross, O.A. Topics in Quantum Computing; CreateSpace Independent Pub: Scotts Valley, CA, USA, 2012. [Google Scholar]
- Dusek, M.; Buzek, V. Quantum-controlled measurement device for quantum-state discrimination. Phys. Rev. A 2002, 66, 022112. [Google Scholar] [CrossRef] [Green Version]
- Fiurásek, J.; Dusek, M.; Filip, R. Universal measurement apparatus controlled by quantum software. Phys. Rev. Lett. 2002, 89, 190401. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, A.A.-B.; Eleuch, H.; Raymond-Ooi, C.-H. Non-locality Correlation in Two Driven Qubits Inside an Open Coherent Cavity: Trace Norm Distance and Maximum Bell Function. Sci. Rep. 2019, 9, 19632. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, A.; Eleuch, H. Quantum correlation control for two semiconductor microcavities connected by an optical fiber. Phys. Scr. 2017, 92, 065101. [Google Scholar] [CrossRef]
- Bruß, D. Optimal Eavesdropping in Quantum Cryptography with Six States. Phys. Rev. Lett. 1998, 81, 3018–3021. [Google Scholar] [CrossRef] [Green Version]
- Bennett, C.-H.; Brassard, G.; Mermin, N.-D. Quantum cryptography without Bell’s theorem. Phys. Rev. Lett. 1992, 68, 557. [Google Scholar] [CrossRef] [PubMed]
- Rusca, D.; Boaron, A.; Curty, M.; Martin, A.; Zbinden, H. Security proof for a simplified Bennett-Brassard 1984 quantum-key-distribution protocol. Phys. Rev. A 2018, 98, 052336. [Google Scholar] [CrossRef] [Green Version]
- Kalra, M.; Poonia, R.-C. Design a New Protocol and Compare with BB84 Protocol for Quantum Key Distribution. In Soft Computing for Problem Solving Advances in Intelligent Systems and Computing; Springer: Singapore, 2019. [Google Scholar]
- Serna, E.-H. Quantum Key Distribution from a Random Seed. arXiv 2013, arXiv:1311.1582v2. [Google Scholar]
- Chong, S.-K.; Hwang, T. Quantum key agreement protocol based on BB84. Opt. Commun. 2010, 283, 1192–1195. [Google Scholar] [CrossRef]
- Furrer, F.; Franz, T.; Berta, M.; Leverrier, A.; Scholz, V.; Tomamichel, M.; Werner, R. Erratum: Continuous variable quantum key distribution: Finite-key analysis of composable security against coherent attacks. Phys. Rev. Lett. 2014, 112, 019902. [Google Scholar] [CrossRef]
- Bechmann-Pasquinucci, H.; Gisin, N. Incoherent and coherent eavesdropping in the 6-state protocol of quantum cryptography. Phys. Rev. A 1999, 59, 4238. [Google Scholar] [CrossRef] [Green Version]
- Pirandola, S.; Andersen, U.L.; Banchi, L.; Berta, M.; Bunandar, D.; Colbeck, R.; Englund, D.; Gehring, T.; Lupo, C.; Ottaviani, C.; et al. Advances in Quantum Cryptography. Adv. Opt. Photonics 2020, 12, 1012–1236. [Google Scholar] [CrossRef] [Green Version]
- Boyer, M.; Liss, R.; Mor, T. Security Against Collective Attacks of a Modified BB84 QKD Protocol with Information only in One Basis. In Proceedings of the 2nd International Conference on Complexity, Future Information Systems and Risk, Porto, Portugal, 24–26 April 2017; Volume 1, pp. 23–29. [Google Scholar]
- Nikolopoulos, G.M.; Khalique, A.; Alber, G. Provable entanglement and information cost for qubit-based quantum key-distribution protocols. Eur. Phys. J. D 2015, 37, 441–450. [Google Scholar] [CrossRef] [Green Version]
- Lo, H.; Ma, X.; Chen, K. Decoy State Quantum Key Distribution. Phys. Rev. Lett. 2005, 94, 230504. [Google Scholar] [CrossRef] [Green Version]
- Zhao, B.; Zha, X.; Chen, Z.; Shi, R.; Wang, D.; Peng, T.; Yan, L. Performance Analysis of Quantum Key Distribution Technology for Power Business. Appl. Sci. 2020, 10, 2906. [Google Scholar] [CrossRef]
- He, W.; Guha, S.; Shapiro, J.; Bash, B. Performance analysis of free-space quantum key distribution using multiple spatial modes. Opt. Express 2021, 29, 19305. [Google Scholar] [CrossRef] [PubMed]
- Lim, C.; Xu, F.; Pan, J.; Ekert, A. Security Analysis of Quantum Key Distribution with Small Block Length and Its Application to Quantum Space Communications. Phys. Rev. Lett. 2021, 126, 100501. [Google Scholar] [CrossRef] [PubMed]
- Gottesman, D.; Lo, H. Proof of security of quantum key distribution with two-way classical communications. IEEE Trans. Inf. Theory 2003, 49, 457–475. [Google Scholar] [CrossRef] [Green Version]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 181–182. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Wen, Q.; Gao, F.; Zhu, F. Robust variations of the Bennett-Brassard 1984 protocol against collective noise. Phys. Rev. A 2003, 80, 032321. [Google Scholar] [CrossRef]
- Shu, H. Asymptotically Optimal Quantum Key Distribution Protocols. arXiv 2021, arXiv:2110.01973v3. [Google Scholar]
- Breuer, H.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Eleuch, H.; Rotter, I. Nearby states in non-Hermitian quantum systems I: Two states. Eur. Phys. J. D 2015, 69, 229. [Google Scholar] [CrossRef] [Green Version]
- Scheel, S.; Pachos, J.; Hinds, E.; Knight, P. Quantum Gates and Decoherence. In Quantum Coherence; Springer: Singapore, 2006. [Google Scholar]
- Ash Saki, A.; Alam, M.; Ghosh, S. Study of Decoherence in Quantum Computers: A Circuit-Design Perspective. arXiv 2019, arXiv:1904.04323v1. [Google Scholar]
- Kjaergaard, M.; Schwartz, M.; Braumüller, J.; Krantz, P.; Wang, J.; Gustavsson, S.; Oliver, W. Physics Superconducting Qubits: Current State of Play. Annu. Rev. Condens. Matter 2019, 11, 95. [Google Scholar]
- Diamanti, E.; Lo, H.; Qi, B.; Yuan, Z. Practical challenges in quantum key distribution. npj Quantum Inf. 2016, 2, 16025. [Google Scholar] [CrossRef] [Green Version]
- Courtois, N.; Finiaz, M.; Sendrier, N. How to achieve a McEliece-based Digital Signature Scheme. In Advances in Cryptology—ASIACRYPT 2001. Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2248, pp. 157–174. [Google Scholar]
- Bunandar, D.; Govia, L.; Krovi, H.; Englund, D. Numerical finite-key analysis of quantum key distribution. npj Quantum Inf. 2020, 6, 104. [Google Scholar] [CrossRef]

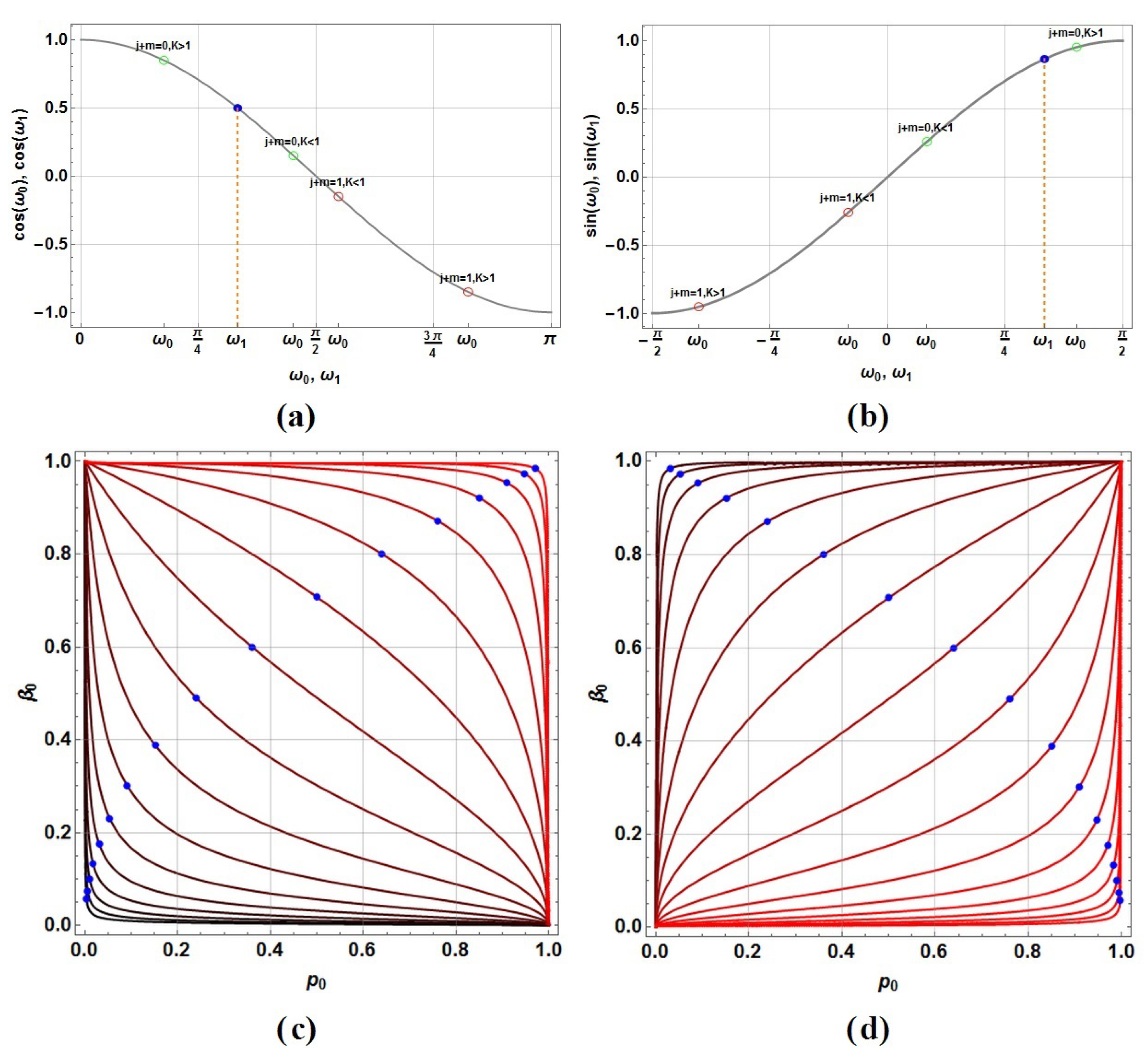
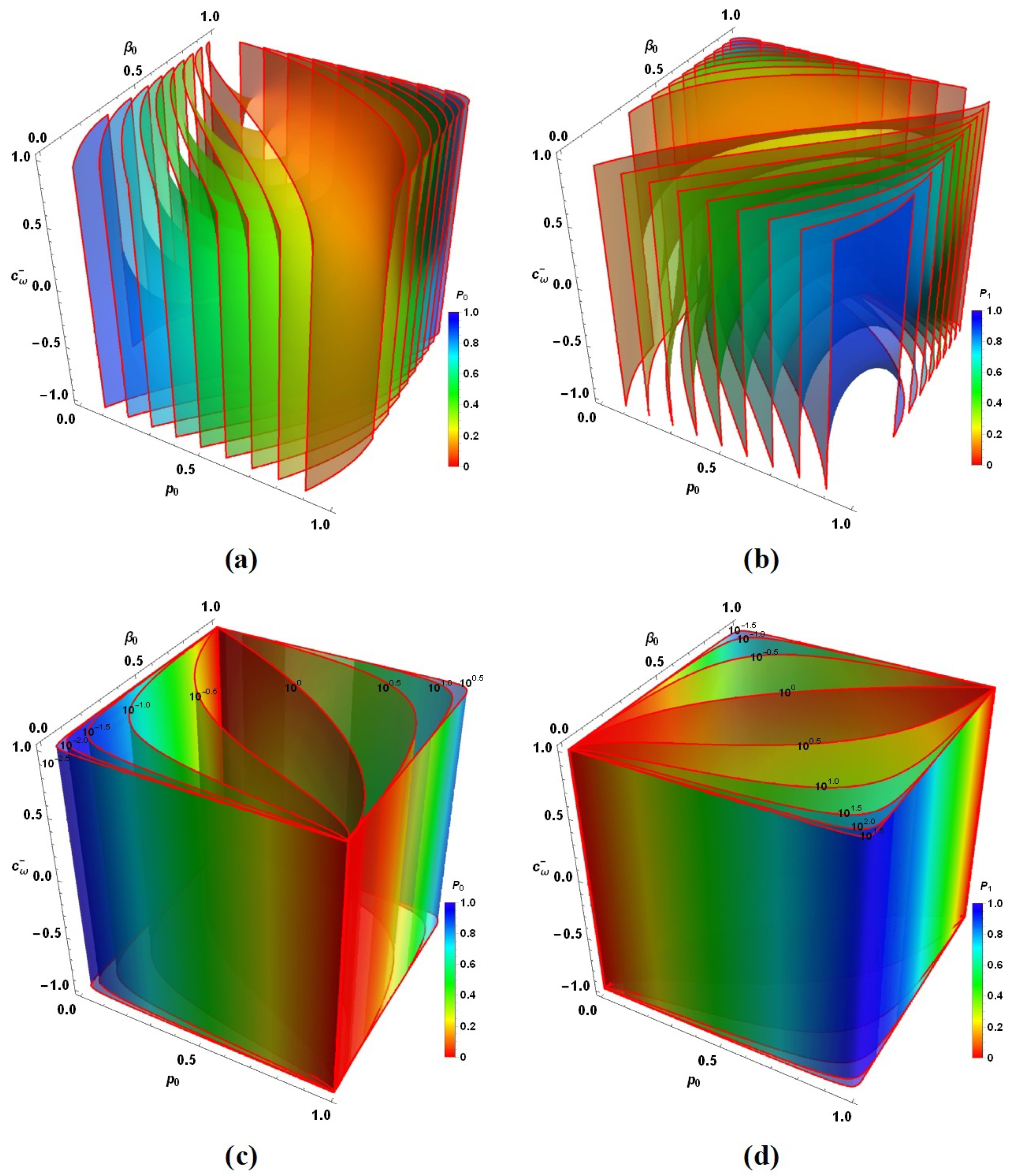
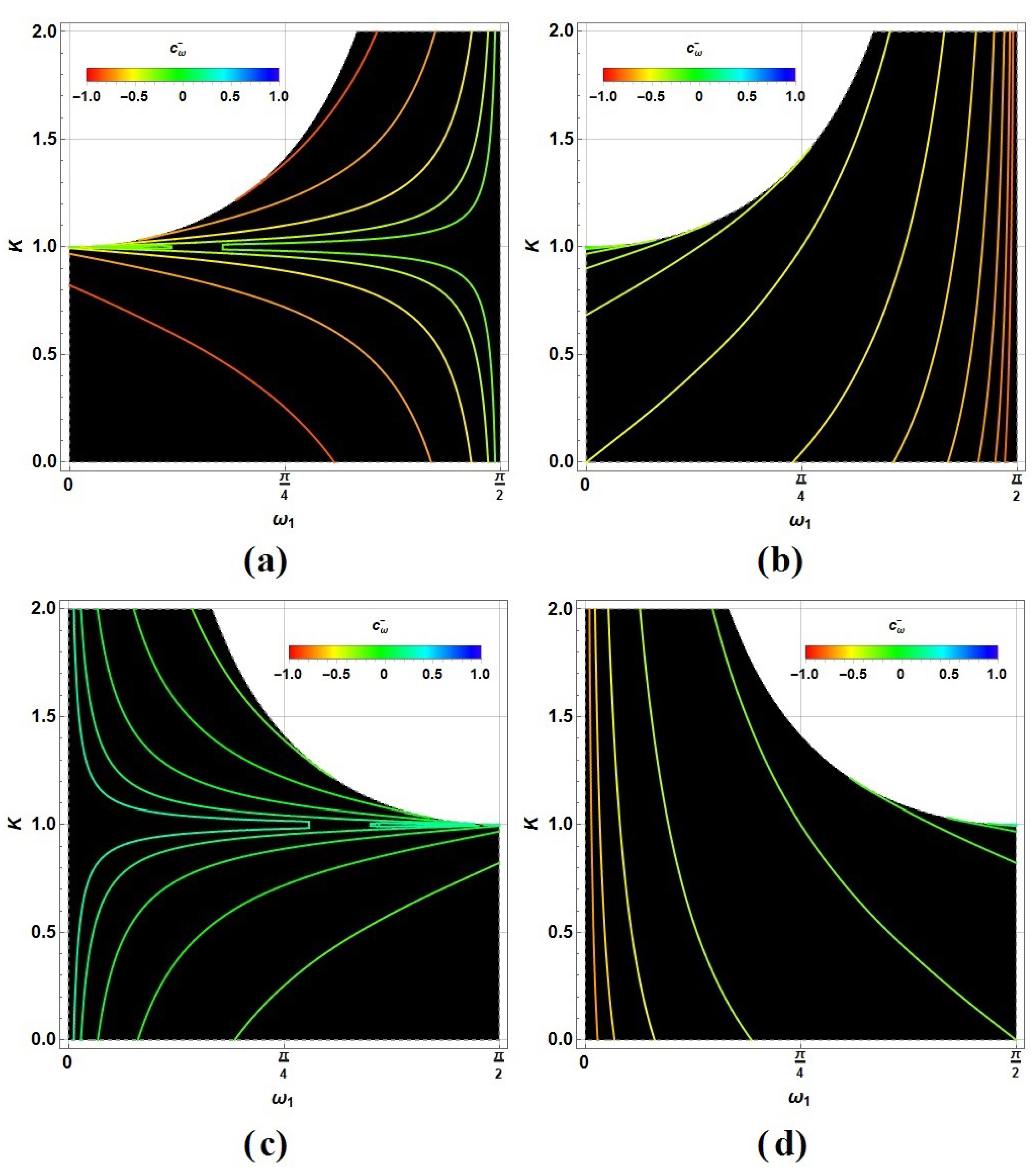
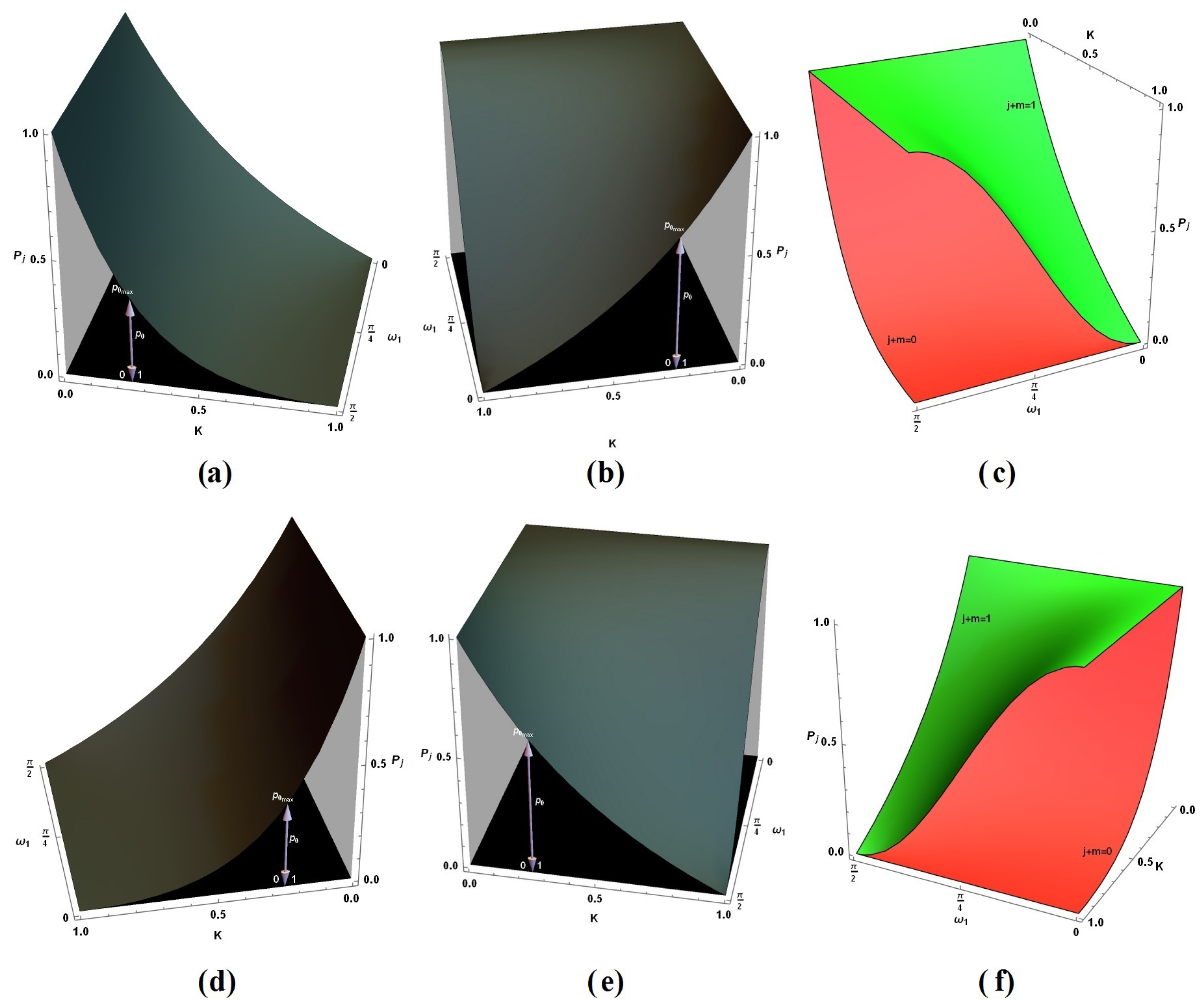

| Symbol | Process | Description |
|---|---|---|
| DT | Original qubit state to be teleported | |
| DT | Control state to manage the final receiver in double teleportation | |
| DT | Superposition probabilities for each receiver in double teleportation | |
| DT | Entangled resources for teleportation in the for of Bell states | |
| DT | Controlled and Hadamard gates to manage the double teleportation | |
| DT | Initial state and pre-measurement state during the double teleportation process | |
| DT | Post-measurement and corrected states at the end of double teleportation process | |
| PP | Local processing operators on the qubit k in possession of party i | |
| PP | Parametric continuous characterization of each local processing | |
| PP | Controlled operation to apply local processing on each receiver | |
| PP | Output state from the each local processing on | |
| PP | Local processing operators on the qubit k in possession of party i | |
| TC | Parameters for the basis measurement of the control state | |
| TC | Success probability for each outcome of the control measurement | |
| QKD | Key parameters in the QKD process | |
| P | QKD | Absolute rate of the success eavesdropper without reconciliation |
| QKD | Relative rate of the success eavesdropper with reconciliation | |
| QKD | Absolute and relative QBER |
| Setup | Selection | Measurement | Sharing | Decision | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Alice | Alice | Alice | Bob | Alice | Bob | Alice/Bob | ||||||
| j | m | A/R | key | |||||||||
| 0 | H | 0 | 1 | 0 | H | H | H | ✓ | 0 | |||
| D | 1 | 0 | D | × | D | ✗ | - | |||||
| 0 | H | 1 | 0 | D | H | D | ✗ | - | ||||
| D | 1 | 0 | D | D | D | ✓ | 1 | |||||
| D | 1 | 0 | 0 | H | × | H | ✗ | - | ||||
| 0 | H | 0 | 1 | 0 | H | H | H | ✓ | 1 | |||
| D | 0 | 1 | D | D | D | ✓ | 0 | |||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| Basis Selection and Outcomes Classes | Alice | Eve | Bob | P | |||
|---|---|---|---|---|---|---|---|
| Basis | Out | Basis | Out | Basis | Out | ||
| 1: Basis selections completely meets | |||||||
| 2: Eve basis fails but Bob output not | |||||||
| 3: Bob basis meets but output fails | |||||||
| 4: Bob basis and output fail | |||||||
| Process & Qubits | 1 | 2 | 3 | Total | ||||
|---|---|---|---|---|---|---|---|---|
| X | Z | Hadamard | Toffoli | |||||
| DT | 4 | 2 | 1 | 0 | 0 | 0 | 2 | 9 |
| PP | 4 | 1 | 1 | 1 | 1 | 10 | 1 | 19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cardoso-Isidoro, C.; Delgado, F. Shared Quantum Key Distribution Based on Asymmetric Double Quantum Teleportation. Symmetry 2022, 14, 713. https://doi.org/10.3390/sym14040713
Cardoso-Isidoro C, Delgado F. Shared Quantum Key Distribution Based on Asymmetric Double Quantum Teleportation. Symmetry. 2022; 14(4):713. https://doi.org/10.3390/sym14040713
Chicago/Turabian StyleCardoso-Isidoro, Carlos, and Francisco Delgado. 2022. "Shared Quantum Key Distribution Based on Asymmetric Double Quantum Teleportation" Symmetry 14, no. 4: 713. https://doi.org/10.3390/sym14040713







