Lie-Group Shooting/Boundary Shape Function Methods for Solving Nonlinear Boundary Value Problems

Abstract

In the numerical integration of the second-order nonlinear boundary value problem (BVP), the right boundary condition plays the role as a target equation, which is solved either by the half-interval method (HIM) or a new derivative-free Newton method (DFNM) to be presented in the paper. With the help of a boundary shape function, we can transform the BVP to an initial value problem (IVP) for a new variable. The terminal value of the new variable is expressed as a function of the missing initial value of the original variable, which is determined through a few integrations of the IVP to match the target equation. In the new boundary shape function method (NBSFM), we solve the target equation to obtain a highly accurate missing initial value, and then compute a precise solution. The DFNM can find more accurate left boundary values, whose performance is superior than HIM. Apparently, DFNM converges faster than HIM. Then, we modify the Lie-group shooting method and combine it to the BSFM for solving the nonlinear BVP with Robin boundary conditions. Numerical examples are examined, which assure that the proposed methods together with DFNM can successfully solve the nonlinear BVPs with high accuracy.

1. Introduction

There are numerous numerical methods to tackle the boundary value problems (BVPs) in [1,2,3,4,5,6,7,8,9,10]. The present paper will derive a very powerful numerical solver with a derivative-free Newton method to solve the target equation in terms of the Robin type boundary conditions. Recently, Liu and Li [11] designed the bases of solution by transforming the nonhomogeneous Robin boundary conditions to the homogeneous ones by using the homogenization function technique, and then seeking the polynomial bases to satisfy the homogeneous Robin boundary conditions. They introduced the energetic Robin boundary functions as the bases, whose processes are quite complicated.

For the first-order system of ordinary differential equations (ODEs), the group-preserving scheme (GPS) has been developed by Liu [12] for the solutions of initial value problems (IVPs). The main difference between the GPS and the traditional numerical integration methods is that those schemes are all formulated directly in the usual Euclidean space, while the GPS is formulated in the Minkowski space. A major advantage of the formulation of ODEs in the Minkowski space is that we can develop group preserving schemes to retain the inherent Lie-symmetry of the augmented ODEs in the Minkowski space. Recently, Xu and Wu [13] combined the GPS with a midpoint technique to improve the accuracy and convergence property. Liu [14] extended and modified the GPS for solving second-order BVPs, based on the Lie-symmetry of the proper orthochronous Lorentz group, who introduced one-step GPS by utilizing the closure property of the Lie-group and labelled it as the Lie-group shooting method (LGSM). Moreover, Liu [15] developed the LGSM for solving nonlinear singularly perturbed boundary value problems. Recently, Hajiketabi and Abbasbandy [16] developed a simple, efficient and accurate Lie-group shooting method for solving nonlinear boundary value problems.

The paper is outlined as follows. In Section 2, the boundary shape function for automatically satisfying the Robin boundary conditions is introduced, where two cases are considered. In Section 3, we transform the BVP to a new IVP for the new variable $y\left(x\right)$, with its terminal value $y\left(1\right)$ being expressed as a function of the missing initial value of the original variable $u\left(x\right)$. This new version is a modification of the original boundary shape function method (BSFM). In Section 4, we develop an iterative algorithm relying on the new boundary shape function method (NBSFM), and the half-interval method (HIM) is used to solve the target equation. In Section 5, the Lie-group shooting method is combined with the BSFM for developing a new iterative algorithm of LGSBSFM. Here, a main contribution is developing a derivative-free Newton method to solve the target equation. In Section 6, we test numerical examples by using these algorithms. We introduce the general Robin boundary value problems in Section 7, the corresponding NBSFM is derived, and two numerical examples are given. Finally, Section 8 makes the conclusions.

2. Boundary Shape Function

Consider the boundary value problem (BVP):

$$\begin{array}{ccc}\hfill & & u^{″}\left(x\right)=F(x,u\left(x\right),u^{\prime }\left(x\right)),0<x<1,\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill & & a_{1}u\left(0\right)+b_1{u}^{\prime }\left(0\right)=c_1,\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill & & u\left(1\right)=c_2\mathrm{or}{u}^{\prime }\left(1\right)=c_2.\hfill \end{array}$$

(3)

A more general BVP with two-side Robin boundary conditions will be considered in Section 7. We first discuss the right boundary condition with $u\left(1\right)=c_2$. For $u^{\prime }\left(1\right)=c_2$, the processes are similar.

For Equation (2), we consider two cases: (a) $a_1-b_1\ne 0$ and (b) $a_1-b_1=0$. Suppose that

$$\begin{array}{ccc}\hfill & & a_1{s}_1\left(0\right)+b_1{s}_1^{\prime }\left(0\right)=1,s_1\left(1\right)=0,\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill & & a_1{s}_2\left(0\right)+b_1{s}_2^{\prime }\left(0\right)=0,s_2\left(1\right)=1.\hfill \end{array}$$

(5)

For cases (a) and (b), we have, respectively,

$$\begin{array}{ccc}\hfill & & \mathrm{Case}\left(\mathrm{a}\right):s_1\left(x\right)=\frac{1-x}{a_1-b_1},s_2\left(x\right)=\frac{a_{1}x-b_1}{a_1-b_1},\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill & & \mathrm{Case}\left(\mathrm{b}\right):s_1\left(x\right)=\frac{1}{a_1}-\frac{x^2}{a_1},s_2\left(x\right)=1-x+x^2.\hfill \end{array}$$

(7)

A translation function $G\left(x\right)$ in terms of $s_1\left(x\right)$ and $s_2\left(x\right)$ reads as

$$G\left(x\right):=s_1\left(x\right)[a_{1}y\left(0\right)+b_1{y}^{\prime }\left(0\right)-c_1]+s_2\left(x\right)[y\left(1\right)-c_2],$$

(8)

where $y\left(x\right)$ is a new variable.

Theorem 1.

The boundary shape function $u\left(x\right)$ is given by

$$u\left(x\right)=y\left(x\right)-G\left(x\right),$$

(9)

which satisfies

$$a_{1}u\left(0\right)+b_1{u}^{\prime }\left(0\right)=c_1,u\left(1\right)=c_2.$$

(10)

Proof. 

Inserting $x=0$ into Equation (9) and using Equation (8),

$$u\left(0\right)=y\left(0\right)-s_1\left(0\right)[a_{1}y\left(0\right)+b_1{y}^{\prime }\left(0\right)-c_1]-s_2\left(0\right)[y\left(1\right)-c_2].$$

(11)

Taking the differential of Equation (9), inserting $x=0$ and using Equation (8), we have

$$u^{\prime }\left(0\right)=y^{\prime }\left(0\right)-s_1^{\prime }\left(0\right)[a_{1}y\left(0\right)+b_1{y}^{\prime }\left(0\right)-c_1]-s_2^{\prime }\left(0\right)[y\left(1\right)-c_2].$$

(12)

A combination of Equations (11) and (12) leads to

$$\begin{array}{ccc}& & a_{1}u\left(0\right)+b_1{u}^{\prime }\left(0\right)=a_{1}y\left(0\right)+a_1{s}_1\left(0\right)[c_1-a_{1}y\left(0\right)-b_1{y}^{\prime }\left(0\right)]+a_1{s}_2\left(0\right)[c_2-y\left(1\right)]\hfill \\ & & +b_1{y}^{\prime }\left(0\right)+b_1{s}_1^{\prime }\left(0\right)[c_1-a_{1}y\left(0\right)-b_1{y}^{\prime }\left(0\right)]+b_1{s}_2^{\prime }\left(0\right)[c_2-y\left(1\right)]\hfill \\ & & =a_{1}y\left(0\right)+b_1{y}^{\prime }\left(0\right)+[a_1{s}_1\left(0\right)+b_1{s}_1^{\prime }\left(0\right)][c_1-a_{1}y\left(0\right)-b_1{y}^{\prime }\left(0\right)]+[a_1{s}_2\left(0\right)+b_1{s}_2^{\prime }\left(0\right)][c_2-y\left(1\right)],\hfill \end{array}$$

by Equations (4) and (5), which becomes

$$a_{1}u\left(0\right)+b_1{u}^{\prime }\left(0\right)=a_{1}y\left(0\right)+b_1{y}^{\prime }\left(0\right)+c_1-a_{1}y\left(0\right)-b_1{y}^{\prime }\left(0\right)=c_1.$$

(13)

Inserting $x=1$ into Equation (9) and using Equation (8),

$$u\left(1\right)=y\left(1\right)+s_1\left(1\right)[c_1-a_{1}y\left(0\right)-b_1{y}^{\prime }\left(0\right)]+s_2\left(1\right)[c_2-y\left(1\right)],$$

(14)

which, due to Equations (4) and (5), becomes

$$u\left(1\right)=y\left(1\right)+c_2-y\left(1\right)=c_2.$$

(15)

The proof of Equation (10) is ended. □

3. The Initial Value Problem

For Equation (1), if very accurate initial conditions $u\left(0\right)$ and $u^{\prime }\left(0\right)$ are determined, one can obtain a very precise solution of $u\left(x\right)$ by using a higher order numerical integrator to integrate the ODE. Therefore, it is an important topic to precisely determine $B_0:=u\left(0\right)$ and $A_0:=u^{\prime }\left(0\right)$ by an efficient numerical method. Based on Theorem 1, we can develop an iterative algorithm to solve Equation (1) subjected to Equations (2) and (3). Inserting Equation (9) for $u\left(x\right)$ into Equation (1), we can achieve

$$y^{″}\left(x\right)=H(x,y\left(x\right),y^{\prime }\left(x\right);y\left(1\right)):=G^{″}\left(x\right)+F(x,y\left(x\right)-G\left(x\right),y^{\prime }\left(x\right)-G^{\prime }\left(x\right)),$$

(16)

where $G\left(x\right)$ involves $y\left(1\right)$ as unknown constant in Equation (8), but $y\left(0\right)$ and $y^{\prime }\left(0\right)$ are given initial values.

In order to calculate the unknown value $y\left(1\right)$ in Equation (16) and achieve a deeper analysis, we carry out the following works. If $a_1\ne 0$, we assume that

$$u^{\prime }\left(0\right)=A_0$$

(17)

is a constant to be determined and $u\left(0\right)$ is given by $u\left(0\right)=(c_1-b_1{A}_0)/a_1$. Alternatively, if $b_1\ne 0$, we assume that

$$u\left(0\right)=B_0$$

(18)

is a constant to be determined and $u^{\prime }\left(0\right)$ is given by $u^{\prime }\left(0\right)=(c_1-a_1{B}_0)/b_1$.

Under the condition $a_1\ne 0$ for case (a), it follows from Equations (6), (9) and (17) that

$$y\left(1\right)=y\left(0\right)+y^{\prime }\left(0\right)+c_2-\frac{c_1}{a_1}+\left(\frac{b_1}{a_1}-1\right)A_0.$$

(19)

For case (b), it follows from Equations (7), (9) and (17), that

$$y\left(1\right)=A_0+c_2-y^{\prime }\left(0\right).$$

(20)

On the other hand, under the condition $b_1\ne 0$ and for case (a), it follows from Equations (6), (9) and (18) that

$$y\left(1\right)=y\left(0\right)+y^{\prime }\left(0\right)+c_2-\frac{c_1}{b_1}+\left(\frac{a_1}{b_1}-1\right)B_0.$$

(21)

For case (b), it follows from Equations (7), (9) and (18) that

$$y\left(1\right)=\frac{c_1}{a_1}+c_2-B_0-y^{\prime }\left(0\right).$$

(22)

The above equations reveal that $y\left(1\right)$ can be computed from $A_0$ or $B_0$. Inserting these $y\left(1\right)$ into Equation (16), we can obtain a definite ODE in terms of $A_0$ or $B_0$:

$$\begin{array}{ccc}\hfill & & y^{″}\left(x\right)=H_1(x,y\left(x\right),y^{\prime }\left(x\right);A_0),\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill & & y^{″}\left(x\right)=H_2(x,y\left(x\right),y^{\prime }\left(x\right);B_0),\hfill \end{array}$$

(24)

which, upon giving $y\left(0\right)$ and $y^{\prime }\left(0\right)$, are initial value problems (IVPs) endowed with one unknown parameter $A_0$ or $B_0$ to be determined.

Notice that in the original BSFM developed in [17], $y\left(1\right)$ in Equation (8) is determined by an iterative method, which repeatedly integrates Equation (16) to obtain the new value of $y\left(1\right)$ until convergence. To improve the slower convergence and slightly lower accuracy of the original BSFM, we recast Equation (16) to Equation (23) or (24), which may be called a new boundary shape function method (NBSFM). Powerful methods will be developed below to determine $A_0$ or $B_0$ by solving the target equation. Deng et al. [18] have extended the BSFM to solve the nonlinear BVP under nonlinear boundary conditions.

4. The Iterative Algorithm of NBSFM

Because the initial values $y\left(0\right)=y^{\prime }\left(0\right)=0$ are given, we can integrate Equation (23) or (24) from $x=0$ to $x=1$, with a given $A_0$ or $B_0$ to obtain $y\left(1\right)$ and $y^{\prime }\left(1\right)$; hence, inserting $x=1$ into Equation (9) and using Equations (8) and (3) yields

$$\begin{array}{ccc}\hfill & & u(1;A_0)=y\left(1\right)-s_1\left(1\right)[a_{1}y\left(0\right)+b_1{y}^{\prime }\left(0\right)-c_1]-s_2\left(1\right)[y\left(1\right)-c_2]=c_2,\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill & & u^{\prime }(1;B_0)=y^{\prime }\left(1\right)-s_1^{\prime }\left(1\right)[a_{1}y\left(0\right)+b_1{y}^{\prime }\left(0\right)-c_1]-s_2^{\prime }\left(1\right)[y\left(1\right)-c_2]=c_2,\hfill \end{array}$$

(26)

which can determine $A_0$ or $B_0$ by solving a scalar equation, where $y\left(1\right)$ and $y^{\prime }\left(1\right)$ are obtained by integrating Equation (23) or (24).

The curve of $u(1;A_0)$ vs. $A_0$ or $u^{\prime }(1;B_0)$ vs. $B_0$ is a curve of a target function. We can adjust the value of $A_0$ or $B_0$ until $u(1;A_0)$ or $u^{\prime }(1;B_0)$ satisfies $|u(1;A_0)-c_2|<\epsilon$ or $|u^{\prime }(1;B_0)-c_2|<\epsilon$, where $\epsilon$ is a given tolerance of the error to mismatch the right-end boundary condition (3), which is an implicit equation to determine $A_0$ or $B_0$. We can apply the half-interval method to solve Equation (25) or (26), where we repeatedly integrate Equation (23) or (24) with N steps from $x=0$ to $x=1$ to obtain $y\left(1\right)$ and $y^{\prime }\left(1\right)$, and then $u(1;A_0)$ by Equation (25) or $u^{\prime }(1;B_0)$ by Equation (26).

The half-interval method (HIM) is described as follows. We can decide two initial guesses $A_0$ and A, such that $u(1;A_0)u(1;A)<0$. Then, we repeat the following process until convergence:

$$\begin{array}{ccc}& & u_0=u(1;A_0),u_A=u(1;A)\hfill \\ & & 1A_1=(A_0+A)/2\hfill \\ & & u_1=u(1;A_1)\hfill \\ & & \mathrm{If}{u}_0{u}_1\le 0\mathrm{Then}\hfill \\ & & A=A_1\hfill \\ & & u_A=u(1;A)\hfill \\ & & \mathrm{Else}\hfill \\ & & A_0=A_1\hfill \\ & & u_0=u(1;A_0)\hfill \\ & & \mathrm{Endif}\hfill \\ & & \mathrm{If}|u_0-c_2|<\epsilon \mathrm{And}|u_A-c_2|<\epsilon \mathrm{Then}\hfill \\ & & A=(A_0+A)/2\hfill \\ & & \mathrm{Return}\hfill \\ & & \mathrm{Else}\hfill \\ & & \mathrm{Go}\mathrm{To}1\hfill \\ & & \mathrm{Endif}\hfill \end{array}$$

In the half-interval method twice integrations to obtain the right-end values of u at each iteration are required.

The processes to solve $u\left(x\right)$ are summarized as follows:

(i)

Give $y\left(0\right)=y^{\prime }\left(0\right)=0$, the initial guesses of $A_0$ and A, $ϵ$, and $\Delta x=1/N$.

(ii)

Integrate Equation (23) to $x=1$ to obtain $y\left(1\right)$ and apply the HIM to solve Equation (25) until $|u\left(1\right)-c_2|<ϵ$.

The process to determine $B_0$ can be done similarly, by using Equations (24) and (26).

5. Lie-Group Shooting BSFM

5.1. A Combination of LGSM and BSFM

The original Lie-group shooting method developed by Liu [14] was applicable to the nonlinear BVP with simple Dirichlet or Neumann boundary conditions. For solving Equations (1)–(3), we can combine the Lie-group shooting method and the BSFM as a new Lie-group shooting boundary shape function method (LGSBSFM), which is used to solve $y\left(x\right)$ in Equation (16). Here, with case (a) and $a_1\ne 0$ as a demonstrative case, we let

$$\begin{array}{ccc}\hfill & & y_1^{\prime }\left(x\right)=y_2\left(x\right),\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill & & y_2^{\prime }\left(x\right)=H(x,y_1,y_2),\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill & & y_1\left(0\right)=c,y_1\left(1\right)=c,\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill & & y_2\left(0\right)=A,y_2\left(1\right)=B,\hfill \end{array}$$

(30)

where A and B are two unknown constants, and c is a given constant.

Based on the Lie-group shooting method [14], without going into the details, we can derive A for the case $A>0$:

$$\begin{array}{ccc}\hfill & & g_1\left(r\right):=exp\left(-\frac{\widehat{f}}{c}\right),\hfill \end{array}$$

(31)

$$\begin{array}{ccc}\hfill & & D_1\left(r\right):=g_1+{(1-g_1)}^2(r-r^2)>0,\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill & & A\left(r\right)=\sqrt{\frac{{(r-1)}^2{(1-g_1^2)}^2{c}^2}{4D_1{g}_1}},\hfill \end{array}$$

(33)

where

$$\begin{array}{ccc}\hfill & & \widehat{f}=s_1^{″}\left(r\right)[a_{1}c+a_{2}A-c_1]+s_2^{″}\left(r\right)[c-c_2]\hfill \\ & & +H(r,c-s_1\left(r\right)[a_{1}c+a_{2}A-c_1]-s_2\left(r\right)[c-c_2],-s_1^{\prime }\left(r\right)[a_{1}c+a_{2}A-c_1]-s_2^{\prime }\left(r\right)[c-c_2]),\hfill \end{array}$$

(34)

and for the case $A<0$:

$$\begin{array}{ccc}\hfill & & g_2\left(r\right):=exp\left(\frac{\widehat{f}}{c}\right),\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill & & D_2\left(r\right):=g_2+{(1-g_2)}^2(r-r^2)>0,\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\hfill & & A\left(r\right)=-\sqrt{\frac{{(r-1)}^2{(1-g_2^2)}^2{c}^2}{4D_2{g}_2}}.\hfill \end{array}$$

(37)

For a trial $r\in [0,1]$, we can iteratively solve A from Equations (33), (34), and (37). The advantage is that we can determine the slope of the new variable $y\left(x\right)$ in terms of a factor r within a unit interval, which, however, has a drawback of the Lie-group shooting method to iteratively solve A for each r. As a modification, we directly determine A by integrating Equations (27)–(30) to obtain the right-end value $y(1,A)$, and then compare it to the desired one $y\left(1\right)=c$. If $\left|y\right(1,A)-c|$ is smaller than a given error tolerance $ϵ$, then the process to find A is finished. Similarly, the iteration process can be performed by HIM to find a suitable value of A by starting from two given values $A_0$ and $A_2$ with $[y(1,A_0)-c][y(1,A_2)-c]<0$.

When $y\left(x\right)$ is determined, we can obtain $u\left(x\right)$ by $u\left(x\right)=y\left(x\right)-G\left(x\right)$. On the other hand, according to Equations (19), (29), and (30), we can derive

$$A_0=\frac{a_{1}A+a_1{c}_2-c_1}{a_1-b_1},$$

(38)

wherein c is eliminated and $y^{\prime }\left(0\right)=A$ is used. The initial conditions for $u\left(x\right)$ are available as follows:

$$u\left(0\right)=\frac{c_1-b_1{A}_0}{a_1}=\frac{c_1-b_1{c}_2-b_{1}A}{a_1-b_1},u^{\prime }\left(0\right)=A_0=\frac{a_{1}A+a_1{c}_2-c_1}{a_1-b_1}.$$

(39)

In addition, then, we can integrate Equation (1) using the derived initial conditions $u\left(0\right)$ and $u^{\prime }\left(0\right)$ to obtain $u\left(x\right)$.

5.2. A Derivative-Free Newton Method

We can counter the number of iterations for the half-interval method (HIM), which needs 50 iterations for reducing an initial error 1 to a final error with $1/2^{50}=8.882\times {10}^{-16}$. If the error tolerance is $ϵ={10}^{-15}$ to satisfy the right boundary condition, the HIM will spend $50\times 2N$ steps in the numerical integrations of the ODE to obtain the right-end values. To reduce the computational burden, a derivative-free Newton method (DFNM) for solving a scalar equation $f\left(x\right)=0$ is motivated by the Newton iterative method:

$$x_{n+1}=x_n-\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},n=0,1,\dots .$$

(40)

Unfortunately, the derivative term $f^{\prime }\left(x_n\right)$ hinders the use of the Newton method in LGSBSFM, since the scalar target equation $y(1,A)-c=0$ is an implicit function of A.

Suppose that $x^{*}$ is a simple root with $f\left(x^{*}\right)=0$ and $f^{\prime }\left(x^{*}\right)\ne 0$. In order to get rid of the derivative term $f^{\prime }\left(x_n\right)$ in Equation (40), we consider

$$f^{\prime }\left(x_n\right)=f^{\prime }\left(x^{*}\right)+f^{″}\left(x^{*}\right)(x_n-x^{*})+\frac{1}{2}{f}^{‴}\left(x^{*}\right){(x_n-x^{*})}^2+\cdots .$$

(41)

Neglecting the higher-order terms and inserting it into Equation (40), we have

$$x_{n+1}=x_n-\frac{f\left(x_n\right)}{f^{\prime }\left(x^{*}\right)+f^{″}\left(x^{*}\right)(x_n-x^{*})}.$$

(42)

On the other hand, we have

$$f\left(x_n\right)=f^{\prime }\left(x^{*}\right)(x_n-x^{*})+\frac{1}{2}{f}^{″}\left(x^{*}\right){(x_n-x^{*})}^2+\cdots .$$

(43)

Neglecting the higher-order terms and replacing $x_n-x^{*}$ in Equation (42) by $f\left(x_n\right)/f^{\prime }\left(x^{*}\right)$, we can derive a derivative-free Newton method (DFNM):

$$x_{n+1}=x_n-\frac{f\left(x_n\right)}{a+bf\left(x_n\right)},$$

(44)

where

$$a=f^{\prime }\left(x^{*}\right),b=\frac{f^{″}\left(x^{*}\right)}{f^{\prime }\left(x^{*}\right)}.$$

(45)

Next, we turn our attention to the determination of a and b in Equation (45), whose values will influence the convergence speed. Like the half-interval method, the first step is choosing two initial guesses $x_0$ and $x_2$ such that $f\left(x_0\right)f\left(x_2\right)<0$ to render $x^{*}\in (x_0,x_2)$. Then, we take $x_1=(x_0+x_2)/2$. As the approximations of a and b in Equation (45), we can evaluate them by using the technique of finite difference:

$$a=\frac{f\left(x_2\right)-f\left(x_0\right)}{x_2-x_0},b=\frac{1}{a}\frac{f\left(x_2\right)-2f\left(x_1\right)+f\left(x_0\right)}{{(x_1-x_0)}^2}=\frac{4f\left(x_2\right)-8f\left(x_1\right)+4f\left(x_0\right)}{(x_2-x_0)[f\left(x_2\right)-f\left(x_0\right)]}.$$

(46)

In summary, the procedures of the DFNM are given as follows:

(i)

Give the initial guesses of $x_0$ and $x_2$ to render $f\left(x_0\right)f\left(x_2\right)<0$.

(ii)

Compute a and b by Equation (46).

(iii)

For n = 0,1,…, doing

$$x_{n+1}=x_n-\frac{f\left(x_n\right)}{a+bf\left(x_n\right)},\mathrm{until}\left|f\left(x_n\right)\right|<ϵ.$$

The LGSBSFM together with the DFNM for solving $u\left(x\right)$ in Equations (1)–(3) is summarized as follows:

(i)

Give $y\left(0\right)=c$, the initial guesses of $A_0$ and $A_2$ to render $[y(1,A_0)-c][y(1,A_2)-c]<0$, and give $ϵ$, and $\Delta x=1/N$.

(ii)

Compute $A_1=(A_0+A_2)/2$, $y(1,A_1)$, and a and b by

$$a=\frac{y(1,A_2)-y(1,A_0)}{A_2-A_0},b=\frac{1}{a}\frac{y(1,A_2)-2y(1,A_1)+y(1,A_0)}{{(A_1-A_0)}^2}.$$

(iii)

Let $A=A^0$ and for n = 0,1,…, doing

$$A^{n+1}=A^n-\frac{y(1,A^n)-c}{a+b[y(1,A^n)-c]},$$

until $\left|y\right(1,A^n)-c|<ϵ$.

In each iteration, the integration of Equations (27)–(30) to obtain the right-end value $y(1,A^n)$ is required, which is saving more than twice the integrations at each iteration used in the HIM. For saving computational time, the DFNM is suggested to be used.

For solving a scalar equation $f\left(x\right)=0$, the numerically computed order of convergence (COC) is approximated by [19,20]

$$\mathrm{COC}:=\frac{ln|(x_{n+1}-r)/(x_n-r)|}{ln|(x_n-r)/(x_{n-1}-r)|},$$

(47)

where r is a solution of $f\left(x\right)=0$ and the sequence $x_n$ is generated from an iterative scheme. In the computation of COC, we store the values of $A^n$ where $n\le k_0-1$, and take $r=A^{k_0}$, with $k_0$ the number of iterations for the convergence.

6. Examples

To solve Equations (1)–(3), we have developed two iterative algorithms of the NBSFM and LGSBSFM, which can be combined with the HIM or DFNM to solve the target equation. Some examples are given below to explore the performance of these algorithms.

6.1. Example 1

The following BVP is given in [21]:

$$\begin{array}{ccc}\hfill & & u^{″}=\frac{3}{2}{u}^2,\hfill \end{array}$$

(48)

$$\begin{array}{ccc}\hfill & & u\left(0\right)=4,u\left(1\right)=1.\hfill \end{array}$$

(49)

An exact solution is

$$u\left(x\right)=\frac{4}{{(1+x)}^2}.$$

(50)

6.1.1. Case (a)

Instead of Equation (49), we consider a left Robin boundary condition:

$$2u\left(0\right)+u^{\prime }\left(0\right)=0,u\left(1\right)=1.$$

(51)

Due to $a_1=2$, $b_1=1$, and $a_1-b_1=1$, this is a case (a) problem in Section 2 and Section 3.

By using the conventional shooting method, we take

$$u\left(0\right)=-\frac{A_0}{2},u^{\prime }\left(0\right)=A_0,$$

(52)

where $A_0$ is an unknown constant to match the target equation $u\left(1\right)=1$. We can employ HIM to solve the scalar equation $u\left(1\right)-1=0$. Under $N=2000$ and $ϵ={10}^{-15}$, we find that the conventional shooting method does not converge within 1000 iterations, although the solution of $u\left(x\right)$ is accurate with the maximum error (ME) being $2.44\times {10}^{-13}$.

In the NBSFM with HIM, we take $s_1\left(x\right)=1-x$, $s_2\left(x\right)=2x-1$, and

$$y\left(1\right)=y\left(0\right)+y^{\prime }\left(0\right)+1-\frac{A_0}{2}.$$

(53)

Under the parameters $y\left(0\right)=y^{\prime }\left(0\right)=0$, $N=2000$, and $ϵ={10}^{-15}$, the NBSFM with HIM converges with 42 iterations with ME = $2.55\times {10}^{-13}$. The result is more accurate than that in [14]. If we raise $N=4000$, the ME is reduced to $2.31\times {10}^{-14}$, and it is with 48 iterations for convergence. If we employ the NBSFM with DFNM, it is convergent with 14 iterations to obtain the same results. Since only 14 iterations are required, the CPU time is short with 0.6 s. Although with the HIM the CPU time is 0.9 s, its number of iterations is 42. COC = 1.6122 obtained by DFNM reveals that the present method is convergent very fast.

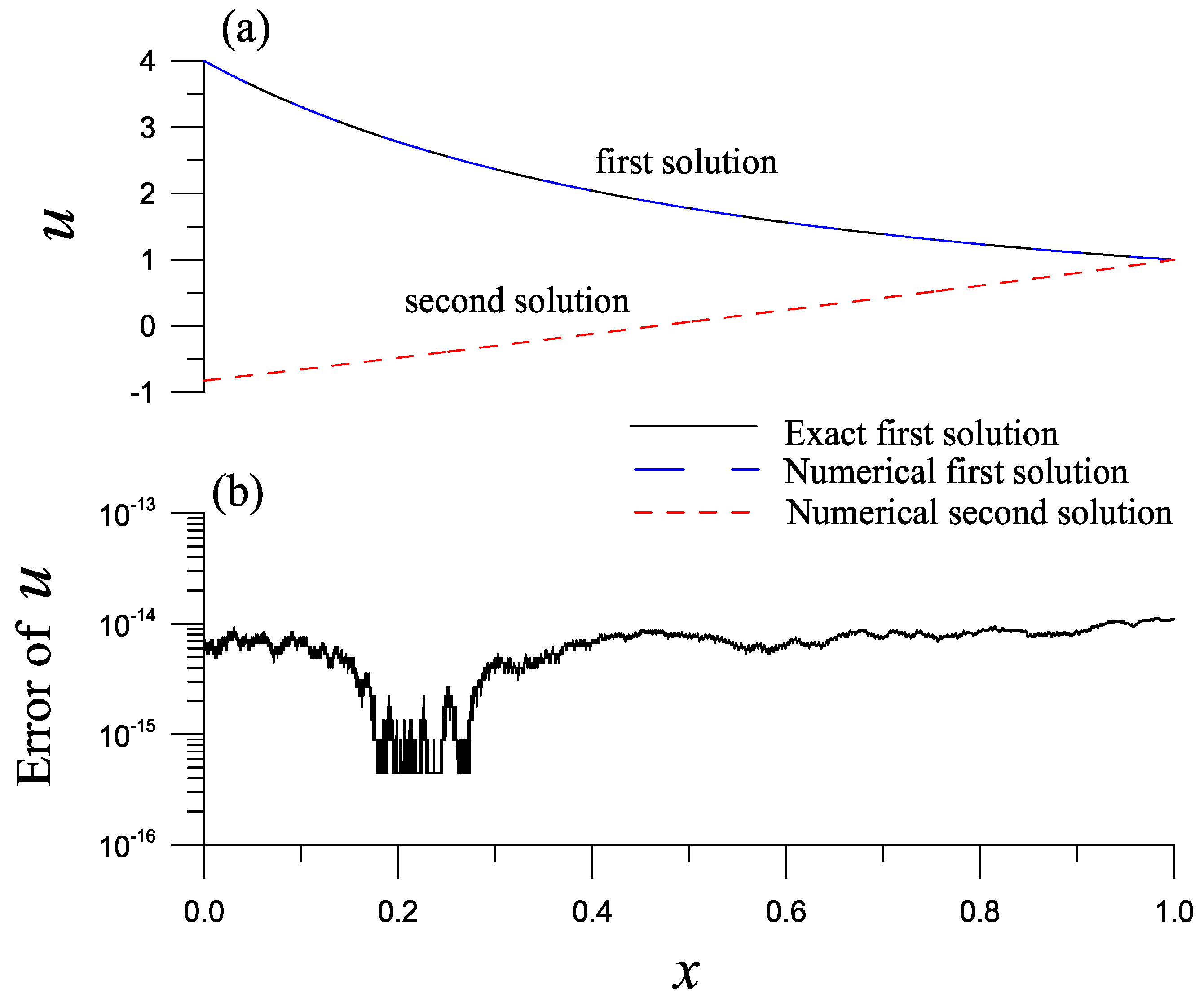
Next, we apply the LGSBSFM in Section 5 together with HIM to solve this problem with $c=0$, $A_0=-5.1$, $A_2=-4.95$, $N=5000$, and $ϵ={10}^{-15}$, which is convergent with 48 iterations, and the numerical solution coincides wth the exact one as shown in Figure 1a, whose errors are plotted in Figure 1b with ME = $1.13\times {10}^{-14}$. If we employ the LGSBSFM with DFNM, it is convergent with 10 iterations to obtain the same results with ME = $1.13\times {10}^{-14}$. The CPU time is very short with 0.46 s, and COC = 1.2546 is obtained, which indicates that the LGSBSFM with DFNM is effective.

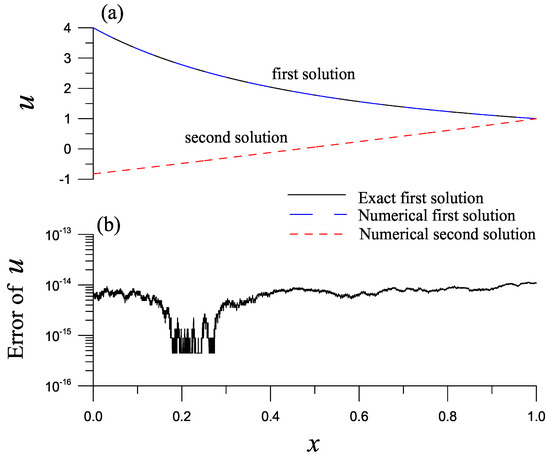
Figure 1. For example 1, (a) comparing the first and second solutions obtained by the Lie-group shooting BSFM and (b) displaying the errors of the first solution.

When we take $c=1$, $A_0=-0.8$, $A_2=0$, we obtain the second solution as shown in Figure 1a by dashed line. The LGSBSFM with HIM is convergent with 47 iterations and with the right boundary error being $1.44\times {10}^{-15}$. If we employ the LGSBSFM with DFNM, it is convergent with 16 iterations and with the right boundary error being $2.22\times {10}^{-16}$.

In Table 1, we tabulate the absolute errors and compare that obtained in [17]. The accuracy upon comparing to that computed in [17] using the boundary shape function method is raised about five orders.

Table 1. For example 1, comparing errors at different x.

x	Present	[17]
0.1	$1.07\times {10}^{-14}$	$5.99\times {10}^{-10}$
0.2	$1.33\times {10}^{-14}$	$1.06\times {10}^{-9}$
0.3	$9.33\times {10}^{-15}$	$1.51\times {10}^{-9}$
0.4	$1.07\times {10}^{-14}$	$2.04\times {10}^{-9}$
0.5	$8.22\times {10}^{-15}$	$2.68\times {10}^{-9}$
0.6	$8.88\times {10}^{-15}$	$3.46\times {10}^{-9}$
0.7	$9.33\times {10}^{-15}$	$4.41\times {10}^{-9}$
0.8	$9.55\times {10}^{-15}$	$5.56\times {10}^{-9}$
0.9	$1.22\times {10}^{-14}$	$6.91\times {10}^{-9}$

In Table 2, we tabulate the numerical value at different x and compare it to the exact one. The accuracy is up to ${10}^{-15}$ to ${10}^{-14}$.

Table 2. For example 1, list the numerical values and errors at different x.

x	0.1	0.3	0.7	0.9
Exact u	3.305785123967	2.366863905325	1.384083044983	1.108033240997
Numerical u	3.305785123967	2.366863905325	1.384083044983	1.108033240997
Error	$1.07\times {10}^{-14}$	$9.33\times {10}^{-15}$	$9.33\times {10}^{-15}$	$1.22\times {10}^{-14}$

6.1.2. Case (b)

Next, we consider other boundary conditions for Equation (48):

$$u\left(0\right)+u^{\prime }\left(0\right)=-4,u\left(1\right)=1.$$

(54)

Due to $a_1=1$, $b_1=1$, and $a_1-b_1=0$, this is a case (b) problem in Section 2 and Section 3.

By using the NBSFM with DFNM, $s_1\left(x\right)=1-x^2$ and $s_2\left(x\right)=1-x+x^2$ and $y\left(1\right)$ is given by

$$y\left(1\right)=A_0+1-y^{\prime }\left(0\right).$$

(55)

Under the parameters $y\left(0\right)=y^{\prime }\left(0\right)=0$, $N=4000$ and $ϵ={10}^{-15}$, the NBSFM with DFNM converges with nine iterations with ME = $3.04\times {10}^{-14}$. Then, we apply the LGSBSFM together with DFNM to solve this problem with $c=1$, $A_0=-10.018$, $A_2=-2.462$, $N=4000$ and $ϵ={10}^{-15}$, which is convergent with 13 iterations, and the numerical solution coincides with the exact one with ME = $1.11\times {10}^{-14}$.

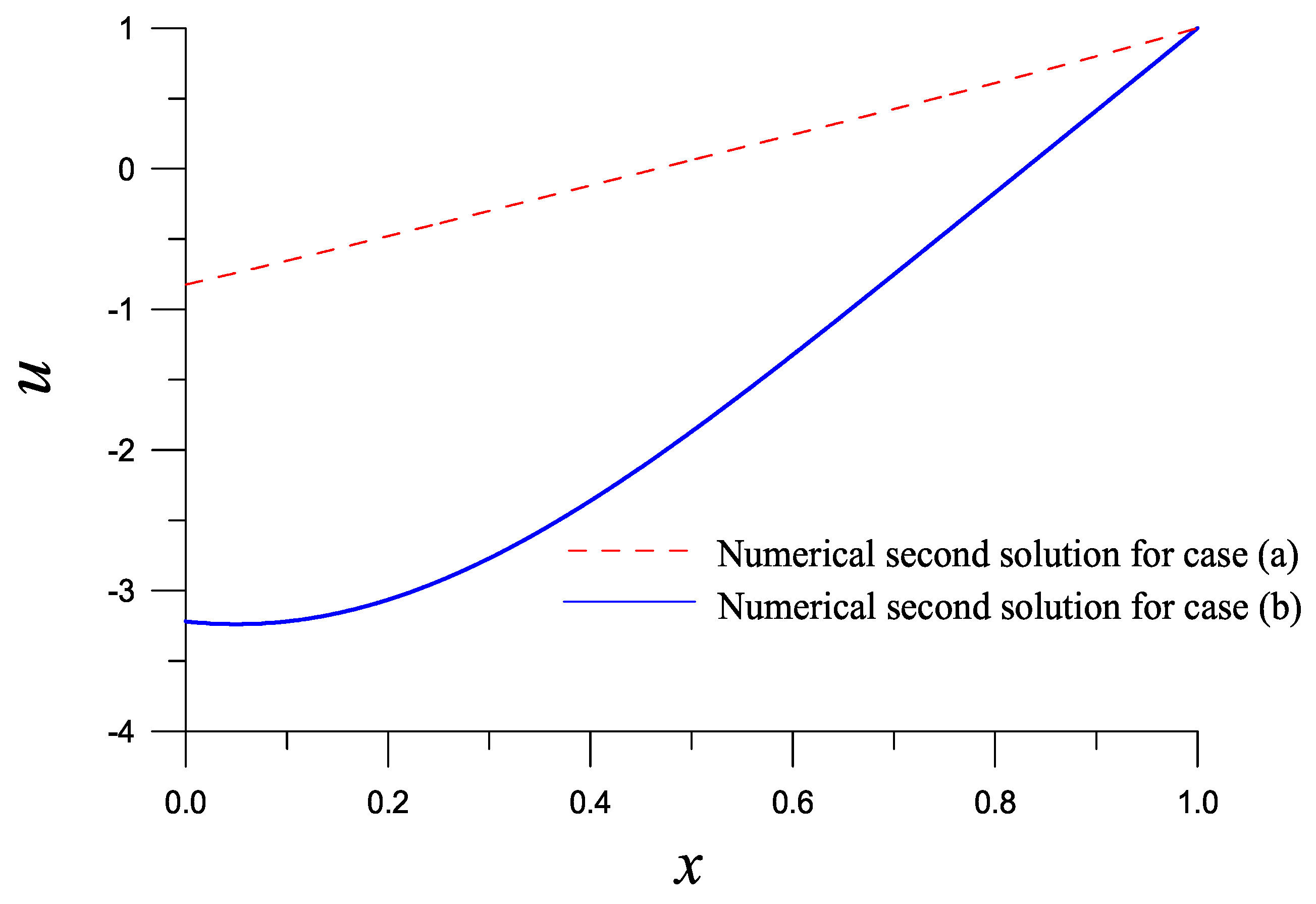
When we change c to $c=2.1$, the LGSBSFM together with DFNM obtains the second solution, which is convergent with 10 iterations. We obtain $u\left(0\right)=-3.21891943$ and $u^{\prime }\left(0\right)=-4+3.21891943=-0.78108057$, and the second numerical solution of case (b) is compared to that of case (a) in Figure 2.

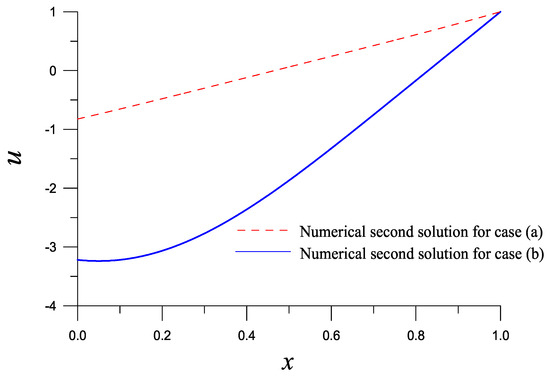
Figure 2. For example 1, comparing the second solutions of cases (a) and (b) obtained by the Lie-group shooting BSFM with DFNM.

6.2. Example 2

Consider a reaction problem [22]:

$$\begin{array}{ccc}\hfill & & u^{″}=Pe(u^{\prime }+R{u}^n),\hfill \end{array}$$

(56)

$$\begin{array}{ccc}\hfill & & Peu\left(0\right)-u^{\prime }\left(0\right)=Pe,u^{\prime }\left(1\right)=0.\hfill \end{array}$$

(57)

For this problem, we assume that $B_0$ in Equation (18) is a constant to be determined and $u^{\prime }\left(0\right)$ is given by $u^{\prime }\left(0\right)=Pe(B_0-1)$. By using the NBSFM with the DFNM, we take $s_1\left(x\right)=1/Pe$ and $s_2\left(x\right)=1/Pe+x$ and $y^{\prime }\left(1\right)$ is given by

$$y^{\prime }\left(1\right)=y^{\prime }\left(0\right)+Pe(1-B_0).$$

(58)

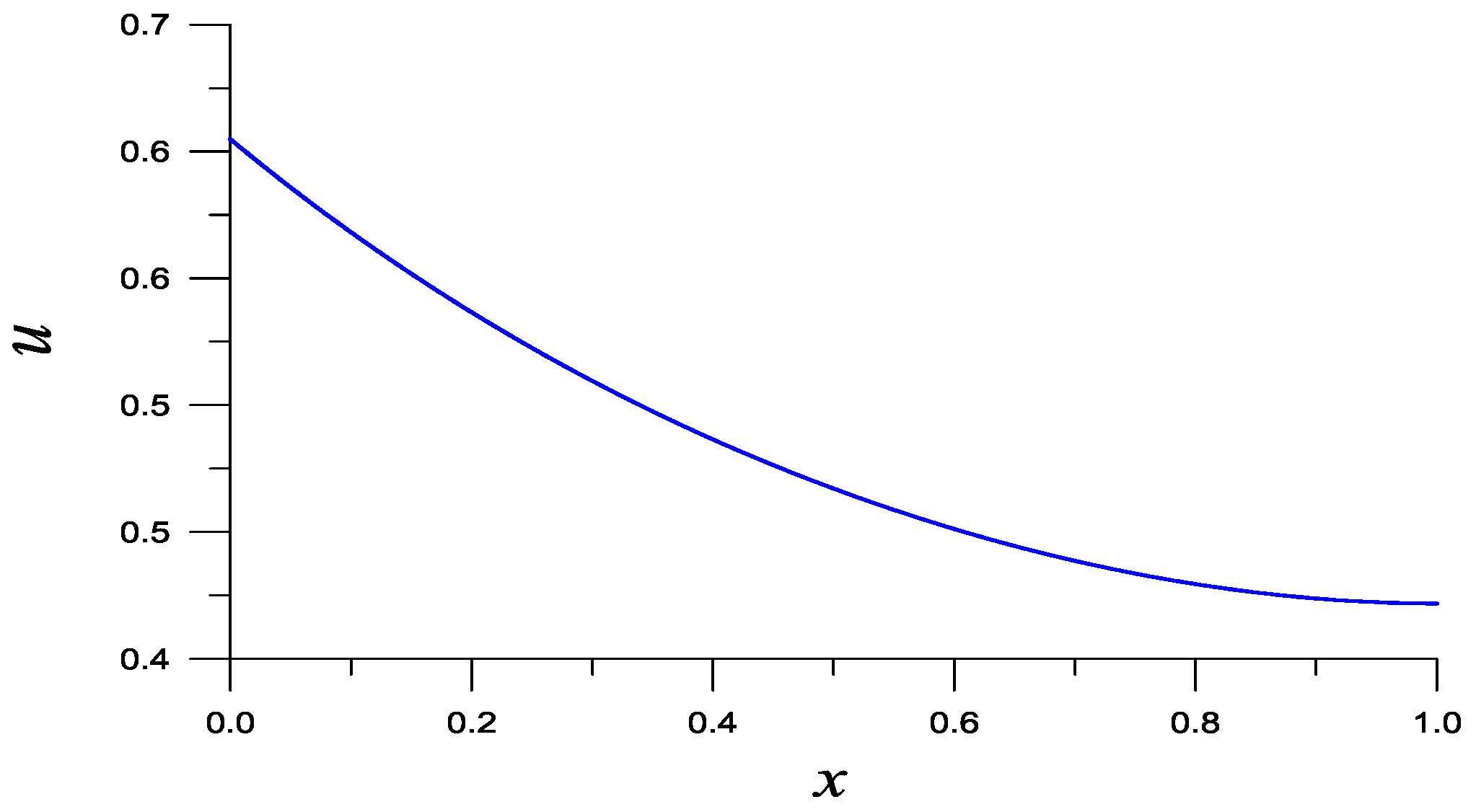
Under the parameters $Pe=1$, $R=3.5$, $n=2.5$, $y\left(0\right)=y^{\prime }\left(0\right)=0$, $N=4000$, and $ϵ={10}^{-15}$, the NBSFM with HIM by two initial guesses $B_0=0.6$ and $B_2=0.61$ to render $u^{\prime }(1,B_0)u^{\prime }(1,B_2)<0$ converges with 45 iterations with the right boundary error being $7.8\times {10}^{-15}$. In contrast, by using the NBSFM with DFNM, it converges with seven iterations with the same right boundary error $7.8\times {10}^{-15}$. The numerical solution is plotted in Figure 3. Since only seven iterations are required, the CPU time is very short with 0.35 s, and COC = 1.0044 is obtained by DFNM.

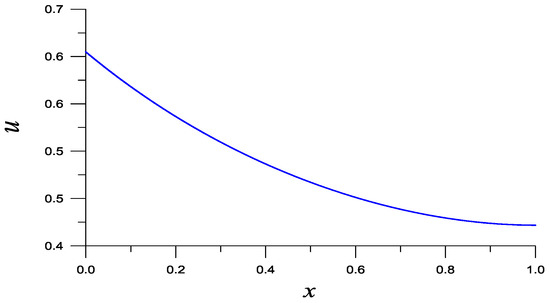
Figure 3. For example 2, showing the solution obtained by the NBSFM with DFNM.

6.3. Example 3

Consider a nonlinear model of diffusion and reaction in porous catalysts [23,24,25,26,27,28]:

$$\begin{array}{ccc}\hfill & & u^{″}\left(x\right)-{\Psi }^2{u}^m\left(x\right)=0,\hfill \end{array}$$

(59)

$$\begin{array}{ccc}\hfill & & u^{\prime }\left(0\right)=0,u\left(1\right)=1.\hfill \end{array}$$

(60)

For this problem, we assume that $B_0$ in Equation (18) is a constant to be determined by

$$B_0=c-G\left(0\right),$$

(61)

where $G\left(x\right)=(x-1)y^{\prime }\left(0\right)+(2x^2-1)[c-1]$, when the LGSM is used.

Under the parameter $m=-3/4$, Magyari [26] has derived an implicit solution:

$$x=\frac{2\sqrt{2}{c}_0^{7/8}}{35\Psi }\sqrt{{\left(\frac{u}{c_0}\right)}^{1/4}}\left[16+8{\left(\frac{u}{c_0}\right)}^{1/4}+6{\left(\frac{u}{c_0}\right)}^{1/2}+5{\left(\frac{u}{c_0}\right)}^{3/4}\right].$$

(62)

If $\Psi =0.8$, $c_0=0.1836751649400644$ for the first solution and $c_0=0.533047876754385$ for the second solution. It is obvious that the exact value is $u\left(0\right)=B_0=c_0$.

With $y\left(0\right)=y^{\prime }\left(0\right)=0$, $N=10000$ and $ϵ={10}^{-15}$, the NBSFM with the HIM by two initial guesses $B_0=c_0-0.01$ and $B=c_0+0.01$ to render $[u(1,B_0)-1][u(1,B)-1]<0$, converges with 42 iterations with the maximum error of the first solution being $3.22\times {10}^{-11}$. Similarly, by using the NBSFM with DFNM, it converges with eight iterations with the same error.

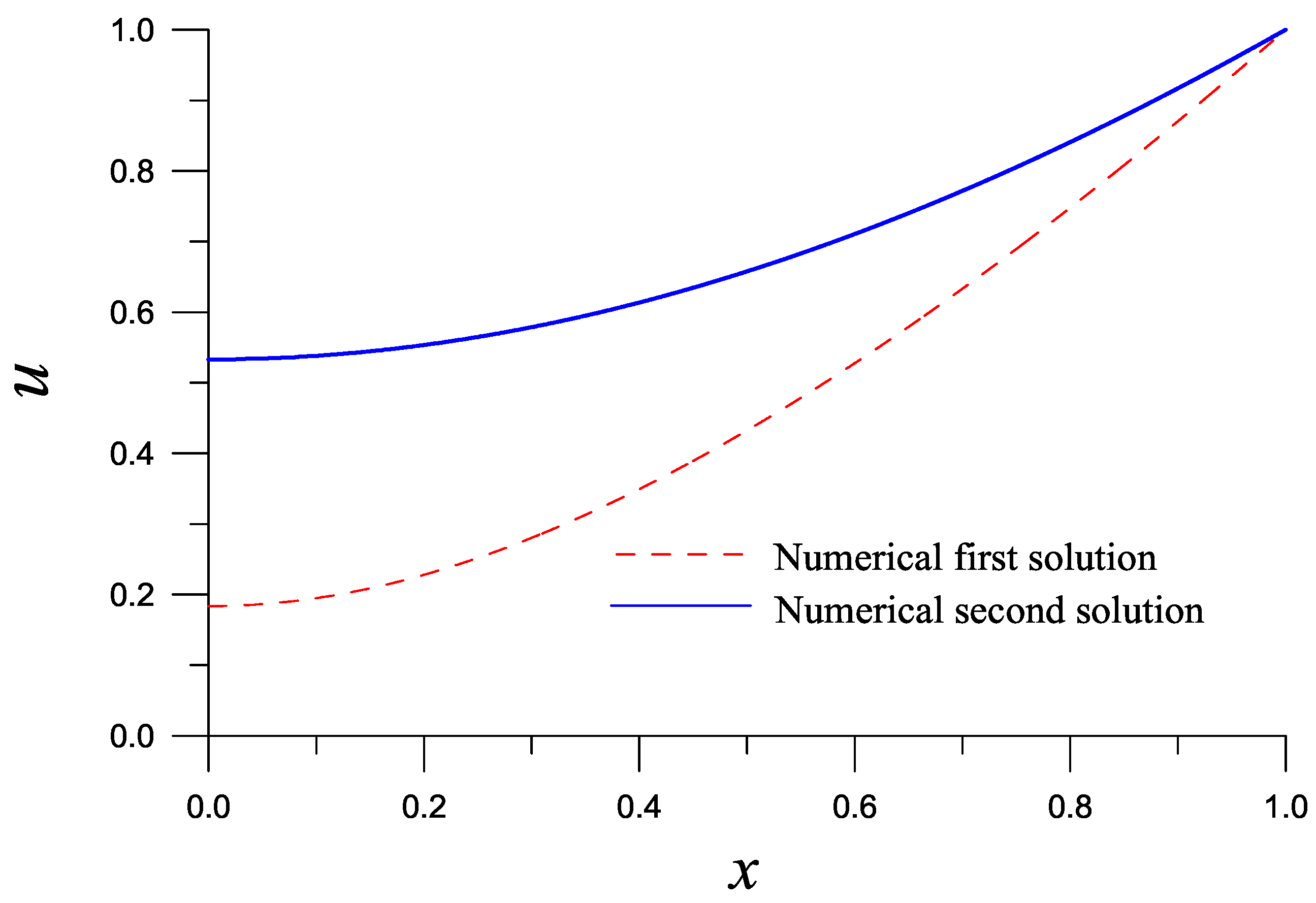
Then, we apply the LGSBSFM together with HIM or DFNM to solve this problem with $c=0.95$, $A_0=-0.76$, $A_2=-0.66$, $N=10000$, and $ϵ={10}^{-15}$, which is convergent with 39 iterations for the HIM, and with nine iterations for the DFNM. The numerical first solution coincides with the exact one in Equation (62) with $c_0=0.1836751649400605$ with ME = $3.22\times {10}^{-11}$, which is plotted in Figure 4 with the dashed line. When we take $c=1$, $A_0=-0.473$, $A{.}_2=-0459$, and LGSBSFM together with DFNM converges with seven iterations. The second numerical solution coincides with the exact one in Equation (62) with $c_0=0.5330478767543923$ with ME = $9.02\times {10}^{-13}$, which is plotted in Figure 4 by the solid line. The accuracy is better than that obtained in [16] about five orders.

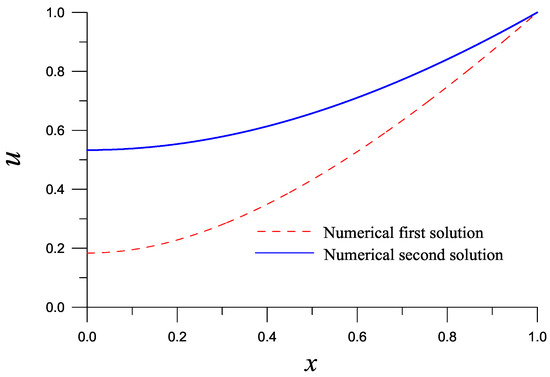
Figure 4. For example 3, comparing the first and second solutions obtained by the Lie-group shooting BSFM with DFNM.

6.4. Example 4

Let us solve the Bratu equation [29]:

$$\begin{array}{ccc}\hfill & & u^{″}\left(x\right)+\lambda e^{u\left(x\right)}=0,\hfill \end{array}$$

(63)

$$\begin{array}{ccc}\hfill & & u\left(0\right)=0,u\left(1\right)=0,\hfill \end{array}$$

(64)

which has an exact solution:

$$u\left(x\right)=-2ln\left[\frac{cosh\left(x-\frac{1}{2}\right)\frac{\theta }{2}}{cosh\frac{\theta }{4}}\right],$$

(65)

where $\theta$ satisfies

$$\sqrt{2\lambda }cosh\frac{\theta }{4}=\theta .$$

(66)

The Bratu problem has zero, one, and two solutions when $\lambda >{\lambda }_c$, $\lambda ={\lambda }_c$ and $\lambda <{\lambda }_c$, respectively, where ${\lambda }_c=3.513830719$.

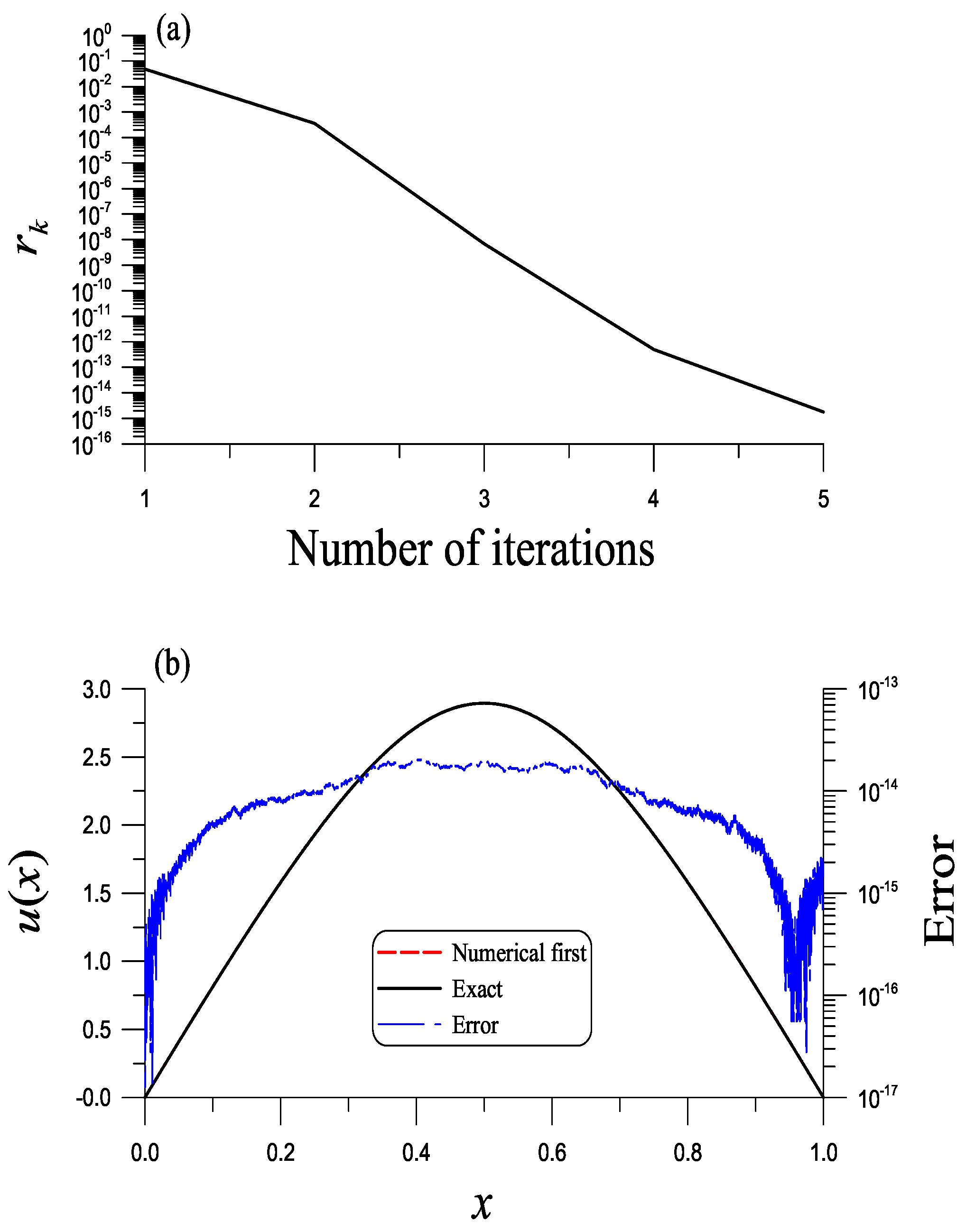
In the NBSFM with DFNM, we assume that $u^{\prime }\left(0\right)=A$ as an initial slope to be determined. We take $\lambda =2$, $N=10000$, $ϵ={10}^{-14}$ and $(A_0,A_2)=(8.1,8.3)$, obtaining $A=8.268763180545168$, which is very close to the exact one with an error $2.84\times {10}^{-14}$. With five iterations as shown in Figure 5 for the convergence, we obtain the solution as shown in Figure 5b by a solid line. Since only five iterations are required, the CPU time is very short with 0.49 s, and COC=1.0204 reveals that the present method is convergent fast—although, for HIM, the CPU time is 0.87 s. The numerical solution coincides with the exact one in Equation (65), and the numerical error is shown in Figure 5b by a dotted-dashed line with ME = $3.84\times {10}^{-14}$.

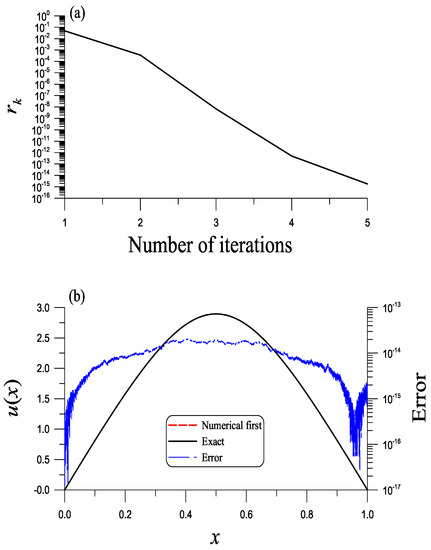
Figure 5. For example 4, (a) convergence rate and (b) comparing the present solution obtained by the NBSFM with DFNM to the exact one and showing error.

In Table 3, we tabulate the absolute errors and compare that obtained in [29,30,31].

Table 3. For example 4 with $\lambda =2$, comparing errors at different x.

x	Present	[29]	[30]	[31]
0.1	$4.50\times {10}^{-15}$	$4.03\times {10}^{-6}$	$1.52\times {10}^{-2}$	$2.13\times {10}^{-3}$
0.2	$8.22\times {10}^{-15}$	$5.70\times {10}^{-6}$	$1.47\times {10}^{-2}$	$4.21\times {10}^{-3}$
0.3	$1.29\times {10}^{-14}$	$5.22\times {10}^{-6}$	$5.89\times {10}^{-3}$	$6.19\times {10}^{-3}$
0.4	$1.95\times {10}^{-14}$	$3.08\times {10}^{-6}$	$3.25\times {10}^{-3}$	$8.00\times {10}^{-3}$
0.5	$2.00\times {10}^{-14}$	$1.46\times {10}^{-6}$	$6.98\times {10}^{-3}$	$9.60\times {10}^{-3}$
0.6	$1.78\times {10}^{-14}$	$3.05\times {10}^{-6}$	$3.25\times {10}^{-3}$	$1.09\times {10}^{-3}$
0.7	$1.15\times {10}^{-14}$	$5.20\times {10}^{-6}$	$5.89\times {10}^{-3}$	$1.19\times {10}^{-2}$
0.8	$6.66\times {10}^{-15}$	$5.68\times {10}^{-6}$	$1.47\times {10}^{-2}$	$1.24\times {10}^{-2}$
0.9	$3.00\times {10}^{-15}$	$4.01\times {10}^{-6}$	$1.52\times {10}^{-2}$	$1.09\times {10}^{-2}$

7. Two-Side Robin Boundary Conditions and Examples

In this section, we extend the NBSFM and DFNM to the following nonlinear BVP under the two-side Robin boundary conditions:

$$\begin{array}{ccc}\hfill & & u^{″}\left(x\right)=F(x,u\left(x\right),u^{\prime }\left(x\right)),0<x<1,\hfill \end{array}$$

(67)

$$\begin{array}{ccc}\hfill & & a_{1}u\left(0\right)+b_1{u}^{\prime }\left(0\right)=c_1,a_{2}u\left(1\right)+b_2{u}^{\prime }\left(1\right)=c_2.\hfill \end{array}$$

(68)

7.1. A New Methodology

As that done in [17], two shape functions are determined by

$$\begin{array}{ccc}\hfill & & a_1{s}_1\left(0\right)+b_1{s}_1^{\prime }\left(0\right)=1,a_2{s}_1\left(1\right)+b_2{s}_1^{\prime }\left(1\right)=0,\hfill \end{array}$$

(69)

$$\begin{array}{ccc}\hfill & & a_1{s}_2\left(0\right)+b_1{s}_2^{\prime }\left(0\right)=0,a_2{s}_2\left(0\right)+b_2{s}_2^{\prime }\left(1\right)=1.\hfill \end{array}$$

(70)

Then, the following variable transformation is employed:

$$u\left(x\right)=y\left(x\right)-s_1\left(x\right)[a_{1}y\left(0\right)+b_1{y}^{\prime }\left(0\right)-c_1]-s_2\left(x\right)[a_{2}y\left(1\right)+b_2{y}^{\prime }\left(1\right)-c_2],$$

(71)

which guarantees that $u\left(x\right)$ satisfies Equation (68) when $y\left(x\right)$ is solved.

In [17], the authors determine $y\left(1\right)$ and $y^{\prime }\left(1\right)$ in Equation (71) by the iteration method until the convergence of $y\left(1\right)$ and $y^{\prime }\left(1\right)$. Here, we let

$$\begin{array}{ccc}\hfill & & \alpha :=a_{2}y\left(1\right)+b_2{y}^{\prime }\left(1\right),\hfill \end{array}$$

(72)

$$\begin{array}{ccc}\hfill & & u\left(x\right)=y\left(x\right)-s_1\left(x\right)[a_{1}y\left(0\right)+b_1{y}^{\prime }\left(0\right)-c_1]-s_2\left(x\right)[\alpha -c_2],\hfill \end{array}$$

(73)

where $\alpha$ is an unknown constant to be determined.

As before, we let $u\left(0\right)=A$ be an unknown constant to be determined, and, after inserting $x=0$, it follows from Equation (73) that

$$\alpha =\frac{1}{s_2\left(0\right)}\{y\left(0\right)-s_1\left(0\right)[a_{1}y\left(0\right)+b_1{y}^{\prime }\left(0\right)-c_1]-A\}+c_2.$$

(74)

Like that in Equations (19)–(22), where $y\left(1\right)$ is expressed in terms of $A_0$ or $B_0$, for the present BVP with a right Robin boundary condition, $\alpha =a_{2}y\left(1\right)+b_2{y}^{\prime }\left(1\right)$ as a combination of $y\left(1\right)$ and $y^{\prime }\left(1\right)$ is expressed in terms of $A:=u\left(0\right)$ in Equation (74) or $B:=u^{\prime }\left(0\right)$ as follows:

$$\alpha =\frac{1}{s_2^{\prime }\left(0\right)}\{y^{\prime }\left(0\right)-s_1^{\prime }\left(0\right)[a_{1}y\left(0\right)+b_1{y}^{\prime }\left(0\right)-c_1]-B\}+c_2,$$

(75)

which is obtained by inserting $x=0$ into the differential of Equation (73).

Inserting Equation (74) into Equation (73) yields

$$u\left(x\right)=y\left(x\right)-G\left(x\right),$$

(76)

where

$$G\left(x\right)=s_1\left(x\right)[a_{1}y\left(0\right)+b_1{y}^{\prime }\left(0\right)-c_1]+s_2\left(x\right)\left[\frac{1}{s_2\left(0\right)}\{y\left(0\right)-s_1\left(0\right)[a_{1}y\left(0\right)+b_1{y}^{\prime }\left(0\right)-c_1]-A\}\right].$$

(77)

In addition, then inserting $u\left(x\right)$ into Equation (67), a new ODE for $y\left(x\right)$ is generated, like that in Equation (16), which through $G\left(x\right)$ involves A as a parameter. Then, we employ the DFNM in Section 5.2 to iteratively determine A by matching the Robin type target equation:

$$a_2[y(1;A)-G\left(1\right)]+b_2[y^{\prime }(1;A)-G^{\prime }\left(1\right)]-c_2=0.$$

(78)

The numerical procedure is similar if we employ Equation (75) to express $\alpha$.

We can also develop a similar LGSBSFM for solving the BVP with two-side Robin boundary conditions by

$$\begin{array}{ccc}\hfill & & u\left(x\right)=y\left(x\right)-s_1\left(x\right)[a_{1}c+b_{1}A-c_1]-s_2\left(x\right)[a_{2}c+b_{2}B-c_2],\hfill \end{array}$$

(79)

$$\begin{array}{ccc}\hfill & & B=\frac{1}{b_2{s}_2\left(0\right)}\{c-s_1\left(0\right)[a_{1}c+b_{1}A-c_1]-A_0\}+\frac{c_2-a_{2}c}{b_2},\hfill \end{array}$$

(80)

where c and A are given constants and $u\left(0\right)=A_0$ is determined by matching the Dirichlet type target equation:

$$y(1;A_0)-c=0.$$

(81)

7.2. Example 5

Following [21], we consider a second-order BVP:

$$u^{″}=\frac{3}{2}{u}^2,2u\left(0\right)+u^{\prime }\left(0\right)=0,u\left(1\right)+u^{\prime }\left(1\right)=0.$$

(82)

The exact solution is given in Equation (50).

We apply the NBSFM together with DFNM to solve this problem, where $s_1\left(x\right)=(2-x)/3$ and $s_2\left(x\right)=1-2x+4x^2/3$. With $y\left(0\right)=-1$, $y^{\prime }\left(0\right)=-1$, $N=5000$, and $ϵ={10}^{-14}$, we take $(A_0,A_2)=(3.9,4.1)$, and the DFNM is convergent with eight iterations, where COC = 1.0379 and the CPU time is 0.53 s. The numerical solution coincides with the exact one (50) with ME = $5.71\times {10}^{-8}$.

By using the LGSBSFM and DFNM with $c=-1$ and $A=-1$, it is convergent with eight iterations. The numerical solution coincides with the exact one in Equation (50) with ME = $6.12\times {10}^{-8}$. The CPU time is very short with 0.35 s for eight iterations, and COC = 1.17223 is obtained by DFNM.

7.3. Example 6

We calculate a nonlinear singular perturbation problem:

$$\begin{array}{ccc}\hfill & & \epsilon u^{″}+2u^{\prime }+e^u=\frac{\epsilon }{{(1+x)}^2}+\frac{2^{[1-e^{-2x/\epsilon }]}-2}{1+x},\hfill \end{array}$$

(83)

$$\begin{array}{ccc}\hfill & & u\left(0\right)-u^{\prime }\left(0\right)=1-\frac{2ln2}{\epsilon },2u\left(1\right)+\epsilon u^{\prime }\left(1\right)=-\frac{\epsilon }{2}.\hfill \end{array}$$

(84)

The exact solution is

$$u\left(x\right)=ln\frac{2}{1+x}-e^{-2x/\epsilon }ln2.$$

(85)

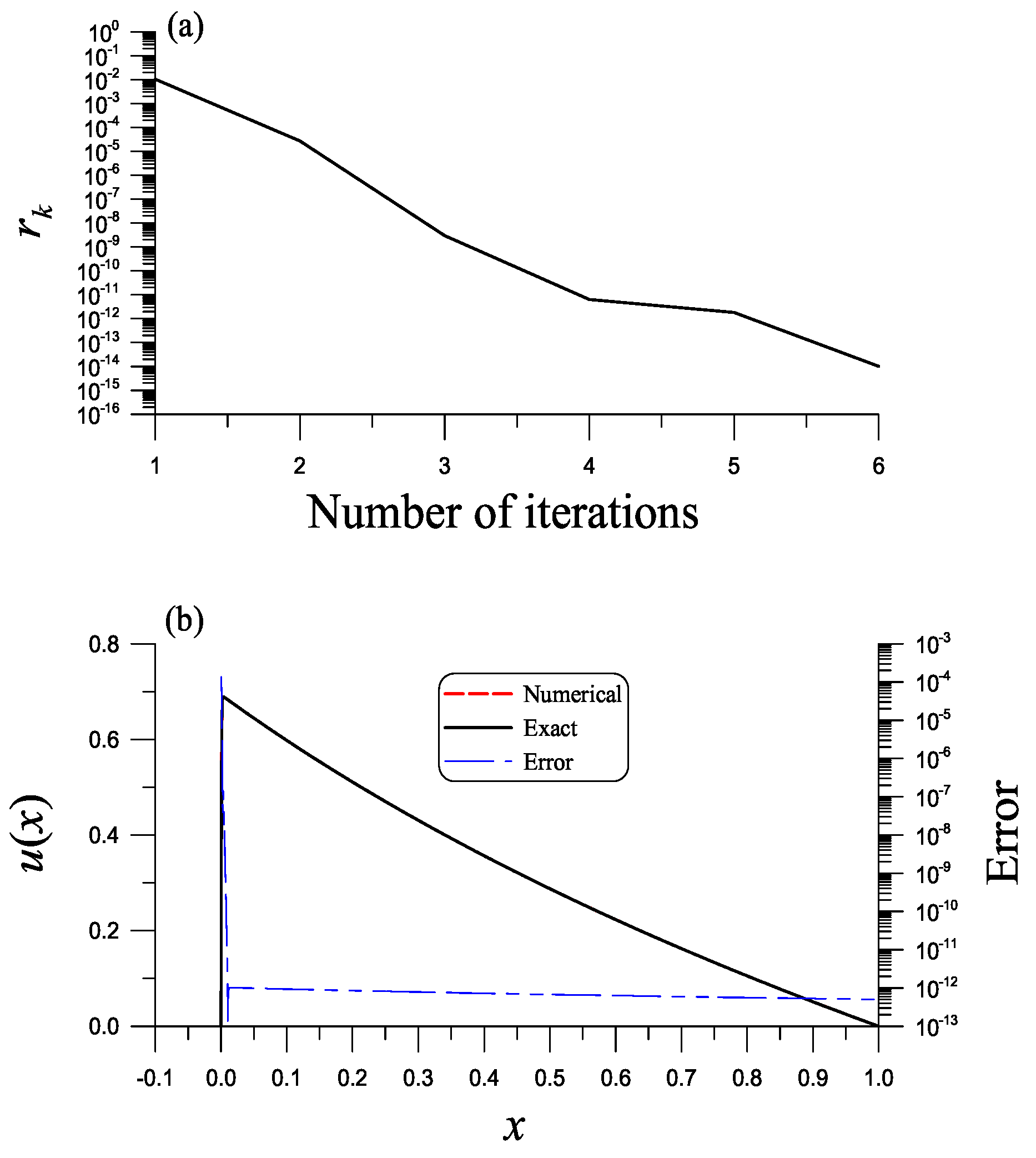
Using the original boundary shape function method through 221 iterations, Liu and Chang [17] find the numerical solution with ME = $1.993\times {10}^{-4}$ for $\epsilon =0.02$. Here, we consider a severely singular case with $\epsilon =0.001$. With $s_1\left(x\right)=(2+\epsilon -2x)/(4+\epsilon )$ and $s_2\left(x\right)=(1+x)/(4+\epsilon )$, $y\left(0\right)=-1$, $y^{\prime }\left(0\right)=-1$, $N=5000$, and $ϵ={10}^{-12}$, and $(A_0,A_2)=(-0.1,0.1)$, the DFNM is convergent with six iterations as shown in Figure 6a. We obtain the solution as shown in Figure 6b by a solid line, which coincides with the exact one in Equation (85), and, in Figure 6b, the numerical error is shown by a dotted-dashed line with ME = $1.35\times {10}^{-4}$. The CPU time is very short with 0.32 s for six iterations, and COC = 1.5375 is obtained by DFNM.

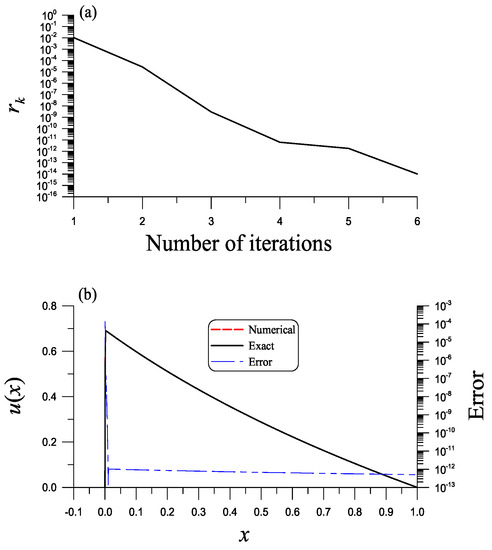
Figure 6. For example 6 of a highly singular problem, (a) the convergence rate and (b) comparing the solution obtained by the NBSFM with DFNM to the exact one and showing error.

In Table 4, we tabulate the numerical value at different x and compare it to the exact value. Besides at the point within the boundary layer, the accuracy is up to ${10}^{-14}$ to ${10}^{-13}$.

Table 4. For example 6 with $\epsilon =0.001$ list errors at different x.

x	0.001	0.1	0.5	0.7	0.9
Exact u	0.5983404102211	0.5978370007566	0.2876820724518	0.1625189294978	0.05129329438755
Numerical u	0.5983602577324	0.5978370007566	0.2876820724525	0.1625189294978	0.05129329438808
Error	$1.9\times {10}^{-5}$	$9.3\times {10}^{-14}$	$6.8\times {10}^{-13}$	$5.9\times {10}^{-13}$	$5.3\times {10}^{-13}$

8. Conclusions

In the numerical integration of nonlinear BVP, a key issue is how to determine the missing initial value $A_0$ or $B_0$ quickly and accurately. In the present paper, we have further modified the boundary shape function method (BSFM) for a new variable, of which the resulting initial value problem with its ODE involves the missing initial value of the original variable as a parameter. Owing to the implicit and nonlinear property of the target equation, we employed a new derivative free Newton method (DFNM) to solve the target equation, which can find very accurate left boundary values within a few iterations, and its performance is better than the half-interval method. In the new boundary shape function method (NBSFM), we solve a target equation to render a highly precise missing initial value and then the solution obtained is very accurate. Through the tests of numerical examples, we found that the CPU time is less than one second, and the COC is located between one and two. We combined the techniques of the Lie-group shooting method to the BSFM, whose advantage is that we can determine the missing slope of the new variable or missing initial value of the original variable in terms of a simple Dirichlet type target equation. Furthermore, we can easily find the multiple solutions of the considered problems. These numerical results clearly showed that the proposed methods can provide excellent approximation to the true solution of the nonlinear BVP with high accuracy.