Abstract
This study aims to symmetrically improve the economy and environmental protection of combined cooling, heating and power microgrid. Hence, the characteristics of configuration ways of energy storage devices in traditional combined cooling, heating and power systems are analyzed, and a scheme for the operator to establish an energy storage station is designed. An improved aquila optimizer for the optimal configuration of the system is proposed to symmetrically enhance the economic and environmental protection performance. The feasibility of the proposed scheme is verified through experiments in three different places. The results show that the economic cost and exhaust emission of the system with energy storage station are reduced to varying degrees compared with the system with energy storage equipment alone and the system without energy storage equipment based on symmetry concept. Especially in Place 1, the scheme with energy storage station in the system can reduce the electric energy purchased from power grid by 43.29% and 61.09%, respectively, compared with other schemes. This study is conducive to promoting the development of clean energy, alleviating the energy crisis, reducing the power supply pressure of power grid, and improving the profits of operators by symmetrically considering the economic and environmental performance of the system.
1. Introduction
With the increasingly serious energy crisis and environmental problems, the traditional distributed energy system is gradually being replaced by the integrated energy system, which will become the first choice for the future energy system [1]. The combined cooling, heating, and power (CCHP) system is a typical integrated energy system, and the use of this operating structure can improve the energy utilization efficiency of the system to more than 85% [2]. Heat storage devices can improve the utilization rate of waste heat [3]. Adding renewable energy generation methods, such as photovoltaic power generation and wind power generation, to the traditional CCHP system can improve the environmental protection of the CCHP system and reduce the dependence of the system on non-renewable energy. Increasing the use of clean energy helps reduce carbon emissions [4]. Rising wind power penetration can threaten the stability of the power system [5]. Compared to wind power, photovoltaic power is highly predictable and stable [6,7]. The introduction of photovoltaic/thermal systems can reduce pollutant gas emissions of the combined heat and power system and improve economic efficiency [8]. However, due to the influence of weather factors by temperature, solar irradiance, wind speed, etc., CCHP systems with renewable energy generation methods have uncertainty in electricity production, which will increase the dependence on the grid [9]. The addition of energy storage batteries can alleviate the pressure on the grid [10]. The way that the user installs energy storage batteries in the CCHP system alone will increase the economic cost of the system, and it will also have little effect on reducing the system’s dependence on the grid. Therefore, the research on the construction method and capacity configuration of energy storage devices is of great value [11]. There are many variables and constraints involved in the CCHP system, and the uncertainty of the load will also affect the optimal configuration and operation of the system. Consequently, it is relatively difficult to determine the optimal operation of the CCHP system [12,13]. The reasonable construction method of energy storage devices and the optimal configuration of the CCHP system can help the further promotion and application of integrated energy systems.
The various devices in the CCHP system determine how the energy is converted. Currently, CCHP systems are mainly divided into two categories: CCHP systems without energy storage equipment and CCHP systems of self-built energy storage equipment by users themselves [14,15]. Both types of CCHP systems can meet the needs of users, but they also have their own problems. During the peak periods of electricity consumption, CCHP systems without energy storage equipment can only be supplemented by the power grid, which increases the power supply pressure of the power grid [16]. Although the CCHP system of self-built energy storage equipment can reduce the dependence of the system on the power grid, the economic cost of the system itself will increase, and the optimization of the entire system will become more complex [17]. By combining the characteristics of the two systems, this study proposes a multi-microgrid operation method based on energy storage station (ESS) services. Operators establish ESS and take advantage of the scale effects of ESS to serve CCHP systems with different load requirements. While reducing the investment cost of the CCHP system, ESS can make profits by charging electricity service fees, so as to achieve a win-win effect between ESS and CCHP systems. Dealing with the coordinated operation between ESS and CCHP systems is a typical system optimization configuration problem.
Methods for optimal system configuration typically include mathematical programming and intelligent optimization algorithms [18]. Intelligent optimization algorithms can solve objective functions quickly and accurately without changing the system model [19]. Intelligent optimization algorithms have greater advantages in dealing with multi-variable, multi-constraint, and nonlinear problems such as system optimization configuration. In previous studies, classical and emerging algorithms, such as particle swarm optimization (PSO), genetic algorithm (GA), and salp swarm algorithm (SSA), have been applied to the optimal configuration of CCHP systems and achieved considerable results [20,21,22]. The aquila optimizer (AO) algorithm is a heuristic intelligent optimization algorithm proposed in 2021. Its performance is superior to the traditional PSO algorithm, GA, and novel algorithms such as SSA [23]. Similar to other intelligent optimization algorithms, the AO algorithm also has the problem of slow convergence and tendency to fall into local extremes when dealing with complex problems, so the AO algorithm needs to be improved [24]. The chaos strategy increases the randomness of individuals during the initialization stage, the mutation strategy increases the diversity of the population during the iteration, and the levy flight strategy can prevent individuals from falling into local extremes [25,26]. Therefore, by introducing the above strategies, the improved aquila optimizer (IAO) algorithm is proposed. In this study, the IAO algorithm is applied as the optimization algorithm, and the comparison results are better than those of the compared algorithms.
In this study, we analyze the form of energy storage battery configuration of traditional CCHP system and innovatively propose a storage battery configuration scheme. By introducing the improved strategies into the original AO algorithm, the IAO algorithm is proposed and used for the optimal configuration of the CCHP microgrid model. The addition of photovoltaic power generation equipment improves the sustainability and environmental friendliness of the CCHP microgrid. The proposed method reduces the power supply pressure of the grid, improves the profits of operators, and is conducive to promoting the development of clean energy, alleviating the energy crisis.
The research hypothesis of this study is to reduce the economic cost and exhaust emissions of the CCHP system through optimizing the configuration of the CCHP multi-microgrid system based on ESS service. Through the establishment of ESS by operators, the dependence of the CCHP system on the grid decreases, and the operator makes a profit by providing electrical energy services to the CCHP system. The main work and contributions of this study can be summarized as follows: (1) establishing an optimal configuration model symmetrically considering the economic and environmental benefits of ESS and the CCHP system; (2) proposing the IAO algorithm for optimal system configuration based on the AO algorithm; (3) the proposed algorithm has better optimization performance compared to the original AO algorithm; (4) reducing the dependence of the CCHP system on the grid by establishing ESS; (5) a new energy storage configuration scheme is proposed, which is beneficial to the economic and environmental protection and stable operation of the CCHP system.
The rest of this study is organized as follows: Section 2 briefly analyzes the literature related to the design and optimal configuration of CCHP systems. Section 3 describes the system model proposed in this study. Section 4 describes the original algorithm and the improvement process. Section 5 conducts an actual case study. Section 6 discusses the implications of this study. Finally, conclusions are provided.
2. Literature Review
Conventional power plants are used at about 30% efficiency for fuel energy, with most of the remaining energy lost in the form of waste heat [27]. After more than a century of development, the CCHP system has been proven to be an efficient and energy-efficient device operation mode [28]. The advancement of technology has gradually changed the fuel source and energy circulation mode of CCHP systems. Nami et al. [29] established a model of the solar-assisted biomass energy CCHP system, and analyzed the key factors of system performance optimization. The results show that the energy provided by the system can meet the energy demand of household users. However, the system’s technological maturity is low, and the complexity is too high. Moreover, the literature does not evaluate the economics of the system. Wei et al. [30] proposed a CCHP system based on proton exchange membrane fuel cells, optimized the system from the aspects of economy and environmental protection by using the improved mayfly optimizer, and obtained the system configuration that is more economical and environmentally friendly than the original algorithm. However, the system lacks clean energy and the optimization process does not consider the problem of environmental friendliness. Tonekaboni et al. [31] applied nanofluid and porous media to a solar collector and used the collector in a CCHP system to improve the energy absorption efficiency of the system. However, the literature lacks a discussion of the economics and environmental protection of the system. Li et al. [32] used the heat pump as the heat source of the CCHP system. Through the analysis of the primary energy saving rate, the carbon dioxide emission reduction rate, and the annual cost saving rate, the system was optimized and analyzed in practical application. However, this system lacks energy storage equipment, which will cause waste of energy. Nazari et al. [33] investigated the effect of electric boiler, hydro storage, and heat storage tank on the scheduling problem of conventional trigeneration system. The results indicated that the use of the model could improve the profits of the system. However, this system does not contain renewable energy, and the environmental protection of the system needs to be improved. Additionally, this system does not contain energy storage devices, and the lack of energy storage devices can cause energy waste. Previous studies have optimized the design of traditional CCHP systems from the perspective of system energy source, equipment material selection, and energy circulation mode. However, due to the difficulty of promoting and applying new materials, the high economic cost of installation, and the instability of new energy sources, the above-mentioned CCHP systems are still in the theoretical research stage.
The energy crisis and environmental issues have promoted the development of clean and renewable energy, and CCHP systems with clean and renewable energy have become a new trend in recent research [34]. Leonzio et al. [35] used software to design and simulate a trigeneration system powered by biogas. The results showed that the system has significant improvements in power generation and carbon dioxide emissions relative to conventional CCHP systems. However, the application scenarios of biogas power generation methods are limited to rural areas and other areas, and large-scale popularization applications cannot be carried out. Dong et al. [36] designed a CCHP system including wind power generation and photovoltaic power generation equipment as the coupling hub of the electric-gas system. Although this system is more economical than separated systems, the cost of wind turbines installation is still too high for the ordinary user, and the wind turbines are often far away from the user side, which is contrary to the installation concept of CCHP systems integrated on the user side. Zhang et al. [37] used a multi-objective particle swarm algorithm to optimize the CCHP system containing photovoltaic power generation, so that different buildings can achieve a balance between economy and environmental protection. Compared with wind power plants, photovoltaic power generation units can be better used in most scenarios, especially in areas where large equipment and power supply from the grid cannot be installed due to geographical constraints [38]. As a relatively mature clean power generation method, photovoltaic power generation is applied to the CCHP system model built in this study. Photovoltaic power generation equipment often needs to be used in conjunction with energy storage devices to alleviate the intermittent characteristics of power generation [39]. However, in previous studies, energy storage devices were generally configured by the user side of the CCHP system [40]. Considering factors such as installation costs and supporting management, the capacity configuration of the energy storage device is smaller, and it plays a less influential role in buffering and relieving the pressure on the grid. This study proposes that using the ESS operating mode, the operator can establish a large capacity of energy storage devices to serve the CCHP system. The CCHP system needs to pay only the service fee in exchange for the power usage and storage rights of the ESS.
The establishment of ESS increases the difficulty of optimizing the configuration of the CCHP system. Mathematical programming and intelligent optimization algorithms are two commonly used methods for optimizing the configuration. Compared to mathematical programming methods, the use of intelligent optimization algorithms does not require extensive mathematical proofs or changing nonlinear terms in the original model [41]. In the previous studies, GA and PSO have often been used in the optimal configuration and scheduling of the system [42,43]. However, the original algorithm has unstable performance and is easy to fall into local extremums, which has spawned scholars to improve the algorithm and produce new algorithms. Wang et al. [44] introduced the chaos and elite strategies into the original PSO algorithm, which improved the search range and search ability of the original algorithm. Cao et al. [2] replaced the random parameter β in the original owl search algorithm with a circular mapping based on the chaotic mechanism to improve the premature convergence problem of the original algorithm. Abualigah et al. [23] proposed the AO algorithm by simulating the process of finding, tracking, and capturing prey by the aquila. The AO algorithm has been applied to optimize scheduling, parameter tuning, and feature extraction, and has shown superior performance to other algorithms [45,46]. However, when the AO algorithm deals with the multi-variable and multidimensional optimal configuration model proposed in this study, there are still problems of slow convergence speed and low convergence accuracy similar to other algorithms. Therefore, this study proposes the IAO algorithm by improving the different stages of the original AO algorithm.
3. System Description
The structure of the CCHP multi-microgrid system combined with ESS is shown in Figure 1. In this study, the number of the CCHP microgrid is three. Considering the relevant policy restrictions and technical demands, the CCHP system is stipulated not to sell electricity to the grid. The system can be divided into power supply equipment, heating equipment, and cooling equipment. Among them, the power supply equipment includes photovoltaic generator unit (PV), micro turbine (MT), and energy storage station (ESS). Heating equipment includes gas boiler (GB), heat recovery (HR), heat exchanger (HE), and thermal storage tank (TST). Cooling equipment includes electric chiller (EC) and absorption chiller (AC). The mathematical model of the main equipment of the system is described below.
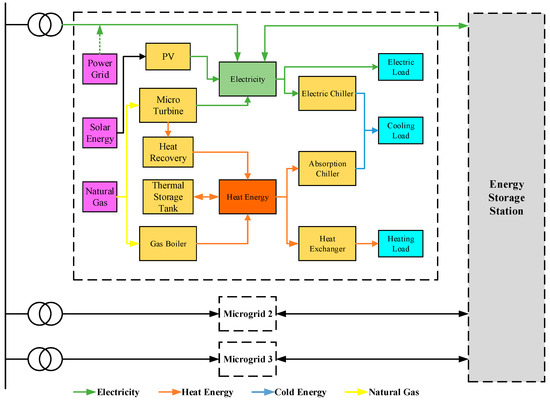
Figure 1.
The structure of the CCHP multi-microgrid system combined with ESS.
3.1. Equipment Description
3.1.1. Power Supply Equipment
(1) Photovoltaic power generation model.
Photovoltaic power generation is introduced into the CCHP system as a clean power generation method. It converts solar energy into electrical energy through the photovoltaic effect. The PV output electrical energy is expressed as follows:
where, Ppv denotes the power output of PV, Npv denotes the installed capacity of PV, Gpv and Tpv denote the solar irradiation intensity received by photovoltaic panels and the surface temperature of photovoltaic panels, GSTC and TSTC denote the solar irradiation intensity received by photovoltaic panels and the surface temperature of photovoltaic panels under standard test conditions, taking values of 1000 W/m2 and 25 °C, and k denotes the correlation coefficient.
(2) Micro turbine model.
MT is not only responsible for supplying electricity to the load, but the waste heat generated will also be further utilized through HR. The expression of MT output electricity is as follows:
where Pmt denotes the electrical power output of MT, Fmt denotes the consumption volume of natural gas, α is the calorific value of natural gas with a value of 9.7 kWh/m3, and denotes the power generation efficiency of MT.
(3) Energy storage station model.
The energy storage station is one of the crucial devices in the system. The regulating effect of ESS further improves the performance of the system. Meanwhile, ESS operators can make a profit.
where and denote the power of ESS at time t and t − 1, denotes the self-discharge rate of ESS, and denote the power purchased and sold by ESS from the CCHP system at time t, and and denote the charging efficiency and discharging efficiency of the energy storage battery.
3.1.2. Heating Equipment
(1) Gas boiler model.
GB plays a crucial role as the final guarantee of heating energy. GB will produce heat when the rest of the equipment cannot meet the heat demand of the user. The expression for its heat generation is as follows:
where Hgb denotes the heat generated by GB, Fgb denotes the consumption volume of natural gas, and denotes the heat production efficiency of GB.
(2) Heat recovery model.
HR makes full use of the fuel consumption of MT. It recovers the waste heat generated by MT in the process of producing electricity. The mathematical expression of HR is as follows:
where Hhr denotes the heat recovered by HR from MT and COPmt denotes the correlation coefficient of heat production by MT.
(3) Heat exchanger model.
HE connects the heat production of the system with the heat load. The mathematical expression for HE is as follows:
where Hhe denotes the heat required by HE, Hload denotes the heat load demand of the user, and denotes the efficiency of HE.
(4) Thermal storage tank model.
TST is a buffering device for heat. TST is preferentially used to store and release excess heat and lack of heat of the system. The state expression of TST is as follows:
where and denote the heat of TST at time t and t − 1, denotes the self-release rate of TST, and denote the heat stored or released at time t, and and denote the efficiency of TST in storing and releasing heat, respectively.
3.1.3. Cooling Equipment
AC and EC produce cooling to meet the demand of the user. Their mathematical expressions are shown as follows:
where Cac and Cec denote the cold generated by AC and EC, Hac denotes the heat consumption of AC, denotes the cooling efficiency of AC, Pec denotes the power consumption of EC, and COPec denotes the cooling coefficient of EC.
3.2. Problem Description
This study aims to optimize the configuration of the CCHP multi-microgrid system combined with ESS. In the solution process, both the economic and environmental protection of the CCHP system and the profitability of the ESS should be satisfied. The decision variables, objective function, constraints, and operating scheme are described as follows.
3.2.1. Decision Variables
The decision variables are as follows:
where Npv, Nmt, Ngb, and Ntst denote the installed capacity of PV, MT, GB, and TST, Ngrid denotes the upper limit of power purchased from the grid, Nbat denotes the capacity of storage batteries to be allocated, and r denotes the ratio of EC cooling production to the cooling load.
3.2.2. Objective Function
The objective function considers the net investment cost of the CCHP system, the cost of consumed natural gas, the ESS service charge, the cost of electricity purchased from the grid, and the cost of waste gas treatment.
where F denotes the value of the objective function, CI denotes the daily investment cost of the equipment, CF denotes the cost of consuming natural gas, CS denotes the service cost of ESS, CG denotes the cost of purchasing electricity from the grid, and CE denotes the cost of treating the waste gas. The specific cost expressions are as follows:
where β denotes the investment recovery coefficient, Ni denotes the installed capacity of the i-th equipment, Ci denotes the unit investment cost, L denotes the life of the equipment, and a denotes the discount rate, taking the value of 0.08.
where Cf denotes the price of natural gas, denotes the electricity purchases from the grid at time t, and is the price of electricity at time t.
where and represent the electricity sold and bought by ESS to the CCHP system at time t, and represent the prices of electricity sold and purchased by ESS at time t, and represents the service charge of ESS taking the value of 0.0079 $/kWh.
where and are the electricity and heat waste at time t, λ is the penalty factor, , , and are the electricity generated by MT, the heat produced by GB, and the electricity purchased from the grid at time t, , , and are the emissions of the g-th pollutant gas emitted by MT, GB, and the grid, and denotes the cost required to treat the g-th pollutant gas.
3.2.3. Constraints
The constraints include the balance of electricity, heating and cooling, and the capacity limits of the equipment.
(1) Equality constraints.
The electricity balance is as follows:
where indicates the required electricity of the system at time t, and and are the shortage and waste of electricity at time t.
The heating balance is as follows:
where and represent the shortage and waste of heat at time t, respectively.
The cooling balance is as follows:
where denotes the cooling load required by the user at time t.
(2) Inequality constraints.
The inequality constraints are mainly the capacity limits of the equipment. The inequality constraints involved in this study are listed in Table 1.

Table 1.
Inequality constraints of the system.
3.3. Operation Schemes
The addition of storage batteries improves the utilization of electricity. However, the configuration of storage batteries alone will increase the investment cost. Additionally, the smaller configuration size has less effect on electricity regulation. Therefore, this study proposes a CCHP system based on ESS service. The earnings of ESS come from two sources. First, the electricity used and stored in ESS is calculated for each CCHP system: charging in the form of electricity sales and purchases. Second, ESS charges a service fee for the electricity used and stored by the CCHP system. In this study, two other operation schemes are chosen for comparison. The three operation schemes are described as follows.
- Scheme 1: ESS service model
Each CCHP system operates independently without configuring energy storage batteries, and the ESS services the CCHP system. Excess power is sold to ESS when PV and MT generation is sufficient. Conversely, electricity is first purchased from ESS when there is insufficient electricity. If the ESS does not have enough electricity, the customer purchases the shortage from the grid.
- Scheme 2: Users configure energy storage equipment by themselves
Each CCHP system operates independently and is equipped with energy storage batteries. The operation process is similar to scheme 1. However, under this scheme, the cost of energy storage batteries needs to be included in the net investment cost.
- Scheme 3: CCHP system is not equipped with energy storage equipment
Each CCHP system operates independently without the configuration of energy storage batteries. When PV and MT generation is sufficient, surplus electricity is wasted. Conversely, electricity is purchased from the grid if there is insufficient generation.
The heating and cooling load demands are met in the same way for the three operating schemes. First, it is determined whether the waste heat recovered by HR meets the system heat demand. If the waste heat is larger than the demand, the excess heat is saved in the TST. If the waste heat is insufficient, TST is given priority for heat release. When TST still cannot meet the demand, GB starts heat production.
4. Optimization Algorithm
This section gives a detailed description of the original AO algorithm and its improvement process.
4.1. AO Algorithm
The aquila optimizer is a novel intelligent optimization algorithm based on the predation process of the aquila [17]. According to the different flight behaviors of the aquila, the predation process includes two stages: searching for prey and catching prey. The exact procedure of the original algorithm is as follows.
4.1.1. Search Stage
When the number of iterations is less than two-thirds of the maximum iterations, the aquila individual updates the position by Equation (22) or Equation (24). The specific position update equation is determined by judging the size of the random number. The search stage is as follows:
where X1(t + 1) denotes the position of the individual after the update, t denotes the current iteration number, Xbest(t) denotes the position of the best individual, XM(t) denotes the average of all individual positions, T denotes the maximum iteration number, N is the number of individuals, and rand is a random value between 0 and 1.
where X2(t + 1) denotes the position of the individual after the update, XR(t) denotes the position of a random individual in the current population, D denotes the dimension of the search space, Levy denotes the levy flight function, and y and x are used to represent the spiral process of the aquila. The corresponding mathematical expressions are as follows:
where β takes the value of 1.5, u and v are two random numbers taking values between 0 and 1, r1 denotes the number of search periods and takes values between 1 and 20, U and ω are fixed values of 0.0565 and 0.005, respectively, and D1 is an integer between 1 and D.
4.1.2. Catch Stage
When the number of iterations is greater than two-thirds of the maximum iterations, the aquila individual updates the position by Equation (28) or Equation (29). Again, the specific position update equation is determined by judging the size of the random number. The catch stage is as follows:
where X3(t + 1) denotes the position of the individual after the update, and are adjustment parameters taking fixed values of 0.1, and UB and LB denote the upper and lower bounds of the search space.
where X4(t + 1) denotes the position of the individual after the update, QF(t) denotes the search function, G1 denotes the movement parameter, and G2 denotes the flight slope.
4.2. IAO Algorithm
The original performance of the AO algorithm is better than most intelligent algorithms already. However, similar to other heuristic algorithms, the AO algorithm still has the problem of slow convergence and the tendency to fall into local optimum. The AO algorithm is improved to increase the convergence speed and convergence accuracy. First, the logistic chaotic mapping is used for the initialization process of the population. Thus, the initial distribution of individuals in the aquila population is improved. Second, mutation, hybridization, and competition strategies from the differential evolution algorithm are introduced into the population update to improve the diversity of the population. Finally, the aquila in the optimal position will execute the levy flight strategy, thus preventing it from falling into local extremes.
4.2.1. Logistic Chaos Mapping Strategy
The initialization quality of the population affects the entire population search process. In the initial stage, a more random initial distribution enables individuals to perform a better search for the global. Individuals have a greater probability of approaching the optimal solution, thus increasing the accuracy and iteration speed of the algorithm. In this study, the logistic chaotic mapping is selected for the initialization process of the population. The specific expressions are as follows:
where ri denotes the i-th random value generated by the chaotic mapping, Xi denotes the initialized position of the individual after the chaotic mapping, and UB and LB are the upper and lower bounds of the search space.
4.2.2. Mutation, Hybridization, and Competition Strategies
To improve the diversity of the aquila population during the predation, and thus, to solve the problems caused by the lack of diversity during the search process, mutation, hybridization, and competition strategies are introduced after each iteration of the population. The execution process is as follows:
where Xq1(t), Xq2(t) and Xq3(t) are three different individuals within the population after the t-th iteration, Ui(t) is the new individual position generated by mutation, and F is the dynamic mutation parameter. Then, the new population generated by mutation and the original population are crossed to produce the hybrid population by hybridization. The specific hybridization process is as follows:
where Vi(t) denotes the position of the new individual produced by hybridization, and CR is a random parameter taking values between 0.5 and 1. Finally, the new population produced after the mutation and hybridization process competes with the original population to keep the superior individuals. The specific competition process is as follows:
where Xnew_i(t) denotes the location of the individual generated after the competition, and f denotes the fitness function, which is the objective function in this study.
Compared with the original population, the positions of all individuals in the new population undergo a larger perturbation. The search range is wider in the early iterative stage, thus avoiding falling into the local optimum. The introduction of the competition strategy retains the better individuals in the population and eliminates the worse ones, which further improves the convergence accuracy of the algorithm.
4.2.3. Levy Flight Strategy
The levy flight strategy is already involved in the position update formulation of the original algorithm, but it is necessary to execute the strategy again for the optimal individual. After all individuals in the population have completed one complete iteration, the current best individual is selected for levy flight. The fitness values of the individual are compared before and after the execution of levy flight strategy to update the optimal individual position. The process is shown as follows:
where Xbest(t) denotes the optimal individual position in the population after the t-th iteration, Xlevy_best(t) denotes the updated position of the optimal individual position after the levy flight strategy, and Xnew_best(t) is the optimal individual position after the selection.
Figure 2 shows the flow chart of the optimal configuration of the CCHP system based on the IAO algorithm. The specific steps are as follows:
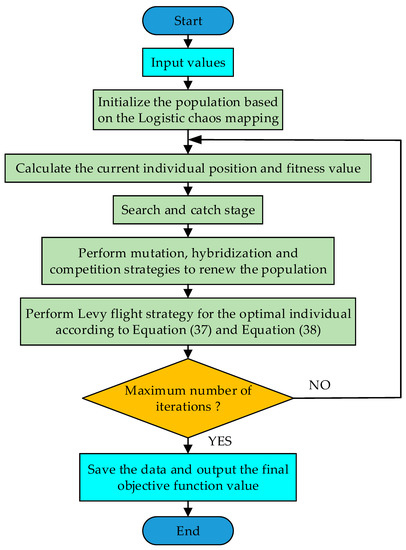
Figure 2.
The flow chart of optimal configuration based on the IAO.
Step 1 Input load and weather data, and parameters of equipment and the algorithm;
Step 2 Initializing the population with the logistic chaos mapping;
Step 3 Calculate the current position of the individual and the fitness value;
Step 4 The aquila individual enters the search and catch stage;
Step 5 The population obtained from Step 4 performs mutation, hybridization, and competition strategies through Equations (33), (35), and (36) to obtain a new population, thereby retaining the individuals with low fitness value;
Step 6 The optimal individual performs the Levy flight strategy according to Equations (37) and (38);
Step 7 Judge whether the maximum number of iterations is reached, and if not, return to Step 3, otherwise execute the next step;
Step 8 Save data and output the objective function value.
5. Case Study
To evaluate the effectiveness of the operation scheme and optimization algorithm proposed in this study, the load data of a large hotel, a supermarket, and a primary school in 16 typical buildings provided by the US Department of Energy Building Technologies program are selected as cases for analysis [47,48]. Figure 3 shows the load curves of the three buildings. Figure 4 shows the temperature and solar irradiance curves. Table 2 lists the relevant parameters of the equipment in the system. Table 3 shows the installation cost and life of the equipment. Table 4 shows the price of electricity and natural gas. Table 5 shows the pollutant gas emission factors and treatment costs.
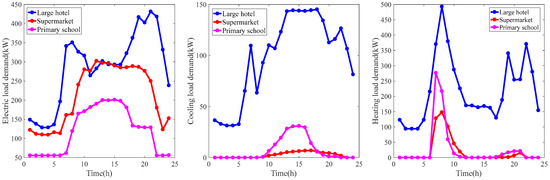
Figure 3.
The load demand of the buildings.
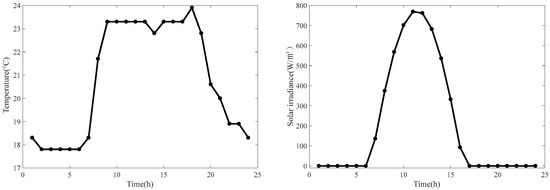
Figure 4.
Temperature and solar irradiance curves.

Table 2.
The value of the equipment parameters.

Table 3.
The investment cost and the life of the equipment.

Table 4.
The price of electricity and natural gas.

Table 5.
Pollutant gas emission and treatment parameters.
In this study, the population size of the algorithm is 30, and the number of iterations is 500. The experiments were performed on MATLAB R2016b software. The computer is configured with Intel® CoreTM i5-6200U, 2.4 GHz, 12 GB RAM, and is made in China.
5.1. Optimization Results
This study aims to improve the economy and environmental protection of the system by combining ESS. By arranging the energy flow of the CCHP system properly, it can reduce the pressure on the grid and the pollutant gas emissions. Meanwhile, ESS makes a profit by serving the CCHP system. The improvements to the original AO algorithm have improved its performance. The gray wolf optimizer (GWO), the whale optimization algorithm (WOA), and the original AO algorithm are selected as comparison algorithms to verify the performance of the IAO algorithm. Based on the different schemes, four algorithms are used to optimize the system, respectively. Section 3.3 provides a specific description of the schemes. The results are the average values of 50 runs based on the program. The convergence curves of the four algorithms are shown in Figure 5, Figure 6 and Figure 7.
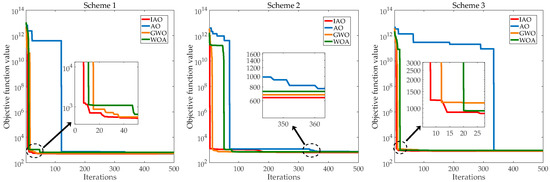
Figure 5.
The convergence curves of Place 1 under different schemes.
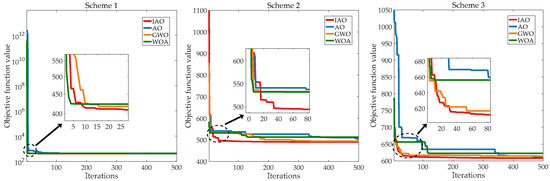
Figure 6.
The convergence curves of Place 2 under different schemes.
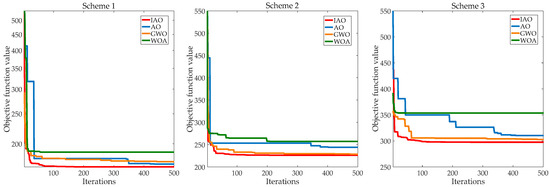
Figure 7.
The convergence curves of Place 3 under different schemes.
The analysis of the convergence curves reveals the following conclusions.
(1) The convergence speed of the IAO algorithm is significantly improved compared to the original AO algorithm. At the iteration number of 100, the IAO algorithm can already converge to a smaller value. Moreover, the convergence speed of the IAO algorithm is faster compared with GWO and WOA.
(2) The convergence accuracy of the IAO algorithm is higher. When reaching the maximum number of iterations, the convergence value of the IAO algorithm is smaller than the convergence values of the other three compared algorithms.
(3) For the same place and optimization algorithm, the convergence values of the iterative curves based on different schemes have significant differences. Specifically, the convergence value of the iteration curve is smaller when the system is operating with scheme 1.
The above results show that the improvement to the AO algorithm is effective. The convergence speed and convergence accuracy of the IAO algorithm are better than the comparison algorithms. Meanwhile, the operation scheme proposed in this study has better economy and environmental protection.
Table 6 shows the objective function values and pollutant gas emissions for different operation schemes.

Table 6.
Objective function values and pollutant gas emissions.
The data in Table 6 more intuitively show the effectiveness of the optimal configuration using the IAO algorithm. For different places and different schemes, the proposed algorithm can obtain the minimum objective function value. Therefore, the IAO algorithm has better search capability and stability than other algorithms. Meanwhile, the calculation shows that the daily economic cost obtained by the IAO algorithm is lower when the systems of the three places are operating with scheme 1. Compared with the cost of scheme 2, the values decreased by 20.54%, 17.95%, and 25.46%, respectively. Compared with the cost when the systems of three places are operating with scheme 3, the values decreased by 37.88%, 33.88%, and 43.38%, respectively. The values for pollutant gas emissions decreased by 16.8%, 28.57%, 32.93% and 32.45%, 43.37%, 49.39%, respectively. The results indicate that the construction of ESS is beneficial to the operation of the CCHP system. Therefore, scheme 1 achieves both economic and environmental improvements for the user side of the CCHP system.
This study aims to take advantage of the scale of ESS to improve the performance of the CCHP system. At the same time, the ESS operator can be profitable. Table 7 shows the capacity configurations and daily investment costs of the energy storage batteries and the revenue of the operator.

Table 7.
Energy storage configuration results.
From the data in Table 7, it can be found that compared to the CCHP system in scheme 2, which is configured with energy storage equipment alone, in scheme 1, ESS can be configured with larger capacity energy storage batteries. Compared with scheme 2, although the form of building ESS will increase the investment cost in energy storage equipment, the merchant still has room for profit. Therefore, the configuration of energy storage equipment proposed in this study is feasible. We consider the profitability of the merchant, and also take into account the economy and environmental protection of the CCHP system. A win-win situation can be achieved by operating ESS with multiple CCHP systems.
5.2. Scheduling Results
Taking Place 1 as an example, Figure 8, Figure 9 and Figure 10 show the electricity balance and heating balance of the CCHP system obtained by the IAO algorithm under different schemes.
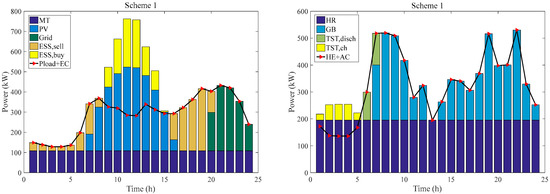
Figure 8.
The electricity balance and heating balance under scheme 1.
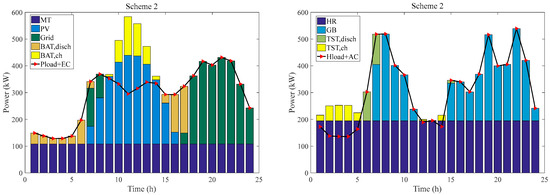
Figure 9.
The electricity balance and heating balance under scheme 2.
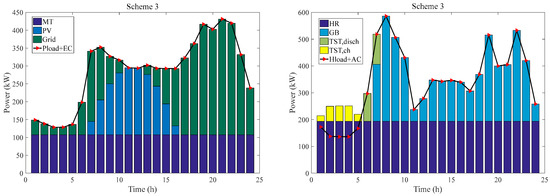
Figure 10.
The electricity balance and heating balance under scheme 3.
The electricity balance shows that all three operating schemes can meet the electricity demand of Place 1 during the day. For scheme 1, from 01:00 to 19:00, the ESS regulates the electrical energy balance of the CCHP system by selling and purchasing electricity. ESS and MT work together to meet the electricity demand of the system when weather conditions do not allow for PV generation. When the PV can generate electricity, ESS, MT, and PV together meet the electricity balance of the system. From 20:00 to 24:00, ESS, MT, and the grid work together to meet the electricity demand of the system. For scheme 2, the scale of self-configured energy storage equipment in CCHP systems is smaller. Therefore, its adjustable range for electricity reduces accordingly. As a result, the electricity required from the grid increases. For scheme 3, the lack of energy storage equipment prevents the system from configuring large-capacity photovoltaic power generation equipment. The system still requires a significant amount of electricity from the grid to meet demand. In summary, ESS can guarantee the electricity balance of the CCHP system by taking advantage of its scale. I In addition, it makes a profit by selling electricity and charging service fees. Meanwhile, the CCHP system reduces economic costs by eliminating energy storage equipment and selling surplus electricity.
The heating balance shows that all three operating schemes can meet the heating demand of Place 1 during the day. The heat production from 1:00 to 11:00 and 15:00 to 24:00 is essentially the same for the different equipment under the three schemes. From 12:00 to 14:00, PV produces sufficient electricity. Due to the electricity regulation by energy storage equipment, the system can be configured with higher capacity photovoltaic generation equipment when operating through scheme 1 and scheme 2. As a result, the percentage of the cooling load allocated to EC will increase. Consequently, less heat will be required to meet the cooling load, indirectly reducing the heat production of GB, thus reducing the emission of polluting gases. On the contrary, when the system is operating with scheme 3, the capacity of the configured photovoltaic power generation equipment is less due to the lack of energy storage equipment. Hence, EC receives less electricity and reduces its cooling production, and more heat is needed to meet the demand for AC. More heat needs to be provided by GB, thus increasing the emission of polluting gases.
Table 8 shows the electricity generated by different equipment under the three operating schemes. With Scheme 1 operation, the PV and the grid provide 34.38% and 15.08% of the total electricity. When run with scheme 2, the corresponding values are 29.19% and 28.27%. When run with scheme 3, the corresponding values are 17.92% and 44.76%, respectively. The percentage of electricity provided by energy storage equipment under the three schemes is 17.95%, 8.04%, and 0%, respectively. Therefore, for the same load demand, increasing the proportion of PV can reduce the pressure on the grid to supply electricity. Compared with scheme 2 and scheme 3, the electricity provided by the grid is decreased by 43.29% and 61.09% when operating with scheme 1. The intermittency of PV needs to be balanced by energy storage equipment. ESS purchases excess electricity during the peak generation period of PV, and sells electricity preferentially when the system lacks electricity. The combined model of ESS and PV produces almost zero pollution in the production and utilization of electricity. The scheme also makes more sense for environmental protection.

Table 8.
The electricity production of the equipment.
In summary, the CCHP system based on ESS service proposed in this study has more competitive advantages. The system is more economical and emits fewer pollutant gases. Moreover, ESS has room for profitability. The energy storage space provided by ESS can better alleviate the intermittency of PV, regulate the electricity balance of the system, and reduce the pressure on the grid.
6. Discussion
Compared with the original AO algorithm, the improved algorithm improves the convergence speed and convergence accuracy and can obtain better objective function values in fewer iterations. Based on the better objective function value, it can be concluded that the economic cost of the system is reduced and the exhaust emissions are reduced. This study contributes to the optimal configuration of the CCHP system. The optimal configuration model based on the IAO algorithm has played an essential role in influencing and promoting the related fields.
In terms of reducing economic costs, this study proposes a new energy storage equipment configuration scheme. Through the coordination of energy storage equipment and photovoltaic power generation equipment, the demand of the system for grid power supply is reduced. Therefore, the exhaust gas emissions from grid power generation are reduced, thus symmetrically reducing the economic investment required for exhaust gas treatment. Meanwhile, the reduced power supply can reduce the pressure on the grid and improve the flexibility of the CCHP system. The CCHP system can still maintain a relatively stable operation when an accident occurs on the grid. In addition, through the construction of ESS, the intermittency of photovoltaic power generation can be further alleviated, and the ESS operator can still get the revenue to keep operating normally.
In terms of exhaust emissions, the system emits the least quantity of exhaust gases when operating with the scheme proposed in this study. The quantity of the exhaust emissions is linked to the cost required to treat the exhaust gas. In addition, the reduction of exhaust emissions can also decrease the damage to the atmosphere. With lower emissions, the cost of treating the exhaust gas is reduced, thus saving the economic investment of the system. As an important part of the ecological environment, reducing exhaust gas pollution and maintaining a clean atmosphere can promote the green cycle of the entire ecosystem. This study provides a sustainable and effective new idea for the green development of the microgrid.
This study makes full use of clean energy to reduce the consumption of non-renewable energy sources. Under the premise of meeting the load requirements from users, this study is committed to finding an effective system configuration solution. In the context of energy crisis and environmental problems, energy conservation and emission reduction are important issues that both companies and individuals cannot ignore. The CCHP system has raised the utilization rate of energy to a new level. The emergence of CCHP systems provides an effective implementation way for energy cascade utilization. Based on the traditional CCHP system, the introduction of photovoltaic power generation equipment can improve the environmental protection benefits of the system and save fossil fuels. Considering the current rising prices of non-renewable energy, reducing the consumption of natural gas raw materials and making full use of clean power generation methods can reduce dependence on imported energy. This study provides an effective way to reduce energy consumption and reduce carbon emissions, which can promote sustainable development.
7. Concluding Remarks
This study designed a CCHP system including photovoltaic power generation equipment and energy storage equipment. According to the characteristics of the two typical configuration schemes of energy storage equipment, the operation scheme based on ESS service was proposed, and a mathematical model considering economy and environmental protection was established. Additionally, the IAO algorithm was proposed by introducing improved strategies. The optimal configurations of the system under different operating schemes were obtained by the IAO algorithm and other compared algorithms. The conclusions are as follows.
(1) The IAO algorithm has better seeking ability than the original algorithm and other compared algorithms. The IAO algorithm has a faster convergence speed and higher convergence accuracy. When other conditions are consistent, using the IAO algorithm to optimize the system can get better results.
(2) The operating scheme proposed in this study is more feasible. For the system in the same place when operating with three different schemes, scheme 1 shows a greater advantage in terms of economy and environmental protection. Compared with scheme 2 and scheme 3, the daily economic cost of the three places decreased by 20.54%, 17.95%, 25.46% and 37.88%, 33.88%, 43.38%, respectively, and the pollutant gas emissions decreased by 16.8%, 28.57%, 32.93% and 32.45%, 43.37%, 49.39% respectively.
(3) Whether to configure energy storage equipment and how to configure energy storage equipment directly affect the configured capacity of PV in CCHP microgrid, thus affecting the pressure of power grid supporting system. Although the three operation schemes can meet the load demand of the system, their economy is different. Scheme 1 can configure a larger scale of PV to reduce the power supply pressure of power grid by matching the PV with the ESS. Taking Place 1 as an example, the electricity provided by the grid is decreased by 43.29% and 61.09%, respectively, when operating with scheme 1 compared to scheme 2 and scheme 3, which improves the system’s economic performance.
We put forward a new scheme for the energy storage configuration of CCHP system, and propose the IAO algorithm to optimize the system. The proposed method reduces the power supply pressure of the grid, improves the profits of operators, and is conducive to promoting the development of clean energy, alleviating the energy crisis. However, this study has some limitations. There is only one renewable energy in the system, namely photovoltaic energy, and more kinds of renewable energy can be taken into account in future research.
Author Contributions
Conceptualization, N.N. and Y.-W.L.; methodology, Y.-W.L. and L.-L.L.; software N.N. and H.-Y.Y.; writing—original draft preparation, N.N. and Y.-W.L.; writing—review and editing, N.N. and Y.-W.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the key project of the Tianjin Natural Science Foundation (Project No. 19JCZDJC32100) and the Natural Science Foundation of Hebei Province of China (Project No. E2018202282).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not Applicable.
Acknowledgments
The authors thank Bimenyimana Samuel for valuable help in the final version of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| AC | absorption chiller |
| AO | aquila optimizer |
| bat | battery |
| CCHP | combined cooling, heating and power |
| ch | charge |
| COP | coefficient of performance |
| disch | discharge |
| EC | electric chiller |
| ESS | energy storage station |
| f | fitness function |
| F | objective function value |
| G | pollutant gas emission |
| GA | genetic algorithm |
| GB | gas boiler |
| GWO | gray wolf optimizer |
| H | heat energy |
| HE | heat exchanger |
| HR | heat recovery |
| IAO | improved aquila optimizer |
| MT | micro turbine |
| P | power |
| PSO | particle swarm optimization |
| PV | photovoltaic generator unit |
| SSA | salp swarm algorithm |
| TST | thermal storage tank |
| WOA | whale optimization algorithm |
| efficiency |
References
- Zhang, Y.; Jiang, J.; Zhang, X.; Sun, L. A hierarchical genetic algorithm and mixed-integer linear programming-based stochastic optimization of the configuration of integrated trigeneration energy systems. Clean Technol. Environ. Policy 2021, 23, 1913–1927. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, Q.; Wang, Z.; Jermsittiparsert, K.; Shafiee, M. A new optimized configuration for capacity and operation improvement of CCHP system based on developed owl search algorithm. Energy Rep. 2020, 6, 315–324. [Google Scholar] [CrossRef]
- Hassan, R.; Das, B.; Al-Abdeli, Y. Investigation of a hybrid renewable-based grid-independent electricity-heat nexus: Impacts of recovery and thermally storing waste heat and electricity. Energy Convers. Manag. 2022, 252, 115073. [Google Scholar] [CrossRef]
- Peng, D.; Wu, H.; Wang, L. Comprehensive energy cooperative optimization model based on energy conversion efficiency considering investment benefit. Int. J. Energy Res. 2021, 45, 2997–3015. [Google Scholar] [CrossRef]
- Li, N.; Zhao, X.; Shi, X.; Pei, Z.; Mu, H.; Taghizadeh-Hesary, F. Integrated energy systems with CCHP and hydrogen supply: A new outlet for curtailed wind power. Appl. Energy 2021, 303, 117619. [Google Scholar] [CrossRef]
- Das, B.; Al-Abdeli, Y.; Kothapalli, G. Integrating renewables into stand-alone hybrid systems meeting electric, heating, and cooling loads: A case study. Renew. Energy 2021, 180, 1222–1236. [Google Scholar] [CrossRef]
- Dong, H.; Fang, Z.; Ibrahim, A.; Cai, J. Optimized Operation of Integrated Energy Microgrid with Energy Storage Based on Short-Term Load Forecasting. Electronics 2022, 11, 22. [Google Scholar] [CrossRef]
- Namnabat, M.; Nazari, M.E. The effects of PV/T utilization on short-term scheduling of integrated distributed CHP system. In Proceedings of the 24th Electrical Power Distribution Conference, Khoramabad, Iran, 29 June 2019; pp. 1–6. [Google Scholar]
- Yan, R.; Lu, Z.; Wang, J.; Chen, H.; Wang, J.; Yang, Y.; Huang, D. Stochastic multi-scenario optimization for a hybrid combined cooling, heating and power system considering multi-criteria. Energy Convers. Manag. 2021, 233, 113911. [Google Scholar] [CrossRef]
- Li, L.; Liu, Z.; Tseng, M.; Zheng, S.; Lim, M. Improved tunicate swarm algorithm: Solving the dynamic economic emission dispatch problems. Appl. Soft Comput. 2021, 108, 107504. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, Z.; Zhou, C.; Wu, T.; Wu, T.; Wang, Y. Capacity allocation of HESS in micro-grid based on ABC algorithm. Int. J. Low-Carbon Technol. 2020, 15, 496–505. [Google Scholar] [CrossRef]
- Fragiacomo, P.; Lucarelli, G.; Genovese, M.; Florio, G. Multi-objective optimization model for fuel cell-based poly-generation energy systems. Energy 2021, 237, 121823. [Google Scholar] [CrossRef]
- Gu, W.; Tang, Y.; Peng, S.; Wang, D.; Sheng, W.; Liu, K. Optimal configuration and analysis of combined cooling, heating, and power microgrid with thermal storage tank under uncertainty. J. Renew. Sustain. Energy 2015, 7, 2125–2141. [Google Scholar] [CrossRef]
- Olamaei, J.; Nazari, M.; Bahravar, S. Economic environmental unit commitment for integrated CCHP-thermal-heat only system with considerations for valve-point effect based on a heuristic optimization algorithm. Energy 2018, 159, 737–750. [Google Scholar] [CrossRef]
- Kuang, J.; Zhang, C.; Bo, S. Stochastic dynamic solution for off-design operation optimization of combined cooling, heating, and power systems with energy storage. Appl. Therm. Eng. 2019, 163, 114356. [Google Scholar] [CrossRef]
- Soheyli, S.; Mehrjoo, M.; Mayam, M. Modeling and optimal resources allocation of a novel tri-distributed generation system based on sustainable energy resources. Energy Convers. Manag. 2017, 143, 1–22. [Google Scholar] [CrossRef]
- Li, F.; Sun, B.; Zhang, C.; Liu, C. A hybrid optimization-based scheduling strategy for combined cooling, heating, and power system with thermal energy storage. Energy 2019, 188, 115948. [Google Scholar] [CrossRef]
- Faridnia, N.; Habibi, D.; Lachowicz, S.; Kavousifard, A. Optimal scheduling in a microgrid with a tidal generation. Energy 2019, 171, 435–443. [Google Scholar] [CrossRef]
- Sun, X.; Wang, G.; Xu, L.; Yuan, H.; Youse, N. Optimal performance of a combined heat-power system with a proton exchange membrane fuel cell using a developed marine predators algorithm. J. Clean. Prod. 2021, 284, 124776. [Google Scholar] [CrossRef]
- Mao, Y.; Wu, J.; Zhang, W. An Effective Operation Strategy for CCHP System Integrated with Photovoltaic/Thermal Panels and Thermal Energy Storage. Energies 2020, 13, 6418. [Google Scholar] [CrossRef]
- Chen, K.; Pan, M. Operation optimization of combined cooling, heating, and power superstructure system for satisfying demand fluctuation. Energy 2021, 237, 121599. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, X.; Wang, Y.; Li, B.; Lu, H. A dynamic decision-making method for energy transaction price of CCHP microgrids considering multiple uncertainties. Int. J. Electr. Power Energy Syst. 2021, 127, 106592. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.; Al-qaness, M.; Gandomi, A. Aquila Optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Wang, S.; Jia, H.; Abualigah, L.; Liu, Q.; Zheng, R. An Improved Hybrid Aquila Optimizer and Harris Hawks Algorithm for Solving Industrial Engineering Optimization Problems. Processes 2021, 9, 1551. [Google Scholar] [CrossRef]
- Li, L.; Liu, Z.; Tseng, M.; Jantarakolica, K.; Lim, M. Using enhanced crow search algorithm optimization-extreme learning machine model to forecast short-term wind power. Expert Syst. Appl. 2021, 184, 115579. [Google Scholar] [CrossRef]
- Ma, B.; Lu, P.; Liu, Y.; Zhou, Q.; Hu, Y. Shared seagull optimization algorithm with mutation operators for global optimization. AIP Adv. 2021, 11, 125217. [Google Scholar] [CrossRef]
- Cho, H.; Smith, A.; Mago, P. Combined cooling, heating and power: A review of performance improvement and optimization. Appl. Energy 2014, 136, 168–185. [Google Scholar] [CrossRef]
- Liu, Z.; Li, L.; Liu, Y.; Liu, J.; Li, H.; Shen, Q. Dynamic economic emission dispatch considering renewable energy generation: A novel multi-objective optimization approach. Energy 2021, 235, 121407. [Google Scholar] [CrossRef]
- Nami, H.; Anvari-Moghaddam, A.; Nemati, A. Modeling and analysis of a solar boosted biomass-driven combined cooling, heating and power plant for domestic applications. Sustain. Energy Technol. Assess. 2021, 47, 101326. [Google Scholar] [CrossRef]
- Wei, D.; Ji, J.; Fang, J.; Yousefi, N. Evaluation and optimization of PEM Fuel Cell-based CCHP system based on Modified Mayfly Optimization Algorithm. Energy Rep. 2021, 7, 7663–7674. [Google Scholar] [CrossRef]
- Tonekaboni, N.; Feizbahr, M.; Tonekaboni, N.; Jiang, G.; Chen, H. Optimization of Solar CCHP Systems with Collector Enhanced by Porous Media and Nanofluid. Math. Probl. Eng. 2021, 2021, 9984840. [Google Scholar] [CrossRef]
- Li, H.; Kang, S.; Lu, L.; Liu, L.; Zhang, X.; Zhang, G. Optimal design and analysis of a new CHP-HP integrated system. Energy Convers. Manag. 2017, 146, 217–227. [Google Scholar] [CrossRef]
- Nazari, M.E.; Bahravar, S.; Olamaei, J. Effect of storage options on price-based scheduling for a hybrid trigeneration system. Int. J. Energy Res. 2020, 44, 7342–7356. [Google Scholar] [CrossRef]
- Li, G.; Wang, R.; Zhang, T.; Ming, M. Multi-Objective Optimal Design of Renewable Energy Integrated CCHP System Using PICEA-g. Energies 2018, 11, 743. [Google Scholar] [CrossRef] [Green Version]
- Leonzio, G. An innovative trigeneration system using biogas as renewable energy. Chin. J. Chem. Eng. 2018, 26, 1179–1191. [Google Scholar] [CrossRef]
- Dong, X.; Quan, C.; Jiang, T. Optimal Planning of Integrated Energy Systems Based on Coupled CCHP. Energies 2018, 11, 2621. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Cho, H.; Mago, P.; Zhang, H.; Yang, F. Multi-Objective Particle Swarm Optimization (MOPSO) for a Distributed Energy System Integrated with Energy Storage. J. Therm. Sci. 2019, 28, 1221–1235. [Google Scholar] [CrossRef]
- Mohsenipour, M.; Ebadollahi, M.; Rostamzadeh, H.; Amidpour, M. Design and evaluation of a solar-based trigeneration system for a nearly zero energy greenhouse in arid region. J. Clean. Prod. 2020, 254, 119990. [Google Scholar] [CrossRef]
- De Souza, R.; Casisi, M.; Micheli, D.; Reini, M. A Review of Small-Medium Combined Heat and Power (CHP) Technologies and Their Role within the 100% Renewable Energy Systems Scenario. Energies 2021, 14, 5338. [Google Scholar] [CrossRef]
- Zhao, H.; Lu, H.; Wang, X.; Li, B.; Wang, Y.; Liu, P.; Ma, Z. Research on Comprehensive Value of Electrical Energy Storage in CCHP Microgrid with Renewable Energy Based on Robust Optimization. Energies 2020, 13, 6526. [Google Scholar] [CrossRef]
- Gao, L.; Hwang, Y.; Cao, T. An overview of optimization technologies applied in combined cooling, heating and power systems. Renew. Sustain. Energy Rev. 2019, 114, 109344. [Google Scholar] [CrossRef]
- Wen, Q.; Liu, G.; Wu, W.; Liao, S. Genetic algorithm-based operation strategy optimization and multi-criteria evaluation of distributed energy system for commercial buildings. Energy Convers. Manag. 2020, 226, 113529. [Google Scholar] [CrossRef]
- Yousif, M.; Ai, Q.; Gao, Y.; Wattoo, W.; Jiang, Z.; Hao, R. Application of Particle Swarm Optimization to a Scheduling Strategy for Microgrids Coupled with Natural Gas Networks. Energies 2018, 11, 3499. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Zhou, L.; Wang, B.; Wang, Z.; Shafie-Khah, M.; Catalao, J. Modified Chaos Particle Swarm Optimization-Based Optimized Operation Model for Stand-Alone CCHP Microgrid. Appl. Sci. 2017, 7, 754. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z.; Yang, B.; Han, Y.; He, T.; He, P.; Meng, X.; He, X. Optimal PID Tuning of PLL for PV Inverter Based on Aquila Optimizer. Front. Energy Res. 2022, 9, 812467. [Google Scholar] [CrossRef]
- Fatani, A.; Dahou, A.; Al-qaness, M.; Lu, S.; Elaziz, M. Advanced Feature Extraction and Selection Approach Using Deep Learning and Aquila Optimizer for IoT Intrusion Detection System. Sensors 2022, 22, 140. [Google Scholar] [CrossRef] [PubMed]
- Deru, M.; Field, K.; Studer, D. U.S. Department of Energy Commercial Reference Building Models of the National Building Stock. 2011. Available online: https://www.energy.gov/eere/buildings/commercial-reference-buildings (accessed on 9 September 2020).
- Wilson, E. Commercial and Residential Hourly Load Profiles for all TMY3 Locations in the United States. 2020. Available online: https://openei.org/doe-opendata/dataset/commercial-and-residential-hourly-load-profiles-for-all-tmy3-locations-in-the-united-states (accessed on 9 September 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).