Optimal Design for a Bivariate Step-Stress Accelerated Life Test with Alpha Power Exponential Distribution Based on Type-I Progressive Censored Samples
Abstract
:1. Introduction
- (1)
- PSO’s core algorithm is straightforward.
- (2)
2. Model and Assumptions
Assumption
3. Likelihood Function and Fisher Information Matrix
4. Confidence Intervals
4.1. Approximate Confidence Intervals
4.2. Bootstrap Confidence Intervals
| Algorithm 1: The algorithm of the bootstrap confidence intervals. |
Step 0 Babic setup: Set b = 1 Calculate the MLE values of denoted by . Step 1 sampling: Obtain the bth bootstrap resample from , where is the MLE obtained in Step 0. Step 2 Bootstrap estimates: Calculate the bth bootstrap estimates using the resample obtained in Step 1. Step 3 Repetition: Set Repeat Steps 1–3 until b = B. Step 4. Arranging in ascending order Organize each estimate in ascending order so that we have and . |
5. Optimization Criterion
6. Bayesian Estimators
6.1. Prior Information and Loss Function
6.2. Posterior Analysis by SLF
7. Simulation Study
- (a)
- From a uniform (0, 1) distribution, generate a random sample of size n and arrange them in ascending order to produce order statistics .
- (b)
- Find such that for a given stress change time and parameter ,
- (c)
- units were randomly removed from non-failed items at time . Assume that follows a binomial distribution with a chance of removal of .
- (d)
- Find such that for a given stress change time and parameter ,
- (e)
- units were randomly removed from non-failed items at time . Assume that follows a binomial distribution with a chance of removal of .
- (f)
- Find such that for a given prefixed censoring time and parameter ,
- (g)
- units were randomly removed from non-failed items at time .
- (h)
- The following demonstrates how to obtain ordered observations:
- (i)
- The following are the model parameters and time:
- (j)
- The probability for binomial distribution has been changed to 0.3 and 0.5.
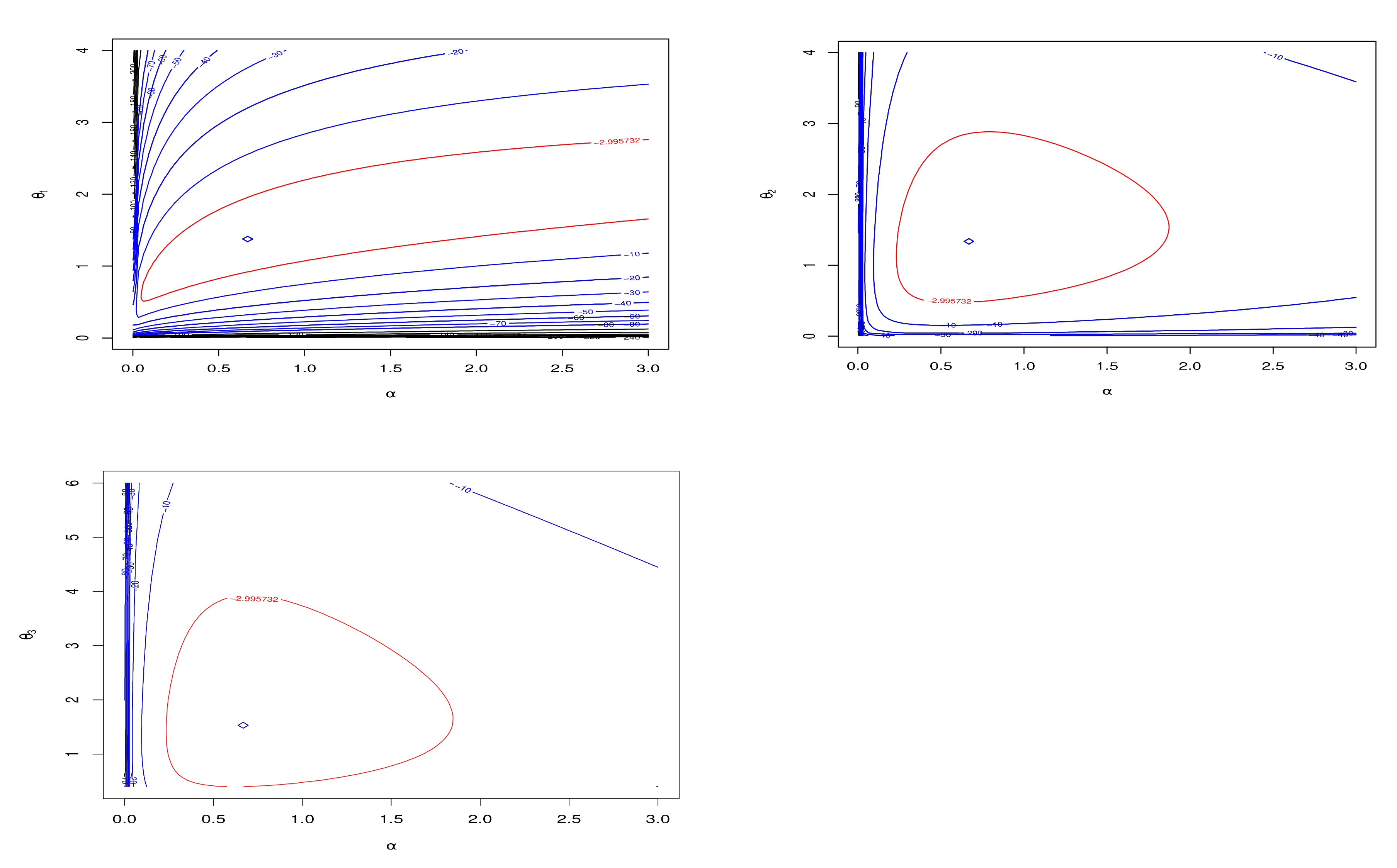
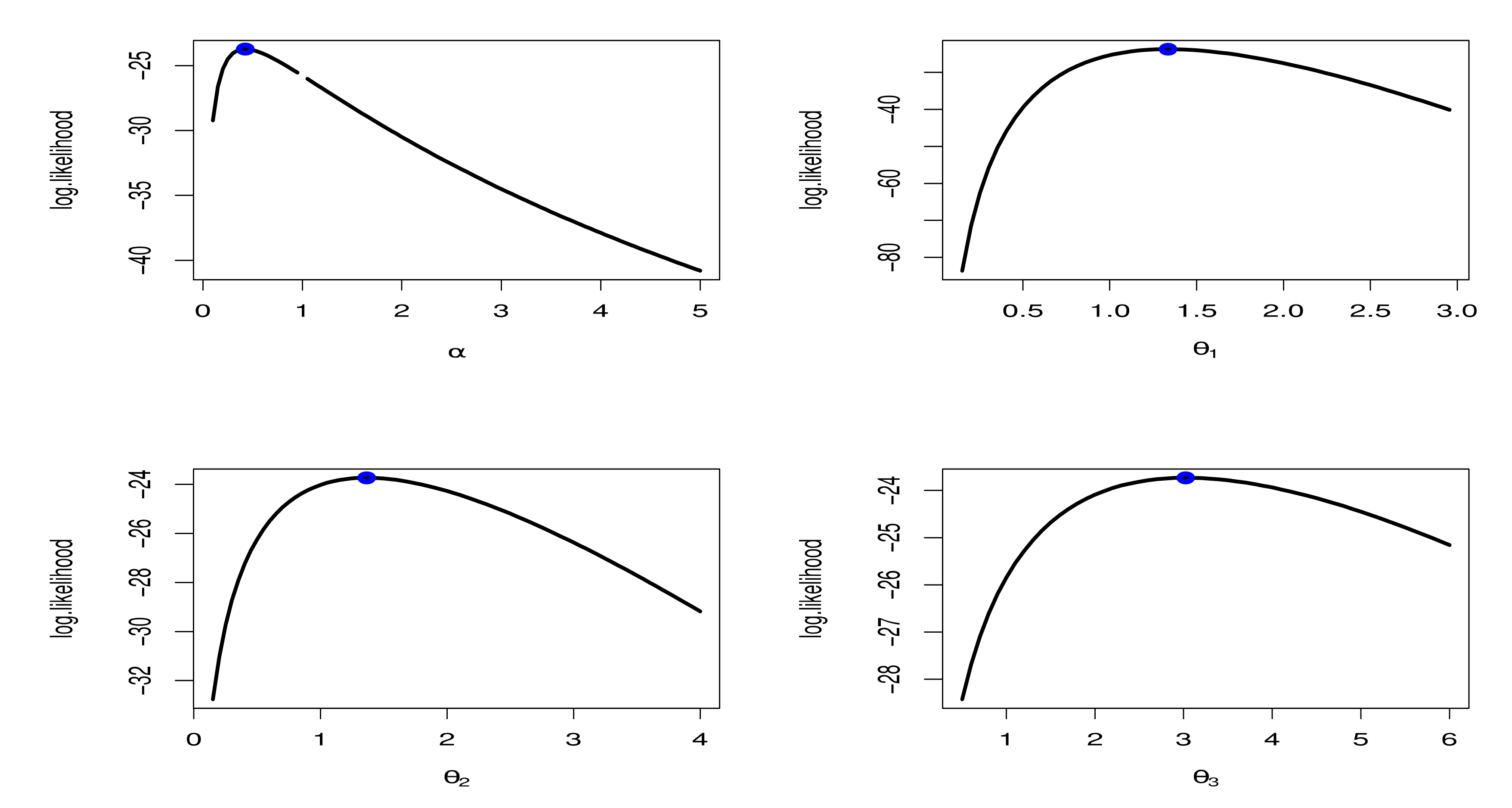
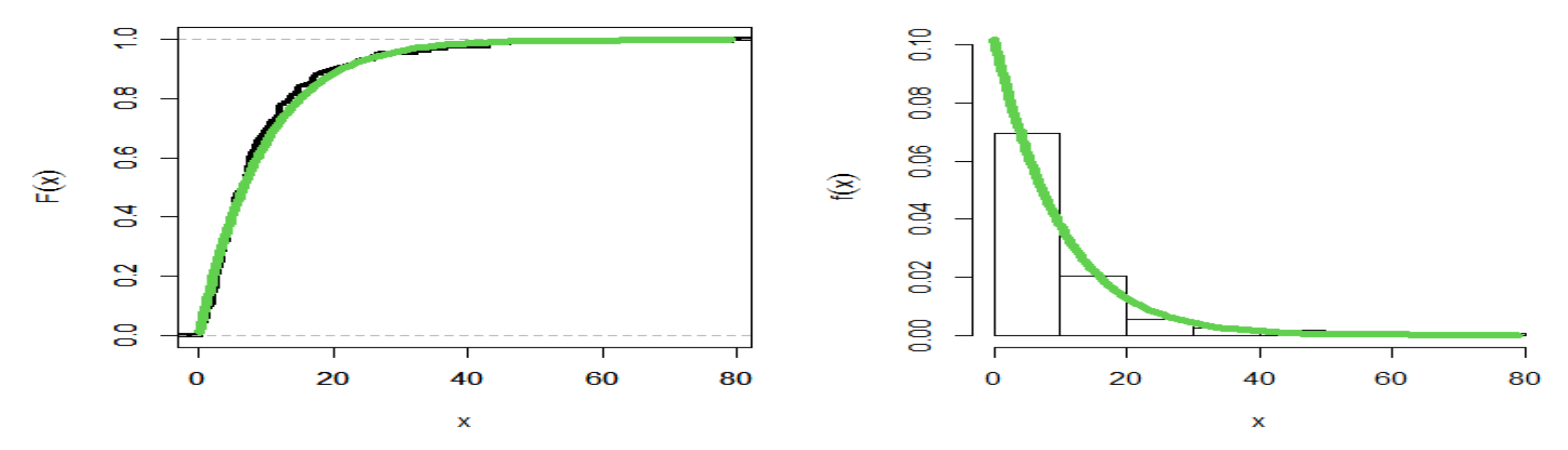
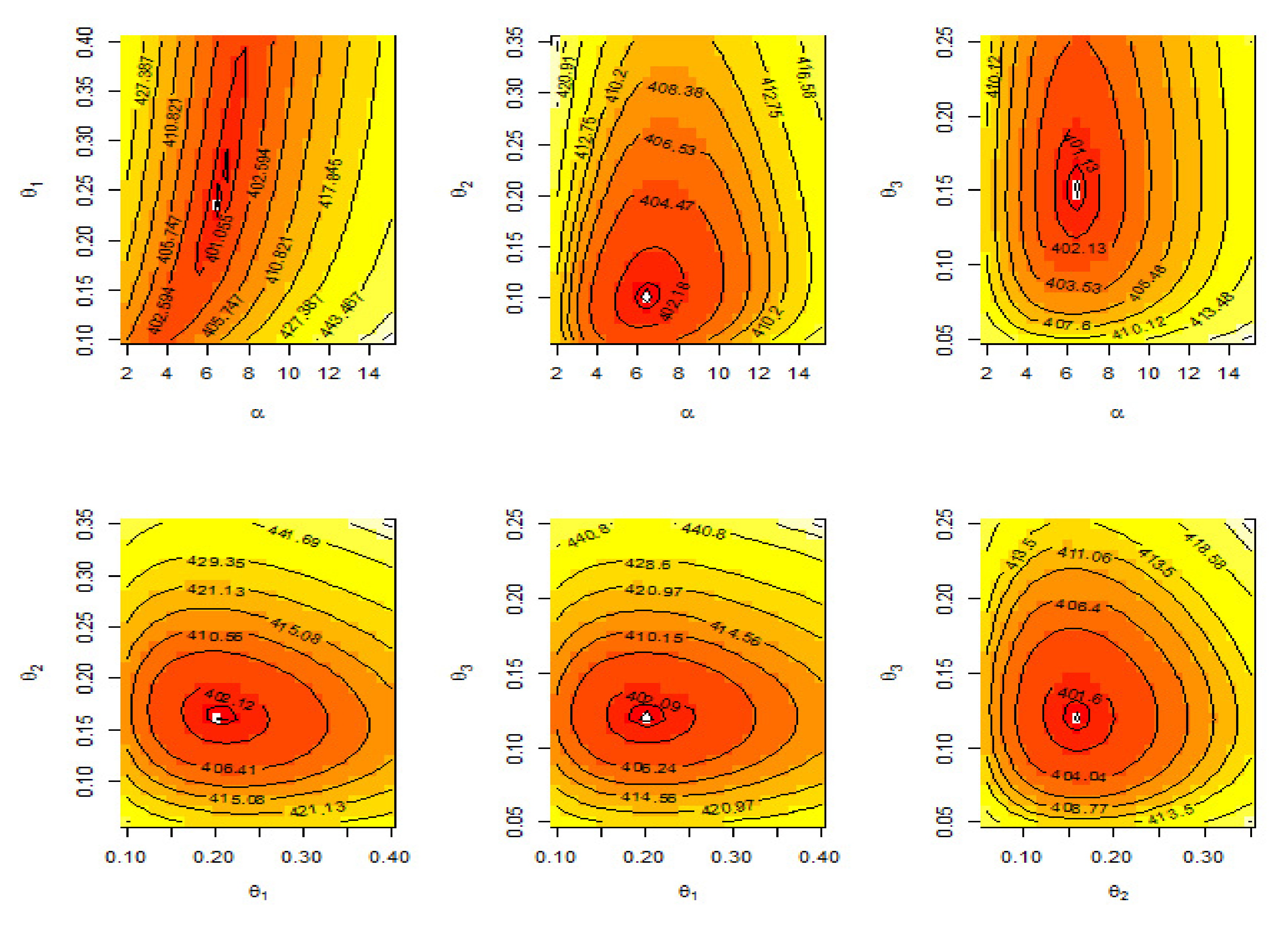
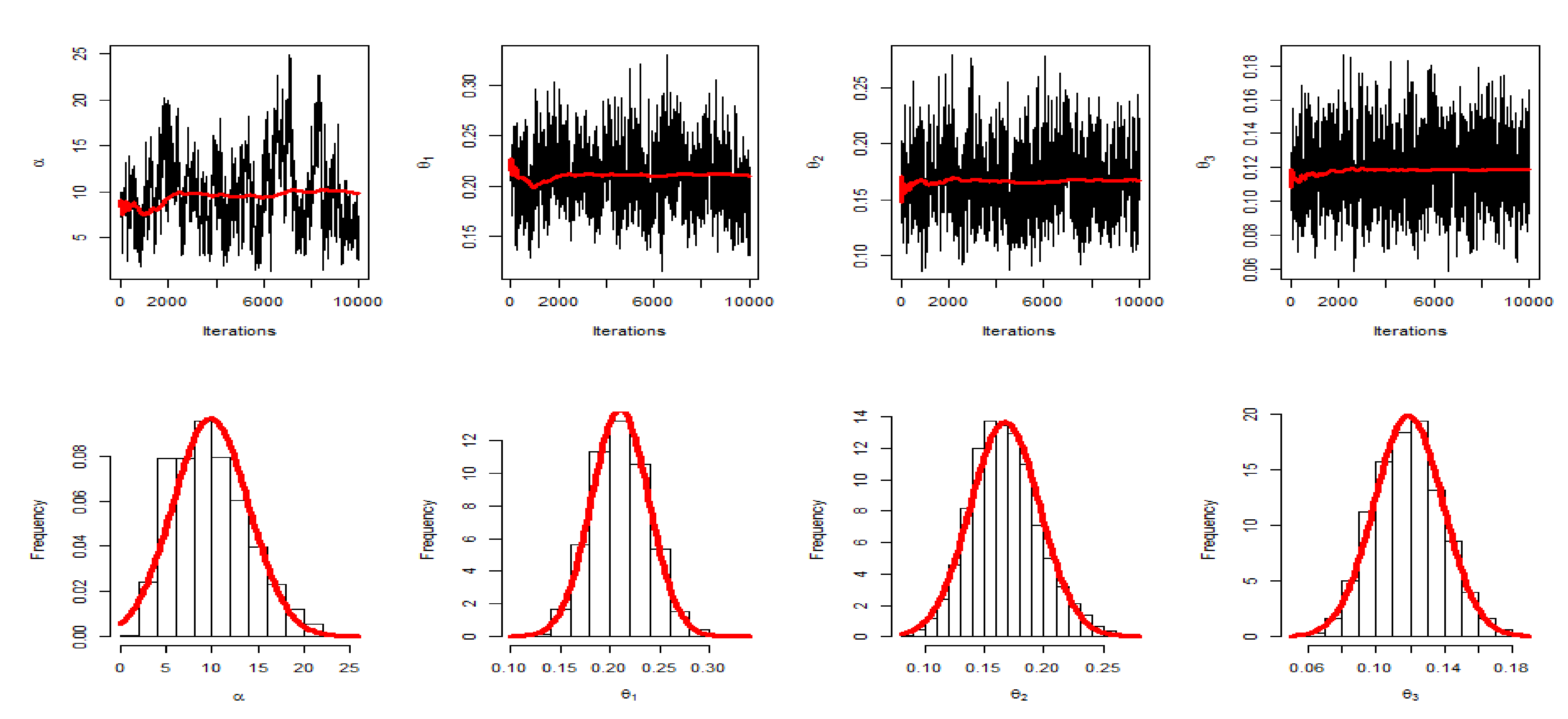
8. Application of Real Data
8.1. Cancer Patient Data
8.2. Failure Times
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meeker, W.Q.; Escobar, L.A. Statistical Methods for Reliability Data; John Wiley & Sons: New York, NY, USA, 2014. [Google Scholar]
- Nelson, W.B. Accelerated Testing: Statistical Models, Test Plans, and Data Analyses; John Wiley & Sons: New York, NY, USA, 2009. [Google Scholar]
- Pascual, F.G.; Meeker, W.Q.; Escobar, L.A. Accelerated Life Test Models and Data Analysis. In Handbook of Engineering Statistics; Pham, H., Ed.; Springer: New York, NY, USA, 2006; Chapter 22. [Google Scholar]
- Ramadan, S.Z. Effect of progressive Type-I right censoring on bayesian statistical inference of simple step-stress acceleration life testing plan under Weibull life distribution. World Acad. Sci. Eng. Technol. Int. J. Mech. Aerosp. Ind. Mechatron. Manuf. Eng. 2014, 8, 327–331. [Google Scholar]
- Balakrishnan, N.; Aggarwala, R. Progressive Censoring: Theory, Methods, and Applications; Birkh€auser: Boston, MA, USA, 2000. [Google Scholar]
- Balakrishnan, N. Progressive censoring methodology: An appraisal. Test 2007, 16, 211–259. [Google Scholar] [CrossRef]
- Almongy, H.M.; Alshenawy, F.Y.; Almetwally, E.M.; Abdo, D.A. Applying transformer insulation using Weibull extended distribution based on progressive censoring scheme. Axioms 2021, 10, 100. [Google Scholar] [CrossRef]
- Wu, S.J. Estimation for the two darameter Pareto distribution under progressive censoring with uniform removals. J. Stat. Comput. Simul. 2003, 73, 125–134. [Google Scholar] [CrossRef]
- Gouno, E.; Sen, A.; Balakrishnan, N. Optimal step-stress test under progressive Type-I censoring. IEEE Trans. Reliab. 2004, 53, 388–393. [Google Scholar] [CrossRef]
- El-Din, M.M.; Abu-Youssef, S.E.; Aly, N.S.; El-Raheem, A.A. Estimation in step-stress accelerated life tests for Weibull distribution with progressive first-failure censoring. J. Stat. Appl. Probab. 2014, 3, 403–411. [Google Scholar]
- Hakamipour, N. Time and cost constrained optimal designs of multiple step stress tests under progressive censoring. Int. J. Qual. Reliab. Manag. 2019, 36, 1721–1733. [Google Scholar] [CrossRef]
- Li, C.; Fard, N. Optimum bivariate step-stress accelerated life test for censored data. IEEE Trans. Reliab. 2007, 56, 77–84. [Google Scholar] [CrossRef]
- Ling, L.; Xu, W.; Li, M. Optimal bivariate step-stress accelerated life test for Type-I hybrid censored data. J. Stat. Comput.Simul. 2011, 81, 1175–1186. [Google Scholar] [CrossRef]
- Mahdavi, A.; Kundu, D. A New Method for Generating Distributions with an Application to Exponential Distribution. Commun. Stat. Theory Methods 2017, 46, 6543–6557. [Google Scholar] [CrossRef]
- Nassar, M.; Alzaatreh, A.; Mead, M.; Abo-Kasem, O. Alpha power Weibull distribution: Properties and applications. Commun. Stat. Theory Methods 2017, 46, 10236–10252. [Google Scholar] [CrossRef]
- Dey, A.; Alzaatreh, A.; Zhang, C.; Kumar, D.A. new extension of generalized exponential distribution with application to ozone data. Ozone Sci. Eng. 2017, 39, 273–285. [Google Scholar] [CrossRef]
- Nadarajah, S.; Okorie, I.E. On the moments of the alpha power transformed generalized exponential distribution. Ozone Sci. Eng. 2018, 40, 330–335. [Google Scholar] [CrossRef]
- Ibrahim, G.M.; Hassan, A.S.; Almetwally, E.M.; Almongy, H.M. Parameter estimation of alpha power inverted Topp–Leone distribution with applications. Intell. Autom. Soft Comput. 2021, 29, 353–371. [Google Scholar] [CrossRef]
- Nassar, M.; Kumar, D.; Dey, S.; Cordeiro, G.M.; Afify, A.Z. The Marshall–Olkin alpha power family of distributions with applications. J. Comput. Appl. Math. 2019, 351, 41–53. [Google Scholar] [CrossRef]
- Almetwally, E.M. Marshall olkin alpha power extended Weibull distribution: Different methods of estimation based on type i and type II censoring. Gazi Univ. J. Sci. 2022, 35, 293–312. [Google Scholar]
- Han, D.; Kundu, D. Inference for a step-stress model with competing risks for failure from the generalized exponential distribution under type-I censoring. IEEE Trans. Reliab. 2014, 64, 31–43. [Google Scholar] [CrossRef]
- Ismail, A.A. Statistical inference for a step-stress partially-accelerated life test model with an adaptive Type-I progressively hybrid censored data from Weibull distribution. Stat. Pap. 2016, 57, 271–301. [Google Scholar] [CrossRef]
- Sharon, V.A.; Vaidyanathan, V.S. Analysis of simple step-stress accelerated life test data from Lindley distribution under type-I censoring. Statistica 2016, 76, 233–248. [Google Scholar]
- Han, D. Optimal accelerated life tests under a cost constraint with non-uniform stress durations. Qual. Eng. 2017, 29, 409–430. [Google Scholar] [CrossRef]
- Zhang, C.; Shi, Y. Statistical prediction of failure times under generalized progressive hybrid censoring in a simple step-stress accelerated competing risks model. J. Syst. Eng. Electron. 2017, 28, 282–291. [Google Scholar]
- Engelbrecht, A.P. Fundamentals of Computational Swarm Intelligence; John Wiley & Sons: West Sussex, UK, 2005. [Google Scholar]
- Kennedy, J.; Eberhart, R.C.; Shi, Y. Swarm Intelligence; Morgan Kaufmann Publishers: San Francisco, CA, USA, 2001. [Google Scholar]
- Li, L.; Liu, F. Application of Particle Swarm Optimization Algorithm to Engineering Structures, Group Search Optimization for Applications in Structural Design; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Kulkarni, M.N.K.; Patekar, M.S.; Bhoskar, M.T.; Kulkarni, M.O.; Kakandikar, G.M.; Nandedkar, V.M. Particle swarm optimization applications to mechanical engineering-A review. Mater. Today Proc. 2015, 2, 2631–2639. [Google Scholar] [CrossRef]
- Nelson, W. Accelerated life testing step-stress models and data analysis. IEEE Trans. Reliab. 1980, 29, 103–108. [Google Scholar] [CrossRef]
- Neyman, J. Outline of a theory of statistical estimation based on the classical theory of probability. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1937, 236, 333–380. [Google Scholar]
- Khan, M.A.; Chandra, N. Estimation and optimal plan for bivariate step-stress accelerated life test under progressive Type-I censoring. Pak. J. Stat. Oper. Res. 2021, 17, 683–694. [Google Scholar] [CrossRef]
- Tibshirani, R.; Efron, B. An Introduction to the Bootstrap; Chapman & Hall, Inc.: London, UK, 1993. [Google Scholar]
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Application; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Khalili-Damghani, K.; Abtahi, A.R.; Tavana, M. A new multi-objective particle swarm optimization method for solving reliability redundancy allocation problems. Reliab. Eng. Syst. Saf. 2013, 111, 58–75. [Google Scholar] [CrossRef]
- Almetwally, E.M.; Abdo, D.A.; Hafez, E.H.; Jawa, T.M.; Sayed-Ahmed, N.; Almongy, H.M. The new discrete distribution with application to COVID-19 Data. Results Phys. 2022, 32, 104–127. [Google Scholar] [CrossRef]
- Metwally, A.S.M.; Hassan, A.S.; Almetwally, E.M.; Kibria, B.M.; Almongy, H.M. Reliability Analysis of the New Exponential Inverted Topp–Leone Distribution with Applications. Entropy 2021, 23, 1662. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Rubin, D.B. Bayesian Data Analysis, 2nd ed.; Chapman and Hall/CRC: London, UK, 2004. [Google Scholar]
- Lynch, S.M. Introduction to Applied Bayesian Statistics and Estimation for Social Scientists; Springer: New York, NY, USA, 2007. [Google Scholar]
- Murthy, D.P.; Xie, M.; Jiang, R. Weibull Models; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Lee, E.T.; Wang, J.W. Statistical Methods for Survival Data Analysis, 3rd ed.; Wiley: New York, NY, USA, 2003. [Google Scholar]






| , T = 3.2 | MLE | Bayesian | ||||||
|---|---|---|---|---|---|---|---|---|
| n | p | Bias | MSE | L.CI | Bias | SE | L.CCI | |
| 70 | 0.3 | 0.7278 | 2.3043 | 8.5740 | 0.0258 | 1.5258 | 0.6027 | |
| 0.9449 | 1.2160 | 2.2305 | −0.2753 | 0.2247 | 0.2476 | |||
| 0.0774 | 0.0484 | 0.8081 | −0.0610 | 0.0330 | 0.4087 | |||
| −0.0738 | 0.1004 | 1.2093 | −0.0668 | 0.0943 | 0.5564 | |||
| 0.5 | 0.7099 | 2.2405 | 8.5399 | 0.0293 | 1.5293 | 0.5990 | ||
| 0.9413 | 1.2086 | 2.2284 | −0.2806 | 0.2194 | 0.2437 | |||
| 0.0801 | 0.0517 | 0.8353 | −0.0798 | 0.0302 | 0.4081 | |||
| −0.0783 | 0.0997 | 1.2000 | −0.0648 | 0.0904 | 0.5323 | |||
| 150 | 0.3 | 0.2799 | 1.2221 | 5.7453 | 0.0741 | 0.2595 | 0.5537 | |
| 0.9374 | 1.0627 | 1.6834 | −0.3800 | 0.1448 | 0.0793 | |||
| 0.0859 | 0.0258 | 0.5319 | −0.2106 | 0.0246 | 0.1588 | |||
| −0.0961 | 0.0455 | 0.7474 | −0.1615 | 0.0369 | 0.3548 | |||
| 0.5 | 0.4512 | 1.7213 | 6.2263 | 0.0522 | 0.1705 | 0.4576 | ||
| 0.9710 | 1.1580 | 1.8199 | −0.4082 | 0.1667 | 0.0407 | |||
| 0.0776 | 0.0338 | 0.6542 | −0.1527 | 0.0277 | 0.2461 | |||
| −0.0646 | 0.0971 | 1.2440 | −0.0366 | 0.0129 | 0.4132 | |||
| 300 | 0.3 | 0.1903 | 0.9224 | 4.0323 | 0.1040 | 0.0255 | 0.4505 | |
| 0.9682 | 1.0532 | 1.3347 | −0.4256 | 0.1428 | 0.0322 | |||
| 0.0892 | 0.0184 | 0.4020 | −0.2694 | 0.0173 | 0.0861 | |||
| −0.0968 | 0.0267 | 0.5171 | −0.2592 | 0.0171 | 0.2171 | |||
| 0.5 | 0.1711 | 0.9239 | 3.9434 | 0.0614 | 0.0131 | 0.3684 | ||
| 0.9704 | 1.0545 | 1.3174 | −0.4345 | 0.1589 | 0.0238 | |||
| 0.0938 | 0.0230 | 0.4678 | −0.2295 | 0.0205 | 0.1225 | |||
| −0.0890 | 0.0461 | 0.7671 | −0.0780 | 0.0123 | 0.3278 | |||
| n | p | Mean | Bias | MSE | Lower | Upper |
|---|---|---|---|---|---|---|
| 70 | 0.3 | 0.3018 | 0.0018 | 0.0069 | 0.1389 | 0.4648 |
| 0.5 | 0.3180 | −0.1820 | 0.0070 | 0.1194 | 0.5167 | |
| 150 | 0.3 | 0.2993 | −0.0007 | 0.0031 | 0.1909 | 0.4076 |
| 0.5 | 0.4972 | −0.0028 | 0.0037 | 0.3787 | 0.6156 | |
| 300 | 0.3 | 0.2983 | −0.0017 | 0.0014 | 0.2258 | 0.3709 |
| 0.5 | 0.5014 | 0.0014 | 0.0019 | 0.4161 | 0.5866 |
| , T = 4 | MLE | Bayesian | ||||||
|---|---|---|---|---|---|---|---|---|
| n | p | Bias | MSE | L.CI | Bias | MSE | L.CCI | |
| 70 | 0.3 | 0.3473 | 1.4360 | 7.1447 | 0.0423 | 0.0239 | 0.5597 | |
| −0.0048 | 0.0238 | 0.6046 | −0.0038 | 0.0147 | 0.0663 | |||
| −0.0065 | 0.0179 | 0.5240 | −0.0023 | 0.0156 | 0.1898 | |||
| 0.0068 | 0.0271 | 0.6449 | −0.0028 | 0.0219 | 0.3028 | |||
| 0.5 | 0.3265 | 1.2711 | 6.9803 | 0.0281 | 0.0176 | 0.5024 | ||
| −0.0002 | 0.0273 | 0.6484 | −0.0039 | 0.0136 | 0.0463 | |||
| 0.0046 | 0.0267 | 0.6410 | −0.0015 | 0.0207 | 0.2706 | |||
| 0.0141 | 0.0563 | 0.9293 | −0.0114 | 0.0262 | 0.3937 | |||
| 150 | 0.3 | 0.0667 | 0.9947 | 5.5357 | 0.0532 | 0.0197 | 0.5077 | |
| −0.0072 | 0.0131 | 0.4479 | −0.4294 | 0.0128 | 0.0270 | |||
| −0.0026 | 0.0091 | 0.3745 | −0.2948 | 0.0081 | 0.0715 | |||
| −0.0073 | 0.0110 | 0.4110 | −0.3676 | 0.0102 | 0.1152 | |||
| 0.5 | 0.2033 | 0.9216 | 5.7859 | 0.0309 | 0.0129 | 0.4391 | ||
| −0.0018 | 0.0133 | 0.4527 | −0.4330 | 0.0129 | 0.0236 | |||
| −0.0055 | 0.0123 | 0.4355 | −0.2466 | 0.0121 | 0.1160 | |||
| 0.0175 | 0.0214 | 0.5698 | −0.2376 | 0.0206 | 0.2538 | |||
| 300 | 0.3 | 0.1297 | 0.8214 | 4.2928 | 0.0397 | 0.0128 | 0.4195 | |
| −0.0019 | 0.0079 | 0.3476 | −0.4458 | 0.0062 | 0.0235 | |||
| −0.0070 | 0.0050 | 0.2757 | −0.3205 | 0.0031 | 0.0554 | |||
| 0.0002 | 0.0060 | 0.3049 | −0.3979 | 0.0059 | 0.0693 | |||
| 0.5 | 0.0906 | 0.8317 | 4.4886 | 0.0373 | 0.0088 | 0.3168 | ||
| −0.0023 | 0.0079 | 0.3478 | −0.4473 | 0.0061 | 0.0219 | |||
| −0.0015 | 0.0064 | 0.3128 | −0.2803 | 0.0061 | 0.0796 | |||
| 0.0016 | 0.0098 | 0.3875 | −0.2872 | 0.0084 | 0.1556 | |||
| n | p | Mean | Bias | MSE | Lower | Upper |
|---|---|---|---|---|---|---|
| 70 | 0.3 | 0.3046 | 0.0046 | 0.0027 | 0.2028 | 0.4065 |
| 0.5 | 0.4989 | −0.0011 | 0.0035 | 0.3824 | 0.6155 | |
| 150 | 0.3 | 0.3014 | 0.0014 | 0.0012 | 0.2322 | 0.3706 |
| 0.5 | 0.4963 | −0.0037 | 0.0017 | 0.4165 | 0.5761 | |
| 300 | 0.3 | 0.2988 | −0.0012 | 0.0006 | 0.2504 | 0.3471 |
| 0.5 | 0.5011 | 0.0011 | 0.0008 | 0.4463 | 0.5559 |
| , T = 2 | MLE | Bayesian | ||||||
|---|---|---|---|---|---|---|---|---|
| n | p | Bias | MSE | L.CI | Bias | MSE | L.CCI | |
| 70 | 0.3 | 1.0029 | 9.1615 | 11.2060 | 0.2264 | 0.0749 | 0.6125 | |
| −0.0018 | 0.4202 | 2.5437 | −0.9248 | 0.3865 | 0.3596 | |||
| −0.0370 | 0.2480 | 1.9485 | −0.1631 | 0.0570 | 0.6684 | |||
| 0.1087 | 0.8958 | 3.6894 | −0.0565 | 0.0303 | 0.6574 | |||
| 0.5 | 1.1488 | 11.6938 | 12.6384 | 0.2000 | 0.0549 | 0.4745 | ||
| −0.0151 | 0.4272 | 2.5640 | −0.9322 | 0.3087 | 0.2679 | |||
| −0.0968 | 0.2449 | 1.9043 | −0.0749 | 0.0214 | 0.4901 | |||
| 0.3101 | 2.3934 | 5.9473 | −0.0106 | 0.0145 | 0.4704 | |||
| 150 | 0.3 | 0.4012 | 3.2915 | 6.9427 | 0.3073 | 0.0711 | 0.5364 | |
| −0.0521 | 0.2512 | 1.9562 | −1.1279 | 0.2273 | 0.1210 | |||
| −0.0828 | 0.1283 | 1.3677 | −0.4008 | 0.0483 | 0.5557 | |||
| −0.0140 | 0.2345 | 1.8995 | −0.1698 | 0.0257 | 0.6306 | |||
| 0.5 | 0.4554 | 3.3671 | 6.9749 | 0.2536 | 0.0474 | 0.3998 | ||
| −0.0459 | 0.2884 | 2.0995 | −1.0900 | 0.2189 | 0.1140 | |||
| −0.0452 | 0.1512 | 1.5154 | −0.1732 | 0.0214 | 0.4536 | |||
| 0.0530 | 0.6104 | 3.0587 | −0.0247 | 0.0128 | 0.4374 | |||
| 300 | 0.3 | 0.1610 | 1.5009 | 4.7655 | 0.3445 | 0.0701 | 0.4165 | |
| −0.0611 | 0.1732 | 1.6152 | −1.1707 | 0.1371 | 0.0992 | |||
| −0.0750 | 0.0751 | 1.0345 | −0.5436 | 0.0363 | 0.3864 | |||
| −0.0063 | 0.1354 | 1.4436 | −0.2500 | 0.0248 | 0.5730 | |||
| 0.5 | 0.2145 | 1.5309 | 4.7815 | 0.2684 | 0.0382 | 0.3761 | ||
| −0.0515 | 0.1719 | 1.6144 | −1.1196 | 0.1254 | 0.1125 | |||
| −0.0407 | 0.0800 | 1.0981 | −0.2723 | 0.0179 | 0.4126 | |||
| 0.0620 | 0.3102 | 2.1720 | −0.0340 | 0.0118 | 0.4008 | |||
| n | p | Mean | Bias | MSE | Lower | Upper |
|---|---|---|---|---|---|---|
| 70 | 0.3 | 0.3015 | 0.0015 | 0.0047 | 0.1664 | 0.4367 |
| 0.5 | 0.5001 | 0.0001 | 0.0065 | 0.3416 | 0.6587 | |
| 150 | 0.3 | 0.3016 | 0.0016 | 0.0025 | 0.2033 | 0.3998 |
| 0.5 | 0.4991 | −0.0009 | 0.0029 | 0.3929 | 0.6053 | |
| 300 | 0.3 | 0.2992 | −0.0008 | 0.0011 | 0.2331 | 0.3653 |
| 0.5 | 0.4985 | −0.0015 | 0.0015 | 0.4222 | 0.5748 |
| , T = 2 | MLE | Bayesian | ||||||
|---|---|---|---|---|---|---|---|---|
| n | p | Bias | MSE | L.CI | Bias | MSE | L.CCI | |
| 70 | 0.3 | 0.5885 | 2.5151 | 5.7787 | 0.4140 | 0.1925 | 0.5559 | |
| 0.1436 | 0.4858 | 2.6761 | −0.8796 | 0.3799 | 0.6027 | |||
| −0.0158 | 0.3424 | 2.2952 | −0.0512 | 0.0264 | 0.5635 | |||
| 0.3021 | 2.3486 | 5.8955 | −0.0324 | 0.0262 | 0.6167 | |||
| 0.5 | 0.4762 | 1.6822 | 4.7339 | 0.4161 | 0.1916 | 0.5124 | ||
| 0.1011 | 0.4350 | 2.5573 | −0.8834 | 0.3804 | 0.5714 | |||
| −0.0218 | 0.3681 | 2.3791 | −0.0483 | 0.0257 | 0.5562 | |||
| 0.3672 | 2.8932 | 6.5170 | −0.0307 | 0.0249 | 0.6062 | |||
| 150 | 0.3 | 0.2412 | 0.6417 | 2.9975 | 0.5195 | 0.1846 | 0.4525 | |
| 0.0198 | 0.3039 | 2.1619 | −1.0911 | 0.2922 | 0.1661 | |||
| −0.0643 | 0.1796 | 1.6435 | −0.1522 | 0.0245 | 0.5701 | |||
| 0.1011 | 0.6331 | 3.0969 | −0.0736 | 0.0259 | 0.5340 | |||
| 0.5 | 0.2525 | 0.5780 | 2.8138 | 0.4607 | 0.1822 | 0.3634 | ||
| 0.0464 | 0.2898 | 2.1045 | −1.0534 | 0.2111 | 0.1412 | |||
| −0.0387 | 0.2225 | 1.8447 | −0.0610 | 0.0164 | 0.4280 | |||
| 0.1954 | 1.2317 | 4.2869 | −0.0112 | 0.0115 | 0.4150 | |||
| 300 | 0.3 | 0.1083 | 0.2218 | 1.7985 | 0.5743 | 0.1820 | 0.4319 | |
| −0.0070 | 0.1894 | 1.7077 | −1.1404 | 0.1530 | 0.1158 | |||
| −0.0529 | 0.1078 | 1.2716 | −0.2949 | 0.0211 | 0.5324 | |||
| −0.0065 | 0.1922 | 1.7202 | −0.1361 | 0.0237 | 0.5119 | |||
| 0.5 | 0.1165 | 0.3155 | 2.1562 | 0.4865 | 0.0944 | 0.3435 | ||
| −0.0291 | 0.2024 | 1.7618 | −1.0808 | 0.1693 | 0.1271 | |||
| −0.0555 | 0.1266 | 1.3790 | −0.1047 | 0.0122 | 0.4076 | |||
| 0.0988 | 0.5235 | 2.8126 | −0.0152 | 0.0106 | 0.3929 | |||
| n | p | Mean | Bias | MSE | Lower | Upper |
|---|---|---|---|---|---|---|
| 70 | 0.3 | 0.3001 | 0.0001 | 0.0088 | 0.1164 | 0.4839 |
| 0.5 | 0.3339 | −0.1661 | 0.0091 | 0.0950 | 0.5729 | |
| 150 | 0.3 | 0.2984 | −0.0016 | 0.0039 | 0.1752 | 0.4217 |
| 0.5 | 0.4921 | −0.0079 | 0.0051 | 0.3529 | 0.6312 | |
| 300 | 0.3 | 0.2979 | −0.0021 | 0.0020 | 0.2105 | 0.3852 |
| 0.5 | 0.5035 | 0.0035 | 0.0023 | 0.4099 | 0.5971 |
| p | Sample Size | Failure Times | Censored Data |
|---|---|---|---|
| 0.3 | 0.0120, 0.0208, 0.0225, 0.0227, 0.0484, 0.0529, 0.0634, 0.0666, 0.0730, 0.0753, 0.0779, 0.0810, 0.1141, 0.1204, 0.1303, 0.1313, 0.1400, 0.1537, 0.1596, 0.1690, 0.1702, 0.1918, 0.1993, 0.2322, 0.2369, 0.2450, 0.2670, 0.2713, 0.2721, 0.2958, 0.2980, 0.3042, 0.3089, 0.3122, 0.3216, 0.3337, 0.3893, 0.4084, 0.4175, 0.4294, 0.4445, 0.4736, 0.5427, 0.5676, 0.5836, 0.6056, 0.6298, 0.6338, 0.6646 | ||
| 0.7734, 0.7879, 0.8797, 0.9038, 0.9560, 0.9647, 1.1626 | |||
| 1.2900, 1.3263, 1.3430, 1.7225, 1.8973 | |||
| 0.5 | 0.0052, 0.0329, 0.0450, 0.0481, 0.0646, 0.0657, 0.0757, 0.0764, 0.0793, 0.0821, 0.0992, 0.1066, 0.1074, 0.1085, 0.1085, 0.1253, 0.1622, 0.1760, 0.1956, 0.2006, 0.2124, 0.2208, 0.2216, 0.2300, 0.2300, 0.2429, 0.2519, 0.2612, 0.2794, 0.2881, 0.3410, 0.3560, 0.3920, 0.4025, 0.4227, 0.4280, 0.4338, 0.4670, 0.5015, 0.5550, 0.6055, 0.6245, 0.6305, 0.6445, 0.6503, 0.6602 | ||
| 0.7253 0.8509 0.9028 0.9039 1.0172 1.1254 1.1374 1.1419 | |||
| 1.4019 1.4843 1.5290 1.9690 1.9768 |
| MLE | Bayesian | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimates | SE | Lower | Upper | Estimates | SE | Lower | Upper | ||
| 0.3 | 0.4260 | 0.9371 | 0.0041 | 2.2626 | 1.2811 | 0.4866 | 0.3997 | 2.2355 | |
| 1.3353 | 1.0563 | 0.0074 | 3.4056 | 0.2054 | 0.0609 | 0.1066 | 0.3117 | ||
| 1.3649 | 0.7775 | 0.0016 | 2.8889 | 1.1852 | 0.4833 | 0.3710 | 2.0742 | ||
| 3.0237 | 1.4760 | 0.1307 | 5.9166 | 2.1696 | 1.0009 | 0.5887 | 4.2216 | ||
| 0.5 | 0.6613 | 1.0077 | 0.0031 | 2.6365 | 2.3943 | 0.9352 | 0.6052 | 4.4307 | |
| 1.3650 | 0.7497 | 0.0010 | 2.8344 | 0.2429 | 0.0760 | 0.1179 | 0.3790 | ||
| 1.3199 | 0.5822 | 0.1788 | 2.4610 | 1.1281 | 0.3870 | 0.4135 | 1.8778 | ||
| 1.5370 | 0.7223 | 0.1214 | 2.9527 | 1.1173 | 0.4894 | 0.3090 | 2.0967 | ||
| p | 0.3 | 0.5 |
|---|---|---|
| OA | 4.7769 | 2.4382 |
| OB | 0.0204 | 0.0049 |
| Estimates | SE | KSD | KSPV | AIC | BIC | |
|---|---|---|---|---|---|---|
| 1.1744 | 0.8437 | 0.0793 | 0.3963 | 832.6364 | 838.3404 | |
| 0.1113 | 0.0226 |
| MLE | Bayesian | |||||||
|---|---|---|---|---|---|---|---|---|
| Estimates | SE | Lower | Upper | Estimates | SE | Lower | Upper | |
| 8.5483 | 4.1609 | 0.3930 | 16.7036 | 9.8196 | 4.1350 | 2.6035 | 17.7296 | |
| 0.2072 | 0.0401 | 0.1287 | 0.2858 | 0.2100 | 0.0287 | 0.1548 | 0.2644 | |
| 0.1636 | 0.0295 | 0.1057 | 0.2216 | 0.1673 | 0.0292 | 0.1107 | 0.2268 | |
| 0.1179 | 0.0210 | 0.0767 | 0.1591 | 0.1190 | 0.0201 | 0.0809 | 0.1587 | |
| Estimates | SE | KSD | KSPV | AIC | BIC | |
|---|---|---|---|---|---|---|
| 1 | 41.8597 | 35.5371 | 0.0685 | 0.9604 | 309.7250 | 313.5490 |
| 2 | 0.2132 | 0.0269 |
| p | Scheme | Data |
|---|---|---|
| 0.1 | 1.578, 1.582, 1.858, 2.595, 2.710, 2.899, 2.940, 3.087, 3.669, 3.848, 4.740, 4.848, 5.170, 5.783, 5.866, 5.872, 6.152, 6.406, 6.839, 7.042, 7.187, 7.262, 7.466, 7.479, 7.481 | |
| 8.292, 8.443, 8.475, 8.587, 9.053, 9.172, 9.229, 9.352, 10.046, 11.182, 11.270, 11.490, 11.623, 11.848 | ||
| 14.369, 16.410 | ||
| 0.3 | 1.578, 1.582, 1.858, 2.595, 2.710, 2.899, 2.940, 3.087, 3.669, 3.848, 4.740, 4.848, 5.170, 5.783, 5.866, 5.872, 6.152, 6.406, 6.839, 7.042, 7.187, 7.262, 7.466, 7.479, 7.481 | |
| 8.292, 8.443, 8.587, 9.053, 9.172, 9.229, 9.352, 10.046, 11.270, 11.490, 11.623 | ||
| 14.812 | ||
| 0.5 | . | 1.578, 1.582, 1.858, 2.595, 2.710, 2.899, 2.940, 3.087, 3.669, 3.848, 4.740, 4.848, 5.170, 5.783, 5.866, 5.872, 6.152, 6.406, 6.839, 7.042, 7.187, 7.262, 7.466, 7.479, 7.481 |
| 8.292, 8.443, 8.587, 9.229, 9.352, 11.490, 11.623 | ||
| 14.369, 14.812 |
| MLE | Bayesian | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| p | Estimates | SE | Lower | Upper | Estimates | SE | Lower | Upper | |
| 0 | 101.9995 | 141.3574 | 0 | 379.0600 | 171.9544 | 124.2122 | 2.1979 | 381.6562 | |
| 0.2397 | 0.0459 | 0.1497 | 0.3297 | 0.1856 | 0.0389 | 0.1083 | 0.2592 | ||
| 0.2507 | 0.0625 | 0.1283 | 0.3731 | 0.1311 | 0.0447 | 0.0550 | 0.2239 | ||
| 0.1532 | 0.0608 | 0.0340 | 0.2724 | 0.0471 | 0.0261 | 0.0068 | 0.0974 | ||
| 0.1 | 100.9999 | 139.1585 | 0 | 373.7505 | 88.9375 | 69.7446 | 0.7274 | 238.8796 | |
| 0.2396 | 0.0458 | 0.1498 | 0.3293 | 0.1202 | 0.0307 | 0.0569 | 0.1789 | ||
| 0.2816 | 0.0697 | 0.1449 | 0.4183 | 0.1472 | 0.0494 | 0.0567 | 0.2467 | ||
| 0.0696 | 0.0485 | 0.0060 | 0.1646 | 0.0684 | 0.0456 | 0.0003 | 0.1553 | ||
| 0.3 | 101.00 | 139.3159 | 0 | 374.0591 | 98.2779 | 67.8543 | 1.1924 | 221.0414 | |
| 0.2400 | 0.0458 | 0.1502 | 0.3299 | 0.0868 | 0.0253 | 0.0330 | 0.1300 | ||
| 0.2722 | 0.0762 | 0.1229 | 0.4215 | 0.1278 | 0.0494 | 0.0434 | 0.2271 | ||
| 0.0623 | 0.0614 | 0.00581 | 0.1827 | 0.1008 | 0.0692 | 0.0000 | 0.2247 | ||
| 0.5 | 101.9997 | 141.6590 | 0 | 379.6513 | 141.1278 | 92.6898 | 8.6789 | 319.6637 | |
| 0.2406 | 0.0460 | 0.1504 | 0.3308 | 0.0798 | 0.0211 | 0.0379 | 0.1193 | ||
| 0.2248 | 0.0791 | 0.0697 | 0.3799 | 0.1910 | 0.0769 | 0.0592 | 0.3491 | ||
| 0.1113 | 0.0769 | 0.00394 | 0.2620 | 0.1038 | 0.0828 | 0.00003 | 0.2687 | ||
| p | 0 | 0.1 | 0.3 | 0.5 |
|---|---|---|---|---|
| OA | 19,981.9181 | 19,365.0904 | 19,408.9293 | 20,067.2795 |
| OB | 0.00037 | 0.00033 | 0.00025 | 0.00015 |
| AIC | 284.8944 | 260.9252 | 239.6899 | 227.7883 |
| BIC | 292.5424 | 268.5733 | 247.3380 | 235.4364 |
| p | 0 | 0.1176 | 0.3030 | 0.4063 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alotaibi, R.; Mutairi, A.A.; Almetwally, E.M.; Park, C.; Rezk, H. Optimal Design for a Bivariate Step-Stress Accelerated Life Test with Alpha Power Exponential Distribution Based on Type-I Progressive Censored Samples. Symmetry 2022, 14, 830. https://doi.org/10.3390/sym14040830
Alotaibi R, Mutairi AA, Almetwally EM, Park C, Rezk H. Optimal Design for a Bivariate Step-Stress Accelerated Life Test with Alpha Power Exponential Distribution Based on Type-I Progressive Censored Samples. Symmetry. 2022; 14(4):830. https://doi.org/10.3390/sym14040830
Chicago/Turabian StyleAlotaibi, Refah, Aned Al Mutairi, Ehab M. Almetwally, Chanseok Park, and Hoda Rezk. 2022. "Optimal Design for a Bivariate Step-Stress Accelerated Life Test with Alpha Power Exponential Distribution Based on Type-I Progressive Censored Samples" Symmetry 14, no. 4: 830. https://doi.org/10.3390/sym14040830
APA StyleAlotaibi, R., Mutairi, A. A., Almetwally, E. M., Park, C., & Rezk, H. (2022). Optimal Design for a Bivariate Step-Stress Accelerated Life Test with Alpha Power Exponential Distribution Based on Type-I Progressive Censored Samples. Symmetry, 14(4), 830. https://doi.org/10.3390/sym14040830








