Study of α-Decay Energy by an Artificial Neural Network Considering Pairing and Shell Effects
Abstract
:1. Introduction
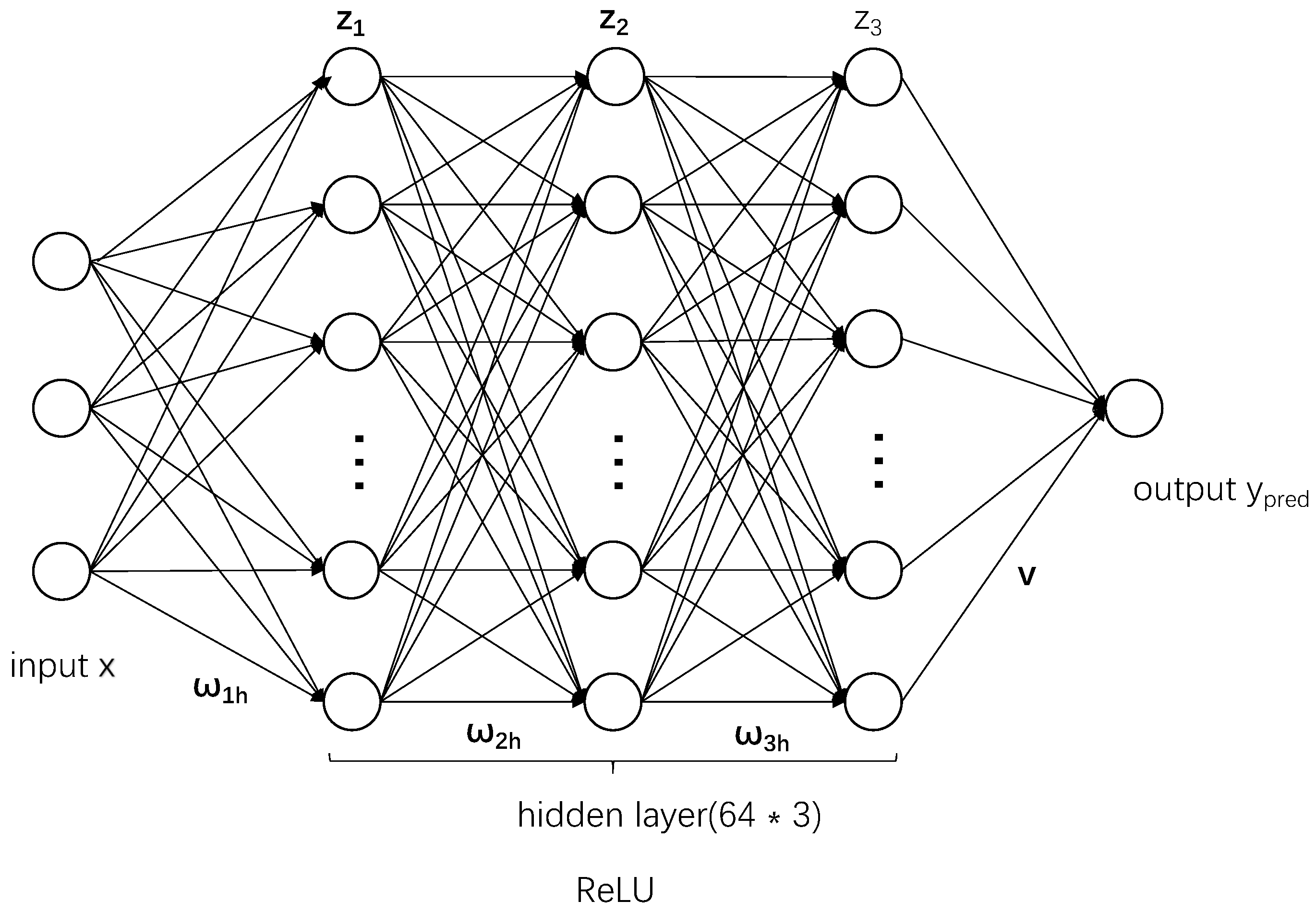
2. Theoretical Framework
3. Results and Discussions
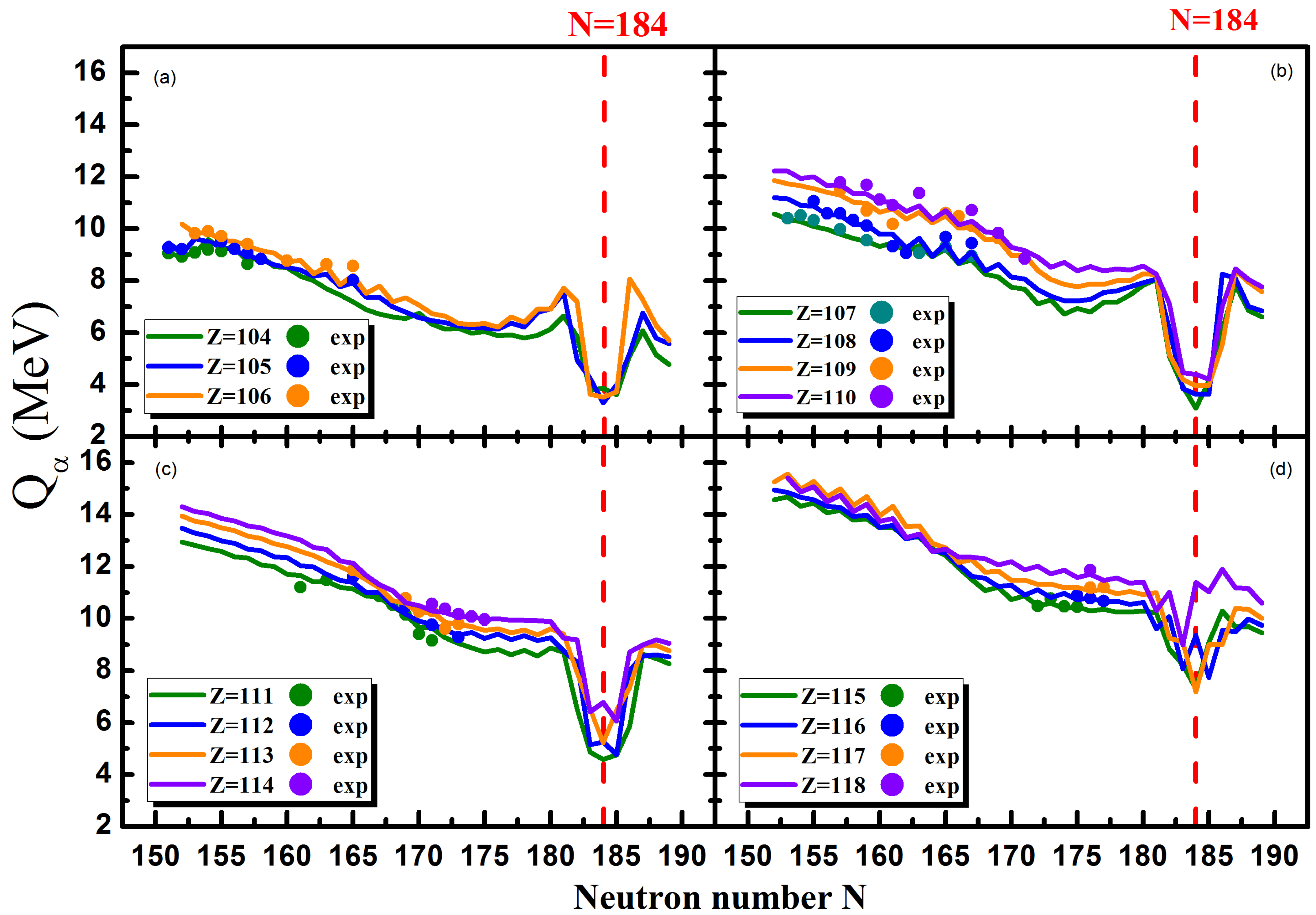
3.1. Prediction of the -Decay Energy Based on the Experimental Data
3.2. Extrapolation of the -Decay Energy in the Superheavy Nuclei Mass Region
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hofmannand, S.; Munzenberg, G. The discovery of the heaviest elements. Rev. Mod. Phys. 2000, 72, 733–767. [Google Scholar] [CrossRef]
- Ren, Z.Z.; Xu, G.G. Reduced alpha transfer rates in a schematic model. Phys. Rev. C 1987, 36, 456–459. [Google Scholar] [CrossRef]
- Hodgson, P.E.; Běták, E. Cluster emission, transfer and capture in nuclear reactions. Phys. Rep. 2003, 374, 1–89. [Google Scholar] [CrossRef]
- Seweryniak, D.; Starosta, K.; Davids, C.N.; Gros, S.; Hecht, A.A.; Hoteling, N.; Khoo, T.L.; Lagergren, K.; Lotay, G.; Peterson, D.; et al. α decay of 105Te. Phys. Rev. C 2006, 73, 061301. [Google Scholar] [CrossRef]
- Duflo, J.; Zuker, A.P. Microscopic mass formulas. Phys. Rev. C 1995, 52, R23–R27. [Google Scholar] [CrossRef] [Green Version]
- Vogt, K.; Hartmann, T.; Zilges, A. Simple parametrization of single- and two-nucleon separation energies in terms of the neutron to proton ratio N/Z. Phys. Lett. B 2001, 517, 255–260. [Google Scholar] [CrossRef] [Green Version]
- Bethe, H.A.; Bacher, R.F. Nuclear Physics A. Stationary States of Nuclei. Rev. Mod. Phys. 1936, 8, 82–229. [Google Scholar] [CrossRef] [Green Version]
- Möller, P.; Myers, W.D.; Sagawa, H.; Yoshida, S. New Finite-Range Droplet Mass Model and Equation-of-State Parameters. Phys. Rev. Lett. 2012, 108, 052501. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.; Liu, M.; Wu, X.; Meng, J. Surface diffuseness correction in global mass formula. Phys. Lett. B 2014, 734, 215–219. [Google Scholar] [CrossRef] [Green Version]
- Goriely, S.; Chamel, N.; Pearson, J.M. Skyrme-Hartree-Fock-Bogoliubov Nuclear Mass Formulas: Crossing the 0.6 MeV Accuracy Threshold with Microscopically Deduced Pairing. Phys. Rev. Lett. 2009, 102, 152503. [Google Scholar] [CrossRef] [Green Version]
- Goriely, S.; Chamel, N.; Pearson, J.M. Further explorations of Skyrme-Hartree-Fock-Bogoliubov mass formulas. XVI. Inclusion of self-energy effects in pairing. Phys. Rev. C 2016, 93, 034337. [Google Scholar] [CrossRef]
- Von-Eiff, D.; Freyer, H.; Stocker, W.; Weigel, M.K. The relativistic spin-orbit force near the neutron-drip line. Phys. Lett. B 1995, 344, 11–17. [Google Scholar] [CrossRef]
- Vretenar, D.; Afanasjev, A.V.; Lalazissis, G.A.; Ring, P. Relativistic Hartree-Bogoliubov theory: Static and dynamic aspects of exotic nuclear structure. Phys. Rep. 2005, 409, 101–259. [Google Scholar] [CrossRef]
- Meng, J.; Peng, J.; Zhang, S.Q.; Zhou, S.G. Possible existence of multiple chiral doublets in 106Rh. Phys. Rev. C 2006, 73, 037303. [Google Scholar] [CrossRef] [Green Version]
- L, H.Z.; Giai, N.V.; Meng, J. Spin-Isospin Resonances: A Self-Consistent Covariant Description. Phys. Rev. Lett. 2008, 101, 122502. [Google Scholar] [CrossRef] [Green Version]
- Niu, Z.M.; Niu, Y.F.; Liang, H.Z.; Long, W.H.; Meng, J. Self-consistent relativistic quasiparticle random-phase approximation and its applications to charge-exchange excitations. Phys. Rev. C 2017, 95, 044301. [Google Scholar] [CrossRef] [Green Version]
- Kirson, M.W. Mutual influence of terms in a semi-empirical mass formula. Nucl. Phys. A 2008, 798, 29–60. [Google Scholar] [CrossRef]
- Möller, P.; Nix, J.R.; Kratz, K.L. Nuclear Properties for Astrophysical and Radioactive-Ion-Beam Applications. At. Data Nucl. Data Tables 1997, 66, 131–343. [Google Scholar] [CrossRef] [Green Version]
- Jia, J.H.; Qian, Y.B.; Ren, Z.Z. Systematics of α-decay energies in the valence correlation scheme. Phys. Rev. C 2021, 103, 024314. [Google Scholar] [CrossRef]
- Dong, T.; Ren, Z.Z. α-decay energy formula for superheavy nuclei based on the liquid-drop model. Phys. Rev. C 2010, 82, 034320. [Google Scholar] [CrossRef]
- Ni, D.D.; Ren, Z.Z. Binding energies, α-decay energies, and α-decay half-lives for heavy and superheavy nuclei. Nucl. Phys. A 2012, 893, 13–26. [Google Scholar] [CrossRef]
- Jiang, H.; Fu, G.J.; Sun, B.; Liu, M.; Wang, N.; Wang, M.; Ma, Y.G.; Lin, C.J.; Zhao, Y.M.; Zhang, Y.H.; et al. Predictions of unknown masses and their applications. Phys. Rev. C 2012, 85, 054303. [Google Scholar] [CrossRef]
- Dong, J.; Wei, Z.; Scheid, W. Correlation between alpha-decay Energies of Superheavy Nuclei Involving Effect of Symmetry Energy. Phys. Rev. Lett. 2011, 107, 012501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hao, X.; Zhang, G.; Ma, S. Deep learning; World Scientific: Singapore, 2016; Volume 10, pp. 417–439. [Google Scholar]
- Niu, Z.M.; Liang, H.Z. Nuclear mass predictions based on Bayesian neural network approach with pairing and shell effects. Phys. Lett. B 2018, 778. [Google Scholar] [CrossRef]
- Neufcourt, L.; Cao, Y.; Nazarewicz, W.; Viens, F. Bayesian approach to model-based extrapolation of nuclear observables. Phys. Rev. C 2018, 98, 034318. [Google Scholar] [CrossRef] [Green Version]
- Neufcourt, L.; Cao, Y.; Nazarewicz, W.; Olsen, E.; Viens, F. Neutron Drip Line in the Ca Region from Bayesian Model Averaging. Phys. Rev. Lett. 2019, 122, 062502.1–062502.6. [Google Scholar] [CrossRef] [Green Version]
- Yüksel, E.; Soydaner, D.; Bahtiyar, H. Nuclear mass predictions using neural networks: Application of the multilayer perceptron. Int. J. Mod. Phys. E 2021, 30. [Google Scholar] [CrossRef]
- Saxena, G.; Sharma, P.K.; Saxena, P. Modified empirical formulas and machine learning for α-decay systematics. J. Phys. G Nucl. Part. Phys. 2021, 48, 055103. [Google Scholar] [CrossRef]
- Rodríguez, U.B.; Vargas, C.Z.; Gonçalves, M.G.; Barbosa, S.D.; Guzman, F. Alpha half-lives calculation of superheavy nuclei with Qα-values predictions based on Bayesian neural network approach. J. Phys. G Nucl. Part. Phys. 2019, 46, 115109. [Google Scholar] [CrossRef]
- Akkoyun, S.; Bayram, T.; Kara, S.O.; Sinan, A. An artificial neural network application on nuclear charge radii. J. Phys. G Nucl. Part. Phys. 2013, 40, 055106-1–055106-7. [Google Scholar] [CrossRef]
- Available online: https://www.nndc.bnl.gov/ensdf/ (accessed on 25 March 2022).
- Dnmez, P. Introduction to Machine Learning, 2nd ed.; Alpaydn, E., Ed.; The MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Rumelhart, D.; Hinton, G.E.; Williams, R.J. Learning Representations by Back Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jeff, H. Ian Goodfellow, Yoshua Bengio, and Aaron Courville: Deep learning. In Genetic Programming and Evolvable Machines; Springer: Berlin, Germany, 2017; pp. 1–3. [Google Scholar]
- Htike, K.K.; Hogg, D. Unsupervised detector adaptation by joint dataset feature learning. In Proceedings of the International Conference on Computer Vision and Graphics, Warsaw, Poland, 15–17 September 2014; pp. 270–277. [Google Scholar]
- Kortelainen, M.; Mcdonnell, J.; Nazarewicz, W.; Reinhard, P.G.; Sarich, J.; Schunck, N.; Stoitsov, M.V.; Wild, S.M. Nuclear energy density optimization: Large deformations. Phys. Rev. C 2011, 85, 024304. [Google Scholar] [CrossRef]
- Qian, Y.B.; Ren, Z.Z. Robustness of heavy and superheavy nuclei against α decay: Progress toward identifying the possible location of the “island of stability”. Phys. Rev. C 2019, 100, 061302. [Google Scholar] [CrossRef]
- Nilsson, S.; Nix, J.; Sobiczewski, A.; Szymański, Z.; Wycech, S.; Gustafson, C.; Möller, P. On the spontaneous fission of nuclei with Z near 114 and N near 184. Nucl. Phys. A 1968, 115, 545–562. [Google Scholar] [CrossRef] [Green Version]
- Sobiczewski, A.; Gareev, F.; Kalinkin, B. Closed shells for Z> 82 and N> 126 in a diffuse potential well. Phys. Lett. 1966, 22, 500–502. [Google Scholar] [CrossRef]
- Mosel, U.; Greiner, W. On the stability of superheavy nuclei against fission. Z. Phys. A Hadron. Nucl. 1969, 222, 261–282. [Google Scholar] [CrossRef]

| ANN Model | XGBoost [29] | DZ+BNN Model [30] | |||||
|---|---|---|---|---|---|---|---|
| input x | () | (,) | () | (,) | - | () | |
| (MeV) | training set | 0.150 | 0.135 | 0.115 | 0.090 | - | 0.178 |
| test set | 0.303 | 0.220 | 0.176 | 0.105 | 0.403 | 0.274 | |
| Parent Nuclei | (MeV) | (MeV) | (MeV) | Parent Nuclei | (MeV) | (MeV) | (MeV) | ||
|---|---|---|---|---|---|---|---|---|---|
| Rf | 255 | 9.055 | 9.065 | Db | 270 | 9.265 | 9.458 | ||
| Rf | 256 | 8.926 | 8.955 | Db | 263 | 9.206 | 9.057 | ||
| Rf | 257 | 9.083 | 9.065 | Db | 262 | 9.501 | 9.620 | ||
| Rf | 258 | 9.193 | 9.588 | Db | 257 | 9.620 | 9.507 | ||
| Rf | 259 | 9.131 | 9.242 | Db | 261 | 9.500 | 9.302 | ||
| Rf | 261 | 8.648 | 8.758 | 0.173 | Db | 256 | 9.218 | 9.163 | |
| Sg | 271 | 9.821 | 9.815 | Db | 260 | 9.050 | 8.960 | ||
| Sg | 269 | 9.901 | 9.861 | Db | 258 | 8.834 | 8.808 | ||
| Sg | 266 | 9.714 | 9.546 | Db | 259 | 8.020 | 7.928 | 0.127 | |
| Sg | 263 | 9.403 | 9.333 | Bh | 274 | 10.401 | 10.367 | ||
| Sg | 261 | 8.763 | 8.721 | Bh | 270 | 10.503 | 10.278 | ||
| Sg | 259 | 8.631 | 8.552 | Bh | 272 | 10.319 | 10.076 | ||
| Sg | 260 | 8.561 | 8.202 | 0.156 | Bh | 266 | 9.967 | 9.781 | |
| Hs | 270 | 11.059 | 10.872 | Bh | 264 | 9.550 | 9.496 | ||
| Hs | 269 | 10.591 | 10.539 | Bh | 262 | 9.061 | 9.344 | ||
| Hs | 275 | 10.586 | 10.528 | Bh | 260 | 9.301 | 9.228 | ||
| Hs | 273 | 10.335 | 10.162 | Bh | 261 | 8.951 | 8.795 | 0.179 | |
| Hs | 267 | 10.110 | 10.148 | Mt | 278 | 11.480 | 11.284 | ||
| Hs | 266 | 9.315 | 9.790 | Mt | 276 | 10.695 | 10.971 | ||
| Hs | 265 | 9.070 | 9.256 | Mt | 270 | 10.181 | 10.774 | ||
| Hs | 264 | 9.670 | 9.428 | Mt | 275 | 10.600 | 10.488 | ||
| Hs | 263 | 9.440 | 9.110 | 0.235 | Mt | 274 | 10.481 | 10.021 | |
| Ds | 281 | 11.780 | 11.692 | Mt | 268 | 10.101 | 10.049 | ||
| Ds | 279 | 11.680 | 11.336 | Mt | 266 | 9.631 | 9.581 | 0.315 | |
| Ds | 277 | 11.117 | 11.022 | Rg | 282 | 11.197 | 11.648 | ||
| Ds | 271 | 10.899 | 11.029 | Rg | 281 | 11.481 | 11.435 | ||
| Ds | 270 | 11.371 | 10.879 | Rg | 280 | 10.851 | 10.797 | ||
| Ds | 273 | 10.710 | 10.282 | Rg | 279 | 10.520 | 10.461 | ||
| Ds | 269 | 9.840 | 9.833 | Rg | 278 | 10.147 | 10.139 | ||
| Ds | 267 | 8.853 | 9.158 | 0.289 | Rg | 272 | 9.415 | 9.664 | |
| Cn | 285 | 11.595 | 11.388 | Rg | 274 | 9.160 | 9.652 | 0.271 | |
| Cn | 283 | 10.450 | 10.160 | Nh | 285 | 11.851 | 11.775 | ||
| Cn | 281 | 9.761 | 9.778 | Nh | 286 | 10.781 | 10.583 | ||
| Cn | 277 | 9.291 | 9.367 | 0.182 | Nh | 283 | 10.261 | 10.192 | |
| Fl | 289 | 10.561 | 10.295 | Nh | 284 | 10.281 | 10.251 | ||
| Fl | 288 | 10.370 | 10.230 | Nh | 282 | 9.615 | 9.851 | ||
| Fl | 287 | 10.161 | 10.059 | Nh | 278 | 9.791 | 9.765 | 0.133 | |
| Fl | 286 | 10.072 | 10.089 | Mc | 290 | 10.471 | 10.477 | ||
| Fl | 285 | 9.961 | 9.963 | 0.141 | Mc | 289 | 10.751 | 10.579 | |
| Lv | 293 | 11.001 | 10.954 | Mc | 287 | 10.456 | 10.387 | ||
| Lv | 292 | 10.891 | 10.714 | Mc | 288 | 10.451 | 10.441 | 0.092 | |
| Lv | 291 | 10.774 | 10.802 | Ts | 293 | 11.184 | 11.061 | ||
| Lv | 290 | 10.671 | 10.616 | 0.095 | Ts | 294 | 11.201 | 11.113 | 0.106 |
| Og | 294 | 11.861 | 11.697 | 0.164 | all nuclei | 0.204 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, H.-Q.; Qu, Z.-Z.; Wu, R.-H.; Su, H.-Z.; He, X.-T. Study of α-Decay Energy by an Artificial Neural Network Considering Pairing and Shell Effects. Symmetry 2022, 14, 1006. https://doi.org/10.3390/sym14051006
You H-Q, Qu Z-Z, Wu R-H, Su H-Z, He X-T. Study of α-Decay Energy by an Artificial Neural Network Considering Pairing and Shell Effects. Symmetry. 2022; 14(5):1006. https://doi.org/10.3390/sym14051006
Chicago/Turabian StyleYou, Hong-Qiang, Zheng-Zhe Qu, Ren-Hang Wu, Hao-Ze Su, and Xiao-Tao He. 2022. "Study of α-Decay Energy by an Artificial Neural Network Considering Pairing and Shell Effects" Symmetry 14, no. 5: 1006. https://doi.org/10.3390/sym14051006
APA StyleYou, H.-Q., Qu, Z.-Z., Wu, R.-H., Su, H.-Z., & He, X.-T. (2022). Study of α-Decay Energy by an Artificial Neural Network Considering Pairing and Shell Effects. Symmetry, 14(5), 1006. https://doi.org/10.3390/sym14051006






