A Multi-Strategy Improved Arithmetic Optimization Algorithm
Abstract
:1. Introduction
2. Arithmetic Optimization Algorithm
3. The Improved Arithmetic Optimization Algorithm
3.1. Initial Population Based on Circle Chaotic Mapping
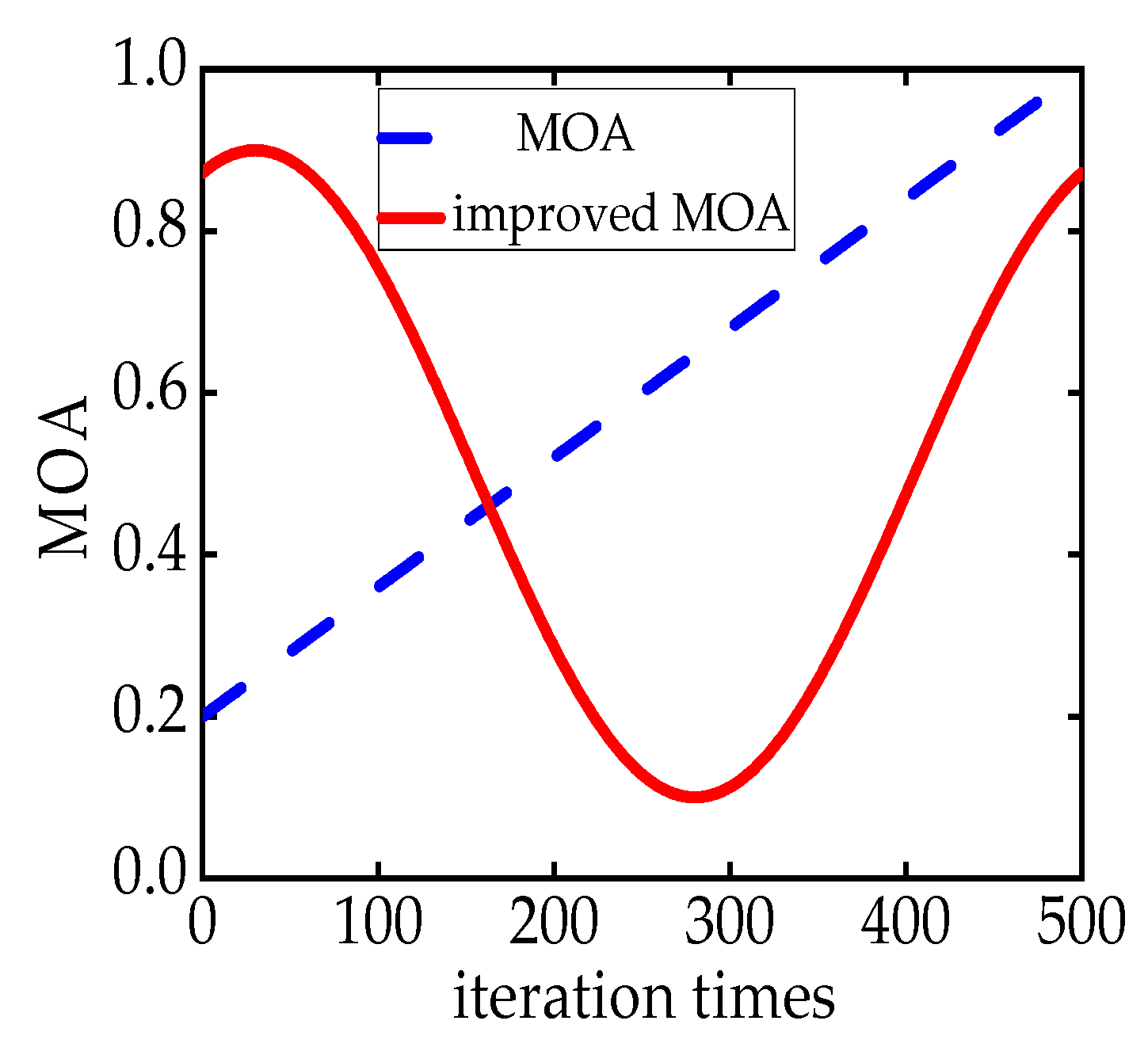
3.2. MOA Optimized by Means of A Compound Cycloid
3.3. The Optimal Mutation Strategy, Combining Sparrow Elite Mutation with the Adaptive Water Wave Factor and Cauchy Disturbances
3.3.1. Sparrow Elite Mutation
3.3.2. Cauchy Disturbance
| Algorithm 1. The pseudo-code of the improved arithmetic optimization algorithm. | |
| 01 | Initialization |
| 02 | Initialize the population size (n), dimension (m), and the number of iterations (Tmax) |
| 03 | Initialize the individuals of population Xi (i = 1, 2, 3, …, n) using circle chaotic mapping, as shown in Equation (7). |
| 04 | Evaluate the fitness value and find the current best individual and best fitness value |
| 05 | Set the parameters α, μ, ubj, and lbj |
| 06 | Main loop{ |
| 07 | While (t ≤ Tmax) |
| 08 | Calculate the MOP by Equation (5) |
| 09 | Calculate the MOA by Equations (8) and (9) |
| 10 | For each search agent |
| 11 | If r1 > MOA |
| 12 | Update position by Equation (3) |
| 13 | Else |
| 14 | Update position by Equation (6) |
| 15 | End if |
| 16 | Calculate the fitness values of the individuals and rankings according to the fitness values |
| 17 | Calculate the water wave factor |
| 18 | Update the top 20% of the individuals with the current fitness value according to Equation (11) |
| 19 | Update current best individual and best fitness value |
| 20 | Disturb the current optimal individual with Equation (13). Compare its fitness value with that before disturbance |
| 21 | Update current best individual and best fitness value |
| 22 | End for |
| 23 | t = t + 1 |
| 24 | End While} |
| 25 | Return best fitness value and current best individual |
4. Test of Algorithm
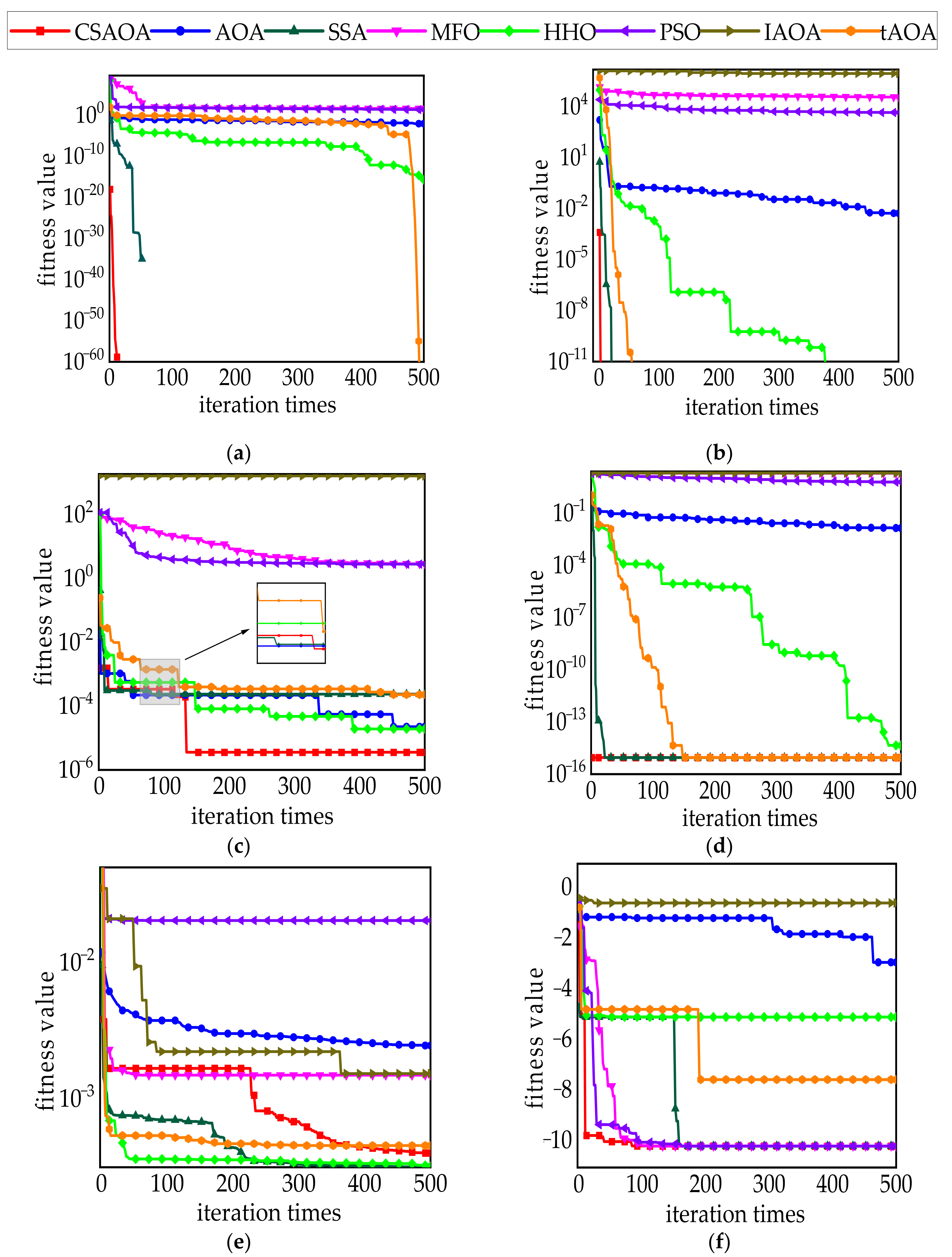
4.1. Effectiveness Test of Algorithm Improvement Strategy
4.2. Benchmark Function Test
4.3. Time Complexity of the Algorithm
4.4. Wilcoxon Rank-Sum Test
4.5. CEC2019 Test Set
5. Engineering Application of Algorithm
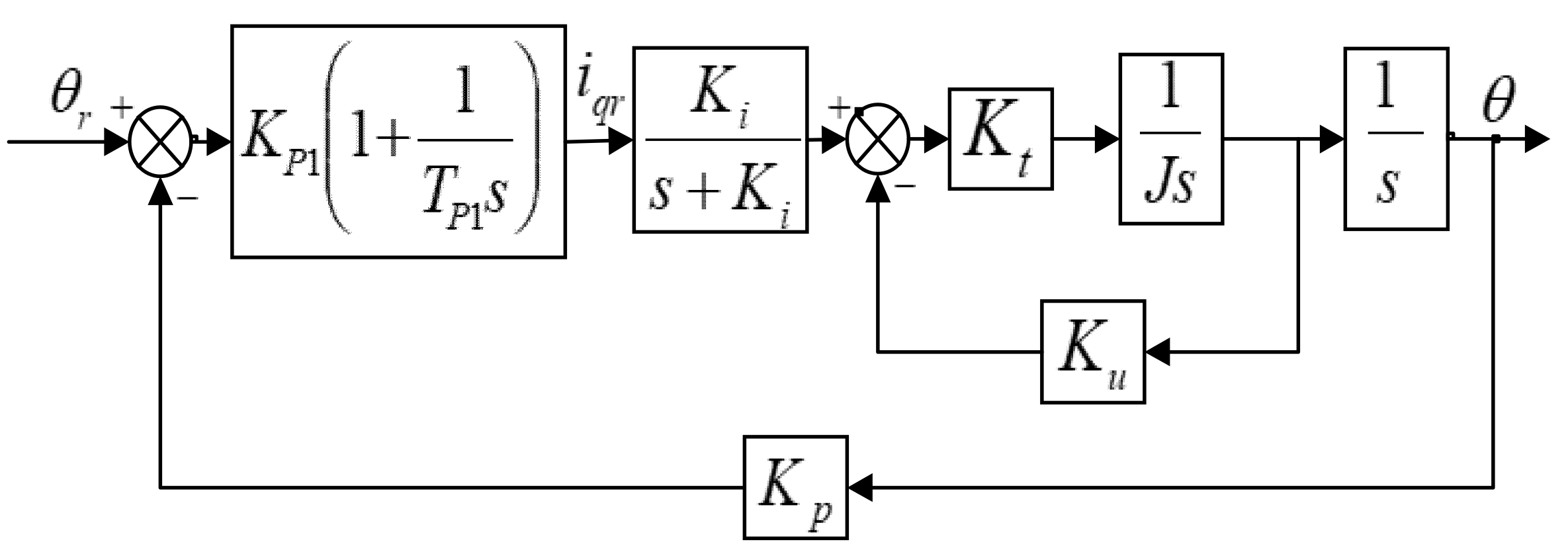
5.1. The Problem of AC Motor PID Control
5.2. Pressure Vessel Design Problem
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chaudhary, K.; Chaudhary, H. Optimal dynamic design of planar mechanisms using teaching learning based optimization algorithm. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 3442–3456. [Google Scholar] [CrossRef]
- Wang, B.; Xiang, T.; Li, N. A Symmetric Sine Cosine Algorithm with Adaptive Probability Selection. IEEE Access 2020, 8, 25272–25285. [Google Scholar] [CrossRef]
- Hekimoğlu, B. Sine-cosine algorithm-based optimization for automatic voltage regulator system. Trans. Inst. Meas. Control 2018, 41, 1761–1771. [Google Scholar] [CrossRef]
- Ye, A.; Zhou, X.; Miao, F. Innovative Hyperspectral Image Classification Approach Using Optimized CNN and ELM. Electronics 2022, 11, 775. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Heidari, A.A.; Gandomi, A.H.; Chu, X.; Chen, H. RUN beyond the metaphor: An efficient optimization algorithm based on Runge Kutta method. Expert Syst. Appl. 2021, 181, 115079. [Google Scholar] [CrossRef]
- Wongkhuenkaew, R.; Auephanwiriyakul, S.; Chaiworawitkul, M.; Theera-Umpon, N. Three-Dimensional Tooth Model Reconstruction Using Statistical Randomization-Based Particle Swarm Optimization. Appl. Sci. 2021, 11, 2363. [Google Scholar] [CrossRef]
- Kotyrba, M.; Volna, E.; Habiballa, H.; Czyz, J. The Influence of Genetic Algorithms on Learning Possibilities of Artificial Neural Networks. Computers 2022, 11, 70. [Google Scholar] [CrossRef]
- Bu, S.J.; Kang, H.B.; Cho, S.B. Ensemble of Deep Convolutional Learning Classifier System Based on Genetic Algorithm for Database Intrusion Detection. Electronics 2022, 11, 745. [Google Scholar] [CrossRef]
- Fan, Q.; Chen, Z.; Xia, Z. A novel quasi-reflected Harris hawks optimization algorithm for global optimization problems. Soft Comput. 2020, 24, 14825–14843. [Google Scholar] [CrossRef]
- Hussain, K.; Zhu, W.; Salleh, M. Long-Term Memory Harris’ Hawk Optimization for High Dimensional and Optimal Power Flow Problems. IEEE Access 2019, 7, 147596–147616. [Google Scholar] [CrossRef]
- Yi, H.; Wang, J.; Hu, Y. Mechanism isomorphism identification based on artificial fish swarm algorithm. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 5421–5433. [Google Scholar] [CrossRef]
- Ouyang, C.; Zhu, D.; Qiu, Y. Lens Learning Sparrow Search Algorithm. Math. Probl. Eng. 2021, 2, 9935090. [Google Scholar] [CrossRef]
- Song, C.; Yao, L.; Hua, C. Comprehensive water quality evaluation based on kernel extreme learning machine optimized with the sparrow search algorithm in Luoyang River Basin, China. Environ. Earth Sci. 2021, 80, 16. [Google Scholar] [CrossRef]
- Xu, X.; Peng, L.; Ji, Z. Research on Substation Project Cost Prediction Based on Sparrow Search Algorithm Optimized BP Neural Network. Sustainability 2021, 13, 13746. [Google Scholar] [CrossRef]
- Meidani, K.; Hemmasian, A.; Mirjalili, S.; Barati Farimani, A. Adaptive grey wolf optimizer. Neural Comput. Appl. 2022, 34, 7711–7731. [Google Scholar] [CrossRef]
- He, Q.; Luo, S. Hybrid improved chimpanzee optimization algorithm and its mechanical application. Control Decis. 2022, 1, 11. [Google Scholar]
- Jia, H.; Sun, K.; Zhang, W.; Leng, X. An enhanced chimp optimization algorithm for continuous optimization domains. Complex Intell. Syst. 2022, 8, 65–82. [Google Scholar] [CrossRef]
- Wang, W.C.; Xu, L.; Chau, K.W. Yin-Yang firefly algorithm based on dimensionally Cauchy mutation. Expert Syst. Appl. 2020, 150, 113216. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, F. A Modified Whale Optimization Algorithm. Comput. Eng. 2018, 44, 208–213. [Google Scholar]
- Saremi, S.; Mirjalili, S.Z.; Mirjalili, S.M. Evolutionary population dynamics and grey wolf optimizer. Neural Comput. Appl. 2015, 26, 1257–1263. [Google Scholar] [CrossRef]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.M. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Lan, Z.; He, Q. Multi-trategy Fusion Algorithm and Its Engineering Optimization. Appl. Res. Comput. 2022, 39, 758–763. [Google Scholar]
- Yang, W.; He, Q. Optimization algorithm of multi-head reverse series algorithm with activation mechanism. Appl. Res. Comput. 2022, 39, 151–156. [Google Scholar]
- Abualigah, L.; Diabat, A.; Sumari, P. A Novel Evolutionary Arithmetic Optimization Algorithm for Multilevel Thresholding Segmentation of COVID-19 CT Images. Processes 2021, 9, 1155. [Google Scholar] [CrossRef]
- Khatir, S.; Tiachacht, S.; Thanh, C.L.; Ghandourah, E.; Wahab, M.A. An improved artificial neural network using arithmetic optimization algorithm for damage assessment in FGM composite plates. Compos. Struct. 2021, 273, 114287. [Google Scholar] [CrossRef]
- Zheng, R.; Jia, H.; Abualigah, L.; Liu, Q.; Wang, S. An improved arithmetic optimization algorithm with forced switching mechanism for global optimization problems. Math. Biosci. Eng. 2022, 19, 473–512. [Google Scholar] [CrossRef]
- Li, S.Y.; Gu, K.R. Smart Fault-Detection Machine for Ball-Bearing System with Chaotic Mapping Strategy. Sensors 2019, 19, 2178. [Google Scholar] [CrossRef] [Green Version]
- Dósa, G.; Newman, N.; Tuza, Z.; Voloshin, V. Coloring Properties of Mixed Cycloids. Symmetry 2021, 13, 1539. [Google Scholar] [CrossRef]
- Li, M.; Liu, Z.; Wang, M.; Pang, G.; Zhang, H. Design of a Parallel Quadruped Robot Based on a Novel Intelligent Control System. Appl. Sci. 2022, 12, 4358. [Google Scholar] [CrossRef]
- Feng, Z.K.; Liu, S.; Niu, W.J.; Liu, Y.; Luo, B.; Miao, S.M.; Wang, S. Optimal Operation of Hydropower System by Improved Grey Wolf Optimizer Based on Elite Mutation and Quasi-Oppositional Learning. IEEE Access 2019, 7, 155513–155529. [Google Scholar] [CrossRef]
- Martín, J.; Parra, M.I.; Pizarro, M.M.; Sanjuán, E.L. Baseline Methods for the Parameter Estimation of the Generalized Pareto Distribution. Entropy 2022, 24, 178. [Google Scholar] [CrossRef] [PubMed]
- Zheng, T.; Liu, S.; Ye, X. Improved arithmetic optimization algorithm of adaptive t distribution and dynamic boundary strategy. Comput. Appl. Res. 2022, 39, 1410–1414. [Google Scholar]
- Abbassi, A.; Ben Mehrez, R.; Bensalem, Y.; Abbassi, R.; Kchaou, M.; Jemli, M.; Abualigah, L.; Altal, M. Improved Arithmetic Optimization Algorithm for Parameters Extraction of Photovoltaic Solar Cell Single-Diode Model. Arab. J. Sci. Eng. 2022, 139, 1–17. [Google Scholar] [CrossRef]
- Bezdan, T.; Stoean, C.; Naamany, A.A.; Bacanin, N.; Rashid, T.A.; Zivkovic, M.; Venkatachalam, K. Hybrid Fruit-Fly Optimization Algorithm with K-Means for Text Document Clustering. Mathematics 2021, 9, 1929. [Google Scholar] [CrossRef]
- Wang, Y. Study on Pressure Balance Control of Piston Pressure Sensor. Master’s Thesis, Hefei University of Technology, Hefei, China, 2018. [Google Scholar]
- Kıran, M.S. An Implementation of Tree-Seed Algorithm (TSA) for Constrained Optimization. Intell. Evol. Syst. 2016, 5, 189–197. [Google Scholar] [CrossRef]





| Algorithm | Mean Value | Standard Deviation | ||
|---|---|---|---|---|
| Dimensional | 30 | 50 | 30 | 50 |
| AOA | 0.0120 | 0.0271 | 0.0312 | 0.0647 |
| CAOA | 9.1050 × 10−5 | 0.0040 | 0.0013 | 0.0041 |
| SAOA | 9.5750 × 10−4 | 0.0017 | 0.0178 | 0.0392 |
| CSAOA | 1.0912 × 10−7 | 1.7104 × 10−4 | 6.8177 × 10−7 | 1.5102 × 10−10 |
| F | Function | Dimensional | Domain | Optimal Value |
|---|---|---|---|---|
| F1 | 30/100 | [−100,100] | 0 | |
| F2 | 30/100 | [−10,10] | 0 | |
| F3 | 30/100 | [−100,100] | 0 | |
| F4 | 30/100 | [−100,100] | 0 | |
| F5 | 30/100 | [−30,30] | 0 | |
| F6 | 30/100 | [−10,10] | 0 | |
| F7 | 30/100 | [−1.28,1.28] | 0 | |
| F8 | 30/100 | [−600,600] | 0 | |
| F9 | 30/100 | [−5.12,5.12] | 0 | |
| F10 | 30/100 | [−32,32] | 0 | |
| F11 | 30/100 | [−600,600] | 0 | |
| F12 | 30/100 | [−50,50] | 0 | |
| F13 | 30/100 | [−50,50] | 0 | |
| F14 | 2 | [−65,65] | 1 | |
| F15 | 4 | [−5,5] | 0.1484 | |
| F16 | 2 | [−5,5] | −1 | |
| F17 | 2 | [−5,5] | 0.3 | |
| F18 | 2 | [−5,5] | 3 | |
| F19 | 3 | [1,3] | −3 | |
| F20 | 4 | [0,10] | −1 |
| F | Algorithm | d = 30 | d = 100 | ||||
|---|---|---|---|---|---|---|---|
| Optimal Value | Standard Deviation | Mean Value | Optimal Value | Standard Deviation | Mean Value | ||
| F1 | CSAOA | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| AOA | 1.3697 × 10−2 | 7.5626 × 10−3 | 2.2228 × 10−2 | 2.1635 × 10−2 | 5.9715 × 10−3 | 2.8779 × 10−2 | |
| tAOA | 6.0359 × 10−243 | 0.0000 | 1.3240 × 10−196 | 2.1929 × 10−244 | 0.0000 | 3.4896 × 10−185 | |
| IAOA | 2.3852 × 105 | 1.8367 × 104 | 2.6226 × 105 | 2.4203 × 105 | 1.6107 × 104 | 2.6472 × 105 | |
| SSA | 0.0000 | 3.8612 × 10−70 | 1.2210 × 10−70 | 3.2493 × 10−252 | 5.8498 × 10−64 | 2.6161 × 10−64 | |
| MFO | 4.1769 × 104 | 1.1343 × 104 | 6.1448 × 104 | 3.8511 × 104 | 2.0171 × 104 | 6.4982 × 104 | |
| HHO | 1.3821 × 10−108 | 3.9119 × 10−96 | 1.3335 × 10−96 | 5.7961 × 10−103 | 1.3175 × 10−93 | 5.8958 × 10−94 | |
| PSO | 3.0264 × 103 | 3.7812 × 103 | 5.9509 × 103 | 1.4261 × 103 | 6.3480 × 103 | 5.2815 × 103 | |
| F2 | CSAOA | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| AOA | 6.7015 × 10−126 | 4.8715 × 10−65 | 1.8559 × 10−65 | 2.9511 × 10−112 | 1.1059 × 10−87 | 4.9459 × 10−88 | |
| tAOA | 3.7605 × 10−201 | 2.5231 × 10−103 | 7.9788 × 10−104 | 4.9927 × 10−157 | 2.0300 × 10−118 | 9.0785 × 10−119 | |
| IAOA | 1.1290 × 1035 | 7.2497 × 1042 | 2.4022 × 1042 | 1.2191 × 1037 | 1.4926 × 1043 | 6.6814 × 1042 | |
| SSA | 0.0000 | 5.4268 × 10−29 | 1.7161 × 10−29 | 0.0000 | 4.2946 × 10−38 | 2.0106 × 10−38 | |
| MFO | 1.9997 × 102 | 4.6211 × 101 | 2.6686 × 102 | 2.5107 × 102 | 2.4185 × 101 | 2.7995 × 102 | |
| HHO | 3.7321 × 10−57 | 4.9387 × 10−53 | 5.9955 × 10−53 | 3.9098 × 10−55 | 1.6429 × 10−51 | 1.3727 × 10−51 | |
| PSO | 1.0347 × 102 | 4.8000 × 101 | 1.7509 × 102 | 1.4143 × 102 | 5.3238 × 101 | 2.2226 × 102 | |
| F3 | CSAOA | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| AOA | 2.7419 × 10−1 | 5.3244 × 10−1 | 6.6035 × 10−1 | 3.2951 × 10−1 | 3.9231 × 10−1 | 7.1837 × 10−1 | |
| tAOA | 1.0365 × 10−218 | 0.0000 | 9.6478 × 10−176 | 4.4972 × 10−231 | 0.0000 | 1.1412 × 10−173 | |
| IAOA | 6.3870 × 105 | 7.1026 × 104 | 7.4294 × 105 | 6.4921 × 105 | 4.8333 × 104 | 7.1367 × 105 | |
| SSA | 0.0000 | 0.0000 | 1.7346 × 10−200 | 0.0000 | 6.5412 × 10−122 | 2.9253 × 10−122 | |
| MFO | 1.4995 × 105 | 9.0594 × 104 | 2.0952 × 105 | 1.6427 × 105 | 4.8054 × 104 | 2.2954 × 105 | |
| HHO | 1.3408 × 10−84 | 6.6239 × 10−75 | 2.9892 × 10−75 | 3.0461 × 10−89 | 2.1092 × 10−67 | 9.4328 × 10−68 | |
| PSO | 7.8597 × 104 | 5.0613 × 104 | 1.3898 × 105 | 1.2535 × 105 | 5.9520 × 104 | 1.6895 × 105 | |
| F4 | CSAOA | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| AOA | 7.5159 × 10−2 | 1.3982 × 10−2 | 9.1227 × 10−2 | 8.2203 × 10−2 | 1.1301 × 10−2 | 9.3750 × 10−2 | |
| tAOA | 2.1545 × 10−115 | 2.0561 × 10−96 | 9.2816 × 10−97 | 3.7202 × 10−104 | 1.1302 × 10−94 | 5.0544 × 10−95 | |
| IAOA | 9.5448 × 101 | 7.8251 × 10−1 | 9.6471 × 101 | 9.3059 × 101 | 1.2238 | 9.4969 × 101 | |
| SSA | 0.0000 | 9.6027 × 10−58 | 4.2944 × 10−58 | 0.0000 | 4.6888 × 10−39 | 2.0969 × 10−39 | |
| MFO | 9.1040 × 101 | 2.3321 | 9.4580 × 10 | 8.9873 × 101 | 2.1850 | 9.3124 × 10 | |
| HHO | 1.7164 × 10−54 | 3.8730 × 10−50 | 1.7338 × 10−50 | 3.4508 × 10−51 | 6.1853 × 10−50 | 5.1528 × 10−50 | |
| PSO | 2.0289 × 101 | 1.4869 | 2.2811 × 101 | 1.6643 × 101 | 4.2802 | 2.1232 × 101 | |
| F5 | CSAOA | 2.8910 × 10−3 | 1.2243 × 10−2 | 1.3436 × 10−2 | 7.9052 × 10−4 | 7.6104 × 10−2 | 5.4217 × 10−2 |
| AOA | 9.8905 × 101 | 3.1023 × 10−2 | 9.8941 × 101 | 9.8819 × 101 | 6.9540 × 10−2 | 9.8904 × 101 | |
| tAOA | 9.8858 × 101 | 1.2841 × 10−2 | 9.8873 × 101 | 9.8866 × 101 | 9.0567 × 10−3 | 9.8875 × 101 | |
| IAOA | 1.1471 × 109 | 4.2754 × 107 | 1.2011 × 109 | 1.0705 × 109 | 1.2350 × 108 | 1.1855 × 109 | |
| SSA | 6.1471 × 10−2 | 6.4823 × 10−2 | 1.3251 × 10−1 | 3.3717 × 10−2 | 1.9198 × 10−1 | 1.8190 × 10−1 | |
| MFO | 6.5409 × 107 | 8.6820 × 107 | 1.8203 × 108 | 4.0630 × 107 | 1.1197 × 108 | 1.7326 × 108 | |
| HHO | 3.7312 × 10−3 | 2.2197 × 10−2 | 2.6143 × 10−2 | 1.4050 × 10−3 | 7.3666 × 10−2 | 7.9354 × 10−2 | |
| PSO | 1.9830 × 105 | 1.8568 × 107 | 9.2024 × 106 | 5.2993 × 105 | 5.5151 × 105 | 1.2947 × 106 | |
| F6 | CSAOA | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| AOA | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| tAOA | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| IAOA | 2.7492 × 108 | 5.9874 × 107 | 3.3817 × 108 | 2.9878 × 108 | 1.0220 × 108 | 4.0924 × 108 | |
| SSA | 0.0000 | 2.1406 × 10−93 | 9.5732 × 10−94 | 1.0696 × 10−286 | 8.7194 × 10−72 | 3.8994 × 10−72 | |
| MFO | 1.0873 × 104 | 4.4717 × 107 | 2.0021 × 107 | 1.9622 × 104 | 5.4764 × 107 | 4.0018 × 107 | |
| HHO | 6.6623 × 10−108 | 7.3828 × 10−98 | 3.3020 × 10−98 | 1.1054 × 10−110 | 1.0168 × 10−94 | 4.5478 × 10−95 | |
| PSO | 1.3601 × 106 | 3.5205 × 106 | 5.7181 × 106 | 4.5861 × 106 | 4.9289 × 107 | 4.2768 × 107 | |
| F7 | CSAOA | 2.9267 × 10−6 | 2.3722 × 10−5 | 2.8044 × 10−5 | 9.1698 × 10−6 | 2.0147 × 10−5 | 3.5667 × 10−5 |
| AOA | 4.2757 × 10−6 | 5.9644 × 10−5 | 5.9879 × 10−5 | 5.4595 × 10−5 | 1.3258 × 10−4 | 2.0102 × 10−4 | |
| tAOA | 1.0078 × 10−5 | 6.4877 × 10−5 | 6.8564 × 10−5 | 2.8181 × 10−5 | 1.1090 × 10−4 | 9.3297 × 10−5 | |
| IAOA | 1.6981 × 103 | 2.0348 × 102 | 1.9295 × 103 | 1.5203 × 103 | 2.3306 × 102 | 1.8371 × 103 | |
| SSA | 2.6432 × 10−5 | 4.5348 × 10−4 | 4.4236 × 10−4 | 1.7974 × 10−4 | 3.7072 × 10−4 | 5.6990 × 10−4 | |
| MFO | 1.5975 × 102 | 1.9347 × 102 | 2.9386 × 102 | 1.0539 × 102 | 1.2845 × 102 | 2.1167 × 102 | |
| HHO | 2.0064 × 10−5 | 1.2755 × 10−4 | 1.9150 × 10−4 | 2.0187 × 10−5 | 1.2515 × 10−4 | 1.2073 × 10−4 | |
| PSO | 1.0825 | 5.6768 × 101 | 4.5013 × 101 | 9.6292 | 3.9483 × 101 | 5.0622 × 101 | |
| F8 | CSAOA | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| AOA | 1.3418 × 10−4 | 2.9923 × 10−4 | 5.0244 × 10−4 | 2.9660 × 10−4 | 1.1015 × 10−4 | 3.9687 × 10−4 | |
| tAOA | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| IAOA | 6.3157 × 101 | 3.2242 | 6.8351 × 101 | 6.9486 × 101 | 2.5146 | 7.2765 × 101 | |
| SSA | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| MFO | 1.1117 × 101 | 3.7540 | 1.6059 × 101 | 1.5147 × 101 | 1.4293 | 1.6984 × 101 | |
| HHO | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| PSO | 1.4107 | 1.7084 | 2.4831 | 2.0968 | 1.4855 | 3.4349 | |
| F9 | CSAOA | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| AOA | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| tAOA | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| IAOA | 1.6102 × 103 | 3.1635 × 101 | 1.6402 × 103 | 1.5785 × 103 | 3.3781 × 101 | 1.6346 × 103 | |
| SSA | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| MFO | 8.1370 × 102 | 8.0360 × 101 | 8.9231 × 102 | 7.5818 × 102 | 5.1659 × 101 | 8.1717 × 102 | |
| HHO | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| PSO | 8.7786 × 102 | 9.1631 × 101 | 9.5337 × 102 | 9.2307 × 102 | 6.6515 × 101 | 9.9908 × 102 | |
| F10 | CSAOA | 8.8818 × 10−16 | 0.0000 | 8.8818 × 10−16 | 8.8818 × 10−16 | 0.0000 | 8.8818 × 10−16 |
| AOA | 8.8818 × 10−16 | 4.7666 × 10−4 | 2.1317 × 10−4 | 8.8818 × 10−16 | 1.0928 × 10−3 | 1.1372 × 10−3 | |
| tAOA | 8.8818 × 10−16 | 0.0000 | 8.8818 × 10−16 | 8.8818 × 10−16 | 0.0000 | 8.8818 × 10−16 | |
| IAOA | 2.0471 × 101 | 3.0222 × 10−2 | 2.0506 × 101 | 2.0382 × 101 | 6.4016 × 10−2 | 2.0477 × 101 | |
| SSA | 8.8818 × 10−16 | 0.0000 | 8.8818 × 10−16 | 8.8818 × 10−16 | 0.0000 | 8.8818 × 10−16 | |
| MFO | 1.9868 × 101 | 3.3033 × 10−2 | 1.9924 × 101 | 1.9755 × 101 | 7.4727 × 10−2 | 1.9880 × 101 | |
| HHO | 8.8818 × 10−16 | 0.0000 | 8.8818 × 10−16 | 8.8818 × 10−16 | 0.0000 | 8.8818 × 10−16 | |
| PSO | 1.3243 × 101 | 1.6071 | 1.5113 × 101 | 1.4995 × 101 | 1.8789 | 1.7506 × 101 | |
| F11 | CSAOA | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| AOA | 1.2203 × 102 | 2.6186 × 102 | 4.8193 × 102 | 2.4244 × 102 | 2.4150 × 102 | 4.8551 × 102 | |
| tAOA | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| IAOA | 2.2522 × 103 | 1.2950 × 102 | 2.4163 × 103 | 2.3306 × 103 | 1.5393 × 102 | 2.5064 × 103 | |
| SSA | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| MFO | 3.7195 × 102 | 1.2642 × 102 | 5.1564 × 102 | 5.0258 × 102 | 9.5333 × 101 | 5.7926 × 102 | |
| HHO | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| PSO | 3.3916 × 101 | 5.4661 | 4.1221 × 101 | 1.9851 × 101 | 5.5612 | 2.5891 × 101 | |
| F12 | CSAOA | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| AOA | 2.8126 | 1.6248 | 4.7728 | 1.3210 | 1.4682 | 3.1535 | |
| tAOA | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| IAOA | 2.5552 × 105 | 1.7410 × 104 | 2.7892 × 105 | 2.5568 × 105 | 6.4507 × 103 | 2.6388 × 105 | |
| SSA | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| MFO | 5.7450 × 104 | 1.9759 × 104 | 7.7476 × 104 | 3.1256 × 104 | 1.9452 × 104 | 6.5136 × 104 | |
| HHO | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| PSO | 3.4242 × 103 | 1.4911 × 103 | 4.5739 × 103 | 4.2942 × 103 | 2.1801 × 103 | 6.7126 × 103 | |
| F13 | CSAOA | 7.7892 × 10−8 | 5.4511 × 10−5 | 4.6380 × 10−5 | 1.0178 × 10−6 | 2.1624 × 10−5 | 1.5606 × 10−5 |
| AOA | 9.7578 | 5.8550 × 10−2 | 9.8453 | 9.9285 | 4.1098 × 10−2 | 9.9813 | |
| tAOA | 9.9859 | 2.4972 × 10−3 | 9.9891 | 9.9841 | 2.8709 × 10−3 | 9.9886 | |
| IAOA | 4.6601 × 109 | 4.9023 × 108 | 5.1856 × 109 | 4.9443 × 109 | 4.1623 × 108 | 5.5553 × 109 | |
| SSA | 5.0924 × 10−4 | 1.0188 × 10−3 | 1.4685 × 10−3 | 8.8230 × 10−5 | 1.1020 × 10−2 | 5.5947 × 10−3 | |
| MFO | 2.1222 × 108 | 3.4180 × 108 | 6.0517 × 108 | 2.7935 × 108 | 3.9204 × 108 | 7.0479 × 108 | |
| HHO | 4.1771 × 10−6 | 9.8017 × 10−5 | 8.9227 × 10−5 | 5.5344 × 10−6 | 9.6250 × 10−5 | 8.4396 × 10−5 | |
| PSO | 6.0808 × 101 | 8.3371 × 104 | 9.3264 × 104 | 3.0820 × 102 | 4.1416 × 104 | 5.4588 × 104 | |
| F | Algorithm | Tmax = 500 | Tmax = 1000 | ||||
|---|---|---|---|---|---|---|---|
| Optimal Value | Standard Deviation | Mean Value | Optimal Value | Standard Deviation | Mean Value | ||
| F14 | CSAOA | 5.9288 | 1.5366 × 10−13 | 5.9288 | 5.9288 | 3.0150 | 7.2772 |
| AOA | 7.8740 | 1.9654 | 10.9480 | 5.9288 | 3.2338 | 10.3630 | |
| tAOA | 9.9800 × 10−1 | 5.2590 | 7.6354 | 2.9821 | 5.0191 | 8.4137 | |
| IAOA | 9.9801 × 10−1 | 2.6881 × 10−4 | 9.9822 × 10−1 | 9.9800 × 10−1 | 8.8731 × 10−1 | 1.3948 | |
| SSA | 2.9821 | 4.3328 | 10.7330 | 9.9800 × 10−1 | 5.6778 | 8.5956 | |
| MFO | 1.9920 | 1.6460 | 4.3572 | 9.9800 × 10−1 | 2.0442 | 2.3818 | |
| HHO | 9.9800 × 10−1 | 8.8250 × 10−11 | 9.9800 × 10−1 | 9.9800 × 10−1 | 1.4927 × 10−10 | 9.9800 × 10−1 | |
| PSO | 9.9800 × 10−1 | 3.2980 × 10−10 | 9.9800 × 10−1 | 9.9800 × 10−1 | 3.0115 × 10−10 | 9.9800 × 10−1 | |
| F15 | CSAOA | 3.1135 × 10−4 | 2.2550 × 10−5 | 3.4556 × 10−4 | 3.0804 × 10−4 | 7.7145 × 10−6 | 3.1364 × 10−4 |
| AOA | 2.0151 × 10−3 | 7.4864 × 10−3 | 7.8982 × 10−3 | 3.3393 × 10−4 | 9.0278 × 10−3 | 5.6261 × 10−3 | |
| tAOA | 3.3949 × 10−4 | 9.3537 × 10−3 | 1.5406 × 10−2 | 3.8758 × 10−4 | 1.0277 × 10−3 | 1.8579 × 10−3 | |
| IAOA | 1.5193 × 10−3 | 3.2671 × 10−3 | 3.4810 × 10−3 | 1.5141 × 10−3 | 8.5690 × 10−4 | 2.1570 × 10−3 | |
| SSA | 3.1621 × 10−4 | 2.3664 × 10−5 | 3.3133 × 10−4 | 3.0826 × 10−4 | 5.7720 × 10−4 | 5.7235 × 10−4 | |
| MFO | 4.9014 × 10−4 | 5.1649 × 10−4 | 1.1770 × 10−3 | 6.9306 × 10−4 | 3.8080 × 10−4 | 1.0286 × 10−3 | |
| HHO | 3.2187 × 10−4 | 4.0765 × 10−5 | 3.4526 × 10−4 | 3.1063 × 10−4 | 2.1931 × 10−5 | 3.2805 × 10−4 | |
| PSO | 1.6554 × 10−3 | 8.9768 × 10−3 | 7.3008 × 10−3 | 1.6554 × 10−3 | 8.4166 × 10−3 | 8.6256 × 10−3 | |
| F16 | CSAOA | −1.0316 | 2.2288 × 10−11 | −1.0316 | −1.0316 | 1.5954 × 10−12 | −1.0316 |
| AOA | −1.0316 | 1.3946 × 10−7 | −1.0316 | −1.0316 | 8.4764 × 10−8 | −1.0316 | |
| tAOA | −1.0316 | 1.6411 × 10−7 | −1.0316 | −1.0316 | 1.3202 × 10−7 | −1.0316 | |
| IAOA | −1.0290 | 3.3750 × 10−3 | −1.0251 | −1.0252 | 6.4286 × 10−3 | −1.0185 | |
| SSA | −1.0316 | 1.4550 × 10−7 | −1.0316 | −1.0316 | 5.9986 × 10−9 | −1.0316 | |
| MFO | −1.0316 | 0.0000 | −1.0316 | −1.0316 | 0.0000 | −1.0316 | |
| HHO | −1.0316 | 1.6503 × 10−10 | −1.0316 | −1.0316 | 8.2136 × 10−13 | −1.0316 | |
| PSO | −1.0316 | 1.7876 × 10−5 | −1.0316 | −1.0316 | 1.2757 × 10−5 | −1.0316 | |
| F17 | CSAOA | 3.9789 × 10−1 | 1.7207 × 10−6 | 3.9789 × 10−1 | 3.9789 × 10−1 | 2.6523 × 10−7 | 3.9789 × 10−1 |
| AOA | 3.9920 × 10−1 | 6.9016 × 10−3 | 4.0607 × 10−1 | 4.0060 × 10−1 | 1.0145 × 10−2 | 4.0984 × 10−1 | |
| tAOA | 3.9826 × 10−1 | 8.4643 × 10−3 | 4.0736 × 10−1 | 3.9800 × 10−1 | 9.1688 × 10−3 | 4.0481 × 10−1 | |
| IAOA | 3.9798 × 10−1 | 3.8876 × 10−3 | 4.0362 × 10−1 | 3.9790 × 10−1 | 3.5639 × 10−3 | 4.0178 × 10−1 | |
| SSA | 3.9789 × 10−1 | 7.0847 × 10−7 | 3.9789 × 10−1 | 3.9789 × 10−1 | 3.9668 × 10−8 | 3.9789 × 10−1 | |
| MFO | 3.9789 × 10−1 | 0.0000 | 3.9789 × 10−1 | 3.9789 × 10−1 | 0.0000 | 3.9789 × 10−1 | |
| HHO | 3.9789 × 10−1 | 4.3690 × 10−8 | 3.9789 × 10−1 | 3.9789 × 10−1 | 3.9874 × 10−9 | 3.9789 × 10−1 | |
| PSO | 3.9789 × 10−1 | 1.0920 × 10−6 | 3.9789 × 10−1 | 3.9789 × 10−1 | 4.8865 × 10−1 | 5.5241 × 10−1 | |
| F18 | CSAOA | 3.0000 | 6.9354 × 10−11 | 3.0000 | 3.0000 | 4.5769 × 10−11 | 3.0000 |
| AOA | 3.0000 | 1.5252 × 10−8 | 3.0000 | 3.0000 | 1.1297 × 101 | 8.3583 | |
| tAOA | 3.0000 | 1.2072 × 101 | 8.4046 | 3.0000 | 7.5751 | 5.3955 | |
| IAOA | 3.0181 | 1.3154 | 4.4153 | 3.0125 | 6.8648 × 10−1 | 3.7742 | |
| SSA | 3.0000 | 1.1655 × 10−6 | 3.0000 | 3.0000 | 1.9297 × 10−7 | 3.0000 | |
| MFO | 3.0000 | 1.1322 × 10−15 | 3.0000 | 3.0000 | 2.0134 × 10−15 | 3.0000 | |
| HHO | 3.0000 | 1.0688 × 10−7 | 3.0000 | 3.0000 | 1.5775 × 10−8 | 3.0000 | |
| PSO | 3.0000 | 1.2094 × 10−4 | 3.0001 | 3.0000 | 2.8097 × 10−5 | 3.0000 | |
| F19 | CSAOA | −3.8628 | 3.4487 × 10−6 | −3.8628 | −3.8628 | 2.0503 × 10−6 | −3.8628 |
| AOA | −3.8541 | 2.0932 × 10−3 | −3.8521 | −3.8573 | 3.4847 × 10−3 | −3.8524 | |
| tAOA | −3.8589 | 6.1122 × 10−3 | −3.8511 | −3.8603 | 3.1827 × 10−3 | −3.8534 | |
| IAOA | −3.8270 | 1.1869 × 10−1 | −3.7383 | −3.8493 | 1.0174 × 10−1 | −3.7700 | |
| SSA | −3.8628 | 2.3691 × 10−5 | −3.8628 | −3.8628 | 1.0027 × 10−6 | −3.8628 | |
| MFO | −3.8628 | 0.0000 | −3.8628 | −3.8628 | 9.3622 × 10−16 | −3.8628 | |
| HHO | −3.8626 | 4.6271 × 10−4 | −3.8618 | −3.8628 | 2.2493 × 10−3 | −3.8614 | |
| PSO | −3.8628 | 3.5228 × 10−3 | −3.8612 | −3.8628 | 4.0691 × 10−3 | −3.8596 | |
| F20 | CSAOA | −1.0153 × 101 | 9.9270 × 10−5 | −1.0153 × 101 | −1.0153 × 101 | 1.4965 × 10−5 | −1.0153 × 101 |
| AOA | −5.3422 | 1.1597 | −3.6184 | −5.0130 | 7.2225 × 10−1 | −3.5994 | |
| tAOA | −7.9372 | 1.6177 | −5.1167 | −9.0817 | 1.8651 | −5.3548 | |
| IAOA | −2.0531 | 3.1992 × 10−01 | −1.5500 | −6.8960 | 1.8733 | −2.2640 | |
| SSA | −1.0153 × 101 | 4.4744 × 10−4 | −1.0153 × 101 | −1.0153 × 101 | 6.5870 × 10−5 | −1.0153 × 101 | |
| MFO | −1.0153 × 101 | 2.2595 | −9.1427 | −1.0153 × 101 | 3.0171 | −7.3715 | |
| HHO | −5.0548 | 1.1872 × 10−3 | −5.0534 | −5.0551 | 1.4752 × 10−3 | −5.0541 | |
| PSO | −1.0149 × 101 | 2.7849 | −7.0881 | −1.0152 × 101 | 1.6090 | −9.6342 | |
| F | AOA | tAOA | IAOA | SSA | MFO | HHO | PSO |
|---|---|---|---|---|---|---|---|
| F1 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.7016 × 10−8 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 |
| F2 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.6572 × 10−11 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 |
| F3 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 3.4526 × 10−7 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 |
| F4 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 5.7720 × 10−11 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 |
| F8 | 1.2118 × 10−12 | NAN | 1.2118 × 10−12 | NAN | 1.2118 × 10−12 | NAN | 1.2118 × 10−12 |
| F9 | NAN | NAN | 1.2118 × 10−12 | NAN | 1.2118 × 10−12 | NAN | 1.2118 × 10−12 |
| F10 | 3.1335 × 10−4 | NAN | 1.2118 × 10−12 | NAN | 1.2118 × 10−12 | NAN | 8.9713 × 10−13 |
| F11 | 1.2118 × 10−12 | NAN | 1.2118 × 10−12 | NAN | 1.2118 × 10−12 | NAN | 1.2118 × 10−12 |
| F20 | 1.2118 × 10−12 | 1.7769 × 10−10 | 3.0199 × 10−11 | 8.8411 × 10−7 | 1.5510 × 10−1 | 4.0772 × 10−11 | 2.6099 × 10−10 |
| Function | Dimensional | Algorithm | Optimal Value | Standard Deviation | Mean Value |
|---|---|---|---|---|---|
| CEC01 | 9 | CSAOA | 1.0000 | 9.9362 × 10−11 | 1.0000 |
| AOA | 1.0000 | 2.0992 × 101 | 1.9396 | ||
| tAOA | 1.0000 | 5.9761 × 103 | 6.3787 × 102 | ||
| IAOA | 7.6618 × 103 | 1.5845 × 104 | 1.5918 × 104 | ||
| SSA | 1.0000 | 9.5074 × 101 | 5.2818 | ||
| MFO | 2.7674 × 101 | 5.3492 × 103 | 1.1279 × 103 | ||
| HHO | 1.0000 | 1.7750 × 104 | 1.2836 × 103 | ||
| PSO | 5.1698 × 102 | 7.9872 × 103 | 2.0578 × 103 | ||
| CEC02 | 16 | CSAOA | 4.3008 | 1.9870 × 10−1 | 4.4720 |
| AOA | 4.8822 | 3.0697 | 5.3359 | ||
| tAOA | 4.6721 | 6.1232 | 5.2510 | ||
| IAOA | 5.4774 × 101 | 1.4310 × 101 | 6.2534 × 101 | ||
| SSA | 5.0000 | 6.1930 × 10−1 | 5.0301 | ||
| MFO | 6.4186 × 101 | 2.3793 × 101 | 7.1883 × 101 | ||
| HHO | 5.0000 | 1.3384 × 101 | 6.1740 | ||
| PSO | 2.4646 × 101 | 1.0274 × 101 | 3.2307 × 101 | ||
| CEC03 | 18 | CSAOA | 1.4791 | 3.0558 | 4.2609 |
| AOA | 4.4274 | 8.0300 × 10−1 | 4.6550 | ||
| tAOA | 5.8347 | 1.2666 | 6.5828 | ||
| IAOA | 1.2712 × 101 | 1.0040 × 10−1 | 1.2730 × 101 | ||
| SSA | 5.6212 | 9.5340 × 10−1 | 6.6439 | ||
| MFO | 1.0712 × 101 | 7.3540 × 10−1 | 1.1880 × 101 | ||
| HHO | 8.2746 | 6.7500 × 10−1 | 8.6720 | ||
| PSO | 9.4749 | 4.9620 × 10−1 | 9.6062 | ||
| CEC04 | 10 | CSAOA | 3.7850 × 101 | 2.4151 × 101 | 6.1721 × 101 |
| AOA | 6.4291 × 101 | 5.8293 | 6.6431 × 101 | ||
| tAOA | 3.2929 × 101 | 6.4355 | 3.5815 × 101 | ||
| IAOA | 5.0192 × 101 | 2.1434 × 101 | 6.1235 × 101 | ||
| SSA | 7.4627 × 101 | 6.5244 | 7.6946 × 101 | ||
| MFO | 6.2439 × 101 | 1.2302 × 101 | 6.5784 × 101 | ||
| HHO | 5.7328 × 101 | 1.5165 × 101 | 7.3943 × 101 | ||
| PSO | 6.4824 × 101 | 7.0026 | 6.9592 × 101 | ||
| CEC05 | 10 | CSAOA | 1.3758 × 101 | 4.2440 × 101 | 4.0781 × 101 |
| AOA | 5.7798 × 101 | 2.2018 | 5.8757 × 101 | ||
| tAOA | 2.8283 × 101 | 2.5955 | 2.8973 × 101 | ||
| IAOA | 1.2654 × 101 | 1.6715 × 101 | 2.0529 × 101 | ||
| SSA | 1.6138 × 101 | 3.7191 × 101 | 3.7237 × 101 | ||
| MFO | 1.0359 × 101 | 2.6354 × 101 | 1.6591 × 101 | ||
| HHO | 1.6947 | 1.8314 × 101 | 1.9929 × 101 | ||
| PSO | 2.0462 × 101 | 1.4811 × 101 | 2.3161 × 101 |
| Algorithm | Kp | Ki | Kd | Fitness Value |
|---|---|---|---|---|
| CSAOA | 0.0000 | 0.0238 | 0.5000 | 120.3124 |
| AOA | 0.4074 | 0.3279 | 0.2194 | 127.4984 |
| tAOA | 0.0604 | 0.0000 | 0.5000 | 123.3777 |
| IAOA | 0.4074 | 0.0788 | 0.3279 | 126.2875 |
| SSA | 0.4074 | 0.0439 | 0.1230 | 127.4984 |
| MFO | 0.4074 | 0.3279 | 0.2194 | 127.4984 |
| HHO | 0.4074 | 0.3279 | 0.2194 | 127.4984 |
| PSO | 0.4074 | 0.3279 | 0.2194 | 127.4984 |
| Algorithm | Ts | Th | R | L | Fitness Value |
|---|---|---|---|---|---|
| CSAOA | 1.3250 | 0.7248 | 67.6089 | 10.0440 | 8861.4469 |
| tCAOA | 1.6194 | 0.6908 | 70.5038 | 10.0000 | 10,567.4419 |
| IAOA | 1.3543 | 0.6834 | 69.3791 | 10.0000 | 9016.5015 |
| AOA | 1.9331 | 0.7133 | 68.6411 | 67.5328 | 17,440.9848 |
| SSA | 1.3023 | 0.6437 | 67.4747 | 24.0520 | 8925.9204 |
| MFO | 1.3006 | 0.6473 | 67.3861 | 100.0000 | 13,478.2491 |
| HHO | 1.3031 | 0.6469 | 67.3860 | 65.6424 | 11,433.7792 |
| PSO | 1.9304 | 0.9545 | 100.0000 | 10.0000 | 25,684.5813 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Li, M.; Pang, G.; Song, H.; Yu, Q.; Zhang, H. A Multi-Strategy Improved Arithmetic Optimization Algorithm. Symmetry 2022, 14, 1011. https://doi.org/10.3390/sym14051011
Liu Z, Li M, Pang G, Song H, Yu Q, Zhang H. A Multi-Strategy Improved Arithmetic Optimization Algorithm. Symmetry. 2022; 14(5):1011. https://doi.org/10.3390/sym14051011
Chicago/Turabian StyleLiu, Zhilei, Mingying Li, Guibing Pang, Hongxiang Song, Qi Yu, and Hui Zhang. 2022. "A Multi-Strategy Improved Arithmetic Optimization Algorithm" Symmetry 14, no. 5: 1011. https://doi.org/10.3390/sym14051011
APA StyleLiu, Z., Li, M., Pang, G., Song, H., Yu, Q., & Zhang, H. (2022). A Multi-Strategy Improved Arithmetic Optimization Algorithm. Symmetry, 14(5), 1011. https://doi.org/10.3390/sym14051011






