A New Approach of Knowledge Reduction in Knowledge Context Based on Boolean Matrix

Abstract

Knowledge space theory (KST) is a mathematical framework for the assessment of knowledge and learning in education. An important task of KST is to achieve all of the atoms. With the development of KST, considering its relationship with formal concept analysis (FCA) has become a hot issue. The atoms of the knowledge space with application in knowledge reduction based on FCA is examined in this paper. The knowledge space and its properties based on FCA are first discussed. Knowledge reduction and its relationship with molecules in the knowledge context are then investigated. A Boolean matrix is employed to determine molecules and meet-irreducible elements in the knowledge context. The method of the knowledge-reduction-based Boolean matrix in the knowledge space is also explored. Furthermore, an algorithm for finding the atoms of the knowledge space in the knowledge context is developed using a Boolean matrix.

1. Introduction

Formal concept analysis (FCA), as a supplement of a rough set, is a mathematical method of data analysis with applications in various areas [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. In particular, it provides a theoretical framework for the discovery and design of concept hierarchies from relational information systems. Concept hierarchies are built on a binary relation between the sets of objects and attributes in a given formal context. FCA derives from the fact that it provides an easy-to-understand diagram rooted in data, the so-called concept lattice. Moreover, the concept lattice is the collection of all formal concepts, which consists of extents and intents that are determined by each other. In general, the research of formal contexts has mainly focused on two aspects: one is the construction of the concept lattice; the other is knowledge reduction. For the first aspect, Berry [15] presented an approach to generate concepts by discussing the relationship between concept lattices and the underlying graphs. After that, Kuznetsov [16] thoroughly compared and summarized several well-known algorithms. On the other hand, the second aspect is knowledge reduction, which includes two parts: concept reduction, which reduces the size of the concept lattices [17,18,19,20,21], and attribute reduction, as well as object reduction, which preserve the hierarchical structure of concept lattices [22,23,24,25,26,27,28,29]. Several important investigations arose at these points. Kumar [17] proposed a method based on fuzzy K-means clustering for reducing the size of the concept lattices. Reference [18] derived the mean value of cardinality of the reduced hierarchical-structure-based graph-theoretical point of view on FCA together with simple probabilistic arguments. To reduce redundant information, Wu et al. [22] illustrated a method of granular reduction based on a discernibility matrix in a formal context. Kumar [23] put forward a non-negative matrix factorization to address the knowledge reduction. Li et al. [24,25,26] formulated heuristic knowledge reduction approaches for finding a minimum granular reduct in decision formal contexts.

Knowledge space theory (KST) [30,31,32,33], proposed by Doignon and Falmagne provides a valuable mathematical framework for computerized web-based systems for the assessment of knowledge and learning in education. The knowledge state, the key notion of KST, is represented by the subset K of items (or problems) in the finite domain of knowledge Q that an individual is capable of solving correctly, barring careless errors and lucky guesses. A pair $(Q,\mathcal{K})$ represents a knowledge structure by convention, where $\mathcal{K}$ is the collection of all the knowledge states called the knowledge structure always containing at least the following special constituent parts: $\left(1\right)$ the empty state, i.e., corresponding to a student knowing nothing about the subject; $\left(2\right)$ Q, which is the state of a student knowing everything about the subject. Subsequently, a knowledge space is closed under union when any two states K and L are given in the space, then union $K\cup L$ is in $\mathcal{K}$. In essence, at some point, the knowledge of students arising from the union of their initial knowledge states is plausible if they have different knowledge states that are involved in an extensive interaction. Therefore, it is unnecessary to reserve any union of states in a description of the knowledge space.

With the growth of KST, the research about its relationship with other approaches has become a research topic. KST has the same mathematical background as FCA. Both of them aim to order two sets of elements simultaneously. There is an intimate relationship between FCA and KST [34]. The relationship between the attribute implications and the entailed relations was considered by Falmagne et al. [33]. References [35,36,37] built a knowledge space by querying an expert to interpret an entailed relation. They showed that the implication systems are in essence closure systems. This is not just in FCA, but also applies in KST via taking set-theoretic complements.

At present, our study focuses on the framework of FCA. In this paper, we use the FCA for the knowledge reduction in the knowledge space. However, FCA could lead to potentially high combinatorial complexity, and the structure obtained, even from small dataset, may become prohibitively large [38]. To overcome this limitation, we applied a Boolean matrix to construct the intents (extents) of molecules (meet-irreducible elements) in knowledge contexts. This model avoids making the concept lattice from the knowledge context and aims to maintain both the object relation and attribute relation simultaneously. We first introduce the relationships between concepts in the knowledge context from the viewpoint of molecule lattice. A novel method based on a Boolean matrix is further proposed for finding the knowledge reduction of a knowledge space.

The remainder of this paper is organized as follows. In Section 1, we briefly review some basic notations of FCA and KST and their relationships. In Section 2, we investigate the relationships between the molecule lattice and the concept lattice from the knowledge context. Then, the judgment theorems of the molecule, as well as meet-irreducible elements of concept lattices are proposed. In Section 3, we conclude that each member in the concept lattice from the knowledge context is the union (intersection) of some molecules (meet-irreducible elements), present a simple way to compute the molecules and meet-irreducible elements in a knowledge context using a Boolean matrix, and discuss an algorithm for the knowledge reduction of a knowledge space in detail. The final summary and further research are drawn in Section 4.

2. Preliminaries

2.1. Formal Concept Analysis Theory

Partial order ≤ is a relation on a set X with reflexivity, anti-symmetry, and transitivity. Then, the set X satisfying the partial order is called the partially ordered set (for short, a poset). For a subset Y of a poset X, we define the lower set and the upper set as follows, respectively:

$$\downarrow Y=\{y\in X:\exists x\in Y\Rightarrow y\le x\};$$

$$\uparrow Y=\{y\in X:\exists x\in Y\Rightarrow x\le y\}.$$

when Y is a singleton set $\left\{x\right\}$; we denote the lower $\downarrow x$ and upper sets $\uparrow x$ for short. Furthermore, a subset Y of X is a lower set if $Y=\downarrow Y$. Analogously, Y is an upper set if $Y=\uparrow Y$. One can see [39] for the details.

A subset Z of a partially ordered set is called a chain if any two members of Z are comparable. Generally, alternative names for a chain are a linearly ordered set and a totally ordered set. Therefore, if Z is a chain and $x,y\in Z$, then either $x\le y$ or $y\le x$ (see [40]).

An element $a\in X$ is named maximal if there exists $a\le x$ such that $x=a$, that is there is no element in X following a except a. Similarly, an element $a\in X$ is called minimal if whenever $x\le a$ then $x=a$, that is there is no element in X preceding a except a itself.

Lemma 1

(Kuratowski). Let X be a poset. Then, each chain in X is contained by a maximal chain.

A formal context is a triple $F=(U,A,R)$, where $U=\{g_1,\cdots ,g_n\}$ and $A=\{a_1,\cdots ,a_m\}$ are two nonempty finite sets of objects and attributes, respectively. R is a binary relation between U and A, where $(g,a)\in R$ means that the object g possesses attribute a.

In fact, the representation of the binary relation contains values 1 and 0, where 1 means the row object possesses the column attribute. In this paper, we suppose that the binary relation R is $regular$, which holds the following forms: for any $(g,a)\in U\times A$:

• There exist $a_i,a_j\in A$ with $(g,a_i)\in R$ and $(g,a_j)\notin R$;
• There are $g_i,g_j\in U$ satisfying $(g_i,a)\in R$ and $(g_j,a)\notin R$.

For $G\subseteq U$ and $B\subseteq A$, one defines the following two operators [1,2]:

• $G^{*}=\{a\in A:\forall g\in G,(g,a)\in R\}$;
• $B^{*}=\{g\in U:\forall a\in B,(g,a)\in R\}$.

$G^{*}$ is the maximal set of attributes that possesses all objects in G, and $B^{*}$ is the maximal set of objects shared by B. If a pair $(G,B)$ satisfies $G^{*}=B$ and $B^{*}=G$, we say that the pair $(G,B)$ is a formal concept, in which G is called the extent and B is called the intent. In addition, for any $g\in U$, ${\left\{g\right\}}^{*}$ is denoted as $g^{*}$ for short. Similarly, for any $a\in A$, denote $a^{*}$ for convenience instead of ${\left\{a\right\}}^{*}$.

It is easy to observe that $G^{*}=\{a\in A:G\subseteq a^{*}\}={\bigcap }_{g\in G}{g}^{*}$ and $B^{*}=\{g\in U:B\subseteq g^{*}\}={\bigcap }_{a\in A}{a}^{*}$. With the hypothesis of $regular$, we have $\left(1\right)$ $U^{*}={\varnothing }_A$ and ${\varnothing }_A^{*}=U$; $\left(2\right)$ ${\varnothing }_U^{*}=A$ and $A^{*}=\varnothing$.

The collection of all formal concepts of F is denoted by $L(U,A,R)$, in which the corresponding partial order relation ≤ is given as follows: for any $(G_1,B_1),(G_2,B_2)\in L(U,A,R)$,

$$(G_1,B_1)\le (G_2,B_2)\iff G_1\subseteq G_2\iff B_1\supseteq B_2,$$

then $(G_1,B_1)$ is a sub-concept of $(G_2,B_2)$ and the relation ≤ is called the hierarchical order of concepts. Since $L(U,A,R)$ is closed under union and intersection [1], that is, for any $(G_1,B_1),(G_2,B_2)\in L(U,A,R)$,

$$\begin{array}{c}(G_1,B_1)\cap (G_2,B_2)=(G_1\cap G_2,{(B_1\cup B_2)}^{**}),\\ (G_1,B_1)\cup (G_2,B_2)=({(G_1\cup G_2)}^{**},B_1\cap B_2),\end{array}$$

then $L(U,A,R)$ forms a complete lattice denoted as the concept lattice.

A closure system is a collection of subsets that is closed under intersection and contains ∅, U. Caspard and Davey [41,42] introduced a closure system induced by the concept lattice. Denote:

$$L_U(U,A,R)=\{G^{**}:G\subseteq U\},$$

$$L_A(U,A,R)=\{B^{**}:B\subseteq A\}.$$

Then, $L_U(U,A,R)$ and $L_A(U,A,R)$ in fact form the closure systems on U and A with respect to $L(U,A,R)$, respectively.

2.2. Knowledge Space Theory

In this subsection, we recall several notions of KST; for more details, refer [31,32].

For a partial knowledge structure $(Q,\mathcal{K})$, Q is a nonempty finite set of items or problems, which is called the domain of the knowledge structure, and $\mathcal{K}$ is family of subsets of Q containing at least Q. The subsets of $\mathcal{K}$ are knowledge states. If $\varnothing \in \mathcal{K}$, then the partial knowledge structure is denoted as a knowledge structure. When $\mathcal{K}$ is closed under union, $(Q,\mathcal{K})$ is called a knowledge space; equivalently, $\mathcal{K}$ is a knowledge space on Q. The dual of $\mathcal{K}$ on Q is the knowledge structure $\overline{\mathcal{K}}$ containing all the complements of the states of $\mathcal{K}$, i.e., $\overline{\mathcal{K}}=\{K\in 2^Q:Q\backslash K\in \mathcal{K}\}$. The minimal subfamily of a knowledge space spanning the original knowledge space is called a base. It should be pointed out that each finite knowledge space has a base.

Furthermore, the states of the base have an important property. Assume that $\mathcal{F}$ is a nonempty family of sets. Each atom at $q\in \bigcup \mathcal{F}$ is a minimal set in $\mathcal{F}$ containing q. A set $X\in \mathcal{F}$ is an atom if it is an atom at q for some $q\in \bigcup \mathcal{F}$. We can conclude that a base of a knowledge space is formed by the collection of all atoms.

There is an intimate relation between FCA and KST [34]. The core connection between FCA and KST is the property that both the collection of extents, as well as the collection of intents of the concepts yield the closure systems. Consider the following formal context:

Definition 1

([34]). Let $(U,Q,R)$ be a formal context where U and Q are individuals and the knowledge domain. For any $x\in U$ and $q\in Q$, $(x,q)\in R\subseteq U\times Q$, if individual x is not capable of solving problem q, then $(U,Q,R)$ is defined as a knowledge context.

Example 1

([31]). Let $U=\{x_1,x_2,x_3,x_4,x_5\}$ be a set of individuals and $Q=\{p,q,r,s\}$ be knowledge domains. Then, the solution behavior is characterized by the relation R in the formal context defined in the following table.

The collection of intents derived from the knowledge context of Table 1 is:

$$L_Q(U,Q,R)=\{\varnothing ,\left\{r\right\},\left\{q\right\},\{p,r\},\{r,s\},\{p,r,q\},\{p,r,s\},Q\}.$$

Table 1. Formal context of individuals $x_1$ to $x_5$.

	p	q	r	s
$x_1$	0	0	1	1
$x_2$	1	0	1	1
$x_3$	0	1	0	0
$x_4$	1	1	1	1
$x_5$	1	1	1	0

It is easy to determine that $L_Q(U,Q,R)$ is closed under intersection forming a closure system on Q with respect to a knowledge context. Now, taking the set-theoretic complements of all the intents, we obtain a family of Q, which contains ∅ and Q and is closed under union, then it forms a knowledge space:

$$\mathcal{K}=\{\varnothing ,\{q\},\{s\},\{p,q\},\{q,s\},\{p,r,s\},\{p,q,s\},Q\}.$$

It is easily seen that a base of knowledge space $\mathcal{K}$ is $\left\{\right\{q\},\{s\},\{p,q\},\{p,r,s\left\}\right\}$, the collection of the subset of solved items for all individuals.

3. Molecular Lattice

Lemma 2.

Let $L(U,A,R)$ be a concept lattice of a formal context $F=(U,A,R)$. For any $(G_1,M_1),(G_2,M_2),(G_3,M_3)\in L(U,A,R)$, then

1. 

$(G_1,M_1)\cup ((G_2,M_2)\cap (G_3,M_3))=((G_1,M_1)\cup (G_2,M_2))\cap ((G_1,M_1)\cup (G_3,M_3))$.

2. 

$(G_1,M_1)\cap ((G_2,M_2)\cup (G_3,M_3))=((G_1,M_1)\cap (G_2,M_2))\cup ((G_1,M_1)\cap (G_3,M_3))$.

Proof. 

We only present the course of proof for $\left(1\right)$. For any $(G,M),(Y,C)\in L(U,A,I)$, we have $G^{**}=G$ and $Y^{**}=Y$, then ${(G\cap Y)}^{*}=G^{*}\cup Y^{*}$ and ${(G^{*}\cap Y^{*})}^{*}=G\cup Y$. Similarly, ${(M\cap C)}^{*}=M^{*}\cup C^{*}$ and ${(M^{*}\cap C^{*})}^{*}=M\cup C$. As we know, $G_i^{**}=G_i$ and $M_i^{**}=M_i$ for $i=1,2,3$, then we have $G_2^{*}\cup G_3^{*}={(G_2\cap G_3)}^{*}$.

$$\begin{array}{l}(G_1,M_1)\cup ((G_2,M_2)\cap (G_3,M_3))=({(G_1\cup (G_2\cap G_3))}^{**},{(M_2\cup M_3)}^{**}\cap M_1),\\ ((G_1,M_1)\cup (G_2,M_2))\cap ((G_1,M_1)\cup (G_3,M_3))=({(G_1^{*}\cap (G_2^{*}\cup G_3^{*}))}^{*},{(M_1\cap (M_2\cup M_3))}^{**}),\end{array}$$

and ${(G_1^{*}\cap (G_2^{*}\cup G_3^{*}))}^{*}={(G_1^{*}\cap {(G_2\cap G_3)}^{*})}^{*}={(G_1\cup (G_2\cap G_3))}^{**}$. Thus $(G_1,M_1)\cup ((G_2,M_2)\cap (G_3,M_3))=((G_1,M_1)\cup (G_2,M_2))\cap ((G_1,M_1)\cup (G_3,M_3))$.    □

By the above the lemma, the complete lattice $L(U,A,R)$ satisfying the distribution laws is called a completely distributive lattice. Note that for any $\mathcal{B},\mathcal{C}\subseteq L(U,A,R)$, if $\forall (G_1,M_1)\in \mathcal{B}$, there exists $(G_2,M_2)\in \mathcal{C}$ with $(G_1,M_1)\le (G_2,M_2)$, then we call $\mathcal{B}$ the refinement of $\mathcal{C}$, denoted as $\mathcal{B}\le \mathcal{C}$. If $\forall (G_1,M_1)\in \mathcal{B}$, there exists $(G_2,M_2)\in \mathcal{C}$ such that $(G_2,M_2)\le (G_1,M_1)$, then we say $\mathcal{C}$ is thinner than $\mathcal{B}$, denoted by $\mathcal{C}⪯\mathcal{B}$.

Definition 2.

Let $F=(U,A,R)$ be a formal context, and for $(G,M)\in L(U,A,R)$, $\mathcal{B}\subset L(U,A,R)$. If:

1. 

$inf\mathcal{B}=(G,M)$, i.e., ${\bigcap }_{(G_1,M_1)\in \mathcal{B}}(G_1,M_1)=(G,M)$,

2. 

and for $\mathcal{C}\subset L(U,A,R)$ with $inf\mathcal{C}\le (G,M)$ such that $\mathcal{C}⪯\mathcal{B}$,

where “inf” means the infimum. Then, $\mathcal{B}$ is referred to as a maximal set of $(G,M)$.

The minimal sets of $(G,M)\in L(U,A,R)$ can be defined under antithesis.

Definition 3.

Let $F=(U,A,R)$ be a formal context and for $(G,M)\in L(U,A,R)$, $\mathcal{B}\subset L(U,A,R)$. If:

1. 

$sup\mathcal{B}=(G,M)$, i.e., ${\bigcup }_{(G_1,M_1)\in \mathcal{B}}(G_1,M_1)=(G,M)$,

2. 

and for $\mathcal{C}\subset L(U,A,R)$ with $(G,M)\le sup\mathcal{C}$ such that $\mathcal{B}\le \mathcal{C}$,

where “sup” means the supremum, then $\mathcal{B}$ is called a minimal set of $(G,M)$.

It is enough to show that $(U,\varnothing )$ and $(\varnothing ,A)$ are the minimal set and maximal set in $L(U,A,R)$ of ∅, respectively, since $L(U,A,R)$ is a complete concept, that is $sup\varnothing =(\varnothing ,A)$ and $inf\varnothing =(U,\varnothing )$. Actually, the union of some maximal sets of $(G,M)$ is also a maximal set of $(G,M)$. Then, the biggest maximal set will inevitably exist, and we denote it as $\alpha \left(\right(G,M\left)\right)$. Similarly, the union of some minimal sets of $(G,M)$ remains a minimal set of $(G,M)$ since $L(U,A,R)$ is complete. Thus, there exists the biggest minimal set of $(G,M)$ denoted by $\beta \left(\right(G,M\left)\right)$. Next, we aim to conduct an investigation on the relationship between $(G,M)$ and its biggest maximal set.

By virtue of the complete distributive lattice $L(U,A,R)$, $\alpha \left(\right(G,M\left)\right)$ is in correspondence with $(G,M)\in L(U,A,R)$ and uniquely exists, which can be seen as a image of $(G,M)$ with a mapping from $L(U,A,R)$ to $2^{L(U,A,R)}$.

Definition 4.

Let $F=(U,A,R)$ be a formal context. For any $(G,M)$, suppose $\alpha \left(\right(G,M\left)\right)$ corresponds to $(G,M)$, then an obtained mapping $\alpha :$$L(U,A,R)\to 2^{L(U,A,R)}$ is defined as the maximal mapping on $L(U,A,R)$.

Theorem 1.

Suppose $F=(U,A,R)$ is a formal context. Then:

1. 

For any $(G,M)\in L(U,A,R)$, $\alpha \left(\right(G,M\left)\right)$ is an upper set, that is $\forall (G_1,M_1)\in \alpha \left((G,M)\right)$, there is $(G_2,M_2)\in \alpha \left((G,M)\right)$ with $(G_2,M_2)\le (G_1,M_1)$.

2. 

$\alpha :$$L(U,A,R)\to 2^{L(U,A,R)}$ is an intersection–union mapping, that is suppose $\mathcal{A}=\{(G_i,M_i)\in L(U,A,R):i\in \Delta \}\subset L(U,A,R)$, then $\alpha \left({\bigcap }_{i\in \Delta }(G_i,M_i)\right)={\bigcup }_{i\in \Delta }\alpha \left((G_i,M_i)\right)$.

Proof. 

(1) Suppose $(G_1,M_1)\in \uparrow \alpha \left((G,M)\right)$ is the upper set of $\alpha \left(\right(G,M\left)\right)$, then there exists $(G_2,M_2)\in \alpha \left((G,M)\right)$ such that $(G_2,M_2)\le (G_1,M_1)$. Let $\mathcal{B}=\alpha \left((G,M)\right)\cup \left\{(G_1,M_1)\right\}$. Evidently, $inf\mathcal{B}=(G,M)$. For $\mathcal{C}\subset L(U,A,R)$ with $inf\mathcal{C}\le (G,M)$, then $\mathcal{C}⪯\alpha \left(\right(G,M\left)\right)$ by virtue of the maximal set $\alpha \left(\right(G,M\left)\right)$. In addition, $(G_2,M_2)\in \alpha \left((G,M)\right)$ meets that $(G_2,M_2)\le (G_1,M_1)$. It is easy to see that $\mathcal{C}⪯\mathcal{B}$. Then, $\mathcal{B}$ is a maximal set of $(G,M)$. On account of $\alpha \left(\right(G,M\left)\right)$ being the biggest maximal set of $(G,M)$, it only has $\left(B\right)=\alpha \left(\right(G,M\left)\right)$, for which $(G_1,M_1)\in \alpha \left((G,M)\right)$. Then, $\alpha \left(\right(G,M\left)\right)=\uparrow \alpha \left(\right(G,M\left)\right)$.

(2) Suppose $\mathcal{A}=\{(G_i,M_i)\in L(U,A,R):i\in \Delta \}\subset L(U,A,R)$ and ${\bigcap }_{i\in \Delta }(G_i,M_i)=(G,M)$. We only have to prove that $\mathcal{B}={\bigcup }_{i\in \Delta }\alpha \left((G_i,M_i)\right)$ is the biggest maximal set of $(G,M)$. In reality,

$$inf\mathcal{B}=in{f}_{i\in \Delta }\left(inf\alpha \left((G_i,M_i)\right)\right)={\bigcap }_{i\in \Delta }(G_i,M_i)=(G,M)$$

.

On the other hand, due to ${\mathcal{B}}_1\subset L(U,A,R)$ with $inf{\mathcal{B}}_1\le (G,M)$ and for any $i\in \Delta$, we have $inf{\mathcal{B}}_1\le (G_i,M_i)$. This implies there exists $(Y,C)\in {\mathcal{B}}_1$ such that $(Y,C)\le (G_{i_j},M_{i_j})$ for any $(G_{i_j},M_{i_j})\in \alpha \left((G_i,M_i)\right)$. Then, $\mathcal{B}⪯{\mathcal{B}}_1$, which yields that $\mathcal{B}$ is a maximal set of $(G,M)$. Furthermore, for any maximal set $\mathcal{C}$ of $(G,M)$ and $\mathcal{B}\ne \mathcal{C}$, by the definition of the maximal set, we conclude that $\mathcal{C}⪯\mathcal{B}$, i.e., for any $(Z,D)\in \mathcal{C}$, there exists $(G_j,M_j)\in \mathcal{B}={\bigcup }_{i\in \Delta }\alpha \left((G_i,M_i)\right)$ satisfying $(G_j,M_j)\le (Z,D)$. Assume $(G_j,M_j)\in \alpha \left((G_{i_0},M_{i_0})\right)$, then $(Z,D)\in \alpha \left((G_{i_0},M_{i_0})\right)\subset \mathcal{B}$ by the condition of $\alpha \left((G_{i_0},M_{i_0})\right)=\uparrow \alpha \left((G_{i_0},M_{i_0})\right)$, which indicates $\mathcal{C}\subset \mathcal{B}$. Thus, $\mathcal{B}$ is the biggest maximal set of $(G,M)$, that is $\mathcal{B}=\alpha \left(\right(G,M\left)\right)$.    □

Definition 5.

Let $F=(U,A,R)$ be a formal context. For any $(G,M)$, suppose $\beta \left(\right(G,M\left)\right)$ corresponds to $(G,M)$, then an obtained mapping $\beta :$$L(U,A,R)\to 2^{L(U,A,R)}$ is referred to as the minimal mapping on $L(U,A,R)$.

Theorem 2.

Suppose $F=(U,A,R)$ is a formal context. Then:

1. 

For any $(G,M)\in L(U,A,R)$, $\beta \left(\right(G,M\left)\right)$ is a lower set, that is, $\forall (G_1,M_1)\in \beta \left((G,M)\right)$, there is $(G_2,M_2)\in \beta \left((G,M)\right)$ with $(G_1,M_1)\le (G_2,M_2)$.

2. 

$\beta :$$L(U,A,R)\to 2^{L(U,A,R)}$ is a union-preserved mapping, that is, suppose $\mathcal{A}=\{(G_i,M_i)\in L(U,A,R):i\in \Delta \}\subset L(U,A,R)$, then $\beta \left({\bigcup }_{i\in \Delta }(G_i,M_i)\right)={\bigcup }_{i\in \Delta }\beta \left((G_i,M_i)\right)$.

Proof. 

This is similar to the proof of Theorem 1.    □

Lemma 3.

Let $F=(U,A,R)$ be a formal context and $(G,M)\in L(U,A,R)$ with $(Y,C)\in \alpha \left(\right(X,B\left)\right)$. Then, there exists $(Z,D)\in L(U,A,R)$ satisfying $(Z,D)\in \alpha \left(\right(G,M\left)\right)$ and $(Y,C)\in \alpha \left(\right(Z,D\left)\right)$.

Proof. 

Notice that $inf\alpha \left(\right(G,M\left)\right)=(G,M)$ and $\alpha :$$L(U,A,R)\to 2^{L(U,A,R)}$ is an intersection–union mapping, so then

$$(Y,C)\in \alpha \left((G,M)\right)=\alpha \left(inf\alpha \left((G,M)\right)\right)=\bigcup \{\alpha \left((G_1,M_1)\right):(G_1,M_1)\in \alpha \left((G,M)\right)\},$$

Thus, there is $(Z,D)=(G_1,M_1)$ such that $(Y,D)\in \alpha \left(\right(Z,D\left)\right)$ and $(Z,D)\in \alpha \left(\right(G,M\left)\right)$.    □

Corollary 1.

Let $F=(U,A,R)$ be a formal context and $(G,M)\in L(U,A,R)$ with $(Y,C)\in \alpha \left(\right(G,M\left)\right)$. Then, there are $(G_1,M_1),\cdots ,(G_t,M_t)\in L(U,A,R)$ following that:

1. 

$(G_1,M_1)\in \alpha \left((G,M)\right)$ and $(G_{k+1},M_{k+1})\in \alpha \left((G_k,M_k)\right)$, $k=1,2,\cdots ,t-1$.

2. 

$(Y,C)\in \alpha \left((G_k,M_k)\right)$, $k=1,\cdots ,t$.

Proof. 

This follows immediately by applying Lemma 3.    □

If $(Y,C)\in \alpha \left(\right(G,M\left)\right)$, then we can discover $(G_1,M_1),\cdots ,(G_t,M_t)\in L(U,Q,R)$ such that $(G,M)\le (G_1,M_1)\le \cdots \le (G_t,M_t)\le (Y,C)$.

Definition 6.

Let $F=(U,A,R)$ be a formal context. For any $\varnothing \ne \mathcal{I}\subset L(U,A,R)$, the following properties hold:

1. 

$(U,\varnothing )\notin \mathcal{I}$ and $\forall (G_1,M_1),(G_2,M_2)\in \mathcal{I}$, $\exists (G_3,M_3)\in \mathcal{I}$ such that $(G_1,M_1)\le (G_3,M_3)$ and $(G_2,M_2)\le (G_3,M_3)$;

2. 

$\mathcal{I}=\downarrow \mathcal{I}$, that is, $\forall (G_1,M_1)\in \mathcal{I}$, $\exists (G_2,M_2)\in \mathcal{I}$ such that $(G_1,M_1)\le (G_2,M_2)$.

Then, we call $\mathcal{I}$ an ideal in $L(U,A,R)$.

Theorem 3.

Let $F=(U,A,R)$ be a formal context and $(G_1,M_1),(G_2,M_2)\in L(U,A,R)$ with $(G_2,M_2)\in \alpha \left((G_1,M_1)\right)$. Then, there exists an ideal $\mathcal{I}$ in $L(U,A,R)$ satisfying the following properties:

1. 

$(G_1,M_1)\in \mathcal{I}\subset \{(G,M)\in L(U,A,R):(G,M)\le (G_2,M_2)\}=\downarrow (G_2,M_2)$;

2. 

For any $(G,M)\in L(U,A,R)-\mathcal{I}$, there exists a minimal element $(Y,C)$ in $L(U,A,R)-\mathcal{I}$ such that $(Y,C)\le (G,M)$.

Proof. 

There exist $(Y_1,C_1),\cdots ,(Y_t,C_t)\in L(U,A,R)$ satisfying the properties of the above corollary. Let $\mathcal{I}={\bigcup }_{i=1}^t(\downarrow (Y_i,C_i))$. Then, $\mathcal{I}$ is a lower set, obviously. Second, for any $(Y_{i_0},C_{i_0}),(Y_{j_0},C_{j_0})\in \mathcal{I}$, there are $(Y_i,C_i),(Y_j,C_j)\in \mathcal{I}$ with $(Y_{i_0},C_{i_0})\le (Y_i,C_i)$ and $(Y_{j_0},C_{j_0})\le (Y_j,C_j)$. Owing to $(Y_{k+1},C_{k+1})\in \alpha \left((Y_k,C_k)\right)$ for $k=1,\cdots ,t-1$, it has either $(Y_i,C_i)\le (Y_j,C_j)$ or $(Y_j,C_j)\le (Y_i,C_i)$. These yield that $\mathcal{I}$ is an ideal in $L(U,A,R)$ and $(G_1,M_1)\in \mathcal{I}\subset \downarrow (G_2,M_2)$. The following certify $\left(2\right)$.

Suppose $(G,M)\in L(U,A,R)-\mathcal{I}$, then $\left\{\right(G,M\left)\right\}$ is a chain. By Kuratowski, there exists a maximal chain $\mathcal{H}$ containing $\left\{\right(G,M\left)\right\}$. Assume $(Y,C)=inf\mathcal{H}$. Next, we prove $(Y,C)\notin \mathcal{I}$. Actually, if $(Y,C)\in \mathcal{I}$, then there is a natural number $k\le t-1$ such that $(Y,C)\in \downarrow (Y_k,C_k)$. $(Y,C)\le (Y_k,C_k)$, i.e., $inf\mathcal{H}\le (Y_k,C_k)$ as a result. However, $(Y_{k+1},C_{k+1})\in \alpha (Y_k,C_k)$, and in light of the definition of the maximal set, there exists $(Z,D)\in \mathcal{H}$ with $(Z,D)\le (Y_{k+1},C_{k+1})$, which indicates $(Z,D)\in \downarrow (Y_{k+1},C_{k+1})\subset \mathcal{I}$, in conflict with $(Z,D)\in \mathcal{H}\subset L(U,A,R)-\mathcal{I}$.    □

Definition 7.

Let $F=(U,A,R)$ be a formal context. For $(G_1,M_1),(G_2,M_2),(G_3,M_3)\in L(U,A,R)$:

1. 

$(G_1,M_1)$ is called a complement-prime element if $(G_1,M_1)\le (G_2,M_2)\cup (G_3,M_3)$ implies $(G_1,M_1)\le (G_2,M_2)$ or $(G_1,M_1)\le (G_3,M_3)$.

2. 

$(G_1,M_1)$ is defined a join-irreducible element if $(G_1,M_1)\le (G_2,M_2)\cup (G_3,M_3)$ implies $(G_1,M_1)=(G_2,M_2)$ or $(G_1,M_1)=(G_3,M_3)$.

3. 

$(G_1,M_1)$ is seen as a prime element if $(G_2,M_2)\cap (G_3,M_3)\le (G_1,M_1)$ implies $(G_2,M_2)\le (G_1,M_1)$ or $(G_3,M_3)\le (G_1,M_1)$.

4. 

$(G_1,M_1)$ is called a meet-irreducible element if $(G_2,M_2)\cap (G_3,M_3)=(G_1,M_1)$ implies $(G_2,M_2)=(G_1,M_1)$ or $(G_3,M_3)=(G_1,M_1)$.

Lemma 4.

$(G,M)\in L(U,A,R)$ is a prime element if and only if ${(G,M)}^{{}^{\prime }}$ is a complement-prime element, where ${(G,M)}^{{}^{\prime }}\in L_C(U,A,R_C)$ is called the complement of $(G,M)$ and $R_C$ is defined as follows:

$$(x,a)\in R_C if and only if (x,a)\notin R,x\in U,a\in A.$$

Theorem 4.

Let $F=(U,A,R)$ be a formal context. Then:

1. 

$(G,M)\in L(U,A,R)$ is a complement-prime element if and only if $(G,M)$ is a join-irreducible element;

2. 

$(G,M)\in L(U,A,R)$ is a prime element if and only if $(G,M)$ is a meet-irreducible element.

Proof. 

We only prove the first. Note that $(G,M)$ is a join-irreducible element and $(G,M)\le (Y,C)\cup (Z,D)$ with $(Y,C),(Z,D)\in L(U,A,R)$. By distributive laws, $(G,M)=(G,M)\cap \left(\right(Y,C)\cup (Z,D\left)\right)=\left(\right(G,M)\cap (Y,C\left)\right)\cup \left(\right(G,M)\cap (Z,D\left)\right)$, then $(G,M)=(G,M)\cap (Y,C)$ or $(G,M)=(G,M)\cap (Z,D)$. These yield that $(G,M)\le (Y,C)$ or $(G,M)\le (Z,D)$. Conversely, if $(G,M)$ is a complement-prime element and $(G,M)=(Y,C)\cup (Z,D)$, then $(G,M)\le (Y,C)\cup (Z,D)$. Thus, $(G,M)\le (Y,C)$ or $(G,M)\le (Z,D)$. However, $(G,M)=(Y,C)\cup (Z,D)$, we obtain $(Y,C)\le (G,M)$ and $(Z,D)\le (G,M)$. Then, $(G,M)=(Y,C)$ or $(G,M)=(Z,D)$, that is $(G,M)$ is a join-irreducible element.    □

Normally, a join-irreducible element is not distinguished from a complement-prime element in this paper. Obviously, $(\varnothing ,A)$ is a join-irreducible element. Every join-irreducible element is called a molecule except $(\varnothing ,Q)$. Therefore, if $(G,M)\in L(U,A,R)$ is a molecule, then $(\varnothing ,A)\ne (G,M)$ is a join-irreducible element.

Theorem 5.

Let $F=(U,A,R)$ be a formal context. For any $(G,M)\in L(U,A,R)$, $(G,M)$ is a molecule if and only if, whenever $(G_1,M_1),(G_2,M_2)\in \beta \left((G,M)\right)$, then there exists $(G_3,M_3)\in \beta \left((G,M)\right)$ such that $(G_1,M_1)\le (G_3,M_3)$ and $(G_2,M_2)\le (G_3,M_3)$.

Proof. 

Suppose $(G,M)\in M\left(L\right(U,A,R\left)\right)$, for any $(G_1,M_1),(G_2,M_2)\in \beta \left((G,M)\right)$, and let

$$\begin{array}{c}\mathcal{A}=\{(Y,C)\in \beta \left((G,M)\right):(G_1,M_1)\le (Y,C)\},\\ \mathcal{B}=\{(Y,C)\in \beta \left((G,M)\right):(G_1,M_1)\nleqq (Y,C)\},\end{array}$$

then $\beta \left(\right(G,M\left)\right)=\mathcal{A}\cup \mathcal{B}$ and $(G,M)=sup\beta \left(\right(G,M\left)\right)=sup\mathcal{A}\cup sup\mathcal{B}$. Then, $(G,M)=sup\mathcal{A}$ or $(G,M)=sup\mathcal{B}$ since $(G,M)$ is a molecule. Actually, $(G,M)\ne sup\mathcal{B}$. Otherwise, $(G,M)=sup\mathcal{B}$, and in light of $\beta \left(\right(G,M\left)\right)$, the minimal set of $(G,M)$ and $(G_1,M_1)\in \beta \left((G,M)\right)$, we have $(Y_1,C_1)\in \mathcal{B}$ such that $(G_1,M_1)\le (Y_1,C_1)$, a contradiction. Hence, $(G,M)=sup\mathcal{A}$. In addition, according to $(G_2,M_2)\in \beta \left((G,M)\right)$, there exists $(Y_2,C_2)\in \mathcal{A}$ meeting $(G_2,M_2)\le (Y_2,C_2)$, which implies $(Y_2,C_2)\in \beta \left((G,M)\right)$, $(G_1,M_1)\le (Y_2,C_2)$, and $(G_2,M_2)\le (Y_2,C_2)$.

Conversely, suppose $(G_1,M_1),(G_2,M_2)\in \beta \left((G,M)\right)$; there exists $(G_3,M_3)\in \beta \left((G,M)\right)$ such that $(G_1,M_1)\le (G_3,M_3)$ and $(G_2,M_2)\le (G_3,M_3)$. If $(G,M)$ is not a molecule, then we have $(Y_1,C_1),(Y_2,C_2)\in L(U,A,R)$ with $(G,M)=(Y_1,C_1)\cup (Y_2,C_2)$, $(G,M)\ne (Y_1,C_1)$, and $(G,M)\ne (Y_2,C_2)$, that is $(G,M)\nleqq (Y_1,C_1)$ and $(G,M)\nleqq (Y_2,C_2)$. Therefore, there are $(G_1,M_1),(G_2,M_2)\in \beta \left((G,M)\right)$ satisfying $(G_1,M_1)\nleqq (Y_1,C_1)$ and $(G_2,M_2)\nleqq (Y_2,C_2)$. According to the hypothesis, we have $(G_3,M_3)\in \beta \left((G,M)\right)$ with $(G_3,M_3)\nleqq (Y_1,C_1)$ and $(G_3,M_3)\nleqq (Y_2,C_2)$. On the other hand, on the basis of $(G,M)\le (Y_1,C_1)\cup (Y_2,C_2)$ and the definition of $\beta \left(\right(G,M\left)\right)$, we can conclude that $(G_3,M_3)\le (Y_1,C_1)$ and $(G_3,M_3)\le (Y_2,C_2)$, which is a contradiction. Therefore, $(X,B)$ is a molecule in $L(U,Q,R)$.    □

Corollary 2.

If $(G,M)\in L(U,A,R)$ is a molecule, then there exists $(Y,C)\in L(U,A,R)$ such that $(G,M)\le (Y,C)$.

Proof. 

This is trivial based on Theorem 5.    □

Corollary 3.

For any $(G,M)\in L(U,A,R)$, if there exists $(Y,C),(Z,D)\in L(U,A,R)$ with neither $(Y,C)\le (Z,D)$ nor $(Z,D)\le (Y,C)$ yielding $(Y,C)\le (G,M)$ and $(Z,D)\le (G,M)$, then $(G,M)$ is not a molecule.

Proof. 

This follows immediately from Theorem 5.    □

Theorem 6.

Let $F=(U,A,R)$ be a formal context. For any $(G,M)\in L(U,A,R)$, $(G,M)$ is a meet-irreducible element if and only if, whenever $(G_1,M_1),(G_2,M_2)\in \alpha \left((G,M)\right)$, then there exists $(G_3,M_3)\in \alpha \left((G,M)\right)$ such that $(G_3,M_3)\le (G_1,M_1)$ and $(G_3,M_3)\le (G_2,M_2)$.

Proof. 

Necessity. Let $(G,M)\in L(U,A,R)$ be a meet-irreducible element and $(G_1,M_1)$, $(G_2,M_2)\in \alpha \left((G,M)\right)$. Denote $\mathcal{C}=\{(Y,C)\in \alpha \left((G,M)\right):(Y,C)\le (G_1,M_1)\}$ and $\mathcal{D}=\{(Y,C)\in \alpha \left((G,M)\right):(Y,C)\nleqq (G_1,M_1)\}$, then $\alpha \left(\right(G,M\left)\right)=\mathcal{C}\cup \mathcal{D}$ and $(G,M)=inf\alpha \left(\right(G,M\left)\right)=inf\mathcal{C}\cap inf\mathcal{D}$. Hence, $(G,M)=inf\mathcal{C}$ or $(G,M)=inf\mathcal{D}$. We next prove that it is impossible for $(G,M)=inf\mathcal{D}$. Inversely, if $(G,M)=inf\mathcal{D}$, by the definition of $\alpha \left(\right(G,M\left)\right)$ and $(G_1,M_1)\in \alpha \left((G,M)\right)$, we have $(Y_1,C_1)\in \mathcal{D}$ such that $(Y_1,C_1)\le (G_1,M_1)$. This is a contradiction. Thus, there can only be $(G,M)=inf\mathcal{C}$. Moreover, owning to $(G_2,M_2)\in \alpha \left((G,M)\right)$, there exists $(Y_2,C_2)\in \mathcal{C}$ with $(Y_2,C_2)\le (G_2,M_2)$. This yields $(Y_2,C_2)\in \alpha \left((G,M)\right)$ with $(Y_2,C_2)\le (G_1,M_1)$ and $(Y_2,C_2)\le (G_2,M_2)$.

Sufficiency. Suppose $(G_1,M_1),(G_2,M_2)\in \alpha \left((G,M)\right)$, then there exists $(G_3,M_3)\in \alpha \left((G,M)\right)$ such that $(G_3,M_3)\le (G_1,M_1)$ and $(G_3,M_3)\le (G_2,M_2)$. If $(G,M)$ is not a meet-irreducible element, then there are $(Y_1,C_1),(Y_2,C_2)\in L(U,Q,R)$ satisfying $(G,M)=(Y_1,C_1)\cap (Y_2,C_2)$ and $(G,M)\ne (Y_1,C_1)$ and $(G,M)\ne (Y_2,C_2)$, i.e., $(Y_1,C_1)\nleqq (G,M)$ and $(Y_2,C_2)\nleqq (G,M)$. Then, we have $(G_1,M_1),(G_2,M_2)\in \alpha \left((G,M)\right)$ such that $(Y_1,C_1)\nleqq (G_1,M_1)$ and $(Y_2,C_2)\nleqq (G_2,M_2)$. According to the known condition, there is $(G_3,M_3)\in \alpha \left((G,M)\right)$ meeting $(Y_1,C_1)\nleqq (G_3,M_3)$ and $(Y_2,C_2)\nleqq (G_3,M_3)$. However, $(G,M)=(Y_1,B_1)\cap (Y_2,B_2)$ and $\alpha \left(\right(G,M\left)\right)$ is the biggest maximal set of $(G,M)$; for the above $(G_3,M_3)\in \alpha \left((G,M)\right)$, there is either $(Y_1,C_1)\le (G_3,M_3)$ or $(Y_2,C_2)\le (G_3,M_3)$, a contradiction. Therefore, $(G,M)$ is a meet-irreducible element.    □

Corollary 4.

Let $F=(U,A,R)$ be a formal context. For $(G,M)\in L(U,A,R)$, if there exists $(Y,C),(Z,D)\in L(U,A,R)$ with neither $(Y,C)\le (Z,D)$ nor $(Z,D)\le (Y,C)$ such that $(G,M)\le (Y,C)$ and $(G,M)\le (Z,D)$, then $(G,M)$ is not a meet-irreducible element.

Corollary 5.

Let $F=(U,A,R)$ be a formal context. For $(G,M)\in L(U,A,R)$, $(G,M)$ is a meet-irreducible element iff $\left|sup\right(G,M\left)\right|=1$, where $|·|$ is the cardinality of a set.

Corollary 6.

For $(G,M)\in L(U,A,R)$, if $\left|sup\right(G,M\left)\right|=1$ and $\left|inf\right(G,M\left)\right|=1$, then $(G,M)$ is not only a molecule, but also a meet-irreducible element.

4. Knowledge Reduction of Knowledge Context Based on FCA

4.1. Classification of Concepts

In the case of knowledge spaces encountered in education, the cardinality of the base of a knowledge space $\mathcal{K}$ is typically much smaller than the cardinality of $\mathcal{K}$. Furthermore, a knowledge space admits at most one base, which is formed by the collection of all the atoms. An atom is a minimal set in $\mathcal{K}$ containing an element of knowledge domain Q. In fact, an atom at $q\in Q$ in the knowledge space is in correspondence with a maximal set at q in the collection of the intents of concepts in the knowledge context.

Let $M\left(L\right(U,A,R\left)\right)=\left\{\right(G,M)\in L(U,A,R):(G,M)$$is$ $molecule\}$ be the collection of all molecules in $L(U,A,R)$.

Theorem 7.

Let $F=(U,A,R)$ be a formal context, then every formal concept in $L(U,A,R)$ is the union of some molecules.

Proof. 

Suppose $(G,M)\in L(U,A,R)$. If $(G,M)=(\varnothing ,A)$, then we have $sup\varnothing =(\varnothing ,A)$. Now, note that $(G,M)\ne (\varnothing ,A)$. Let

$$\pi \left(\right(G,M\left)\right)=\left\{\right(Y,C)\in L(U,A,R):(Y,C)\le (G,M)\wedge (Y,C) is molecule\}.$$

Then, $sup\pi \left(\right(G,M\left)\right)\le (G,M)$. Next, we only have to prove $(G,M)\le \pi \left(\right(G,M\left)\right)$. In fact, let $sup\pi \left(\right(G,M\left)\right)=(Z,D)$ and assume $(G,M)\le (Z,D)$ is not true. By this, there is $(G_1,M_1)\in \alpha \left((Z,D)\right)$ with $(G,M)\nleqq (G_1,M_1)$. In accordance with Theorem 3, an ideal $\mathcal{I}$ such that $(Z,D)\in \mathcal{I}\subset \downarrow (G_1,M_1)$ is existent. Since $(G,M)\notin \downarrow (G_1,M_1)$, we have $(G,M)\notin \mathcal{I}$, that is $(G,M)\in L(U,A,R)-\mathcal{I}$. Then, there exists a minimal element $(Y,C)$ in $L(U,A,R)-\mathcal{I}$ satisfying $(Y,C)\le (G,M)$. Inevitably, $(Y,C)$ is a molecule. In reality, $(\varnothing ,A)\in \mathcal{I}$, while $(Y,C)\in L(U,A,R)-\mathcal{I}$, then $(Y,C)\ne (\varnothing ,A)$. Meanwhile, $(Y,C)$ is a join-irreducible element. If not, there exist $(Y_1,C_1),(Y_2,C_2)\in L(U,A,R)$ such that $(Y,C)=(Y_1,C_1)\cup (Y_2,C_2)$, but $(Y,C)\ne (Y_1,C_1)$ and $(Y,C)\ne (Y_2,C_2)$, which yield $(Y_1,C_1)<(Y,C)$ and $(Y_2,C_2)<(Y,C)$. On the other hand, $(Y_1,C_1),(Y_2,C_2)\in \mathcal{I}$ and $(Y,C)$ is a minimal set. This implies $(Y,C)=(Y_1,C_1)\cup (Y_2,C_2)\in \mathcal{I}$, a contradiction. Hence, $(Y,C)$ is a join-irreducible element. Then, $(Y,C)\in \pi \left(\right(X,B\left)\right)$, that is $(Y,C)\le (Z,D)$. In accordance with $(Z,D)\in \mathcal{I}$ and $\mathcal{I}$ being a lower set, we have $(Y,C)\in \mathcal{I}$. This contradicts $(Y,C)\in L(U,Q,R)-\mathcal{I}$. Therefore, $(G,M)\le sup\pi \left(\right(G,M\left)\right)$.    □

Theorem 8.

Let $F=(U,A,R)$ be a formal context, then every formal concept in $L(U,A,R)$ is the intersection of some prime elements.

Proof. 

This is similar to the above theorem.    □

Definition 8.

Let $F=(U,A,R)$ be a formal context; $L(U,A,R)$ is referred to as a molecular lattice.

Because $L(U,A,R)$ is a complete distributive lattice, in which molecules, as well as meet-irreducible elements can be regarded as the basic unit generating $L(U,A,R)$, it is therefore a molecule is an intersection of some meet-irreducible elements. In order to demonstrate not all the meet-irreducible elements are necessary to show all the molecules, we research the following example.

Example 2.

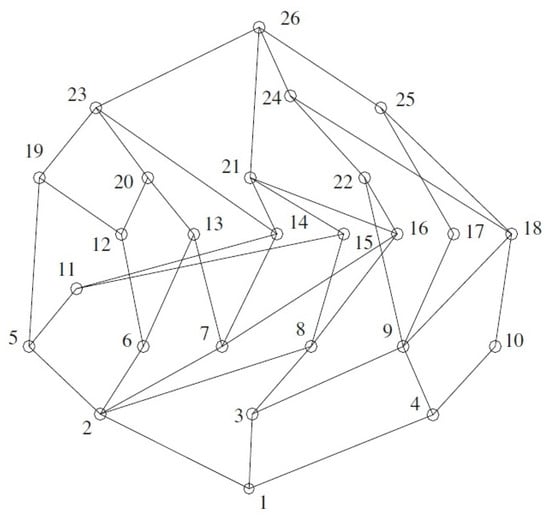
Figure 1 is a Hasse diagram of a concept lattice generated from a formal context $(U,A,R)$, in which a dot represents a formal concept. Dots 1 and 26 in the diagram correspond to $(\varnothing ,A)$ and $(U,\varnothing )$, respectively. It is easy to see that Concepts $2,3,4,5,6,7,10,11,12,17$ are molecules and $10,13,15,17,19,20,21,22,23,24,25$ are meet-irreducible elements. We have

Figure 1. The Hasse diagram of $L(U,A,I)$.

• $2=6\cap 7$
• $3=15\cap 17\cap 21\cap 22$,
• $4=10\cap 17\cap 22$,
• $5=15\cap 19\cap 21\cap 22$,
• $6=13\cap 19\cap 20$,
• $7=21\cap 22\cap 23$,
• $11=15\cap 21\cap 23$,
• $12=19\cap 20$.

In other words, in this way, all molecules can be represented by some meet-irreducible elements except for Concepts 24 and 25. Namely, not all meet-irreducible elements are necessary absolutely, similar to molecules.

Therefore, we have the following definition.

Definition 9.

Let $F=(U,A,R)$ be a formal context. For any $(G,M)\in L(U,A,R)$, if $(G,M)$ is both a meet-irreducible element and a molecule, then $(G,M)$ is called a necessary concept in $L(U,A,R)$; if $(G,M)$ is either a meet-irreducible element or a molecule, then $(G,M)$ is called a relatively necessary concept; otherwise, $(G,M)$ is called a relatively unnecessary concept.

Example 3

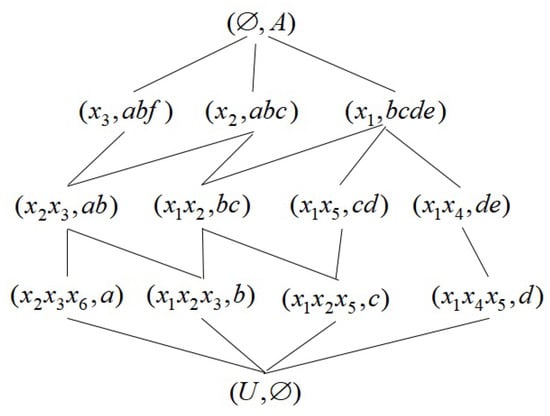
([15]). The formal context $F=(U,A,R)$ is given in Table 2, and the Hasse graph of the corresponding concept lattice is shown in Figure 2.

Table 2. Formal context.

I	a	b	c	d	e	f
$x_1$	0	1	1	1	1	0
$x_2$	1	1	1	0	0	0
$x_3$	1	1	0	0	0	1
$x_4$	0	0	0	1	1	0
$x_5$	0	0	1	1	0	0
$x_6$	1	0	0	0	0	0

Figure 2. The Hasse diagram of $L(U,A,I)$.

We can see that $(x_1,bcde),(x_2,abc),(x_3,abf),(x_1{x}_4,de),(x_1{x}_5,cd),(x_2{x}_3{x}_6,a)$ are all the molecules in $L(U,A,R)$ and $(x_1{x}_4,de),(x_2{x}_3{x}_6,a),(x_1{x}_2{x}_3,b),(x_1{x}_2{x}_5,c),(x_1{x}_4{x}_5,d)$ are all the meet-irreducible elements in $L(U,A,R)$. Then, both $(x_1{x}_4,de)$ and $(x_2{x}_3{x}_6,a)$ are necessary concepts, $(x_2{x}_3,ab)$ and $(x_1{x}_2,bc)$ are relatively unnecessary concepts, and the others are relatively necessary concepts.

4.2. Representing a Concept Lattice Based on a Boolean Matrix

A concept lattice is an ordering of the maximal rectangles defined by a binary relation. In this subsection, we carry out the relationship between the concept lattice and Boolean matrix. Then, a one-to-one correspondence between the set of elements of the concept lattices and the Boolean vector is established. Furthermore, we explain how to use the properties of the Boolean matrix to research the molecules.

Given a formal context $F=(U,A,R)$, for each $(x_i,a_j)\in U\times A$, $(x_i,a_j)\in R$ iff object $x_i$ has a value of 1 in attribute $a_j$ and $(x_i,a_j)\notin R$ iff object $x_i$ has a value of 0 in attribute $a_j$, i.e., $x_i$ has no value in attribute $a_j$. In other words, a formal context can be seen as a Boolean matrix $M_R={\left(c_{ij}\right)}_{n\times m}$, defined by

$$c_{ij}=\left\{\begin{array}{cc}\hfill 1& (x_i,a_j)\in R\\ \hfill 0& (x_i,a_j)\notin R\end{array}\right.$$

We call $M_R$ the relation matrix of F. This point of view enables us to establish a relationship between the concept lattice and Boolean matrix. This may prove important in many applications. It is well known that, for a relation matrix $M_R$ of a formal context, a row vector is the feature vector of $x^{*}$, $x\in U$, and a column vector is the eigenvector of the corresponding $a^{*}$, $a\in A$, denoted as $\lambda \left(x^{*}\right)$ and $\lambda \left(a^{*}\right)$, respectively. As a consequence, we can use Boolean matrices to characterize the formal context, a subset of the objects, or a subset of the properties is characterized by eigenvectors.

Definition 10

([43]). Let $F=(U,A,R)$ be a formal context. M denotes a Boolean matrix composed of all $\lambda \left(x^{**}\right)$ ($\forall x\in U$), and N denotes a Boolean matrix consisting of all $\lambda \left(a^{**}\right)$ ($\forall a\in A$). Then, we call M and N the object relation matrix and attribute relation matrix in $F=(U,A,R)$, respectively.

Lemma 5.

Let $H={\left(h_{ij}\right)}_{n\times m}$, $L={\left(l_{ij}\right)}_{n\times m}$ and $K={\left(k_{ij}\right)}_{m\times p}$ be Boolean matrices. Then:

1. 

$H\le L$ if and only if $h_{ij}\le l_{ij}$ for $i=1,\cdots ,n$, $j=1,\cdots ,m$;

2. 

$H\vee L={(h_{ij}\vee l_{ij})}_{n\times m}$, $H\wedge L={(h_{ij}\wedge l_{ij})}_{n\times m}$;

3. 

$H·K={\left(d_{ij}\right)}_{n\times p}$, where $d_{ij}={\vee }_{1\le k\le m}(h_{ik}\wedge k_{kj})$;

4. 

$H-L={(h_{ij}\wedge (1-l_{ij}))}_{n\times m}$, $\sim H={(1-h_{ij})}_{n\times m}$.

Theorem 9

([43]). Let $F=(U,A,R)$ be a formal context with the relation matrix $M_R={\left(c_{ij}\right)}_{n\times m}$ with respect to R. For any $X\subseteq U$ and $B\subseteq A$, then $\lambda \left(X^{*}\right)=\sim (\lambda \left(X\right)·(\sim M_R))$ and $\lambda \left(B^{*}\right)=\sim (\lambda \left(B\right)·(\sim M_R^T))$.

Proof. 

We assume that $\lambda \left(X\right)=(t_1,t_2,\cdots ,t_n)$ and $E={\left(e_i\right)}_{1\times m}$. Since $e_i=1-{\vee }_{k=1}^m(t_k\wedge (1-c_{ik}))$, we have

$$\begin{array}{cc}\hfill X^{*}& =\{a_i\in A:\forall x\in X,(x,a_i)\in R\}\hfill \\ \hfill & =\{a_i\in A:\forall x\in X,x\in a_i^{*}\}\hfill \\ \hfill & =\{a_i\in A:X\subseteq a_i^{*}\}\hfill \\ \hfill & =\{a_i\in A:X\cap (\sim a_i^{*})=\varnothing \}\hfill \\ \hfill & =\{a_i\in A:{\vee }_{k=1}^n(t_k\wedge (1-c_{ik}))=0\}\hfill \\ \hfill & =\{a_i\in A:e_i=1\}\hfill \end{array}$$

Hence, $\lambda \left(X^{*}\right)=E=\sim (\lambda \left(X\right)·(\sim M_R))$. Similarly, $\lambda \left(B^{*}\right)=\sim (\lambda \left(B\right)·(\sim M_R^T))$    □

Corollary 7.

Let $F=(U,A,R)$ be a formal context with the relation matrix $M_R={\left(c_{ij}\right)}_{n\times m}$ with respect to R. For any $X\subseteq U$ and $B\subseteq A$, then $\lambda \left(X^{**}\right)=\sim ((\sim (\lambda \left(X\right)·(\sim M_R)))·(\sim M_R^T))$ and $\lambda \left(B^{**}\right)=\sim ((\sim (\lambda \left(B\right)·(\sim M_R^T)))·(\sim M_R))$.

The following theorems can help us determine whether or not a concept is a molecule or a meet-irreducible element.

Theorem 10.

Let $F=(U,A,R)$ be a formal context and $(G,M)\in L(U,A,R)$. Then, $(G,M)$ is a molecule in $L(U,A,R)$ iff one of the following two conditions holds:

1. 

There does not exist $\varnothing \ne Y\subset G$ such that $\lambda \left(Y\right)=\lambda \left(Y^{**}\right)$, $\lambda \left(G^{*}\right)\le \lambda \left(Y^{*}\right)$ and $\lambda \left(G^{*}\right)\ne \lambda \left(Y^{*}\right)$, i.e., $\{Y\subset G:Y\ne \varnothing ,\lambda \left(Y\right)=\lambda \left(Y^{**}\right),\lambda \left(G^{*}\right)<\lambda \left(Y^{*}\right)\}=\varnothing$;

2. 

$R\left(G\right)=\{Y\subset G:Y\ne \varnothing ,\lambda \left(Y\right)=\lambda \left(Y^{**}\right),\lambda \left(G^{*}\right)<\lambda \left(Y^{*}\right)\}\ne \varnothing$ and ${\wedge }_{Y\in R\left(G\right)}\lambda (Y^{*}-G^{*})\ne \lambda (\varnothing )$.

Proof. 

If there does not exist $\varnothing \ne Y\subset G$ such that $\lambda \left(Y\right)=\lambda \left(Y^{**}\right)$ and $\lambda \left(G^{*}\right)<\lambda \left(Y^{*}\right)$, then by the definition, it is obvious that $(G,M)$ is a molecule in $L(U,A,R)$.

Now, we assume that $R\left(G\right)\ne \varnothing$. If ${\wedge }_{Y\in R\left(G\right)}\lambda (Y^{*}-G^{*})\ne \lambda (\varnothing )$, we can find an attribute $a\in \bigcap \{Y^{*}-G^{*}:Y\in R\left(G\right)\}$. Since $a\notin B$, there exists $x\in G$ such that $(x,a)\notin R$. On the other hand, for any $\varnothing \ne Y\subset G$ satisfying $\lambda \left(Y\right)=\lambda \left(Y^{**}\right)$ and $\lambda \left(G^{*}\right)<\lambda \left(Y^{*}\right)$, we have $(y,a)\in R$ for $y\in Y$. Consequently, we conclude that $inf(G,M)=\left\{(Y,Y^{*})\right\}$, then $(G,M)$ is a molecule in $L(U,A,R)$.

Under the other situation of ${\wedge }_{Y\in R\left(G\right)}\lambda (Y^{*}-G^{*})=\lambda (\varnothing )$, we cannot find any attribute $a\in A$ such that $a\in Y^{*}$ and $a\notin G^{*}$ for any $\varnothing \ne Y\subset G$ satisfying $\lambda \left(Y\right)=\lambda \left(Y^{**}\right)$ and $\lambda \left(G^{*}\right)<\lambda \left(Y^{*}\right)$. Alternatively, it is hard to find any attribute $a\in A$ such that $(x,a)\notin R$ for an $x\in G$ and $(y,a)\in R$ for all $y\in Y\subset G$ satisfying $\lambda \left(Y\right)=\lambda \left(Y^{**}\right)$ and $\lambda \left(G^{*}\right)<\lambda \left(Y^{*}\right)$. Thus, we can conclude that $\left|inf\right(G,M\left)\right|\ge 2$, then $(G,M)$ is not a molecule in $L(U,A,R)$.    □

Theorem 11.

Let $F=(U,A,R)$ be a formal context and $(G,M)\in L(U,A,R)$. Then, $(G,M)$ is a meet-irreducible element in $L(U,A,R)$ iff one of the following two conditions holds:

1. 

There does not exist $\varnothing \ne C\subset M$ such that $\lambda \left(C\right)=\lambda \left(C^{**}\right)$, $\lambda \left(M^{*}\right)\le \lambda \left(C^{*}\right)$, that is, $\{C\subset M:C\ne \varnothing ,\lambda \left(C\right)=\lambda \left(C^{**}\right),\lambda \left(M^{*}\right)\le \lambda \left(C^{*}\right)\}=\varnothing$;

2. 

$R\left(M\right)=\{C\subset M:C\ne \varnothing ,\lambda \left(C\right)=\lambda \left(C^{**}\right),\lambda \left(M^{*}\right)<\lambda \left(C^{*}\right)\}\ne \varnothing$ and ${\wedge }_{C\in R\left(M\right)}\lambda (C^{*}-M^{*})\ne \lambda (\varnothing )$.

It should be pointed out that we are interested in receiving the intents of all molecules without generating the concept lattice. As we know, $(a^{*},a^{**})\in L(U,A,R)$ for any $a\in A$ and $(x^{**},x^{*})\in L(U,A,R)$, which imply a row in the relation matrix is an intent of a concept and a column is an extent of a concept in $L(U,A,R)$.

It should be noted that there is a concept $(G,M)\in L(U,A,R)$ such that $\left|G\right|=|a^{*}|$ for any attribute $a\in A$ proposed by Mao et al. [44]. Moreover, Mao et al. [44] proposed a proposition that any concept $(G,M)$ in $L(U,A,R)$ is either equivalent to $(b^{*},b^{**})$ ($\exists b\in M$) satisfying $|b^{*}|=|G|$ or the intersection of its two father concepts, that is there are $(G_1,M_1),(G_2,M_2)\in sup(X,B)$ with $(G,M)=(G_1,M_1)\cap (G_2,M_2)$. Then, we write two results as follows.

Lemma 6.

Let $F=(U,A,R)$ be a formal context and $x\in U$. There exists $(G,M)\in L(U,A,R)$ such that $\left|M\right|=|x^{*}|$.

Proof. 

We assume that $|x^{*}|=t$. There are $b_1,\cdots ,b_t\in A$ satisfying $(x,b_i)\in R$, $i\le t$. Note that $M=\{b:(x,b)\in R\}$ and, obviously, $\left|M\right|=t$. Since $(x^{**},x^{*})\in L(U,A,R)$, then $G=x^{**}$, $M=x^{*}$.    □

Theorem 12.

Let $F=(U,A,R)$ be a formal context. For any $(G,M)\in L(U,A,R)$, it satisfies one of the following conditions:

1. 

There exists $x\in G$ such that $|x^{*}|=|M|$ and $(G,M)=(x^{**},x^{*})$;

2. 

There exist $(G_1,M_1)$ and $(G_2,M_2)$ with $G_i\subset G$$(i=1,2)$ such that $(G,M)=(G_1,M_1)\cup (G_2,M_2)$, i.e., $(G,M)$ can be represented by the union of its two sub-concepts.

Proof. 

Now, we assume that $\left|M\right|=t$.

Case 1. If there exists $x\in G$ such that $|x^{*}|=t$, then $(x,b)\in R$ for any $b\in M$, namely, $M\subseteq x^{*}$. Then, $(G,M)=(x^{**},x^{*})$ by $|x^{*}|=|M|=t$.

Case 2. Suppose $\forall x\in G$, $x^{*}\ne \left|M\right|$. In such a case, by the definition of a concept, $(x,b)\in R$ for any $x\in G$ and $a\in M$, then $M\subset x^{*}$ since $x^{*}\ne \left|M\right|$. Consequently, by the property of the complete lattice, there are $(G_1,M_1)$ and $(G_2,M_2)$ with $G_i\subset G$$(i=1,2)$ such that $(G,M)=(G_1,M_1)\cup (G_2,M_2)$.    □

Wu et al. [22] showed that each pair $(x^{**},x^{*})$, $x\in U$, may be a join-irreducible element, i.e., a molecule in $L(U,A,R)$. It is asserted above that a concept $(G,M)$ in $L(U,A,R)$ is not a molecule if it is represented by the union of its two sub-concepts. Therefore, the object relation matrix can be used to achieve the molecules in formal contexts without generating concept lattices. The algorithm (Algorithm 1) of concept reduction in a formal context is shown as follows, and its time complexity is less than $O\left(\right|U{|}^2)$.

Furthermore, in general, an atom in a knowledge space is a non-join-irreducible element that corresponds to a non-meet-irreducible element of the intents of concepts in $L(U,A,R)$. Therefore, the object relation matrix can be used to achieve the molecules in formal contexts without generating concept lattices. The time complexity of algorithm-based concept reduction in a formal context is less than $O\left(n^2\right)$.

Algorithm 1: Concept reduction in formal contexts

Input: A knowledge context $F=(U,A,R)$, where $U=\{x_1,x_2,\cdots ,x_n\}$ and $A=\{a_1,\cdots ,a_m\}$ Output:$\mathcal{B}$//the collection of intents of all concepts 1: Generate the relation matrix $M_R={\left(c_{ij}\right)}_{n\times m}$ 2: Complement of object relation matrix $M={\left(m_{ij}\right)}_{n\times n}$←$M_R^T·(\sim M_R)$ 3: for $j=1$ton 4:    if $\left|M(:,j)\right|={\sum }_{t=1}^{n}M(t,j)=1$ and $M(i,j)=1$$i\le n$ 5:       $\mathcal{B}$←$\mathcal{B}\cup {\lambda }^{-1}\left(M(i,:)\right)$, $n-1$, $M^{{}^{\prime }}$←$M-M(i,:)-M(:,j)$ // delete $M(i,:)$ and $M(:,j)$ in M 6:    end if 7: end for 8: for $i=1$ton 9:    if $|M^{{}^{\prime }}(i,:)|=1$ and $M^{{}^{\prime }}(i,j)=1$ $j\le n$ 10:       find $M(i,:)$ corresponding to $M^{{}^{\prime }}(i,:)$ 11:       $\mathcal{B}$←$\mathcal{B}\cup {\lambda }^{-1}\left(M(i,:)\right)$, $n-1$, $M^{{}^{\prime }}$←$M^{{}^{\prime }}-M^{{}^{\prime }}(i,:)-M^{{}^{\prime }}(:,j)$ 12:    end if 13: end for 14: while $sign=1$ 15:    if $M^{{}^{\prime }}\ne \varnothing$ // empty matrix 16:       $N=\varnothing$ 17:       make $M^{{}^{\prime }}$ uniquely so that each pair of rows in $M^{{}^{\prime }}$ is different 18:       $H={\left(h_{ij}\right)}_{x\times y}$←$\{M^{{}^{\prime }}(i,:):|M^{{}^{\prime }}(i,:)|=mi{n}_{t\le n}|M^{{}^{\prime }}(t,:)\left|\right\}$ 19:       for $i=1$tox 20:          find the $i_1$th, ⋯, $i_t$th rows in M corresponding to $H(i,:)$ 21:          L ← $\{M^{{}^{\prime }}(:,j):M^{{}^{\prime }}(i,j)=1\}$ 22:       end for 23:       $M^{{}^{\prime }}$←$M^{{}^{\prime }}-M^{{}^{\prime }}(i,:)-L$, N←$N\cup \{M(i_j,:):1\le j\le t\}$ 24:       $\mathcal{B}$←$\mathcal{B}\cup \{{\lambda }^{-1}\left(M(i,:)\right):M(i,:)\in M\}$ 25:    else $sign=0$ 26:    end if 27 end while 28: $\mathcal{B}$←$\sim \mathcal{B}$

5. Conclusions

Knowledge reduction is a necessary issue to delete redundant and worthless knowledge in information representation and processing. In addition, KST has a homologous mathematical background based on FCA. In this correspondence paper, we first specifically discussed the lattice structure relationships, i.e., the molecule lattice and the concept lattice. Inspired by this, the acquisition approach of the molecules and meet-irreducible elements was characterized. Finally, numerical algorithms were designed to find the atoms of the knowledge space in the knowledge context via a Boolean matrix. This paper mainly studied the knowledge reduction of the knowledge context, whereas we did not consider the fuzzy circumstances. In reality, various concepts have been investigated from different viewpoints to meet the requirements such as the fuzzy concept, three-way concept, and object-oriented concept. In further work, we will plan to research a knowledge reduction framework in fuzzy knowledge spaces.