Landau–Lifshitz and Weinberg Energy Distributions for the Static Regular Simpson–Visser Space-Time Geometry
Abstract
:1. Introduction
2. The Simpson–Visser Gravitational Background
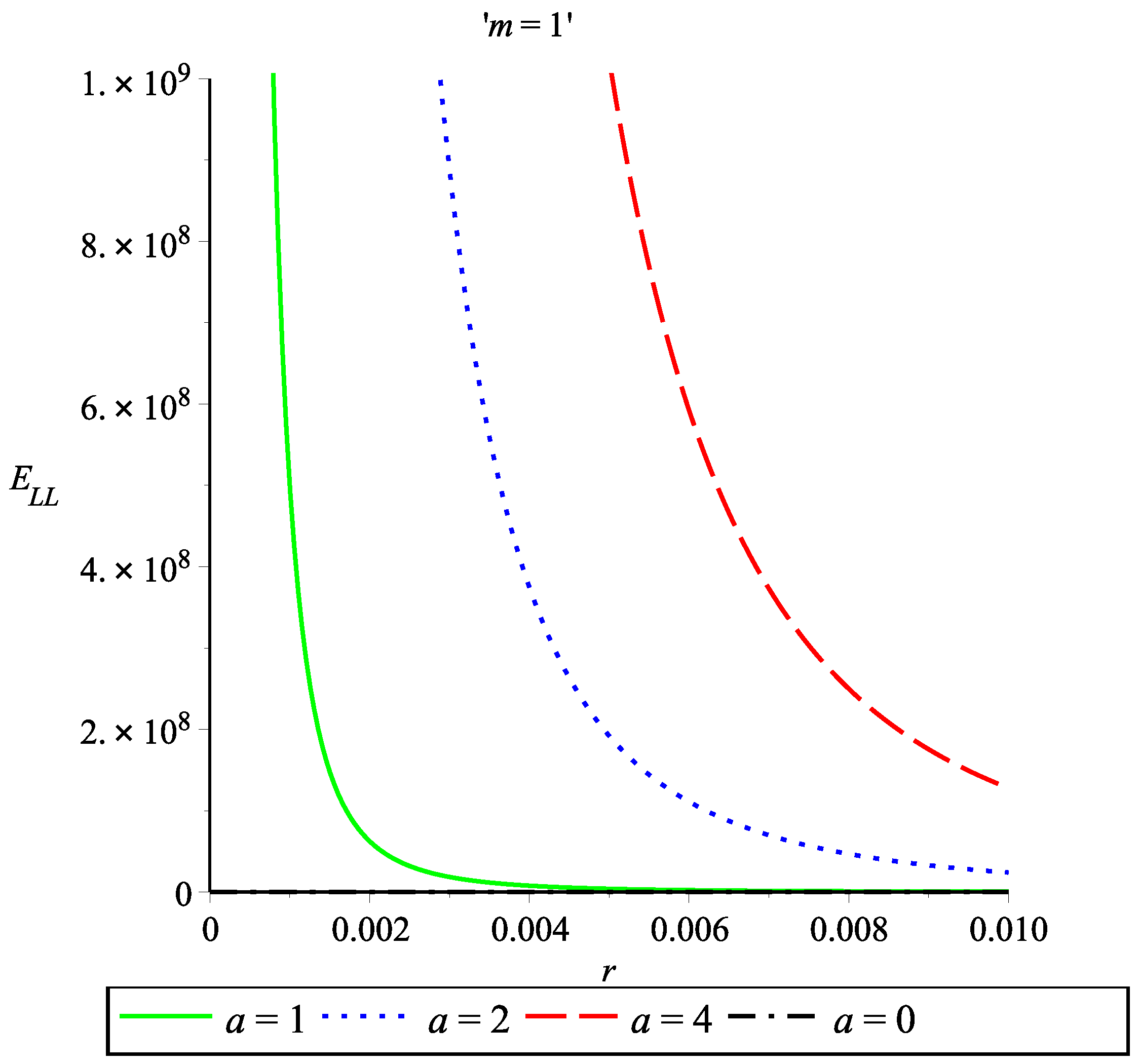
3. Energy-Momentum Distribution of the Simpson–Visser Space-Time in the Landau–Lifshitz Prescription
4. Energy-Momentum Distribution of the Simpson–Visser Space-Time in the Weinberg Prescription
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Einstein, A. On the general theory of relativity. In Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin; Deutsche Akademie der Wissenschaften zu Berlin: Berlin, Germany, 1915; Volume 47, pp. 778–786, Addendum: Volume 47, pp. 799–801; Available online: https://einsteinpapers.press.princeton.edu/vol6-doc/ (accessed on 15 June 2021).
- Trautman, A. Conservation laws in general relativity. In Gravitation: An Introduction to Current Research; Witten, L., Ed.; John Wiley & Sons: New York, NY, USA, 1962; p. 169. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Pergamon Press: New York, NY, USA, 1987; p. 280. [Google Scholar]
- Papapetrou, A. Equations of motion in general relativity. Proc. Phys. Soc. A 1951, 64, 57. [Google Scholar] [CrossRef]
- Bergmann, P.G.; Thomson, R. Spin and angular momentum in general relativity. Phys. Rev. 1953, 89, 400–407. [Google Scholar] [CrossRef]
- Møller, C. On the localization of the energy of a physical system in the general theory of relativity. Ann. Phys. 1958, 4, 347–371. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of General Theory of Relativity; John Wiley & Sons: New York, NY, USA, 1972; p. 165. [Google Scholar]
- Bergqvist, G. Positivity and definitions of mass. Class. Quantum Gravity 1992, 9, 1917. [Google Scholar] [CrossRef]
- Chen, C.-M.; Nester, J.M. Quasi local quantities for general relativity and other gravity theories. Class. Quantum Gravity 1999, 16, 1279. [Google Scholar] [CrossRef] [Green Version]
- Sinha, A.K.; Pandey, G.K.; Bhaskar, A.K.; Rai, B.C.; Jha, A.K.; Kumar, S.; Xulu, S.S. Effective gravitational mass of the Ayón-Beato and García metric. Mod. Phys. Lett. 2015, 30, 1550120. [Google Scholar] [CrossRef] [Green Version]
- Tripathy, S.K.; Mishra, B.; Pandey, G.K.; Singh, A.K.; Kumar, T.; Xulu, S.S. Energy and momentum of Bianchi type VIh universes. Adv. High Energy Phys. 2015, 2015, 705262. [Google Scholar] [CrossRef] [Green Version]
- Saleh, M.; Thomas, B.B.; Kofane, T.C. Energy distribution and thermodynamics of the quantum-corrected Schwarzschild black hole. Chin. Phys. Lett. 2017, 34, 080401. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, P.K.; Mahanta, K.L.; Goit, D.; Sinha, A.K.; Xulu, S.S.; Das, U.R.; Prasad, A.; Prasad, R. Einstein energy-momentum complex for a phantom black hole metric. Chin. Phys. Lett. 2015, 32, 020402. [Google Scholar] [CrossRef] [Green Version]
- Yang, I.-C. Some characters of the energy distribution for a charged wormhole. Chin. J. Phys. 2015, 53, 110108-1–110108-4. [Google Scholar]
- Radinschi, I.; Rahaman, F.; Ghosh, A. On the energy of charged black holes in generalized dilaton-axion gravity. Int. J.Theor. Phys. 2010, 49, 943–956. [Google Scholar] [CrossRef] [Green Version]
- Yang, I.-C.; Lin, C.-L.; Radinschi, I. The energy of a regular black hole in general relativity coupled to nonlinear electrodynamics. Int. J. Theor. Phys. 2009, 48, 248–255. [Google Scholar] [CrossRef] [Green Version]
- Vagenas, E.C. Energy distribution in 2d stringy black hole backgrounds. Int. J. Mod. Phys. 2003, 18, 5781–5794. [Google Scholar] [CrossRef] [Green Version]
- Grammenos, T.; Radinschi, I. Energy distribution in a Schwarzschild-like spacetime. Int. J. Theor. Phys. 2007, 46, 1055–1064. [Google Scholar] [CrossRef] [Green Version]
- Radinschi, I.; Rahaman, F.; Grammenos, T.; Islam, S. Einstein and Møller energy-momentum complexes for a new regular black hole solution with a nonlinear electrodynamics source. Adv. High Energy Phys. 2016, 2016, 9049308. [Google Scholar] [CrossRef]
- Abdel-Megied, M.; Gad, R.M. Møller’s Energy in the Kantowski-Sachs Space-Time. Adv. High Energy Phys. 2010, 2010, 379473. [Google Scholar] [CrossRef] [Green Version]
- Radinschi, I.; Grammenos, T.; Rahaman, F.; Cazacu, M.M.; Spanou, A.; Chakraborty, J. On the energy of a non-singular black hole solution satisfying the weak energy condition. Universe 2020, 6, 169. [Google Scholar] [CrossRef]
- Balart, L. Energy distribution of (2+1)-dimensional black holes with nonlinear electrodynamics. Mod. Phys. Lett. A 2009, 24, 2777–2785. [Google Scholar] [CrossRef]
- Yang, I.-C.; Lin, C.-L.; Radinschi, I. Energy distribution of a regular class of exact black hole solutions. Int. J. Theor. Phys. 2009, 48, 2454–2461. [Google Scholar] [CrossRef] [Green Version]
- Gad, R.M.; Alharbi, H.A. Gravitational energy in Van Stockum space-time. Indian J. Phys. 2022, 96, 1591–1597. [Google Scholar] [CrossRef]
- Aguirregabiria, J.M.; Chamorro, A.; Virbhadra, K.S. Energy and angular momentum of charged rotating black holes. Gen. Relativ. Gravit. 1996, 28, 1393–1400. [Google Scholar] [CrossRef] [Green Version]
- Virbhadra, K.S. Naked singularities and Seifert’s conjecture. Phys. Rev. D 1999, 60, 104041. [Google Scholar] [CrossRef] [Green Version]
- Xulu, S.S. Bergmann–Thomson energy-momentum complex for solutions more general than the Kerr-Schild class. Int. J. Theor. Phys. 2007, 46, 2915–2922. [Google Scholar] [CrossRef] [Green Version]
- Radinschi, I.; Grammenos, T.; Rahaman, F.; Spanou, A.; Islam, S.; Chattopadhyay, S.; Pasqua, A. Energy-momentum for a charged nonsingular black hole solution with a nonlinear mass function. Adv. High Energy Phys. 2017, 2017, 7656389. [Google Scholar] [CrossRef]
- Radinschi, I.; Sahoo, P.K.; Grammenos, T.; Chattopadhyay, S.; Cazacu, M.-M. Localization of Energy and Momentum in an Asymptotically Reissner-Nordström Non-Singular Black Hole Space-Time Geometry. Universe 2020, 6, 69. [Google Scholar] [CrossRef]
- Bel, L. Définition d’une densité d’énergie et d’un état de radiation totale généralisée. Comptes Rendus Hebd. Seances Acad. Sci. 1958, 246, 3015–3018. [Google Scholar]
- Bonilla, M.A.G.; Senovilla, J.M.M. Some properties of the Bel and Bel-Robinson tensors. Gen. Relativ. Gravit. 1997, 29, 91–116. [Google Scholar] [CrossRef]
- Senovilla, J.M. Super-energy tensors. Class. Quantum Gravity 2000, 17, 2799–2841. [Google Scholar] [CrossRef] [Green Version]
- Penrose, R. Quasi-local mass and angular momentum in general relativity. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1982, 381, 53–63. [Google Scholar]
- Tod, K.P. Some examples of Penrose’s quasilocal mass construction. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1983, 388, 457–477. [Google Scholar]
- Brown, J.D.; York, J.W. Quasilocal energy and conserved charges derived from the gravitational action. Phys. Rev. D 1993, 47, 1407. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hayward, S.A. Quasilocal gravitational energy. Phys. Rev. D 1994, 49, 831–839. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.T.; Yau, S.T. Isometric embeddings into the Minkowski space and new quasi-local mass. Commun. Math. Phys. 2019, 288, 919–942. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.-M.; Liu, J.-L.; Nester, J.M. Quasi-local energy from a Minkowski reference. Gen. Relativ. Gravit. 2018, 50, 158. [Google Scholar] [CrossRef] [Green Version]
- Møller, C. The four-momentum of an insular system in general relativity. Nucl. Phys. 1964, 57, 330–338. [Google Scholar] [CrossRef]
- Hayashi, K.; Shirafuji, T. New general relativity. Phys. Rev. D 1979, 19, 3524. [Google Scholar] [CrossRef]
- Maluf, J.W.; Veiga, M.V.O.; da Rocha-Neto, J.F. Regularized expression for the gravitational energy-momentum in teleparallel gravity and the principle of equivalence. Class. Quantum Gravity 2007, 39, 227–240. [Google Scholar] [CrossRef] [Green Version]
- Nester, J.M.; So, L.L.; Vargas, T. Energy of homogeneous cosmologies. Phys. Rev. D 2008, 78, 044035. [Google Scholar] [CrossRef] [Green Version]
- Nashed, G.G.L. Energy of spherically symmetric space-times on regularizing teleparallelism. Int. J. Mod. Phys. A 2010, 25, 28–83. [Google Scholar] [CrossRef] [Green Version]
- Sousa, A.; Pereira, R.B.; Silva, A.C. Energy and angular momentum densities in a Gödel-type universe in teleparallel geometry. Gravit. Cosmol. 2010, 16, 25–33. [Google Scholar] [CrossRef]
- Sharif, M.; Jawad, A. Energy contents of some well-known solutions in teleparallel gravity. Astrophys. Space Sci. 2011, 331, 257–263. [Google Scholar] [CrossRef] [Green Version]
- Aygün, S.; Baysal, H.; Aktaş, C.; Yilmaz, I.; Sahoo, P.K.; Tarhan, I.S. Teleparallel energy-momentum distribution of various black hole and wormhole metrics. Int. J. Mod. Phys. A 2018, 33, 1850184. [Google Scholar] [CrossRef]
- Ganiou, M.G.; Houndjo, M.J.S.; Tossa, J. f(T) gravity and energy distribution in Landau–Lifshitz prescription. Int. J. Mod.Phys. D 2018, 27, 1850039. [Google Scholar] [CrossRef] [Green Version]
- Simpson, A.; Visser, M. Black-bounce to traversable wormhole. J. Cosmol. Astropart. Phys. 2019, 2, 42. [Google Scholar] [CrossRef] [Green Version]
- Simpson, A.; Martin-Moruno, P.; Visser, M. Vaidya spacetimes, black-bounces, and traversable wormholes. Class. Quantum Gravity 2019, 36, 145007. [Google Scholar] [CrossRef] [Green Version]
- Lobo, F.S.N.; Rodrigues, M.E.; Silva, M.V.d.; Simpson, A.; Visser, M. Novel black-bounce spacetimes: Wormholes, regularity, energy conditions, and causal structure. Phys. Rev. D 2021, 103, 0840521. [Google Scholar] [CrossRef]
- Wheeler, J.A. Geometrodynamics; Academic Press: Cambridge, MA, USA, 1962. [Google Scholar]
- Izmailov, R.N.; Zhdanov, E.R.; Bhattacharya, A.; Potapov, A.A.; Nandi, K.K. Can massless wormholes mimic a Schwarzschild black hole in the strong field lensing? Eur. Phys. J. Plus 2019, 134, 384. [Google Scholar] [CrossRef]
- Yusupova, R.M.; Karimov, R.K.; Izmailov, R.N.; Nandi, K.K. Accretion Flow onto Ellis–Bronnikov Wormhole. Universe 2021, 7, 177. [Google Scholar] [CrossRef]
- Mazza, J.; Franzin, E.; Liberati, S. A novel family of rotating black hole mimickers. J. Cosmol. Astropart. Phys. 2021, 4, 82. [Google Scholar] [CrossRef]
- Islam, S.U.; Kumar, J.; Ghosh, S.G. Strong gravitational lensing by rotating Simpson–Visser black holes. arXiv 2021, arXiv:2104.00696. [Google Scholar] [CrossRef]
- Radinschi, I.; Grammenos, T.; Chakraborty, G.; Chattopadhyay, S.; Cazacu, M.M. Einstein and Møller Energy-Momentum Distributions for the Static Regular Simpson–Visser Space-Time. Symmetry 2021, 13, 9. [Google Scholar] [CrossRef]
- Virbhadra, K.S.; Ellis, G.F.R. Schwarzschild black hole lensing. Phys. Rev. D 2000, 62, 084003. [Google Scholar] [CrossRef] [Green Version]
- Jafarzade, K.; Zangeneh, M.K.; Lobo, F.S.N. Observational optical constraints of the Simpson–Visser black-bounce geometry. arXiv 2021, arXiv:2106.13893. [Google Scholar]
- Nascimento, J.R.; Petrov, A.Y.; Porfirio, P.J.; Soares, A.R. Gravitational lensing in black-bounce spacetimes. Phys.Rev. D 2020, 102, 044021. [Google Scholar] [CrossRef]
- Tsukamoto, N. Gravitational lensing in the Simpson–Visser black-bounce spacetime in a strong deflection limit. Phys. Rev. D 2021, 103, 024033. [Google Scholar] [CrossRef]
- Pirani, F. Measurement of classical gravitation fields. In The Role of Gravitation in Physics: Report from the 1957 Chapel Hill Conference; DeWitt, C.M., Rickles, D., Eds.; Max-Planck-Gesellschaft zur Förderung der Wissenschaften: Berlin, Germany, 2011. [Google Scholar]
- Tegmark, M. Measuring Spacetime: From Big Bang to Black Holes. Science 2002, 296, 1427. [Google Scholar] [CrossRef] [Green Version]
- Perche, T.R.; Martín-Martínez, E. Geometry of spacetime from quantum measurements. Phys. Rev. D 2022, 105, 066011. [Google Scholar] [CrossRef]
- Kulkarni, R.S. Curvature and metric. Ann. Math. 1970, 91, 311. [Google Scholar] [CrossRef]
- Karlhede, A. A review of the geometrical equivalence of metrics in general relativity. Gen. Relat. Gravit. 1980, 12, 693. [Google Scholar] [CrossRef]
- Izumi, K.; Hagiwara, C.; Nakajima, K.; Kitamura, T.; Asada, H. Gravitational lensing shear by an exotic lens object with negative convergence or negative mass. Phys. Rev. D 2013, 88, 024049. [Google Scholar] [CrossRef] [Green Version]
- Virbhadra, K.S.; Ellis, G.F.R. Gravitational lensing by naked singularities. Phys. Rev. D 2002, 65, 103004. [Google Scholar] [CrossRef]







| Energy | |||||
|---|---|---|---|---|---|
| m | ∞ | ||||
| m | ∞ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radinschi, I.; Grammenos, T.; Spanou, A.; Chattopadhyay, S.; Cazacu, M.M. Landau–Lifshitz and Weinberg Energy Distributions for the Static Regular Simpson–Visser Space-Time Geometry. Symmetry 2022, 14, 900. https://doi.org/10.3390/sym14050900
Radinschi I, Grammenos T, Spanou A, Chattopadhyay S, Cazacu MM. Landau–Lifshitz and Weinberg Energy Distributions for the Static Regular Simpson–Visser Space-Time Geometry. Symmetry. 2022; 14(5):900. https://doi.org/10.3390/sym14050900
Chicago/Turabian StyleRadinschi, Irina, Theophanes Grammenos, Andromahi Spanou, Surajit Chattopadhyay, and Marius Mihai Cazacu. 2022. "Landau–Lifshitz and Weinberg Energy Distributions for the Static Regular Simpson–Visser Space-Time Geometry" Symmetry 14, no. 5: 900. https://doi.org/10.3390/sym14050900









