The Branched Schiff Base Cationic Complexes of Iron(III) with Different Counter-Ions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Physical Measurements
2.3. Langmuir–Blodgett Technology
3. Results
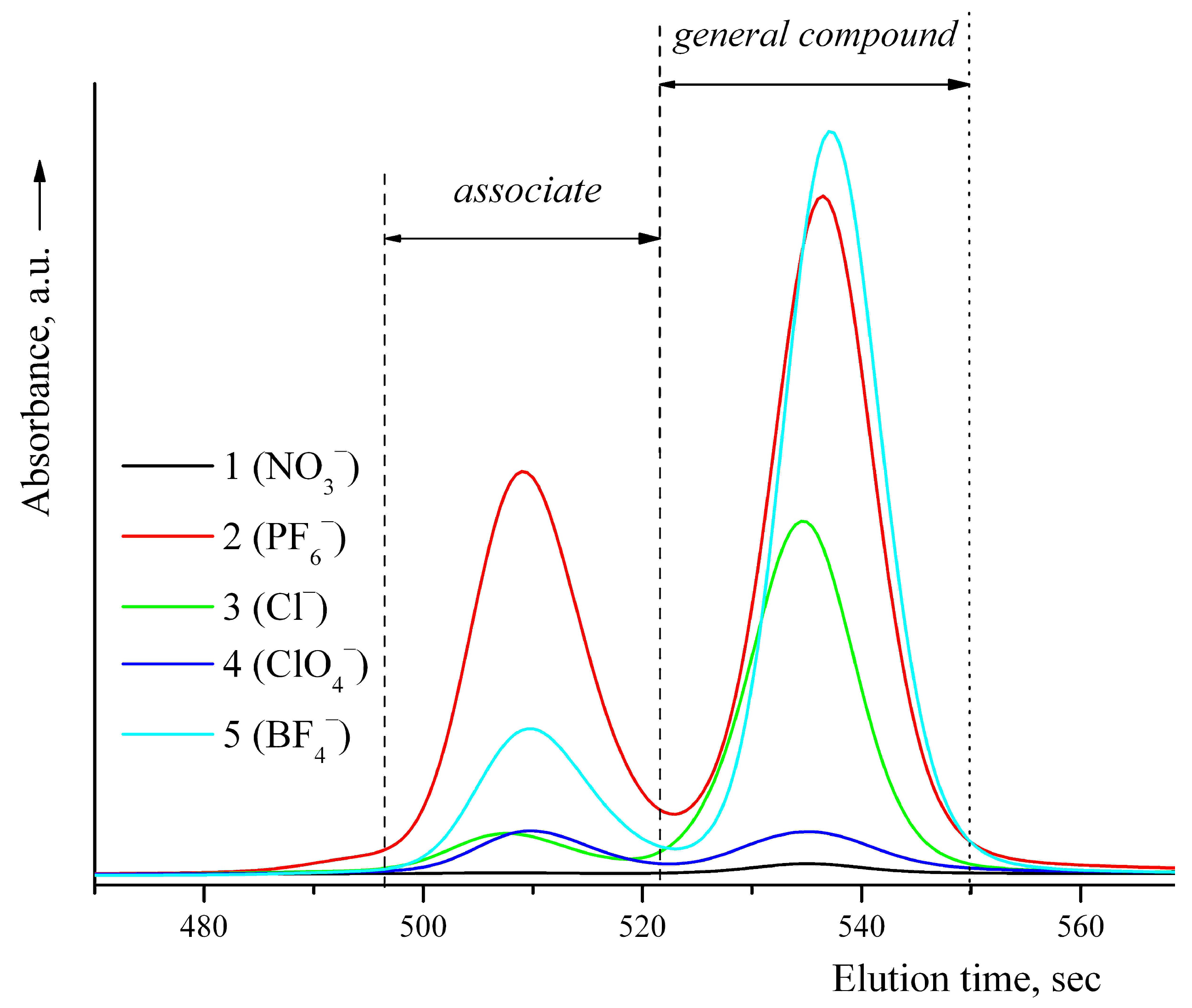
3.1. Synthesis and Characterization
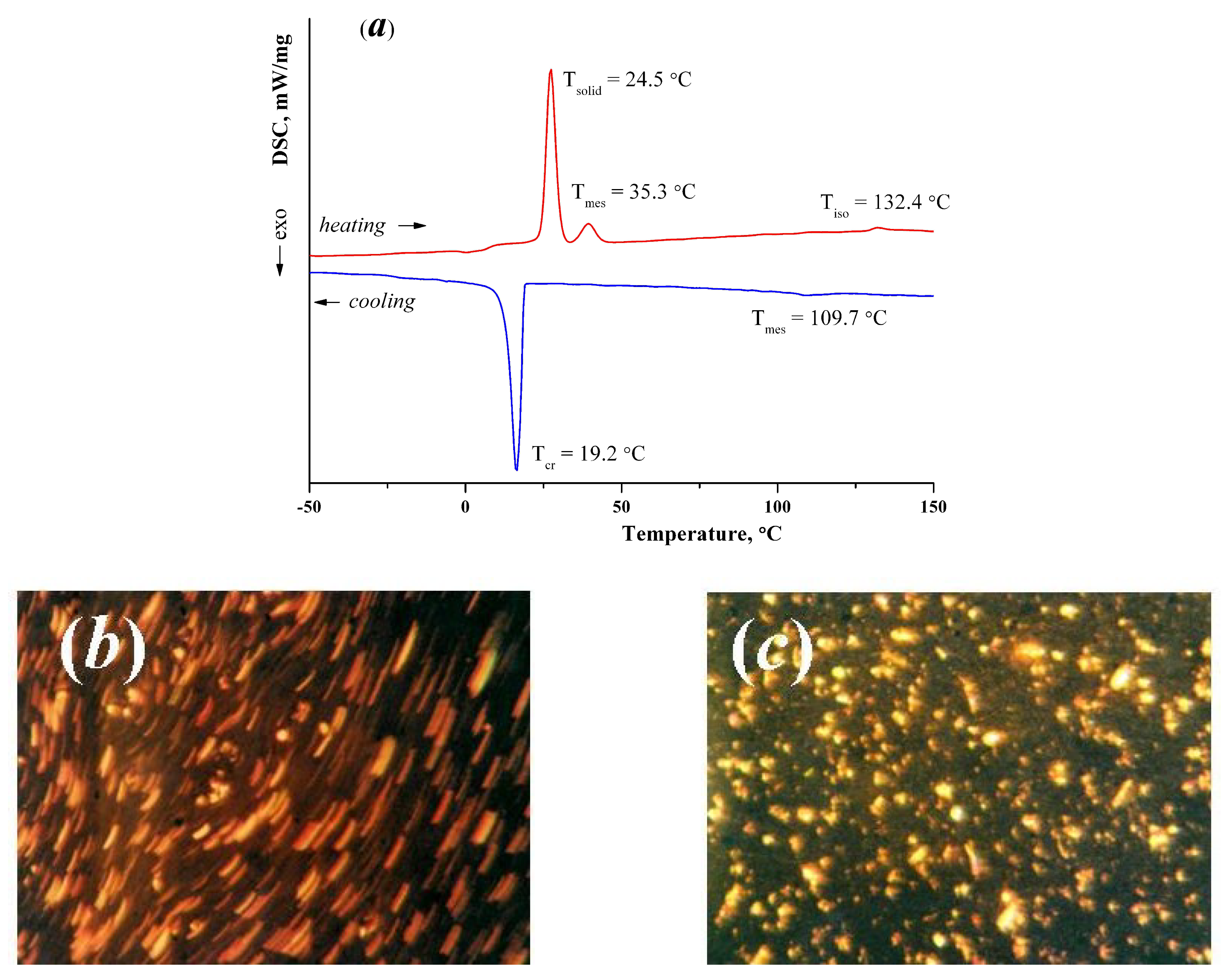
3.2. Thermal Analysis
3.2.1. Phase Transitions in Complex with NO3− Counter-Ion 1
3.2.2. Phase Transitions in Complex with PF6− Counter-Ion 2
3.2.3. Phase Transitions in Complex with Cl− Counter-Ion 3
3.2.4. Phase Transitions in Complex with ClO4− Counter-Ion 4
3.2.5. Phase Transitions in Complex with BF4− Counter-Ion 5
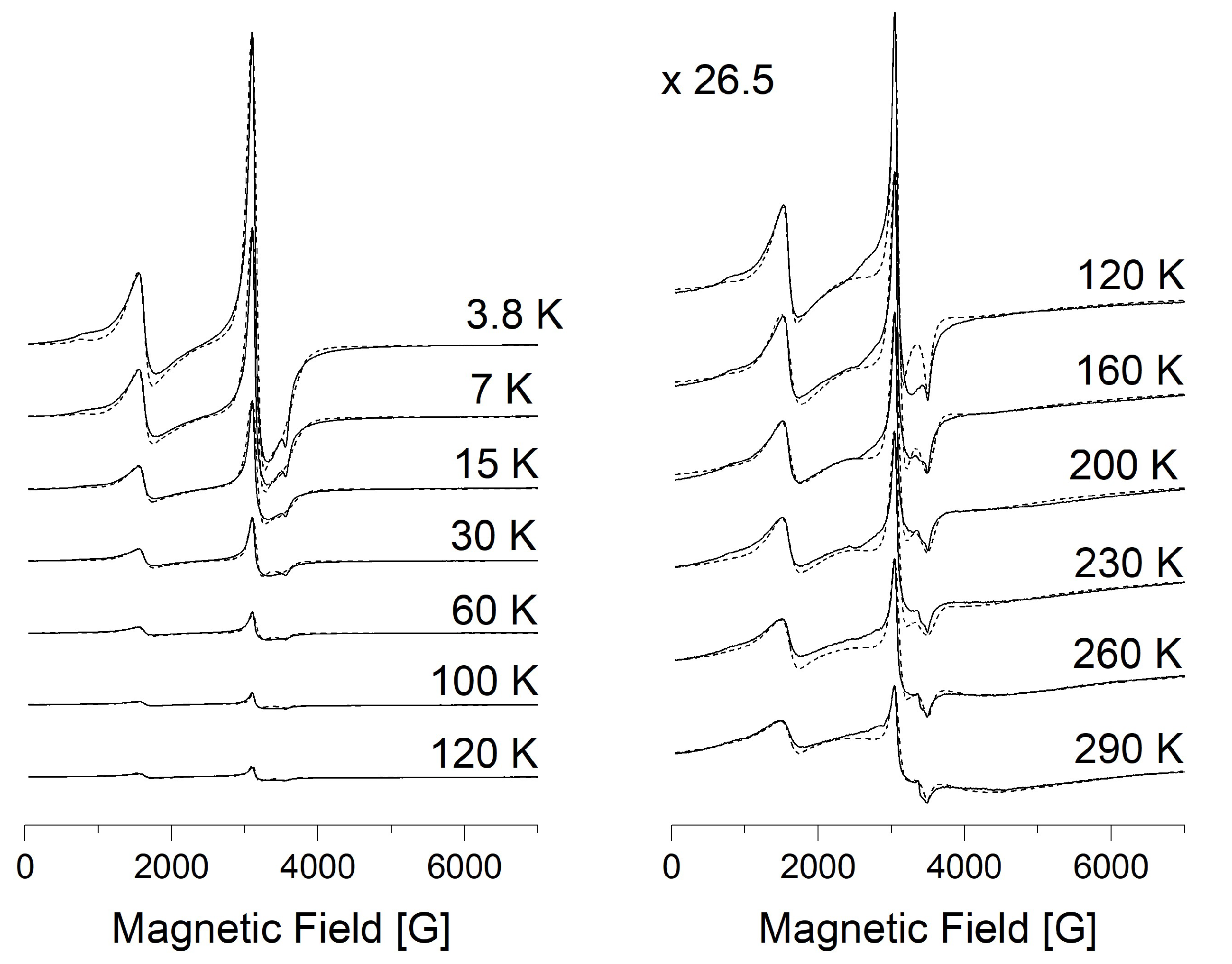
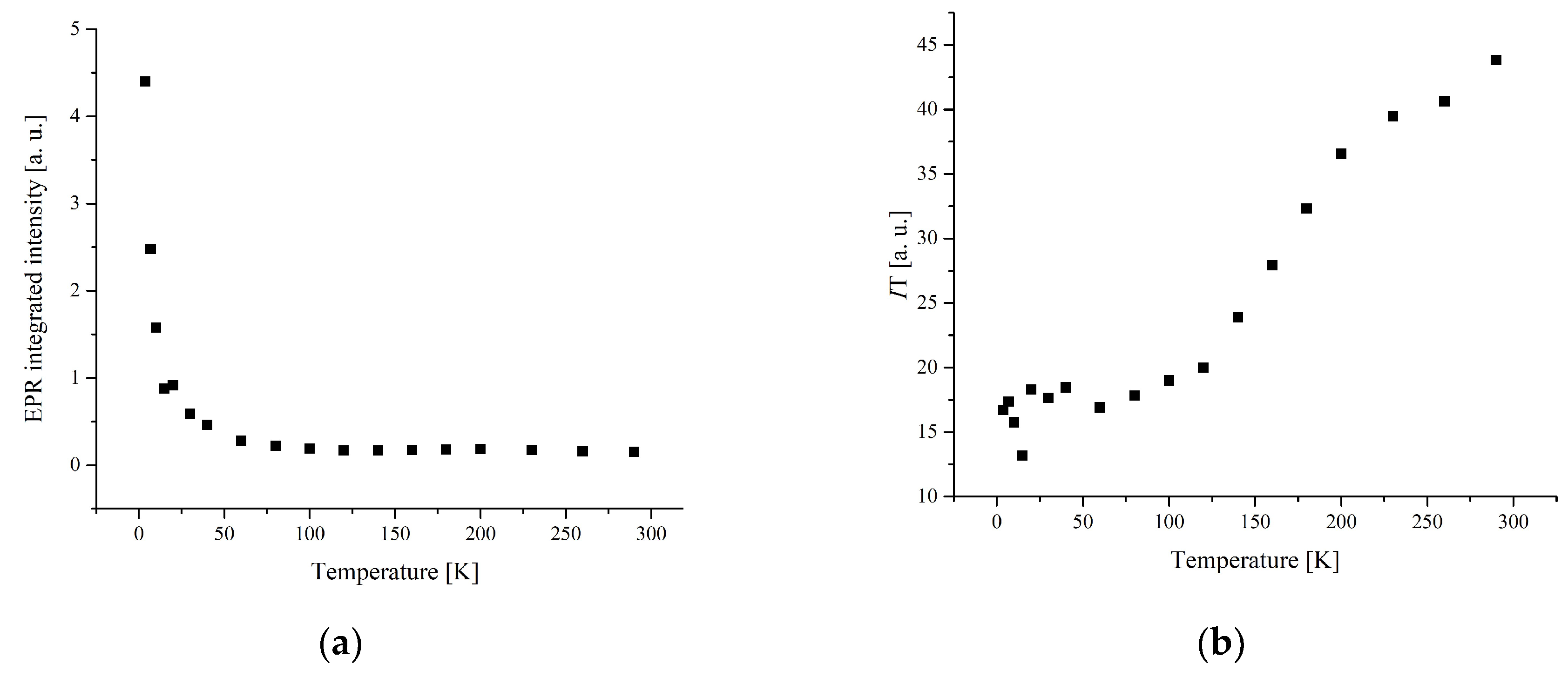
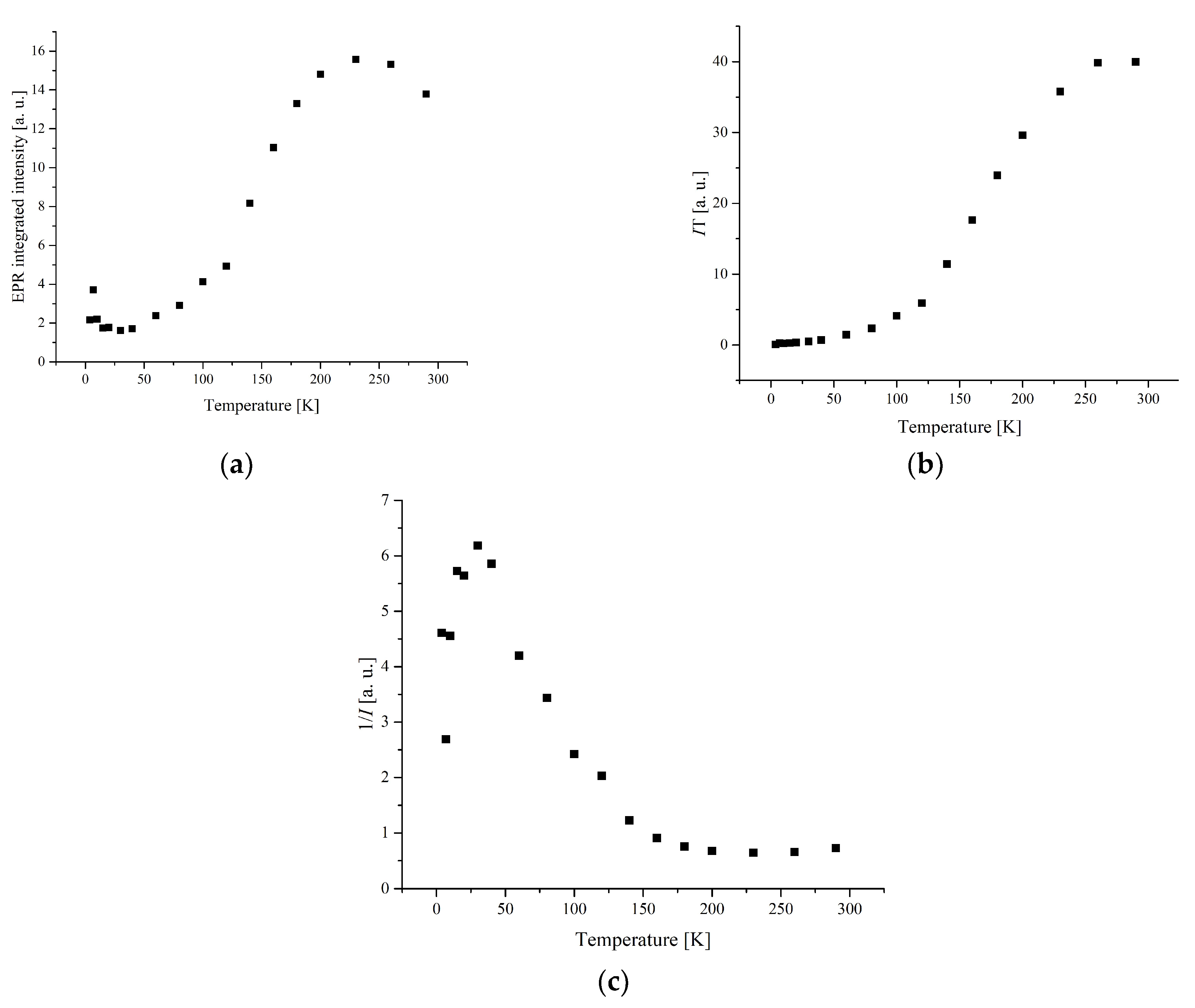
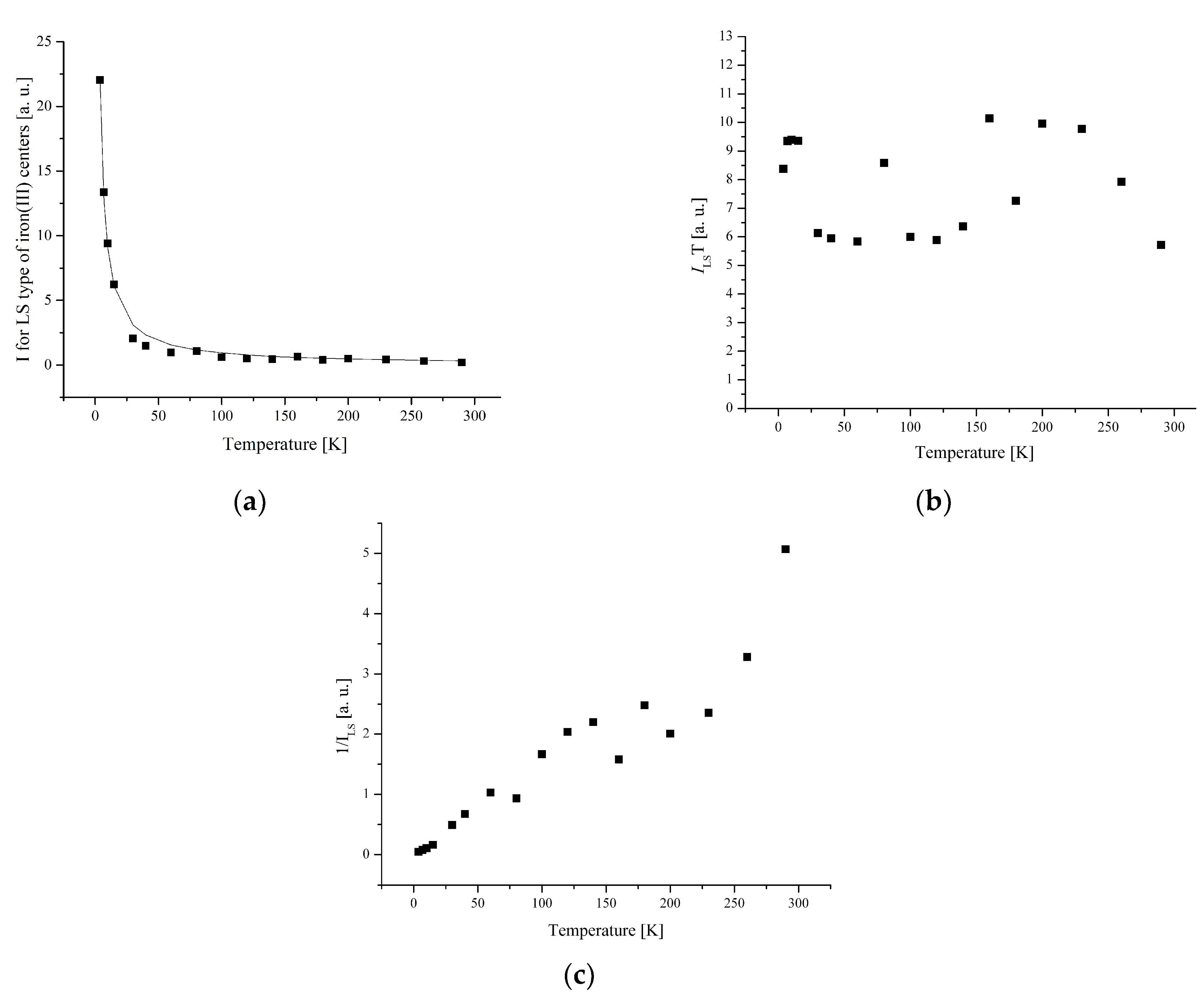
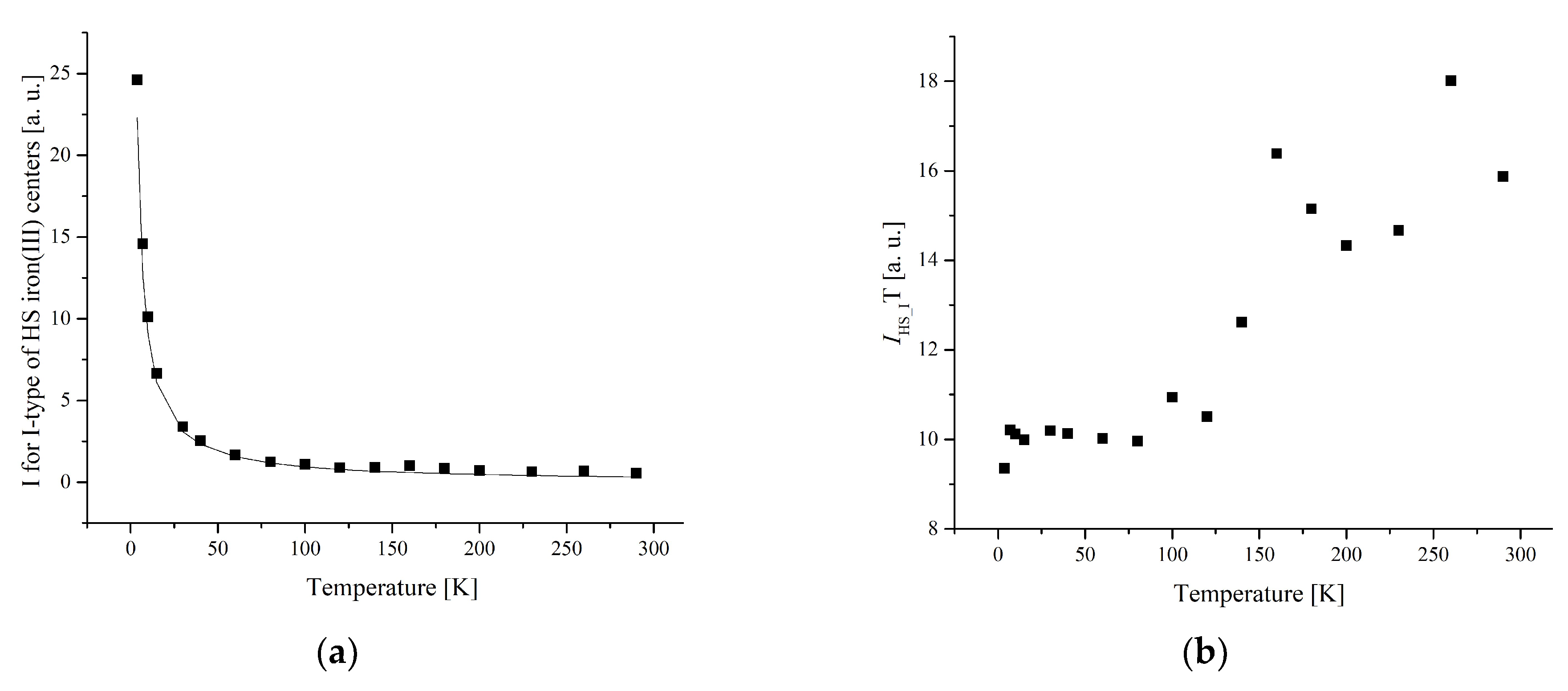
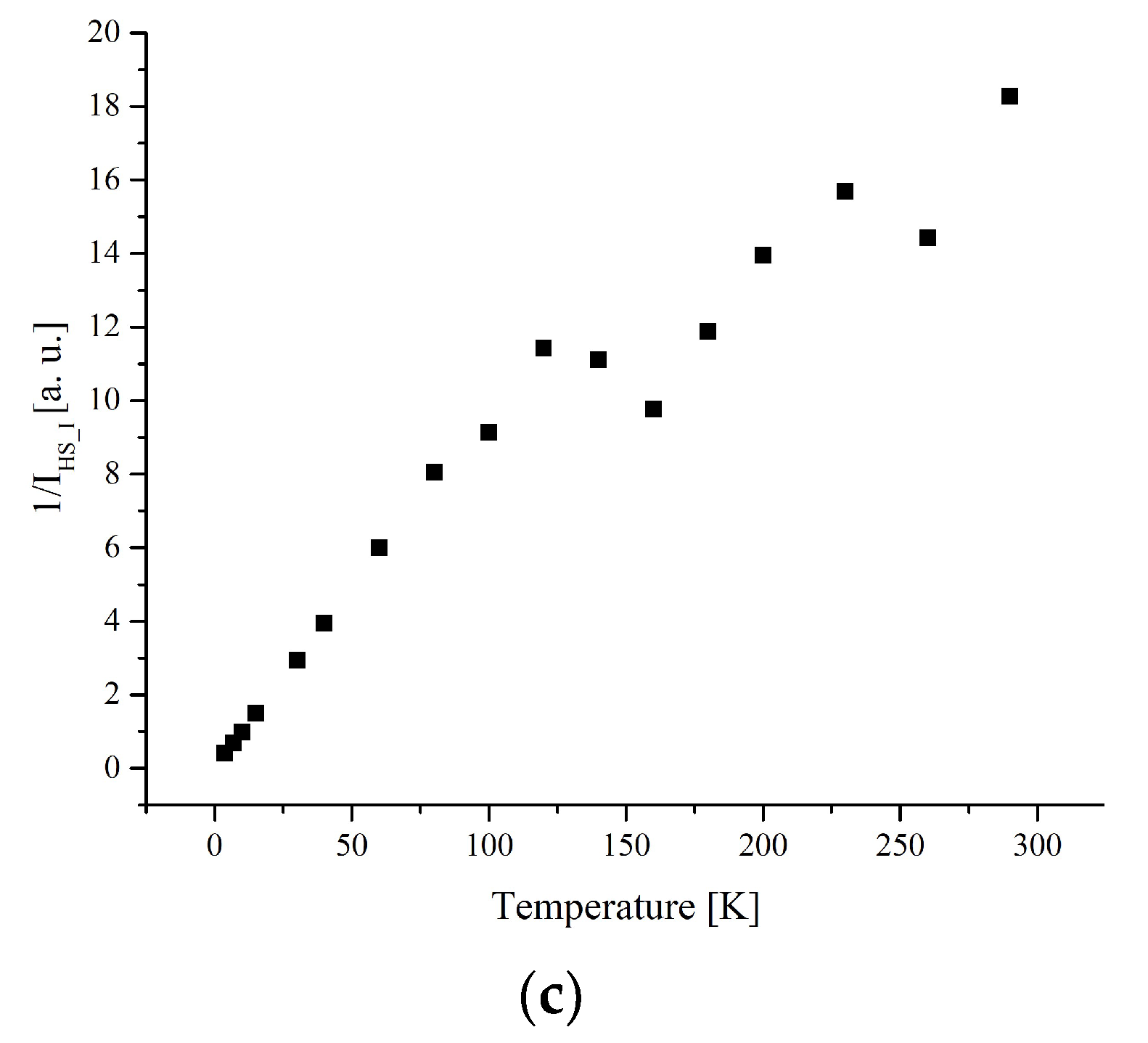
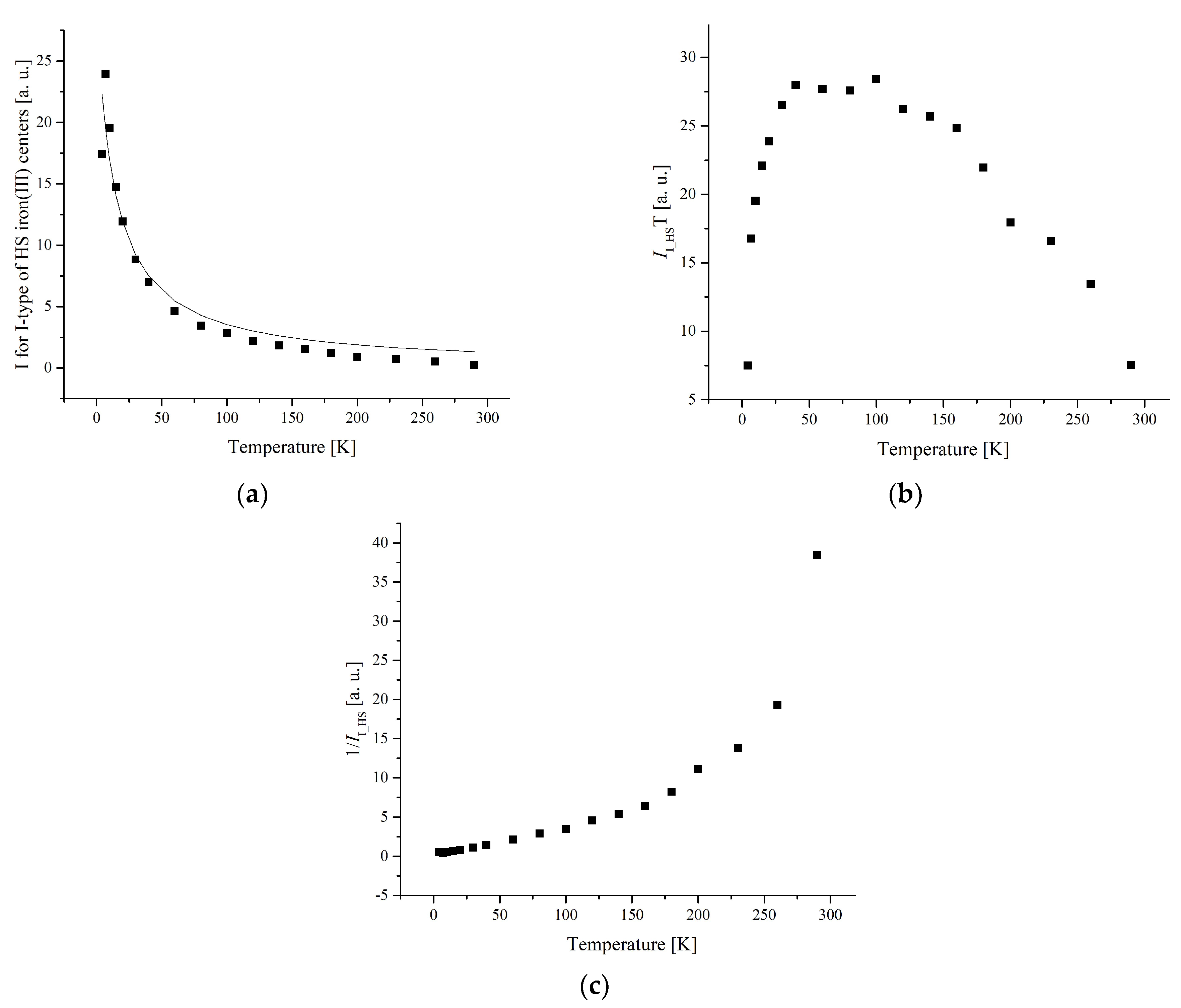
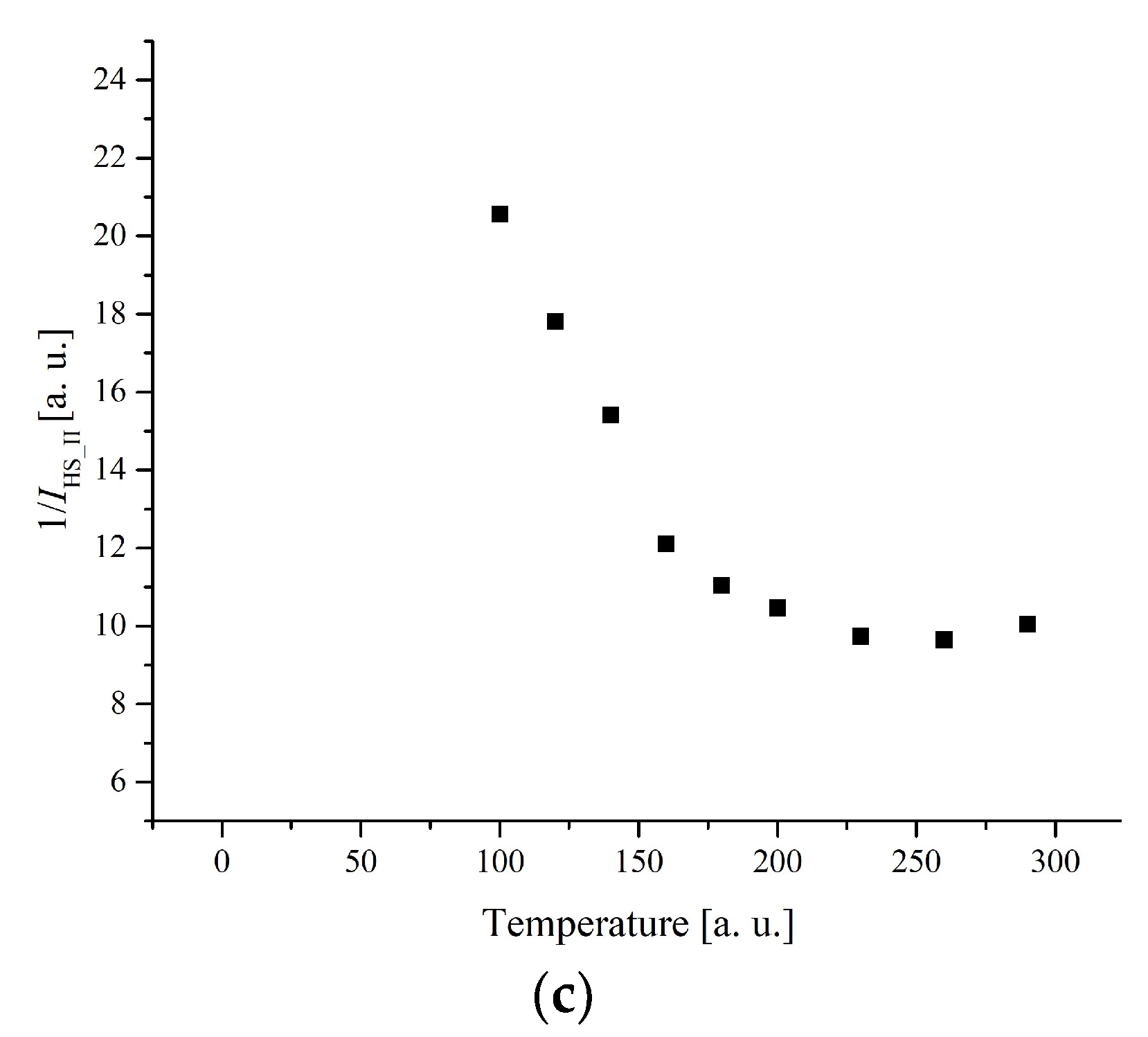
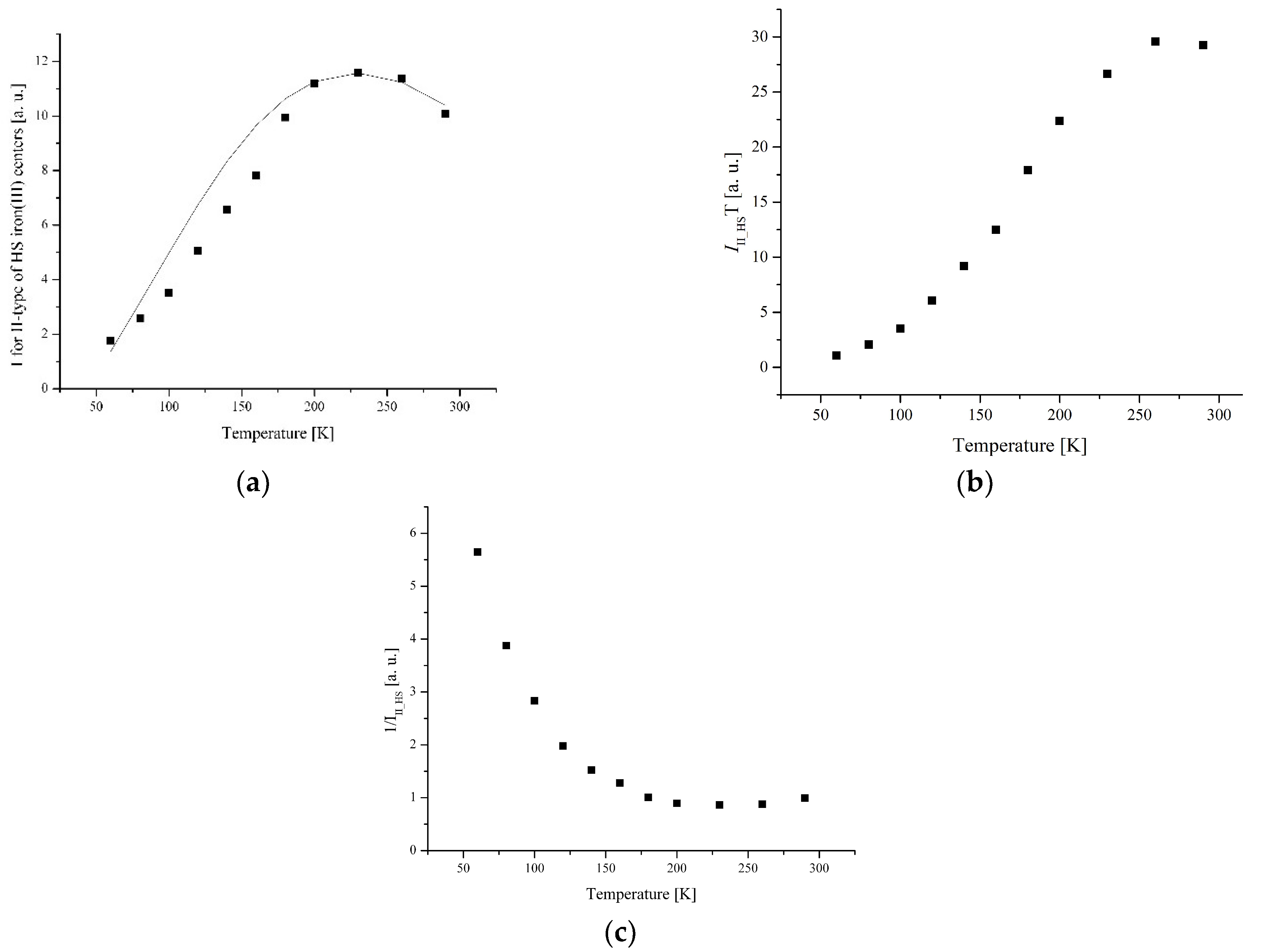
3.3. Electron Paramagnetic Resonance Measurements
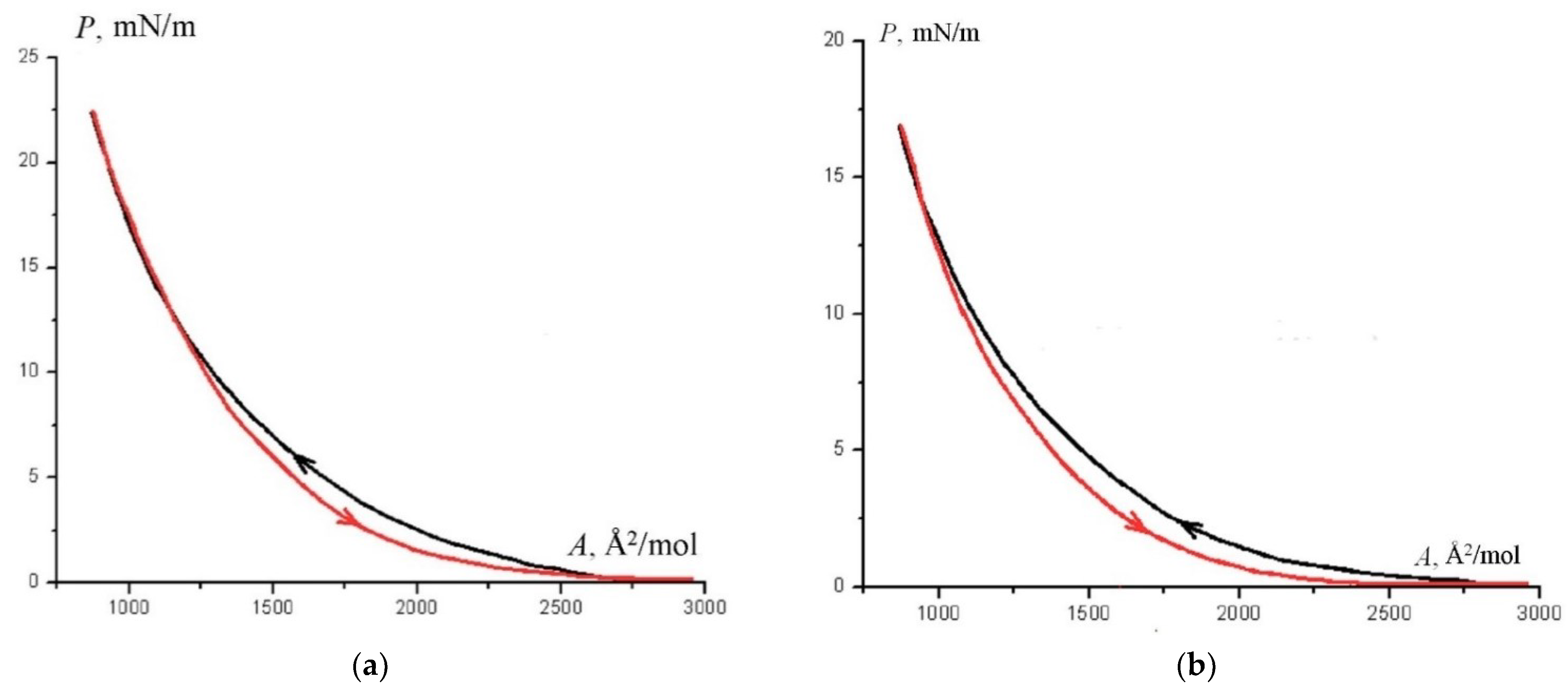
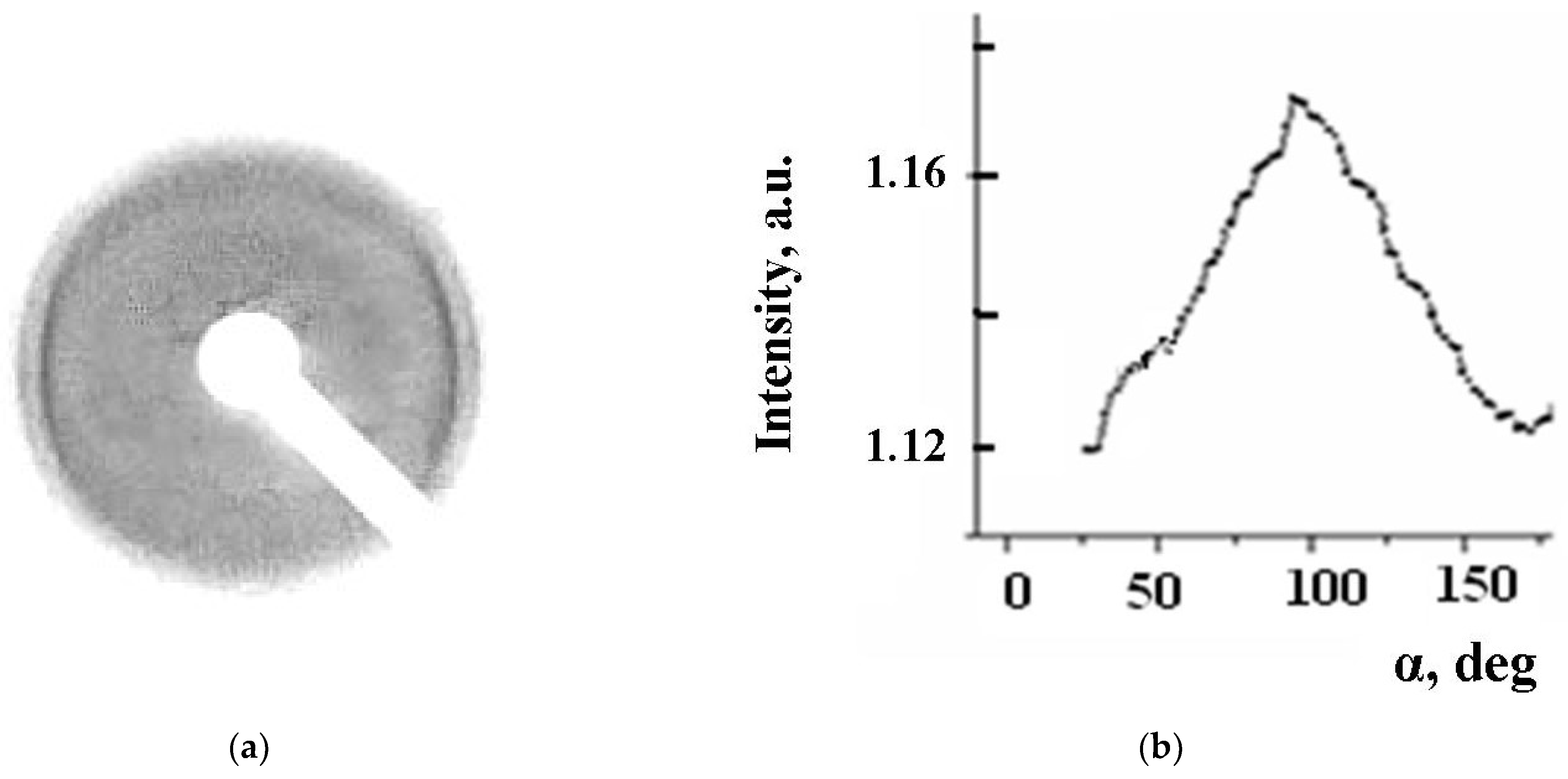
3.4. Structural-Phase Transformations in Floating Layers and Langmuir–Blodgett Films
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Garnovskii, A.D.; Vasil’chenko, I.S. Rational design of metal coordination compounds with azomethine ligands. Russ. Chem. Rev. 2002, 71, 943–968. [Google Scholar] [CrossRef]
- Collinson, S.R.; Fenton, D.E. Metal complexes of bibracchial Schiff base macrocycles. Coord. Chem. Rev. 1996, 148, 19–40. [Google Scholar] [CrossRef]
- Newkome, G.; Moorefield, C.; Vogtle, F. Dendrimers and Dendrons: Concepts, Syntheses, Applications; Wiley-VCH: Weinheim, Germany, 2001. [Google Scholar]
- Frechet, J.; Tomalia, D. Dendrimers and Other Dendritic Polymers; Wiley: Chichester, UK, 2002. [Google Scholar]
- Vogtle, F.; Gestermann, S.; Hesse, R.; Schwierz, H.; Windisch, B. Functional dendrimers. Prog. Polym. Sci. 2000, 25, 987–1041. [Google Scholar] [CrossRef]
- Newkome, G.R.; Shreiner, C.D. Poly(amidoamine), polypropylenimine, and related dendrimers and dendrons possessing different 1 → 2 branching motifs: An overview of the divergent procedures. Polymer 2008, 49, 1–173. [Google Scholar] [CrossRef] [Green Version]
- Maraval, V.; Laurent, R.; Donnadieu, B.; Mauzac, M.; Caminade, A.-M.; Majoral, J.-P. Rapid synthesis of phosphorus-containing dendrimers with controlled molecular architectures: First example of surface-block, layer-block, and segment-block dendrimers issued from the same dendron. J. Am. Chem. Soc. 2000, 122, 2499–2511. [Google Scholar] [CrossRef]
- Yamamoto, K.; Takanashi, K. Synthesis and functionality of dendrimer with finely controlled metal assembly. Polymer 2008, 49, 4033–4041. [Google Scholar] [CrossRef] [Green Version]
- Cruz, C.; Figueirinhas, J.; Sebastiao, P. NMR of Liquid Crystal Dendrimers; Pan Stanford Publishing: Singapore, 2017. [Google Scholar]
- Holm, R.H.; Everett, G.W., Jr.; Chakravorty, A. Metal complexes of Schiff bases and β-ketoamines. In Progress in Inorganic Chemistry; Cotton, F.A., Ed.; John Wiley and Sons, Inc.: New York, NY, USA, 1966; Volume 7, pp. 83–214. [Google Scholar]
- Holm, R.H.; O’Connor, M.J. The Stereochemistry of Bis-chelate Metal(II) Complexes. In Progress in Inorganic Chemistry; Lippard, S.J., Ed.; John Wiley and Sons, Inc.: New York, NY, USA, 1971; Volume 14, pp. 241–401. [Google Scholar]
- Zoubi, W.A.; Ko, Y.G. Schiff base complexes and their versatile applications as catalysts in oxidation of organic compounds: Part I. Appl. Organomet. Chem. 2017, 31, e3574. [Google Scholar] [CrossRef]
- Liu, X.; Manzur, C.; Novoa, N.; Celedon, S.; Carrillo, D.; Hamon, J.-R. Multidentate unsymmetrically-substituted Schiff bases and their metal complexes: Synthesis, functional materials properties, and applications to catalysis. Coord. Chem. Rev. 2018, 357, 144–172. [Google Scholar] [CrossRef]
- Zoubi, W.A.; Al-Hamdani, A.A.S.; Ahmed, S.D.; Ko, Y.G. Synthesis, characterization, and biological activity of Schiff bases metal complexes. J. Phys. Org. Chem. 2018, 31, e3752. [Google Scholar] [CrossRef]
- Harding, D.J.; Harding, P.; Phonsri, W. Spin crossover in iron(III) complexes. Coord. Chem. Rev. 2016, 313, 38–61. [Google Scholar] [CrossRef]
- Alexandrov, A.I.; Krasnov, A.V.; Pashkova, T.V. Magnetic field effect in floating layers and Langmuir-Blodgett films of mesogenic complexes of lanthanides. Synth. Met. 2004, 147, 205–208. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, UK, 2013. [Google Scholar]
- Domracheva, N.E.; Vorobeva, V.E.; Ovcharenko, V.I.; Bogomyakov, A.S.; Zueva, E.M.; Gruzdev, M.S.; Chervonova, U.V.; Kolker, A.M. Counterion effect on the spin-transition properties of the second generation iron(III) dendrimeric complexes. Inorg. Chim. Acta. 2017, 459, 131–142. [Google Scholar] [CrossRef]
- Gruzdev, M.S.; Chervonova, U.V.; Ksenofontov, A.A.; Krestianinov, M.A.; Alexandrov, A.I.; Pashkova, T.V. Schiff base complexes with different metals incorporating derivatives of 3,6-di-tert-butylcarbazole. Appl. Organomet. Chem. 2021, 35, e6145. [Google Scholar] [CrossRef]
- Gruzdev, M.S.; Chervonova, U.V.; Akopova, O.B.; Kolker, A.M. Synthesis and phase behavior of dendrons derived from 3,4,5-tris(tetradecyloxy)benzoic acid with different functional groups in focal point. J. Chem. Sci. 2015, 127, 1801–1810. [Google Scholar] [CrossRef] [Green Version]
- Domracheva, N.; Vorobeva, V.; Pyataev, A.; Tamura, R.; Suzuki, K.; Gruzdev, M.; Chervonova, U.; Kolker, A. Magnetic properties of novel dendrimeric spin crossover iron(III) complex. Inorg. Chim. Acta. 2016, 439, 186–195. [Google Scholar] [CrossRef]
- Marov, I.; Kostromina, N. EPR and NMR in the Chemistry of Coordination Compounds; Nauka: Moscow, Russia, 1979. (In Russian) [Google Scholar]
- Pretsch, E.; Buhlmann, P.; Affolter, C. Structure Determination of Organic Compounds-Tables of Spectral Data; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Becker, H.; Beckert, R.; Berger, W.; Domschke, G. Organikum, Organisch-chemisches Grundpraktikum; Deutscher Verlag der Wissenschaften Publ.: Berlin, Germany, 1993. [Google Scholar]
- Nakamoto, K. Infrared and Raman Spectra of Inorganic and Coordination Compounds, 6th ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Finch, A.; Gates, P.; Radcliffe, K.; Dickson, F.; Bentley, F. Chemical Applications of Far Infrared Spectroscopy; Academic Press: London, UK; New York, NY, USA, 1970. [Google Scholar]
- Cheremisina, I.M. Frequencies of predominantly stretching vibrations and the nature of the metal-ligand bond. J. Struct. Chem. 1978, 19, 286–300. [Google Scholar] [CrossRef]
- Roberts, G.G. Langmuir-Blodgett Films; Springer: New York, NY, USA, 1990. [Google Scholar] [CrossRef]
- Hussain, S.A.; Dey, B.; Bhattacharjee, D.; Mehta, N. Unique supramolecular assembly through Langmuir-Blodgett (LB) technique. Heliyon 2018, 4, e01038. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alexandrov, A.I.; Barakhtenko, D.V.; Pashkova, T.V.; Pyatunin, A.V. Formation and structural investigations of biaxial fullerene containing Langmuir-Blodgett films. Liq. Cryst. Appl. 2009, 4, 100–105. [Google Scholar]
- Alexandrov, A.I.; Pashkova, T.V.; Barakhtenko, D.V.; Gruzdev, M.S.; Chervonova, U.V. Structural investigations of iron complex in bulk samples, floating layers and Langmuir-Blodgett films. Liq. Cryst. Appl. 2011, 4, 14–22. [Google Scholar]
- Vainshtein, B.K. Diffraction of X-rays by Chain Molecules; USSR Academy of Sciences Publisher: Moscow, Russia, 1963. (In Russian) [Google Scholar]







| № | Compound | M | Color | Yield, % | Found (Calcd), % | ||
|---|---|---|---|---|---|---|---|
| C | H | N | |||||
| 1 | [C232H390N4O26Fe]NO3 | 3769.49 | Brown | 77.03 | 73.05 (73.92) | 9.75 (10.43) | 1.75 (1.86) |
| 2 | [C232H390N4O26Fe]PF6 | 3852.46 | Brown | 66.77 | 71.99 (72.33) | 10.13 (10.20) | 1.67 (1.45) |
| 3 | [C232H390N4O26Fe]Cl | 3742.95 | Brown | 47.37 | 74.70 (74.45) | 10.83 (10.50) | 1.76 (1.50) |
| 4 | [C232H390N4O26Fe]ClO4 | 3806.94 | Brown | 45.95 | 72.84 (73.19) | 9.87 (10.33) | 1.70 (1.47) |
| 5 | [C232H390N4O26Fe]BF4 | 3794.29 | Brown | 71.46 | 73.12 (73.44) | 10.94 (10.36) | 1.31 (1.48) |
| Functional Group | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| C=O | 1717 (s) | 1729 (s) | 1715 (s) | 1731 (s) | 1716 (s) |
| C=N | 1585 (s) | 1591 (s) | 1584 (s) | 1589 (s) | 1587 (s) |
| Counter-ion | 1386 NO3− (s) | 857 PF6− (m) | 544 Cl− (w) | 1119 ClO4− (s) | 1037 BF4− (s) 521–533 |
| NH | 995 (m) | 1002 (m) | 1001 (m) | 1003 (m) | 998 (m) |
| Fe–N | 585 | 582 | 584 | 589 | 582 |
| Fe–O | 419 | 417 | 422 | 418 | 422 |
| Orientation of the Molecule Relative to the Surface | The Area Occupied by the Molecule, Å2 |
|---|---|
| A flat molecule | 1330 |
| A molecule with ligands located at an angle of 30° to the surface | 1215 |
| A molecule with ligands located at an angle of 45° to the surface | 1065 |
| A molecule with ligands located at an angle of 60° to the surface | 885 |
| A molecule with ligands located at an angle of 90° to the surface | 435 |
| Complex | Maximum | dBragg, Å |
|---|---|---|
| 2 | 1 | 2.59 |
| 2 | 2.54 | |
| 3 | 2.40 | |
| 4 | 1.56 | |
| 5 | 1.51 | |
| 5 | 1 | 4.18 |
| 2 | 3.77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gruzdev, M.; Chervonova, U.; Vorobeva, V. The Branched Schiff Base Cationic Complexes of Iron(III) with Different Counter-Ions. Symmetry 2022, 14, 1140. https://doi.org/10.3390/sym14061140
Gruzdev M, Chervonova U, Vorobeva V. The Branched Schiff Base Cationic Complexes of Iron(III) with Different Counter-Ions. Symmetry. 2022; 14(6):1140. https://doi.org/10.3390/sym14061140
Chicago/Turabian StyleGruzdev, Matvey, Ulyana Chervonova, and Valerya Vorobeva. 2022. "The Branched Schiff Base Cationic Complexes of Iron(III) with Different Counter-Ions" Symmetry 14, no. 6: 1140. https://doi.org/10.3390/sym14061140
APA StyleGruzdev, M., Chervonova, U., & Vorobeva, V. (2022). The Branched Schiff Base Cationic Complexes of Iron(III) with Different Counter-Ions. Symmetry, 14(6), 1140. https://doi.org/10.3390/sym14061140






