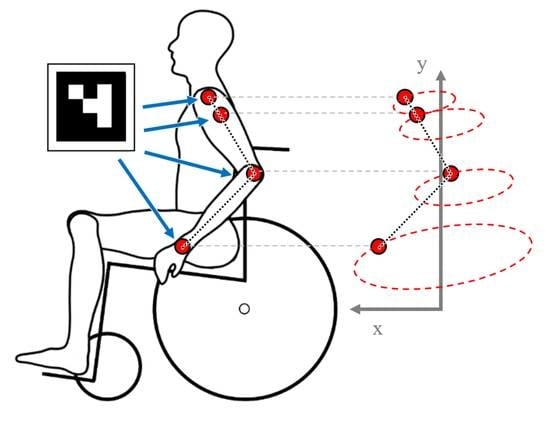
Symmetry Analysis of Manual Wheelchair Propulsion Using Motion Capture Techniques
Abstract
1. Introduction
2. Materials and Methods
2.1. Research Participants
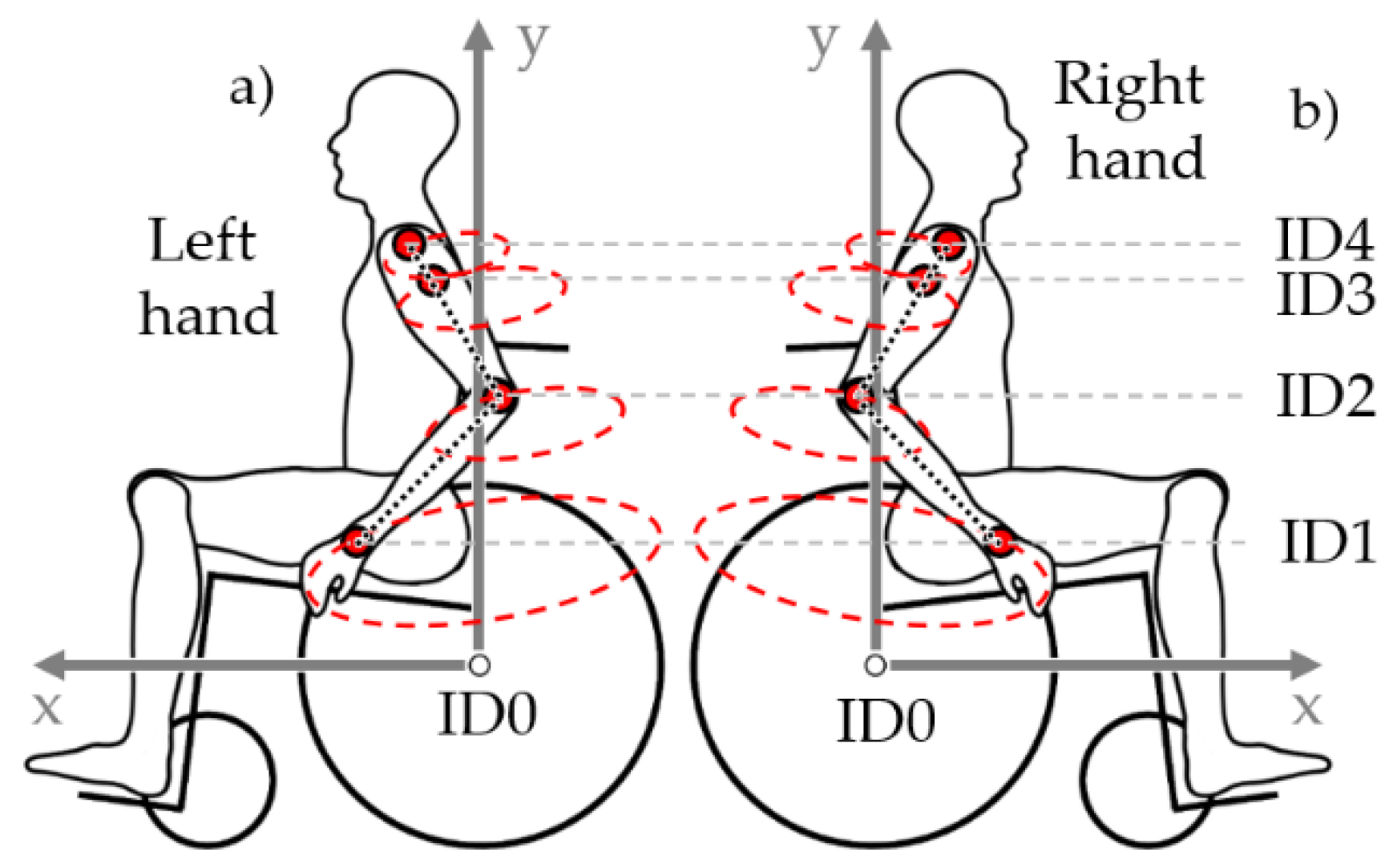
2.2. Data Collection
2.3. Data Processing
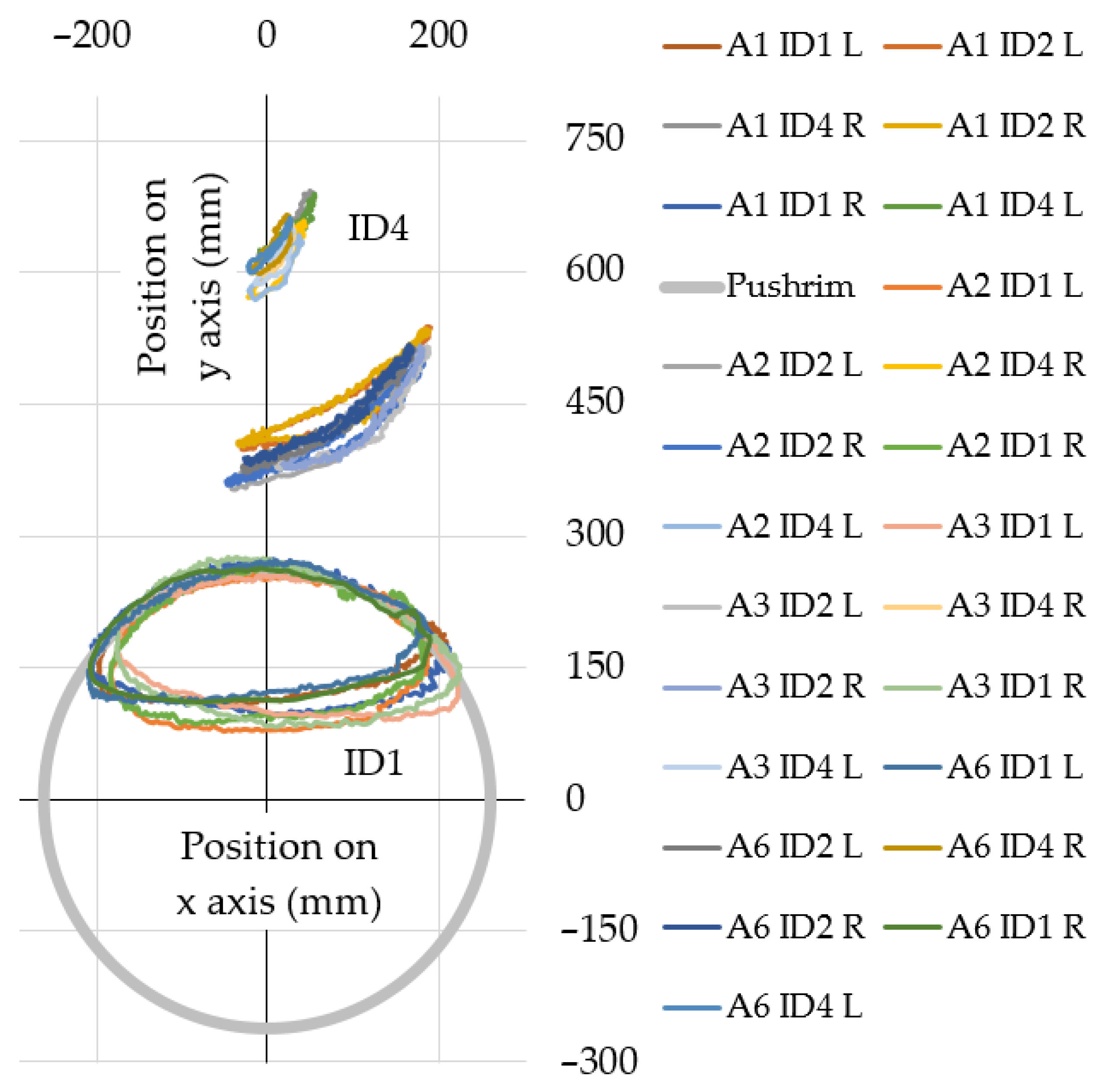
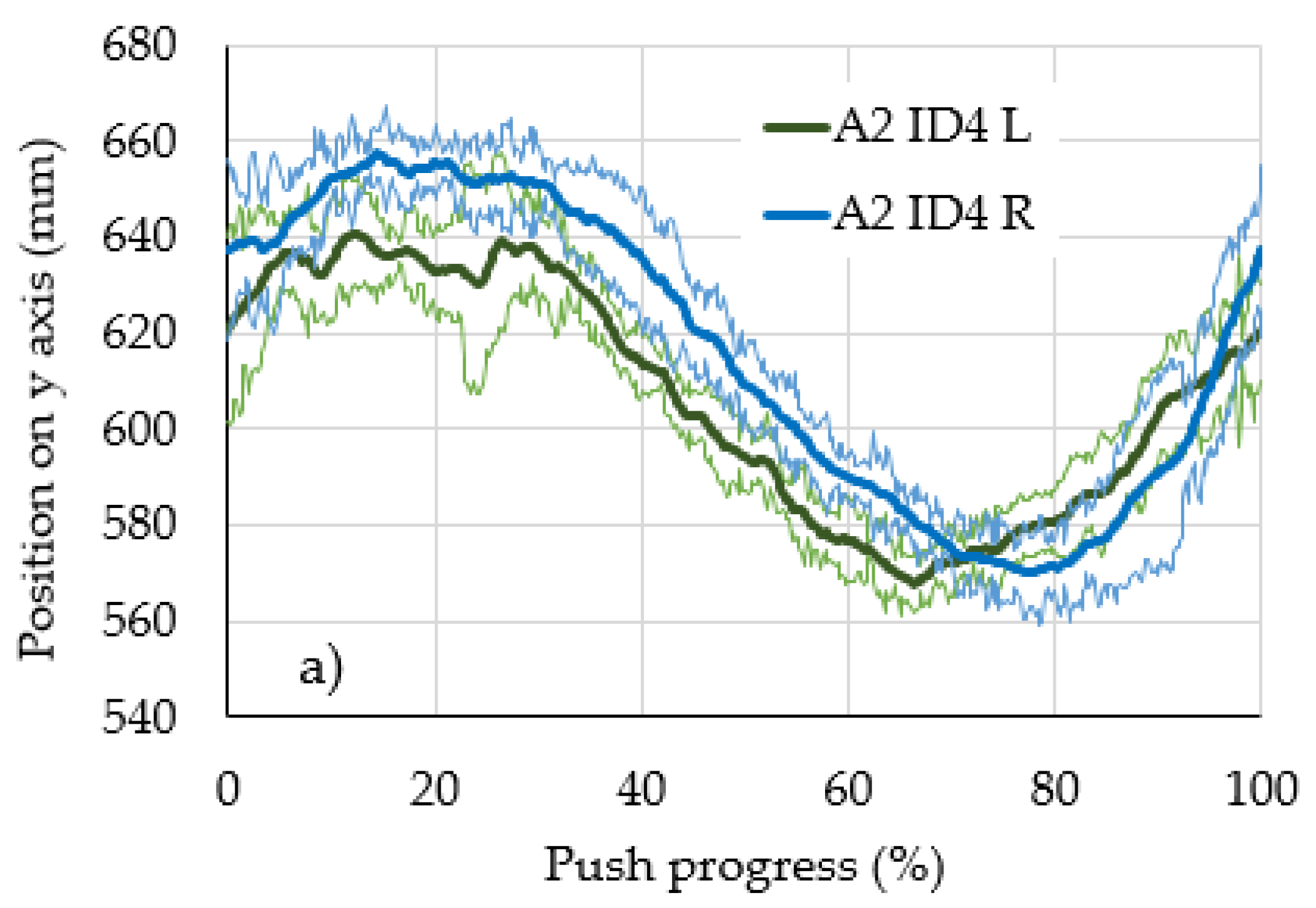
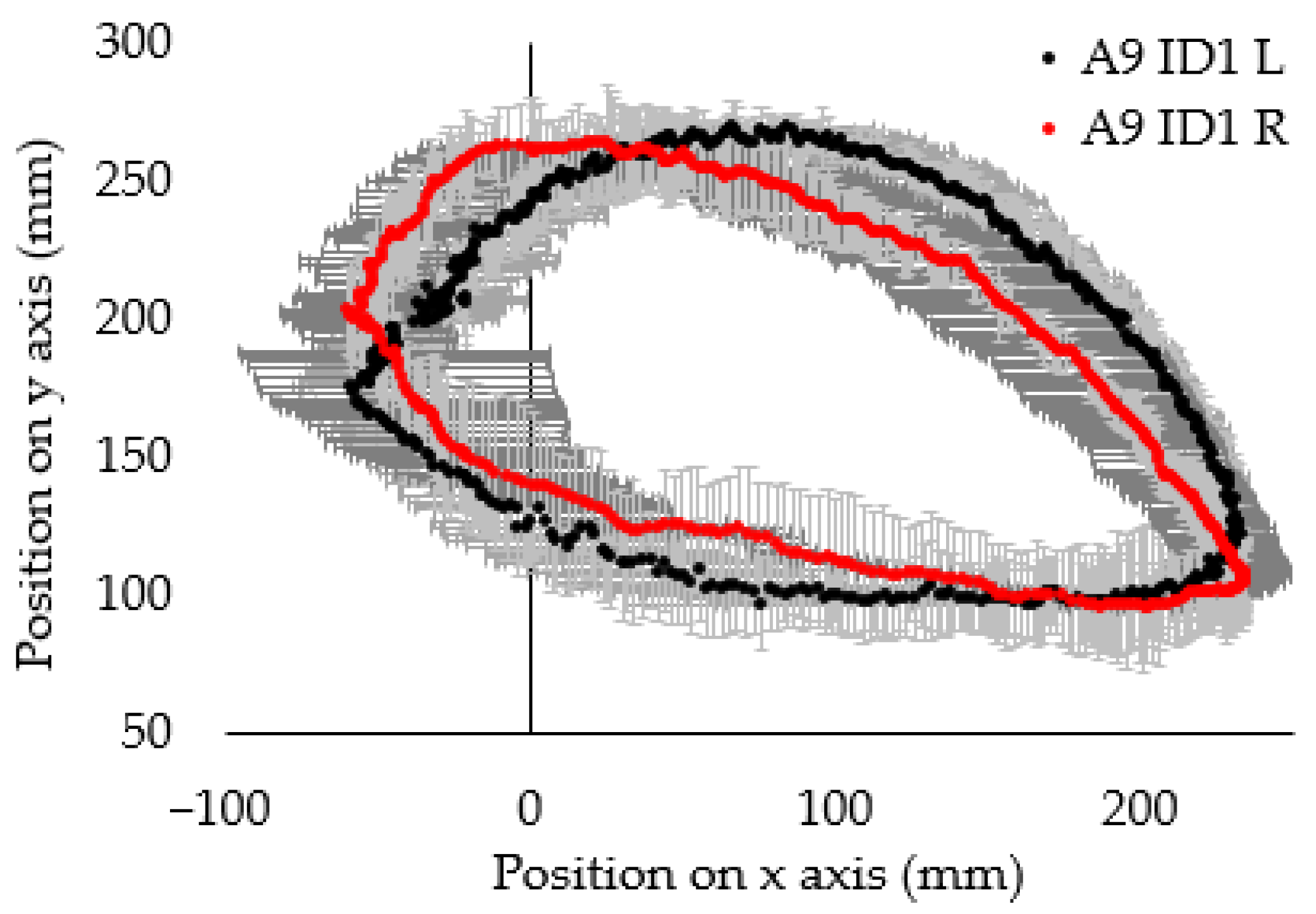
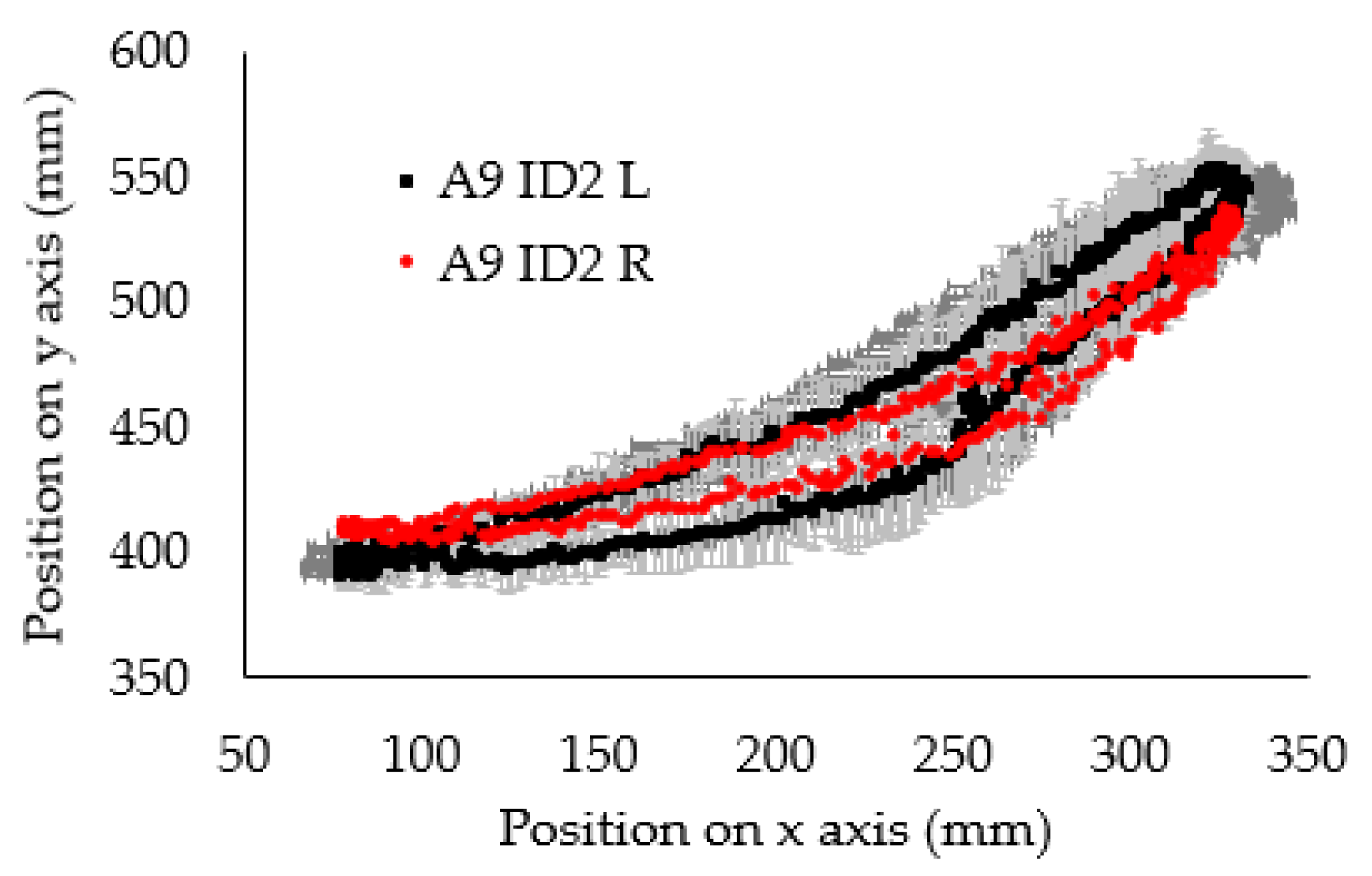
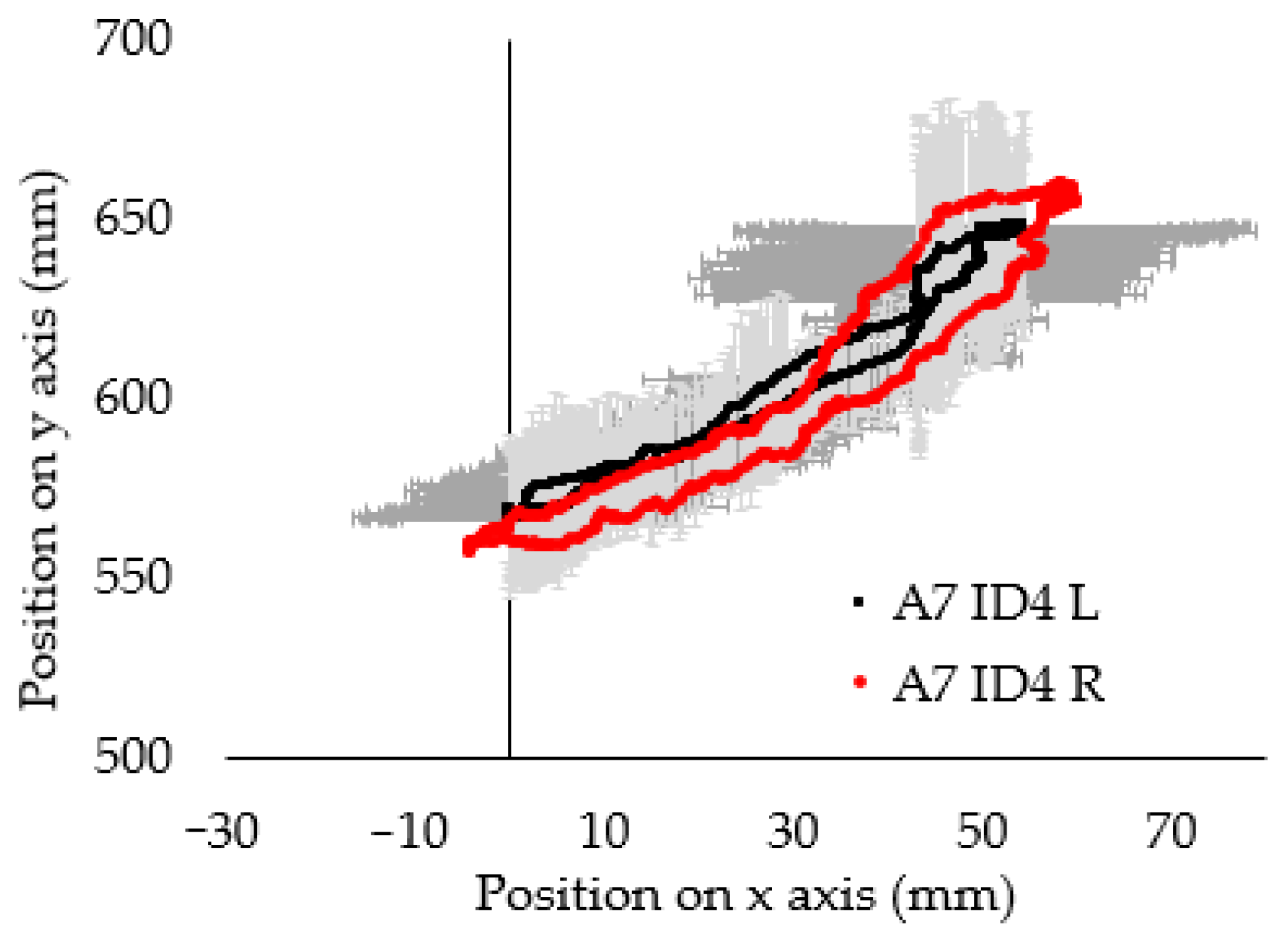
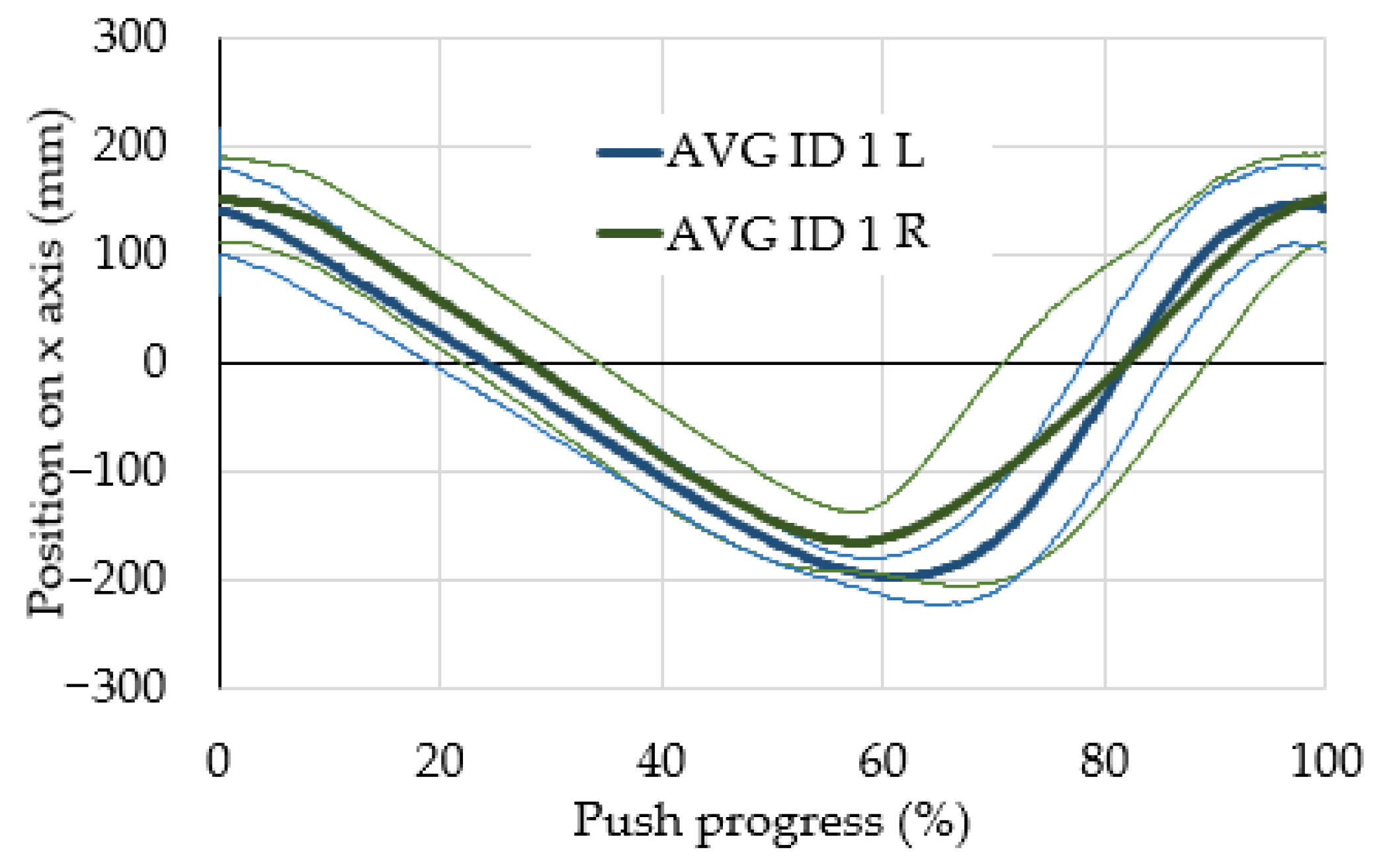
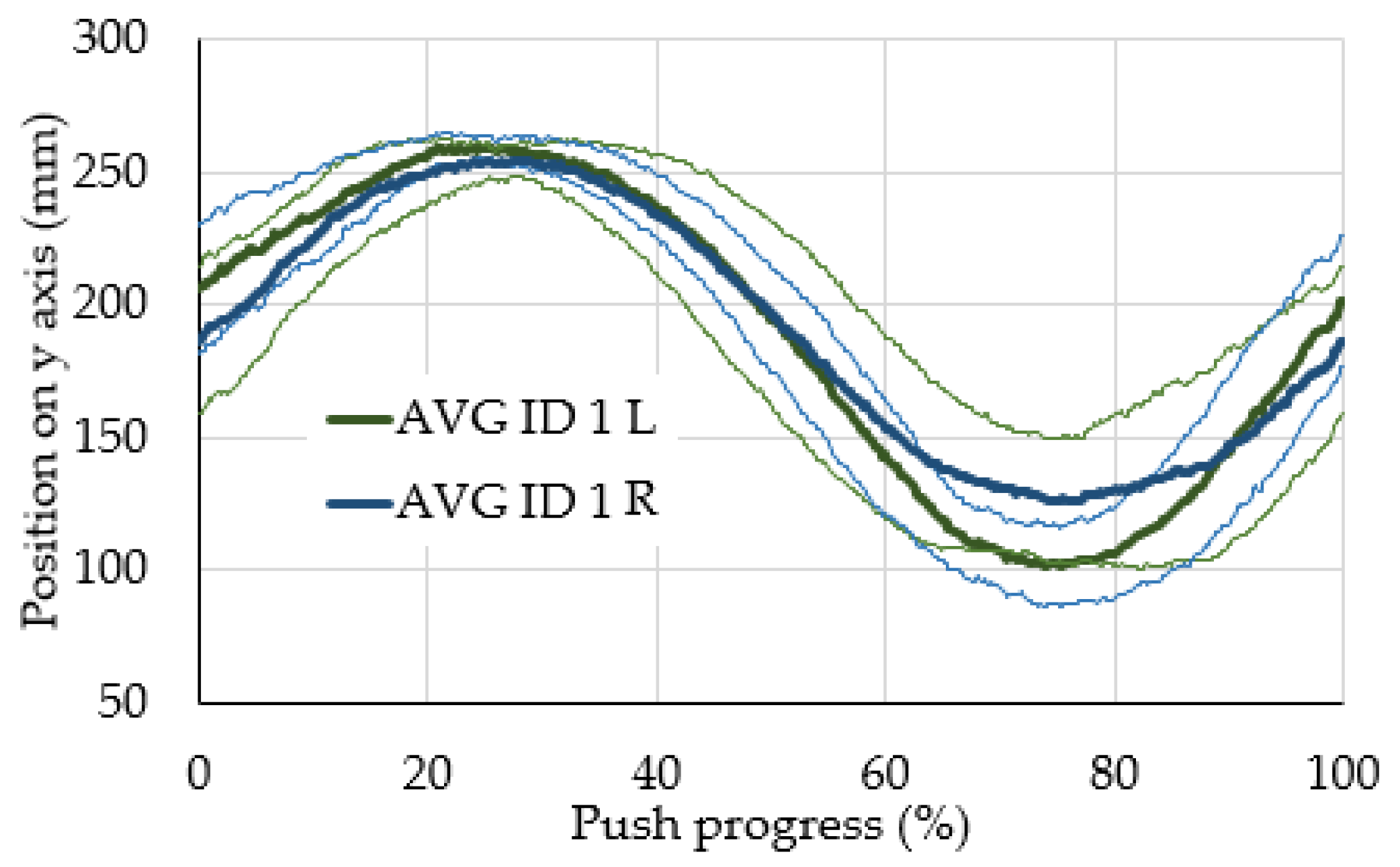
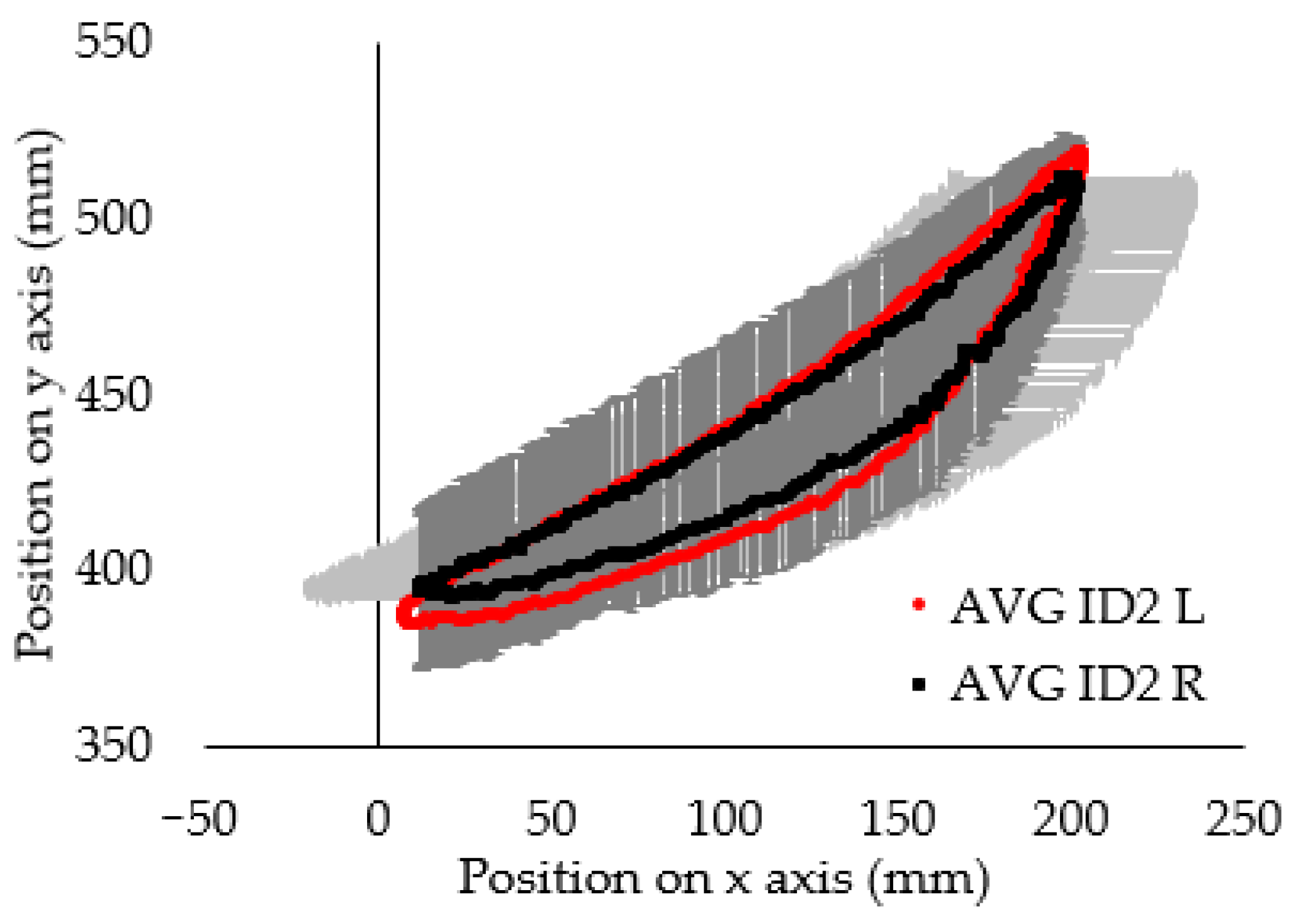
3. Results and Discussion
4. Conclusions
- In some cases, large differences were observed between the average markers’ locations on the left and right limbs.
- The average markers’ locations for individual research participants are characterised by greater asymmetry than the average markers’ locations for the entire group of participants.
- In the group of research participants, the leading hand did not generate a noticeably smaller deviation from the averaged location of the markers.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Warguła, Ł.; Marciniak, A. The Symmetry of the Muscle Tension Signal in the Upper Limbs When Propelling a Wheelchair and Innovative Control Systems for Propulsion System Gear Ratio or Propulsion Torque: A Pilot Study. Symmetry 2022, 14, 1002. [Google Scholar] [CrossRef]
- Vanlandewijck, Y.C.; Theisen, D.; Daly, D. Wheelchair Propulsion Biomechanics. Sports Med. 2001, 31, 339–367. [Google Scholar] [CrossRef] [PubMed]
- Croft, L.; Dybrus, S.; Lenton, J.; Goosey-Tolfrey, V. A Comparison of the Physiological Demands of Wheelchair Basketball and Wheelchair Tennis. Int. J. Sports Physiol. 2022, 5, 301–315. [Google Scholar] [CrossRef] [PubMed]
- Richardson, E.V.; Papathomas, A.; Smith, B.; Victoria, L.G.-T. The psychosocial impact of wheelchair tennis on participants from developing countries. Disabil. Rehabil. 2017, 39, 193–200. [Google Scholar] [CrossRef] [PubMed]
- Bauerfeind, J.; Koper, M.; Wieczorek, J.; Urbański, P.; Tasiemski, T. Sports Injuries in Wheelchair Rugby—A. Pilot Study. J. Hum. Kinet. 2015, 48, 123–132. [Google Scholar] [CrossRef]
- Barfield, J.P.; Malone, L.A.; Arbo, C.; Jung, A.P. Exercise intensity during wheelchair rugby training. J. Sports Sci. 2010, 28, 389–398. [Google Scholar] [CrossRef]
- Wieczorek, B.; Warguła, Ł. Problems of dynamometer construction for wheelchairs and simulation of push motion. MATEC Web Conf. 2019, 254, 01006. [Google Scholar] [CrossRef]
- Wieczorek, B.; Warguła, Ł.; Rybarczyk, D. Impact of a Hybrid Assisted Wheelchair Propulsion System on Motion Kinematics during Climbing up a Slope. Appl. Sci. 2020, 10, 1025. [Google Scholar] [CrossRef]
- Veeger, E.H.; Van Der Woude, L.H.; Rozendal, R.H. Effect of handrim velocity on mechanical efficiency in wheelchair propulsion. Med. Sci. Sports Exerc. 1992, 24, 100–107. [Google Scholar] [CrossRef]
- Gil-Agudo, A.; Del Ama-Espinosa, A.; Pérez-Rizo, E.; Pérez-Nombela, S.; Crespo-Ruiz, B. Shoulder joint kinetics during wheelchair propulsion on a treadmill at two different speeds in spinal cord injury patients. Spinal Cord. 2010, 48, 290–296. [Google Scholar] [CrossRef][Green Version]
- Coutts, K.D. Kinematics of sport wheelchair propulsion. J. Rehabil. Res. Dev. 1990, 27, 21–26. [Google Scholar] [CrossRef]
- Wieczorek, B.; Kukla, M.; Warguła, Ł. Methods for measuring the position of the centre of gravity of an anthropotechnics human-wheelchair system in dynamic conditions. Mater. Sci. Eng. Conf. Ser. 2020, 776, 012062. [Google Scholar] [CrossRef]
- Leary, M.; Gruijters, J.; Mazur, M.; Subic, A.; Burton, M.; Fuss, F.K. A fundamental model of quasi-static wheelchair biomechanics. Med. Eng. Phys. 2012, 34, 1278–1286. [Google Scholar] [CrossRef]
- Mulroy, S.J.; Gronley, J.K.; Newsam, C.J.; Perry, J. Electromyographic activity of shoulder muscles during wheelchair propulsion by paraplegic persons. Arch. Phys. Med. Rehabil. 1996, 77, 187–193. [Google Scholar] [CrossRef]
- Tsai, C.-Y.; Lin, C.-J.; Huang, Y.-C.; Lin, P.-C.; Su, F.-C. The effects of rear-wheel camber on the kinematics of upper extremity during wheelchair propulsion. BioMed. Eng. OnLine 2012, 11, 87. [Google Scholar] [CrossRef]
- Richter, W.M. The effect of seat position on manual wheelchair propulsion biomechanics: A quasi-static model-based approach. Med. Eng. Phys. 2001, 23, 707–712. [Google Scholar] [CrossRef]
- Hughes, C.J.; Weimar, W.H.; Sheth, P.N.; Brubaker, C.E. Biomechanics of wheelchair propulsion as a function of seat position and user-to-chair interface. Arch. Phys. Med. Rehabil. 1992, 73, 263–269. [Google Scholar]
- Kotajarvi, B.R.; Sabick, M.B.; An, K.N.; Zhao, K.D.; Kaufman, K.R.; Basford, J.R. The effect of seat position on wheelchair propulsion biomechanics. J. Rehabil. Res. Dev. 2004, 41, 403–414. [Google Scholar] [CrossRef]
- Kulig, K.; Sreesha, S.R.; Sara, J.M.; Craig, J.N.; JoAnne, K.G.; Ernest, L.B.; Jacquelin, P. Shoulder joint kinetics during the push phase of wheelchair propulsion. Clin. Orthop. Relat. Res. 1998, 354, 132–143. [Google Scholar] [CrossRef] [PubMed]
- de Groot, S.; de Bruin, M.; Noomen, S.P.; van der Woude, L.H. Mechanical efficiency and propulsion technique after 7 weeks of low-intensity wheelchair training. Clin. Biomech. 2008, 23, 434–441. [Google Scholar] [CrossRef]
- Slavens, B.A.; Schnorenberg, A.G.; Aurit, C.M.; Graf, A.; Krzak, J.J.; Reiners, K.; Vogel, L.C.; Harris, G.F. Evaluation of Pediatric Manual Wheelchair Mobility Using Advanced Biomechanical Methods. Biomed. Res. Int. 2015, 2015, 634768. [Google Scholar] [CrossRef]
- Boninger, M.L.; Souza, A.L.; Cooper, R.A.; Fitzgerald, S.G.; Koontz, A.M.; Fay, B.T. Propulsion patterns and pushrim biomechanics in manual wheelchair propulsion. Arch. Phys. Med. Rehabil. 2002, 83, 718–723. [Google Scholar] [CrossRef]
- de Groot, S.; Veeger, H.E.J.; Hollander, A.P.; van der Woude, L.H.V. Effect of wheelchair stroke pattern on mechanical efficiency. Am. J. Phys. Med. Rehabil. 2004, 83, 640–649. [Google Scholar] [CrossRef]
- de Groot, S.; Veeger, D.H.; Hollander, A.P.; Van der Woude, L.H. Wheelchair propulsion technique and mechanical efficiency after 3 weeks of practice. Med. Sci. Sports Exerc. 2002, 34, 756–766. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Goosey, V.L.; Campbell, I.G. Symmetry of the elbow kinematics during racing wheelchair propulsion. Ergonomics 1998, 41, 1810–1820. [Google Scholar] [CrossRef] [PubMed]
- Hurd, W.J.; Morrow, M.M.; Kaufman, K.R.; An, K.N. Influence of varying level terrain on wheelchair propulsion biomechanics. Am. J. Phys. Med. Rehabil. 2008, 87, 984–991. [Google Scholar] [CrossRef] [PubMed]
- Soltau, S.L.; Slowik, J.S.; Requejo, P.S.; Mulroy, S.J.; Neptune, R.R. An investigation of bilateral symmetry during manual wheelchair propulsion. Front. Bioeng. Biotechnol. 2015, 3, 86. [Google Scholar] [CrossRef]
- Hurd, W.J.; Morrow, M.M.; Kaufman, K.R.; An, K.N. Biomechanic evaluation of upper-extremity symmetry during manual wheelchair propulsion over varied terrain. Arch. Phys. Med. Rehabil. 2008, 89, 1996–2002. [Google Scholar] [CrossRef]
- Stephens, C.L.; Engsberg, J.R. Comparison of overground and treadmill propulsion patterns of manual wheelchair users with tetraplegia. Disabil. Rehabil. Assist. Technol. 2010, 5, 420–427. [Google Scholar] [CrossRef] [PubMed]
- Koontz, A.M.; Cooper, R.A.; Boninger, M.L. An autoregressive modeling approach to analyzing wheelchair propulsion forces. Med. Eng. Phys. 2001, 23, 285–291. [Google Scholar] [CrossRef]
- Schnorenberg, A.J.; Slavens, B.A.; Wang, M.; Vogel, L.C.; Smith, P.A.; Harris, G.F. Biomechanical model for evaluation of pediatric upper extremity joint dynamics during wheelchair mobility. J. Biomech. 2014, 47, 269–276. [Google Scholar] [CrossRef] [PubMed]
- Shimada, S.D.; Robertson, R.N.; Bonninger, M.L.; Cooper, R.A. Kinematic characterization of wheelchair propulsion. J. Rehabil. Res. Dev. 1998, 35, 210–218. [Google Scholar] [PubMed]
- Lebedev, I.; Erashov, A.; Shabanova, A. Accurate Autonomous UAV Landing Using Vision-Based Detection of ArUco-Marker. In Proceedings of the 5th International Conference on Interactive Collaborative Robotics (ICR 2020), St. Petersburg, Russia, 7–9 October 2020; pp. 179–188. [Google Scholar]
- Rammer, J.; Brooke, S.; Joseph, K.; Jack, W.; Susan, R.; Gerald, H. Assessment of a markerless motion analysis system for manual wheelchair application. J. Neuroeng. Rehabil. 2018, 15, 96. [Google Scholar] [CrossRef] [PubMed]
- Fay, B.T.; Boninger, M.L.; Fitzgerald, S.G.; Souza, A.L.; Cooper, R.A.; Koontz, A.M. Manual wheelchair pushrim dynamics in people with multiple sclerosis. Arch. Phys. Med. Rehabil. 2004, 85, 935–942. [Google Scholar] [CrossRef]

| Test Subject Number | Right or Left Side, Marker Number, and Axis | |||||
|---|---|---|---|---|---|---|
| R ID1 x | R ID1 y | R ID2 x | R ID2 y | R ID4 x | R ID4 y | |
| A1 | 48.94 | 50.54 | 48.15 | 46.21 | 27.56 | 31.02 |
| A2 | 89.10 | 27.95 | 57.88 | 31.84 | 21.24 | 22.06 |
| A3 | 55.06 | 27.75 | 32.82 | 28.20 | 23.95 | 37.19 |
| A4 | 45.89 | 54.36 | 34.88 | 30.45 | 18.06 | 25.89 |
| A5 | 60.47 | 26.49 | 67.64 | 53.94 | 24.58 | 41.43 |
| A6 | 46.11 | 54.63 | 44.12 | 30.83 | 19.21 | 25.95 |
| A7 | 67.45 | 55.17 | 46.14 | 59.54 | 26.51 | 47.38 |
| A8 | 71.33 | 42.56 | 43.57 | 52.09 | 30.05 | 49.76 |
| A9 | 48.02 | 57.91 | 49.74 | 50.40 | 13.53 | 18.01 |
| A10 | 48.02 | 57.91 | 49.74 | 50.40 | 18.27 | 30.50 |
| AVG | 112.12 | 37.51 | 47.10 | 28.48 | 30.03 | 23.34 |
| L ID1 x | L ID1 y | L ID2 x | L ID2 y | L ID4 x | L ID4 y | |
| A1 | 97.72 | 50.18 | 97.72 | 50.18 | 15.61 | 17.44 |
| A2 | 64.07 | 33.61 | 24.04 | 39.13 | 16.51 | 23.85 |
| A3 | 80.28 | 43.15 | 80.28 | 43.15 | 14.75 | 28.31 |
| A4 | 64.74 | 34.09 | 64.74 | 34.09 | 53.04 | 31.46 |
| A5 | 57.18 | 25.30 | 57.18 | 25.30 | 20.80 | 31.75 |
| A6 | 62.81 | 35.28 | 62.81 | 35.28 | 19.50 | 28.81 |
| A7 | 78.71 | 42.19 | 78.71 | 42.19 | 16.57 | 31.96 |
| A8 | 49.37 | 37.83 | 49.37 | 37.83 | 14.95 | 25.46 |
| A9 | 55.67 | 30.38 | 28.97 | 34.95 | 13.53 | 18.01 |
| A10 | 55.67 | 30.38 | 55.67 | 30.38 | 19.50 | 28.81 |
| AVG | 76.74 | 29.70 | 49.17 | 25.72 | 31.75 | 25.91 |
| Test Subject Number | Right or Left Side and Marker Number | |||||
|---|---|---|---|---|---|---|
| R ID1 | R ID2 | R ID4 | L ID1 | L ID2 | L ID4 | |
| A1 | 30.15 | 9.87 | 4.64 | 38.14 | 9.20 | 2.59 |
| A2 | 10.83 | 7.06 | 3.72 | 21.62 | 8.51 | 3.78 |
| A3 | 21.15 | 6.52 | 6.14 | 23.37 | 7.12 | 4.75 |
| A4 | 32.04 | 6.34 | 4.20 | 23.19 | 7.50 | 4.92 |
| A5 | 21.53 | 10.55 | 6.20 | 16.14 | 7.60 | 4.65 |
| A6 | 46.02 | 7.24 | 4.22 | 21.12 | 9.80 | 4.67 |
| A7 | 38.86 | 13.16 | 7.51 | 31.36 | 7.73 | 5.10 |
| A8 | 27.31 | 10.56 | 7.69 | 26.37 | 6.60 | 3.76 |
| A9 | 23.78 | 10.32 | 2.65 | 30.47 | 7.53 | 2.65 |
| A10 | 27.51 | 11.24 | 4.89 | 43.96 | 8.25 | 4.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kukla, M.; Maliga, W. Symmetry Analysis of Manual Wheelchair Propulsion Using Motion Capture Techniques. Symmetry 2022, 14, 1164. https://doi.org/10.3390/sym14061164
Kukla M, Maliga W. Symmetry Analysis of Manual Wheelchair Propulsion Using Motion Capture Techniques. Symmetry. 2022; 14(6):1164. https://doi.org/10.3390/sym14061164
Chicago/Turabian StyleKukla, Mateusz, and Wojciech Maliga. 2022. "Symmetry Analysis of Manual Wheelchair Propulsion Using Motion Capture Techniques" Symmetry 14, no. 6: 1164. https://doi.org/10.3390/sym14061164
APA StyleKukla, M., & Maliga, W. (2022). Symmetry Analysis of Manual Wheelchair Propulsion Using Motion Capture Techniques. Symmetry, 14(6), 1164. https://doi.org/10.3390/sym14061164