Cornish–Fisher-Based Control Charts Inclusive of Skewness and Kurtosis Measures for Monitoring the Mean of a Process
Abstract
:1. Introduction
2. CF-1 Limits Inclusive of Skewness
3. CF-2 Limits Inclusive of Skewness and Kurtosis
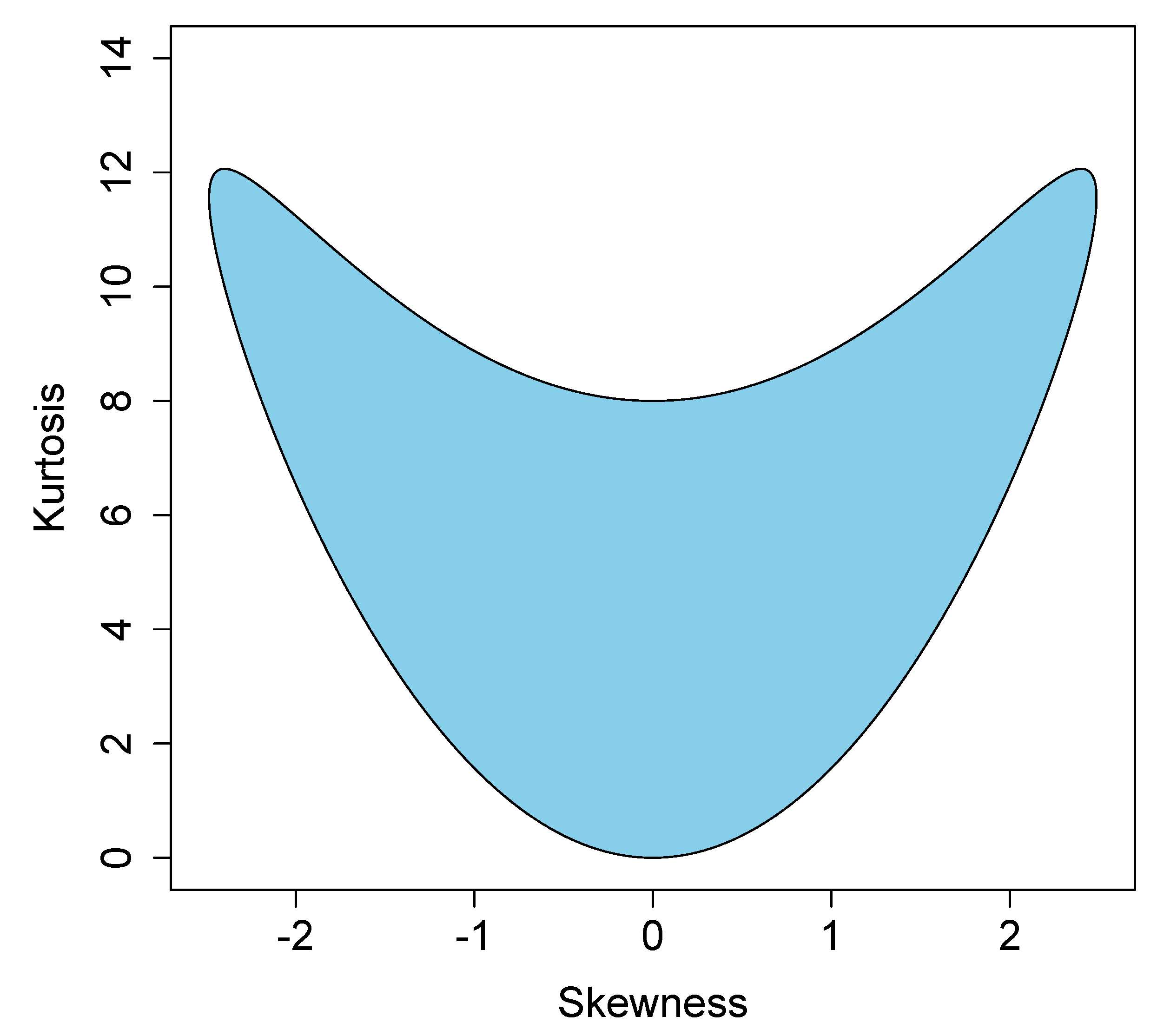
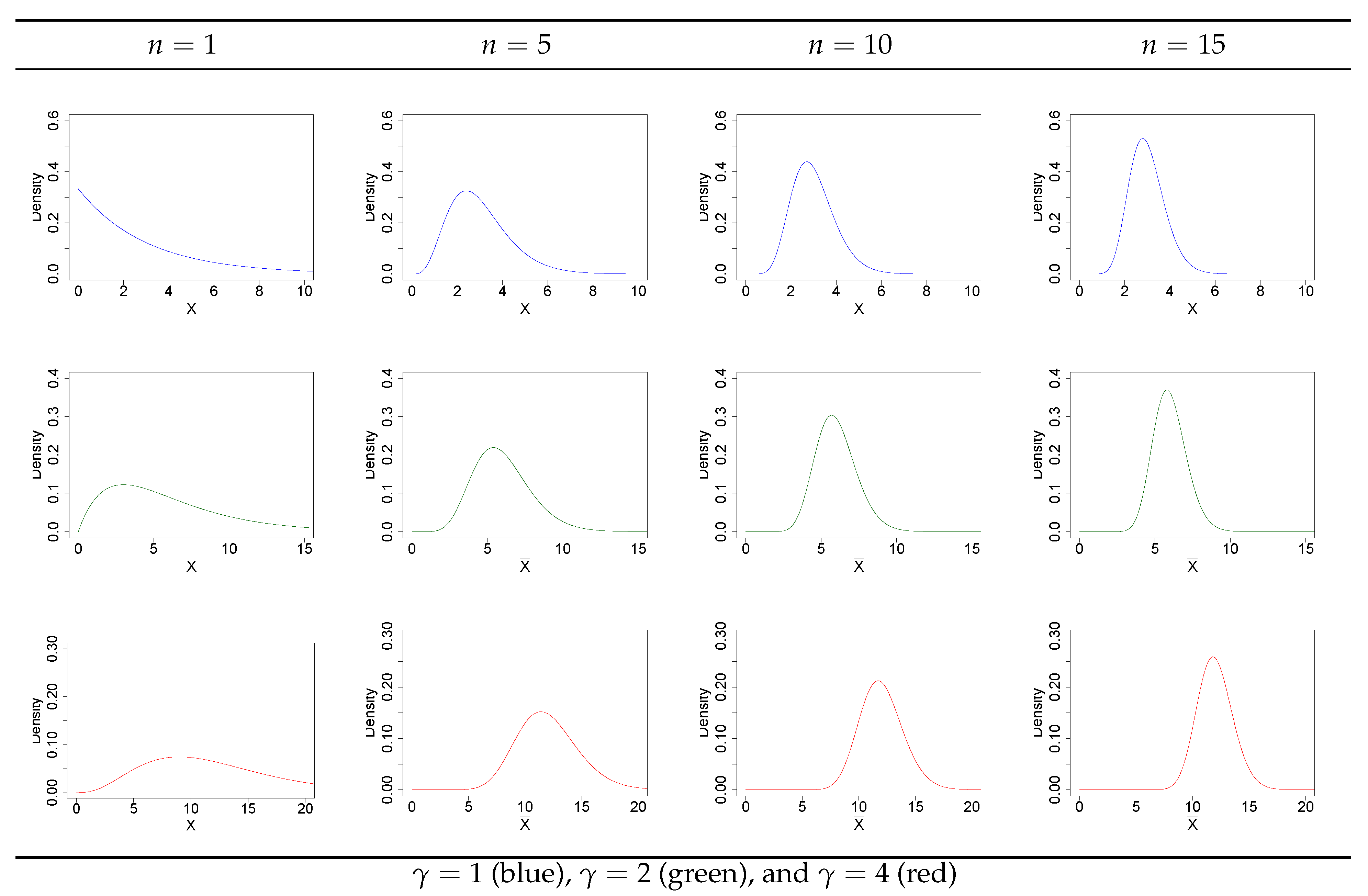
4. Numerical Analysis
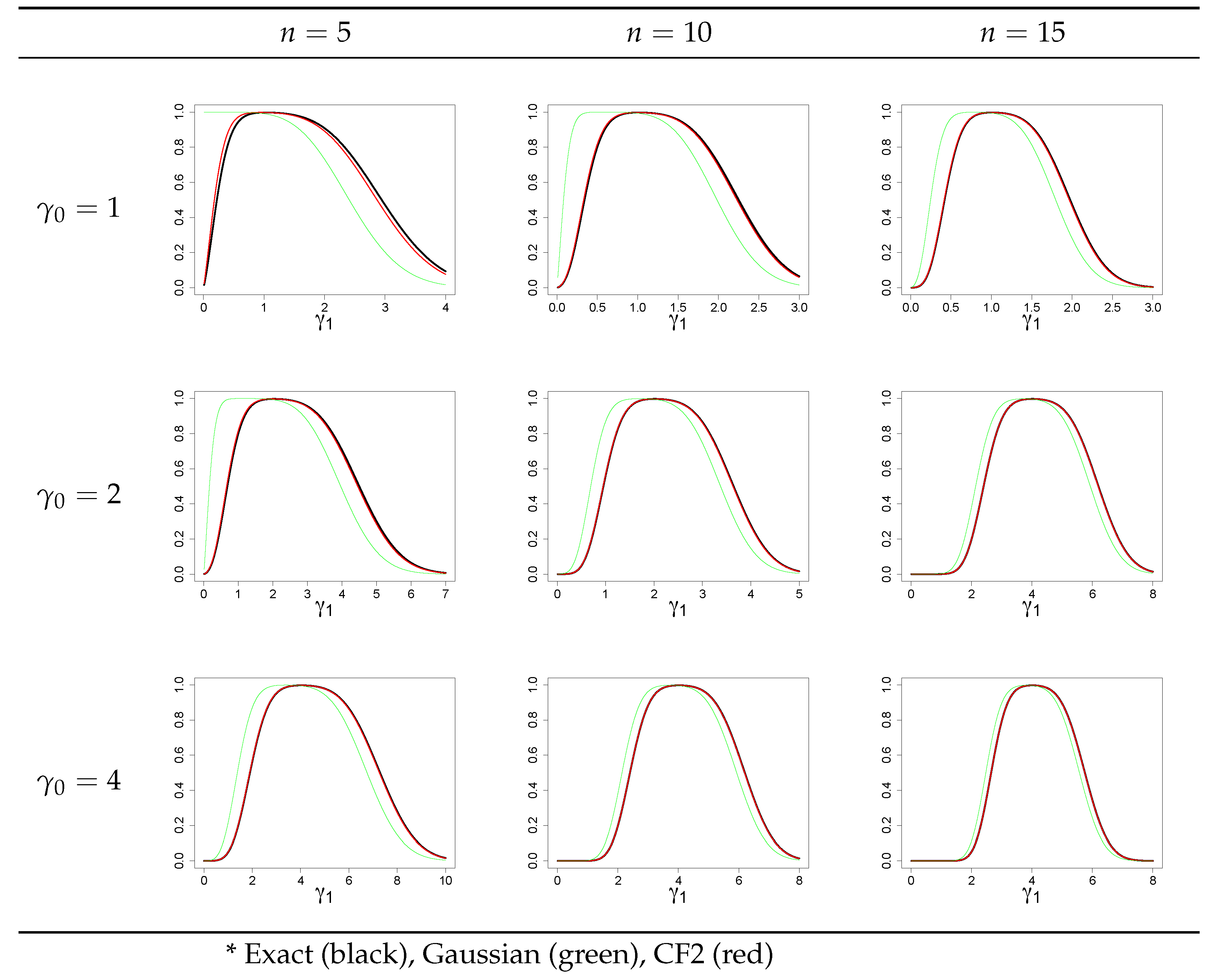
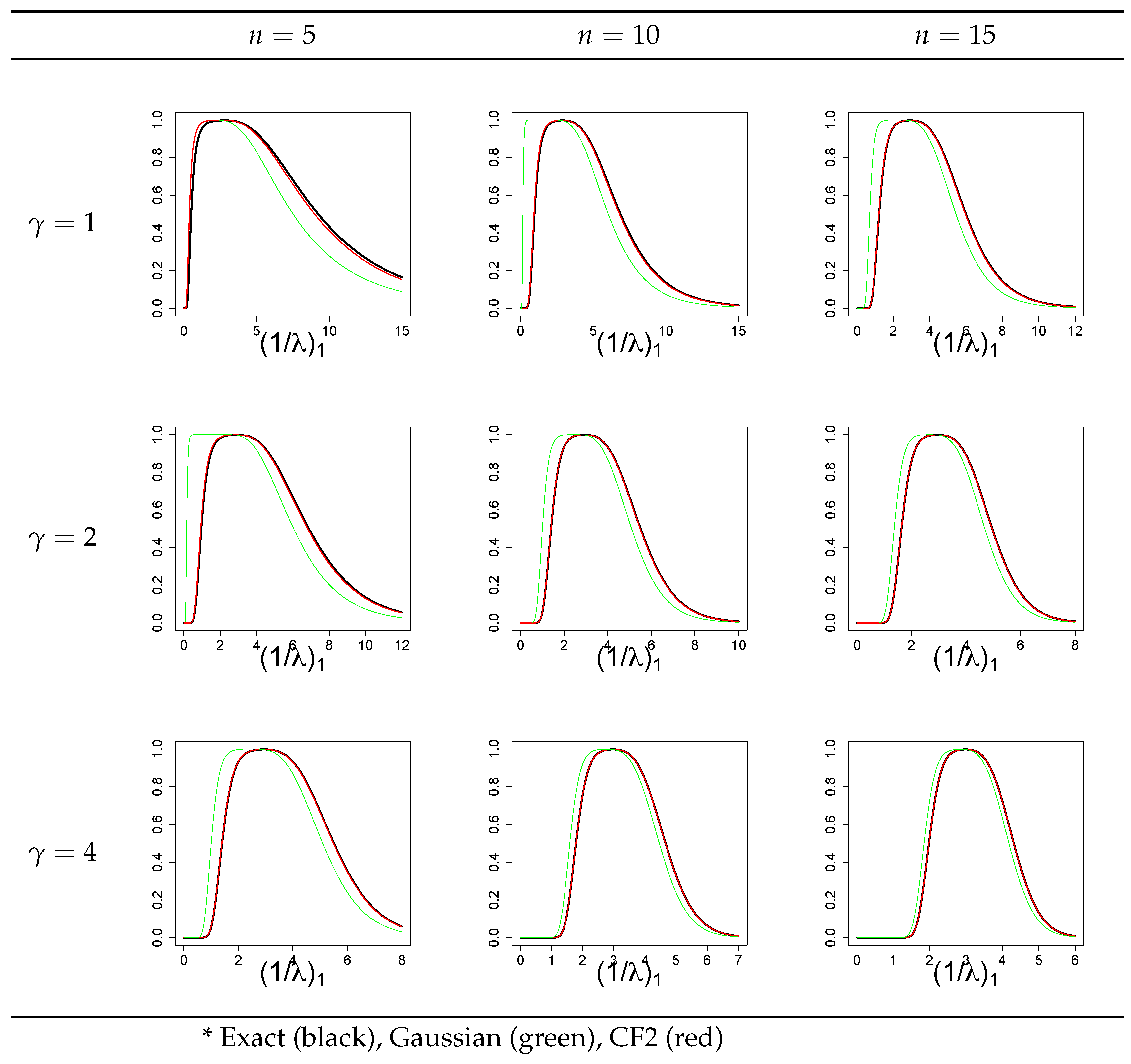
4.1. Known Skewness and Kurtosis Measures
4.2. Estimated Skewness and Kurtosis Measures
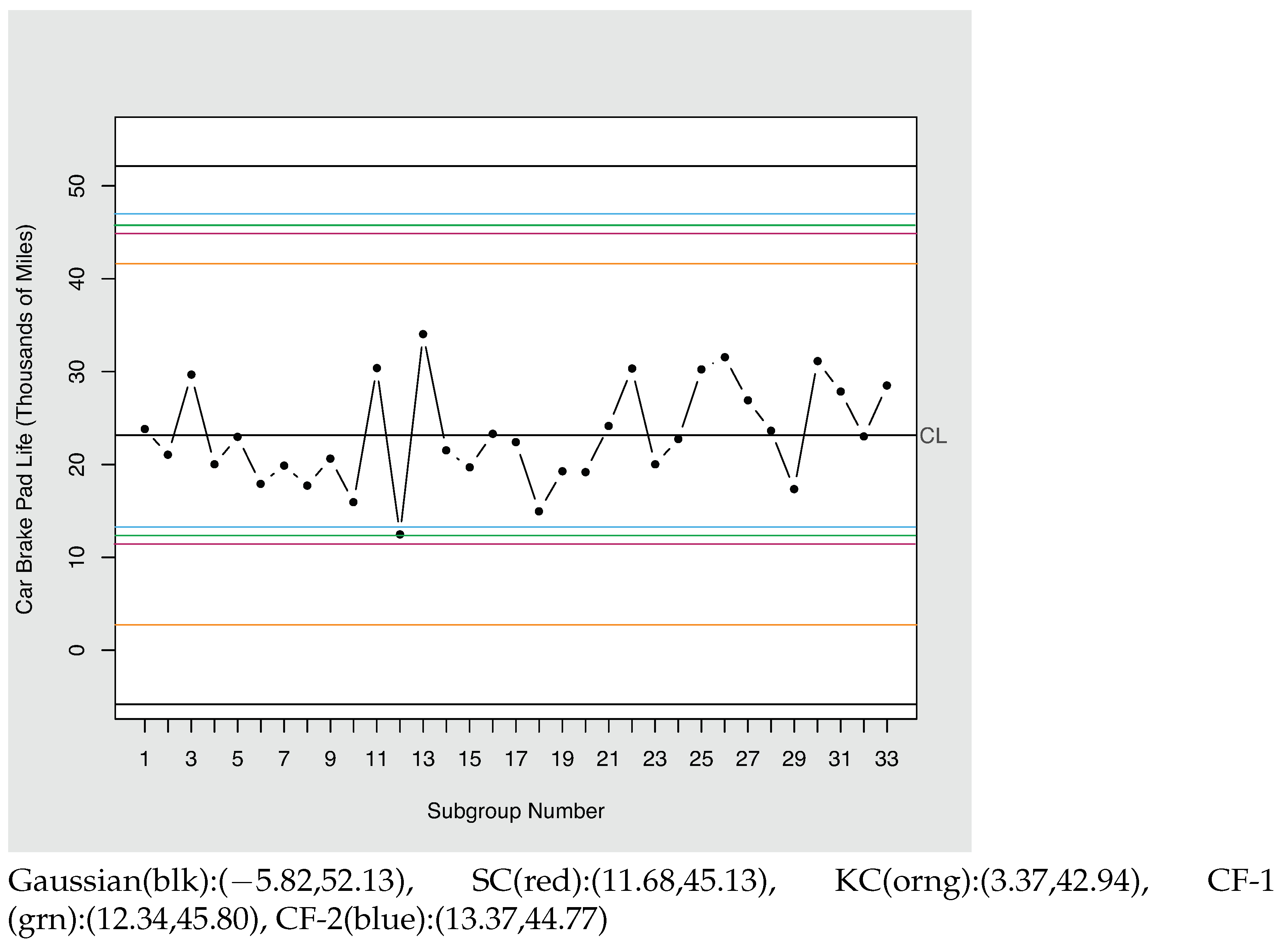
5. Control Charting Application
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Skewness | |
| Excess Kurtosis | |
| n | Subgroup Size |
| m | Number of Subgroups |
| Type I Error Rate, Producer’s Risk | |
| Standard Normal Probability Density Function | |
| Standard Normal Cumulative Density Function | |
| Discriminant | |
| Scale Parameter of distribution | |
| Shape Parameter of distribution |
References
- Zain, Z.; Yahaya, S.S.S.; Ahmad, N.; Atta, A.M.A. New X-bar Control Chart Using Skewness Correction Method for skewed Distributions with Application in Healthcare. Syst. Rev. Pharm. 2020, 11, 120–131. [Google Scholar]
- Dreves, M.; Huang, G.; Peng, Z.; Polyzotis, N.; Rosen, E.; Suganthan, G.C.P. From Data to Models and Back. In Proceedings of the Fourth International Workshop on Data Management for End-to-End Machine Learning, Portland, OR, USA, 14 June 2020; pp. 1–4. [Google Scholar]
- Mehta, R. Self-Assessment Data May Be Significantly Skewed During Global Health Crises. Int. J. Aviat. Res. 2020, 12. [Google Scholar]
- Chan, L.K.; Cui, H.J. Skewness Correction and R Charts for Skewed Distributions. Nav. Res. Logist. 2003, 50, 555–573. [Google Scholar] [CrossRef]
- Tadikamalla, P.; Popescu, D. Kurtosis Correction Method for and Control Charts for Long-Tailed Symmetrical Distributions. Nav. Res. Logist. 2007, 54, 371–384. [Google Scholar] [CrossRef]
- Maillard, D. A User’s Guide to the Cornish Fisher Expansion; SSRN:1997178 2018; pp. 1–14. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1997178 (accessed on 12 April 2022).
- Blanca, M.J.; Arnau, J.; López-Montiel, D.; Bono, R.; Bendayan, R. Skewness and Kurtosis in Real Data Samples. Methodology 2013, 9, 78–84. [Google Scholar]
- Bai, D.S.; Choi, S.I. and R control charts for skewed populations. J. Qual. Technol. 1995, 27, 120–131. [Google Scholar] [CrossRef]
- Shu, L.; Wei, J.; Wu, J. A one-sided EWMA control chart for monitoring process means. Commun. Stat. Comput. 2007, 36, 901–920. [Google Scholar] [CrossRef]
- Jones, A. The statistical design of EWMA control charts with estimated parameters. J. Qual. Technol. 2002, 34, 277–288. [Google Scholar] [CrossRef]
- Jensen, A.; Jones-Farmer, A.; Champ., C.; Woodall, W. Effects of parameter estimation on control chart properties: A literature review. J. Qual. Technol. 2006, 38, 349–364. [Google Scholar] [CrossRef]
- Chakraborti, S. Nonparametric (distribution-free) quality control charts. Encycl. Stat. Sci. 2011, 1–27. [Google Scholar] [CrossRef]
- Chakraborti, S.; Graham, M. Nonparametric (distribution-free) control charts: An updated overview and some results. Qual. Eng. 2019, 31, 1–22. [Google Scholar] [CrossRef]
- Jones-Farmer, L.A.; Jordan, V.; Champ, C.W. Distribution-free Phase I control charts for subgroup location. J. Qual. Technol. 2009, 41, 304–316. [Google Scholar] [CrossRef]
- Gibbons, J.D.; Chakraborti, S. Nonparametric Statistical Inference, 5th ed.; Taylor and Francis: Abingdon, UK, 2010. [Google Scholar]
- Amin, R.W.; Reynolds, M.R.; Bakir, S.T. Nonparametric quality control charts based on the sign statistic. Commun. Stat. Theory Methods 1995, 24, 1597–1623. [Google Scholar] [CrossRef]
- Bakir, S.T. A distribution-free Shewhart quality control chart based on signed-ranks. Qual. Eng. 2004, 16, 613–623. [Google Scholar] [CrossRef]
- Cornish, E.A.; Fisher, R.A. Moments and Cumulants in the Specifications of Distributions. Rev. Int. Stat. Inst. 1937, 4, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Johnson, N.; Kotz, S. Continuous Univariate Distributions; Wiley: New York, NY, USA, 1970; p. 34. [Google Scholar]
- Omar, M.; Arafat, S.; Hossain, M.; Riaz, M. Inverse Maxwell Distribution and Statistical Process Control: An Efficient Approach for Monitoring Positively Skewed Process. Symmetry 2021, 13, 189. [Google Scholar] [CrossRef]
- Chernozhukov, V.; Fernandez-Val, I.; Galichon, A. Improving point and interval estimators of monotone functions by rearrangement. Biometrika 2009, 96, 559. [Google Scholar]
| Gamma (1,3) = Exponential(3) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n = 5 | n = 10 | n = 15 | ||||||||||
| ARL↓ | LCL | UCL | ARL↑ | ARL↓ | LCL | UCL | ARL↑ | ARL↓ | LCL | UCL | ARL↑ | |
| Exact | 740.74 | 0.48 | 8.64 | 740.74 | 740.74 | 0.93 | 6.65 | 740.74 | 740.74 | 1.20 | 5.86 | 740.74 |
| Gaussian | ∞ | (·) | 7.03 | 107.41 | 4.56 × 10 | 0.15 | 5.85 | 148.85 | 3.53 × 10 | 0.68 | 5.23 | 179.09 |
| WSD | - | - | 7.50 | 187.62 | - | - | 6.08 | 234.80 | 9.71 × 10 | 0.52 | 5.48 | 269.40 |
| SC | 2724.80 | 0.35 | 8.40 | 556.79 | 646.24 | 0.89 | 6.59 | 946.97 | 679.81 | 1.18 | 5.83 | 821.70 |
| KC | 333,333 | 0.128 | 8.18 | 422.30 | 14,705.88 | 0.63 | 6.32 | 377.22 | 7575.76 | 0.95 | 5.60 | 363.90 |
| CF1 | 326.58 | 0.58 | 8.62 | 730.99 | 593.82 | 0.95 | 6.65 | 730.46 | 662.25 | 1.21 | 5.86 | 731.53 |
| CF2 | 460.83 | 0.53 | 8.67 | 772.80 | 670.24 | 0.94 | 6.66 | 754.24 | 749.06 | 1.20 | 5.87 | 749.06 |
| Gamma (2,3) | ||||||||||||
| n = 5 | n = 10 | n = 15 | ||||||||||
| ARL↓ | LCL | UCL | ARL↑ | ARL↓ | LCL | UCL | ARL↑ | ARL↓ | LCL | UCL | ARL↑ | |
| Exact | 740.74 | 1.85 | 13.31 | 740.74 | 740.74 | 2.76 | 10.83 | 740.74 | 740.74 | 3.24 | 9.82 | 740.74 |
| Gaussian | 4.56 × 10 | 0.31 | 11.69 | 148.85 | 5.20 × 10 | 1.98 | 10.03 | 203.11 | 1.25 × 10 | 2.71 | 9.29 | 240.16 |
| WSD | - | - | 12.18 | 237.76 | 3.33 × 10 | 1.74 | 10.27 | 296.03 | 3.45 × 10 | 2.56 | 9.45 | 336.47 |
| SC | 946.97 | 1.79 | 13.17 | 646.83 | 783.70 | 2.74 | 10.79 | 696.38 | 732.06 | 3.24 | 9.81 | 712.76 |
| KC | 14,705.88 | 1.26 | 12.64 | 377.22 | 5405.41 | 2.34 | 10.39 | 361.14 | 3703.70 | 2.92 | 9.49 | 366.03 |
| CF1 | 593.82 | 1.91 | 13.29 | 730.46 | 689.66 | 2.775 | 10.82 | 733.14 | 711.74 | 3.25 | 9.82 | 734.21 |
| CF2 | 670.24 | 1.88 | 13.32 | 754.72 | 722.02 | 2.76 | 10.84 | 746.83 | 732.06 | 3.24 | 9.83 | 744.05 |
| Gamma (4,3) | ||||||||||||
| n = 5 | n = 10 | n = 15 | ||||||||||
| ARL↓ | LCL | UCL | ARL↑ | ARL↓ | LCL | UCL | ARL↑ | ARL↓ | LCL | UCL | ARL↑ | |
| Exact | 740.74 | 5.52 | 21.66 | 740.74 | 740.74 | 7.10 | 18.50 | 740.74 | 740.74 | 7.88 | 17.18 | 740.74 |
| Gaussian | 5.20 × 10 | 3.95 | 20.05 | 203.11 | 6765.87 | 6.31 | 17.69 | 268.31 | 3755.31 | 7.35 | 16.65 | 309.84 |
| WSD | 3.33 × 10 | 3.46 | 20.52 | 292.74 | 1.50 × 10 | 6.06 | 17.93 | 358.68 | 6578.95 | 7.19 | 16.80 | 397.61 |
| SC | 783.70 | 5.49 | 21.59 | 696.38 | 735.29 | 7.10 | 18.48 | 720.46 | 744.05 | 7.88 | 17.17 | 728.33 |
| KC | 5405.41 | 4.68 | 20.79 | 361.14 | 2976.19 | 6.58 | 17.96 | 374.81 | 2298.85 | 7.50 | 16.80 | 393.24 |
| CF1 | 689.66 | 5.55 | 21.65 | 733.14 | 720.98 | 7.11 | 18.49 | 735.29 | 729.39 | 7.89 | 17.18 | 736.92 |
| CF2 | 722.02 | 5.53 | 21.67 | 746.83 | 735.29 | 7.10 | 18.50 | 742.94 | 738.01 | 7.88 | 17.19 | 742.39 |
| Exact | Gaussian | CF-1 | CF-2 | ||
|---|---|---|---|---|---|
| ARL↓ | 1 | 2.24 | 8.13 × 10 | 2.06 | 2.16 |
| 2 | 49.48 | 8.13 × 10 | 41.27 | 45.56 | |
| 3 | 740.74 | 4.56 × 10 | 593.82 | 670.24 | |
| ARL↑ | 3 | 740.74 | 148.58 | 520.02 | 754.72 |
| 4 | 31.69 | 12.00 | 31.42 | 32.06 | |
| 5 | 6.87 | 3.70 | 6.79 | 6.87 | |
| for | |||||
| for | |||||
| Gamma (1,3) = Exponential (3) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n = 5 | n = 10 | n =15 | ||||||||
| m = | 100 | 1000 | 10,000 | 100 | 1000 | 10,000 | 100 | 1000 | 10,000 | |
| Exact | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | |
| Gaussian |
Known Sim(Med) Sim(IQR) | · · · | · · · | · · · |
4.56 × 105 · · |
4.56 × 105 · · |
4.56 × 105 · · |
3.53 × 105 (2.44 × 105) (4.24 × 105) |
3.53 × 105 (3.29 × 105) (6.90 × 105) |
3.53 × 105 (3.51 × 105) (1.95 × 105) |
| SC | Known Sim(Med) Sim(IQR) | 2724.80 (16,042.05) (528,697.80) | 2724.80 (3726.37) (5890.05) | 2724.80 (2907.68) (1403.73) | 946.97 (1625.76) (3458.58) | 946.97 (1049.20) (708.76) | 946.97 (956.43) (224.51) | 821.69 (1179.06) (2574.73) | 821.69 (856.85) (538.85) | 821.69 (828.91) (168.45) |
| CF1 | Known Sim(Med) Sim(IQR) | 326.58 (1967.59) (15,430.76) | 326.58 (437.12) (686.78) | 326.58 (341.57) (181.22) | 593.82 (1145.34) (2564.59) | 593.82 (678.78) (515.40) | 593.82 (606.50) (158.59) | 662.25 (899.93) (1862.49) | 662.25 (717.41) (408.27) | 662.25 (668.68) (138.78) |
| CF2 | Known Sim(Med) Sim(IQR) | 460.83 (333.84) (867.29) | 460.83 (358.80) (287.72) | 460.83 (419.56) (164.86) | 670.24 (639.42) (1074.77) | 670.24 (620.09) (311.65) | 670.24 (657.01) (113.83) | 749.06 (703.01) (1285.62) | 749.06 (679.43) (353.41) | 749.06 (699.11) (124.33) |
| Gamma (2,3) | ||||||||||
| n = 5 | n = 10 | n = 15 | ||||||||
| m = | 100 | 1000 | 10,000 | 100 | 1000 | 10,000 | 100 | 1000 | 10,000 | |
| Exact | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | |
| Gaussian |
Known Sim(Med) Sim(IQR) |
4.56 × 109 · · |
4.56 × 109 · · |
4.56 × 109 · · |
5.20 × 104 (3.78 × 104) (3.20 × 105) |
5.20 × 104 (5.00 × 104) (6.15 × 104) |
5.20 × 104 (5.29 × 104) (1.81 × 104) |
1.25 × 104 (1.02 × 104) (3.26 × 104) |
1.25 × 104 (1.23 × 104) (1.24 × 104) |
1.25 × 104 (1.27 × 104) (1092.90) |
| SC | Known Sim(Med) Sim(IQR) | 946.97 (1468.95) (3042.21) | 946.97 (1027.32) (695.96) | 946.97 (950.96) (202.08) | 783.70 (954.67) (1881.77) | 783.70 (802.81) (404.00) | 783.70 (786.45) (136.07) | 758.15 (844.09) (1802.91) | 758.15 (788.49) (438.33) | 758.15 (757.03) (147.69) |
| CF1 | Known Sim(Med) Sim(IQR) | 593.82 (1007.22) (2222.62) | 593.82 (671.91) (501.45) | 593.82 (607.43) (157.25) | 689.66 (876.56) (1860.54) | 689.66 (710.90) (393.75) | 689.66 (692.48) (122.72) | 711.74 (828.37) (1851.38) | 711.74 (719.21) (402.47) | 711.74 (717.05) (131.09) |
| CF2 | Known Sim(Med) Sim(IQR) | 670.24 (540.62) (921.75) | 670.24 (627.39) (327.84) | 670.24 (654.38) (117.87) | 722.02 (703.10) (1044.93) | 722.02 (717.77) (332.00) | 722.02 (720.22) (119.05) | 732.06 (739.27) (1560.88) | 732.06 (710.32) (383.10) | 732.06 (734.96) (128.60) |
| Gamma (4,3) | ||||||||||
| n = 5 | n = 10 | n = 15 | ||||||||
| m = | 100 | 1000 | 10,000 | 100 | 1000 | 10,000 | 100 | 1000 | 10,000 | |
| Exact | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | |
| Gaussian |
Known Sim(Med) Sim(IQR) |
5.20 × 104 (3.80 × 104) (2.15 × 105) |
5.20 × 104 (4.98 × 104) (5.08 × 104) |
5.20 × 104 (5.13 × 104) (1.58 × 104) |
6765.87 (6776.40) (2.01 × 104) |
6765.87 (6859.42) (4749.77) |
6765.87 (6796.99) (1580.69) |
3755.31 (3490.03) (1.13 × 10) | 3755.31 (3787.28) (3102.52) | 3755.31 (3777.15) (901.67) |
| SC | Known Sim(Med) Sim(IQR) | 783.70 (999.26) (1763.86) | 783.70 (814.33) (418.17) | 783.70 (795.62) (124.59) | 749.63 (820.69) (1373.07) | 749.63 (754.47) (363.18) | 749.63 (751.03) (125.95) | 744.05 (795.79) (1867.23) | 744.05 (779.79) (429.59) | 744.05 (736.71) (130.16) |
| CF1 | Known Sim(Med) Sim(IQR) | 689.66 (836.41) (1514.37) | 689.66 (735.83) (396.29) | 689.66 (690.93) (115.72) | 720.98 (810.86) (1305.64) | 720.98 (721.73) (389.33) | 720.98 (729.00) (120.37) | 729.39 (898.95) (1884.96) | 729.39 (732.59) (414.86) | 729.39 (720.67) (123.55) |
| CF2 | Known Sim(Med) Sim(IQR) | 722.02 (668.54) (875.65) | 722.02 (721.95) (326.34) | 722.02 (716.26) (104.11) | 735.29 (772.98) (1219.99) | 735.29 (724.90) (339.82) | 735.29 (734.46) (105.75) | 738.01 (721.21) (1645.47) | 738.01 (710.36) (385.45) | 738.01 (736.69) (133.52) |
| Gamma (1,3) = Exponential(3) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n = 5 | n = 10 | n = 15 | ||||||||
| m = | 100 | 1000 | 10,000 | 100 | 1000 | 10,000 | 100 | 1000 | 10,000 | |
| Exact | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | |
| Gaussian | Known Sim(Med) Sim(IQR) | 107.41 (93.8) (89.33) | 107.41 (103.72) (45.7) | 107.41 (107.2) (13.05) | 148.85 (131.49) (243.43) | 148.85 (148.13) (83.48) | 148.85 (147.73) (24.57) | 179.09 (166.51) (336.02) | 179.09 (174.83) (144.55) | 179.09 (177.68) (33.91) |
| SC | Known Sim(Med) Sim(IQR) | 556.79 (427.45) (941.62) | 556.79 (544.22) (355.33) | 556.79 (551.57) (109.13) | 520.29 (368.39) (901.68) | 520.29 (401.2) (371.98) | 520.29 (523.16) (52.63) | 562.75 (413.22) (1296.71) | 562.75 (527.98) (441.37) | 562.75 (566.73) (56.13) |
| CF1 | Known Sim(Med) Sim(IQR) | 730.99 (363.50) (1062.04) | 730.99 (669.69) (451.69) | 730.99 (724.90) (176.60) | 730.46 (448.43) (1395.73) | 730.46 (693.96) (516.92) | 730.46 (723.59) (166.14) | 731.53 (528.26) (1713.78) | 731.53 (706.96) (511.33) | 731.53 (727.27) (172.94) |
| CF2 | Known Sim(Med) Sim(IQR) | 772.80 (363.50) (999.44) | 772.80 (669.79) (556.76) | 772.80 (755.00) (245.50) | 754.24 (442.48) (1144.96) | 754.24 (664.23) (498.79) | 754.24 (730.19) (177.53) | 749.06 (485.79) (1393.70) | 749.06 (709.72) (601.20) | 749.06 (733.41) (191.97) |
| Gamma (2,3) | ||||||||||
| n = 5 | n = 10 | n = 15 | ||||||||
| m = | 100 | 1000 | 10,000 | 100 | 1000 | 10,000 | 100 | 1000 | 10,000 | |
| Exact | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | |
| Gaussian | Known Sim(Med) Sim(IQR) | 148.85 (144.83) (183.8) | 148.85 (146.9) (55.16) | 148.85 (148.71) (18.7) | 203.11 (180.25) (347.12) | 203.11 (204.12) (101.2) | 203.11 (203.29) (32.13) | 240.16 (209.89) (491.22) | 240.16 (241.84) (149.39) | 240.16 (242.1) (48.1) |
| SC | Known Sim(Med) Sim(IQR) | 646.83 (520.83) (991.86) | 646.83 (616.90) (378.63) | 646.83 (642.26) (127.21) | 696.38 (531.53) (1552.85) | 696.38 (653.60) (723.12) | 696.38 (679.35) (312.16) | 712.76 (569.64) (1626.56) | 712.76 (711.24) (556.22) | 712.76 (717.36) (171.62) |
| CF1 | Known Sim(Med) Sim(IQR) | 730.46 (530.93) (1113.11) | 730.46 (715.31) (491.77) | 730.46 (731.53) (150.66) | 746.83 (562.43) (1462.87) | 746.83 (706.96) (537.50) | 746.83 (728.86) (170.26) | 734.21 (613.69) (1886.49) | 734.21 (725.16) (574.62) | 734.21 (728.33) (188.12) |
| CF2 | Known Sim(Med) Sim(IQR) | 754.72 (445.58) (1073.91) | 754.72 (702.00) (515.41) | 754.72 (728.60) (183.19) | 746.83 (504.42) (1307.47) | 746.83 (718.13) (538.87) | 746.83 (745.71) (179.05) | 744.05 (530.23) (1681.06) | 744.05 (715.56) (592.04) | 744.05 (743.49) (194.31) |
| Gamma (4,3) | ||||||||||
| n = 5 | n = 10 | n = 15 | ||||||||
| m = | 100 | 1000 | 10,000 | 100 | 1000 | 10,000 | 100 | 1000 | 10,000 | |
| Exact | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | 740.74 | |
| Gaussian | Known Sim(Med) Sim(IQR) | 203.11 (195.1) (281.58) | 203.11 (205.38) (75.88) | 203.11 (203.75) (23.93) | 268.31 (245.46) (464.72) | 268.31 (272.38) (138.95) | 268.31 (266.95) (46.10) | 309.84 (292.83) (656.67) | 309.84 (303.21) (198.34) | 309.84 (307.41) (60.53) |
| SC | Known Sim(Med) Sim(IQR) | 696.38 (565.30) (1066.21) | 696.38 (677.05) (400.35) | 696.38 (688.23) (124.86) | 720.46 (602.25) (1508.28) | 720.46 (689.89) (434.75) | 720.46 (717.62) (150.78) | 728.33 (621.70) (1889.65) | 728.33 (714.80) (568.78) | 728.33 (722.80) (159.54) |
| CF1 | Known Sim(Med) Sim(IQR) | 733.14 (590.32) (1062.04) | 733.14 (699.79) (451.69) | 733.14 (724.64) (176.60) | 735.29 (616.71) (1542.17) | 735.29 (706.72) (465.07) | 735.29 (726.74) (147.20) | 736.92 (723.59) (2173.25) | 736.92 (740.47) (540.34) | 736.92 (729.13) (168.02) |
| CF2 | Known Sim(Med) Sim(IQR) | 746.83 (513.88) (1062.04) | 746.83 (693.24) (451.69) | 746.83 (736.11) (176.60) | 742.94 (558.50) (1395.73) | 742.94 (712.25) (516.92) | 742.94 (749.91) (166.14) | 742.39 (594.71) (1713.78) | 742.39 (725.16) (511.33) | 742.39 (736.92) (172.94) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Braden, P.; Matis, T. Cornish–Fisher-Based Control Charts Inclusive of Skewness and Kurtosis Measures for Monitoring the Mean of a Process. Symmetry 2022, 14, 1176. https://doi.org/10.3390/sym14061176
Braden P, Matis T. Cornish–Fisher-Based Control Charts Inclusive of Skewness and Kurtosis Measures for Monitoring the Mean of a Process. Symmetry. 2022; 14(6):1176. https://doi.org/10.3390/sym14061176
Chicago/Turabian StyleBraden, Paul, and Timothy Matis. 2022. "Cornish–Fisher-Based Control Charts Inclusive of Skewness and Kurtosis Measures for Monitoring the Mean of a Process" Symmetry 14, no. 6: 1176. https://doi.org/10.3390/sym14061176
APA StyleBraden, P., & Matis, T. (2022). Cornish–Fisher-Based Control Charts Inclusive of Skewness and Kurtosis Measures for Monitoring the Mean of a Process. Symmetry, 14(6), 1176. https://doi.org/10.3390/sym14061176






