Revealing the Symmetry of Materials through Neutron Diffraction
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
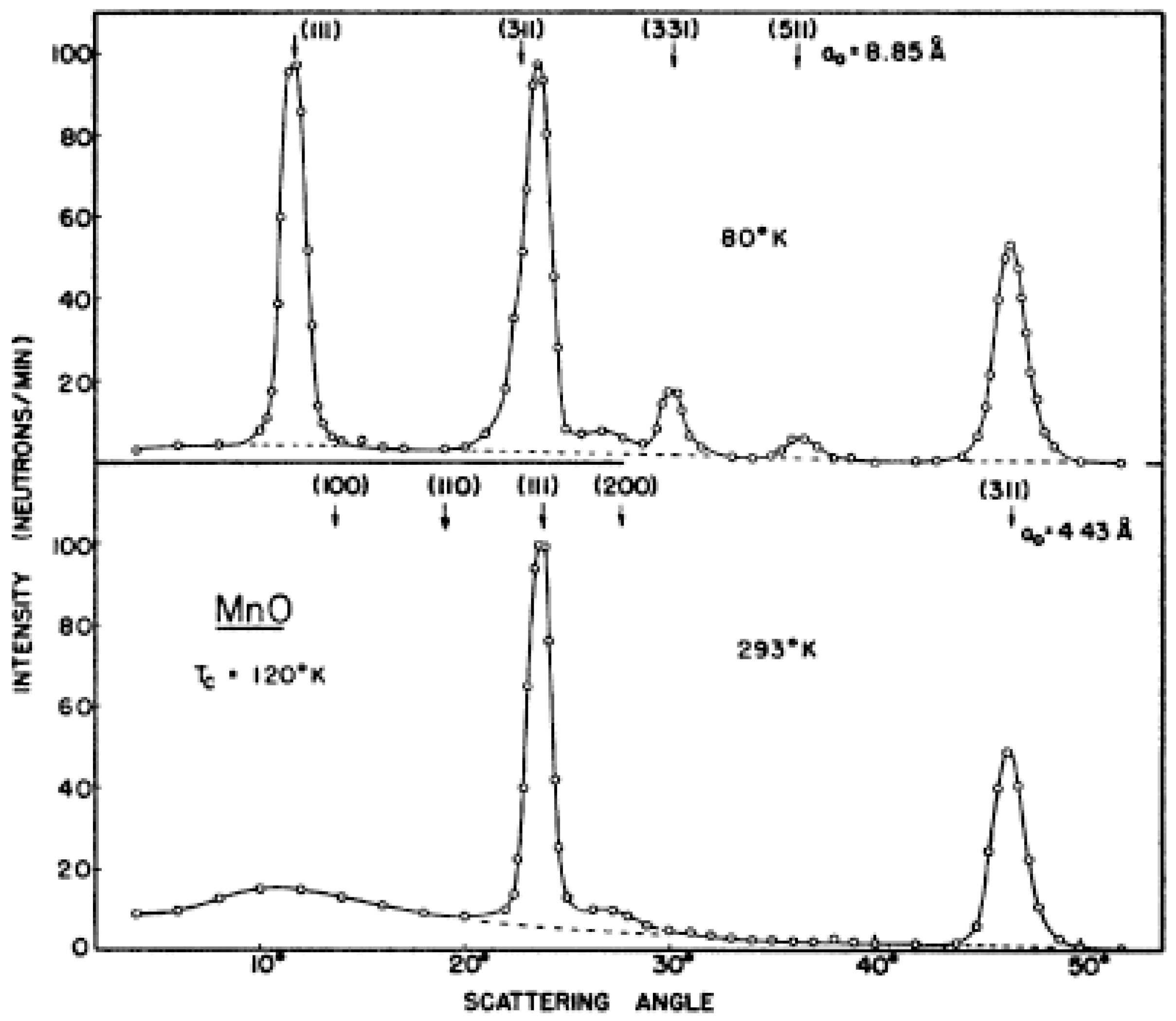
3.1. MnO
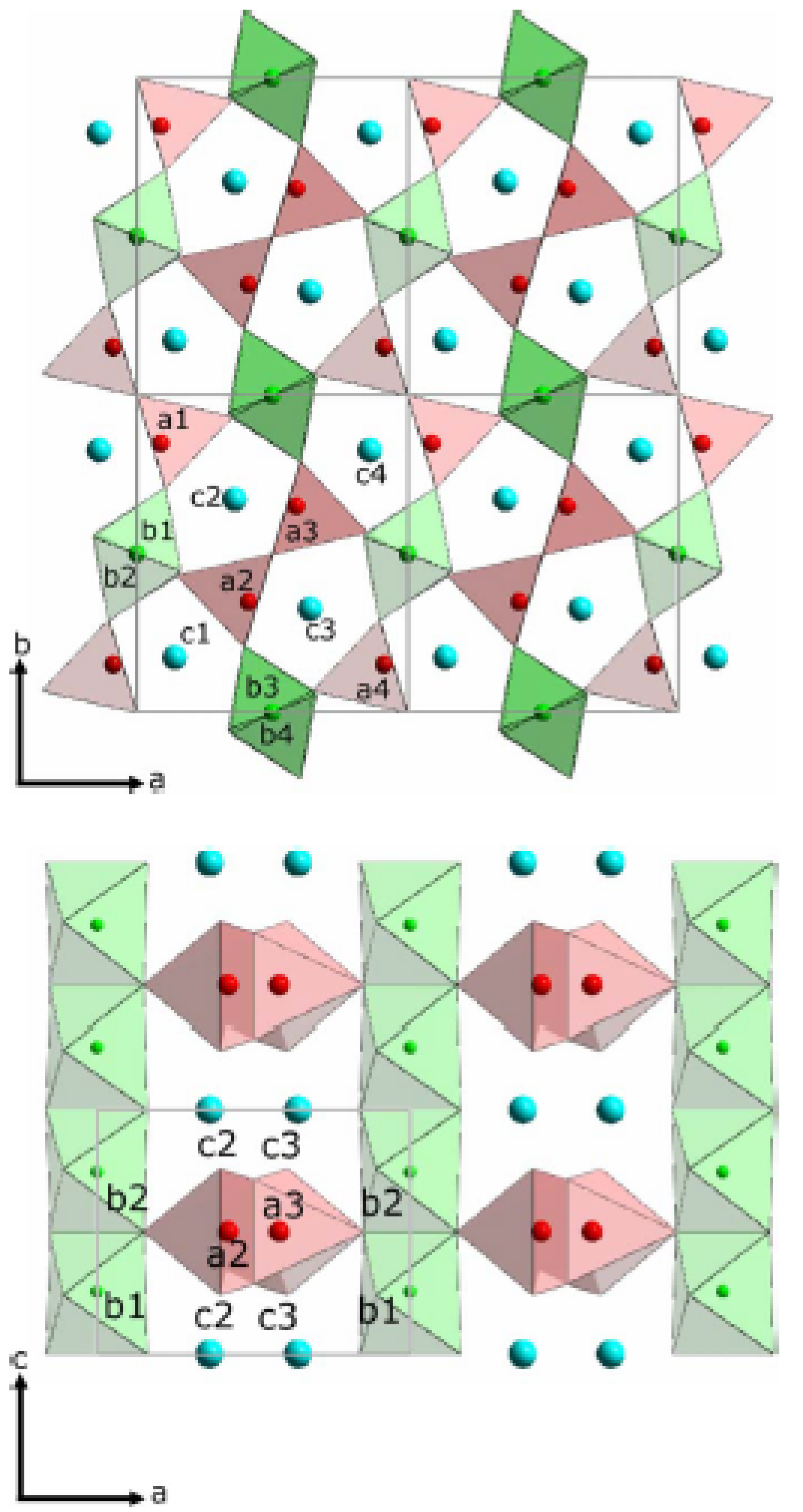
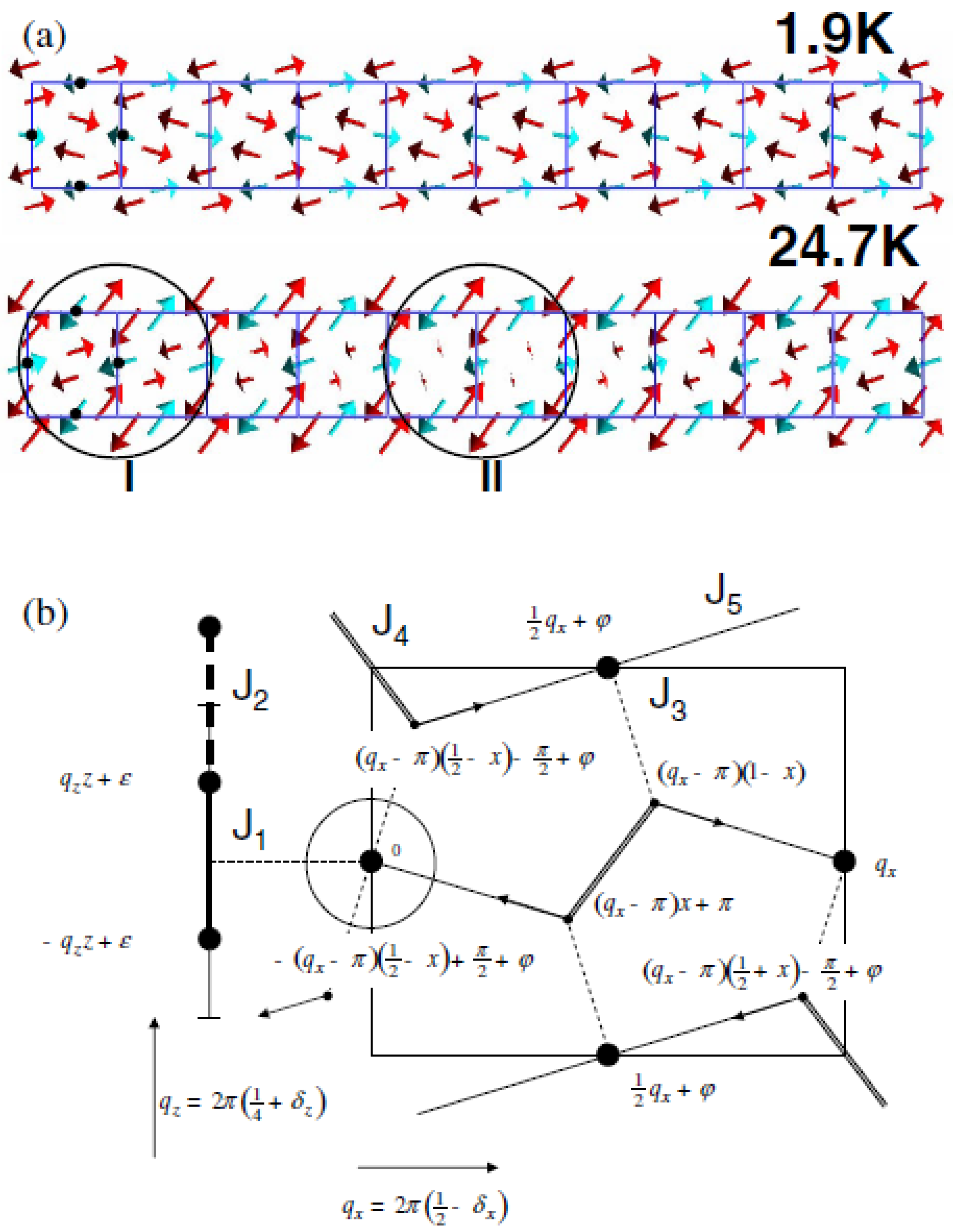
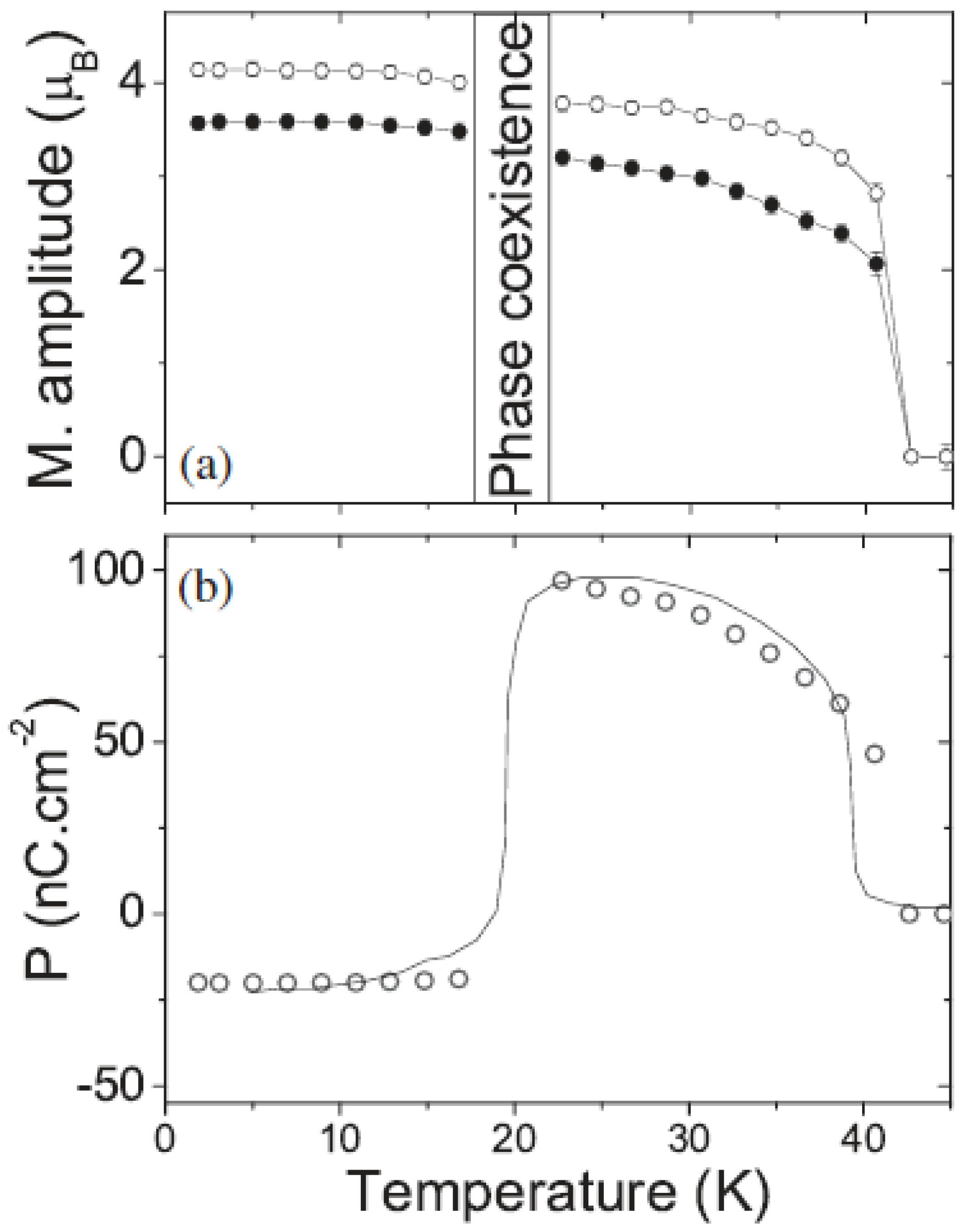
3.2.
4. Tools
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Hammermesh, M. Group Theory and Its Application to Physical Problems, reprint ed.; Dover Publications: Mineola, NY, USA, 1989. [Google Scholar]
- Bradley, C.; Cracknell, A.P. The Mathematical Tehory of Symmetry in Solids; Representation Theory for Point Groups and Space Groups, revised ed.; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Mirman, R. Point Groups, Space Groups, Crystals, Molecules; World Scientific: Singapore, 1999. [Google Scholar]
- Izyumov, Y.A.; Syromyatnikov, V. Phase Transitions and Crystal Symmetry, english ed.; Kluwer Academic Publishers: Boston, MA, USA, 1990. [Google Scholar]
- Rodriguez-Carvajal, J. FULLPROF: A Program for Rietveld Refinement and Pattern Matching Analysis. In Abstracts of the Satellite Meeting on Powder Diffraction of the XV Congress of the IUCr; Toulouse, France, 1990; p. 127. Available online: https://www.scirp.org/(S(351jmbntvnsjt1aadkposzje))/reference/ReferencesPapers.aspx?ReferenceID=868636 (accessed on 20 April 2022).
- Aroyo, M.I.; Perez-Mato, J.M.; Capillas, C.; Kroumova, E.; Ivantchev, S.; Madariaga, G.; Kirov, A.; Wondratschek, H. Bilbao Crystallographic Server: I. Databases and crystallographic computing programs. Z. Krist. 2006, 221, 15–27. [Google Scholar] [CrossRef]
- Aroyo, M.I.; Kirov, A.; Capillas, C.; Perez-Mato, J.M.; Wondratschek, H. Bilbao Crystallographic Server. II. Representations of crystallographic point groups and space groups. Acta Crystallogr. Sect. A 2006, 62, 115–128. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA: A three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]
- Willighagen, E.; Howard, M. Fast and Scriptable Molecular Graphics in Web Browsers without Java3D. Nat. Preced. 2007, 1. [Google Scholar] [CrossRef]
- Pérez-Mato, J.M.; Madariaga, G.; Tello, M.J. Superspace groups and Landau theory. A physical approach to superspace symmetry in incommensurate structures. Phys. Rev. B 1984, 30, 1534–1543. [Google Scholar] [CrossRef]
- Perez-Mato, J.; Gallego, S.; Tasci, E.; Elcoro, L.; de la Flor, G.; Aroyo, M. Symmetry-Based Computational Tools for Magnetic Crystallography. Annu. Rev. Mater. Res. 2015, 45, 217–248. [Google Scholar] [CrossRef]
- Kopský, V. Towards a system in space group representations. Comput. Math. Appl. 1988, 16, 493–505. [Google Scholar] [CrossRef]
- Shull, C.G.; Strauser, W.A.; Wollan, E.O. Neutron diffraction by paramagnetic and antiferromagnetic substances. Phys. Rev. 1951, 83, 333–345. [Google Scholar] [CrossRef]
- Werner, P.E.; Eriksson, L.; Westdahl, M. TREOR, a semi-exhaustive trial-and-error powder indexing program for all symmetries. J. Appl. Crystallogr. 1985, 18, 367–370. [Google Scholar] [CrossRef]
- Boultif, A.; Èr, D.L. Applied Crystallography Powder pattern indexing with the dichotomy method. J. Appl. Crystallogr. 2004, 37. [Google Scholar] [CrossRef]
- Wills, A.S. A new protocol for the determination of magnetic structures using simulated annealing and representational analysis (SARAh). Phys. B Condens. Matter 2000, 276–278, 680–681. [Google Scholar] [CrossRef]
- Blech, I.A.; Averbach, B.L. Long-range magnetic order in MnO. Phys. Rev. 1966, 142, 287–290. [Google Scholar] [CrossRef]
- Rudolf, T.; Kant, C.; Mayr, F.; Loidl, A. Magnetic-order induced phonon splitting in MnO from far-infrared spectroscopy. Phys. Rev. B-Condens. Matter Mater. Phys. 2008, 77, 024421. [Google Scholar] [CrossRef]
- Chung, L.; Paul, M.K.; Balakrishnan, G.; Lees, R.; Ivanov, A.; Yethiraj, M. Role of electronic correlations on the phonon modes of MnO and NiO. Phys. Rev. B 2003, 68, 140406. [Google Scholar] [CrossRef]
- Cheetham, A.K.; Hope, D.A.O. Magnetic ordering and exchange effects in the antiferromagnetic solid solutions MnxN. Phys. Rev. B 1983, 27, 6964–6967. [Google Scholar] [CrossRef]
- Sun, X.; Feng, E.; Su, Y.; Nemkovski, K.; Petracic, O.; Brückel, T. Magnetic properties and spin structure of MnO single crystal and powder. J. Phys. Conf. Ser. 2017, 862. [Google Scholar] [CrossRef]
- Kantor, A.P.; Dubrovinsky, L.S.; Dubrovinskaia, N.A.; Kantor, I.Y.; Goncharenko, I.N. Phase transitions in MnO and FeO at low temperatures: A neutron powder diffraction study. J. Alloys Compd. 2005, 402, 42–45. [Google Scholar] [CrossRef]
- Goodwin, A.L.; Tucker, M.G.; Dove, M.T.; Keen, D.A. Magnetic structure of MnO at 10 K from total neutron scattering data. Phys. Rev. Lett. 2006, 96, 047209. [Google Scholar] [CrossRef]
- Kagomiya, I.; Matsumoto, S.; Kohn, K.; Fukuda, Y.; Shoubu, T.; Kimura, H.; Noda, Y.; Ikeda, N. Lattice Distortion at Ferroelectric Transition of YMn2O5. Ferroelectrics 2011, 286, 167–174. [Google Scholar] [CrossRef]
- Kobayashi, S.; Osawa, T.; Kimura, H.; Noda, Y.; Kagomiya, I.; Kohn, K. Reinvestigation of simultaneous magnetic and ferroelectric phase transitions in YMn2O5. J. Phys. Soc. Jpn. 2004, 73, 1593–1596. [Google Scholar] [CrossRef]
- Kimura, H.; Kobayashi, S.; Fukuda, Y.; Osawa, T.; Kamada, Y.; Noda, Y.; Kagomiya, I.; Kohn, K. Spiral spin structure in the commensurate magnetic phase of multiferroic RMn2O5. J. Phys. Soc. Jpn. 2007, 76, 074706. [Google Scholar] [CrossRef]
- Chapon, L.C.; Radaelli, P.G.; Blake, G.R.; Park, S.; Cheong, S.W. Ferroelectricity induced by acentric spin-density waves in YMn2O5. Phys. Rev. Lett. 2006, 96, 097601. [Google Scholar] [CrossRef] [PubMed]
- Vecchini, C.; Chapon, L.; Brown, P.; Chatterji, T.; Park, S.; Cheong, S.W.; Radaelli, P. Commensurate magnetic structures of RMn2O5 (R = Y,Ho,Bi) determined by single-crystal neutron diffraction. Phys. Rev. B 2008, 77, 134434. [Google Scholar] [CrossRef]
- Noda, Y.; Kimura, H.; Fukunaga, M.; Kobayashi, S.; Kagomiya, I.; Kohn, K. Magnetic and ferroelectric properties of multiferroic RMn2O5. J. Phys. Condens. Matter 2008, 20, 434206. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, S.H.; Park, S.I.; Kenzelmann, M.; Harris, A.B.; Schefer, J.; Chung, J.H.; Majkrzak, C.F.; Takeda, M.; Wakimoto, S.; et al. Spiral spin structures and origin of the magnetoelectric coupling in YMn2O5. Phys. Rev. B 2008, 78, 245115. [Google Scholar] [CrossRef]
- Radaelli, P.G.; Vecchini, C.; Chapon, L.C.; Brown, P.J.; Park, S.; Cheong, S.W. Incommensurate magnetic structure of YMn2O5: A stringent test of the multiferroic mechanism. Phys. Rev. B 2009, 79, 020404. [Google Scholar] [CrossRef]
- Radaelli, P.G.; Chapon, L.C. Symmetry constraints on the electrical polarization in multiferroic materials. Phys. Rev. B-Condens. Matter Mater. Phys. 2007, 76, 054428. [Google Scholar] [CrossRef]
- Harris, A.B.; Kenzelmann, M.; Aharony, A.; Entin-Wohlman, O. Effect of inversion symmetry on the incommensurate order in multiferroic R Mn2O5 (R = rare earth). Phys. Rev. B Condens. Matter Mater. Phys. 2008, 78, 014407. [Google Scholar] [CrossRef]
- Harris, A.B.; Aharony, A.; Entin-Wohlman, O. Order parameters and phase diagram of multiferroic RMn2O5. Phys. Rev. Lett. 2008, 100, 217202. [Google Scholar] [CrossRef]
- Lesniewski, J.E.; Disseler, S.M.; Quintana, D.J.; Kienzle, P.A.; Ratcliff, W.D. Bayesian method for the analysis of diffraction patterns using BLAND. J. Appl. Crystallogr. 2016, 49, 2201–2209. [Google Scholar] [CrossRef]
- Petíček, V.; Fuksa, J.; Dušek, M. Magnetic space and superspace groups, representation analysis: Competing or friendly concepts? Acta Crystallogr. Sect. A Found. Crystallogr. 2010, 66, 649–655. [Google Scholar] [CrossRef] [PubMed]
- Campbell, B.J.; Stokes, H.T.; Tanner, D.E.; Hatch, D.M. ISODISPLACE: A web-based tool for exploring structural distortions. J. Appl. Crystallogr. 2006, 39, 607–614. [Google Scholar] [CrossRef]
- Petrícek, V.; Dušek, M.; Palatinus, L. Crystallographic computing system JANA2006: General features. Z. Krist. 2014, 229, 345–352. [Google Scholar] [CrossRef]
- Toby, B.H.; Von Dreele, R.B. GSAS-II: The genesis of a modern open-source all purpose crystallography software package. J. Appl. Crystallogr. 2013, 46, 544–549. [Google Scholar] [CrossRef]
- White, J.S.; Butykai.; Cubitt, R.; Honecker, D.; Dewhurst, C.D.; Kiss, L.F.; Tsurkan, V.; Bordács, S. Direct evidence for cycloidal modulations in the thermal-fluctuation-stabilized spin spiral and skyrmion states of GaV4S8. Phys. Rev. B 2018, 97, 020401. [Google Scholar] [CrossRef]
- Dally, R.L.; Ratcliff, W.D.; Zhang, L.; Kim, H.S.; Bleuel, M.; Kim, J.W.; Haule, K.; Vanderbilt, D.; Cheong, S.W.; Lynn, J.W. Magnetic phase transitions and spin density distribution in the molecular multiferroic system GaV4S8. Phys. Rev. B 2020, 102, 014410. [Google Scholar] [CrossRef]
- Lee, S.; Choi, T.; Ratcliff, W.; Erwin, R.; Cheong, S.W.; Kiryukhin, V. Single ferroelectric and chiral magnetic domain of single-crystalline BiFeO3 in an electric field. Phys. Rev. B-Condens. Matter Mater. Phys. 2008, 78, 100101. [Google Scholar] [CrossRef]
- Ratcliff, W.; Kan, D.; Chen, W.; Watson, S.; Chi, S.; Erwin, R.; McIntyre, G.J.; Capelli, S.C.; Takeuchi, I. Neutron Diffraction Investigations of Magnetism in BiFeO3 Epitaxial Films. Adv. Funct. Mater. 2011, 21, 1567–1574. [Google Scholar] [CrossRef]
- Qureshi, N. Mag2Pol: A program for the analysis of spherical neutron polarimetry, flipping ratio and integrated intensity data. J. Appl. Crystallogr. 2019, 52, 175–185. [Google Scholar] [CrossRef]
- Maruyama, S.; Anbusathaiah, V.; Fennell, A.; Enderle, M.; Takeuchi, I.; Ratcliff, W.D. Change in the magnetic structure of (Bi,Sm)FeO3 thin films at the morphotropic phase boundary probed by neutron diffraction. APL Mater. 2014, 2, 116106. [Google Scholar] [CrossRef]


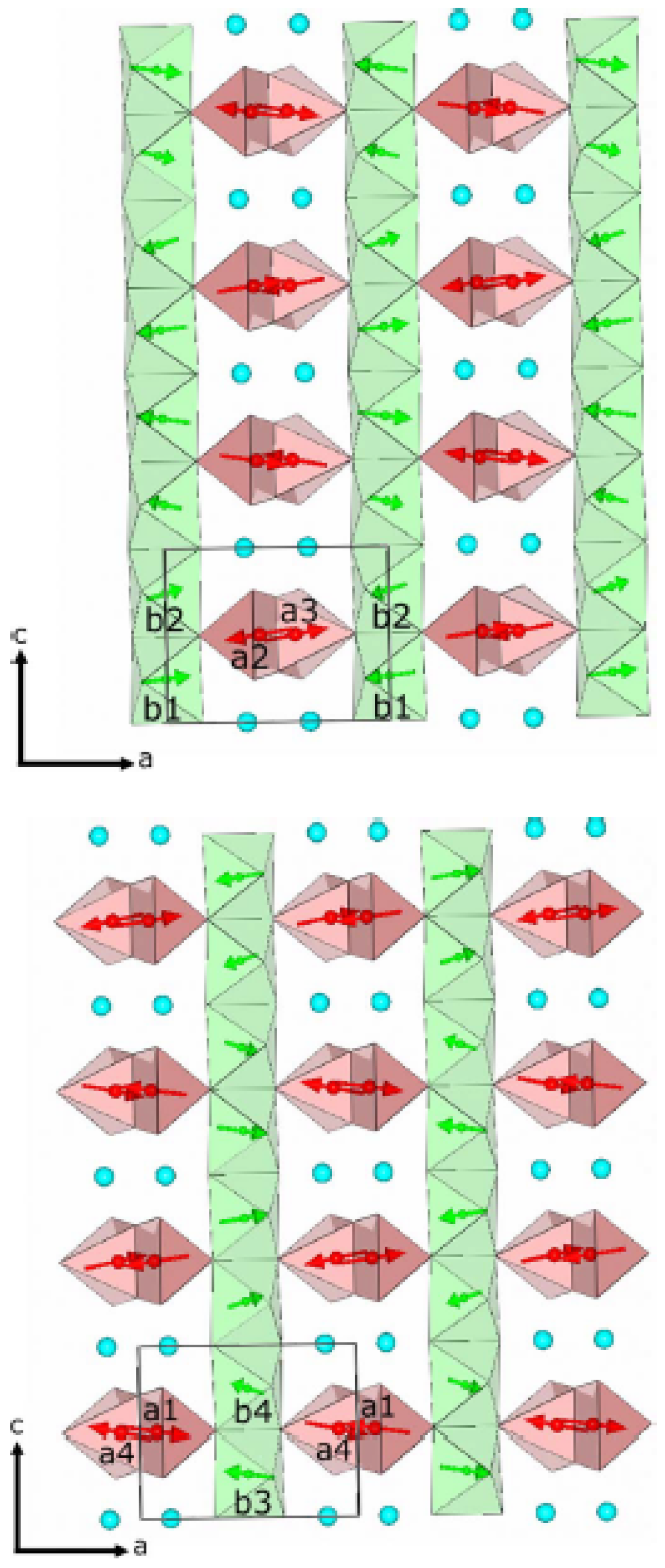
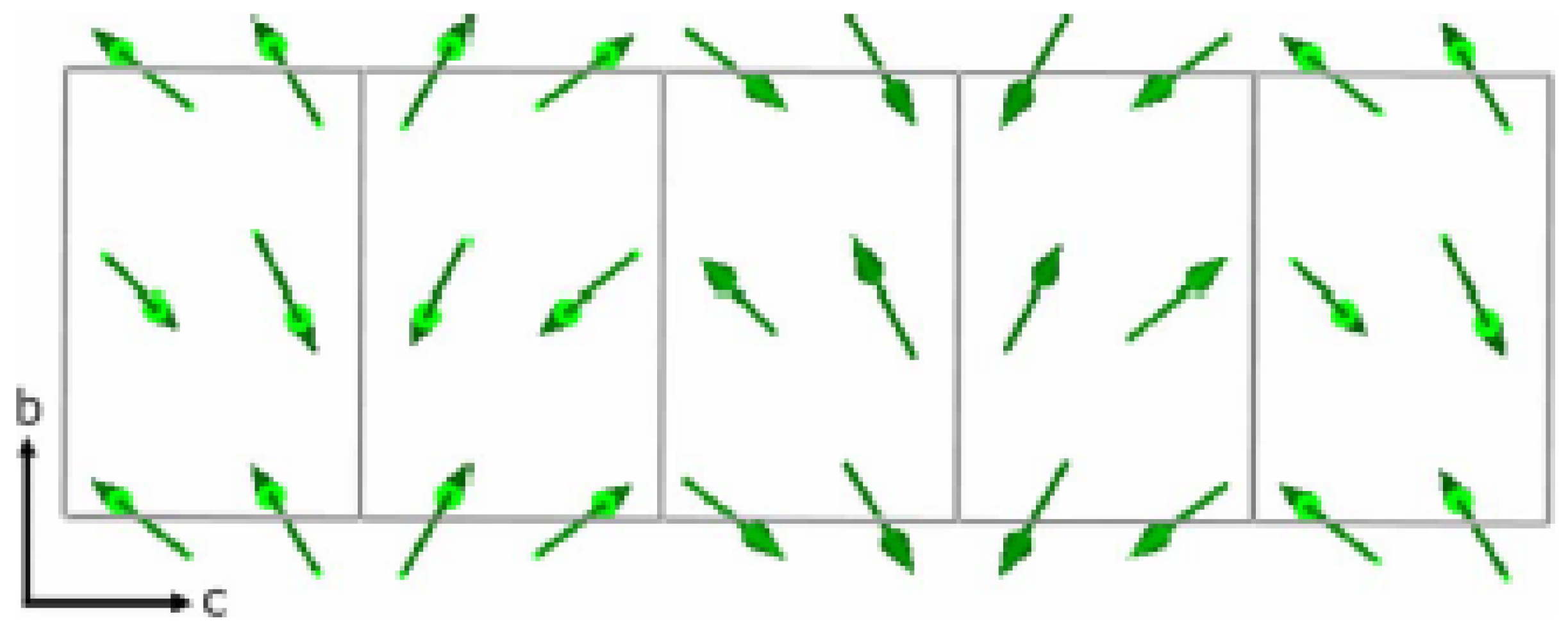
| IR | BV | Atom | BV Components | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | 12 | 12 | 12 | 0 | 0 | 0 | ||
| 1 | 6 | −6 | 0 | 0 | 0 | 0 | ||
| 1 | 3.464 | 3.464 | −6.928 | 0 | 0 | 0 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ratcliff, W. Revealing the Symmetry of Materials through Neutron Diffraction. Symmetry 2022, 14, 1215. https://doi.org/10.3390/sym14061215
Ratcliff W. Revealing the Symmetry of Materials through Neutron Diffraction. Symmetry. 2022; 14(6):1215. https://doi.org/10.3390/sym14061215
Chicago/Turabian StyleRatcliff, William. 2022. "Revealing the Symmetry of Materials through Neutron Diffraction" Symmetry 14, no. 6: 1215. https://doi.org/10.3390/sym14061215
APA StyleRatcliff, W. (2022). Revealing the Symmetry of Materials through Neutron Diffraction. Symmetry, 14(6), 1215. https://doi.org/10.3390/sym14061215






