Dynamic Response of Vibratory Piling Machines for Ground Foundations

Abstract

Vibrating technological equipment for the introduction of piles and columns into the ground of construction foundations (named vibratory piling machines) is crucial in the process of building stable and resilient foundations for civil engineering, hydrotechnical construction, special construction (e.g., military constructions), bridges, roads and industrial platforms. During the works carried out by the construction companies in various geographical areas of Romania, particularities of the dynamic technological regimes influenced by the nature of the land were identified at the deep introduction of the construction elements in the form of piles or circular (tubular) columns. The results of applied research, rheological modeling and optimization of vibrating equipment, highlight the need for an analytical approach that takes into account the parametric variations of the elastic and damping characteristics of some categories of soils on the depth of piles or foundation columns. In this context, the paper presents the calculation model with the dynamic response for the vibrating equipment of insertion with disturbing forces of 200–1250 kN for piles or columns with lengths of 10–30 m. The novelty of the research study consists in the linear rheological model, which was adopted in the form of a Maxwell–Voigt–Kelvin schematic of the type (E-V)–(E|V), with a discrete variation in four values for stiffness and damping of the soil, as the piles or columns vibrate and advance in the ground foundation. Practical experience of the authors in the field of using vibrogenerators for the introduction of piles in various types of ground foundations led to the adoption of the rheological model with variable damping coefficients depending on the depth of penetration into the soil. The curves of the dissipated power confirm the experimental data obtained in situ, in accordance with the rheological indoor tests of the different types of soil foundations.

1. Introduction

The capability level of the vibrating machines in this specialized class is evaluated according to the size of the functional parameters in the working mode, namely: vibration amplitudes, transmitted force to the soil (ground foundation), dynamic insulation in the machine and dissipated energy [1,2].

In Romania, vibrating machines with dynamic action are used, whose operating regime is correlated with the nature of the soil [3,4]. Thus, several distinct classes of foundation soils have been identified, consisting mainly of the following categories: loess-sensitive soils, contractile soils (with volume variations), fine and uniform sands with the possibility of liquefaction, clayey and dusty soils and sandy clay soils [5,6].

An equivalent linear calculation model, which takes into account a complex rheological behavior, is adopted in this paper. Also, for theoretical reasons, numerical analysis is performed using a linear visco-elastic approach [7,8].

According to the Federal Highway Administration (FHWA), the relationships between maximum soil particle velocity and pile peak distance are based on the nominal energy of the vibrogenerator for two types of foundation soil: Class II (soils with standard penetration test values 5–15 strokes per 0.3 m) and Class III (hard soils with standard penetration test values of 15–50 strokes per 0.3 m). In general, there is an increase in the kinematic parameters of the cell (displacements, speeds, accelerations) as the rigidity of the ground and the energy of the vibrogenerator increase [9]. The classification of piles can be made according to the method of installation, through which piles are usually classified into two categories: non-displaced piles and displaced piles. The first category of piles requires the prior removal of the ground, while the trained prefabricated piles (the second category) are characterized by the appearance of ground movements to allow the piles to enter the ground, without the need to remove the ground beforehand [10].

The interaction between piles and foundation soils was studied for the past five decades [11]. The scientific and technical literature presents various models of the interaction between the foundation soil and the prefabricated piles introduced by shocks and/or vibrations; analysis and calculation models are of three types: empirical/experimental models, theoretical models and engineering models [12,13,14,15].

The dynamic interaction between the pile and the foundation soil was not sufficiently studied due to the complexity of the vibrogenerator–pile–foundation soil model [16]. The studied dynamic models of the interactions of vibrogenerator–pile–foundation soil are theoretical models [17,18,19], numerical simulations models [20] and experimental models (in situ or indoor tests) [21,22,23]. Numerical simulation and, especially, analytical modeling of the movement of vibrating piles in saturated soil is quite difficult [24]. Although open-ended piles (circular or rectangular tube type) are common in engineering practice, studies focused mainly on closed-ended piles [25].

Experimental tests are often used to establish numerical simulation models and to validate theoretical models. Some experimental data on the vibration introduction of prefabricated piles into the foundation field are available in the literature. The experimental tests, in the laboratory and in situ, took into account the two types of piles: experiments with closed-ended piles and experiments with open-ended piles [26,27].

For vibratory machines in this technological class, the Maxwell–Voigt–Kelvin rheological model, denoted (E-V)–(E|V), with dynamic force generators (vibrating motors), was realized, so that between the physical–mechanical and terrain-modeling parameters, the rigidity k and the damping coefficient c, the amplitude of the steady-state forced vibrations A and the transmitted force to the ground Q could be determined by an analytical calculation relation [28,29,30].

In this way, the calculation relations and the families of curves were determined, which eloquently reflect the variations of the dynamic parameters for the technological regimes defined by the pulsation ω and the amplitude A of the technological vibrations [31,32].

This paper is organized as follows: Section 2 presents a linear dynamic model of the vibratory piling machine in interaction with the soil foundation; the dynamic analysis, in steady-state forced vibration condition of this model, consists in determination of the amplitude displacements, dynamic forces transmitted to the ground, dynamic transmissibility coefficient and dissipated energy per harmonic cycle function of damping characteristic of the soil and the functional parameters of the vibratory piling machine. Section 3 presents a case study of a vibratory piling machine. It shows graphs of the variation in the dynamic and energetic parameters of the vibrogenerator–pile–foundation soil system considered as an (E-V)–(E|V) rheological model, function of damping ratio $\zeta$ and the relative pulsation $\mathsf{\Omega }$. The plotted parameters of the systems are the amplitudes of the displacements of the mobile mass of the vibrating machine, the amplitudes of the displacements and of the deflections of the components of the rheological model, the amplitudes of the dynamic transmitted force to the ground, the dynamic transmissibility coefficient and the dissipated energy per cycle. Section 4 emphasizes the importance of technological parameter $\mathsf{\Omega }$ on the analysis of the dynamic characteristics of the vibrogenerator–pile–foundation soil system. The final concluding remarks are presented in Section 5.

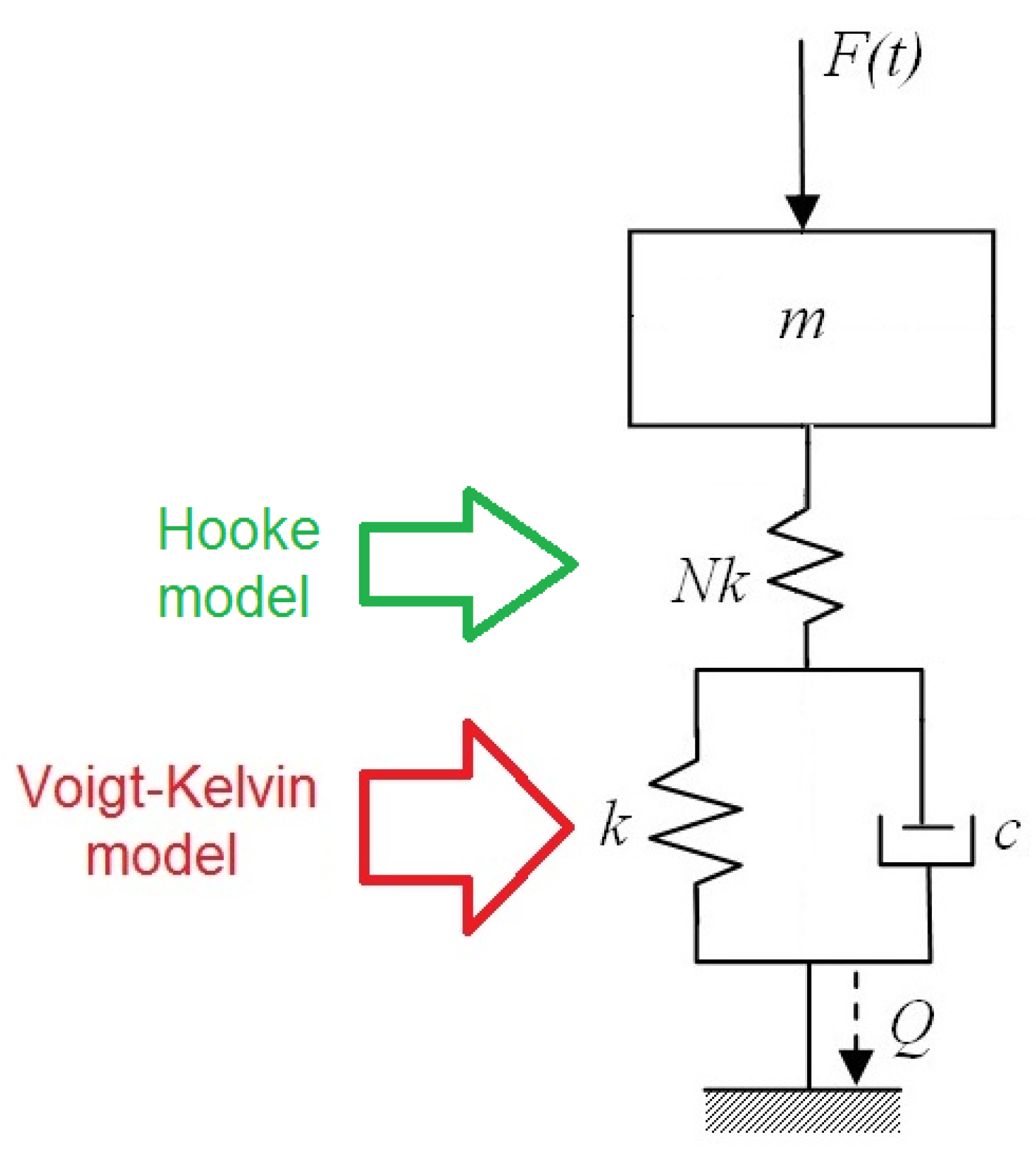
2. Linear Dynamic Model of the Vibratory Piling Machine

The linear dynamical system with unidirectional vertical motion is shown in Figure 1 [32,33]. The serial structure of the system consists of mass m, the rheological Maxwell model type (E-V) and the rheological model Voigt–Kelvin type (E|V). The dynamic model is disturbed by the vertical harmonic force $F\left(t\right)=F_0\sin \omega t$, the coordinates being the vertical displacements: $x=x\left(t\right)$ of the mass m, $y=y\left(t\right)$ in the Voigt–Kelvin model and $z=z\left(t\right)$ of the point of connection of the elements of the Maxwell model.

.

The rheological characteristics (stiffness, damping) of the linear models are $\left(k, c\right)$ for the Voigt–Kelvin (E|V) model and $\left(Nk, Sc\right)$ for the Maxwell (E-V) model, where S and N are positive multiplier numbers and the relation between the two is $S=\lambda N$, where λ is also a positive multiplier number.

2.1. Dynamic Response of the Linear Rheological System

For the dynamic system shown in Figure 1, the governing equations (differential equations of motion), expressed in complex numbers, can be written as follows [34,35],

$$\{\begin{array}{c}m\ddot{\tilde{x}}+cS\left(\dot{\tilde{x}}-\dot{\tilde{z}}\right)+k\tilde{x}=F_0\sin \omega t\\ k\tilde{y}+c\dot{\tilde{y}}-kN\left(\tilde{z}-\tilde{y}\right)=0\\ kN\left(\tilde{z}-\tilde{y}\right)=cS\left(\dot{\tilde{x}}-\dot{\tilde{z}}\right)\end{array}$$

(1)

The steady-state forced vibration responses, in terms of displacements, velocities and accelerations, are

$$\tilde{x}=\tilde{X}{e}^{j\omega t} \stackrel{\frac{d}{dt}}{\to } \dot{\tilde{x}}=j\omega \tilde{X}{e}^{j\omega t} \stackrel{\frac{d}{dt}}{\to } \ddot{\tilde{x}}=-{\omega }^2\tilde{X}{e}^{j\omega t}$$

$$\tilde{y}=\tilde{Y}{e}^{j\omega t} \stackrel{\frac{d}{dt}}{\to } \dot{\tilde{y}}=j\omega \tilde{Y}{e}^{j\omega t} \stackrel{\frac{d}{dt}}{\to } \ddot{\tilde{y}}=-{\omega }^2\tilde{Y}{e}^{j\omega t}$$

$$\tilde{z}=\tilde{Z}{e}^{j\omega t} \stackrel{\frac{d}{dt}}{\to } \dot{\tilde{z}}=j\omega \tilde{Z}{e}^{j\omega t} \stackrel{\frac{d}{dt}}{\to } \ddot{\tilde{z}}=-{\omega }^2\tilde{Z}{e}^{j\omega t} ,$$

which, replaced in (1), lead to the linear algebraic system in complex quantities $\tilde{X}, \tilde{Y}, \tilde{Z}$ in the form

$$\{\begin{array}{c}\left(-m{\omega }^2+jc\omega S\right)\tilde{X}-jc\omega S\tilde{Z}=F_0\\ \left[k\left(1+N\right)+jc\omega \right]\tilde{Y}-kN\tilde{Z}=0\\ -jc\omega S\tilde{X}-kN\tilde{Y}+\left[kN+jc\omega S\right]\tilde{Z}=0\end{array}$$

(2)

The complex determinant $\tilde{D}$ of the linear algebraic system matrix is obtained as follows,

$$\tilde{D}=det\left[\begin{array}{ccc}-m{\omega }^2+jc\omega S& 0& -jc\omega S\\ 0& k\left(1+N\right)+jc\omega & -kN\\ -jc\omega S& -kN& kN+jc\omega S\end{array}\right] ,$$

(3)

from where

$$\begin{gathered} \tilde{D}=\left(-m{\omega }^2+jc\omega S\right)\left\{\left[k\left(1+N\right)+jc\omega \right]\left[kN+jc\omega S\right]-k^2{N}^2\right\} \\ -jc\omega S\left\{jc\omega S\left[k\left(1+N\right)+jc\omega \right]\right\} \end{gathered}$$

(3a)

Using the notations $\alpha =-m{\omega }^2$, $\beta =c\omega$, $\delta =kN$, $\gamma =k\left(1+N\right)$ and $S=\lambda N$, the expression of the determinant $\tilde{D}$ becomes

$$\tilde{D}=\left[\alpha \delta \left(\gamma -\delta \right)-{\beta }^{2}S\left(\alpha +\delta \right)\right]+j\beta \left[\alpha \left(\gamma S+\delta \right)+\delta S\left(\gamma -\delta \right)\right]$$

(4)

Returning to the structural parameters $\left(m,c,k,\omega \right)$ of the system, the determinant $\tilde{D}$ can be written function of the variables $\left(c,\omega \right)$ as follows,

$$\begin{gathered} \tilde{D}\left(c,\omega \right)=\left[-m{\omega }^2{k}^{2}N+c^2{\omega }^2\lambda Nm{\omega }^2-c^2{\omega }^{2}k\lambda N^2\right] \\ +jc\omega \left[-m{\omega }^{2}k\left(N+\lambda N+\lambda N^2\right)+k^2\lambda N^2\right] \end{gathered}$$

(5)

As a function of the dimensionless parameters of the system, $\zeta =\frac{c}{2\sqrt{mk}}$—damping ratio and $\mathsf{\Omega }=\frac{\omega }{{\omega }_n}$ —relative pulsation, the determinant $\tilde{D}$ can be written

$$\tilde{D}\left(\zeta , \mathsf{\Omega }\right)=N{k}^3\left[-{\mathsf{\Omega }}^2-{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda N+{\mathsf{\Omega }}^2{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda \right]+j\left(2\zeta \mathsf{\Omega }\right)N{k}^3\left[\lambda N-{\mathsf{\Omega }}^2\left(1+\mathsf{\lambda }+\mathsf{\lambda }\mathrm{N}\right)\right]$$

(6)

or

$$\tilde{D}\left(\zeta , \mathsf{\Omega }\right)=N{k}^3\left[C+jD\right]$$

(6a)

The complex determinant ${\tilde{D}}_X$ of unknown variable $\tilde{X}$ can be calculated as follows,

$${\tilde{D}}_X=det\left[\begin{array}{ccc}{F}_0& 0& -jc\omega S\\ 0& k\left(1+N\right)+jc\omega & -kN\\ 0& -kN& kN+jc\omega S\end{array}\right],$$

(7)

or

$${\tilde{D}}_X\left(c,\omega \right)=F_0\left[k^{2}N-c^2{\omega }^2\lambda N\right]+jc\omega kN{F}_0\left[1+\lambda +\lambda N\right]$$

(7a)

As a function of the dimensionless parameters $\left(\zeta , \mathsf{\Omega }\right)$, the determinant ${\tilde{D}}_X$ can be written as follows,

$${\tilde{D}}_X\left(\zeta , \mathsf{\Omega }\right)=F_0{k}^{2}N\{[1-{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda ]+j[\left(2\zeta \mathsf{\Omega }\right)\left(1+\lambda +\lambda N\right)]\},$$

(8)

or

$${\tilde{D}}_X\left(\zeta , \mathsf{\Omega }\right)=F_0{k}^{2}N\left[A+jB\right]$$

(8a)

The complex determinant ${\tilde{D}}_Y$ of unknown variable $\tilde{Y}$ can be calculated as

$${\tilde{D}}_Y\left(c,\omega \right)=det\left[\begin{array}{ccc}-m{\omega }^2+jc\omega S& F_0& -jc\omega S\\ 0& 0& -kN\\ -jc\omega S& 0& kN+jc\omega S\end{array}\right]=-j{F}_{0}c\omega k\lambda N^2$$

(9)

Or the function of variables $\left(\zeta , \mathsf{\Omega }\right)$:

$${\tilde{D}}_Y\left(\zeta , \mathsf{\Omega }\right)=-j{F}_0{k}^2\lambda N^2\left(2\zeta \mathsf{\Omega }\right)$$

(10)

With the notation $E=\left(2\zeta \mathsf{\Omega }\right)$, the determinant ${\tilde{D}}_Y$ becomes

$${\tilde{D}}_Y\left(\zeta , \mathsf{\Omega }\right)=F_0{k}^2\lambda N^2\left[-jE\right]$$

(10a)

The complex determinant ${\tilde{D}}_Z$ of unknown variable $\tilde{Z}$ can be calculated as follows,

$${\tilde{D}}_Z=det\left[\begin{array}{ccc}-m{\omega }^2+jc\omega S& 0& F_0\\ 0& k\left(1+N\right)+jc\omega & 0\\ -jc\omega S& -kN& 0\end{array}\right],$$

(11)

from where

$${\tilde{D}}_Z\left(c,\omega \right)=F_{0}c\omega \lambda N\left[-c\omega +jk\left(1+N\right)\right]$$

(11a)

Function of the dimensionless parameters $\left(\zeta , \mathsf{\Omega }\right)$, the determinant ${\tilde{D}}_Z$ can be written

$${\tilde{D}}_Z\left(\zeta , \mathsf{\Omega }\right)=F_0{k}^2\lambda N\left(2\zeta \mathsf{\Omega }\right)\left[-\left(2\zeta \mathsf{\Omega }\right)+j\left(1+N\right)\right]$$

(12)

or, using the notations $a=-2\zeta \mathsf{\Omega }$ and $b=1+N$:

$${\tilde{D}}_Z\left(\zeta , \mathsf{\Omega }\right)=F_0{k}^2\lambda N\left(2\zeta \mathsf{\Omega }\right)\left[a+jb\right]$$

(12a)

2.1.1. Forced Vibration: Amplitude Displacement $x\left(t\right)$ in Steady-State Condition

The harmonic dynamic response in complex displacement $\tilde{X}$ is

$$\tilde{X}=\frac{{\tilde{D}}_X\left(\zeta , \mathsf{\Omega }\right)}{\tilde{D}\left(\zeta , \mathsf{\Omega }\right)}=\frac{F_0{k}^{2}N\left[A+jB\right]}{N{k}^3\left[C+jD\right]}=\frac{F_0}{k}\frac{A+jB}{C+jD}$$

(13)

where it uses the notations

$$\{\begin{array}{c}A=1-{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda ; B=\left(2\zeta \mathsf{\Omega }\right)\left(1+\lambda +\lambda N\right)\hfill \\ C=-{\mathsf{\Omega }}^2-{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda N+{\mathsf{\Omega }}^2{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda \hfill \\ D=\left(2\zeta \mathsf{\Omega }\right)\left[\lambda N-{\mathsf{\Omega }}^2\left(1+\lambda +\lambda N\right)\right] \hfill \end{array}$$

(13a)

From Equation (13) the complex displacement $\tilde{X}$ is obtained as follows,

$$\tilde{X}=\frac{F_0}{k}\frac{1}{C^2+D^2}\left[\left(AC+BD\right)+j\left(BC-AD\right)\right]$$

(14)

with the amplitude of steady-state forced vibration $\left|\tilde{X}\right|=X_0$ obtained by

$$X_0=\frac{F_0}{k}\sqrt{\frac{A^2+B^2}{C^2+D^2}}$$

(15)

As a function of the dimensionless parameters $\left(\zeta , \mathsf{\Omega }\right)$, the amplitude $X_0$ can be written as follows,

$$X_0\left(\zeta , \mathsf{\Omega }\right)=\frac{F_0}{k}\sqrt{\frac{{[1-{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda ]}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2{(1+\lambda +\lambda N)}^2}{{[{\mathsf{\Omega }}^2+{(2\zeta \mathsf{\Omega })}^2\lambda N-{\mathsf{\Omega }}^2{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda ]}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2{[\lambda N-{\mathsf{\Omega }}^2\left(1+\lambda +\lambda N\right)]}^2}}$$

(15a)

2.1.2. Forced Vibration: Amplitude Displacement $y\left(t\right)$ in Steady-State Condition

The harmonic dynamic response in complex displacement $\tilde{Y}$ is

$$\tilde{Y}=\frac{{\tilde{D}}_Y\left(\zeta , \mathsf{\Omega }\right)}{\tilde{D}\left(\zeta , \mathsf{\Omega }\right)}=\frac{F_0}{k}\lambda N\frac{-jE}{C+jD}=\frac{F_0}{k}\lambda N\frac{1}{C^2+D^2}\left(DE-jCE\right)$$

(16)

where E, C and D are obtained by Equations (10a) and (13a).

The amplitude of steady-state forced vibration $\left|\tilde{Y}\right|=Y_0$ can be calculated as follows,

$$Y_0=\frac{F_0}{k}\lambda N\frac{E}{\sqrt{C^2+D^2}}$$

(17)

Using the expressions from (10a) and (13a) for the terms E, C and D, the amplitude $Y_0$ can be written

$$Y_0\left(\zeta , \mathsf{\Omega }\right)=\frac{F_0}{k}\lambda N\frac{2\zeta \mathsf{\Omega }}{\sqrt{C^2+D^2}} ,$$

(18)

or

$$Y_0\left(\zeta , \mathsf{\Omega }\right)=\frac{F_0}{k}\lambda N\frac{2\zeta \mathsf{\Omega }}{\sqrt{{[{\mathsf{\Omega }}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda N-{\mathsf{\Omega }}^2{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda ]}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2{[\lambda N-{\mathsf{\Omega }}^2\left(1+\lambda +\lambda N\right)]}^2}}$$

(18a)

2.1.3. Forced Vibration: Amplitude Displacement $z\left(t\right)$ in Steady-State Condition

Using the notations from Equations (12a) and (13a), the harmonic dynamic response in complex displacement $\tilde{Z}$ is

$$\tilde{Z}=\frac{{\tilde{D}}_Z\left(\zeta , \mathsf{\Omega }\right)}{\tilde{D}\left(\zeta , \mathsf{\Omega }\right)}=\frac{F_0}{k}\lambda \left(2\zeta \mathsf{\Omega }\right)\frac{a+jb}{C+jD} ,$$

(19)

or

$$\tilde{Z}=\frac{F_0}{k}\lambda \left(2\zeta \mathsf{\Omega }\right)\frac{1}{C^2+D^2}\left[\left(aC+bD\right)+j\left(bC-aD\right)\right]$$

(20)

The amplitude of steady-state forced vibration $\left|\tilde{Z}\right|=Z_0$ can be calculated as follows,

$$Z_0=\frac{F_0}{k}\lambda \left(2\zeta \mathsf{\Omega }\right)\sqrt{\frac{a^2+b^2}{C^2+D^2}} ,$$

(21)

from where

$$Z_0=\frac{F_0}{k}\lambda \left(2\zeta \mathsf{\Omega }\right)\sqrt{\frac{{\left(2\zeta \mathsf{\Omega }\right)}^2+{\left(1+N\right)}^2}{C^2+D^2}} ,$$

(22)

or

$$Z_0=\frac{F_0}{k}\lambda \left(2\zeta \mathsf{\Omega }\right)\sqrt{\frac{{\left(2\zeta \mathsf{\Omega }\right)}^2+{\left(1+N\right)}^2}{{[{\mathsf{\Omega }}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda N-{\mathsf{\Omega }}^2{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda ]}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2{[\lambda N-{\mathsf{\Omega }}^2\left(1+\lambda +\lambda N\right)]}^2}}$$

(22a)

2.2. Dynamic Force Transmitted to the Ground Foundation

The dynamic force $\tilde{Q}$ is transmitted to the ground foundation through the spring k and the damper c in the Voigt–Kelvin rheological model, thus, the force $\tilde{Q}$ can be written as a sum of elastic force of the spring and viscous force of the damper

$$\tilde{Q}=k\tilde{y}+c\dot{\tilde{y}}=\left(k+jc\omega \right)\tilde{Y}{e}^{j\omega t} ,$$

(23)

or, using displacement $\tilde{Y}$, obtained by (16), and its derivate

$$\tilde{Q}=\frac{F_0\lambda NE}{C^2+D^2}\left[\left(D-EC\right)+j\left(DE+C\right)\right] ,$$

(24)

where terms E, C and D use the expressions from (10a) and (13a).

The amplitude $\left|\tilde{Q}\right|=Q_0$ of the dynamic force transmitted to the ground foundation is

$$\left|\tilde{Q}\right|=Q_0=F_0\lambda NE\sqrt{\frac{1+E^2}{C^2+D^2}}=F_0\lambda N\left(2\zeta \mathsf{\Omega }\right)\sqrt{\frac{1+{\left(2\zeta \mathsf{\Omega }\right)}^2}{C^2+D^2}} ,$$

(25)

or

$$Q_0\left(\zeta , \mathsf{\Omega }\right)=F_0\lambda N\left(2\zeta \mathsf{\Omega }\right)\sqrt{\frac{1+{\left(2\zeta \mathsf{\Omega }\right)}^2}{{[{\mathsf{\Omega }}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda N-{\mathsf{\Omega }}^2{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda ]}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2{[\lambda N-{\mathsf{\Omega }}^2\left(1+\lambda +\lambda N\right)]}^2}}$$

(26)

2.3. Dynamic Transmissibility Coefficient

The dynamic coefficient of transmissibility of the force $\tilde{Q}=Q_0{e}^{j\left(\omega t+\phi \right)}$ in relation to the harmonic perturbing force $\tilde{F}=F_0{e}^{j\omega t}$ is defined as the ratio between the two amplitudes of the forces, as [36,37]

$$T\left(\zeta , \mathsf{\Omega }\right)=\frac{Q_0\left(\zeta , \mathsf{\Omega }\right)}{F_0}=\lambda N\left(2\zeta \mathsf{\Omega }\right)\sqrt{\frac{1+{\left(2\zeta \mathsf{\Omega }\right)}^2}{C^2+D^2}} ,$$

(27)

where $:$

$$\{\begin{array}{c}C=-{\mathsf{\Omega }}^2-{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda N+{\mathsf{\Omega }}^2{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda \\ D=\left(2\zeta \mathsf{\Omega }\right)\left[\lambda N-{\mathsf{\Omega }}^2\left(1+\lambda +\lambda N\right)\right]\end{array}$$

(28)

2.4. Deflections of the Viscous Dampers in Maxwell–Voigt–Kelvin Model

2.4.1. Deflection of Simple Viscous Damper in Voigt–Kelvin Model

The deflection of the simple viscous damper in the Voigt–Kelvin model (with damping coefficient c) is

$$\tilde{y}=\tilde{Y}{e}^{j\omega t}=Y_0{e}^{j\phi }{e}^{j\omega t}=Y_0{e}^{j\left(\omega t+\phi \right)} ,$$

(29)

where:

$\phi$ is the phase between the displacements $\tilde{y}$ and $\tilde{z}$

$Y_0$ is the amplitude obtained by (18).

2.4.2. Deflection of Viscous Damper in Maxwell Model

The deflection of the viscous damper in the Maxwell model (with damping coefficient cS) is

$$\tilde{u}=\tilde{x}-\tilde{z}=\left(\tilde{X}-\tilde{Z}\right)e^{j\omega t},$$

(30)

where $\tilde{X}$ and $\tilde{Z}$ are obtained by (14) and (20), respectively.

The deflection of the viscous damper in the Maxwell model can be written as

$$\tilde{u}=\tilde{U}{e}^{j\omega t} ,$$

(31)

where:

$$\tilde{U}=\tilde{X}-\tilde{Z}=\frac{F_0}{k}\left[\frac{AC+BD}{C^2+D^2}+j\frac{BC-AD}{C^2+D^2}\right]-\left(2\zeta \mathsf{\Omega }\right)\lambda \frac{F_0}{k}\left[\frac{aC+bD}{C^2+D^2}+j\frac{bC-aD}{C^2+D^2}\right] ,$$

(32)

The deflection $\tilde{U}$ can be written as complex number

$$\tilde{U}=\frac{F_0}{k}\frac{1}{C^2+D^2}\left[G+jH\right] ,$$

(33)

where the expression of the amplitude $\left|\tilde{U}\right|=U_0$ is calculated as follows

$$U_0^2=\frac{F_0^2}{k^2}\frac{1}{{\left[C^2+D^2\right]}^2}\left[G^2+H^2\right] ,$$

(34)

or

$$U_0=\frac{F_0}{k}\frac{\sqrt{G^2+H^2}}{C^2+D^2} ,$$

(35)

with the real constants:

$$\{\begin{array}{c}G=\left(AC+BD\right)+\left(2\zeta \mathsf{\Omega }\right)\lambda \left(aC+bD\right)\\ H=\left(BC-AD\right)+\left(2\zeta \mathsf{\Omega }\right)\lambda \left(bC-aD\right)\end{array}$$

(36)

By substituting the expressions for the constants G and H in Equation (34), the square of the amplitude $U_0$ of the deflection of the viscous damper in the Maxwell model is obtained as

$$U_0^2=\frac{F_0^2}{k^2}\frac{\left(C^2+D^2\right)[\left(A^2+B^2\right)+{\left(2\zeta \mathsf{\Omega }\right)}^2{\lambda }^2\left(a^2+b^2\right)+2\left(2\zeta \mathsf{\Omega }\right)\lambda \left(aA+bB\right)]}{{\left(C^2+D^2\right)}^2} ,$$

(37)

or

$$U_0^2=\frac{F_0^2}{k^2}L ,$$

(38)

where

$$L=\frac{1}{C^2+D^2}[\left(A^2+B^2\right)+{\left(2\zeta \mathsf{\Omega }\right)}^2{\lambda }^2\left(a^2+b^2\right)+2\left(2\zeta \mathsf{\Omega }\right)\lambda \left(aA+bB\right)]$$

(38a)

The amplitude $U_0$ result is

$$U_0=\frac{F_0}{k}\sqrt{L}=\frac{F_0}{k}\sqrt{\frac{\left(A^2+B^2\right)+{\left(2\zeta \mathsf{\Omega }\right)}^2{\lambda }^2\left(a^2+b^2\right)+2\left(2\zeta \mathsf{\Omega }\right)\lambda \left(aA+bB\right)}{C^2+D^2}} ,$$

(39)

where $a=-2\zeta \mathsf{\Omega }$ and $b=1+N$ and the real constants A, B, C, D are obtained by (13a).

2.5. Dissipated Energy in the Viscous Dampers in Maxwell–Voigt–Kelvin Model

The dissipated energy per cycle in the viscous damper in the Voigt–Kelvin model (with damping coefficient c) is

$$W_d^{V-K}=\pi c\omega Y_0^2 ,$$

or, taking into consideration that $c\omega =\left(2\zeta \mathsf{\Omega }\right)k$ and the expression of the amplitude $Y_0$ obtained by (18)

$$W_d^{V-K}=\pi \frac{F_0^2}{k}{\lambda }^2{N}^2\frac{{\left(2\zeta \mathsf{\Omega }\right)}^3}{C^2+D^2}$$

The dissipated energy per cycle in the viscous damper in the Maxwell model (with damping coefficient cS = cλN) is

$$W_d^M=\pi \left(c\lambda N\right)\omega U_0^2 ,$$

or, taking into consideration the square expression of the amplitude $U_0$ obtained by (18)

$$W_d^M=\pi \frac{F_0^2}{k}\left(2\zeta \mathsf{\Omega }\right)\lambda NL$$

The total dissipated energy per cycle is the sum of dissipated energies in each type of viscous damper

$$W_d=W_d^{V-K}+W_d^M ,$$

or

$$W_d\left(\zeta ,\mathsf{\Omega }\right)=\pi \frac{F_0^2}{k}\left[{\lambda }^2{N}^2\frac{{\left(2\zeta \mathsf{\Omega }\right)}^3}{C^2+D^2}+\lambda N\left(2\zeta \mathsf{\Omega }\right)L\right] ,$$

(40)

where the real constants C, D and L are obtained by (13a) and (38a).

3. Dynamic Parameters Analysis of a Vibratory Piling Machine: Case Study

The analysis of the dynamic parameters was performed for a calculus model of a vibratory piling machine with the following inertial and rheological characteristics [33]:

• the mobile mass of the equipment (incl. pile mass) $m={10}^4 \mathrm{kg}$

• two cases of perturbing force:
  (1) harmonic force $F\left(t\right)=F_0\sin \omega t$
  (2) harmonic inertial force $F\left(t\right)=\left(m_{0}r{\omega }^2\right)\sin \omega t$;

• the amplitude of harmonic perturbing force (piling force) $F_0=1250 \mathrm{kN}$;

• the static moment of the dynamic unbalanced masses (for harmonic inertial force) $m_{0}r=5 \mathrm{kg} \mathrm{m}$;

• discrete variable stiffness $k=\left(1÷5\right)\times {10}^{5 }\mathrm{kN}/\mathrm{m}$;

• discrete variable viscous damping $c=\left(2÷15\right)\times {10}^{2 }\mathrm{kNs}/\mathrm{m}$;

• discrete multiplier numbers $N=1÷10$ and $S=1÷10$;

• perturbing force pulsation (steady-state regime) $\omega =\left(200÷500\right) \mathrm{rad}/\mathrm{s}$;

• damping ratio of the ground foundation $\zeta =0.15÷0.32$.

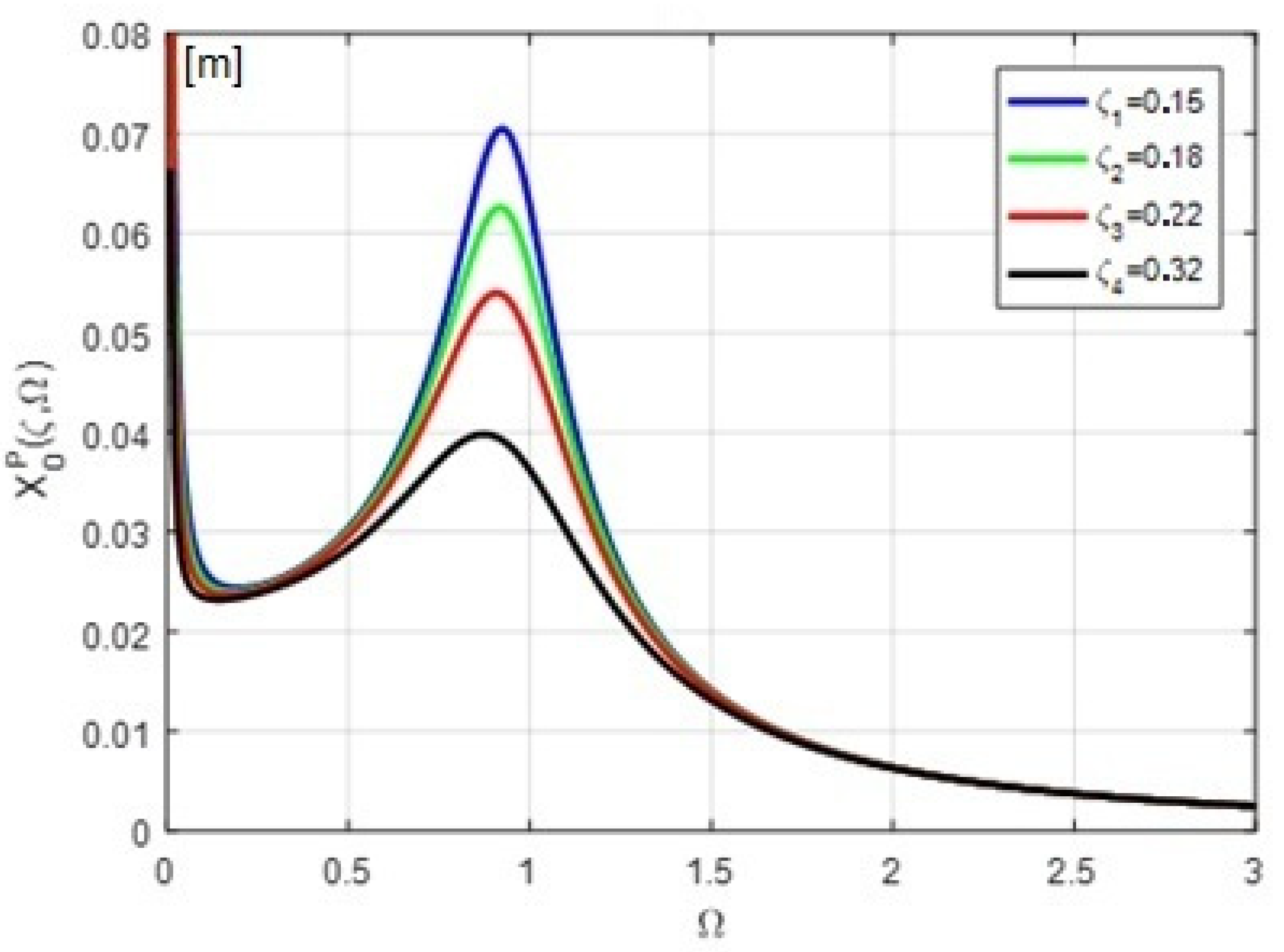
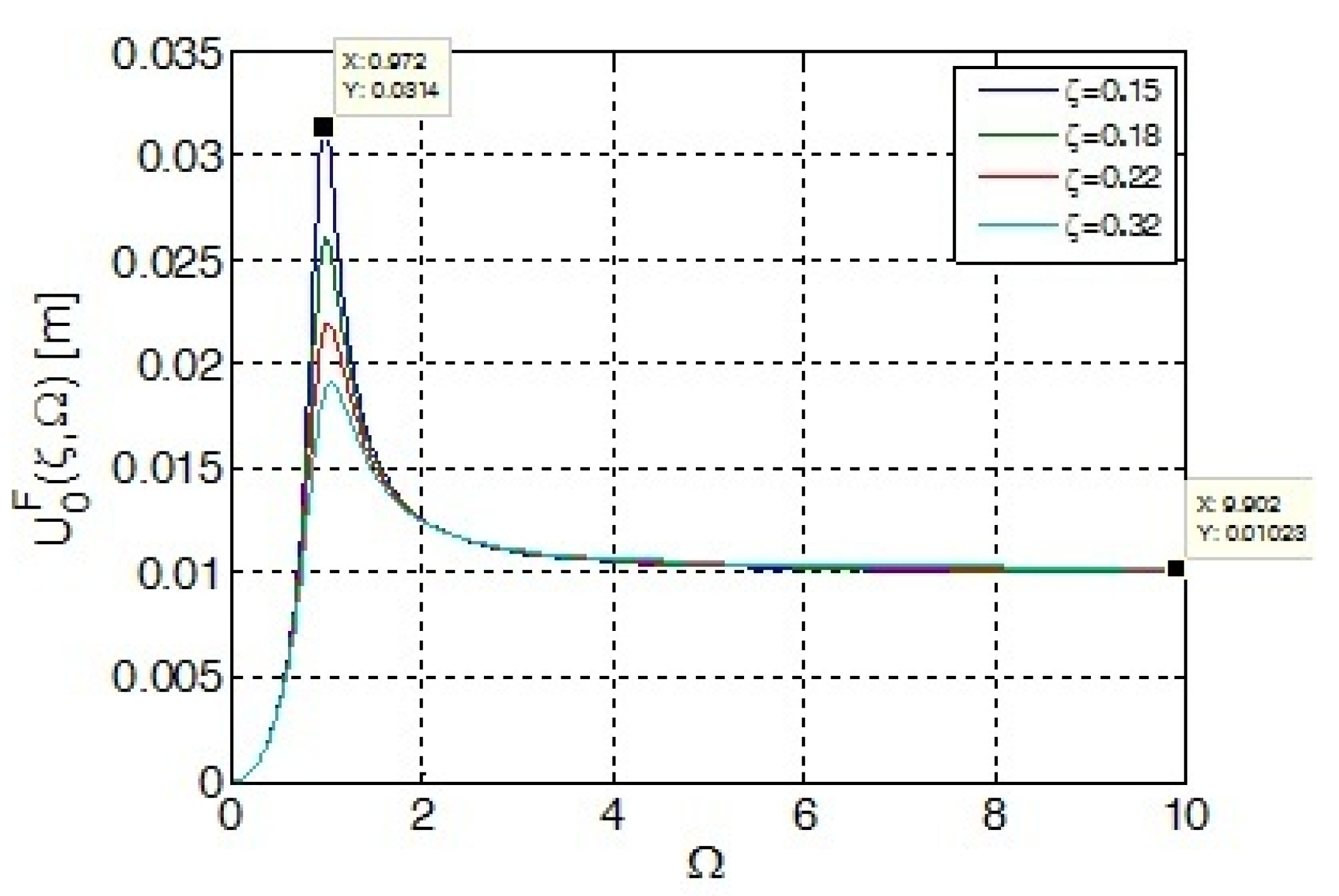
3.1. Amplitude of Steady-State Forced Vibration of Mobile Mass of the Equipment

Figure 2 shows the variation in steady-state vibration amplitudes of the mass m function of relative pulsation $\mathrm{\Omega }$, at four discrete/different values of damping ratio ζ, in the case of harmonic perturbing force $F\left(t\right)=F_0\sin \left(\omega t\right)$ with constant amplitude $F_0=1250 \mathrm{kN}$ and multiplier numbers $N=10$, $S=10$ for the Maxwell model. The curves of the amplitude $X_0\left(\zeta ,\mathsf{\Omega }\right)$ were plotted using Equation (15a).

Figure 3 shows the variation in steady-state vibration amplitudes of the mass m function of relative pulsation $\mathsf{\Omega }$, at four discrete/different values of damping ratio ζ, in the case of inertial harmonic perturbing force $F\left(t\right)=\left(m_{0}r{\omega }^2\right)\sin \left(\omega t\right)=\frac{m_{0}r}{m}k{\mathsf{\Omega }}^2\sin \left(\omega t\right)$ and multiplier numbers $N=10$, $S=10$ for the Maxwell model. The curves of the amplitude $X_0\left(\zeta ,\mathsf{\Omega }\right)$ were plotted using Equation (15a), with $\frac{F_0}{k}=\frac{m_{0}r}{m}{\mathsf{\Omega }}^2$.

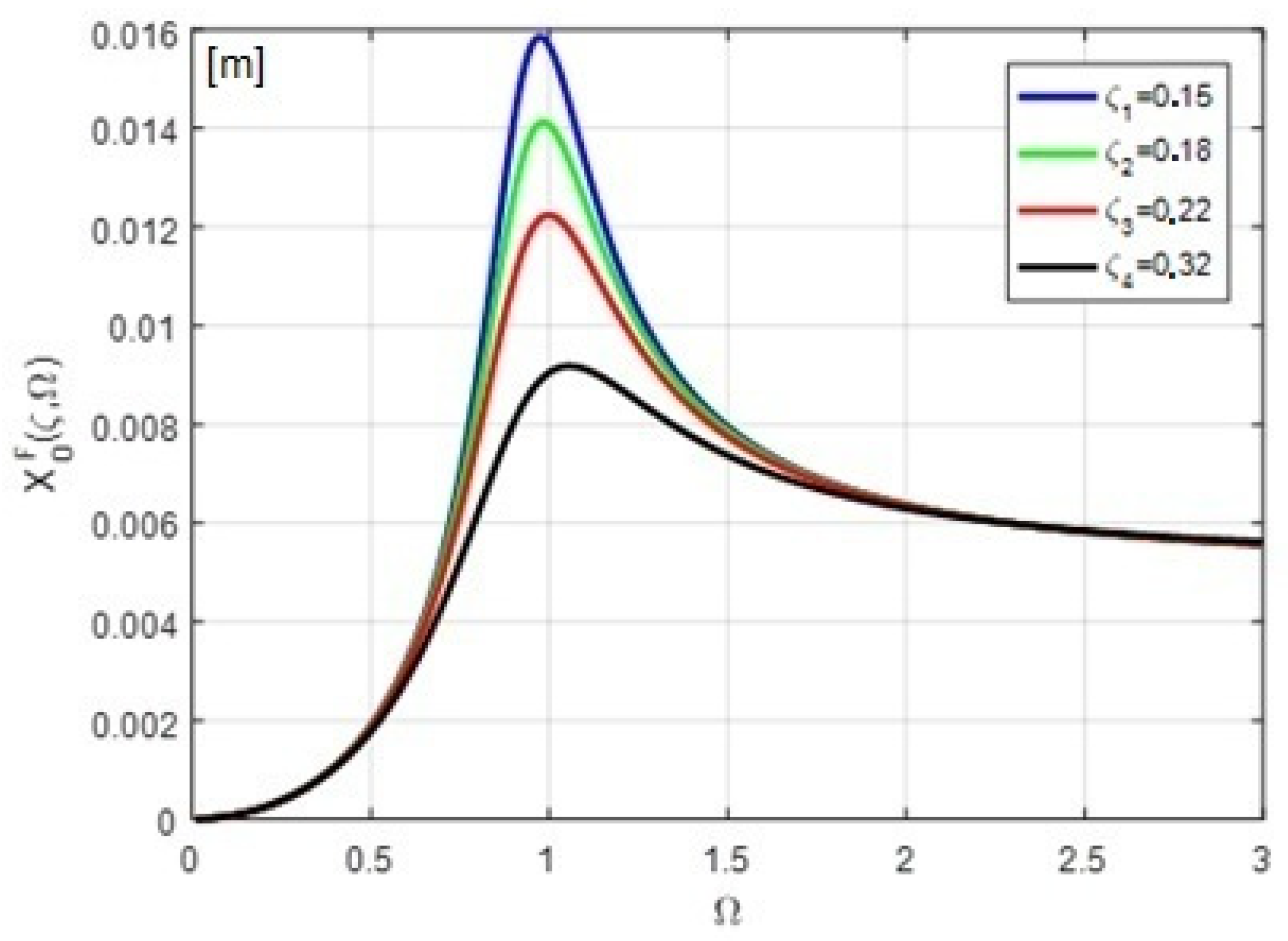
3.2. Amplitude of the Harmonic Deflection in Voigt–Kelvin Model

Figure 4 shows the variation in harmonic deflection in the Voigt–Kelvin model function of relative pulsation $\mathsf{\Omega }$, at four discrete/different values of damping ratio ζ, in the case of harmonic perturbing force $F\left(t\right)=F_0\sin \left(\omega t\right)$ with constant amplitude $F_0=1250 \mathrm{kN}$ and multiplier numbers $N=10$, $S=10$ for the Maxwell model. The curves of the deflection amplitude $Y_0\left(\zeta ,\mathsf{\Omega }\right)$ were plotted using Equation (18a).

Figure 5 shows the variation in harmonic deflection of the Voigt–Kelvin model function of relative pulsation $\mathsf{\Omega }$, at four discrete/different values of damping ratio ζ, in the case of inertial harmonic perturbing force $F\left(t\right)=\left(m_{0}r{\omega }^2\right)\sin \left(\omega t\right)=\frac{m_{0}r}{m}k{\mathsf{\Omega }}^2\sin \left(\omega t\right)$ and multiplier numbers $N=10$, $S=10$ for the Maxwell model. The curves of the deflection amplitude $Y_0\left(\zeta ,\mathsf{\Omega }\right)$ were plotted using Equation (18a), with $\frac{F_0}{k}=\frac{m_{0}r}{m}{\mathsf{\Omega }}^2$.

3.3. Amplitude of the Harmonic Variation in the Displacement in Maxwell Model

Figure 6 shows the variation in harmonic displacement of the connection point CP in the Maxwell model, function of relative pulsation $\mathsf{\Omega }$, at four discrete/different values of damping ratio ζ, in the case of harmonic perturbing force $F\left(t\right)=F_0\sin \left(\omega t\right)$ with constant amplitude $F_0=1250\mathrm{kN}$ and multiplier numbers $N=10$, $S=10$. The curves of the displacement amplitude $Z_0\left(\zeta ,\mathsf{\Omega }\right)$ were plotted using Equation (22a).

Figure 7 shows the variation in harmonic displacement of the connection point CP in the Maxwell model, function of relative pulsation $\mathsf{\Omega }$, at four discrete/different values of damping ratio ζ, in the case of inertial harmonic perturbing force $F\left(t\right)=\left(m_{0}r{\omega }^2\right)\sin \left(\omega t\right)=\frac{m_{0}r}{m}k{\mathsf{\Omega }}^2\sin \left(\omega t\right)$ and multiplier numbers $N=10$, $S=10$. The curves of the displacement amplitude $Z_0\left(\zeta ,\mathsf{\Omega }\right)$ were plotted using Equation (22a), with $\frac{F_0}{k}=\frac{m_{0}r}{m}{\mathsf{\Omega }}^2$.

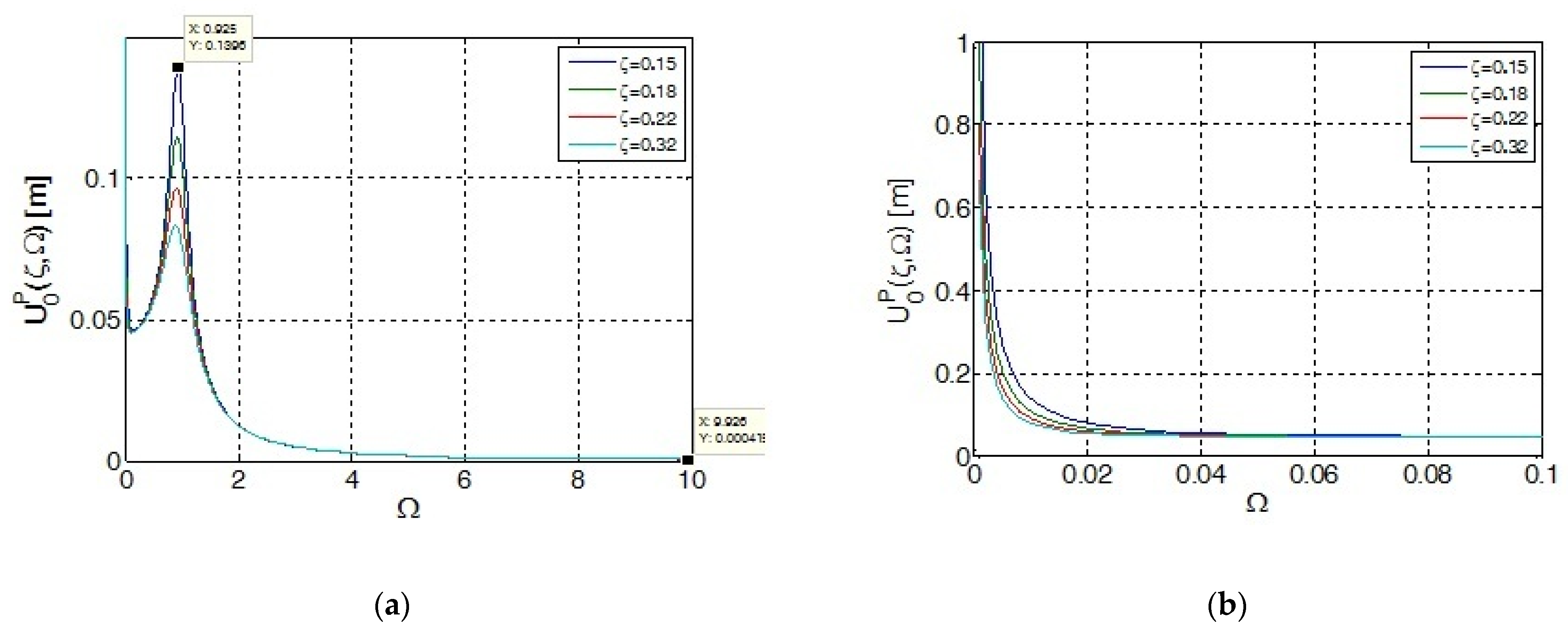
3.4. Dynamic Coefficient of Transmissibility

Figure 8 shows the variation in the coefficient of transmissibility T function of relative pulsation $\mathsf{\Omega }$, at four discrete/different values of damping ratio ζ, in the case of harmonic perturbing force $F\left(t\right)=F_0\sin \left(\omega t\right)$ with constant amplitude $F_0=1250 \mathrm{kN}$ and multiplier numbers $N=10$, $S=10$ for the Maxwell model. The curves of the coefficient of transmissibility $T\left(\zeta ,\mathsf{\Omega }\right)$ were plotted using Equation (27).

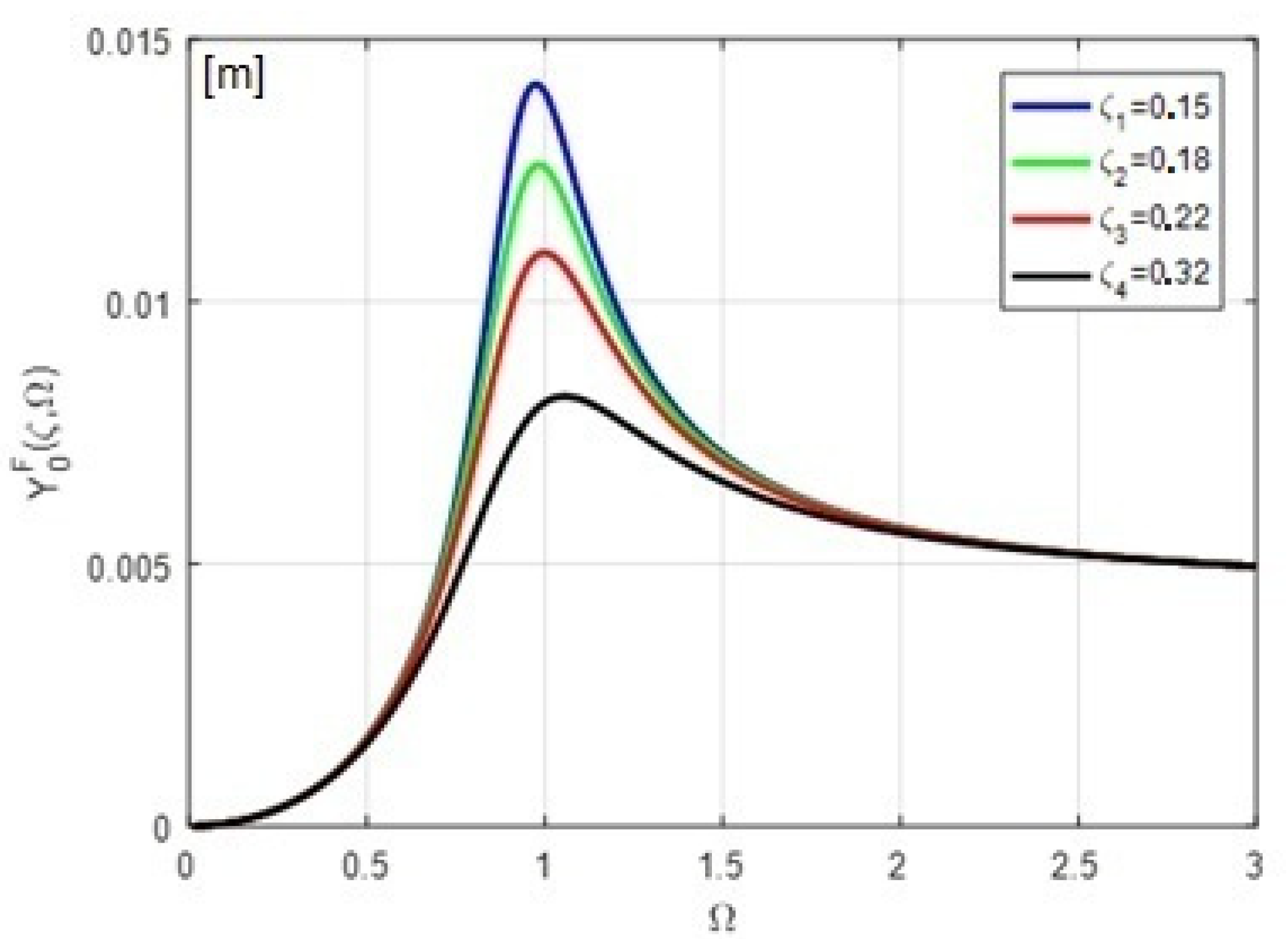
3.5. Amplitude of the Harmonic Deflection in Maxwell Model

Figure 9a,b show the variation in harmonic deflection in the Maxwell model function of relative pulsation $\mathsf{\Omega }$, at four discrete/different values of damping ratio ζ, in the case of harmonic perturbing force $F\left(t\right)=F_0\sin \left(\omega t\right)$ with constant amplitude $F_0=1250 \mathrm{kN}$ and multiplier numbers $N=10$, $S=10$. The curves of the deflection amplitude $U_0\left(\zeta ,\mathsf{\Omega }\right)$ were plotted using Equation (39).

Figure 10 shows the variation in harmonic deflection in the Maxwell model function of relative pulsation $\mathsf{\Omega }$, at four discrete/different values of damping ratio ζ, in the case of harmonic inertial force $F\left(t\right)=\left(m_{0}r{\omega }^2\right)\sin \left(\omega t\right)=\frac{m_{0}r}{m}k{\mathsf{\Omega }}^2\sin \left(\omega t\right)$ and multiplier numbers $N=10$, $S=10$. The curves of the deflection amplitude $U_0\left(\zeta ,\mathsf{\Omega }\right)$ were plotted using Equation (39), with $\frac{F_0}{k}=\frac{m_{0}r}{m}{\mathsf{\Omega }}^2$.

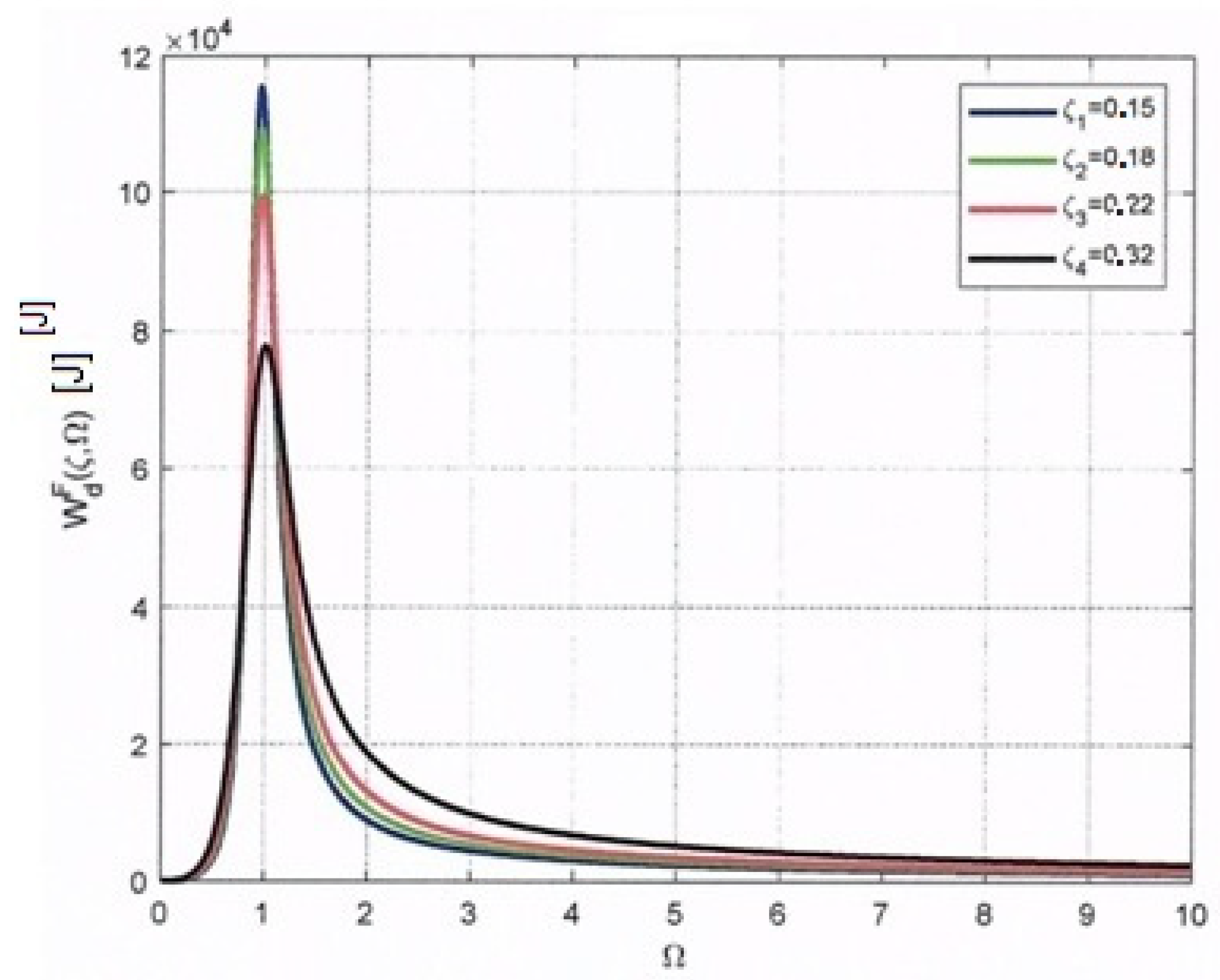
3.6. Dissipated Energy in the Viscous Dampers of Maxwell–Voigt–Kelvin Model

Figure 11 shows the variation in the total dissipated energy per cycle in the dampers of the Maxwell–Voigt–Kelvin model coefficient function of relative pulsation $\mathsf{\Omega }$, at four discrete/different values of damping ratio ζ, in the case of harmonic perturbing force $F\left(t\right)=F_0\sin \left(\omega t\right)$ with constant amplitude $F_0=1250\mathrm{kN}$ and multiplier numbers $N=10$, $S=10$. The curves of the dissipated energy per cycle $W_d\left(\zeta ,\mathsf{\Omega }\right)$ were plotted using Equation (40).

Figure 12 shows the variation in the total dissipated energy per cycle in the dampers of the Maxwell–Voigt–Kelvin model coefficient of relative pulsation $\mathsf{\Omega }$, at four discrete/different values of damping ratio ζ, in the case of inertial harmonic perturbing force $F\left(t\right)=\left(m_{0}r{\omega }^2\right)\sin \left(\omega t\right)=\frac{m_{0}r}{m}k{\mathsf{\Omega }}^2\sin \left(\omega t\right)$ and multiplier numbers $N=10$, $S=10$. The curves of the dissipated energy per cycle $W_d\left(\zeta ,\mathsf{\Omega }\right)$ were plotted using Equation (40), with $\frac{F_0}{k}=\frac{m_{0}r}{m}{\mathsf{\Omega }}^2$.

4. Discussion

(1) Hypothetically, in the case of a very high damping coefficient in the Maxwell rheological model, i.e., $cS\to \infty$ or $\lambda \to \infty$, the dynamic rigidity of the damper increases (theoretical $c\omega S\to \infty$) and the Maxwell model becomes a Hooke rheological model [32,38]. In this case, the Maxwell–Voigt–Kelvin rheological model (see Figure 1) becomes a Hooke–Voigt–Kelvin rheological model as seen in Figure 13. Thus, the amplitude of the dynamic harmonic force transmitted to the ground foundation is

$$Q_0^{HVK}=\underset{\lambda \to \infty }{\lim }{Q}_0^{MVK}=\underset{\lambda \to \infty }{\lim }\frac{F_0\lambda N\left(2\zeta \mathsf{\Omega }\right)\sqrt{1+{\left(2\zeta \mathsf{\Omega }\right)}^2}}{\sqrt{{[-{\mathsf{\Omega }}^2-{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda N+{\mathsf{\Omega }}^2{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda ]}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2{[\lambda N-{\mathsf{\Omega }}^2\left(1+\lambda +\lambda N\right)]}^2}} ,$$

or

$$Q_0^{HVK}=\underset{\lambda \to \infty }{\lim }\frac{F_{0}N\left(2\zeta \mathsf{\Omega }\right)\sqrt{1+{\left(2\zeta \mathsf{\Omega }\right)}^2}}{\sqrt{{\left[-\frac{{\mathsf{\Omega }}^2}{\mathsf{\lambda }}-{\left(2\zeta \mathsf{\Omega }\right)}^{2}N+{\mathsf{\Omega }}^2{\left(2\zeta \mathsf{\Omega }\right)}^2\right]}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2{\left[N-{\mathsf{\Omega }}^2\left(\frac{1}{\lambda }+1+N\right)\right]}^2}}$$

After the limit calculation, the amplitude of dynamic harmonic transmitted force becomes

$$Q_0^{HVK}=\frac{F_{0}N\left(2\zeta \mathsf{\Omega }\right)\sqrt{1+{\left(2\zeta \mathsf{\Omega }\right)}^2}}{\sqrt{{\left(2\zeta \mathsf{\Omega }\right)}^4{\left({\mathsf{\Omega }}^2-\mathrm{N}\right)}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2{[N-{\mathsf{\Omega }}^2\left(1+N\right)]}^2}} ,$$

or

$$Q_0^{HVK}=\frac{F_{0}N\sqrt{1+{\left(2\zeta \mathsf{\Omega }\right)}^2}}{\sqrt{{\left(2\zeta \mathsf{\Omega }\right)}^2{\left({\mathsf{\Omega }}^2-\mathrm{N}\right)}^2+{[N-{\mathsf{\Omega }}^2\left(1+N\right)]}^2}}$$

(2) Under the same hypothesis as in (1), the dynamic coefficient of the transmissibility of Hooke–Voigt–Kelvin rheological model is:

$$T^{HVK}\left(\zeta ,\mathsf{\Omega }\right)=\frac{Q_0^{HVK}}{F_0}=\frac{N\sqrt{1+{\left(2\zeta \mathsf{\Omega }\right)}^2}}{\sqrt{{\left(2\zeta \mathsf{\Omega }\right)}^2{\left({\mathsf{\Omega }}^2-\mathrm{N}\right)}^2+{\left[N-{\mathsf{\Omega }}^2\left(1+N\right)\right]}^2}} ,$$

(3) Considering the Hooke–Voigt–Kelvin rheological model according to (1), the amplitude of steady-state forced vibration of mobile mass m of the piling machine can be written

$$X_0^{HVK}=\underset{\lambda \to \infty }{\lim }{X}_0^{MVK}=\frac{F_0}{k}\underset{\lambda \to \infty }{\lim }\sqrt{\frac{{[1-{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda ]}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2{\left(1+\lambda +\lambda N\right)}^2}{{[{\mathsf{\Omega }}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda N-{\mathsf{\Omega }}^2{\left(2\zeta \mathsf{\Omega }\right)}^2\lambda ]}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2{[\lambda N-{\mathsf{\Omega }}^2\left(1+\lambda +\lambda N\right)]}^2}} ,$$

or

$$X_0^{HVK}=\frac{F_0}{k}\sqrt{\underset{\lambda \to \infty }{\lim }\frac{{\left[\frac{1}{\lambda }-{\left(2\zeta \mathsf{\Omega }\right)}^2\right]}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2{\left[\frac{1}{\lambda }+1+N\right]}^2}{{\left[-\frac{{\mathsf{\Omega }}^2}{\mathsf{\lambda }}-{\left(2\zeta \mathsf{\Omega }\right)}^{2}N+{\mathsf{\Omega }}^2{\left(2\zeta \mathsf{\Omega }\right)}^2\right]}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2{\left[N-{\mathsf{\Omega }}^2\left(\frac{1}{\lambda }+1+N\right)\right]}^2}}$$

$$\Rightarrow X_0^{HVK}=\frac{F_0}{k}\sqrt{\frac{{\left(2\zeta \mathsf{\Omega }\right)}^2+{\left(1+N\right)}^2}{{\left(2\zeta \mathsf{\Omega }\right)}^2{\left({\mathsf{\Omega }}^2-N\right)}^2+{[N-{\mathsf{\Omega }}^2\left(1+N\right)]}^2}}$$

5. Conclusions

Using a dynamic model and the hypothesis of linear behavior in stabilized dynamic regime (steady-state forced vibration), and based on the calculation relations, the parametric quantities defining the operation of the vibratory piling machines (equipment for the introduction of piles/columns in the ground foundation) were evaluated. Thus, the conclusions in the case of perturbing harmonic forces $F\left(t\right)=F_0\sin \left(\omega t\right)$ and $F\left(t\right)=\left(m_{0}r{\omega }^2\right)\sin \left(\omega t\right)$ can be summarized as follows:

(a) The amplitude of the technological vibrations in a post-resonance regime remains relatively constant at the variation of the relative pulsation $\mathsf{\Omega }\ge 2$;

(b) The variation in the maximum displacements and deflections, as internal parameters of the system, expressed by $X_0\left(\zeta ,\mathsf{\Omega }\right)$, $Y_0\left(\zeta ,\mathsf{\Omega }\right)$, $Z_0\left(\zeta ,\mathsf{\Omega }\right)$ and $U_0\left(\zeta ,\mathsf{\Omega }\right)$ in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 and Figure 9 and Figure 10, highlights the internal behavior of the ground foundation in the regime of steady-state harmonic forced vibrations with the maximum force $P=F_0=2000 \mathrm{kN}$ and $F_0\left(\omega \right)=\left(m_{0}r{\omega }^2\right), \mathrm{respectively}$;

(c) The amplitude of the dynamic force $Q_0\left(\zeta , \mathsf{\Omega }\right)$ transmitted to the ground foundation, function of the parameters of the piling machine and the rheological parameters of the soil, can be calculated with Equation (26);

(d) The ability to transmit the technological vibrations at the top of the pilot/column to the ground foundation is given by Equation (27), with the parametric variation in the coefficient of transmissibility T from Figure 8;

(e) The dissipated energy during the process of vibration introduction of the pilot/column into the soil can be calculated with Equation (40), with the parametric variations from Figure 11 and Figure 12;

(f) From the curves of the amplitude of steady-state forced vibration of mobile mass m (Figure 2 and Figure 3), it can be concluded that the stabilized technological regime for the vibratory piling machine is in post-resonance, for $\mathsf{\Omega }\ge 2$ (where the amplitude of forced vibration is the same, regardless of the value of damping ratio $\zeta$). The post-resonance operating condition $\mathsf{\Omega }\ge 2$ can be ensured by increasing the total moving mass m (depending on the mass of the pilot/column, as well as the elasticity of the foundation soil) or by increasing the pulsation ω of the harmonic force, or both;

(g) The use of the vibratory piling machine in the resonance stabilized regime ($\mathsf{\Omega }\approx 1$ regardless of the size of the structural damping ratio $\zeta$ of the ground) could lead to larger amplitudes of the steady-state forced vibration: $40–70 \mathrm{mm}$ in case of harmonic force $F_0\sin \left(\omega t\right)$ see Figure 2, $9–16 \mathrm{mm}$ in case of inertial harmonic force $\left(m_{0}r{\omega }^2\right)\sin \left(\omega t\right)$ see Figure 3. However, although the resonant operating mode could lead to higher forward speeds of the pilot/column into the foundation ground (hence higher productivity of the technological process), with the change of the damping ratio $\zeta$ of the foundation soil, the amplitude of the forced vibrations varies significantly, the process of piling through vibrations becoming technologically unstable and, therefore, uncontrollable. According to the case studies presented in Figure 2 and Figure 3, the amplitude of the forced vibrations in the resonance mode varies significantly depending on the damping ratio $\zeta$, with the linear functions $A_{\mathrm{res}}\left(\zeta \right)=78.9–121.3\zeta \left[\mathrm{mm}\right]$ in the case of harmonic force $F_0\sin \left(\omega t\right)$ and $A_{\omega \mathrm{res}}\left(\zeta \right)=21.8–39.4\zeta \left[\mathrm{mm}\right]$ in the case of inertial harmonic force $\left(m_{0}r{\omega }^2\right)\sin \left(\omega t\right)$;

(h) Considering a technological regime $\mathsf{\Omega }\ge 2$ for the vibratory piling equipment, the transmissibility coefficient of the force is $\mathrm{T}\le 0.5$ regardless of the value of damping ratio $\zeta$ (Figure 8), meaning that the transmitted force to the pile/column is, at maximum, half of the dynamic force of the vibrating motor. In the case of a post-resonance regime with $\mathsf{\Omega }\ge 2$, the higher the damping ratio $\zeta$, the higher the transmissibility coefficient T, due to the forces transmitted by the dampers of the Maxwell and Voigt–Kelvin rheological elements, especially for high deformation speeds. Despite the fact that the operation of the technological equipment is technologically unstable in the resonance work mode, high transmissibility coefficients can be obtained, all the more so as the damping coefficient of the foundation ground decreases. As Figure 8 demonstrates, the transmissibility coefficient at the resonance varies inversely with the damping ratio $\zeta$ of the foundation ground according to the law $T_{\mathrm{res}}\left(\zeta \right)=4–6.07\zeta$ for $0.15\le \zeta \le 0.32$;

(i) The curves in Figure 11 and Figure 12 show that the dissipated energies per cycle are maximum at resonance and the higher the value, the lower the damping ratio $\zeta$ (due to the higher values of the damping deflections at the lower values of the damping coefficients). For the technological regime with $\mathsf{\Omega }\ge 2$, the values of dissipated energy are $50–100 \mathrm{kJ}/\mathrm{cycle}$ for harmonic force $F\left(t\right)=F_0\sin \left(\omega t\right)$ and $10–20\mathrm{kJ}/\mathrm{cycle}$ for inertial harmonic force $F\left(t\right)=\left(m_{0}r{\omega }^2\right)\sin \left(\omega t\right)$.

(j) According to Figure 11, for a hypothetical stabilized resonance work regime, the theoretical value of dissipated energy in the case of harmonic perturbing force is $1300–2600 \mathrm{kJ}/\mathrm{cycle}$, meaning a dissipated power $P\approx 40,000–80,000 \mathrm{kW}$ for a nominal pulsation of $\omega =200 \mathrm{rad}/\mathrm{s}$ ($f=31.8 \mathrm{Hz}$ or $n=1909 {\min }^{-1}$). According to Figure 12, in the same hypotheses as above, the value of dissipated energy in the case of inertial harmonic perturbing force is $77–116 \mathrm{kJ}/\mathrm{cycle}$, meaning a dissipated power $P\approx 2500–3700 \mathrm{kW}$. These huge values of dissipated powers lead to the conclusion that resonant operating modes, even when stable, require very high installed powers of the drive vibro-motors;

(k) For a nominal pulsation of $\omega =200 \mathrm{rad}/\mathrm{s}$, a vibromotor with rotating unbalanced masses and a technological regime with $\mathsf{\Omega }\ge 5$, the dissipated power in damping elements is about $P\approx 60–150 \mathrm{kW}$ or $P\approx 80–200 \mathrm{HP}$. Taking into consideration the mechanical efficiency of the vibratory piling machines used and the in situ experimental test values (for the engines nominal power of $P_N\approx 200–400 \mathrm{HP}$), the complex linear Hooke–Voigt–Kelvin rheological model with variable damping coefficient can be used for the dynamic analysis of the vibrogenerator–pile–foundation soil system;

(l) Regardless of the type of disturbing force generated by the vibratory piling machine, the harmonic force $F_0\sin \left(\omega t\right)$ and inertial harmonic force $\left(m_{0}r{\omega }^2\right)\sin \left(\omega t\right)$, engineering practice on site has shown that the pre-resonant and resonant operating modes are unstable and uncontrollable, therefore, not recommended from a technological perspective.

The dynamic calculation model presented in the paper can be used to evaluate the technological working capacity of a vibratory piling machine or equipment used for inserting piles/columns in various types of soils for the construction of foundations.

The limitations of the presented models are as follows:

• the rheological model has linear elements (elasticity, damping) and cannot describe the possible nonlinear behavior of the foundation soil;
• the dynamic model of the system considers the pilot/column as a rigid solid body with infinite stiffness;
• the pilot’s advancement in the foundation ground does not take into account any possible obstacles in the foundation ground (e.g., very hard rocks) or irregularities (e.g., cavities, liquefied soil, groundwater).