Stability of Euler Methods for Fuzzy Differential Equation

Abstract

The Liu process is a fuzzy process whose membership function is a symmetric function on an expected value. The object of this paper was a fuzzy differential equation driven by Liu process. Since the existing fuzzy Euler solving methods (explicit Euler scheme, semi-implicit Euler scheme, and implicit Euler scheme) have the same convergence, to compare them, we presented four stabilities, i.e., asymptotical stability, mean square stability, exponential stability, and A stability. By choosing special fuzzy differential equation as a test equation, we deduced that mean square stability is equivalent to exponential stability. Furthermore, an explicit fuzzy Euler scheme and semi-implicit fuzzy Euler scheme showed asymptotical stability and mean square stability, while an explicit fuzzy Euler scheme failed to meet A stability but that an implicit fuzzy Euler scheme is A stable, and whether semi-implicit fuzzy Euler scheme is A stable depends on the values of $\alpha$ and $\lambda$.

1. Introduction

To characterize the evolution of fuzzy events, the fuzzy differential equation (FDE) was established. The FDE studied by experts is the fuzzification of the classical differential equation. The essence is generally divided into three cases: (1) converting the coefficients into fuzzy numbers; (2) replacing the initial or boundary values with fuzzy numbers; and (3) the forcing term is a fuzzy-valued function. Therefore, the form of FDE is either one of three cases or a combination thereof. In this context, based on fuzzy set theory, a wealth of results have been achieved. The involving differential is defined according to different fuzzy derivatives, as the representative is the generalized differential and the generalized Hukuhara derivative. On the premise of the Hukuhara derivative, by using linear transformations, Ngo [1] obtained the expression for the exact solution of linear second-order FDE; Zhang and Sun [2] put forward some definitions of the stability of FDE under second-order Hukuhara derivatives by means of Lyapunov function. Related to solving FDE, Khastan et al. [3,4] obtained new fuzzy approximation methods by fuzzy transform; Allahviranloo et al. [5] raised an Euler scheme on the basis of Taylor expansion; and spline collocation methods for systems of fuzzy fractional differential equations were deduced by Alijani et al. [6]. As for FDE under the concept of a generalized differential, Nematollah et al. [7] obtained an analytical solution and numerical solution via the differential transformation method; Chehlabi [8] obtained the continuity and existence conditions of the solution function; the relation between solutions of first-order linear FDE was developed by Khastan and Rodrguez-Lpez [9]; Mosleh and Otadi [10] presented a method to approximate linear FDE. In terms of other fuzzy derivations, we refer the interested reader to [11].

Because a lot of practical problems are self-dual in nature, the possibility measure is not the best tool to characterize fuzzy events. Just under this setting, Liu and Liu [12] set up a credibility measure, provided with self-duality, which created a new branch of fuzzy mathematics. When the fuzzy event is time-varying, Liu [13] described a special dynamic fuzzy phenomenon as a Liu process. Dai [14] contended that Liu process is consistent with reflection principle. Similar to the classical mathematical analysis, Liu [13] presented the a Liu differential, Liu integral and geometric Liu process. Along this line, You et al. [15] extended the Liu process, Liu differential and Liu integral to a multi-dimensional situation. Thereafter, a new FDE driven by Liu process was given via Liu [13] in 2008. Compared with FDE mentioned above, the fuzziness of this kind of equation is more widespread, and its most striking difference is that the driving term is a fuzzy process. In addition, in order to establish an FDE model for complicated practical problems, Zhu [16] gave a multi-dimensional FDE driven by Liu process. With regard to the new FDE, many scholars have carried out studies, for example, Zhu [16] raised some concepts and theorems of stability for FDE driven by Liu process. In contrast with the results of Zhu as for FDE, You and Hao [17] defined stability in credibility and stability in the mean was provided by You and Hao [18], and the conditions for stability in credibility and stability in the mean were given. In fact, there are few FDE that can be solved analytically, and thus scholars focused on the consideration of a numerical solution. Based on the Taylor expansion of homogeneous FDE, the Euler method originated from You and Hao [19]. Furthermore, Cheng and You [20] put forward four new numerical schemes. In the sense of applications, Liu [13] set up the stock model of Liu process, which is of great service to deal with the problem in fuzzy finance. Zhu [21] and Qin et al. [22] applied FDE to fuzzy optimization control and production planning problems, respectively.

Although scholars are exploring different numerical methods of FDE, there is no criterion to judge whether these methods are effective. Considering the explicit fuzzy Euler scheme, the semi-implicit fuzzy Euler scheme and implicit fuzzy Euler scheme have the same convergence; to compare them, we concentrated on the stability of fuzzy Euler methods. The contributions of this paper are: (1) four concepts of stability are defined for numerical solution; (2) four stable properties of the three fuzzy Euler schemes are obtained; (3) by numerical experiments, the images of stable regions are depicted.

The article is arranged as follows. The preparatory knowledge laid in Section 2 is an essential cornerstone for the study of this paper. In Section 3, we mainly prove mean square the (MS) stability of the equation, enumerate three fuzzy Euler methods used in this paper, and propose four kinds of stability for the numerical solution. In Section 4, each Euler scheme is substituted into the test equation to obtain a numerical solution. Furthermore, we discuss the four stable properties one by one for these numerical solutions. In Section 5, the visual stable region image is obtained by numerical experiment. Under the same stability conditions, different numerical methods can be compared by observing the images. Finally, we briefly conclude the results in Section 6.

2. Preliminaries

To make it easier to comprehend this paper, we will briefly introduce the knowledge involved. We use $\mathsf{\Theta }$ to represent a nonempty set, and $\mathcal{P}$ to represent the power set of $\mathsf{\Theta }$. $A\in \mathcal{P}$ is called a fuzzy event. Credibility measure $\mathrm{Cr}$ is a set function satisfying:

(1)

$\mathrm{Cr}\left\{\mathsf{\Theta }\right\}=1$;

(2)

$\mathrm{Cr}\left\{A\right\}\le \mathrm{Cr}\left\{B\right\}$, whenever $A\subset B$;

(3)

$\mathrm{Cr}\left\{A\right\}+\mathrm{Cr}\left\{A^c\right\}=1,$ for any $A\in \mathcal{P}$;

(4)

$\mathrm{Cr}\left\{{\bigcup }_i{A}_i\right\}={sup}_i\mathrm{Cr}\left\{A_i\right\}$ for any collection $A_i$ in $\mathcal{P}$ with ${sup}_i\mathrm{Cr}\left\{A_i\right\}<0.5$.

The triplet $(\mathsf{\Theta },\mathcal{P},\mathrm{Cr})$ is called a credibility space [23]. A fuzzy variable is a function $\zeta \left(\theta \right),\theta \in \mathsf{\Theta }$ (abbreviated as $\zeta$), whose effect is to project credibility space $(\mathsf{\Theta },\mathcal{P},\mathrm{Cr})$ to a real set R. Provided that there exists an index set T, then a function which can convert $T\times (\mathsf{\Theta },\mathcal{P},\mathrm{Cr})$ into a set of real numbers, is called a fuzzy process, indicated by $X(t,\theta )$, where $t\in T,\theta \in \mathsf{\Theta }$. Particularly, $X(t,\theta )$ represents a fuzzy variable if t is set. Correspondingly, if $\theta$ is fixed, then $X(t,\theta )$ refers to the sample trajectory of a fuzzy process. We say that $X(t,\theta )$ is a continuous sample if the sample trajectory of $X(t,\theta )$ is a continuous function of t. For simplification, we write $X_t$ instead of $X(t,\theta )$.

In order to describe a fuzzy variable, we give the definitions of expected value, variance, and k-th moment, which will be used in the discussion of stabilities.

Definition 1

(Liu [12]). Suppose that ζ is a fuzzy variable, then the expected value of ζ is expressed as $E\left[\zeta \right]={\int }_0^{+\infty }\mathrm{Cr}\{\zeta \ge r\}\mathrm{d}r-{\int }_{-\infty }^0\mathrm{Cr}\{\zeta \le r\}\mathrm{d}r,$ where at least one of the two integrals is finite.

The variance of ζ is defined as $Var\left[\zeta \right]=E[{(\zeta -E\left[\zeta \right])}^2]$ and $E\left[{\zeta }^k\right]$ is called the k-th moment of ζ, where k is a positive number.

Since the research object in this paper is FDE driven by Liu process, the definition of the Liu process and its Lipschitz continuity, and the FDE driven by Liu process are listed.

Definition 2

(Liu [13]). A fuzzy process $C_t$ is called a Liu process if the following conditions hold. $\left(i\right)$ $C_0=0$; $\left(ii\right)$ $C_t$ not only has independent increments but also stationary increments; $\left(iii\right)$ the increment in $C_t$ is a normally distributed fuzzy variable with expected value $et$ and variance ${\sigma }^2{t}^2$.

It is noteworthy that $C_t$ is a standard Liu process if $e=0$ and $\sigma =1$. Note that the membership function of a Liu process is a symmetric function about $et$, which is useful in the calculation related to credibility or expected value.

Theorem 1

(Dai [14]). If $\mathrm{Cr}\left\{\theta \right\}>0$ with regard to any given $\theta \in \mathsf{\Theta }$, then the path of the Liu process denoted by $C_t\left(\theta \right)$ possesses Lipschitz continuous property, which reads $|C_t-C_l|\le K\left(\theta \right)|t-l|,$ where K(θ) means Lipschitz constant.

Definition 3

(Fuzzy differential equation, Liu [13]). Provided that $C_t$ refers to a standard Liu process, and p, q are fixed functions. The following equation

$$\mathrm{d}{X}_t=p(t,X_t)\mathrm{d}t+q(t,X_t)\mathrm{d}{C}_t$$

(1)

is known as FDE driven by Liu process, where $X_t$ is a fuzzy process.

Note that it is a special case of fuzzy differential equation, where the driven process is a Liu process.

3. Stability of Numerical Methods

The stability of numerical solutions is to study the solution’s properties under small disturbances. It is an important branch of numerical solutions. In this section, four definitions of stability for numerical solutions of fuzzy differential equation are given.

3.1. Stability in Mean-Square for FDE

Consider the following FED:

$$\mathrm{d}{X}_t=p\left(X_t\right)\mathrm{d}t+q\left(X_t\right)\mathrm{d}{C}_t,t\in [0,T],X_{t_0}=X_0,$$

(2)

where p and q are given functions with a continuous derivative, $C_t$ is a standard Liu process, whose stationary increment is expressed as $\Delta C_t=C_{t+h}-C_t,t,t+h\in [0,T]$. If the step-size h is sufficiently small, then $E[\Delta C_t]=0,Var[{(\Delta C_t)}^2]=E[{(\Delta C_t)}^2]=h^2.$

Definition 4.

If there is always ${lim}_{|X_0-Y_0|\to 0}E\left[\right|X_t-Y_t{|}^2]=0$, then (1) is stable in MS, where $t\ge 0$, $X_t$, and $Y_t$ are the solutions of (1) when the initial values are $X_0$ and $Y_0$, respectively.

Theorem 2.

Suppose that (1) has a unique solution, and if the coefficient satisfies the strong Lipschitz condition

$$\left|p\right(t,x)-p(t,y\left)\right|+\left|q\right(t,x)-q(t,y\left)\right|\le L\left(t\right)|x-y|,$$

then (1) is stable in MS, where $t\ge 0$, $L\left(t\right)$ is an integrable function defined on $[0,+\infty )$.

Proof. 

Suppose $X_t$ and $Y_t$ are solutions of (1) corresponding to two different initial values $X_0$ and $Y_0$, then for any $\theta \in \mathsf{\Theta }$, it follows from Theorem 1 that

$$\begin{array}{ll}\mathrm{d}|X_t-Y_t{|}^2& =2|X_t-Y_t\left|\mathrm{d}\right|X_t-Y_t|=2|X_t-Y_t\left|\right|(p(t,X_t)-p(t,Y_t))\mathrm{d}t+(q(t,X_t)-q(t,Y_t))\mathrm{d}{C}_t|\\ & \le 2|X_t-Y_t\left|\right[L\left(t\right)|X_t-Y_t|\mathrm{d}t+L\left(t\right)K\left(\theta \right)|X_t-Y_t\left|\mathrm{d}t\right]\\ & \le 2L\left(t\right)(1+K\left(\theta \right)){|X_t-Y_t|}^2\mathrm{d}t,\end{array}$$

integrating on both sides of the above formula, we have $|X_t-Y_t{|}^2\le 2{|X_0-Y_0|}^2\exp ((1+K\left(\theta \right)){\int }_{t_0}^t{L}_s\mathrm{d}s),$ then

$$\begin{array}{ll}\underset{|X_0-Y_0|\to 0}{lim}E\left[\right|X_t-Y_t{|}^2]& \le 2\underset{|X_0-Y_0|\to 0}{lim}E[|X_0-Y_0{|}^2\exp ((1+K\left(\theta \right)){\int }_{t_0}^t{L}_s\mathrm{d}s)]\\ & =2(1+K\left(\theta \right))\underset{|X_0-Y_0|\to 0}{lim}E\left[\right|X_0-Y_0{|}^2\exp ({\int }_{t_0}^t{L}_s\mathrm{d}s)]=0.\end{array}$$

Thus, (1) is stable in MS. The proof is completed. □

Generally speaking, the stability of the system itself is the stability of the trivial solution $X_t\equiv 0$. In order to study stability easily, two kinds of linear test equations with complex numbers $\lambda$, $\mu$ and $\sigma$ are given by

$$\mathrm{d}{X}_t=\lambda X_t\mathrm{d}t+\mu X_t\mathrm{d}{C}_t,$$

(3)

$$\mathrm{d}{X}_t=\lambda X_t\mathrm{d}t+\sigma \mathrm{d}{C}_t.$$

(4)

The analytic solution of Equation (3) is $X_t=X_0\exp (\lambda t+\mu C_t).$

Definition 5.

The solution $X_t$ of Equation (3) is p stable, if for any sufficiently small $|X_0|$, we have ${lim}_{t\to \infty }E\left[\right|X_t{|}^p]=0.$ When $p=1$, it is called asymptotically stable, i.e.,

$$\mathrm{Cr}\{\underset{t\to \infty }{lim}E\left[\right|X_t\left|\right]=0\}=1\iff \Re \left\{\lambda \right\}<0,$$

where $\Re \left(\lambda \right)$ means the real part of λ. When $p=2$, it is said to be stable in MS, i.e., ${lim}_{t\to \infty }E\left[\right|X_t{|}^2]=0\iff Equation\left(3\right)isstableinMS.$

3.2. The Concept of Numerical Stability

Stability is a significant basis for judging whether an algorithm is applicable. Based on three commonly used Euler methods, the stability of numerical solutions is studied in this paper. Then, four concepts of stability and three Euler schemes are introduced in this subsection.

Euler methods: The discussion of Euler methods is divided into three types:

(i)

Explicit fuzzy Euler scheme (refer to [19])

$${\tilde{X}}_{t_{n+1}}={\tilde{X}}_{t_n}+hp({\tilde{X}}_{t_n})+q({\tilde{X}}_{t_n})\Delta C_{t_n}.$$

(ii)

Semi-implicit fuzzy Euler scheme (see [20], also called $\theta$-method in classical differential equation)

$${\tilde{X}}_{t_{n+1}}={\tilde{X}}_{t_n}+h[\alpha p({\tilde{X}}_{t_{n+1}})+(1-\alpha )p({\tilde{X}}_{t_n})]+q({\tilde{X}}_{t_n})\Delta C_{t_n},\alpha \in [0,1].$$

(iii)

Implicit fuzzy Euler scheme (mentioned in [20])

$${\tilde{X}}_{t_{n+1}}={\tilde{X}}_{t_n}+hp({\tilde{X}}_{t_{n+1}})+q({\tilde{X}}_{t_{n+1}})\Delta C_{t_n}.$$

In order to facilitate discussion, the iterative formula obtained by Euler methods for Equation (3) iterated in one step is recorded as ${\tilde{X}}_{t_{n+1}}=H(h,\lambda ,\mu ,\Delta C_{t_n}){\tilde{X}}_{t_n}.$ To make the formula simple, let $r=\lambda h,s=\mu h,\Delta C_{t_n}=\xi h$. Naturally $H(h,\lambda ,\mu ,\Delta C_{t_n})$ can be recorded as $H(r,s)$, where $\xi$ is a normal fuzzy variable and $\xi \sim N(0,1)$. We have calculated the k-th $(k=1,\cdots ,4)$ moments of $\xi$ to get $E\left[\xi \right]=0,E\left[{\xi }^2\right]=1,E\left[{\xi }^3\right]=0,E\left[{\xi }^4\right]\approx 7.$

Then, four numerical stabilities are proposed in this paper.

Definition 6.

Let $H_1(r,s)=E\left[H(h,\lambda ,\mu ,\Delta C_{t_n})\right]$. We shall call $H_1(r,s)$ the stable function of the numerical scheme. If $|H_1(r,s)|<1$, then the numerical scheme is called asymptotically stable, and the region of asymptotical stability of the numerical scheme is expressed as $D_{AS}=\left\{(r,s)\right||H_1(r,s)|<1\}$.

Definition 7.

Let $H_2(r,s)=E\left[H^2(h,\lambda ,\mu ,\Delta C_{t_n})\right]$. Then, $H_2(r,s)$ is called the MS stable function of the numerical scheme. The numerical scheme is said to be stable in MS if $|H_2(r,s)|<1$. The domain of MS stability of the numerical scheme is recorded as $D_{MS}=\left\{(r,s)\right||H_2(r,s)|<1\}$.

Definition 8.

For a given step-size h, a numerical method is used to solve FDE, which then yields the discrete solution ${\{{\tilde{X}}_{t_n}\}}_{n=0}^{\infty }$. If there are two positive constants p and Q such that $E\left[\right|{\tilde{X}}_{t_n}{|}^2]\le QE[|X_0\left|{}^2\right]e^{-pnh},\forall n\ge 0$, then the numerical method is exponentially stable in the sense of mean square.

Applying a one-step numerical method to (4), we obtain ${\tilde{X}}_{t_{n+1}}=F\left(\lambda h\right){\tilde{X}}_{t_n}+Z_{t_n},$ where $Z_{t_n}$ is a fuzzy variable that is independent of ${\tilde{X}}_{t_n}$, and the domain of absolute stability for the numerical method is $D_A=\left\{(\lambda ,h)\right|\Re \left(\lambda \right)<0and\left|F\left(\lambda h\right)\right|<1\}.$

Definition 9.

If the domain of absolute stability for the numerical scheme contains the entire left half plane, i.e., $\Re \left(\lambda \right)<0\Rightarrow \left|F\right(\lambda h\left)\right|<1$, then the numerical scheme is said to be A stable.

4. Conditions of Stability and Stability Region of Euler Methods

According to the concepts of asymptotical stability, MS stability, exponential stability, and A stability proposed in the previous section, we apply the three Euler schemes mentioned above to the test equations, and obtain different results, respectively.

4.1. Asymptotical Stability

Theorem 3.

With regard to (3), semi-implicit fuzzy Euler scheme is asymptotically stable if and only if $|1+\frac{r}{1-\alpha r}|<1,\alpha \in [0,1].$

Proof. 

Applying the recurrence formula of the semi-implicit fuzzy Euler scheme to the test Equation (3), we have

$${\tilde{X}}_{t_{n+1}}=\frac{1+(1-\alpha )r+s\xi }{1-\alpha r}{\tilde{X}}_{t_n}.$$

(5)

Denote the asymptotical stable function of semi-implicit fuzzy Euler scheme as $H_1^{se}(r,s)$. Since $E\left[\xi \right]=0$, according to Definition 6, $H_1^{se}(r,s)=E\left[H(r,s)\right]=E[\frac{1+(1-\alpha )r+s\xi }{1-\alpha r}]=1+\frac{r}{1-\alpha r}.$ Thus, the result is easy to obtain. □

Note that for (3), the region of asymptotical stability of the semi-implicit fuzzy Euler scheme is $D_{AS}=\left\{(r,s)\right||1+\frac{r}{1-\alpha r}|<1\}.$

Denote the asymptotically stable function of the explicit fuzzy Euler method as $H_1^{ex}(r,s)$. Since the explicit fuzzy Euler method is a special case of semi-implicit fuzzy Euler scheme, here we only give the stable function $H_1^{ex}(r,s)=1+r.$

Remark 1.

(1)

Applying the implicit fuzzy Euler scheme to (3), we obtain the iterative form ${\tilde{X}}_{t_{n+1}}=H(r,s){\tilde{X}}_{t_n}=\frac{1}{1-r-s\xi }{\tilde{X}}_{t_n}.$ The difficulty is that $H(r,s)$ may approach infinity whenever the value of the normal fuzzy variable ξ is in the neighborhood of $(1-r)/s$. In this case, the implicit Euler scheme is instable for any λ, μ and h. Hence, the value of ξ will also affect the asymptotical stability and MS stability of implicit fuzzy Euler scheme. However, in all other cases, the asymptotically stable function of the implicit fuzzy Euler method expressed by $H_1^{im}(r,s)=\frac{1}{1-r}$ and the region of the implicit fuzzy Euler method coincides with that of the semi-implicit fuzzy Euler scheme when $\alpha =1$. As a result, the implicit method has the best stability properties.

(2)

Under the condition that the value of the normal fuzzy variable ξ is in the neighborhood of $(1-r)/s$, if we increase α, i.e., going towards implicitness, the stability is improving but the fully implicit scheme is unstable again. This reveals that the implicit scheme is not a special case of the semi-implicit one, because the latter one handles the last term fully explicit.

(3)

The original Dahlquist test equation in the not-fuzzy case is a special case of the FDE studied here ($\mu =0$) and for that, the implicit method has extremely good stability properties.

4.2. MS Stability

Theorem 4.

For (3), the semi-implicit fuzzy Euler scheme is stable in MS if and only if

$$|\frac{1+{(1-\alpha )}^2{r}^2+s^2+2(1-\alpha )r}{{(1-\alpha r)}^2}|<1,\alpha \in [0,1].$$

Proof. 

Denote the MS stable function of the semi-implicit fuzzy Euler scheme as $H_2^{se}(r,s)$. Since $E\left[\xi \right]=0,E\left[{\xi }^2\right]=1,$ according to Definition 7, we have

$$\begin{array}{ll}{H}_2^{se}(r,s)=E\left[H^2(r,s)\right]& =E[\frac{1+2r-2\alpha r+r^2+{\alpha }^2{r}^2-2\alpha r^2+s^2{\xi }^2+2s\xi +2(1-\alpha )rs\xi }{{(1-\alpha r)}^2}]\\ & =\frac{1+2r-2\alpha r+r^2+{\alpha }^2{r}^2-2\alpha r^2+s^2}{{(1-\alpha r)}^2}.\end{array}$$

Thus, the result is easy to obtain. □

Note that for (3), the region of MS stability of the semi-implicit fuzzy Euler scheme is

$$D_{MS}^{se}=\left\{(r,s)\right||\frac{1+2r-2\alpha r+r^2+{\alpha }^2{r}^2-2\alpha r^2+s^2}{{(1-\alpha r)}^2}|<1\}.$$

Denote the asymptotically stable function of the explicit fuzzy Euler method as $H_2^{ex}(r,s)$. Since the explicit fuzzy Euler method is a special case of the semi-implicit fuzzy Euler scheme, here we only focus on the stable function $H_2^{ex}(r,s)={(1+r)}^2+s^2.$

Remark 2.

For the same reason in Remark 1, if the value of the normal fuzzy variable ξ is in the neighborhood of $(1-r)/s$, the implicit Euler scheme is unstable for any λ, μ and h. Otherwise, the MS stable function of the implicit fuzzy Euler method expressed by $H_2^{im}(r,s)=\frac{1}{{(1-r)}^2+s^2},$ and the implicit method has the best stability properties.

Theorem 5.

In the mean square sense, the semi-implicit fuzzy Euler method is absolutely unstable under the condition of $0\le \alpha \le \frac{1}{2},r\le {\displaystyle \frac{2}{2\alpha -1}}$.

Proof. 

Let $H_2^{se}(r,s)\ge 1$, i.e., $(1-2\alpha )r^2+2r+s^2\ge 0.$ It is equivalent to $(1-2\alpha )r^2+2r\ge 0.$ Therefore, the establishment of the formula should meet the conditions $0\le \alpha \le \frac{1}{2}$ and $r\le {\displaystyle \frac{2}{2\alpha -1}}$. The proof is completed. □

4.3. Exponential Stability

Theorem 6.

For (3), fuzzy Euler methods are exponentially stable if and only if $|H_2(r,s)|<1,$ where $H_2(r,s)$ means an MS stable function.

Proof. 

Similar to the proof of Theorem 4, $E\left[\right|{\tilde{X}}_{t_{n+1}}{|}^2]=|H_2(r,s)\left|E\right[|{\tilde{X}}_{t_n}{|}^2].$ Replacing $H_2(r,s)$ with $H_2$ and repeating the recurrence of the above formula, we have

$$E\left[\right|{\tilde{X}}_{t_n}{|}^2]=|H_2{|}^n\left|E\right[|X_0{|}^2]={[e^{ln|H_2|}]}^{n}E[|X_0{|}^2].$$

(6)

Firstly, there is the proof of sufficiency. If $|H_2(r,s)|<1$, take $p=-\frac{1}{h}ln\left|H_2\right|$, then for $\forall Q\in N^{+}$, we have

$$QE\left[\right|X_0|{}^2]e^{-pnh}=Q{e}^{-nh(-{\displaystyle \frac{1}{h}}ln|H_2|)}E[|X_0|{}^2]=Q|H_2{|}^{n}E\left[\right|X_0\left|{}^2\right],\forall n\ge 0.$$

Consequently,

$$E\left[\right|{\tilde{X}}_n|{}^2]=|H_2{|}^{n}E\left[\right|X_0|{}^2]\le Q|H_2{|}^{n}E\left[\right|X_0|{}^2]=QE[|X_0\left|{}^2\right]e^{-pnh},\forall n\ge 0.$$

Secondly, there is the proof of necessity. If numerical methods are exponentially stable, according to Definition 8, $E\left[\right|{\tilde{X}}_{t_n}{|}^2]\le QE[|X_0\left|{}^2\right]e^{-pnh},\forall n\ge 0,$ and utilizing (6), we have ${\left[e^{ln|H_2|}\right]}^n\le Q{e}^{-pnh}.$ Take $n=\frac{lnQ}{ph}+1$ for $\forall n\ge 0$, then

$$|H_2{|}^n={[e^{ln|H_2|}]}^n\le Q{e}^{-ph[{\displaystyle \frac{lnQ}{ph}}+1]}=Q{e}^{-lnQ-ph}=e^{-ph}<1.$$

Hence $|H_2(r,s)|<1$. The theorem is proven. □

Theorem 7.

For (3), the exponential stability of the numerical method is equivalent to its MS stability.

Proof. 

By Theorem 6, we can easily draw the conclusion. □

4.4. A Stability

Theorem 8.

With respect to (4), the explicit fuzzy Euler scheme is not A stable but the implicit fuzzy Euler scheme is A stable. Furthermore, the semi-implicit fuzzy Euler scheme is A stable if the parameter α satisfies $1/2\le \alpha \le 1$ and $\Re \left(\lambda \right)<0$, while semi-implicit fuzzy Euler scheme is not A stable if the parameter α satisfies $0\le \alpha <1/2$.

Proof. 

Let $\lambda =a+ib$ in this proof.

(i)

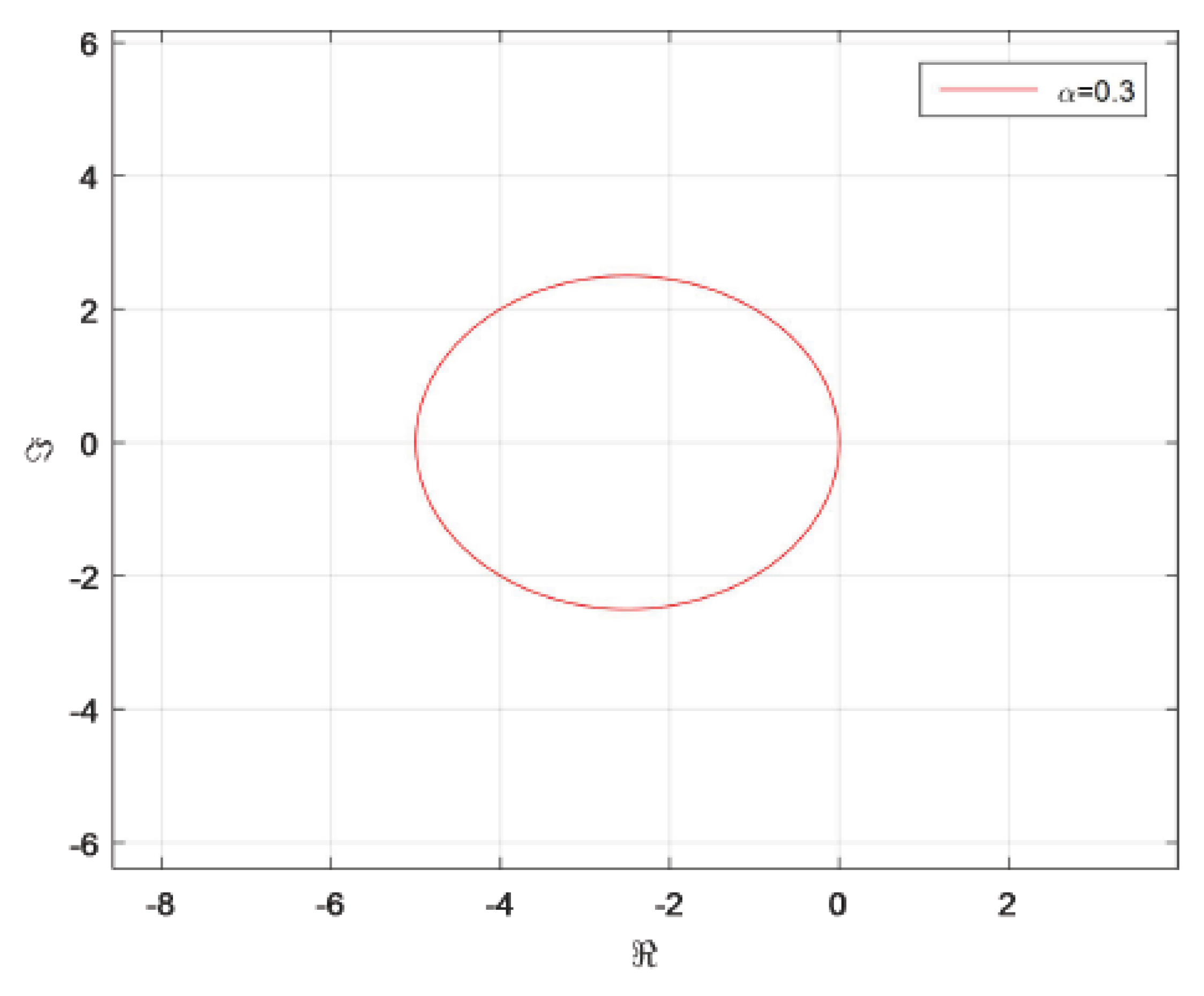
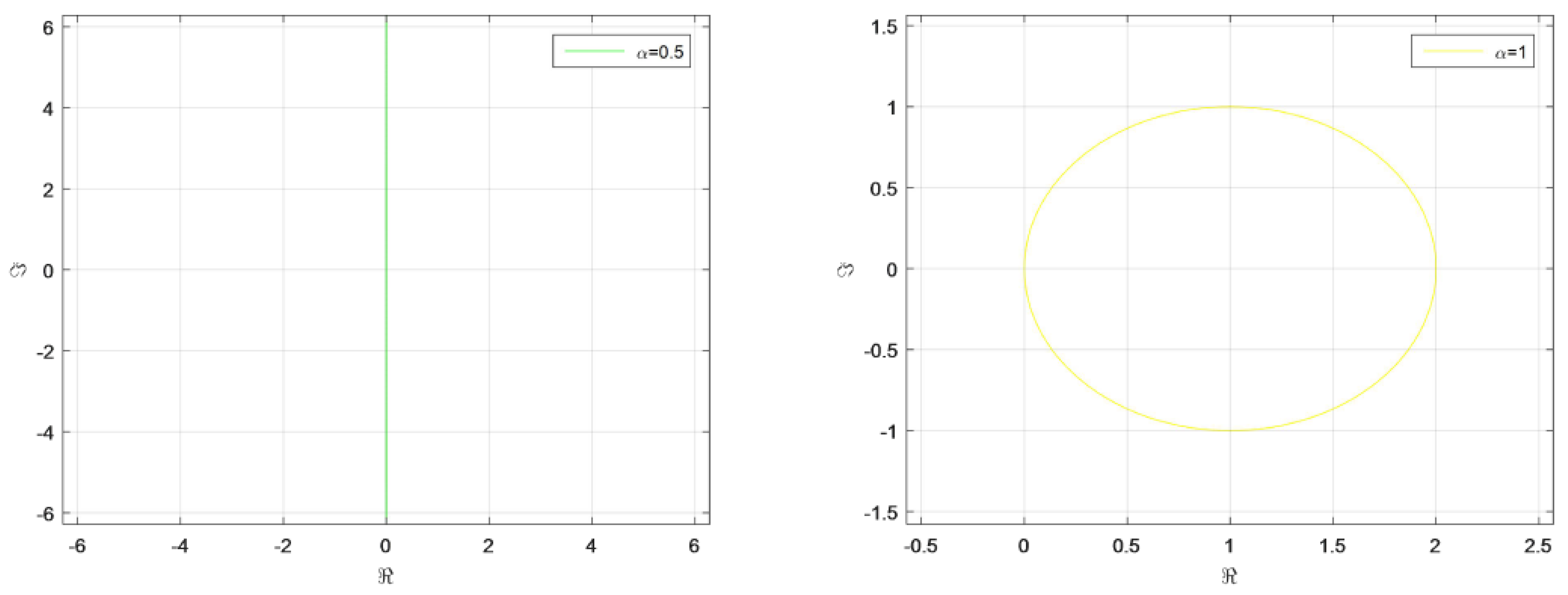
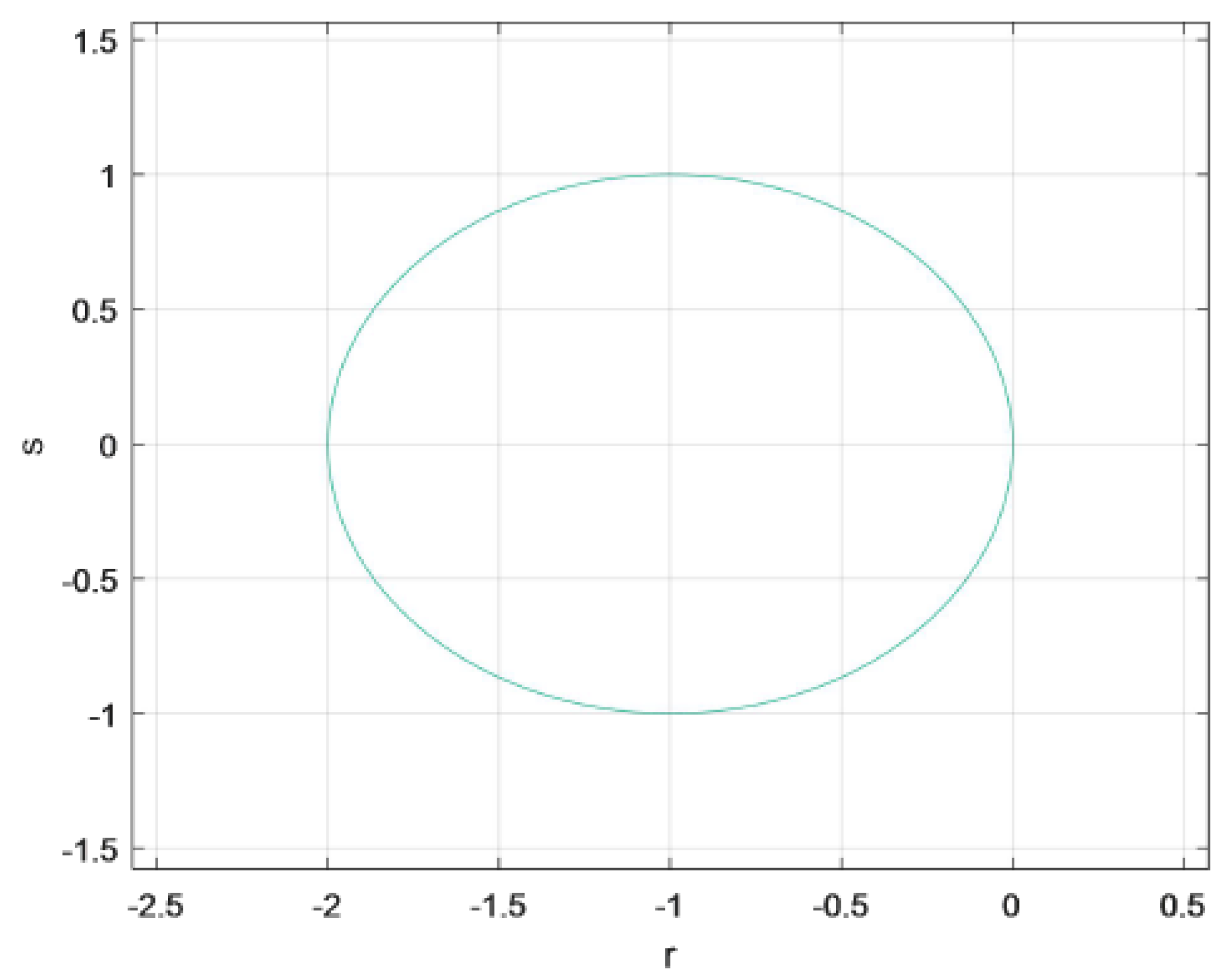
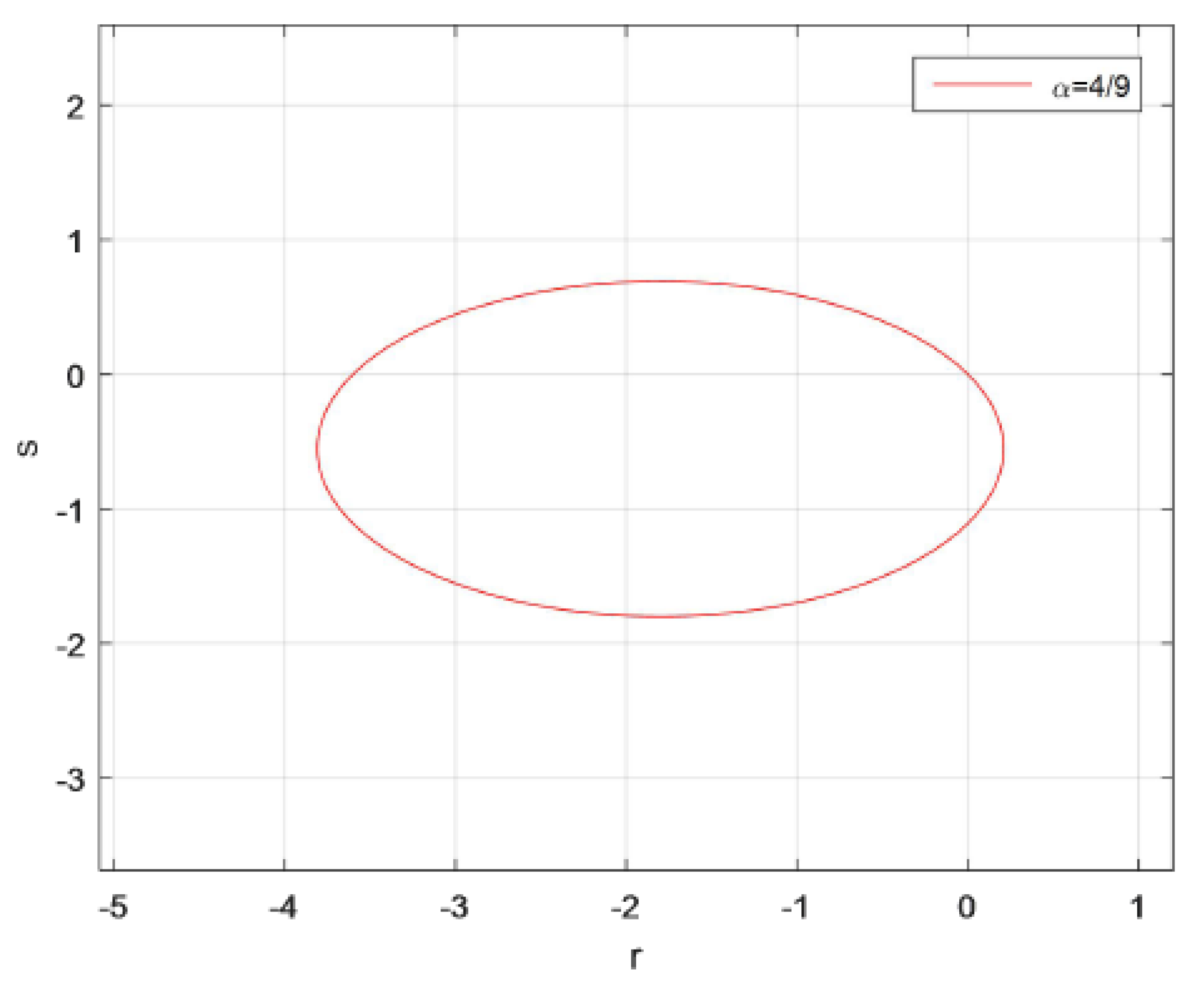
Applying the explicit fuzzy Euler scheme to (4), we yield ${\tilde{X}}_{t_{n+1}}=(1+\lambda h){\tilde{X}}_{t_n}+\sigma \Delta C_{t_n},\mathrm{that}\mathrm{is}F\left(\lambda h\right)=1+\lambda h.$ Let $\left|F\right(\lambda h\left)\right|<1,$, i.e., ${(1+ah)}^2+{\left(bh\right)}^2<1.$ It is easy to see that the absolute stable region of the method is the interior of a circle with $-1+0i$ as its center and 1 as the radius, so the explicit fuzzy Euler scheme is not A stable from Definition 9.

(ii)

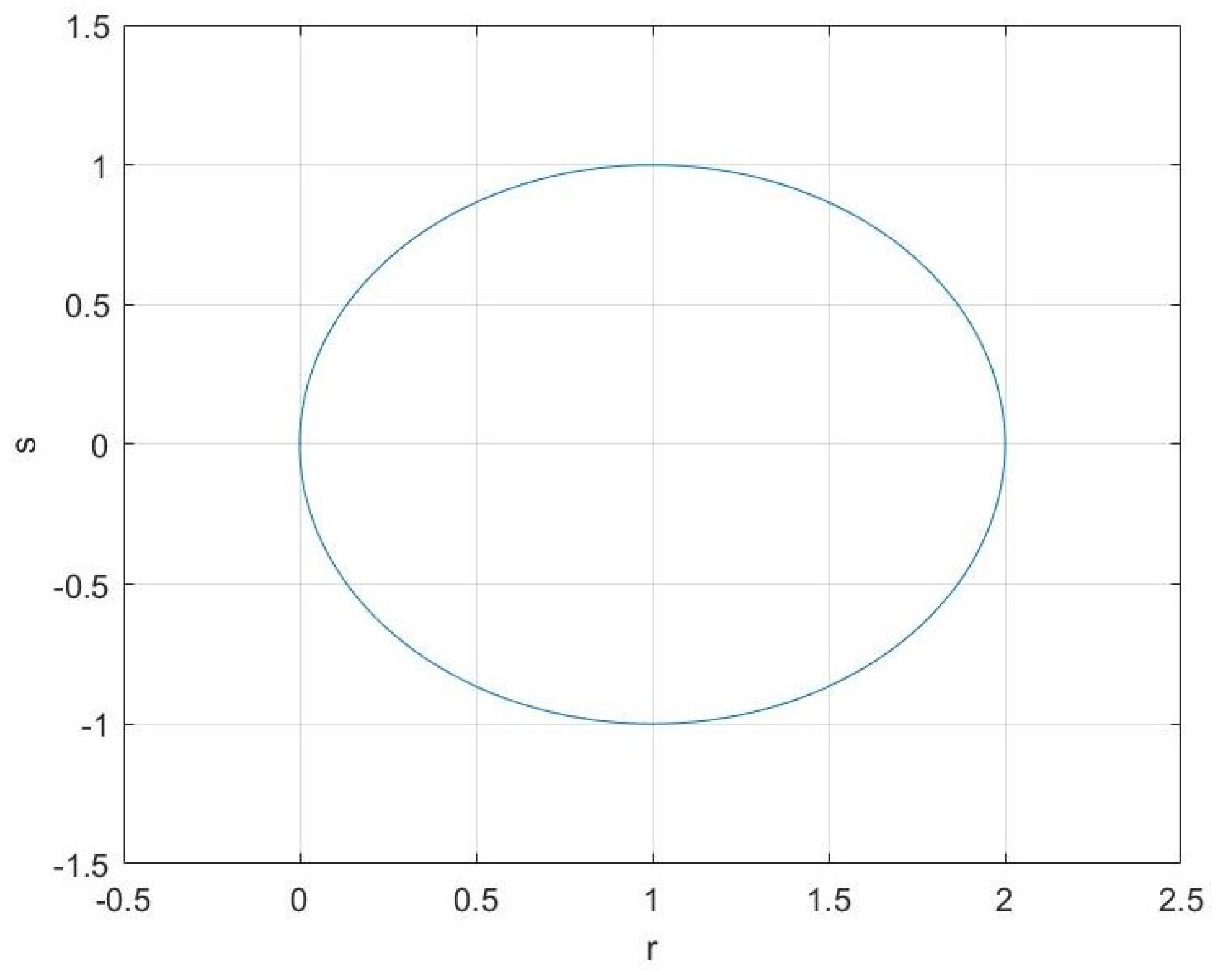
Applying the implicit fuzzy Euler scheme to (4), we similarly gain ${\tilde{X}}_{t_{n+1}}={(1-\lambda h)}^{-1}{\tilde{X}}_{t_n}+\sigma \Delta C_{t_n},\mathrm{that}\mathrm{is}F\left(\lambda h\right)={(1+\lambda h)}^{-1}.$ Let $\left|F\right(\lambda h\left)\right|<1,$ i.e., ${(1-ah)}^2+{\left(bh\right)}^2>1.$ It suffices to show that the absolute stable region of the method is the exterior of a circle with $1+0i$ as its center and 1 as the radius, so the implicit fuzzy Euler scheme is A stable.

(iii)

Applying the semi-implicit fuzzy Euler scheme to (4), we have

$${\tilde{X}}_{t_{n+1}}={(1-\alpha \lambda h)}^{-1}[1+(1-\alpha )\lambda h]{\tilde{X}}_{t_n}+\sigma \Delta C_{t_n},\alpha \in [0,1],$$

that is $F\left(\lambda h\right)={(1-\alpha \lambda h)}^{-1}[1+(1-\alpha )\lambda h].$ Let $\left|F\right(\lambda h\left)\right|<1,$ i.e.,

$$(1-2\alpha )(a^2+b^2)h+2a<0.$$

(7)

We then discuss this in two cases.

• Case 1: $\frac{1}{2}\le \alpha \le 1$. The semi-implicit fuzzy Euler scheme is A stable only if $\Re \left(\lambda \right)=a<0$.
• Case 2: $0\le \alpha <\frac{1}{2}$. We find that (7) can be written as ${(B+ah)}^2+{\left(bh\right)}^2<B^2,\mathrm{where}B={(1-2\alpha )}^{-1}.$

It is obvious that the absolute stable region of the method is the interior of a circle with $-B+0i$ as its center and B as the radius, so the semi-implicit fuzzy Euler scheme is not A stable. □

5. Numerical Experiment

By numerical experiments, this section discusses the effect of $\alpha$ in a semi-implicit fuzzy Euler scheme on MS stability, and compares the effects of three fuzzy Euler schemes in terms of asymptotical stability and MS stability.

5.1. The Effect of $\alpha$ on MS Stability in Semi-Implicit Fuzzy Euler Scheme

The following fuzzy differential equation is used as the experimental equation:

$$\mathrm{d}{X}_t=-50X_t\mathrm{d}t+25X_t\mathrm{d}{C}_t,X_{t_0}=X_0=1,t\in [0,10].$$

(8)

Select $\lambda =-50$, $\mu =25$, which satisfy Theorem 2; thus Equation (8) is stable in MS. Applying the semi-implicit Euler scheme, take $\alpha ={\displaystyle \frac{1}{4}},{\displaystyle \frac{2}{5}},{\displaystyle \frac{3}{7}},{\displaystyle \frac{4}{5}}$, respectively. According to Theorem 4, the corresponding MS stability regions are depicted in Figure 1 by using Matlab software.

It is observed from Figure 1 that when $\alpha =\frac{1}{4}$, the semi-implicit fuzzy Euler scheme is not MS stable. In addition, when $r=-5<{\displaystyle \frac{1}{2\alpha -1}}=-4$, according to Theorem 6, the semi-implicit fuzzy Euler scheme is absolutely unstable, thus Theorem 4 is verified; when $\alpha =\frac{2}{5}$, the semi-implicit fuzzy Euler scheme is not MS stable; when $\alpha =\frac{3}{7}$, the semi-implicit Euler scheme is MS stable; when $\alpha ={\displaystyle \frac{4}{5}}$, the semi-implicit fuzzy Euler scheme is MS stable. In short, the region of MS stability of the semi-implicit fuzzy Euler scheme is larger with the bigger value of $\alpha$.

5.2. Stability of Three Fuzzy Euler Scheme

In this subsection, the MS stability and asymptotical stability of the fuzzy Euler methods are verified by numerical experiments.

(1)

Asymptotical stability

Take the test equation as follows

$$d{X}_t=(-10+10i)X_{t}dt+7X_{t}d{C}_t,X_{t_0}=X_0=1,t\in [0,10].$$

(9)

Since the region of the implicit fuzzy Euler method coincides with that of the semi-implicit fuzzy Euler scheme when $\alpha =1$, we only use the explicit fuzzy Euler schemes and the semi-implicit fuzzy Euler scheme to iterate, and take $\alpha$ in the semi-implicit fuzzy Euler scheme to be $0.3,0.5,1$, respectively. It follows from Section 4.1 that there is no s involved in the asymptotical stable functions $H_1^{se}(r,s),H_1^{ex}(r,s)$, and we divide r into the real part ℜ and imaginary part ℑ. Then, the stable region of the explicit fuzzy Euler method is $D_{AS}^{ex}=\{(\Re ,\Im )|{(1+\Re )}^2+{\Im }^2<1\}$. Similarly, we can deduce the stable region expressed by ℜ and ℑ of the semi-implicit fuzzy Euler method based on Theorem 3. Then, the patterns of the region of asymptotical stability are given in Figure 2, Figure 3 and Figure 4. The stable region of the explicit fuzzy Euler method is the interior of the circle in Figure 2, the stable region of the semi-implicit fuzzy Euler method is the intersection of the left half plane and the exterior of the circles in Figure 3 and the right figure in Figure 4, and the stable region of the semi-implicit fuzzy Euler method is the left half plane in the left figure in Figure 4.

We find that when $\alpha =0.3$, the stable region of the semi-implicit fuzzy Euler scheme is larger than that of the explicit fuzzy Euler scheme; then, the stability is stronger. Therefore, for (9), the asymptotical stability of the semi-implicit fuzzy Euler scheme is better than that of the explicit fuzzy Euler scheme. Integrating Figure 1, we conclude that the implicit method has the best stability properties except for the case of the value of normal fuzzy variable $\xi$ is in the neighborhood of $(1-r)/s$.

(2)

MS stability

Continuing to use (8) as the test equation, three fuzzy Euler schemes are used to iterate, according to Section 4.2, their MS stable regions are shown in Figure 5, Figure 6 and Figure 7 by Matlab software. Since $H_2^{im}(r,s)=\frac{1}{{(1-r)}^2+s^2},$ we have the stable region of the implicit fuzzy Euler scheme as $D_{MS}^{im}=\{(r,s)|{(1-r)}^2+s^2>1\}.$ Therefore, the stable region of the implicit fuzzy Euler scheme is the exterior of the circle in Figure 7, while the stable region of the explicit fuzzy Euler scheme and the semi-implicit fuzzy Euler scheme are the interior of the circle in Figure 5 and Figure 6.

We find that when $\alpha =\frac{4}{9}$, the stable region of the semi-implicit fuzzy Euler scheme is larger than the explicit fuzzy Euler scheme, and the stable region of the implicit fuzzy Euler scheme is the biggest. Therefore, for (8), the MS stability of the semi-implicit fuzzy Euler scheme is better than that of the explicit fuzzy Euler scheme, and the implicit method has the best stability properties except in the case in which the value of the normal fuzzy variable $\xi$ is in the neighborhood of $(1-r)/s$.

6. Conclusions

In this paper, we gave definitions of asymptotical stability, MS stability, exponential stability and A stability, and obtained that MS stability and exponential stability are equivalent. The stability properties of fuzzy Euler methods were studied via the linear test equations. The comparison of the stabilities of three fuzzy Euler methods are listed in

Table 1. Stabilities of three fuzzy Euler methods.

Stabilities	Asymptotical Stability	MS Stability Exponential Stability	A Stability
$\mathrm{explicit}\mathrm{fuzzy}\mathrm{Euler}\mathrm{scheme}$	$\mathrm{stable}$	$\mathrm{stable}$	$\mathrm{stable}$
$\mathrm{semi}-\mathrm{implicit}\mathrm{fuzzy}\mathrm{Euler}\mathrm{scheme}$	$\mathrm{more}\mathrm{stable}$	$\mathrm{more}\mathrm{stable}$	$\mathrm{more}\mathrm{stable}$
${\mathrm{implicit}\mathrm{fuzzy}\mathrm{Euler}\mathrm{scheme}}^1$	$\mathrm{best}\mathrm{stable}$	$\mathrm{best}\mathrm{stable}$	$\mathrm{best}\mathrm{stable}$
${\mathrm{implicit}\mathrm{fuzzy}\mathrm{Euler}\mathrm{scheme}}^2$	$\mathrm{unstable}$	$\mathrm{unstable}$	$\mathrm{unstable}$

.

Note that, in Table 1, the implicit fuzzy Euler scheme ${}^1$ expresses the implicit fuzzy Euler scheme where $\xi$ is out of the neighborhood of $(1-r)/s$ and the implicit fuzzy Euler scheme ${}^2$ expresses the implicit fuzzy Euler scheme where $\xi$ is in the neighborhood of $(1-r)/s$.