Abstract
We propose a separable, reversible watermarking scheme in encrypted images for privacy preservation. The Paillier cryptosystem is used for separable detection and decryption. Users may want to use cloud services without exposing their content. To preserve privacy, the image owner encrypts the original image using a public key cryptosystem before sending it to the cloud. Cloud service providers can embed the watermark into encrypted images by using a data-hiding key without knowing and destroying the original image. Even though the cloud service providers do not know the original image content, they can use the data-hiding key to detect the watermark from the encrypted image for authentication. Besides, the image owner can use the private key to directly decrypt the watermarked encrypted image to get the original image without any distortion due to its homomorphic property. Experimental results show the feasibility of the proposed method, which can provide efficient privacy-preserving authentication without degrading security.
1. Introduction
With the explosive growth in Internet technology, a large number of people may share or process their data over social networks. Cloud-based services are an obvious commercial opportunity that has expanded aggressively into the whole world in recent years. That means cloud-based businesses are booming so much that many cloud service providers are going to enter the cloud-based industry. Cloud service providers provide cloud-based storage services that allow users to upload data into cloud storage. However, image owners may not want to expose their private content to cloud service providers. Semi-trusted cloud service providers impel owners to encrypt their private images before sending them to the cloud [1,2,3,4]. Traditional data hiding or watermarking usually occurs before encryption or after decryption, which exposes private content to the data-hider. Therefore, it is desired that encrypted images can be directly processed without exposing the original image content. Reversible watermarking in encrypted images provides a potential solution for privacy preserving and encrypted image authentication [1].
Zhang [1] first proposed a novel reversible data-hiding scheme for encrypted images. He used a stream cipher to encrypt the image and then embedded the secret data by modifying a small region of the encrypted image. The original image can be perfectly recovered if the embedded data are extracted successfully. Hong et al. [5] proposed an improved version of Zhang’s method [1] in encrypted images. For each block, they used side matching to embed one bit by flipping three least significant bits (LSB) of a set of pixels. The error rate of extracted secret bits can be further decreased by measuring the smoothness of blocks. Previous methods embedded data by reversibly vacating room from the encrypted images, which may lead to some errors upon data extraction and image restoration. In 2013, Ma et al. [6] proposed a reversible data-hiding method by reserving room before encryption. They can achieve real reversibility, which means that data extraction and image recovery are free of any errors.
Cao et al. [7] used the patch level sparse representation to propose a reversible data-hiding method. Sparse coding is applied to generate a large, vacated room, and thus more secret messages can be embedded in the encrypted image. Liu and Pun [8] transferred redundant space of the original image to the encrypted image in order to embed secret data. Fu et al. [9] utilized the block permutation and stream cipher to encrypt the original image and compressed the most significant bit (MSB) layers of embeddable blocks to vacate room for data hiding. In 2020, Su et al. [10] presented reversible data hiding in an encrypted absolute moment block truncation coding (AMBTC) compressed image. AMBTC is lossy image compression that has lower storage costs and computation. The AMBTC compression codes are encrypted to vacate redundant room to embed secret messages.
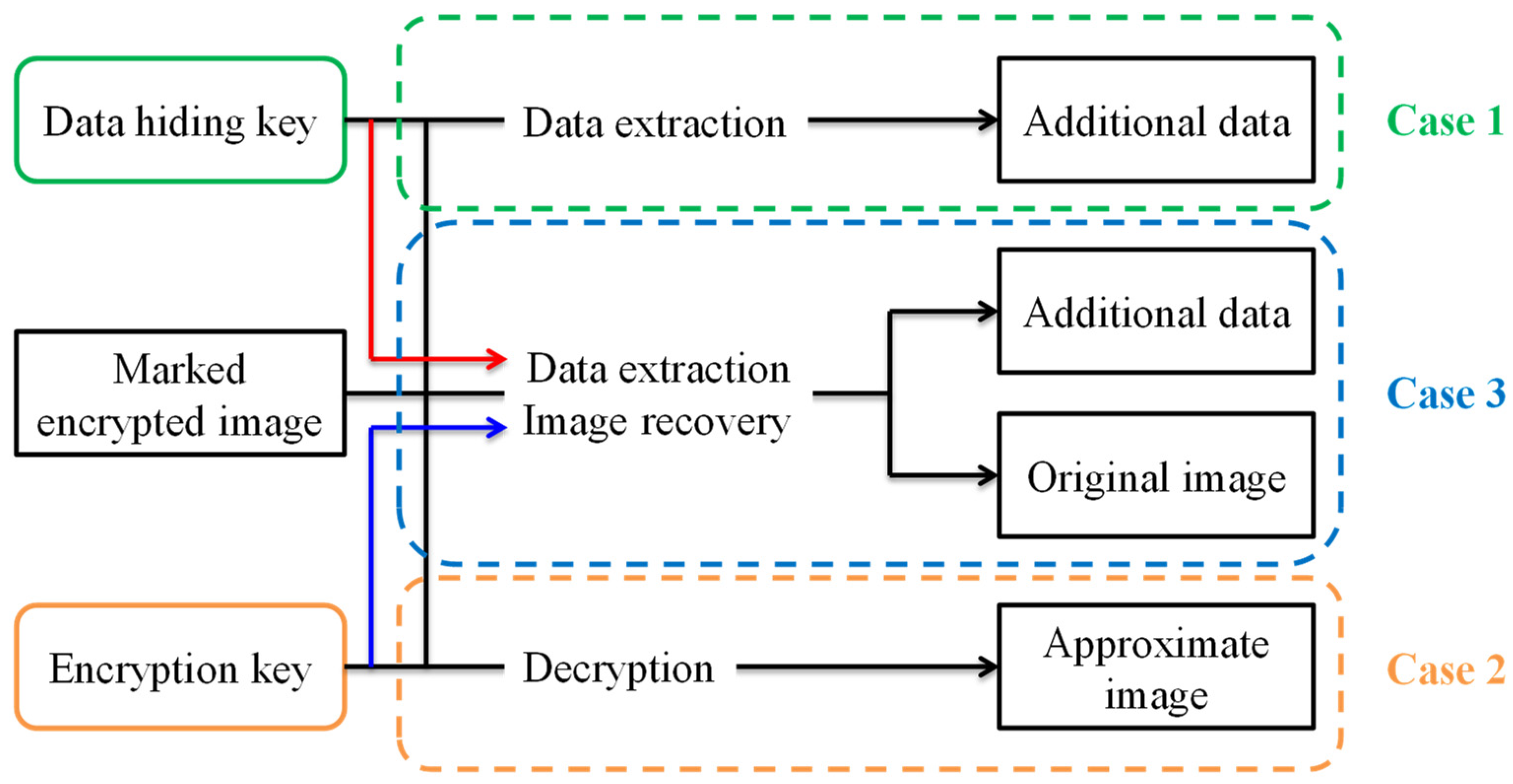
In most methods, image decryption and secret data extraction need to be performed together. The original image has to be revealed in order to extract the secret data. In this way, the receiver who has no decryption key will have unauthorized access to image content. Hence, Zhang [2] first proposed a novel scheme for separable reversible data hiding in encrypted images. Three cases are presented at the receiver side as illustrated in Figure 1. First, if a receiver has the data-hiding key, he can extract the secret data without knowing the image content. Second, if the receiver has the encryption key, he cannot extract the secret data but he can decrypt the encrypted image to get a lossy original image. Third, when the amount of secret data is not too large, if the receiver has both the data-hiding key and the encryption key, he can extract the secret data and completely recover the original image without any errors.
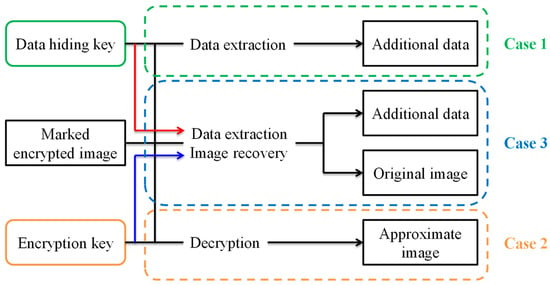
Figure 1.
Three cases at the receiver side.
In 2016, Xu and Wang [11] utilized a stream cipher to encrypt interpolation-error of pixels and reversibly embedded secret data into interpolation-error in an encrypted domain by using histogram shifting and difference expansion. In their method, data extraction can be performed either in the encrypted domain or in the decrypted domain. Huang et al. [3] preserved the correlation between neighboring pixels in the encrypted domain. Therefore, the previously proposed reversible data-hiding schemes can be directly applied to the encrypted image. In their proposed framework, the reversible data-hiding scheme is independent of the image encryption algorithm. Qian and Zhang [4] compressed the bits selected from the encrypted image to make room for embedding secret data. The selected bits are encoded by low density parity check codes. In 2018, Qin et al. [12] proposed a high-capacity reversible data-hiding scheme in encrypted image with separable capability. They used a block-based stream cipher to encrypt the original image. The encrypted blocks were processed by run-length coding to vacate space for embedding additional data. At the receiver size, a directly-decrypted image similar to the original image can be generated using the encryption key, and the additional data can be extracted by using the data-hiding key.
Qin et al. [13] used an analogues stream cipher and block permutation to encrypt the original image blocks. The encrypted blocks were classified into smooth and complex regions, and LSBs of the smooth blocks were compressed to make spare space for embedding additional data. They provided separable operations of data extraction and decryption and image recovery according to the availability of the encryption key and data-hiding key. In 2019, Ge et al. [14] encrypted image blocks using a stream cipher algorithm and embedded additional data into the peak pixels using histogram shifting inside each encrypted block. They further constructed a multi-level approach that iterated the embedding process to generate the watermarked encrypted images. Wu et al. [15] considered spatial correlation in the entire original image and proposed parametric binary tree labeling to label encrypted pixels for embedding secret data. Bhardwaj and Aggarwal [16] improved block-based, joint-encrypted, image-reversible data-hiding algorithms by embedding n secret bits into n sub-blocks.
In 2022, Wang et al. [17] proposed a separable, reversible data-hiding scheme in encrypted images, using pixel rotation to embed data into the encrypted image. Four decrypted rotation states are considered to completely recover the image. Meng et al. [18] used an integer wavelet transform and a chaotic system to reversibly embed a watermark into the encrypted image. They encrypted the LL component of the wavelet domain by the chaotic system and embedded the watermark into the HH component. However, they had to solve the extra pixel overflow problem that occurred when image reconstruction after LL was encrypted.
These methods use a stream cipher algorithm to encrypt the original image. It is difficult to find the extra space for embedding additional data in the encryption domain. Hence, the data-hider has to preprocess the original image or extract some features of the image in order to embed additional data. Preprocessing the original image in advance may leak image content to the data-hider, which does not guarantee preservation of privacy. Furthermore, the image owner may also realize the embedding position and the embedded data. The security of the embedded data cannot be guaranteed. In addition, embedding data into the ciphertext by using symmetric key cryptography inevitably changes the ciphertext, leading to incorrect decryption. We expect that directly decrypting the watermarked encrypted image using only the encryption key shall not completely recover the original image. As shown in Figure 1, data extraction should be performed before image recovery if we want to completely recover the original image without any errors.
In terms of privacy-preserving applications, the security of the image content and the embedded data should be considered. Note that the owner does not allow others to access the image content, and the server manager does not allow others to crack the embedding data and the data-hiding key. The owner can perform the entire reversible data-hiding scheme only if the owner has knowledge of the watermarking technique and the computation capability of data hiding. It may be impractical for the general public if the owner is involved in watermark embedding and extraction. Thus, it is important that only the owner can conduct image encryption and decryption, and only the server manager can conduct the reversible data-hiding algorithm. Alternatively, image encryption and decryption performed at the owner end should be independent of the watermarking algorithm conducted at the server end.
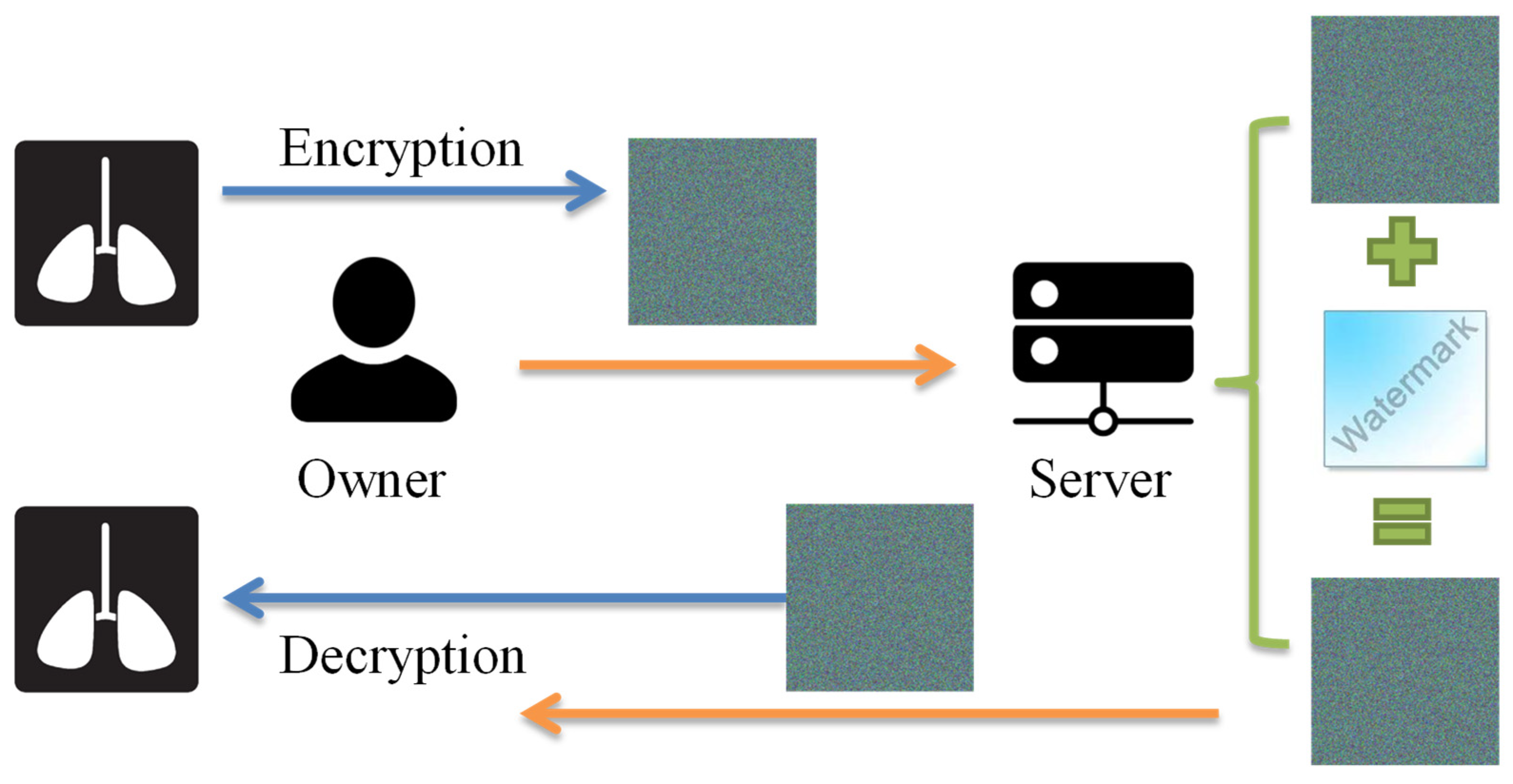
In order to avoid the exposure of private content and completely separate the owner and the data-hider, we proposed a new separable framework for reversible watermarking of encrypted images as shown in Figure 2. To prevent private content from being exposed, the owner first encrypts the original image by using the Paillier cryptosystem before sending it to cloud-based services. For the purpose of image authentication or content notation, the server managers can embed the watermark directly into encrypted images without knowing and destroying the original image content. In our proposed separable framework, only two cases occurred at the receiver side. Watermark extraction and image decryption are totally independent. Though server managers do not know the original content, they can use the data-hiding key to detect the watermark from the watermarked encrypted image for authentication. Besides, the homomorphic property of the Paillier cryptosystem enables the image owner to directly decrypt the watermarked encrypted image to get the original image without any errors despite the fact that the owner does not know what and where the embedded watermark is. Compared with other schemes using a stream cipher for encryption, the proposed separate framework provides more appropriate cloud applications to preserve confidentiality.
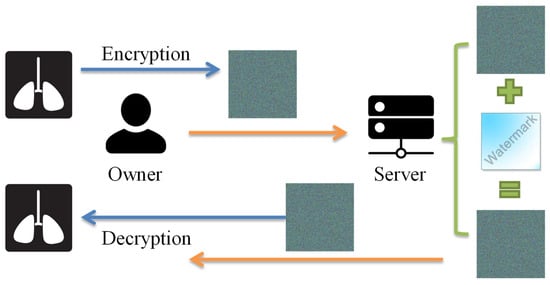
Figure 2.
A separable framework for reversible watermarking in encrypted images.
The paper is organized as follows. In Section 2, we introduce the Paillier cryptosystem and its homomorphic properties. The proposed separable reversible watermarking method in encrypted images is presented in Section 3, where we also describe separate watermark detection and image decryption. The proposed method is experimentally validated in Section 4. Finally, the paper is concluded in Section 5.
2. Paillier Cryptosystem
The Paillier cryptosystem, invented by P. Paillier [19] in 1999, is an asymmetric key encryption algorithm for probabilistic public key cryptography. Security depends on the difficulty of computing discrete logarithms. The Paillier cryptosystem is described as follows.
• Key generation
Choose two large primes p and q randomly such that gcd(pq, (p − 1)(q − 1)) = 1 and compute n = pq, λ = lcm (p − 1, q − 1). The public key is (n, g), where g in is a random integer that should satisfy gcd(L(gλ mod n2), n) = 1, where . The private key is (λ, μ), where μ = (L(gλ mod n2))−1 mod n.
• Encryption
Let m ∈ be a message to be encrypted. Randomly select an integer r ∈ and compute the ciphertext with public key
where c is the ciphertext of m and E is the encryption function.
c = E(m, r) = gm·rn mod n2
• Decryption
Let c ∈ be the ciphertext to decrypt; compute the plaintext with private key
where m is the plaintext of c, and D is the decryption function.
m = D(c) = L(cλ mod n2)·μ mod n
• Homomorphic properties
In the Paillier cryptosystem, homomorphic properties with non-deterministic encryption are suitable features for privacy-preserving applications. Homomorphic addition means the product of two ciphertexts will decrypt to the sum of their corresponding plaintexts. Given two encryption functions E(m1, r1) and E(m2, r2), we can compute
E(m1, r1)·E(m2, r2) = gm1 + m2·(r1r2)n mod n2 = E(m1 + m2, r1r2).
Therefore, we can get
D(E(m1, r1)·E(m2, r2)) = m1 + m2.
Homomorphic multiplication means that a ciphertext raised to the power of a constant will decrypt to the product of the plaintext and the constant. The identity can be described as
D(E(m1, r1)k mod n2) = km1.
The Paillier cryptosystem provides semantic security against chosen-plaintext attacks. The decisional composite residuosity assumption is believed to be intractable. Hence, the Paillier cryptosystem is considered provably secure due to the fact that semantic security can be reduced to solving some hard mathematical problem.
3. Proposed Method
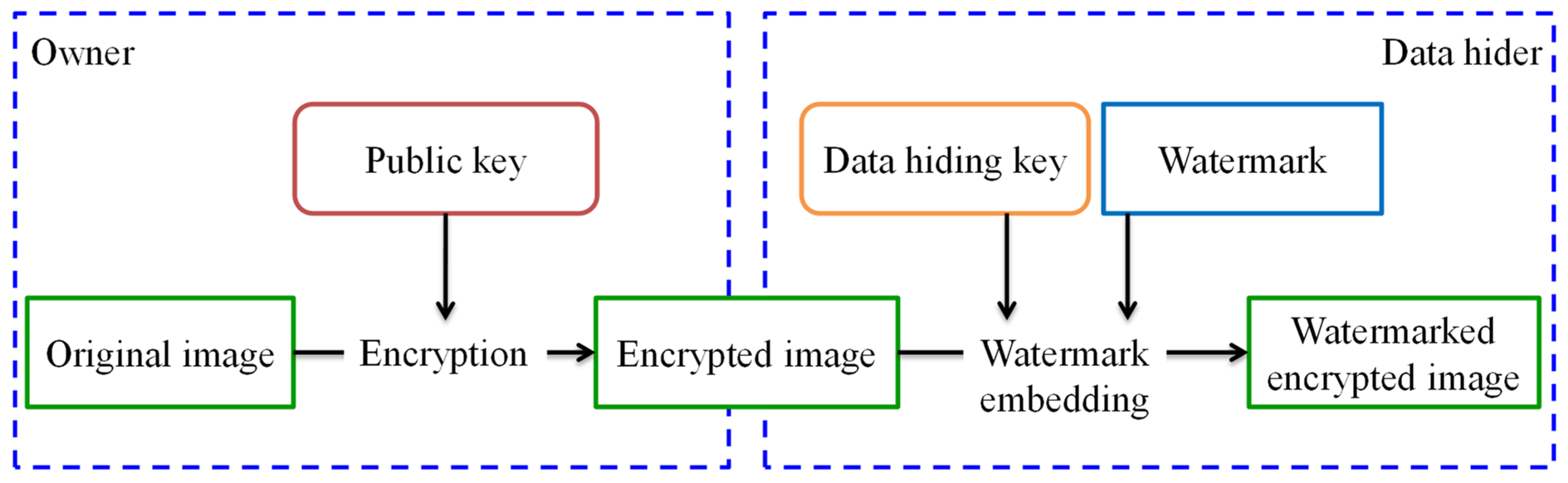
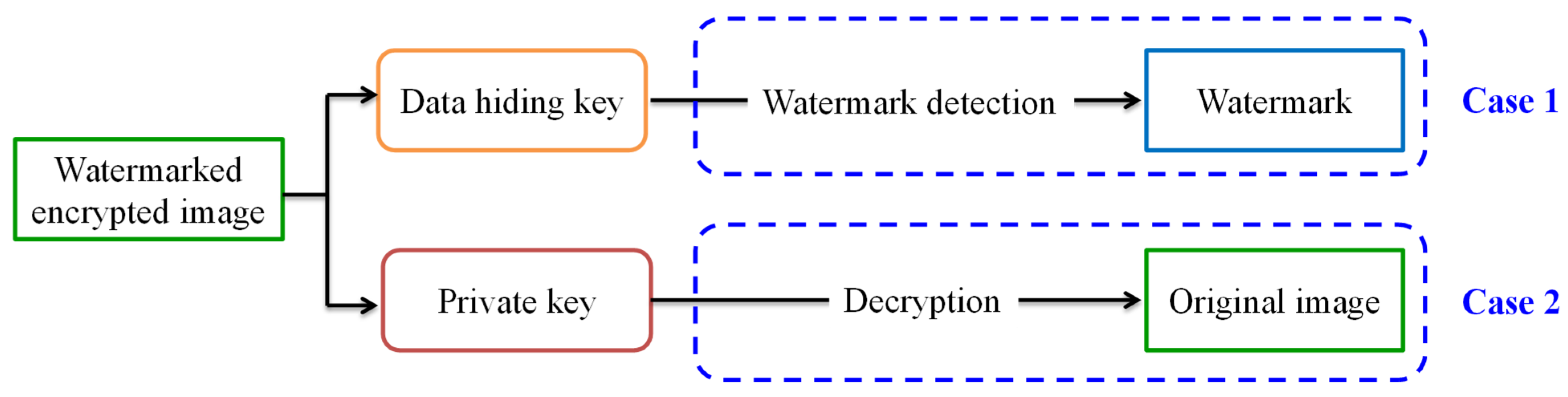
In this section, a new separable framework for reversible watermarking in encrypted images is proposed. The watermarking flowchart is shown in Figure 3. To prevent private content from being exposed to cloud service providers, the owner first encrypts the original image by using the Paillier cryptosystem before sending it to the cloud services. For image authentication or content notation, the cloud service provider embeds the watermark directly into encrypted images without knowing and destroying the original image content. At the receiver side, the proposed separable framework is presented in Figure 4. There are two cases at the receiver side in which watermark detection and image decryption are totally independent. The cloud service provider who has the data-hiding key can detect the watermark from the watermarked encrypted image for authentication, though he does not know the original content. For the image owner who only has the private key, he does not know what and where the embedded watermark is, whereas he can use the homomorphic property of the Paillier cryptosystem to directly decrypt the watermarked, encrypted image to completely recover the original image. In other words, watermark embedding does not affect decryption of the plaintext. Therefore, decryption of the plaintext can be performed before watermark detection. That also means that watermark detection and image decryption are not interactive.
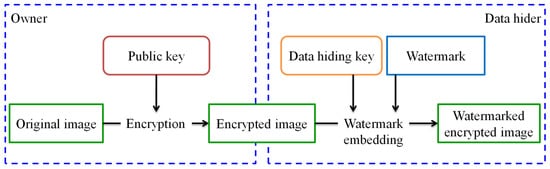
Figure 3.
The watermarking flowchart.
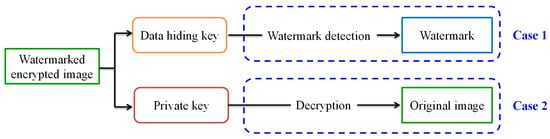
Figure 4.
The proposed separable framework.
3.1. Image Encryption
In this phase, the image owner encrypts the original plaintext image using the Paillier cryptosystem, which is probabilistic public key cryptography. Assume that the original image is an 8-bit grayscale image and the pixel value m(i, j) denotes the pixel value at position (i, j). The detailed encryption procedure is as follows.
- Step 1.
- For each pixel group m(i, j) and m(i, j + 1), compute their corresponding ciphertext values with public keywhere E is the encryption function described in Equation (1) and r is a random value in .c(i, j) = E(m(i, j), r(i, j))·E(m(i, j + 1), r(i, j + 1))
c(i, j + 1) = E(m(i, j), r(i, j))·E(m(i, j + 1), r(i, j + 1))−1 - Step 2.
- Describe each ciphertext value as the 24-bit color pixel values.
3.2. Watermark Embedding
When having access to the encrypted image, the cloud service provider can embed the watermark directly into it without any distortion of the original content. Supposing the encrypted image is a 24-bit color image and pixel value c(i, j) is represented as the ciphertext value at position (i, j).
- Step 1.
- Generate the embedding sequence using the data-hiding key.
- Step 2.
- According to the embedding sequence, embed the watermark in each encrypted pixel group c(i, j) and c(i, j + 1) aswhere w(i, j) denotes the watermarked encrypted pixel value at position (i, j), and b is the watermark bit.
3.3. Watermark Detection
After receiving the watermarked encrypted image, the data hider, who only has the data-hiding key, can detect the watermark. Let w(i, j) be the watermarked encrypted pixel value at position (i, j).
- Step 1.
- Generate the embedding sequence using the data-hiding key.
- Step 2.
- According to the embedding sequence, detect the watermark bit b in each watermarked encrypted pixel group w(i, j) and w(i, j + 1) as
3.4. Image Decryption
When getting the watermarked encrypted image from the cloud service, the owner, who has the private key, can directly decrypt it to obtain the original image even though the watermark has not been removed by the data hider. Let w(i, j) be the watermarked encrypted pixel value at position (i, j). For each watermarked encrypted pixel group w(i, j) and w(i, j + 1), the owner can decrypt it with the private key as
where D is the decryption function described in Equation (2).
Although the encrypted image contains the watermark, the decrypted image is the same as the original image due to the homomorphic properties of the Paillier cryptosystem. We show an example of the proposed method as follows. Let m(i, j) = 128 and m(i, j + 1) = 122 be an original pixel group, (3599, 3600) be the public key, (1740, 1109) be the private key, and b = 1 be the watermark bit. The owner encrypts m(i, j) and m(i, j + 1) as c(i, j) = 10,388,635 and c(i, j + 1) = 10,913,649. The data hider embeds a watermark bit into c(i, j) and c(i, j + 1) to generate w(i, j) = 10,913,649 and w(i, j + 1) = 10,388,635. At the receiver side, the data hider can detect watermark bit 1 since w(i, j) ≥ w(i, j + 1). Without removing the watermark, the owner can directly decrypt the watermarked encrypted pixel by calculating m(i, j) = D(10,913,649 × 10,388,635) × 2−1 mod 3599 = 128 and m(i, j + 1) = |D(10,913,649 × 10,388,635−1) − 3599| × 2−1 mod 3599 = 122. Therefore, our proposed method provides a separate framework for watermark detection and image decryption without leaking private content, which is suitable for privacy-preserving applications.
4. Experimental Results
In this section, we conduct several experiments to evaluate the performance of our proposed scheme. As shown in Figure 5, three representative grayscale images sized 512 × 512, Lena, Baboon, and Peppers, including smooth or complex textures, are used as the original images in the experiments. Figure 6 shows the encrypted images encrypted using the Paillier cryptosystem. From Figure 6, we cannot see any contours of the original image in the encrypted image. The Paillier cryptosystem, which is a probabilistic encryption algorithm, is considered provably secure. Unlike deterministic encryption, plaintext repeatedly encrypted with the same key will yield different ciphertext in the Paillier cryptosystem.

Figure 5.
Original image. (a) Lena. (b) Baboon. (c) Peppers.

Figure 6.
Encrypted image. (a) Lena. (b) Baboon. (c) Peppers.
A total of (512 × 512)/2 = 131,072 watermark bits are embedded in each encrypted image. Figure 7 shows the watermarked encrypted images. The encrypted images seem to be the same as the watermarked encrypted images since no modifications are made in the ciphertext after embedding the watermark. Unlike other methods, we just change the position of ciphertext rather than using LSB embedding to destroy the ciphertext. That also means we can maintain the security of ciphertext after embedding the watermark.

Figure 7.
Watermarked encrypted image. (a) Lena. (b) Baboon. (c) Peppers.
Figure 8 presents the image decryption results. Without removing the watermark in advance, the homomorphic properties of the Paillier cryptosystem enable the owner to directly decrypt the watermarked encrypted image to obtain the original image. In Table 1, we give an example of how fast the embedding based on the Paillier cryptosystem runs on a computer. We simulated embedding 131,072 watermark bits into an image with 512 × 512 pixels. We measured the time taken to perform the encryption, embedding, and decryption on various images. The test was implemented in Python on a personal computer with an Intel Core i7-10510U 1.80 GHz CPU, 16 GB RAM, and 64-bit Windows 10 system. As we know, asymmetric encryption takes relatively more time than symmetric encryption. Our proposed method takes about 30 s for image encryption and 50 s for image decryption. The Paillier cryptosystem takes a little time for image encryption and decryption, whereas it provides the homomorphic properties that allow us to perform a variety of computations on the encrypted image while keeping the content confidential. Different from encryption using a stream cipher, homomorphic encryption is a valuable capability that enables privacy-preserving tasks to be accomplished in untrusted cloud environments. Therefore, the proposed method based on homomorphic properties can provide a separate framework for watermark detection and image decryption without exposing private content to semi-trusted cloud service providers.

Figure 8.
Image decryption. (a) Lena. (b) Baboon. (c) Peppers.

Table 1.
The computation time of the proposed method.
4.1. Encrypted Image Analysis
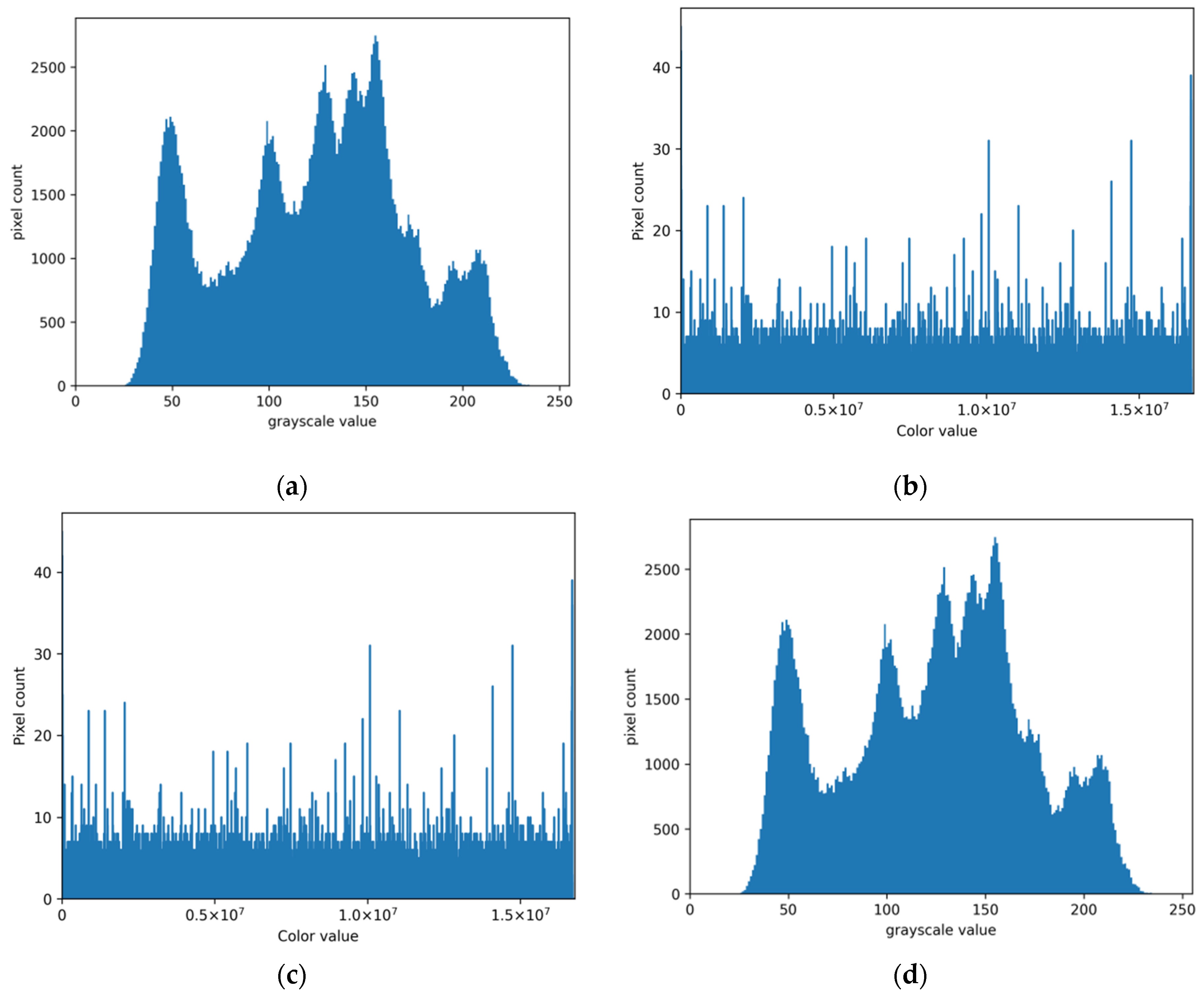
For an encryption realized using public key cryptography, the expected frequency distribution of pixel values is fairly uniform. To see the distribution of encrypted pixel values, we first use histogram analysis to evaluate the encrypted image quality. Figure 9 shows the histograms of images processed by the proposed scheme. We can see in Figure 9 that Figure 9a is the same as Figure 9d since the original image can be directly decrypted from the watermarked encrypted image without any errors. From Figure 9b,c, we also notice that the histograms of the encrypted image before and after watermark embedding are the same due to the fact that the embedding does not change the frequency of each pixel value. Furthermore, every value in the encrypted image occurs roughly the same number of times. It is intuitively clear that the distribution of encrypted pixel values is relatively uniform and has no relationship with the original image histogram.
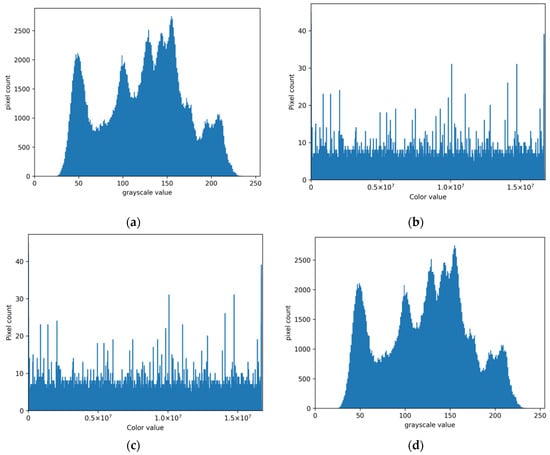
Figure 9.
Histogram analysis. (a) Original Lena image histogram. (b) Encrypted Lena image histogram. (c) Watermarked encrypted Lena image histogram. (d) Decrypted Lena image histogram.
We further use information entropy to measure the randomness and uncertainty in an image. Information entropy can be viewed as the degree of uniformness of a random variable. The information entropy H(X) of an image X is defined as
where x is the pixel and P(x) is probability of x. Table 2 lists the information entropy of each test image. The higher the information entropy of an image, the more the image is disordered. Note that the information entropies of the encrypted image before and after watermark embedding are the same. The information entropy of encrypted images is fairly close to the upper bound of 8, which represents a uniform distribution with 256 levels. Thus, security can be perfectly guaranteed.

Table 2.
Information entropy of each test image.
4.2. Performance Comparison
To better understand how different embedding capacities affect the performance of the proposed method, the embedding rate and peak signal-to-noise ratio (PSNR) are used to evaluate performance. The embedding rate is defined as the average bits that each pixel can carry. PSNR used to measure visual quality between two images is defined as
where MSE denotes the mean square error defined by
where O(i, j) denotes a pixel value of one image at position (i, j), R(i, j) denotes a pixel value of another image at position (i, j), and M × N is the image size.
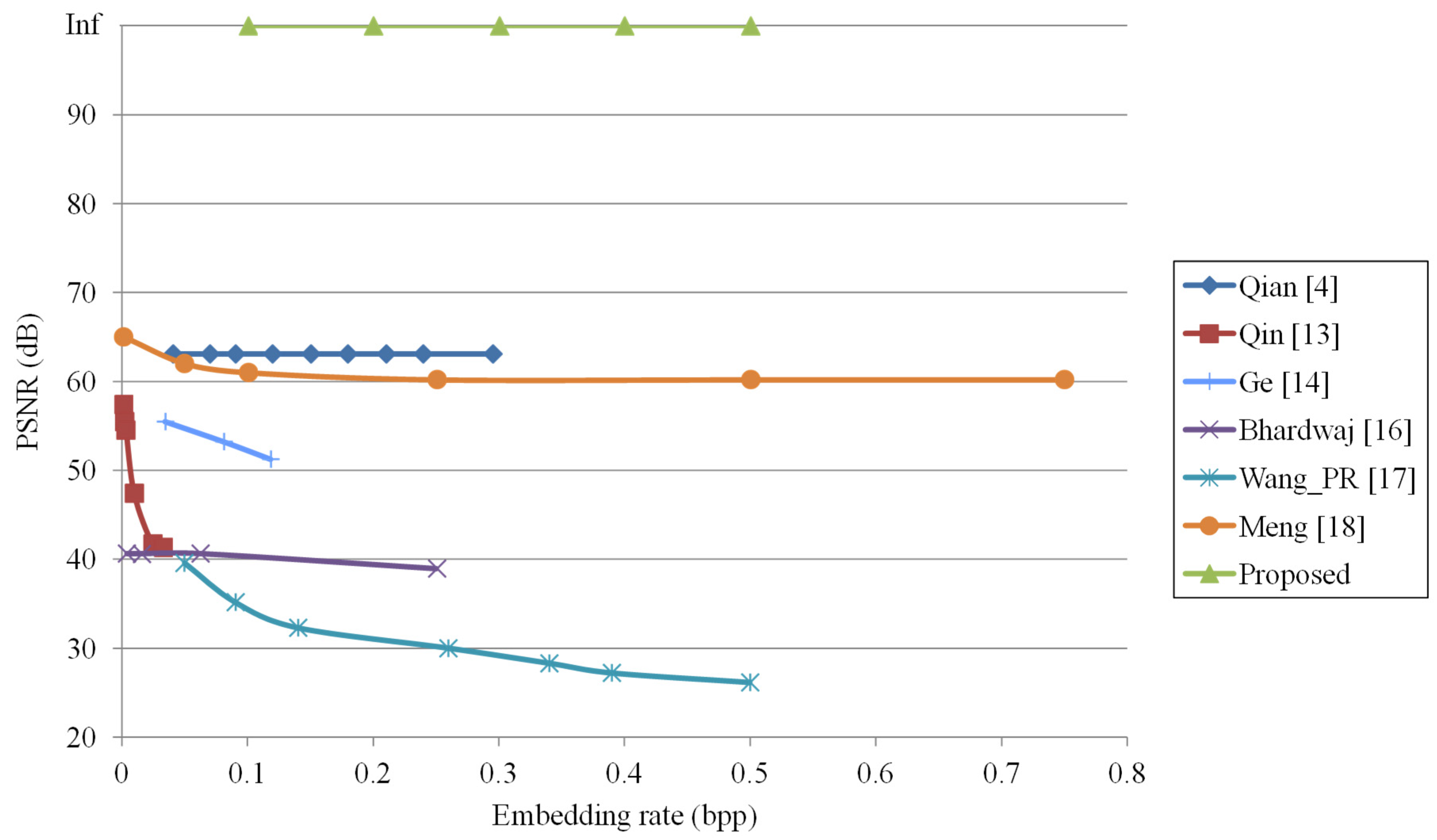
We note that different images do not affect the performance of the proposed method. Figure 10 shows the performance comparison of the embedding rate with PSNR for Lena with other methods [4,13,14,16,17,18]. The PSNR values between the original image and the directly decrypted image are given in our experiments. We can see in Figure 10 that the PSNRs of directly decrypted images in our proposed method are always infinite regardless of the embedding rate since the original image can be completely recovered from the watermarked encrypted image without performing watermark extraction. Other methods [4,13,14,16,17,18] cannot directly recover the original image with only the encryption key. From Figure 10, the performance derived from the proposed method is significantly better than that of other methods [4,13,14,16,17,18]. However, our maximum embedding rate is 0.5 bpp, which is lower than that of method [18] since we use two encrypted pixels to embed the 1-bit watermark.
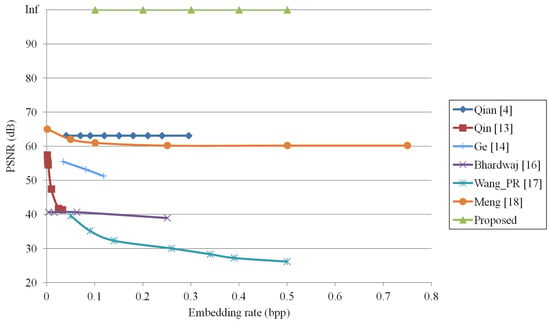
Figure 10.
Performance comparison for Lena with other methods [4,13,14,16,17,18].
Feature comparison with other methods [4,13,14,16,17,18] is further summarized in Table 3. Other methods [4,13,14,16,17,18] use symmetric cryptography to encrypt the original image. We can also see in Table 3 that hiding data in the encrypted image in their methods leads to some direct decryption errors. They cannot directly decrypt the original image due to the distortion introduced by hiding data in the ciphertext. Thus, they need the third case that uses both the encryption key and the data-hiding key to completely recover the original image at the receiving end. This may expose image content or embedded data. In our method, the homomorphic property of the Paillier cryptosystem enables the owner to directly decrypt the watermarked encrypted image to get the original image without using the data-hiding key. As a result, image encryption and decryption conducted at the owner end are independent of the watermarking algorithm conducted at the server end. Note we have a limitation in image encryption since the Paillier cryptosystem will expand the size from plaintext to ciphertext. Although the Paillier cryptosystem expands data, it provides the probabilistic property that can encrypt a single plaintext to many possible ciphertexts.

Table 3.
Feature comparison.
5. Conclusions
Reversible, encrypted data-hiding is useful in cloud services to preserve confidentiality. However, most methods need to preprocess the original image to embed data in the encrypted domain, or to remove embedded data before completely recovering the original image. Besides, embedding data in images encrypted using a stream cipher distorts the cryptographic security. Those preprocessing operations expose private content to the data hider. Therefore, we proposed a new separable framework for reversible watermarking of encrypted images using public key cryptography in order to completely separate the owner and the data hider and avoid leaking private content. In the proposed method, the owner encrypts the original image using the Paillier cryptosystem to prevent private content from being exposed. The data hider embeds the watermark into the encrypted image without preprocessing the original image. In our proposed separable framework, the owner can directly decrypt the watermarked encrypted image without removing the watermark in advance to get the original image using the homomorphic property of the Paillier cryptosystem. Compared with other schemes based on stream cipher encryption, the proposed method provides more appropriate cloud services with higher security for privacy preservation.
Author Contributions
Formal analysis, Y.-F.C. and W.-L.T.; Methodology, Y.-F.C. and W.-L.T.; Writing—original draft, W.-L.T.; Writing—review and editing, Y.-F.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
This work was supported in part by the Ministry of Science and Technology under grants MOST 110-2221-E-025-012- and MOST 110-2221-E-025-014-MY2.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, X. Reversible data hiding in encrypted image. IEEE Signal Process. Lett. 2011, 18, 255–258. [Google Scholar] [CrossRef]
- Zhang, X. Separable reversible data hiding in encrypted image. IEEE Trans. Inf. Forensics Secur. 2012, 7, 826–832. [Google Scholar] [CrossRef]
- Huang, F.; Huang, J.; Shi, Y.Q. New framework for reversible data hiding in encrypted domain. IEEE Trans. Inf. Forensics Secur. 2016, 11, 2777–2789. [Google Scholar] [CrossRef]
- Qian, Z.; Zhang, X. Reversible data hiding in encrypted images with distributed source encoding. IEEE Trans. Circuits Syst. Video Technol. 2016, 26, 636–646. [Google Scholar] [CrossRef]
- Hong, W.; Chen, T.S.; Wu, H.Y. An improved reversible data hiding in encrypted images using side match. IEEE Signal Process. Lett. 2012, 19, 199–202. [Google Scholar] [CrossRef]
- Ma, K.; Zhang, W.; Zhao, X.; Yu, N.; Li, F. Reversible data hiding in encrypted images by reserving room before encryption. IEEE Trans. Inf. Forensics Secur. 2013, 8, 553–562. [Google Scholar] [CrossRef]
- Cao, X.; Du, L.; Wei, X.; Meng, D.; Guo, X. High capacity reversible data hiding in encrypted images by patch-level sparse representation. IEEE Trans. Cybern. 2016, 46, 1132–1143. [Google Scholar] [CrossRef]
- Liu, Z.; Pun, C. Reversible data-hiding in encrypted images by redundant space transfer. Inf. Sci. 2018, 433–434, 188–203. [Google Scholar] [CrossRef]
- Fu, Y.; Kong, P.; Yao, H.; Tang, Z.; Qin, C. Effective reversible data hiding in encrypted image with adaptive encoding strategy. Inf. Sci. 2019, 494, 21–36. [Google Scholar] [CrossRef]
- Su, G.D.; Chang, C.C.; Lin, C.C. A high capacity reversible data hiding in encrypted AMBTC-compressed images. IEEE Access 2020, 8, 26984–27000. [Google Scholar] [CrossRef]
- Xu, D.; Wang, R. Separable and error-free reversible data hiding in encrypted images. Signal Process. 2016, 123, 9–21. [Google Scholar] [CrossRef]
- Qin, C.; He, Z.; Luo, X.; Dong, J. Reversible data hiding in encrypted image with separable capability and high embedding capacity. Inf. Sci. 2018, 465, 285–304. [Google Scholar] [CrossRef]
- Qin, C.; Zhang, W.; Cao, F.; Zhang, X.; Chang, C.C. Separable reversible data hiding in encrypted images via adaptive embedding strategy with block selection. Signal Process. 2018, 153, 109–122. [Google Scholar] [CrossRef]
- Ge, H.; Chen, Y.; Qian, Z.; Wang, J. A high capacity multi-level approach for reversible data hiding in encrypted images. IEEE Trans. Circuits Syst. Video Technol. 2019, 29, 2285–2295. [Google Scholar] [CrossRef]
- Wu, Y.; Xiang, Y.; Guo, Y.; Tang, J.; Yin, Z. An improved reversible data hiding in encrypted images using parametric binary tree labeling. IEEE Trans. Multimed. 2020, 22, 1929–1938. [Google Scholar] [CrossRef] [Green Version]
- Bhardwaj, R.; Aggarwal, A. An improved block based joint reversible data hiding in encrypted images by symmetric cryptosystem. Pattern Recognit. Lett. 2020, 139, 60–68. [Google Scholar] [CrossRef]
- Wang, X.; Chang, C.C.; Lin, C.C.; Chang, C.C. Reversal of pixel rotation: A reversible data hiding system towards cybersecurity in encrypted images. J. Vis. Commun. Image Represent. 2022, 82, 103421. [Google Scholar] [CrossRef]
- Meng, L.; Liu, L.; Wang, X.; Tian, G. Reversible data hiding in encrypted images based on IWT and chaotic system. Multimed. Tools Appl. 2022, 81, 16833–16861. [Google Scholar] [CrossRef]
- Paillier, P. Public-key cryptosystems based on composite degree residuosity classes. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Prague, Czech Republic, 2–6 May 1999; pp. 223–238. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).