A Novel Integrated Method for Harmonic Suppression and Reactive Power Compensation in Distribution Network
Abstract
:1. Introduction
- To restrict harmonic mitigation as per the IEEE 519-2014 standard in such a way that source currents are sinusoidal, irrespective of harmonic content in distorted source voltage and non-linear load.
- To eradicate the effect of poor load power factor, such that it results in an almost united power factor on the supply side.
- To decrease apparent power supplied from the source for given source voltage conditions.
2. Integration Mechanism of Harmonic Suppression and Reactive Power Compensation
2.1. Steps of Integrated Method for Harmonic Suppression and Reactive Power Compensation
- : Call the start and stop interrupt service.
- :Run interrupt service routine.
- :Stop interrupt service routine.
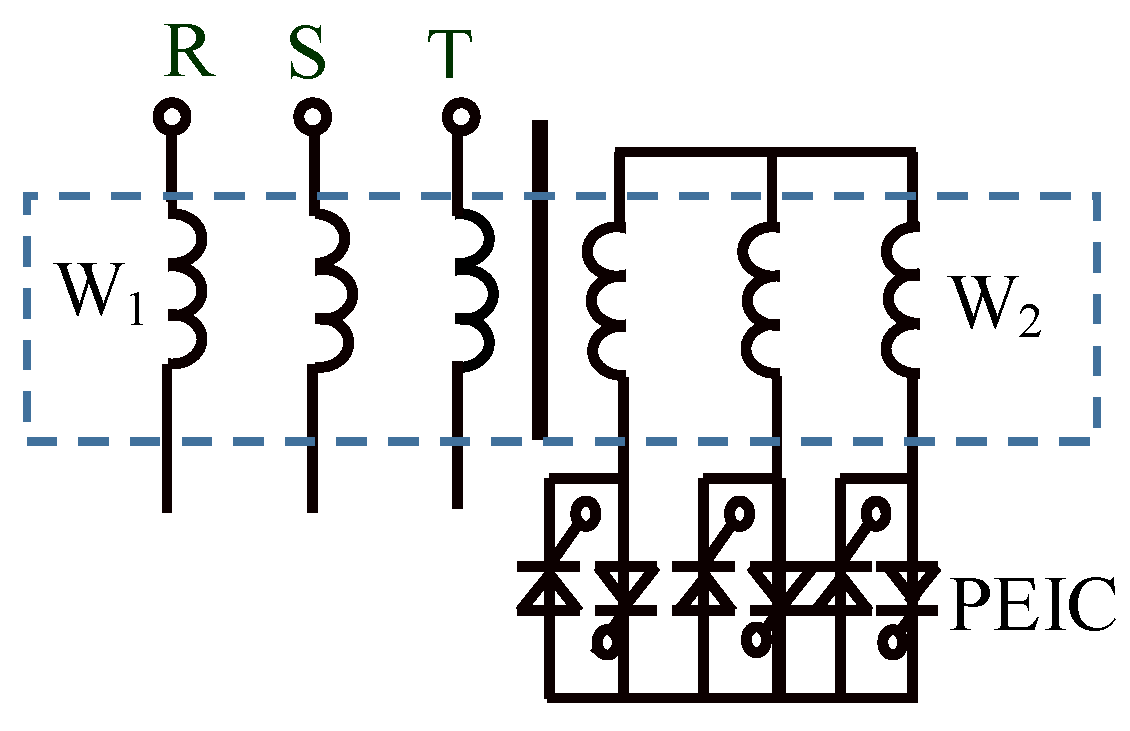
2.2. Topological Structure of the Integrated System
3. Harmonic Current Filtering Method of HFSS
- Propose the constraint conditions that must be met during dynamic tuning so as to improve the stability of HFSS while filtering out the h-order harmonic current;
- Adopt the minimum capacitance method to design the parameters of the electromagnetic coupling reactor (SS) and filter capacitors of the HFSS according to the h-order harmonic current that needs to be filtered out;
- Propose the method for adjusting the inductance of the SS; that is, the power electronic impedance converter (PEIC) adjusts the equivalent inductance of SS to by adjusting its thyristor trigger angle according to the desired control signal ;
- Uses the two-step optimization algorithm to get the control signal needed to make h-order harmonic current flowing into the HFSS to reach the maximum;
- Switch on and off the filter capacitor bank C–C by controlling the on/off of the contactors KM–KM, so as to obtain the equivalent capacitance C required for reactive power compensation. Thus, L and C form a low impedance loop so that the harmonic current in the power distribution system flows directly into the filter subsystem to filter out harmonics.
3.1. Dynamic Tuning Condition for HFSS
- Condition 1: The h-order harmonic current generated by the the nonlinear load must be less than or equal to the maximum h-order harmonic current that the HFSS can filter.
- Condition 2: Let be the allowable h-order harmonic current into the public grid prescribed in the Harmonics standards (IEEE Std 519—2014), and the HFSS is tuned when the h-order harmonic current in the grid is larger than ; otherwise, the HFSS continues to output the control signal (k−1) from the previous moment.
3.2. Parameter Design of Filter Capacitors
3.3. Parameter Design of Electromagnetic Coupling Reactor
- step 1: Inductance of primary reactance windin
- step 2: Rated voltage
- step 3: Rated current
- step 4: Rated capacity of electromagnetic coupling reactor
3.4. Parameter Checking of Filter Capacitor
- Current checking
- Peak voltage
3.5. Parameter Design System of HFSS
- Parameters setting module
- Capacitor design module
- Inductance design module
- Checking capacitance parameters module
- Result output module
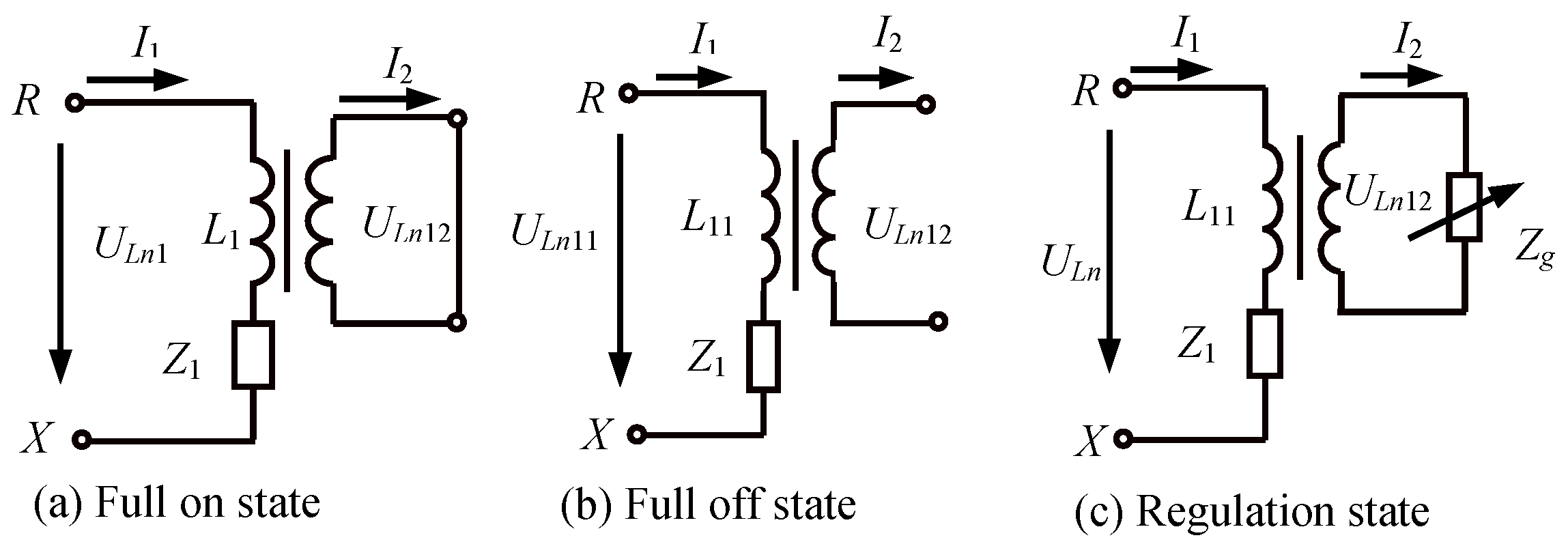
3.6. Inductance Regulation of Electromagnetic Coupling Reactor
- When , the thyristors are fully turned on, in which case the primary inductance of SS is the minimum, denoted by .
- When , the thyristors are fully switched off, in which case the primary inductance of SS is the maximum, denoted by .
- The inductance of SS ranges within [, ]. By adjusting the trigger angle of the thyristor, the primary inductance of SS can be continuously adjusted in this range, and its value will increase with the rising trigger angle .
- When , the linearity of the primary inductance is relatively good, so it is the optimal regulation range.
- The variation of the magnetic circuit of SS is complex and thus difficult to control quantitatively.
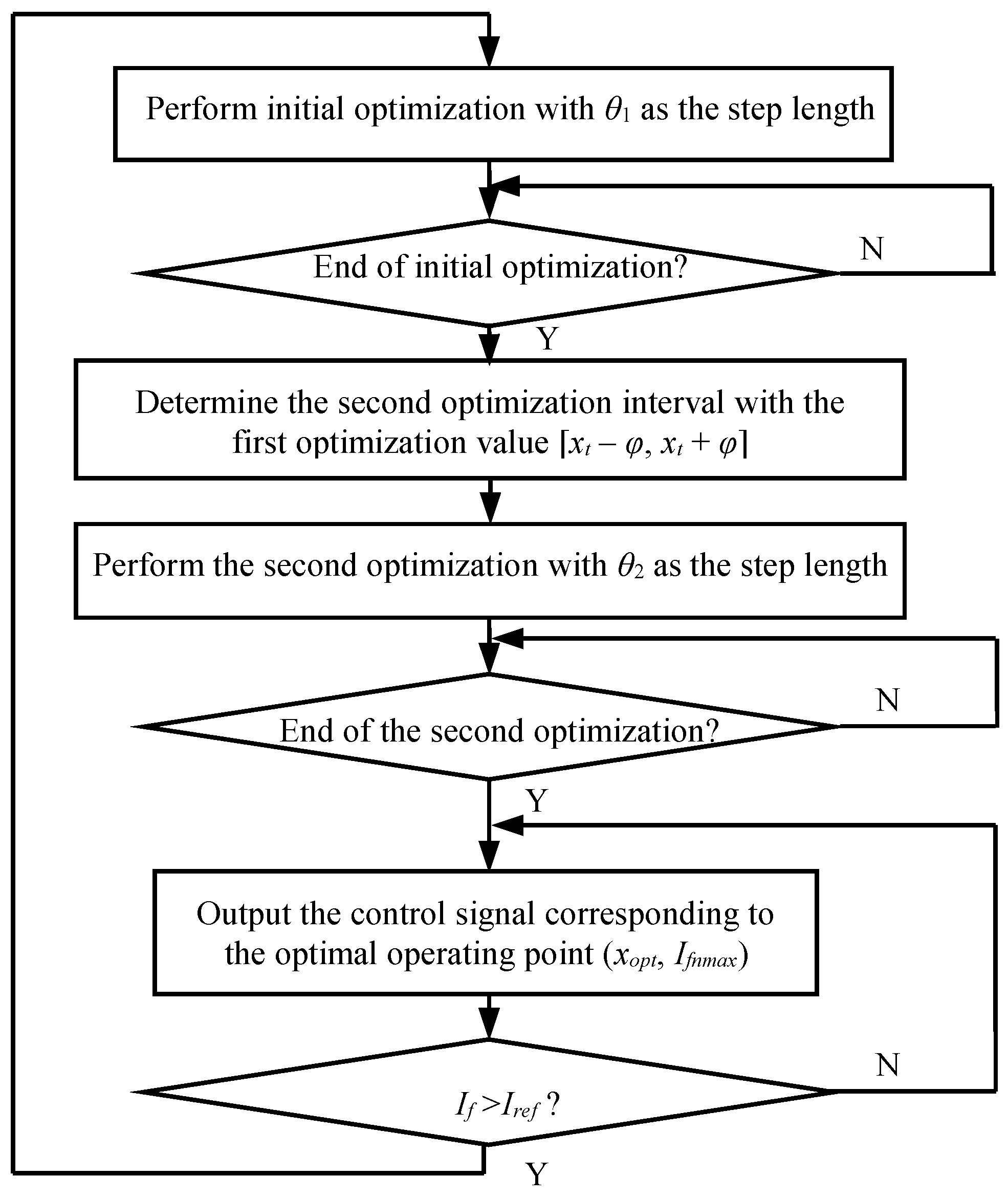
3.7. Two-Step Optimization Algorithm
- Principle of two-step optimization algorithm.
- Advantages of two-step optimization algorithm.
- Process of two-step optimization algorithm.
4. Reactive Power Compensation Method of RPCSS
4.1. Capacitance Determination of Reactive Power Compensation Capacitor
- Required reactive power compensation capacity.
- The total reactive power capacity provided by RPCSS.
- The equivalent capacitance of RPCSS.
4.2. Control Strategy of RPCSS
- When , the reactive power of the system conforms to the standard, and the reactive power compensation is maintained;
5. Integration Simulation of Harmonic Suppression and Reactive Power Compensation
5.1. Simulation Cases Design
5.2. Load Characteristic Analysis
- Scheme I: According to the power quality parameters of a power plant’s distribution network and the simulation model of the integrated system of harmonic suppression and reactive power compensation, the system simulation time of the system is set to 0.1 s after several experiments. The connection mode of the three-phase power supply adopts a star connection, and RMS of the line voltage is 380 V. The frequency is 50 Hz; in the series RLC circuit, , mH, and ; the sampling time s.
- In case of the phase shift angle of the pulses () of 60, the active power P is 8309 W, the reactive power Q is 13,276 Var, and the power factor is 0.4547. In this case, the power factor is too small, so reactive power compensation is required;
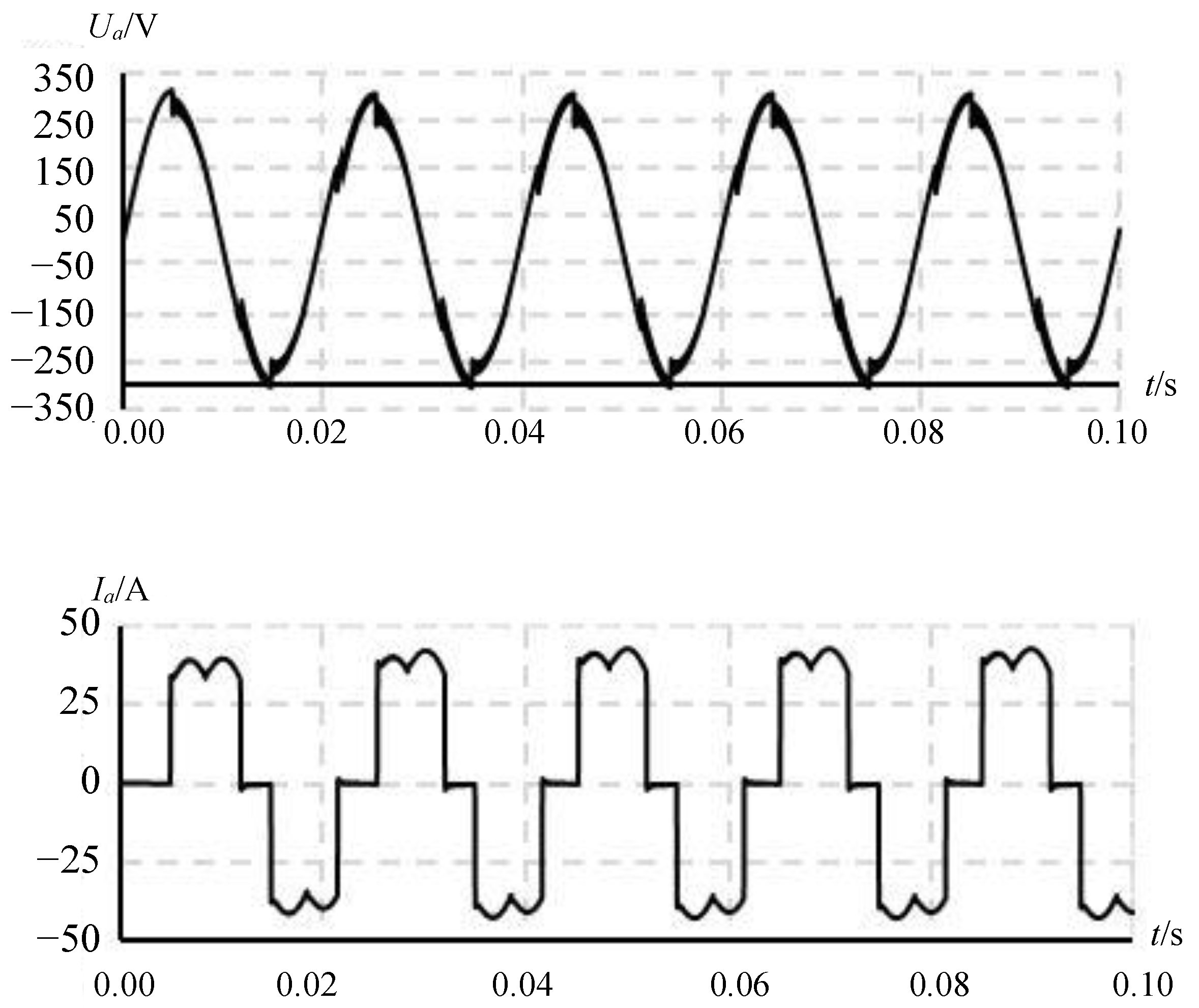
- The waveform distortion of the current in the system is great. The main harmonics exceeding the harmonic current standard are the 5th, 7th, 11th, and 13th harmonics, which need to be filtered.
5.3. Harmonic Suppression Effect Analysis
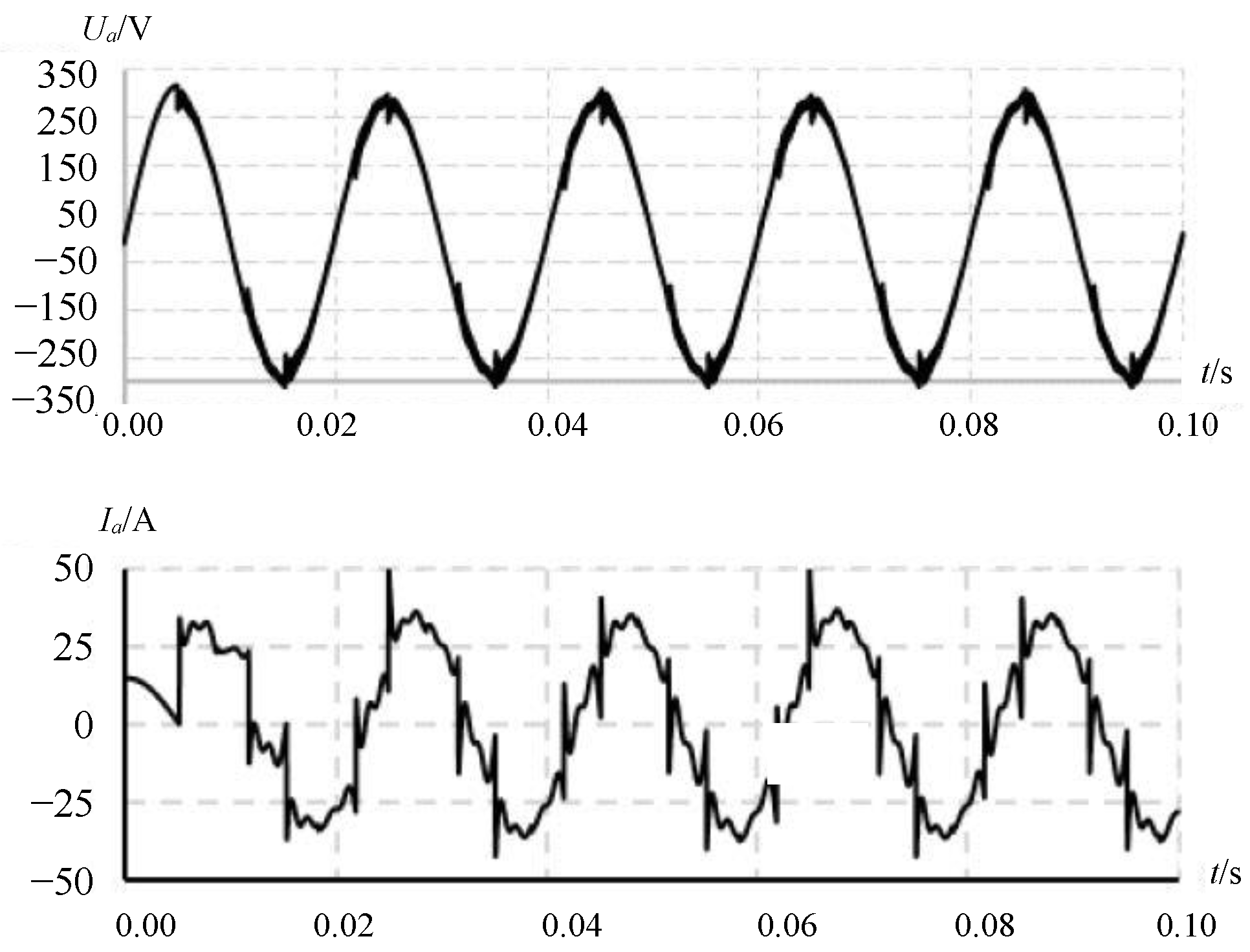
- Scheme II: Only HFSS is put into operation to analyze the suppression effect of HFSS on the harmonics in distribution network in Case I-13. The active power and reactive power and power factor before and after filtering are also analyzed for the next dynamic reactive power compensation.
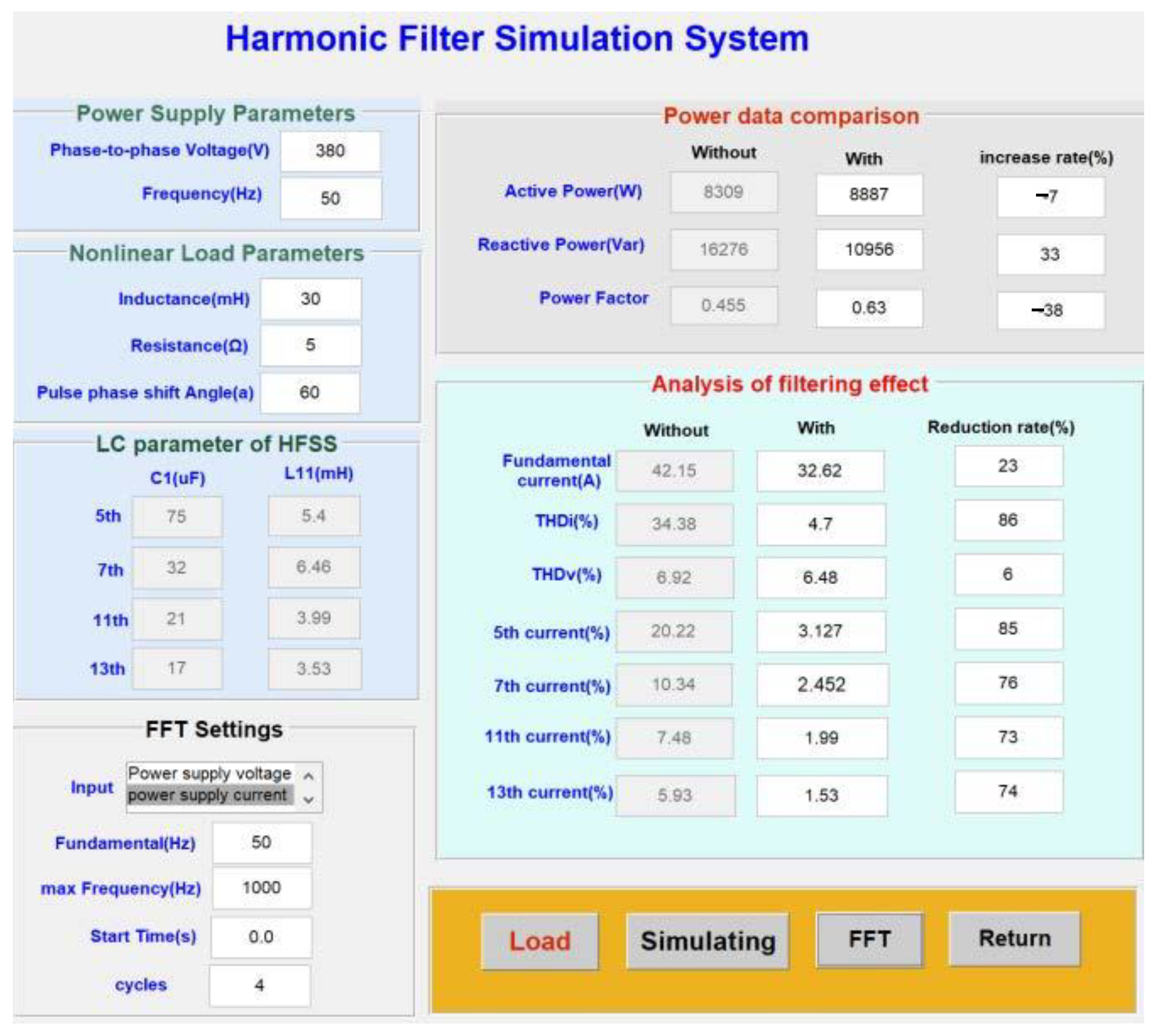
- In Case I-13, after HFSS is put into use, the harmonic currents of the main orders all drop significantly (all above 70%), and the main harmonic current content of the system falls below the national standard. This indicates a significant filtering effect and verifies the rationality of filter parameter design;
- The reactive power reduction rate of the system is about 30%, and the power factor improvement rate is 38%, indicating that the HFSS has a certain effect in reactive power compensation. However, the filtered power factor is still not up to the requirements, so it is necessary to use RPCSS to compensate the system so that the power factor can reach 0.98 or more.
5.4. Analysis of the Comprehensive Effect of Harmonic Suppression and Reactive Power Compensation
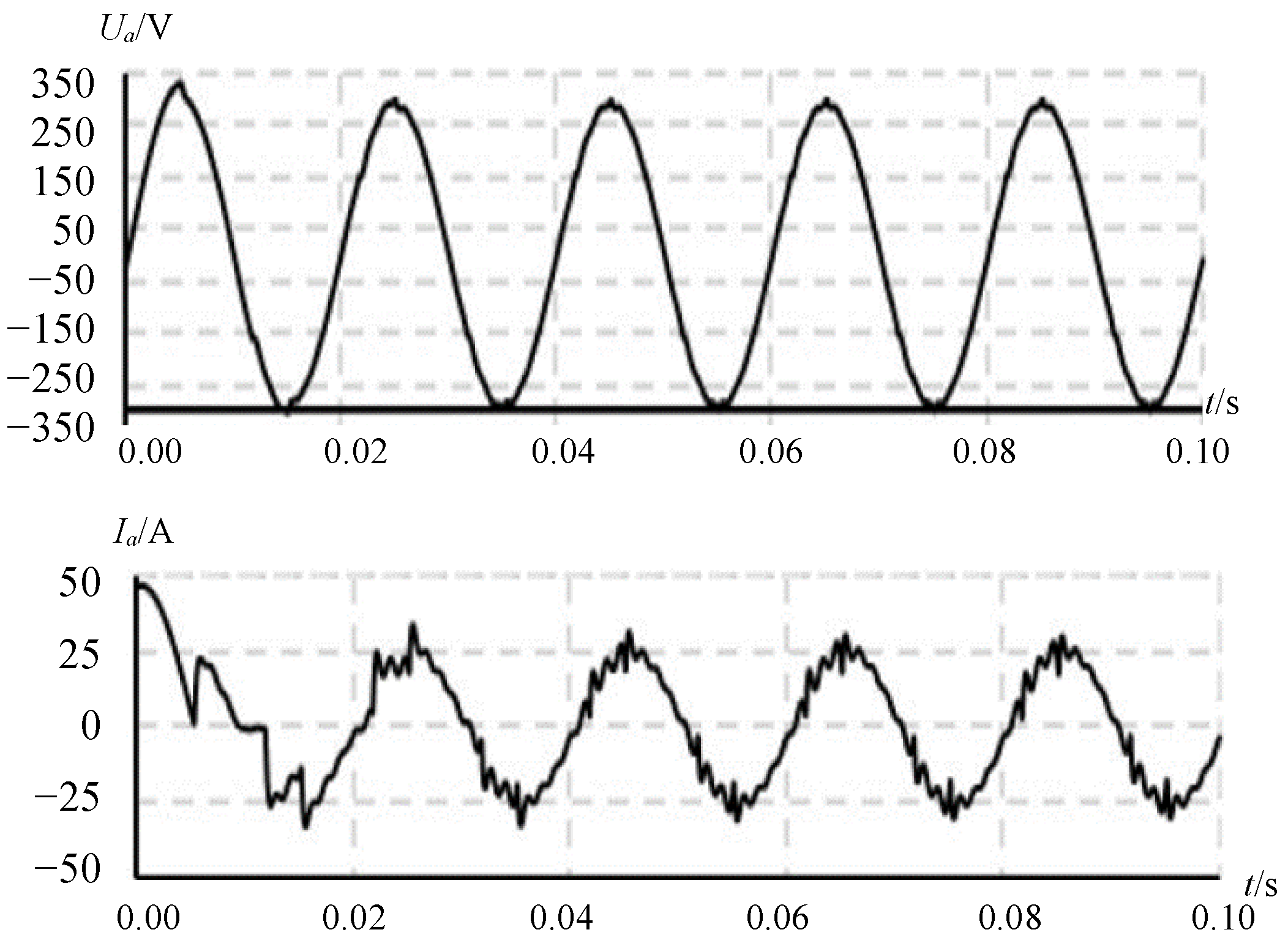
- Scheme III: On the basis of Scheme II, the reactive power compensation subsystem (RPCSS) is added to analyze the active power, reactive power, and power factor of the system.
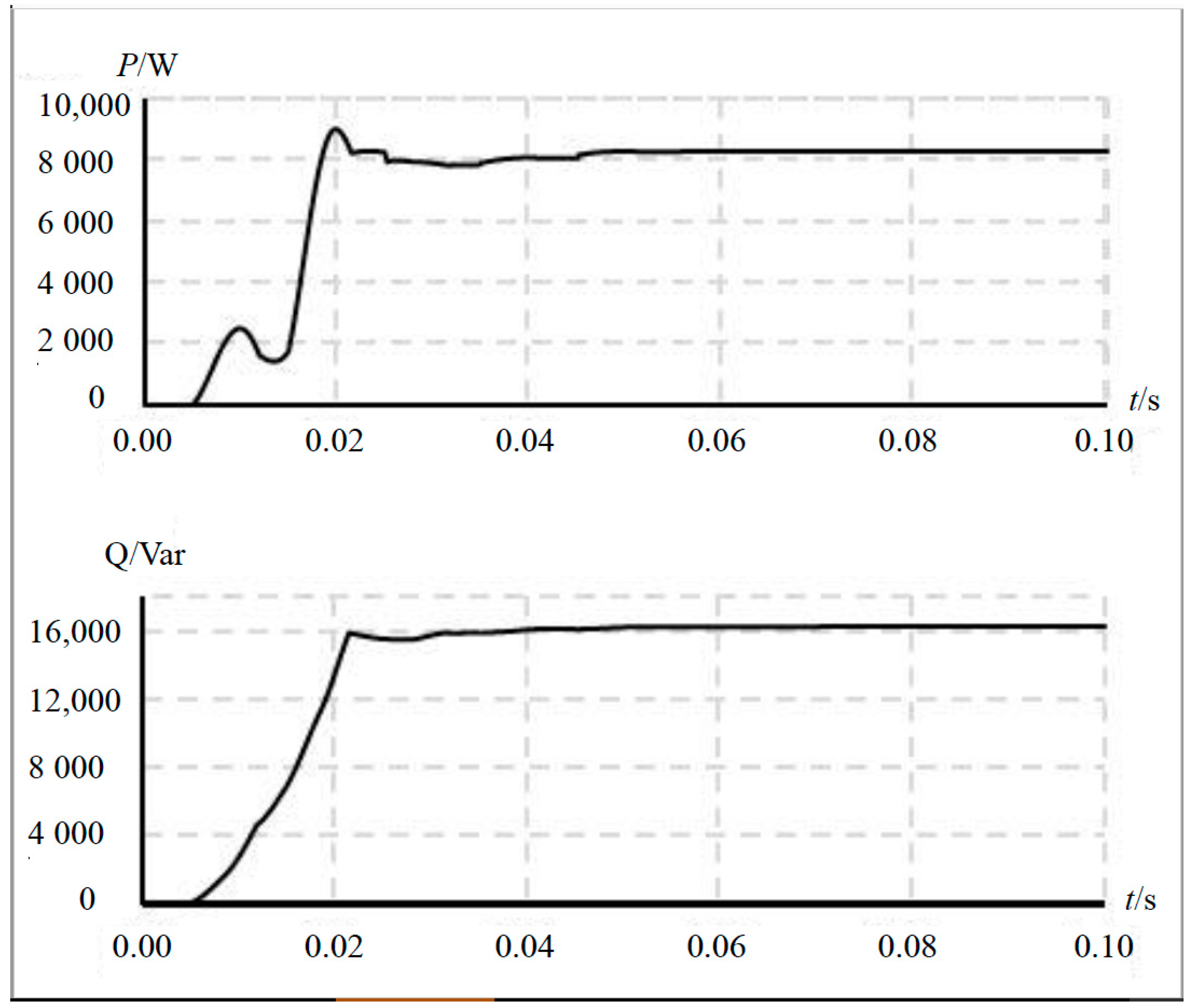
- After HFSS and RPCSS are used, the reactive power of the system is reduced from 16,276 to 1626 Var, with a reduction rate of 90%, and the power factor increases from 0.45 to 0.99. These indicate that the capacitive reactive power and inductive reactive power are roughly balanced, and that the compensation effect is obvious;
- After filtering the 5th, 7th, 11th, and 13th harmonic currents, the current distortion rate is reduced to below 5%, and the reduction rate ranges from 50% to 80%. Moreover, the voltage distortion rate is also reduced by 60% and the harmonic voltage of the power supply is sinusoidal and symmetrical, indicating an obvious filtering effect;
- When there are harmonics in the distribution network, HFSS should be applied for filtering first until the harmonics in the system meet the national regulations. After that, RPCSS is used for reactive power compensation;
- After the comprehensive treatment is completed, HFSS is put into operation first and then switched off later to avoid the harmonic amplification caused by the direct input of RPCSS, the burn out of main power components of RPCSS, and the system oscillation, so as to ensure the smooth operation of the system.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, D.; Yang, K.; Zhu, Z.Q.; Qin, Y. A Novel Series Power Quality Controller with Reduced Passive Power Filter. IEEE Trans. Ind. Electron. 2017, 64, 773–784. [Google Scholar] [CrossRef]
- Lee, T.L.; Wang, Y.C.; Li, J.C.; Guerrero, J.M. Hybrid active filter with variable conductance for harmonic resonance suppression in industrial power systems. IEEE Trans. Ind. Electron. 2015, 62, 746–756. [Google Scholar] [CrossRef] [Green Version]
- Azebaze Mboving, C.S. Investigation on the Work Efficiency of the LC Passive Harmonic Filter Chosen Topologies. Electronics 2015, 10, 896–930. [Google Scholar] [CrossRef]
- Dovgun, V.P.; Egorov, D.E.; Shevchenko, E.S. Parametric synthesis of passive filter-compensating devices. Russ. Electri. Eng. 2016, 87, 28–34. [Google Scholar] [CrossRef]
- Bollen, M.H.; Das, R.; Djokic, S.; Ciufo, P.; Meyer, J.; Rönnberg, S.K.; Zavodam, F. Power quality concerns in implementing smart distribution-grid applications. IEEE Trans. Smart Grid 2017, 8, 391–399. [Google Scholar] [CrossRef] [Green Version]
- Kalaskar, M.N.R.; Holmukhe, M.R. Report On Harmonics Generation and Mitigation in Power System. Int. J. Eng. Res. 2016, 5, 772–774. [Google Scholar]
- Chen, J.; Xiao, L.; Yuan, Y.X.; Yang, K.; Lei, L.; Mao, B.P.; Chen, Z. Development of passive dynamic power filter based on MCU. J. Wuhan Univ. Technol. 2013, 35, 144–146. [Google Scholar]
- Wang, Y.; Yuan, Y.; Chen, J. Study of harmonic suppression of ship electric propulsion systems. J. Power Electron. 2019, 19, 1303–1314. [Google Scholar]
- Wang, Y.F.; Yuan, Y.X. Development of a Soft Starter with Current-Limiting, Reactive Power Compensation and Harmonic Filtering. Appl. Mech. Mater. 2014, 462–463, 658–661. [Google Scholar] [CrossRef]
- Wang, Y.F.; Yuan, Y.X.; Chen, J.; Cheng, Q.J. A Dynamic Reactive Power Compensation Method of Super High-Power and High-Voltage Motor. Appl. Mech. Mater. 2014, 602–605, 2828–2831. [Google Scholar] [CrossRef]
- Wang, Y.F.; Yuan, Y.X. A dynamic reactive power compensation method for high-power and high-voltage electronic motors based on self-adaptive fuzzy PID control. In Proceedings of the 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, 12–14 August 2016; pp. 10–15. [Google Scholar]
- Kalair, A.; Abas, N.; Kalair, A.R.; Saleem, Z.; Khan, N. Review of harmonic analysis, modeling and mitigation techniques. Renew. Sust. Energ. Rev. 2017, 78, 1154–1187. [Google Scholar] [CrossRef]
- Zobaa, A.F. Mixed-Integer Distributed Mixed-Integer Distributed Ant Colony Multi-Objective Optimization of Single-Tuned Passive Harmonic Filter Parameters. IEEE Access 2019, 7, 44862–44870. [Google Scholar] [CrossRef]
- Othman, A.M.; Gabbar, H.A. Enhanced microgrid dynamic performance using a modulated power filter based on enhanced bacterial foraging optimization. Energies 2017, 10, 776. [Google Scholar] [CrossRef] [Green Version]
- Swain, S.D.; Ray, P.K.; Mohanty, K.B. Improvement of power quality using a robust hybrid series active power filter. IEEE Trans. Power Electr. 2016, 32, 3490–3498. [Google Scholar] [CrossRef]
- Omar, R.; Tan, Z.H.; Rasheed, M.; Sulaiman, M. An Improvement of Shunt Active Power Filter using Effective Controller for Different Load Condition. J. Eng. Appl. Sci. 2020, 15, 1311–1321. [Google Scholar] [CrossRef] [Green Version]
- Litrán, S.P.; Salmeron, P. Analysis and design of different control strategies of hybrid active power filter based on the state model. IET Power Electron. 2012, 5, 1341–1350. [Google Scholar] [CrossRef]
- Schffer, G.J.; Moura, F.A.M.; Mendonça, M.V.B.; Júnior, A.J.P.R.; Albertini, M.R.M.C.; Camacho, J.R. Conservative Power Theory (CPT): A New Approach to the Tuned Passive Filter Design. Renew. Energ. Power Qual. J. 2019, 17, 245–250. [Google Scholar] [CrossRef]
- Song, Q.; Chen, S.; Zhao, Z.; Liu, Y.; Alsaadi, F.E. Passive filter design for fractional-order quaternion-valued neural networks with neutral delays and external disturbance. Neural Netw. 2021, 137, 18–30. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, Y.; Chen, J. A novel electromagnetic coupling reactor based passive power filter with dynamic tunable function. Energies 2018, 11, 1647. [Google Scholar] [CrossRef] [Green Version]
- Solatialkaran, D.; Khajeh, K.G.; Zare, F. A Novel Filter Design Method for Grid-Tied Inverters. IEEE Trans. Power Electr. 2021, 36, 5473–5485. [Google Scholar] [CrossRef]
- Ortuzar, M.E.; Carmi, R.E.; Dixon, J.W.; Moran, L. Voltage-source active power filter based on multilevel converter and ultracapacitor DC link. IEEE Trans. Ind. Electron. 2006, 53, 477–485. [Google Scholar] [CrossRef]
- Alasali, F.; Nusair, K.; Foudeh, H.; Holderbaum, W.; Vinayagam, A.; Aziz, A. Modern Optimal Controllers for Hybrid Active Power Filter to Minimize Harmonic Distortionk. Electronics 2022, 11, 1453. [Google Scholar] [CrossRef]
- Tomaszm, B.; Marekm, N.; Stanisławm, P. Power Supply and Reactive Power Compensation of a Single-Phase Higher Frequenc. Energies 2022, 15, 2563. [Google Scholar]
- Sun, L.; Zhang, Z.; Gu, X.; Yu, L. Analysis of Reactive Power Compensation Effect of a New Hybrid Excitation. IEEE Trans. Ind. Electron. 2020, 67, 3562–3572. [Google Scholar] [CrossRef]
- Teleke, S.; Abdulahovic, T.; Thiringer, T. Dynamic performance comparison of synchronous condenser and SVC. IEEE Trans. Power Deliv. 2008, 23, 1606–1612. [Google Scholar] [CrossRef]
- Funaki, T.; Nakagawa, K.; Hikihara, T. The Origin of Nonlinear Phenomena in TCR-SVC Associated With Parametric Excitation of Intrinsic Oscillation and External Excitation. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 2952–2958. [Google Scholar] [CrossRef] [Green Version]







| Case | Scheme | KM KM | Simulation Model Applied |
|---|---|---|---|
| I | Load characteristic analysis | 0 0 | Without |
| II | harmonic suppression effect analysis | 0 1 | HFSS |
| III | analysis of the integration system | 1 1 | HFSS + RPCSS |
| Case | P/W | Q/Var | ph | |
|---|---|---|---|---|
| I-1 | 0 | 32,056 | 467 | 0.9999 |
| I-2 | 5 | 31,825 | 1372 | 0.9991 |
| I-3 | 10 | 31,193 | 3297 | 0.9945 |
| I-4 | 15 | 29,838 | 6351 | 0.9781 |
| I-5 | 20 | 27,741 | 9809 | 0.9428 |
| I-6 | 25 | 25,486 | 12,584 | 0.8967 |
| I-7 | 30 | 23,224 | 14,516 | 0.8480 |
| I-8 | 35 | 20,466 | 16,297 | 0.7823 |
| I-9 | 40 | 17,781 | 17,367 | 0.7154 |
| I-10 | 45 | 14,971 | 17,757 | 0.6446 |
| I-11 | 50 | 11,836 | 17,595 | 0.5581 |
| I-12 | 55 | 9265 | 16,659 | 0.4860 |
| I-13 | 60 | 8309 | 16,276 | 0.4547 |
| I-14 | 65 | 7164 | 15,337 | 0.4232 |
| I-15 | 70 | 4978 | 13,517 | 0.3456 |
| I-16 | 75 | 3043 | 11,050 | 0.2655 |
| I-17 | 80 | 1503 | 7660 | 0.1925 |
| I-18 | 85 | 506 | 4059 | 0.1238 |
| Case | THD | THD | |||||||
|---|---|---|---|---|---|---|---|---|---|
| I-1 | 0 | 86.91 | 23.66 | 18.56 | 12.29 | 6.09 | 4.36 | 1.92 | 8.39 |
| I-2 | 5 | 86.56 | 26.05 | 19.26 | 13.23 | 7.45 | 5.92 | 3.62 | 9.23 |
| I-3 | 10 | 85.55 | 29.16 | 19.91 | 13.97 | 8.66 | 7.35 | 5.31 | 10.26 |
| I-4 | 15 | 83.40 | 30.67 | 20.56 | 13.72 | 9.27 | 7.31 | 6.03 | 11.40 |
| I-5 | 20 | 80.38 | 31.08 | 20.67 | 13.59 | 9.19 | 7.32 | 5.94 | 13.29 |
| I-6 | 25 | 77.20 | 31.09 | 20.85 | 13.41 | 9.20 | 7.27 | 5.94 | 14.53 |
| I-7 | 30 | 73.43 | 31.17 | 21.15 | 13.13 | 9.27 | 7.09 | 5.99 | 11.94 |
| I-8 | 35 | 69.14 | 31.08 | 21.28 | 12.95 | 9.19 | 7.09 | 5.89 | 12.68 |
| I-9 | 40 | 64.30 | 31.00 | 21.32 | 12.83 | 8.97 | 7.17 | 5.69 | 10.06 |
| I-10 | 45 | 58.70 | 31.14 | 21.77 | 12.40 | 9.10 | 6.98 | 5.83 | 9.94 |
| I-11 | 50 | 52.50 | 31.29 | 22.28 | 11.95 | 9.28 | 6.80 | 5.99 | 9.03 |
| I-12 | 55 | 46.05 | 31.25 | 22.46 | 11.81 | 8.95 | 6.90 | 5.60 | 6.72 |
| I-13 | 60 | 42.15 | 34.38 | 20.22 | 10.34 | 7.48 | 5.93 | 3.82 | 6.92 |
| I-14 | 65 | 40.10 | 31.56 | 23.29 | 11.05 | 9.27 | 6.51 | 5.88 | 6.59 |
| I-15 | 70 | 33.22 | 31.74 | 24.07 | 10.25 | 9.13 | 6.31 | 5.72 | 5.24 |
| I-16 | 75 | 26.05 | 31.99 | 25.16 | 9.15 | 8.76 | 6.27 | 5.22 | 4.05 |
| I-17 | 80 | 17.81 | 34.35 | 28.47 | 6.00 | 9.27 | 5.08 | 5.41 | 2.65 |
| I-18 | 85 | 43.83 | 4059 | 36.39 | 1.79 | 10.22 | 2.13 | 6.03 | 1.57 |
| Order | A | uF | Var | mH | A | VA |
|---|---|---|---|---|---|---|
| 5th | 11 | 75 | 25 | 5.67 | 38.27 | 14,583.00 |
| 7th | 6 | 32 | 15 | 6.78 | 25.08 | 9557.00 |
| 11th | 4 | 21 | 15 | 4.19 | 24.86 | 9472.93 |
| 13th | 3 | 17 | 15 | 3.71 | 27.83 | 9761.50 |
| Case | A | ||||||
|---|---|---|---|---|---|---|---|
| I-13 | 42.15 | 34.38 | 20.22 | 10.34 | 7.48 | 5.93 | 6.92 |
| II | 32.62 | 4.7 | 3.13 | 2.45 | 1.99 | 1.53 | 6.48 |
| Reduction rate/% | 23 | 86 | 85 | 76 | 73 | 74 | 6 |
| Case | W | Var | ph |
|---|---|---|---|
| I-13 | 8309 | 16,276 | 0.45 |
| II | 8887 | 10,956 | 0.63 |
| Reduction rate/% | −7 | 33 | −38 |
| Case | A | ||||||
|---|---|---|---|---|---|---|---|
| I-13 | 42.15 | 34.38 | 20.22 | 10.34 | 7.48 | 5.93 | 6.92 |
| III | 25.35 | 7.43 | 3.98 | 4.55 | 3.55 | 2.563 | 2.79 |
| Reduction rate/% | 40 | 78 | 80 | 56 | 53 | 57 | 60 |
| Case | W | Var | ph |
|---|---|---|---|
| I-13 | 8309 | 16,276 | 0.45 |
| III | 11,170 | 1626 | 0.99 |
| Reduction rate/% | −34 | 90 | −120 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yin, K.; Liu, H.; Yuan, Y. A Novel Integrated Method for Harmonic Suppression and Reactive Power Compensation in Distribution Network. Symmetry 2022, 14, 1347. https://doi.org/10.3390/sym14071347
Wang Y, Yin K, Liu H, Yuan Y. A Novel Integrated Method for Harmonic Suppression and Reactive Power Compensation in Distribution Network. Symmetry. 2022; 14(7):1347. https://doi.org/10.3390/sym14071347
Chicago/Turabian StyleWang, Yifei, Kaiyang Yin, Huikang Liu, and Youxin Yuan. 2022. "A Novel Integrated Method for Harmonic Suppression and Reactive Power Compensation in Distribution Network" Symmetry 14, no. 7: 1347. https://doi.org/10.3390/sym14071347






