On Hosoya Polynomial and Subsequent Indices of C4C8(R) and C4C8(S) Nanosheets
Abstract
:1. Introduction
2. Methods
3. Results
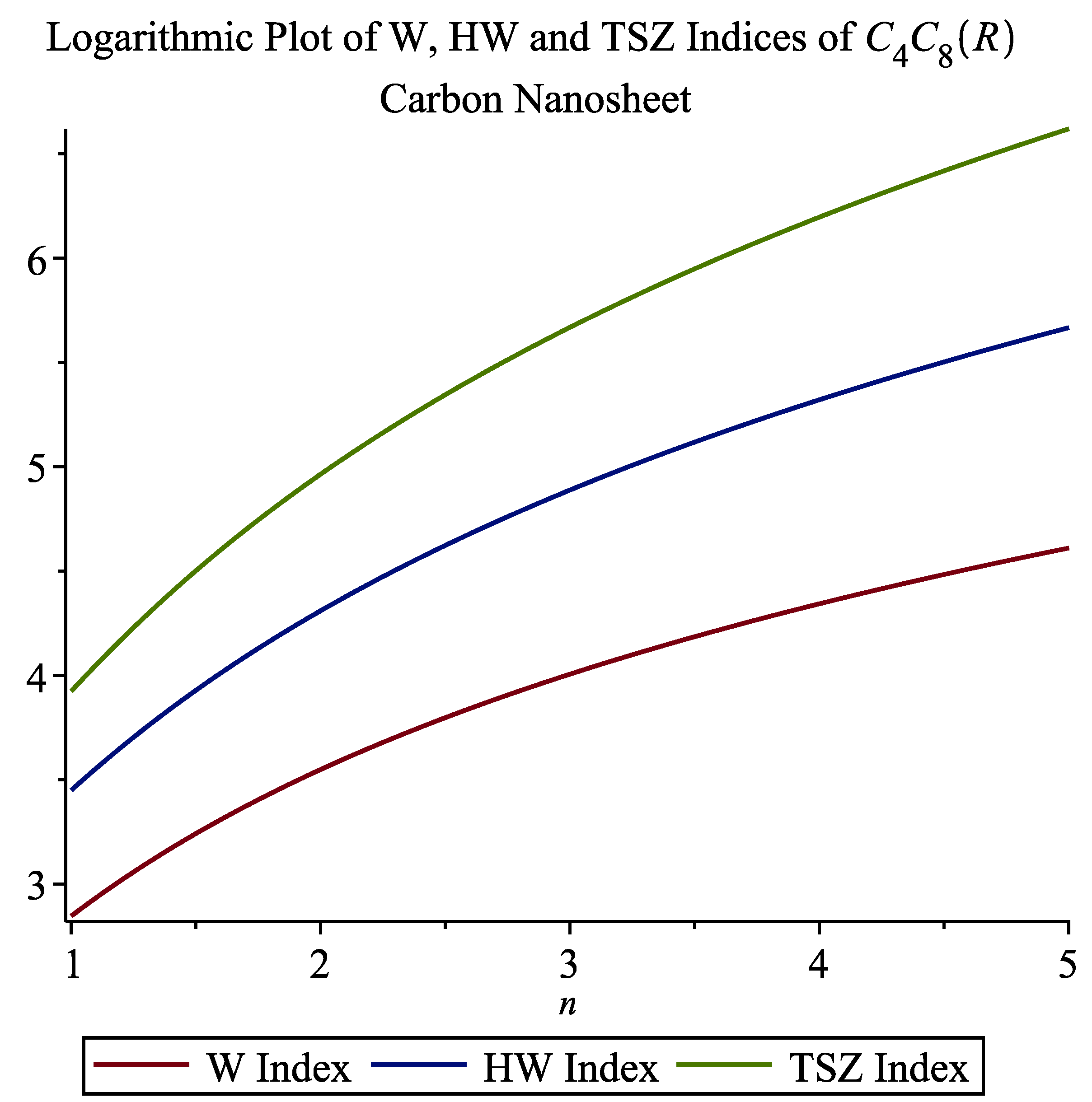
3.1. Carbon Nanosheet
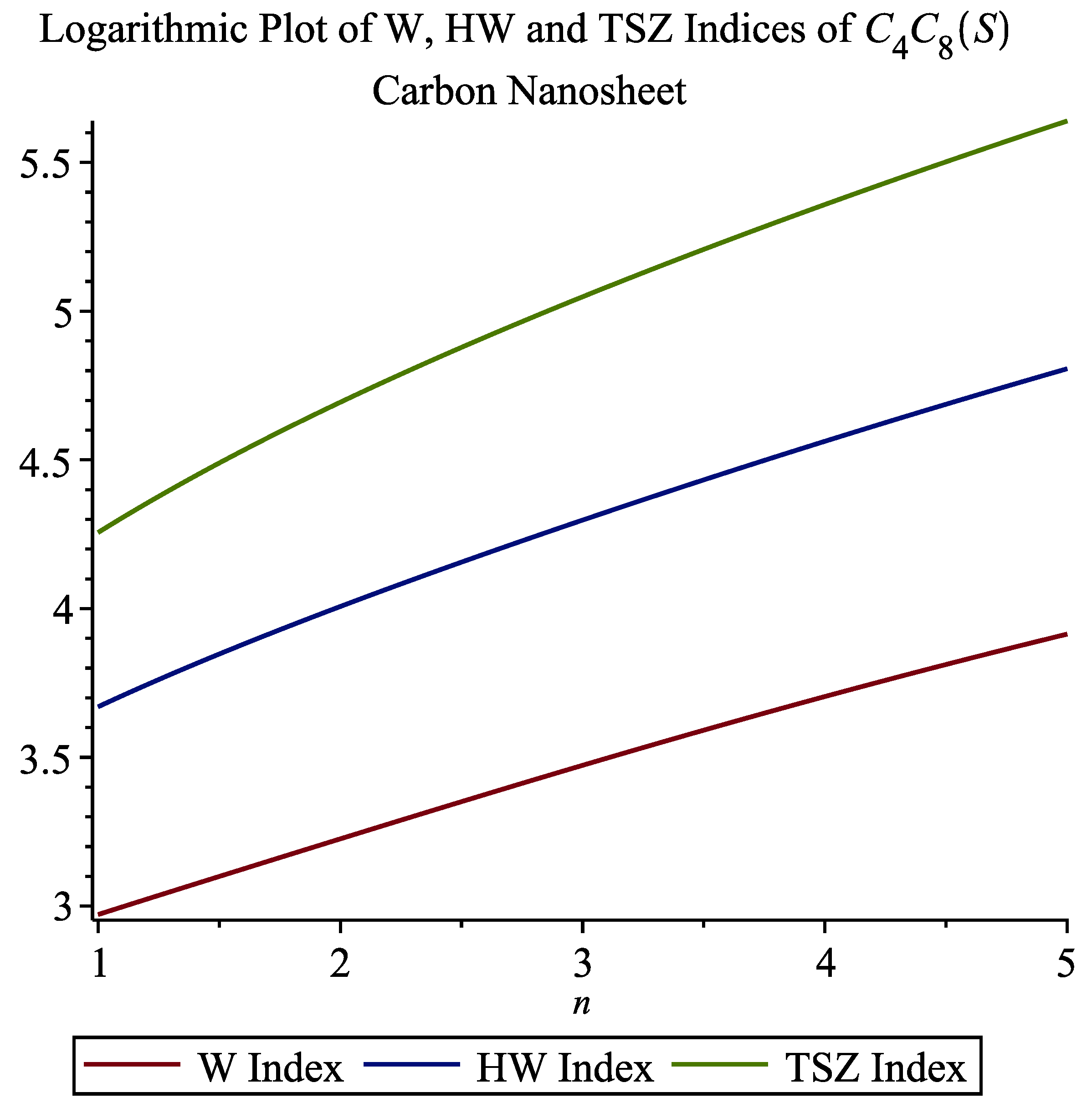
3.2. Carbon Nanosheet
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Joita, D.M.; Jantschi, L. Extending the characteristic polynomial for characterization of C20 fullerene congeners. Mathematics 2017, 5, 84. [Google Scholar] [CrossRef] [Green Version]
- Hosoya, H. On some counting polynomials in chemistry. Discret. Appl. Math. 1988, 19, 239–257. [Google Scholar] [CrossRef] [Green Version]
- Gutman, I.; Klavžar, S.; Petkovšek, M.; Žigert, P. On Hosoya polynomial of benzenoid graphs. MATCH Commun. Math. Comput. Chem. 2001, 43, 49–66. [Google Scholar]
- Cash, G. Relationship between the Hosoya polynomial and the hyper Wiener index. Appl. Math. Lett. 2002, 15, 893–895. [Google Scholar] [CrossRef]
- Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef]
- Ahmad, H.; Hussain, M.; Nazeer, W.; Chu, Y.M. Distance-based invariants of zigzag polyhex nanotube. Math. Methods Appl. Sci. 2020. [Google Scholar] [CrossRef]
- Došlić, T. On the number of spanning trees in alternating polycyclic chains. J. Math. Chem. 2018, 56, 2794–2800. [Google Scholar]
- Došlić, T.; Zubac, I. Partition of π-electrons among the faces of polyhedral carbon clusters. J. Math. Chem. 2018, 56, 2512–2524. [Google Scholar]
- Shirakol, S.; Kalyanshetti, M.; Hosamani, S.M. QSPR analysis of certain distance based topological indices. Appl. Math. Nonlinear Sci. 2019, 4, 371–386. [Google Scholar] [CrossRef] [Green Version]
- Hu, M.; Ali, H.; Binyamin, M.A.; Ali, B.; Liu, J.-B.; Fan, C. On Distance-Based Topological Descriptors of Chemical Interconnection Networks. J. Math. 2021, 2021, 5520619. [Google Scholar] [CrossRef]
- Mozafari, Z.; Chamjangali, M.A.; Beglari, M.; Doosti, R. The efficiency of ligand–receptor interaction information alone as new descriptors in QSAR modeling via random forest artificial neural network. Chem. Biol. Drug Des. 2020, 96, 812–824. [Google Scholar] [CrossRef] [PubMed]
- Suay-García, B.; Bueso-Bordils, J.I.; Falcó, A.; Antón-Fos, G.M.; Alemán-López, P.A. Virtual Combinatorial Chemistry and Pharmacological Screening: A Short Guide to Drug Design. Int. J. Mol. Sci. 2022, 23, 1620. [Google Scholar] [CrossRef] [PubMed]
- Alomari, F.Y.; Sharfalddin, A.A.; Abdellattif, M.H.; Domyati, D.; Basaleh, A.S.; Hussien, M.A. QSAR Modeling, Molecular Docking and Cytotoxic Evaluation for Novel Oxidovanadium (IV) Complexes as Colon Anticancer Agents. Molecules 2022, 27, 649. [Google Scholar] [CrossRef] [PubMed]
- Wadhwa, P.; Mittal, A. Quantitative Structure-Property Relationship (QSPR) Modeling Applications in Formulation Development. In Computer Aided Pharmaceutics and Drug Delivery; Springer: Singapore, 2022; pp. 543–560. [Google Scholar]
- Jaganathan, K.; Tayara, H.; Chong, K.T. An Explainable Supervised Machine Learning Model for Predicting Respiratory Toxicity of Chemicals Using Optimal Molecular Descriptors. Pharmaceutics 2022, 14, 832. [Google Scholar] [CrossRef]
- Lotfi, S.; Ahmadi, S.; Kumar, P. A hybrid descriptor based QSPR model to predict the thermal decomposition temperature of imidazolium ionic liquids using Monte Carlo approach. J. Mol. Liq. 2021, 338, 116465. [Google Scholar] [CrossRef]
- Mahboob, A.; Alrowaili, D.; Alam, S.M.; Ali, R.; Rasheed, M.W.; Siddique, I. Topological Attributes of Silicon Carbide SiC4-IIi,j Based on Ve-Degree and Ev-Degree. J. Chem. 2022, 2022, 3188993. [Google Scholar] [CrossRef]
- Adnan, M.; Bokhary, S.A.U.H.; Imran, M. On Wiener Polarity Index and Wiener Index of Certain Triangular Networks. J. Chem. 2021, 2021, 2757925. [Google Scholar] [CrossRef]
- Adnan, M.; Bokhary, S.A.U.H.; Abbas, G.; Iqbal, T. Degree-based topological indices and QSPR analysis of antituberculosis drugs. J. Chem. 2022, 2022, 5748626. [Google Scholar] [CrossRef]
- Gutman, I.; Körtvélyesi, T. Wiener indices and molecular surfaces. Z. Für Nat. A 1995, 50, 669–671. [Google Scholar] [CrossRef] [Green Version]
- Devillers, J.; Balaban, A.T. (Eds.) Topological Indices and Related Descriptors in QSAR and QSPR; Gordan and Breach Science Publishing: Philadelphia, PA, USA, 1999. [Google Scholar]
- Wang, G.; Liu, Y.; Wei, J.; Liu, J.B. The Edge-Hyper Wiener Index of Zigzag Single-Walled Nanotubes. Polycycl. Aromat. Compd. 2022, 2030764. [Google Scholar] [CrossRef]
- Chu, Y.M.; Imran, M.; Baig, A.Q.; Akhter, S.; Siddiqui, M.K. On M-polynomial-based topological descriptors of chemical crystal structures and their applications. Eur. Phys. J. Plus. 2020, 135, 874. [Google Scholar] [CrossRef]
- Hayat, S.; Imran, M.; Liu, J.B. An efficient computational technique for degree and distance based topological descriptors with examples. IEEE Access 2019, 7, 32276–32296. [Google Scholar] [CrossRef]
- Shao, Z.; Siddiqui, M.K.; Muhammad, M.H. Computing Zagreb indices and zagreb polynomials for symmetrical nanotubes. Symmetry 2018, 10, 244. [Google Scholar] [CrossRef] [Green Version]
- Deutsch, E.; Klavžar, S. Computing Hosoya polynomials of graphs from primary subgraphs. arXiv 2012, arXiv:1212.3179. [Google Scholar]
- Sadeghieh, A.; Alikhani, S.; Ghanbari, N.; Khalaf, A.J.M. Hosoya polynomial of some cactus chains. Cogent Math. 2017, 4, 1305638. [Google Scholar] [CrossRef]
- Zhang, Q.X.; Xu, S.J.; Chen, H.Y. The Hosoya polynomial of one-pentagonal carbon nanocone. Fuller. Nanotub. Carbon Nanostructure 2014, 22, 866–873. [Google Scholar] [CrossRef]
- Ali, A.A.; Ali, A.M. Hosoya Polynomials of Pentachains. MATCH Commun. Math. Comput. Chem. 2011, 65, 807–819. [Google Scholar]
- Arockiaraj, M.; Klavžar, S.; Mushtaq, S.; Balasubramanian, K. Distance-based topological indices of nanosheets, nanotubes and nanotori of SIO2. J. Math. Chem. 2019, 57, 343–369. [Google Scholar] [CrossRef]
- Chen, L.; Mehboob, A.; Ahmad, H.; Nazeer, W.; Hussain, M.; Farahani, M.R. Harary and Hosoya polynomial of TOX(n), RTOX(n), TSL(n), and RTSL(n). Discret. Dyn. Nat. Soc. 2019, 2019, 8696982. [Google Scholar] [CrossRef] [Green Version]
- Nizami, A.R.; Shabir, K.; Sardar, M.S.; Qasim, M.; Cancan, M.; Ediz, S. Base polynomials for degree and distance based topological invariants of n-bilinear straight pentachain. JIOS 2021, 42, 1479–1495. [Google Scholar] [CrossRef]
- Farahani, M.R. On the Schultz polynomial and Hosoya polynomial of circumcoronene series of benzenoid. J. Appl. Math. Comput. 2013, 31, 595–608. [Google Scholar] [CrossRef] [Green Version]
- Farahani, M.R. Hosoya, Schultz, Modified Schultz Polynomials and Their Topological Indices of Benzene Molecules: First Members of Polycyclic Aromatic Hydrocarbons (PAHs). Int. J. Theo. Chem. 2013, 1, 9–16. [Google Scholar]
- Ali, P.; Kirmani, S.A.K.; Al Rugaie, O.; Azam, F. Degree-based topological indices and polynomials of hyaluronic acid-curcumin conjugates. Saudi Pharm. J. 2020, 28, 1093–1100. [Google Scholar] [CrossRef]
- Mortazavi, B.; Shojaei, F.; Zhuang, X.; Pereira, L.F.C. First-principles investigation of electronic, optical, mechanical and heat transport properties of pentadiamond: A comparison with diamond. Carbon Trends 2021, 3, 100036. [Google Scholar] [CrossRef]
- Khanna, V.; Kumar, V.; Bansal, S.A. Mechanical properties of aluminium-graphene/carbon nanotubes (CNTs) metal matrix composites: Advancement, opportunities and perspective. Mater. Res. Bull. 2021, 138, 111224. [Google Scholar] [CrossRef]
- Wieland, L.; Li, H.; Rust, C.; Chen, J.; Flavel, B.S. Carbon nanotubes for photovoltaics: From lab to industry. Adv. Energy Mater. 2021, 11, 2002880. [Google Scholar] [CrossRef]
- Kanu, N.J.; Bapat, S.; Deodhar, H.; Gupta, E.; Singh, G.K.; Vates, U.K.; Verma, G.C.; Pandey, V. An insight into processing and properties of smart carbon nanotubes reinforced nanocomposites. Smart Sci. 2022, 10, 40–55. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, J.; Jiang, F.; Zhao, S.; Su, Q.; Du, G. Microporous carbon nanosheets derived from corncobs for lithium sulfur batteries. Electrochim. Acta 2015, 176, 853–860. [Google Scholar] [CrossRef]
- Sevilla, M.; Fuertes, A.B. Direct Synthesis of Highly Porous Interconnected Carbon Nanosheets and Their Application as High-Performance Supercapacitors. ACS Nano 2014, 8, 5069–5078. [Google Scholar] [CrossRef] [Green Version]
- Wei, W.; Liang, H.; Parvez, K.; Zhuang, X.; Feng, X.; Mãllen, K. Nitrogen-Doped Carbon Nanosheets with Size-Defined Mesopores as Highly Efficient Metal-Free Catalyst for the Oxygen Reduction Reaction. Angew. Chem. 2014, 126, 1596–1600. [Google Scholar] [CrossRef]
- Mahto, A.; Singh, A.; Aruchamy, K.; Maraddi, A.; Bhadu, G.R.; Kotrappanavar, N.S.; Meena, R. A hyperaccumulation pathway to hierarchically porous carbon nanosheets from halophyte biomass for wastewater remediation. Sustain. Mater. Technol. 2021, 29, e00292. [Google Scholar] [CrossRef]
- Cheng, C.; He, S.; Zhang, C.; Du, C.; Chen, W. High-performance supercapacitor fabricated from 3D free-standing hierarchical carbon foam-supported two dimensional porous thin carbon nanosheets. Electrochim. Acta 2018, 290, 98–108. [Google Scholar] [CrossRef]
- Ali, Z.; Basharat, M.; Wu, Z. A Review on the Morphologically Controlled Synthesis of Polyphosphazenes for Electrochemical Applications. ChemElectroChem 2021, 8, 759–782. [Google Scholar] [CrossRef]
- Sreekumar, K.G.; Manilal, K. Hosoya polynomial and Harary index of SM family of graphs. J. Inf. Optim. Sci. 2018, 39, 581–590. [Google Scholar] [CrossRef]
- Xu, S.-J.; Chen, H.; Zhang, Q.-X.; Tu, L. Hosoya polynomials of twisted toroidal polyhexes. Ars Comb. 2014, 114, 417–425. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheikh, U.; Rashid, S.; Ozel, C.; Pincak, R. On Hosoya Polynomial and Subsequent Indices of C4C8(R) and C4C8(S) Nanosheets. Symmetry 2022, 14, 1349. https://doi.org/10.3390/sym14071349
Sheikh U, Rashid S, Ozel C, Pincak R. On Hosoya Polynomial and Subsequent Indices of C4C8(R) and C4C8(S) Nanosheets. Symmetry. 2022; 14(7):1349. https://doi.org/10.3390/sym14071349
Chicago/Turabian StyleSheikh, Umber, Sidra Rashid, Cenap Ozel, and Richard Pincak. 2022. "On Hosoya Polynomial and Subsequent Indices of C4C8(R) and C4C8(S) Nanosheets" Symmetry 14, no. 7: 1349. https://doi.org/10.3390/sym14071349
APA StyleSheikh, U., Rashid, S., Ozel, C., & Pincak, R. (2022). On Hosoya Polynomial and Subsequent Indices of C4C8(R) and C4C8(S) Nanosheets. Symmetry, 14(7), 1349. https://doi.org/10.3390/sym14071349






