A Comparative Study of the Fractional Coupled Burgers and Hirota–Satsuma KdV Equations via Analytical Techniques
Abstract
:1. Introduction
2. Preliminaries
3. The General Implementation of the Elzaki Decomposition Method
4. VITM Formulation
5. Numerical Results
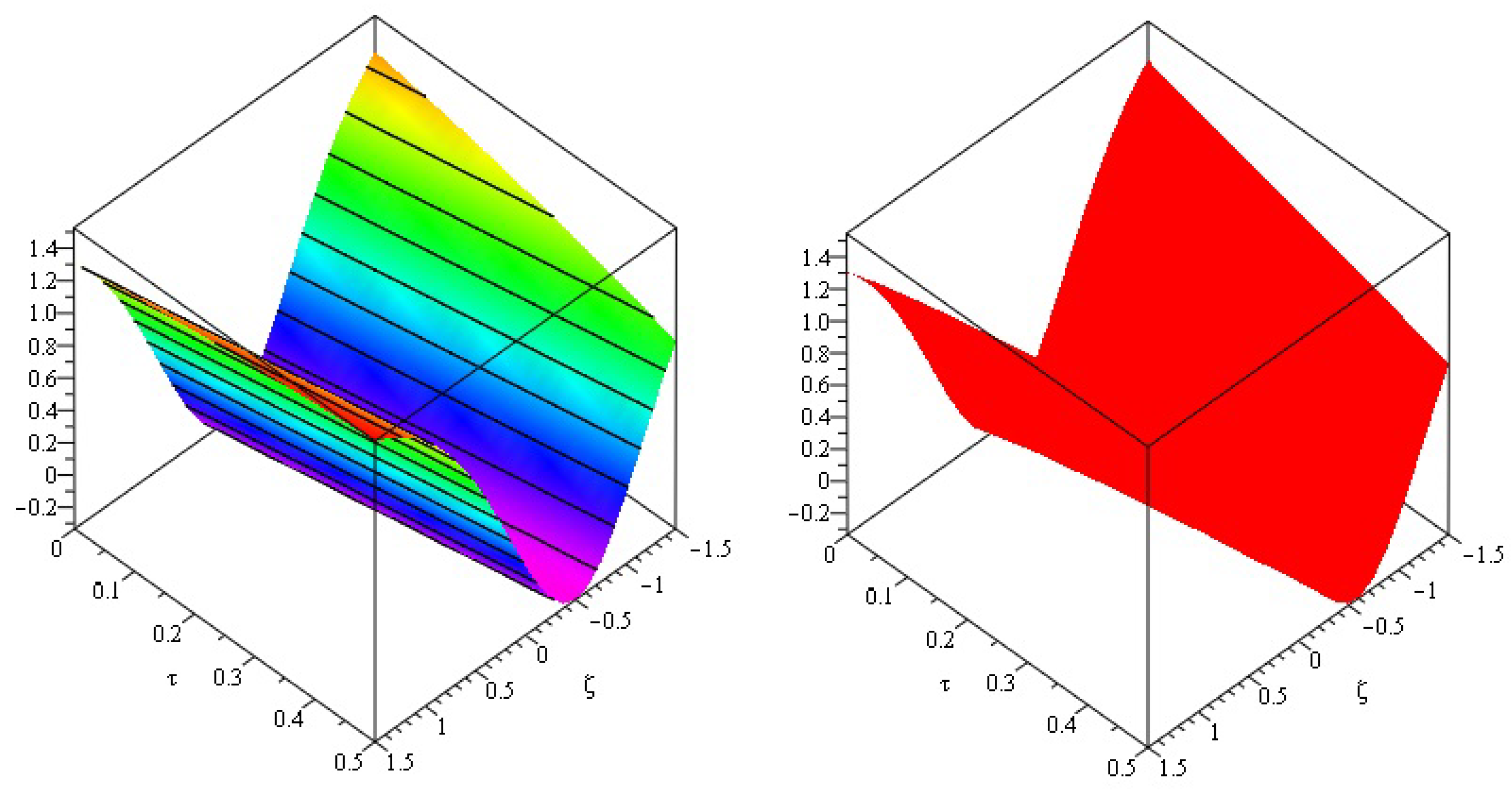
5.1. Problem
5.2. Problem
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nonlaopon, K.; Naeem, M.; Zidan, A.M.; Alsanad, A.; Gumaei, A. Numerical investigation of the time-fractional Whitham-Broer-Kaup equation involving without singular kernel operators. Complexity 2021, 7979365. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent-II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar]
- Iqbal, N.; Yasmin, H.; Ali, A.; Bariq, A.; Al-Sawalha, M.M.; Mohammed, W.W. Numerical Methods for Fractional-Order Fornberg-Whitham Equations in the Sense of Atangana-Baleanu Derivative. J. Funct. Spaces 2021, 2021, 2197247. [Google Scholar] [CrossRef]
- Iqbal, N.; Yasmin, H.; Rezaiguia, A.; Kafle, J.; Almatroud, A.O.; Hassan, T.S. Analysis of the Fractional-Order Kaup–Kupershmidt Equation via Novel Transforms. J. Math. 2021, 2021, 2567927. [Google Scholar] [CrossRef]
- Areshi, M.; Khan, A.; Shah, R.; Nonlaopon, K. Analytical investigation of fractional-order Newell-Whitehead-Segel equations via a novel transform. AIMS Math. 2022, 7, 6936–6958. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 1983, 27, 201–210. [Google Scholar] [CrossRef]
- Baillie, R.T. Long memory processes and fractional integration in econometrics. J. Econom. 1996, 73, 5–59. [Google Scholar] [CrossRef]
- Chow, T.S. Fractional dynamics of interfaces between soft-nanoparticles and rough substrates. Phys. Lett. A 2005, 342, 148–155. [Google Scholar] [CrossRef]
- Chen, C.M.; Liu, F.; Anh, V.; Turner, I. Numerical methods for solving a two-dimensional variable-order anomalous subdiffusion equation. Math. Comput. 2012, 81, 345–366. [Google Scholar] [CrossRef]
- Shah, N.A.; Alyousef, H.A.; El-Tantawy, S.A.; Shah, R.; Chung, J.D. Analytical Investigation of Fractional-Order Korteweg-De-Vries-Type Equations under Atangana-Baleanu-Caputo Operator: Modeling Nonlinear Waves in a Plasma and Fluid. Symmetry 2022, 14, 739. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999; p. 198. [Google Scholar]
- Inc, M. The approximate and exact solutions of the space-and time-fractional Burgers equations with initial conditions by variational iteration method. J. Math. Anal. Appl. 2008, 345, 476–484. [Google Scholar] [CrossRef] [Green Version]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Translated from the 1987 Russian Original; Gordon and Breach: New York, NY, USA, 1993. [Google Scholar]
- Shah, N.A.; Hamed, Y.S.; Abualnaja, K.M.; Chung, J.D.; Khan, A. A comparative analysis of fractional-order kaup-kupershmidt equation within different operators. Symmetry 2022, 14, 986. [Google Scholar] [CrossRef]
- Agrawal, O.P.; Defterli, O.; Baleanu, D. Fractional optimal control problems with several state and control variables. J. Vib. Control 2010, 16, 1967–1976. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Ullah, R.; Khan, A.; Shah, R.; Kafle, J.; Mahariq, I.; Jarad, F. Numerical analysis of the fractional-order nonlinear system of Volterra integro-differential equations. J. Funct. Spaces 2021, 2021, 1537958. [Google Scholar] [CrossRef]
- Aljahdaly, N.H.; Akgul, A.; Shah, R.; Mahariq, I.; Kafle, J. A comparative analysis of the fractional-order coupled Korteweg-De Vries equations with the Mittag-Leffler law. J. Math. 2022, 2022, 8876149. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Aljahdaly, N.H.; Ali, A.; Shah, R.; Mahariq, I.; Tchalla, A.M. ψ-Haar Wavelet Operational Matrix Method for Fractional Relaxation-Oscillation Equations Containing-Caputo Fractional Derivative. J. Funct. Spaces 2021, 2021, 7117064. [Google Scholar] [CrossRef]
- Mukhtar, S.; Shah, R.; Noor, S. The Numerical Investigation of a Fractional-Order Multi-Dimensional Model of Navier-Stokes Equation via Novel Techniques. Symmetry 2022, 14, 1102. [Google Scholar] [CrossRef]
- Alesemi, M.; Iqbal, N.; Hamoud, A.A. The analysis of fractional-order proportional delay physical models via a novel transform. Complexity 2022, 2022, 2431533. [Google Scholar] [CrossRef]
- Alesemi, M.; Iqbal, N.; Botmart, T. Novel analysis of the fractional-order system of non-linear partial differential equations with the exponential-decay kernel. Mathematics 2022, 10, 615. [Google Scholar] [CrossRef]
- Wu, J. Theory and Applications of Partial Functional Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1996; Volume 119. [Google Scholar]
- Yang, X.J.; Baleanu, D. Fractal heat conduction problem solved by local fractional variation iteration method. Therm. Sci. 2013, 17, 625–628. [Google Scholar] [CrossRef]
- Qin, Y.; Khan, A.; Ali, I.; Al Qurashi, M.; Khan, H.; Shah, R.; Baleanu, D. An efficient analytical approach for the solution of certain fractional-order dynamical systems. Energies 2020, 13, 2725. [Google Scholar] [CrossRef]
- Mirmoradia, S.H.; Hosseinpoura, I.; Ghanbarpour, S.; Barari, A. Application of an approximate analytical method to nonlinear Troesch’s problem. Appl. Math. Sci. 2009, 3, 1579–1585. [Google Scholar]
- Kumar, A.; Kumar, S.; Yan, S.P. Residual power series method for fractional diffusion equations. Fundam. Inform. 2017, 151, 213–230. [Google Scholar] [CrossRef]
- Khan, H.; Khan, A.; Al-Qurashi, M.; Shah, R.; Baleanu, D. Modified modelling for heat like equations within Caputo operator. Energies 2020, 13, 2002. [Google Scholar] [CrossRef]
- Khan, H.; Khan, A.; Kumam, P.; Baleanu, D.; Arif, M. An approximate analytical solution of the Navier-Stokes equations within Caputo operator and Elzaki transform decomposition method. Adv. Diff. Equ. 2020, 2020, 1–23. [Google Scholar]
- Keskin, Y.; Oturanc, G. Reduced differential transform method for partial differential equations. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 741–750. [Google Scholar] [CrossRef]
- Evans, D.J.; Raslan, K.R. The Adomian decomposition method for solving delay differential equation. Int. J. Comput. Math. 2005, 82, 49–54. [Google Scholar] [CrossRef]
- Bateman, H. Some recent researches on the motion of fluids. Mon. Weather. Rev. 1915, 43, 163–170. [Google Scholar] [CrossRef]
- Yasmin, H. Numerical Analysis of Time-Fractional Whitham-Broer-Kaup Equations with Exponential-Decay Kernel. Fractal Fract. 2022, 6, 142. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Erfani, E. New analytical method for solving Burgers and nonlinear heat transfer equations and comparison with HAM. Comput. Phys. Commun. 2009, 180, 1539–1544. [Google Scholar] [CrossRef]
- Moslem, W.M.; Sabry, R. Zakharov-Kuznetsov-Burgers equation for dust ion acoustic waves. Chaos Solitons Fractals 2008, 36, 628–634. [Google Scholar] [CrossRef]
- Iqbal, N.; Botmart, T.; Mohammed, W.W.; Ali, A. Numerical investigation of fractional-order Kersten-Krasil’shchik coupled KdV-mKdV system with Atangana-Baleanu derivative. Adv. Contin. Discret. Models 2022, 2022, 1–20. [Google Scholar] [CrossRef]
- Liu, Z.J.; Adamu, M.Y.; Suleiman, E.; He, J.H. Hybridization of homotopy perturbation method and Laplace transformation for the partial differential equations. Therm. Sci. 2017, 21, 1843–1846. [Google Scholar] [CrossRef] [Green Version]
- Hristov, J. An exercise with the He’s variation iteration method to a fractional Bernoulli equation arising in transient conduction with non-linear heat flux at the boundary. Int. Rev. Chem. Eng. 2012, 4, 489–497. [Google Scholar]
- Liu, C.F.; Kong, S.S.; Yuan, S.J. Reconstructive schemes for variational iteration method within Yang-Laplace transform with application to fractal heat conduction problem. Therm. Sci. 2013, 17, 715–721. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef] [Green Version]
- Elzaki, T.M. The new integral transform Elzaki transform. Glob. J. Pure Appl. Math. 2011, 7, 57–64. [Google Scholar]
- Alderremy, A.A.; Elzaki, T.M.; Chamekh, M. New transform iterative method for solving some Klein-Gordon equations. Results Phys. 2018, 10, 655–659. [Google Scholar] [CrossRef]
- Kim, H. The time shifting theorem and the convolution for Elzaki transform. Int. J. Pure Appl. Math. 2013, 87, 261–271. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yasmin, H.; Iqbal, N. A Comparative Study of the Fractional Coupled Burgers and Hirota–Satsuma KdV Equations via Analytical Techniques. Symmetry 2022, 14, 1364. https://doi.org/10.3390/sym14071364
Yasmin H, Iqbal N. A Comparative Study of the Fractional Coupled Burgers and Hirota–Satsuma KdV Equations via Analytical Techniques. Symmetry. 2022; 14(7):1364. https://doi.org/10.3390/sym14071364
Chicago/Turabian StyleYasmin, Humaira, and Naveed Iqbal. 2022. "A Comparative Study of the Fractional Coupled Burgers and Hirota–Satsuma KdV Equations via Analytical Techniques" Symmetry 14, no. 7: 1364. https://doi.org/10.3390/sym14071364
APA StyleYasmin, H., & Iqbal, N. (2022). A Comparative Study of the Fractional Coupled Burgers and Hirota–Satsuma KdV Equations via Analytical Techniques. Symmetry, 14(7), 1364. https://doi.org/10.3390/sym14071364






