Free Vibration Analysis of a Spinning Composite Laminated Truncated Conical Shell under Hygrothermal Environment
Abstract
:1. Introduction
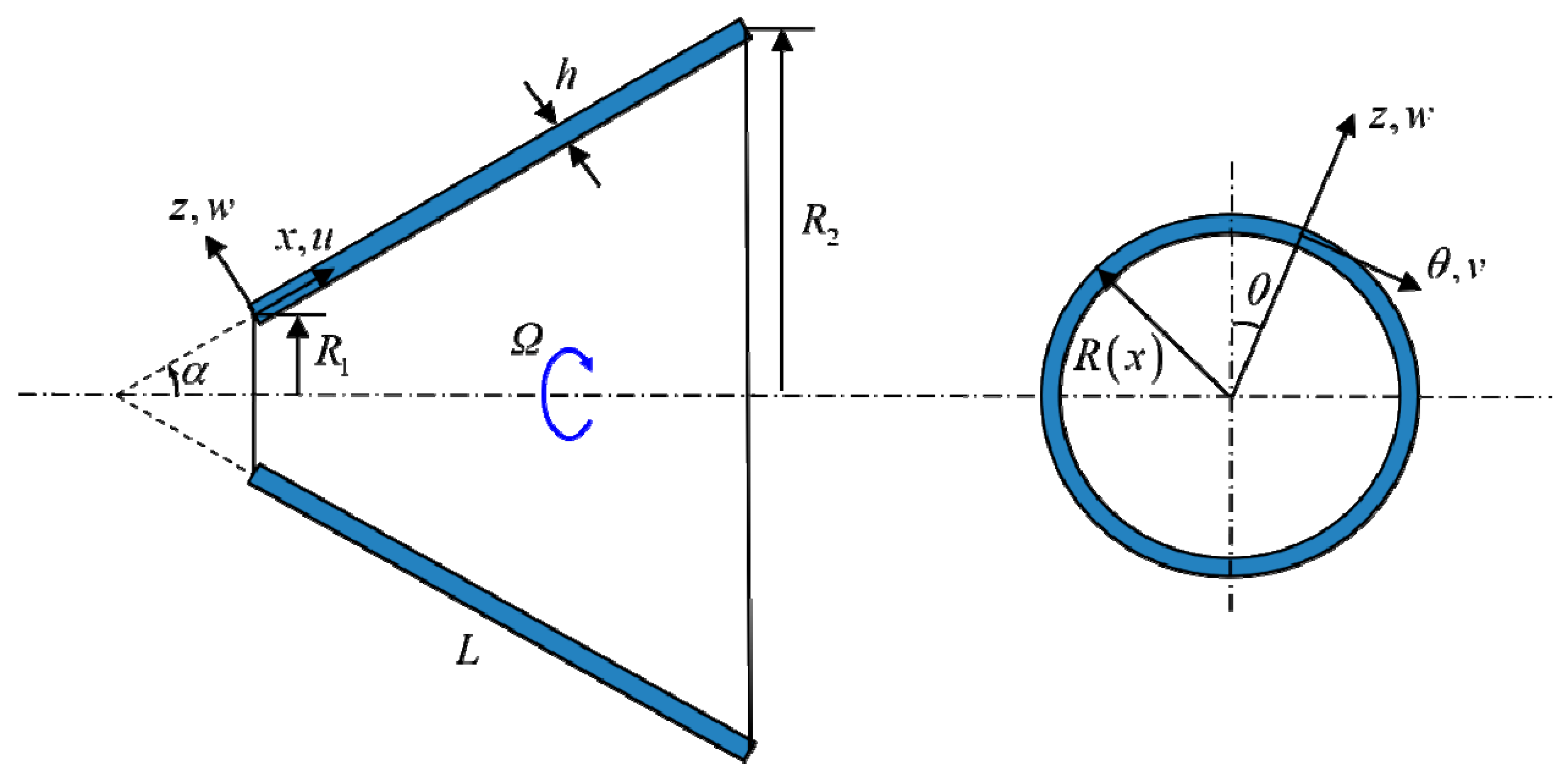
2. Theoretical Formulations
2.1. Constitutive Equations
2.2. Governing Equations
3. Solution Procedure
4. Results and Discussion
4.1. Validation
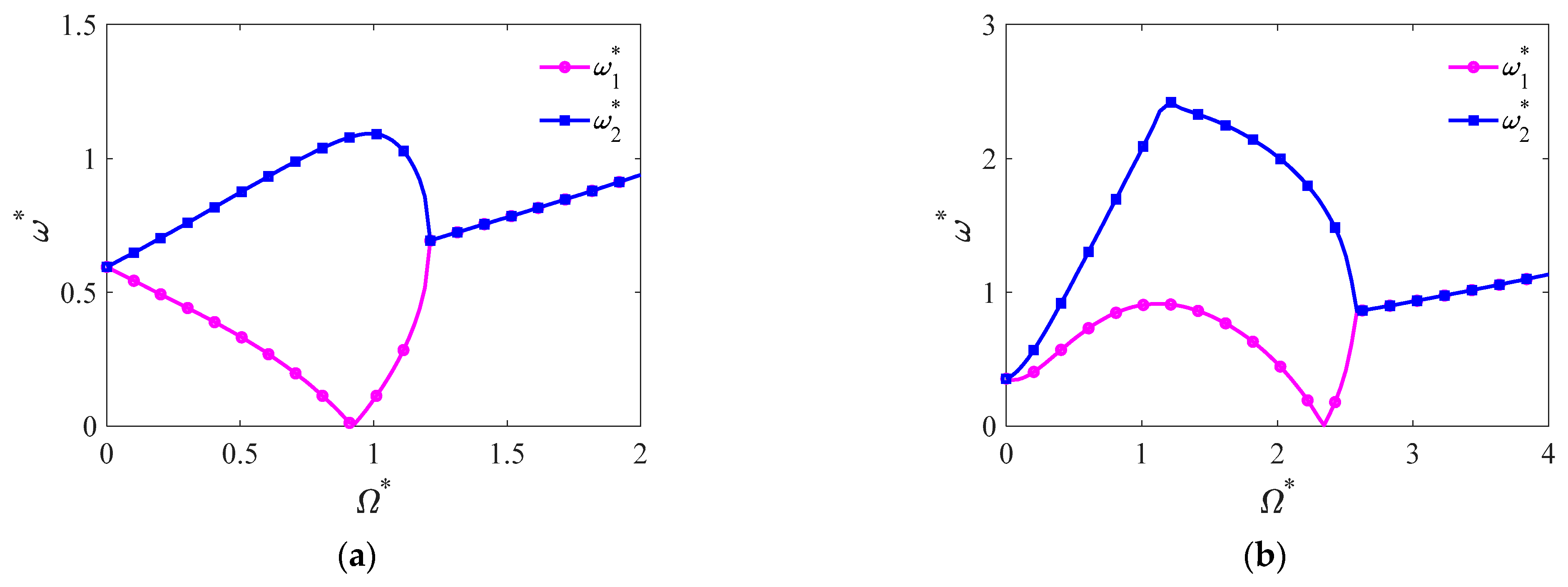
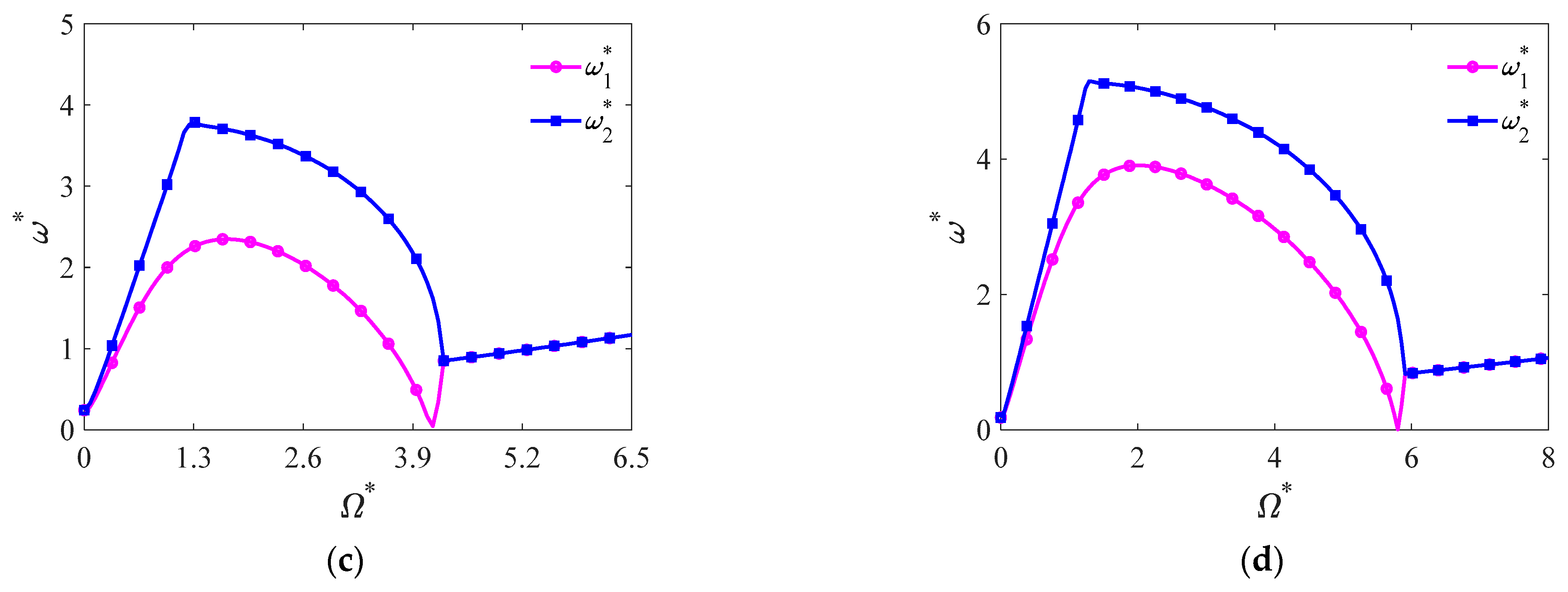
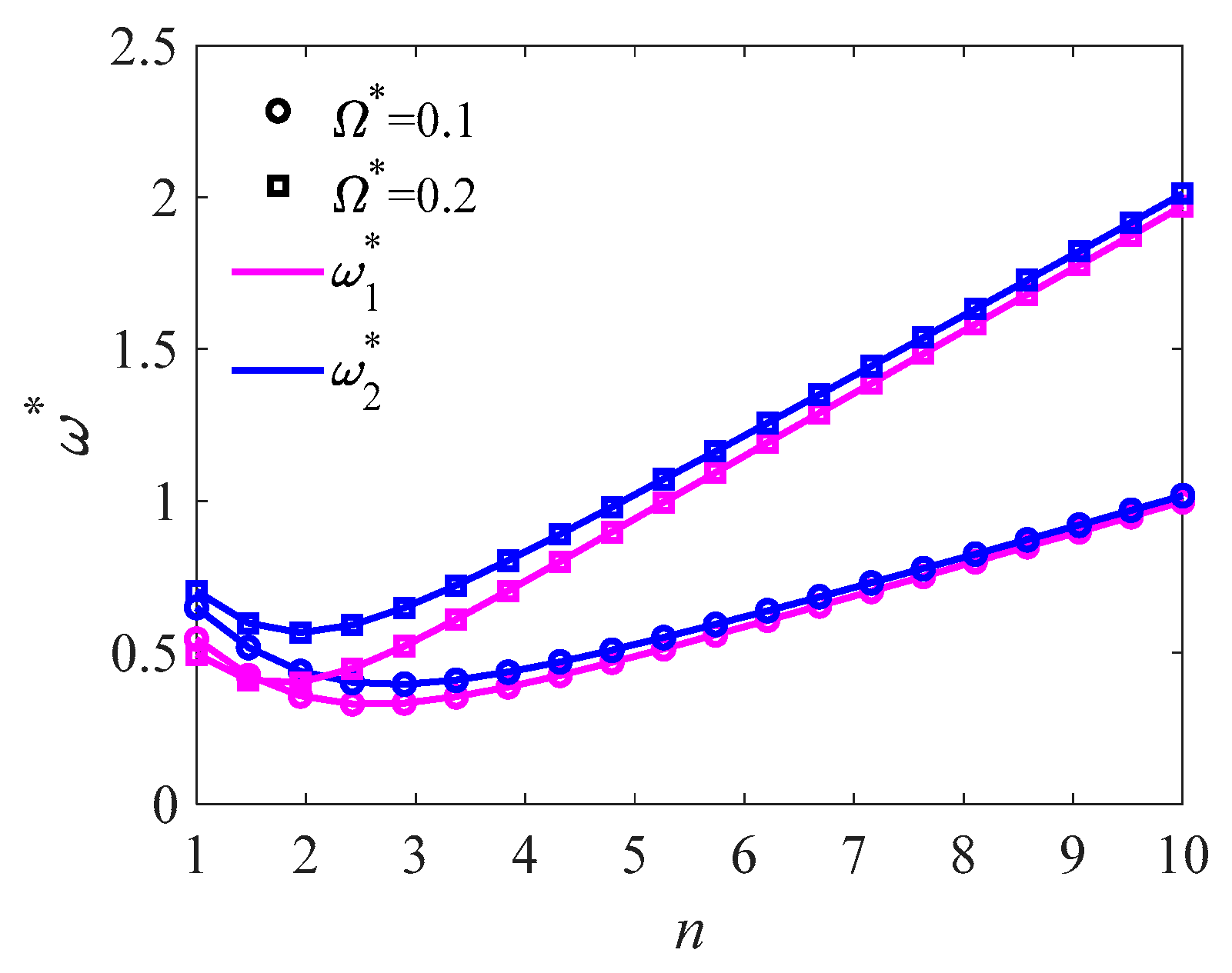
4.2. Natural Frequency and Critical Spinning Angular Speed
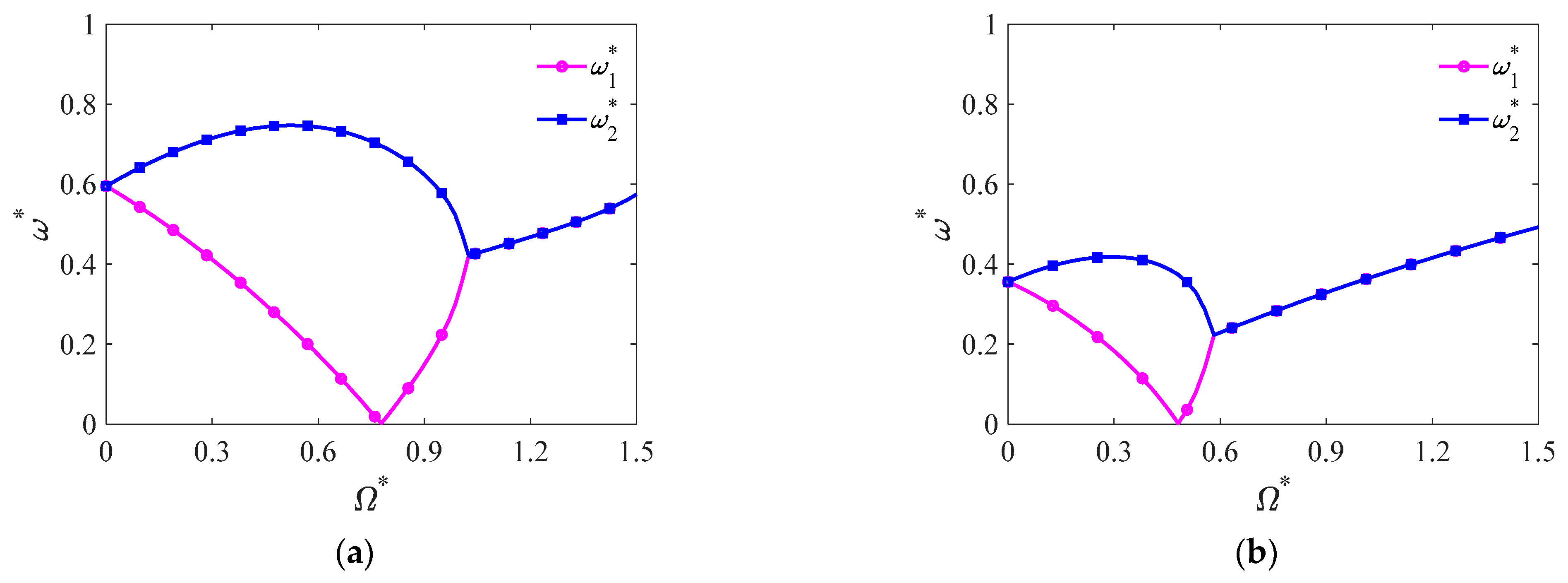
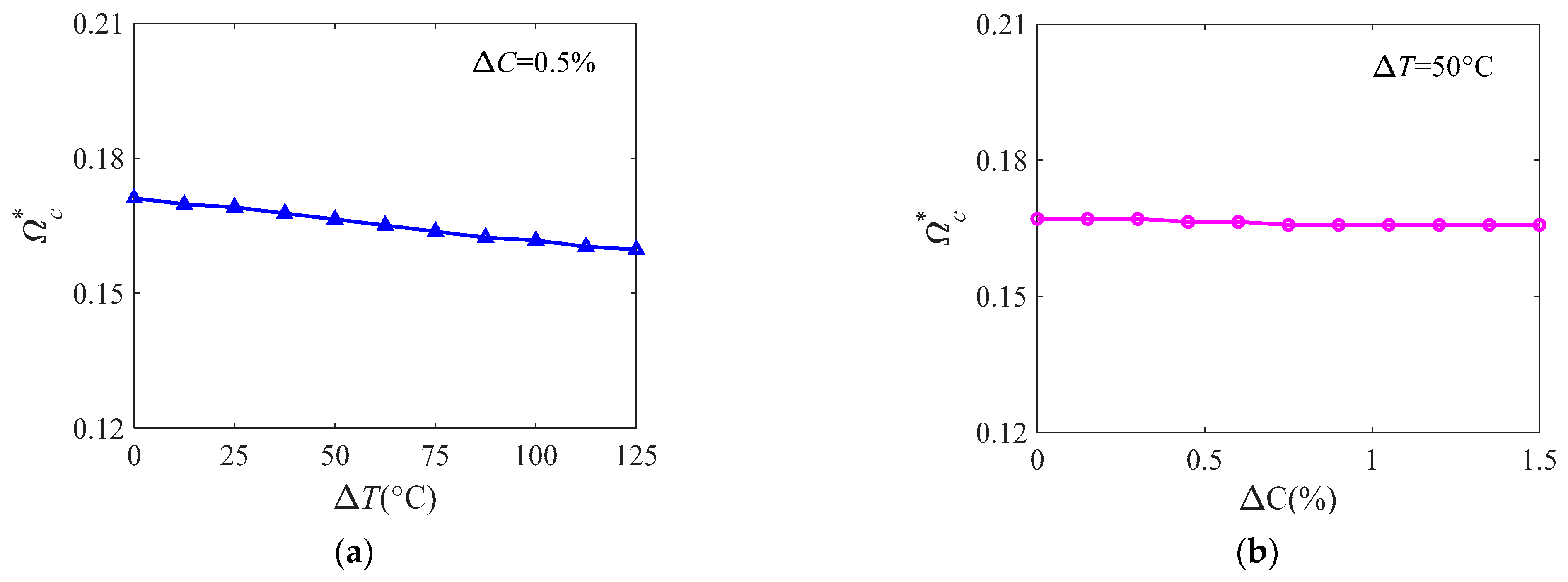
4.3. Hygrothermal Analysis
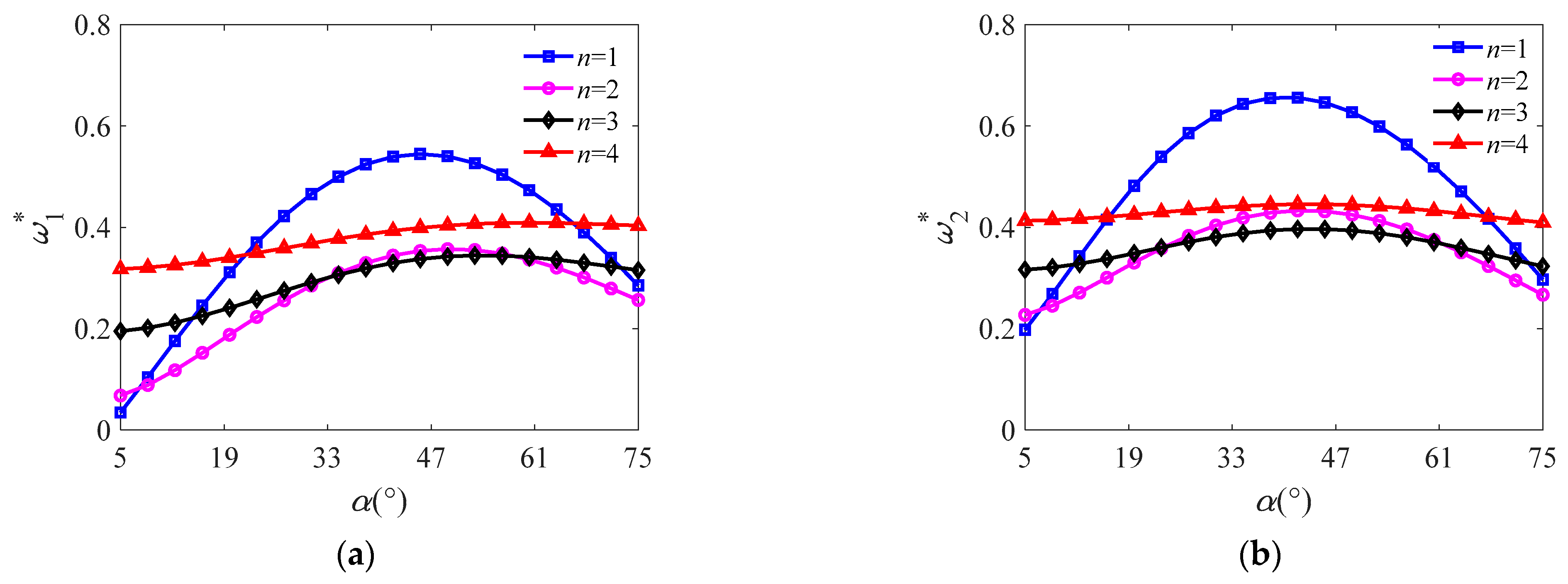
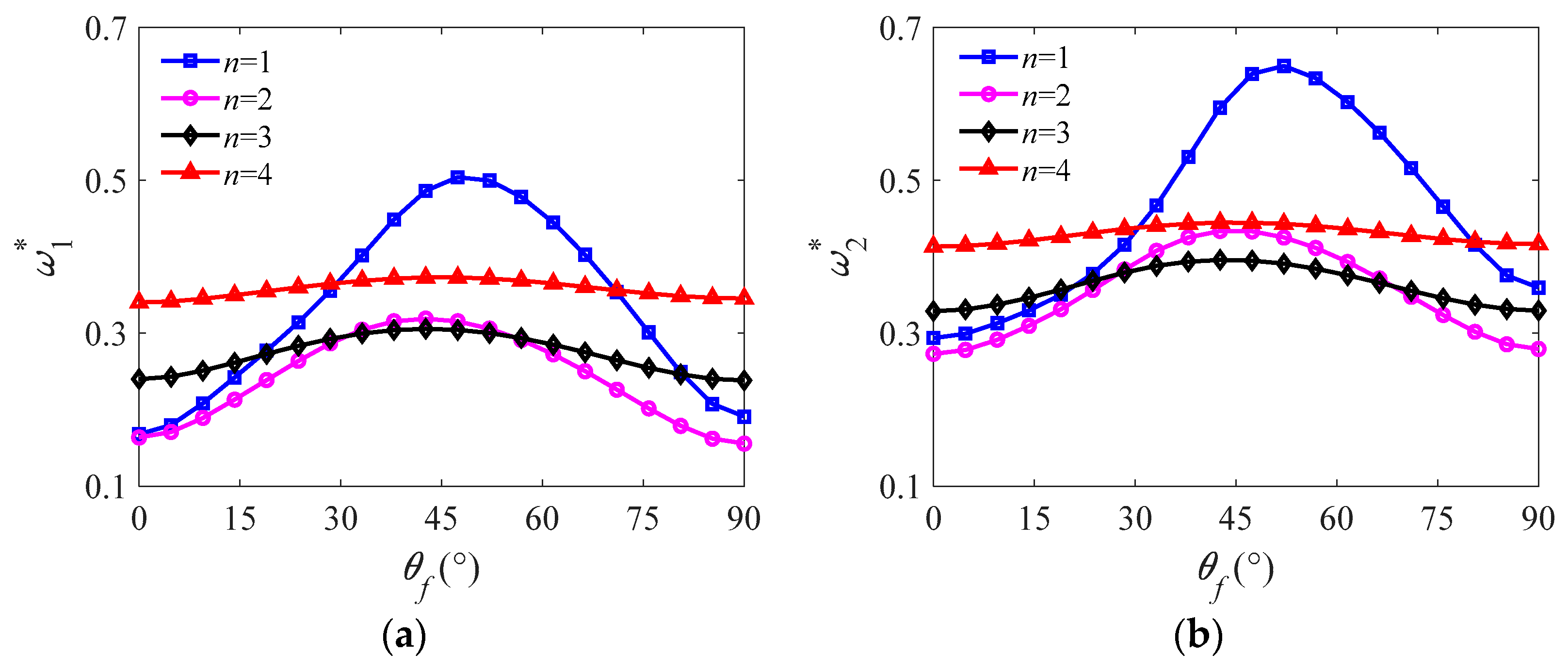
4.4. Effects of Design Parameters on Vibration Characteristics
5. Conclusions
- The Coriolis force is the dominant factor resulting in the asymmetric variation of natural frequencies of forward and backward traveling waves. The centrifugal force would stiffen the conical shell and enhance the frequencies of both traveling waves symmetrically, and initial hoop tension plays a major role in the increase of critical spinning angular speed.
- Temperature and moisture concentration both weaken natural frequencies and critical spinning speeds of the shell, and the influence of temperature on the frequencies and the speed is more prominent than that of moisture concentration. In addition, thermal expansion deformation is nonnegligible in free vibration analysis of spinning composite laminated truncated conical shells.
- Natural frequencies of forward and backward traveling waves all initially increase and then decrease with semivertex angle and fiber orientation angle, which indicates that vibration behavior of the conical shell can be distinctly controlled by using suitable values of design parameters.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Sun, S.P.; Liu, L.; Cao, D.Q. Nonlinear travelling wave vibrations of a rotating thin cylindrical shell. J. Sound Vib. 2018, 431, 122–136. [Google Scholar] [CrossRef]
- Gibson, R.F. A review of recent research on mechanics of multifunctional composite materials and structures. Compos. Struct. 2010, 92, 2793–2810. [Google Scholar] [CrossRef]
- Bryan, G.H. On the beats in the vibrations of a revolving cylinder or bell. Proc. Camb. Philos. Soc. 1890, 7, 101–111. [Google Scholar]
- Srinivasan, A.; Lauterbach, G.F. Traveling waves in rotating cylindrical shells. J. Eng. Ind. 1971, 93, 1229–1232. [Google Scholar] [CrossRef]
- Li, H. Frequency characteristics of a rotating truncated circular layered conical shell. Compos. Struct. 2000, 50, 59–68. [Google Scholar]
- Lam, K.Y.; Li, H. Influence of boundary conditions on the frequency characteristics of a rotating truncated circular conical shell. J. Sound Vib. 1999, 223, 171–195. [Google Scholar] [CrossRef]
- Ng, T.Y.; Li, H.; Lam, K.Y. Generalized differential quadrature for free vibration of rotating composite laminated conical shell with various boundary conditions. Int. J. Mech. Sci. 2003, 45, 567–587. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.H.; Xie, T.F. Vibration characteristics of a rotating composite laminated cylindrical shell in subsonic air flow and hygrothermal environment. Int. J. Mech. Sci. 2019, 150, 356–368. [Google Scholar] [CrossRef]
- Talebitooti, M.; Ghayour, M.; Ziaei-Rad, S.; Talebitooti, R. Free vibrations of rotating composite conical shells with stringer and ring stiffeners. Arch. Appl. Mech. 2009, 80, 201–215. [Google Scholar] [CrossRef]
- Liew, K.M.; Ng, T.Y.; Zhao, X. Free vibration analysis of conical shells via the element-free kp-Ritz method. J. Sound Vib. 2005, 281, 627–645. [Google Scholar] [CrossRef]
- Sivadas, K. Vibration analysis of pre-stressed rotating thick circular conical shell. J. Sound Vib. 1995, 186, 99–109. [Google Scholar] [CrossRef]
- Chen, C.; Dai, L. Nonlinear vibration and stability of a rotary truncated conical shell with intercoupling of high and low order modals. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 254–269. [Google Scholar] [CrossRef]
- Wu, C.P.; Chiu, S.J. Thermally induced dynamic instability of laminated composite conical shells. Int. J. Solids Struct. 2002, 39, 3001–3021. [Google Scholar] [CrossRef]
- Dong, Y.; Li, X.; Gao, K.; Li, Y.; Yang, J. Harmonic resonances of graphene-reinforced nonlinear cylindrical shells: Effects of spinning motion and thermal environment. Nonlinear Dyn. 2020, 99, 981–1000. [Google Scholar] [CrossRef]
- Sun, S.; Cao, D.; Han, Q. Vibration studies of rotating cylindrical shells with arbitrary edges using characteristic orthogonal polynomials in the Rayleigh–Ritz method. Int. J. Mech. Sci. 2013, 68, 180–189. [Google Scholar] [CrossRef]
- Li, X.; Xu, Q.; Li, Y.H. Parametric Instability of a Rotating Axially Loaded FG Cylindrical Thin Shell Under Both Axial Disturbances and Thermal Effects. Z. Nat. A 2018, 73, 1105–1119. [Google Scholar] [CrossRef]
- Li, X.; Du, C.C.; Li, Y.H. Parametric resonance of a FG cylindrical thin shell with periodic rotating angular speeds in thermal environment. Appl. Math. Model. 2018, 59, 393–409. [Google Scholar] [CrossRef]
- Zhang, W.; Niu, Y.; Behdinan, K. Vibration characteristics of rotating pretwisted composite tapered blade with graphene coating layers. Aerosp. Sci. Technol. 2020, 98, 105644. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, D. Free vibration of functionally graded porous cylindrical shell using a sinusoidal shear deformation theory. Aerosp. Sci. Technol. 2017, 66, 83–91. [Google Scholar] [CrossRef]
- Sheikh, A.H.; Asadi, A.; Thomsen, O.T. Vibration of thin-walled laminated composite beams having open and closed sections. Compos. Struct. 2015, 134, 209–215. [Google Scholar] [CrossRef]
- Chen, X.; Chen, L.; Huang, S.; Li, M.; Li, X. Nonlinear forced vibration of in-plane bi-directional functionally graded materials rectangular plate with global and localized geometrical imperfections. Appl. Math. Model. 2021, 93, 443–466. [Google Scholar] [CrossRef]
- Cuong-Le, T.; Nguyen, K.D.; Hoang-Le, M.; Sang-To, T.; Phan-Vu, P.; Wahab, M.A. Nonlocal strain gradient IGA numerical solution for static bending, free vibration and buckling of sigmoid FG sandwich nanoplate. Phys. B Condens. Matter 2022, 631, 413726. [Google Scholar] [CrossRef]
- Cuong-Le, T.; Nguyen, K.D.; Lee, J.; Rabczuk, T.; Nguyen-Xuan, H. A 3D nano scale IGA for free vibration and buckling analyses of multi-directional FGM nanoshells. Nanotechnology 2021, 33, 065703. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Jiang, W.; Chen, X.; Zhou, Z. Nonlinear forced vibration of rotating composite laminated cylindrical shells under hygrothermal environment. Z. Nat. A 2021, 76, 769–786. [Google Scholar] [CrossRef]
- Shakouri, M. Free vibration analysis of functionally graded rotating conical shells in thermal environment. Compos. Part B Eng. 2019, 163, 574–584. [Google Scholar] [CrossRef]
- Civalek, Ö. Discrete singular convolution method for the free vibration analysis of rotating shells with different material properties. Compos. Struct. 2017, 160, 267–279. [Google Scholar] [CrossRef]
- Heydarpour, Y.; Aghdam, M.M.; Malekzadeh, P. Free vibration analysis of rotating functionally graded carbon nanotube-reinforced composite truncated conical shells. Compos. Struct. 2014, 117, 187–200. [Google Scholar] [CrossRef]
- Li, X.; Chen, X.C.; Jiang, W.T. Dynamic stability of graded graphene reinforced truncated conical shells under both periodic spinning speeds and axial loads considering thermal effects. Eng. Struct. 2022, 256, 113963. [Google Scholar] [CrossRef]
- Heydarpour, Y.; Malekzadeh, P.; Aghdam, M.M. Free vibration of functionally graded truncated conical shells under internal pressure. Meccanica 2013, 49, 267–282. [Google Scholar] [CrossRef]
- Zhao, X.; Li, Y. Vibration and Acoustic Responses of an Orthotropic Composite Conical Shell in a Hygroscopic Environment. Int. J. Appl. Mech. 2015, 7, 1550053. [Google Scholar] [CrossRef]
- Shen, H.S.; Xiang, Y. Thermal buckling and postbuckling behavior of FG-GRC laminated cylindrical shells with temperature-dependent material properties. Meccanica 2019, 54, 283–297. [Google Scholar] [CrossRef]
- Patel, B.; Ganapathi, M.; Makhecha, D. Hygrothermal effects on the structural behaviour of thick composite laminates using higher-order theory. Compos. Struct. 2002, 56, 25–34. [Google Scholar] [CrossRef]
- Biswal, M.; Sahu, S.K.; Asha, A.V. Vibration of composite cylindrical shallow shells subjected to hygrothermal loading-experimental and numerical results. Compos. Part B Eng. 2016, 98, 108–119. [Google Scholar] [CrossRef]
- Li, X. Parametric resonances of rotating composite laminated nonlinear cylindrical shells under periodic axial loads and hygrothermal environment. Compos. Struct. 2021, 255, 112887. [Google Scholar] [CrossRef]
- Qin, Y.; Li, X.; Yang, E.C.; Li, Y.H. Flapwise free vibration characteristics of a rotating composite thin-walled beam under aerodynamic force and hygrothermal environment. Compos. Struct. 2016, 153, 490–503. [Google Scholar] [CrossRef]
- Qin, Y.; Li, Y.H. Influences of hygrothermal environment and installation mode on vibration characteristics of a rotating laminated composite beam. Mech. Syst. Signal Process. 2017, 91, 23–40. [Google Scholar] [CrossRef]
- Bandyopadhyay, T.; Karmakar, A.; Kishimoto, K. Transient response of delaminated composite conical shells due to multiple low velocity impacts in hygrothermal environment. Compos. Struct. 2016, 143, 202–219. [Google Scholar] [CrossRef]
- Hajmohammad, M.H.; Azizkhani, M.B.; Kolahchi, R. Multiphase nanocomposite viscoelastic laminated conical shells subjected to magneto-hygrothermal loads: Dynamic buckling analysis. Int. J. Mech. Sci. 2018, 137, 205–213. [Google Scholar] [CrossRef]
- Parhi, A.; Singh, B.N.; Panda, S.K. Nonlinear free vibration analysis of composite conical shell panel with cluster of delamination in hygrothermal environment. Eng. Comput. 2019, 37, 1565–1577. [Google Scholar] [CrossRef]
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity; Cambridge University Press: New York, NY, USA, 2013; Volume 1. [Google Scholar]
- Jones, R.M. Mechanics of Composite Materials; Scripta Book Company: Washington, DC, USA, 1975; Volume 193. [Google Scholar]
- Huang, S.; Hsu, B. Resonant phenomena of a rotating cylindrical shell subjected to a harmonic moving load. J. Sound Vib. 1990, 136, 215–228. [Google Scholar] [CrossRef]
- Wang, Y.Q. Nonlinear vibration of a rotating laminated composite circular cylindrical shell: Traveling wave vibration. Nonlinear Dyn. 2014, 77, 1693–1707. [Google Scholar] [CrossRef]
- Soedel, W. Vibrations of Shells and Plates; Marcel Dekker Incorporated: New York, NY, USA, 1981. [Google Scholar]
- Han, Q.K.; Chu, F.L. Parametric resonance of truncated conical shells rotating at periodically varying angular speed. J. Sound Vib. 2014, 333, 2866–2884. [Google Scholar] [CrossRef]

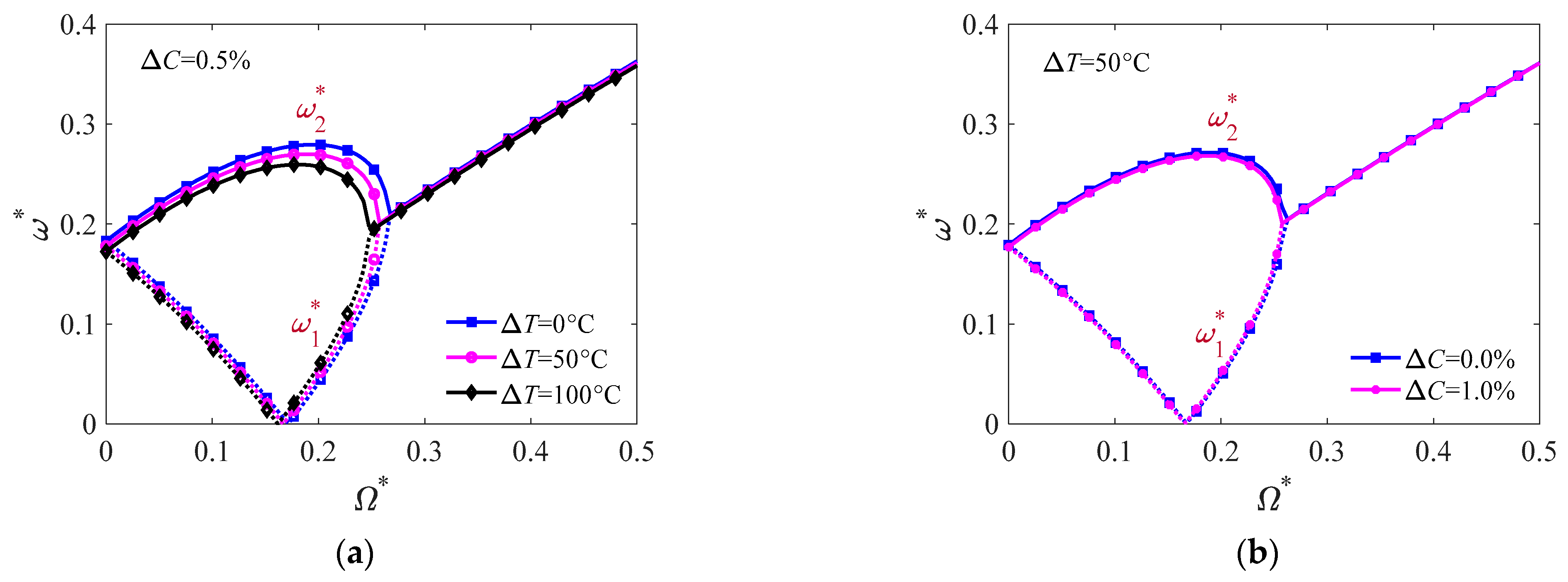



| Modulus (GPa) | (a) Moisture Concentration, ΔC (%) | ||||||
|---|---|---|---|---|---|---|---|
| 0.00 | 0.25 | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 | |
| E1 | 130 | 130 | 130 | 130 | 130 | 130 | 130 |
| E2 | 9.5 | 9.25 | 9.0 | 8.75 | 8.5 | 8.5 | 8.5 |
| G12 | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 |
| (b) Temperature, T (°C) | |||||||
| 25 | 50 | 75 | 100 | 125 | 150 | ||
| E1 | 130 | 130 | 130 | 130 | 130 | 130 | |
| E2 | 9.5 | 8.5 | 8.0 | 7.5 | 7.0 | 6.75 | |
| G12 | 6.0 | 6.0 | 5.5 | 5.0 | 4.75 | 4.5 | |
| n | α = 30° | α = 60° | ||
|---|---|---|---|---|
| Reference [10] | Present | Reference [10] | Present | |
| 2 | 0.7909 | 0.8078 | 0.5719 | 0.5893 |
| 3 | 0.7281 | 0.7314 | 0.5998 | 0.6022 |
| 4 | 0.6347 | 0.6261 | 0.6049 | 0.6139 |
| 5 | 0.5522 | 0.5359 | 0.6071 | 0.6186 |
| Ω* | n | Reference [45] | Reference [6] | Present | |||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 0.7414 | 0.7414 | 0.7414 | 0.7414 | 0.7454 | 0.7454 |
| 2 | 0.4456 | 0.4456 | 0.4456 | 0.4456 | 0.4481 | 0.4481 | |
| 3 | 0.2785 | 0.2785 | 0.2785 | 0.2785 | 0.2855 | 0.2855 | |
| 4 | 0.1888 | 0.1888 | 0.1888 | 0.1888 | 0.1926 | 0.1926 | |
| 0.1 | 1 | 0.6692 | 0.8116 | 0.6735 | 0.8154 | 0.6758 | 0.8248 |
| 2 | 0.4095 | 0.5320 | 0.4177 | 0.5399 | 0.4138 | 0.5334 | |
| 3 | 0.3362 | 0.4308 | 0.3467 | 0.4410 | 0.3418 | 0.4419 | |
| 4 | 0.3797 | 0.4538 | 0.3893 | 0.4633 | 0.3888 | 0.4696 | |
| Temperature Variation and Moisture Concentration | n | Present | FEM | R |
|---|---|---|---|---|
| ΔT = 25 °C, ΔC = 0.25% | 1 | 198.2577 | 197.9374 | 0.16% |
| 2 | 118.5799 | 118.1238 | 0.39% | |
| 3 | 80.7713 | 80.1092 | 0.83% | |
| ΔT = 50 °C, ΔC = 0.50% | 1 | 197.5097 | 197.0924 | 0.21% |
| 2 | 117.9563 | 117.2945 | 0.56% | |
| 3 | 80.1008 | 79.5839 | 0.65% | |
| ΔT = 100 °C, ΔC = 1.00% | 1 | 196.2000 | 195.4958 | 0.36% |
| 2 | 116.9296 | 116.0283 | 0.78% | |
| 3 | 79.1323 | 78.5029 | 0.80% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhang, X.; Zhou, Z. Free Vibration Analysis of a Spinning Composite Laminated Truncated Conical Shell under Hygrothermal Environment. Symmetry 2022, 14, 1369. https://doi.org/10.3390/sym14071369
Li X, Zhang X, Zhou Z. Free Vibration Analysis of a Spinning Composite Laminated Truncated Conical Shell under Hygrothermal Environment. Symmetry. 2022; 14(7):1369. https://doi.org/10.3390/sym14071369
Chicago/Turabian StyleLi, Xiao, Xuanling Zhang, and Zhihong Zhou. 2022. "Free Vibration Analysis of a Spinning Composite Laminated Truncated Conical Shell under Hygrothermal Environment" Symmetry 14, no. 7: 1369. https://doi.org/10.3390/sym14071369
APA StyleLi, X., Zhang, X., & Zhou, Z. (2022). Free Vibration Analysis of a Spinning Composite Laminated Truncated Conical Shell under Hygrothermal Environment. Symmetry, 14(7), 1369. https://doi.org/10.3390/sym14071369





